Реферат рациональные числа: Рациональные Числа Реферат – Telegraph

Рациональные Числа Реферат – Telegraph

➡➡➡ ПОДРОБНЕЕ ЖМИТЕ ЗДЕСЬ!

Рациональные Числа Реферат
Пошаговое изучение математики для начинающих
Тема рациональных чисел достаточно обширна. О ней можно говорить бесконечно и писать целые труды, каждый раз удивляясь новым фишкам.
Чтобы не допускать в будущем ошибок, в данном уроке мы немного углубимся в тему рациональных чисел, почерпнём из неё необходимые сведения и двинемся дальше.
Рациональное число — это число, которое может быть представлено в виде дроби  , где a — это числитель дроби, b — знаменатель дроби. Причем b не должно быть нулём, поскольку деление на ноль не допускается.
К рациональным числам относятся следующие категории чисел:
Каждое число из этой категории может быть представлено в виде дроби .
Пример 1. Целое число 2 может быть представлено в виде дроби . Значит число 2 относится не только к целым числам, но и к рациональным.
Пример 2. Смешанное число может быть представлено в виде дроби . Данная дробь получается путём перевода смешанного числа в неправильную дробь
Значит смешанное число относится к рациональным числам.
Пример 3. Десятичная дробь 0,2 может быть представлена в виде дроби . Данная дробь получилась путём перевода десятичной дроби 0,2 в обыкновенную дробь. Если испытываете затруднения на этом моменте, повторите тему десятичных дробей .
Поскольку десятичная дробь 0,2 может быть представлена в виде дроби , значит она тоже относится к рациональным числам.
Пример 4. Бесконечная периодическая дробь 0, (3) может быть представлена в виде дроби . Данная дробь получается путём перевода чистой периодической дроби в обыкновенную дробь. Если испытываете затруднения на этом моменте, повторите тему периодические дроби .
Поскольку бесконечная периодическая дробь 0, (3) может быть представлена в виде дроби  , значит она тоже относится к рациональным числам.
В дальнейшем, все числа которые можно представить в виде дроби, мы всё чаще будем называть одним словосочетанием — рациональные числа .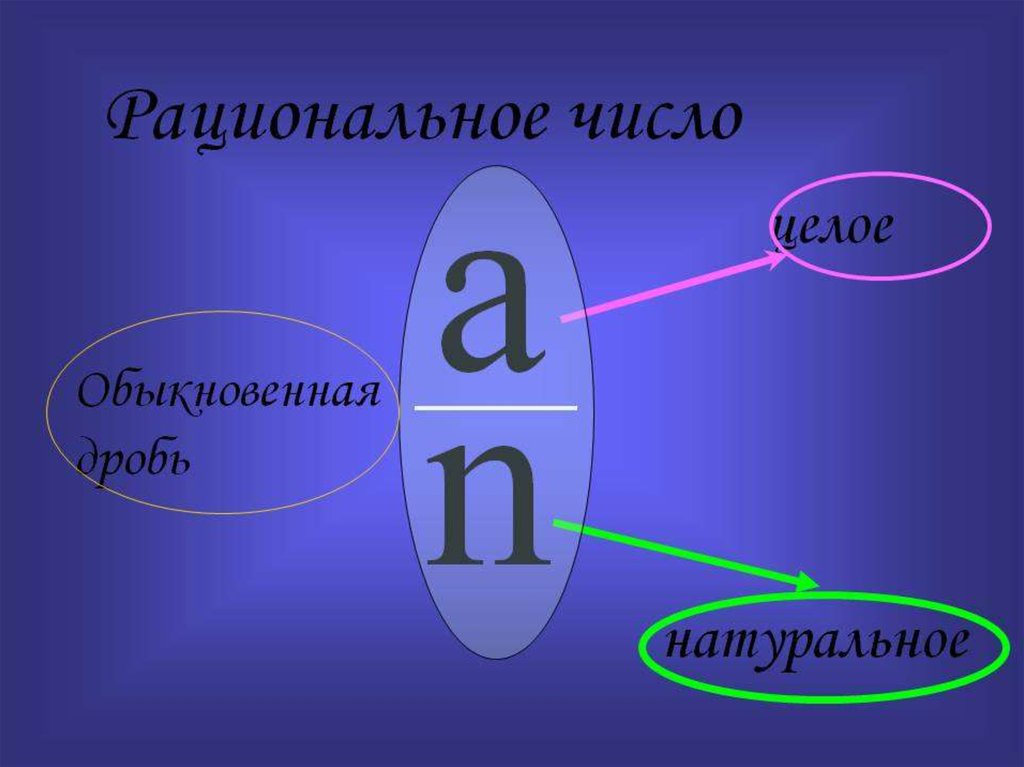
Координатную прямую мы рассматривали, когда изучали отрицательные числа. Напомним, что это прямая линия на которой лежат множество чисел. Выглядит следующим образом:
На этом рисунке приведен небольшой фрагмент координатной прямой от −5 до 5.
Отметить на координатной прямой целые числа вида 2, 0, −3 не составляет особого труда.
Намного интереснее дела обстоят с остальными числами: с обыкновенными дробями, смешанными числами, десятичными дробями и т.д. Эти числа лежат между целыми числами и этих чисел бесконечно много.
Например, отметим на координатной прямой рациональное число . Данное число располагается ровно между нулём и единицей
Попробуем понять, почему дробь  вдруг расположилась между нулём и единицей.
Как уже говорилось выше, между целыми числами лежат остальные числа — обыкновенные дроби, десятичные дроби, смешанные числа и т.д. К примеру, если увеличить участок координатной прямой от 0 до 1, то можно увидеть следующую картину
Видно, что между целыми числами 0 и 1 лежат уже другие рациональные числа, которые являются знакомыми для нас десятичными дробями. Здесь же видна наша дробь , которая расположилась там же, где и десятичная дробь 0,5. Внимательное рассмотрение этого рисунка даёт ответ на вопрос почему дробь расположилась именно там.
Дробь означает разделить 1 на 2. А если разделить 1 на 2, то мы получим 0,5
Десятичную дробь 0,5 можно замаскировать и под другие дроби. Из основного свойства дроби мы знаем, что если числитель и знаменатель дроби умножить или разделить на одно и то же число, то значение дроби не изменится.
Если числитель и знаменатель дроби умножить на любое число, например на число 4, то мы получим новую дробь  , а эта дробь также как и  равна 0,5
А значит на координатной прямой дробь можно расположить там же, где и располагалась дробь
Пример 2. Попробуем отметить на координатной рациональное число . Данное число располагается ровно между числами 1 и 2
Если увеличить участок координатной прямой от 1 до 2, то мы увидим следующую картину:
Видно, что между целыми числами 1 и 2 лежат уже другие рациональные числа, которые являются знакомыми для нас десятичными дробями. Здесь же видна наша дробь , которая расположилась там же, где и десятичная дробь 1,5.
Мы увеличивали определенные отрезки на координатной прямой, чтобы увидеть остальные числа, лежащие на этом отрезке. В результате, мы обнаруживали десятичные дроби, которые имели после запятой одну цифру.
Но это были не единственные числа, лежащие на этих отрезках. Чисел, лежащих на координатной прямой бесконечно много.
Нетрудно догадаться, что между десятичными дробями, имеющими после запятой одну цифру, лежат уже другие десятичные дроби, имеющие после запятой две цифры. Другими словами, сотые части отрезка.
К примеру, попробуем увидеть числа, которые лежат между десятичными дробями 0,1 и 0,2
Ещё пример. Десятичные дроби, имеющие две цифры после запятой и лежащие между нулём и рациональным числом 0,1 выглядят так:
Пример 3. Отметим на координатной прямой рациональное число . Данное рациональное число будет располагаться очень близко к нулю
Если мы увеличим отрезок от 0 до 0,1 то увидим где точно расположилось рациональное число
Видно, что наше рациональное число расположилось там же, где и десятичная дробь 0,02.
Пример 4. Отметим на координатной прямой рациональное число 0, (3)
Рациональное число 0, (3) является бесконечной периодической дробью. Его дробная часть никогда не заканчивается, она бесконечная
0,33333….и так далее до бесконечности..
И поскольку у числа 0,(3) дробная часть является бесконечной, это означает, что мы не сможем найти точное место на координатной прямой, где это число располагается. Мы можем лишь указать это место приблизительно.
Рациональное число 0,33333… будет располагаться очень близко к обычной десятичной дроби 0,3
Данный рисунок не показывает точное место расположения числа 0,(3). Это лишь иллюстрация, показывающая как близко может располагаться периодическая дробь 0,(3) к обычной десятичной дроби 0,3.
Пример 5. Отметим на координатной прямой рациональное число . Данное рациональное число будет располагаться посередине между числами 2 и 3
это есть 2 (две целых) и (одна вторая). Дробь по другому ещё называют «половиной». Поэтому мы отметили на координатной прямой два целых отрезка и ещё половину отрезка.
Если перевести смешанное число в неправильную дробь, то получим обыкновенную дробь . Эта дробь на координатной прямой будет располагаться там же, где и дробь
Если увеличить участок координатной прямой от 2 до 3, то мы увидим следующую картину:
Видно, что наше рациональное число  расположилось там же, где и десятичная дробь 2,5
В предыдущем уроке, который назвался умножение и деление целых чисел мы научились делить целые числа. В роли делимого и делителя могли стоять как положительные, так и отрицательные числа.
В данном выражении делимое (−6) является отрицательным числом.
Здесь уже отрицательным числом является делитель (−2). Но в обоих случаях мы получаем один и тот же ответ −3.
Учитывая, что любое деление можно записать в виде дроби, мы можем рассмотренные выше примеры также записать в виде дроби:
А поскольку в обоих случаях значение дроби одинаково, минус стоящий либо в числителе либо в знаменателе можно сделать общим, поставив его перед дробью
Поэтому между выражениями      и    и    можно поставить знак равенства, потому что они несут одно и то же значение
В дальнейшем работая с дробями, если минус будет нам встречаться в числителе или в знаменателе, мы будем делать этот минус общим, ставя его перед дробью.
Как и целое число, рациональное число имеет своё противоположное число.
Например, для рационального числа противоположным числом является . Располагается оно на координатной прямой симметрично расположению   относительно начала координат. Другими словами, оба этих числа равноудалены от начала координат
Мы знаем что для того, чтобы перевести смешанное число в неправильную дробь, нужно целую часть умножить на знаменатель дробной части и прибавить к числителю дробной части. Полученное число будет числителем новой дроби, а знаменатель остаётся прежним..
Например, переведём смешанное число   в неправильную дробь
Умножим целую часть на знаменатель дробной части и прибавим числитель дробной части:
Полученное число 5 будет числителем новой дроби, а знаменатель останется прежним:
Полностью данная процедура записывается следующим образом:
Чтобы вернуть изначальное смешанное число, достаточно выделить целую часть в дроби
Но этот способ перевода смешанного числа в неправильную дробь применим только в том случае, если смешанное число является положительным. Для отрицательного числа данный способ не сработает.
Рассмотрим дробь . Выделим в этой дроби целую часть. Получим
Чтобы вернуть изначальную дробь нужно перевести смешанное число   в неправильную дробь. Но если мы воспользуемся старым правилом, а именно умножим целую часть на знаменатель дробной части и к полученному числу прибавим числитель дробной части, то получим следующее противоречие:
Мы получили дробь , а должны были получить дробь .
Делаем вывод, что смешанное число в неправильную дробь переведено неправильно:
Чтобы правильно перевести отрицательное смешанное число в неправильную дробь, нужно целую часть умножить на знаменатель дробной части, и из полученного числа вычесть  числитель дробной части. В этом случае у нас всё встанет на свои места
Отрицательное смешанное число является противоположным для смешанного числа . Если положительное смешанное число располагается в правой части и выглядит так
то отрицательное смешанное число будет располагаться в левой части симметрично относительное начала координат
И если читается как «две целых и одна вторая», то читается как «минус две целых и минус одна вторая» . Поскольку числа −2 и располагаются в левой части координатной прямой — они оба являются отрицательными.
Любое смешанное число можно записать в развёрнутом виде. Положительное смешанное число в развёрнутом виде записывается как .
А отрицательное смешанное число записывается как
Теперь мы можем понять, почему смешанное число расположилось в левой части координатной прямой. Минус перед двойкой указывает, что мы сдвинулись от нуля на два шага влево, в результате оказались в точке, где находится число −2
Затем, начиная от числа −2 сдвинулись ещё влево на шага. А поскольку значение равно −0,5 то наш шаг будет половиной от полного шага.
В итоге, мы окажемся посередине между числами −3 и −2
Пример 2. Выделить в неправильной дроби целую часть, затем полученное смешанное число обратно перевести в неправильную дробь
Выполним первую часть задания, а именно выделим в неправильной дроби целую часть
Выполним вторую часть задания, а именно переведём полученное смешанное число в неправильную дробь. Для этого умножим целую часть на знаменатель дробной части и из полученного числа вычтем числитель дробной части:
Если нет желания путаться и привыкать к новому правилу, то можно  смешанное число заключить в скобки, а минус оставить за скобкой. Тогда можно будет применить старое доброе правило: умножить целую часть на знаменатель дробной части и к полученному числу прибавить числитель дробной части.
Выполним предыдущее задание этим способом, а именно переведём смешанное число в неправильную дробь
Понравился урок? Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

Возникло желание поддержать проект?
Используй кнопку ниже
Было бы лучше, чтоб после каждого шага было много задач. Так как без задач, не возможно закрепление и запоминание темы. Только ни в коем случае «один вопрос и пять вариантов ответа». Человек решая, должен быть уверен, что правильно решил задачу.
К каждому шагу дано более одного примера. Вы можете, прочитав условие, самостоятельно попытаться решить примеры.
С большим удовольствием прошёлся по материалу и освежил знания. Жаль нет продолжения. Очень всё доходчиво, спасибо.
Здравствуйте admin! С большим удовольствием повторил математику, скажите пожалуйста какие дальше темы?Очень нужно экспрессом к вышке добраться
Спасибо за сайт с удовольствием изучаю то что пропустил многие годы назад. Но хотелось бы узнать профессию автора и квалификацию и о том дойдет ли админ до разделов высшей математики.
По вашим статьям надо учебники писать. Если бы в у нас в книгах все так понятно писали все бы были отличниками.
Здравствуйте мы продолжаем учится товарищ ленин сказал учиться не поздно а ещё желаю увидеть вышие матиматику в адресе
Very cool site !!!!
Дорабатывать и перерабатывать !!!!
Добавлять примеры !!!! Возможно даже из курса Сканави для школы и тд !!!
Тогда нужно это преобразовать в различные уровни !!!!
Всего 14 дней объяснений и можно первые 3 класса
пропустить в школе !!!!
Very cool site !!!!
Жаль не понимаю почему если в калькуляторе разделить — 27÷5 то выходит — 5,4 а значит — 5 4/5 а значить ошибка. Тежело понят пока ((
5,4 это десятичная дробь, если ее перевести в обычную, то будет 5 4\10 = 5 2\5, а не 5 4\5
5,4 это означает 5 целое четыре десятых. А если сократить, то получится 5 целое две пятых
Хорошо бы отметить ещё тот нюанс, что при сравнении смешанных чисел удобно поменять тот же приём что и при сравнении десятичных дробей, о котором вы пишите. Просто смотрим целую часть смешанной дроби по ней делаем сравнение. Если же целые части дробей равны, то вывод о сравнении смешанных дробей можно сделать по сравнению дробных частей. Перевод в неправильную дробь для сравнения может и имеет право на жизнь для методического понимания, но технически излишен для сравнения смешанных дробей. Кроме того, сравнение описаным обычным способом также дает некоторое понимание сути смешанных дробей.
Ваш адрес email не будет опубликован. Обязательные поля помечены *

Рациональные числа : определения, примеры
Реферат на тему «Развитие понятия о числе » | 3. Рациональные числа .
Реферат — Рациональные числа
Рациональные числа и их свойства простым языком | Студент… | Яндекс Дзен
Рациональные числа
Понятие Денежной Системы Реферат
Государственный Бюджет Реферат По Экономике
Осина Осенью Описание Сочинение
Страховые Взносы Курсовая
Эссе На Тему Модернизация Российского Образования

Реферат — Рациональные числа

Реферат

• формат docx
• размер 126.47 КБ
• добавлен 30 июня 2011 г.

Рациональное число. Множество рациональных чисел.
Что такое ломаное число?
Древнекитайская задача с дробями.
Обыкновенные дроби в Старой Индии.
Дроби в Древнем Египте.
Дроби в Древнем Риме.
Вавилонские шестидесятеричные дроби.
Нумерация и дроби в Древней Греции.
Нумерация и дроби на Руси.
Дроби в других государствах древности.
О простых числах. Евклид, Эратосфен, Чебышев.
О задаче Гольдбаха. Нерешенные задачи теории чисел.

Ал-Хорезми и его «Арифметика».
Абацисты и алгоритмики в средневековой Европе.
От натуральных к дробным числам.
О периодических дробях.
Десятичные дроби.
Из истории нуля.
Число и отношение.
Пропорции в Древней Греции.
Как записывали пропорции в прошлом.
Об измерении земного меридиана Эратосфеном.
Недостаточность рациональных чисел.
От эмпирической к теоретической арифметике.
Список литературы.

Похожие разделы

1. Академическая и специальная литература
2. Военные дисциплины
3. Баллистика и динамика выстрела

1. Академическая и специальная литература
2. Исторические дисциплины
3. История науки и техники

1. Академическая и специальная литература
2. Концепции современного естествознания (КСЕ)

1. Академическая и специальная литература
2. Математика
3. Периодика по математике
4. Историко-математические исследования

1. Академическая и специальная литература
2. Математика
3. Философия математики

1. Академическая и специальная литература
2. Транспорт
3. Судостроение
4. Теория корабля, ТУС, устройство и живучесть судов

1. Академическая и специальная литература
2. Физика
3. Астрономия и астрофизика

1. Академическая и специальная литература
2. Физика
3. Механика

1. Академическая и специальная литература
2. Философские дисциплины
3. История философии

1. Академическая и специальная литература
2. Философские дисциплины
3. Философия науки и техники

1. Документальная литература
2. Жизнь выдающихся людей
3. Ученые, изобретатели, деятели науки

Смотрите также

• формат djvu
• размер 3. 6 МБ
• добавлен 08 июля 2011 г.

Целые числа. Все действия с большими числами. Числа простые и составные. Десятичные дроби. Сложение и вычитание десятичных дробей. Умножение н деление десятичной дроби на целое число. Проценты. Измерение объемов. Простые дроби. Правильные и неправильные дроби. Сложение и вычитание простых дробей. Общее наименьшее кратное. Умножение и деление простых дробей. Изменение суммы и разности. Изменение произведения и частного. Умножение и депение целого…

Статья

• формат docx
• размер 229.2 КБ
• добавлен 24 октября 2011 г.

План: Первые университеты. Леонардо Пизанский. Николь Орем. Решение уравнений третьей и четвертой степеней. Мнимые величины. Алгебра Ф.Виета. Симметрические функции корней. Отрицательные числа. Теория перспективы.rn

Статья

• формат docx
• размер 237.31 КБ
• добавлен 24 октября 2011 г.

План: Источники (Московский папирус, папирус Райнда). Иероглифическая нумерация. Действие над натуральными числами и дробями. Красные числа. Задачи, приводящие к линейным и двучленным квадратным уравнениям. Прогрессии. Геометрические знания. Значение математики древнего Египта.rn

Статья

• формат docx
• размер 279.86 КБ
• добавлен 24 октября 2011 г.

План: Арабская нумерация. Арифметические действия, дроби и задачи. Алгебра и квадратные уравнения. Геометрические построения. Тригонометрия. Теория отношений и действительные числа.rn

Статья

• формат docx
• размер 313.78 КБ
• добавлен 22 октября 2011 г.

План: Источники. Нумерация. Арифметические действия. Дроби. Математика в девяти книгах. Правило двух ложных положений. Системы линейных уравнений со многими неизвестными. Отрицательные числа. Начальные этапы развития тригонометрии. Квадратные уравнения. Теоретико-числовые задачи. Геометрические задачи. Значение математики древнего и средневекового Китая.rn

Статья

• формат docx
• размер 655. 67 КБ
• добавлен 22 октября 2011 г.

План: Источники: труды Ариабхаты, Брахмагупты, Бхаскары, Магавиры. Создание позиционной десятичной нумерации. Арифметика натуральных чисел и дробей. Задачи на пропорции. Алгебраическая символика. Отрицательные и иррациональные числа. Линейные и квадратные уравнения. Неопределенные уравнения. Теорема Пифагора. Площади и объемы. Тригонометрия. Числовые ряды. Комбинаторика. Значение математики древней и средневековой Индии.rn

• формат djvu
• размер 3.47 МБ
• добавлен 12 ноября 2010 г.

Работы по истории понятия числа нужны учителям математики средней школы и студентам физико-математических факультетов педагогических институтов. Некоторые материалы, вошедшие в эту книгу, были ранее опубликованы в «Историко-математических исследованиях», в „Трудах Института истории естествознания АН СССР» и в журнале «Математика в школе».

Презентация

• формат ppt
• размер 106 КБ
• добавлен 03 июня 2011 г.

АлтГПА, 2011 год, 5 курс, предмет — История математики. Комплексные числа. История возникновения. Развитие понятия о числе. На пути к комплексным числам. Утверждение комплексных чисел в математике. Геометрическое представление комплексного числа. Тригонометрическая форма комплексного числа.

Реферат

• формат rtf
• размер 62.95 КБ
• добавлен 12 апреля 2010 г.

Предмет- история математики, 30 страниц. содержание: Зарождение и развитие понятия числа. Проблема несоизмеримых или Первый кризис в основании математики. Следствия первого кризиса и попытки его преодоления. Становление теории предела. Создание теории действительного числа. Карл Вейерштрасс. Георг Кантор. Рихард Дедекинд.

• формат pdf
• размер 136.51 КБ
• добавлен 23 мая 2009 г.

В брошюре доказываются замечательные теоремы великих математиков прошлого — Архимеда (теорема об объёме шара), Ферма (теорема о представлении простых чисел в виде суммы двух квадратов натуральных чисел), Эйлера (равенство e?i=?1), Лагранжа (теорема о представлении любого натурального числа в виде суммы четырёх квадратов целых чисел) и Гаусса (теорема о построении циркулем и линейкой правильного семнадцатиугольника).

Представление абстрактного типа данных с использованием рациональных чисел

Основная идея абстракции данных состоит в том, чтобы структурировать программы таким образом, чтобы они работали с абстрактными данными.

Представление абстрактного типа данных с использованием Rational числа

Основная идея абстракции данных состоит в том, чтобы структурировать программы так, чтобы они оперировали абстрактными данными. То есть наши программы должны использовать данные таким образом, чтобы делать как можно меньше предположений о данных. возможный. В то же время конкретное представление данных определяется как самостоятельная часть программы.

Примечание

В конкретное представление данных, известно определение каждой функции

Любая программа состоит из двух частей. Две части программы: часть которая работает с абстрактными данными и той частью, которая определяет конкретные представление , связано небольшой набор функций, которые реализуют абстрактные данные в терминах конкретных представление. Чтобы проиллюстрировать эту технику, давайте рассмотрим пример для разработать набор функций для работы с рациональными числами.

Пример

Рациональное число — это отношение целых чисел, и рациональные числа составляют важный подкласс действительных чисел. Рациональное такие числа, как 8/3 или 19/23, обычно записываются как:

<числитель>/<знаменатель>

, где и <числитель>, и <знаменатель> — это заполнители для целых значений. Обе части нужны чтобы точно охарактеризовать значение рационального числа. Фактически деление integers производит аппроксимацию с плавающей запятой, теряя точную точность целых чисел.

8/3 =2,6666666666666665

Однако вы можете создать точное представление для рациональных чисел путем объединения числителя и знаменателя.

Как мы знаем из функциональных абстракций, мы можем начать продуктивно программировать до того, как у вас будет реализация некоторых части нашей программы. Давайте начнем с предположения, что у вас уже есть способ построение рационального числа из числителя и знаменателя. Вы тоже предположим, что для рационального числа у вас есть способ выбрать его числитель и его компонент знаменателя. Далее предположим, что конструктор и также доступны селекторы.

Здесь мы используем мощную стратегию для разработка программ: «принятие желаемого за действительное» . Мы еще не сказали, как представляется рациональное число или как конструктор и селекторы должны быть реализованы.

Примечание

Принятие желаемого за действительное – это формирование убеждений и принимать решения в соответствии с тем, что было бы приятно представить, а не апеллируя к реальности.

Пример: АТД для рациональных чисел

— конструктор

— строит рациональное число с числителем n, знаменателем d

рациональное(n, d)

— селектор

число(x) → возвращает числитель рационального числа x

denom(y) → возвращает знаменатель рационального числа y

Теперь у вас есть операции над рациональными числами определяется в терминах функций селектора numer и denom, а конструктор функция рациональная, но вы еще не определили эти функции.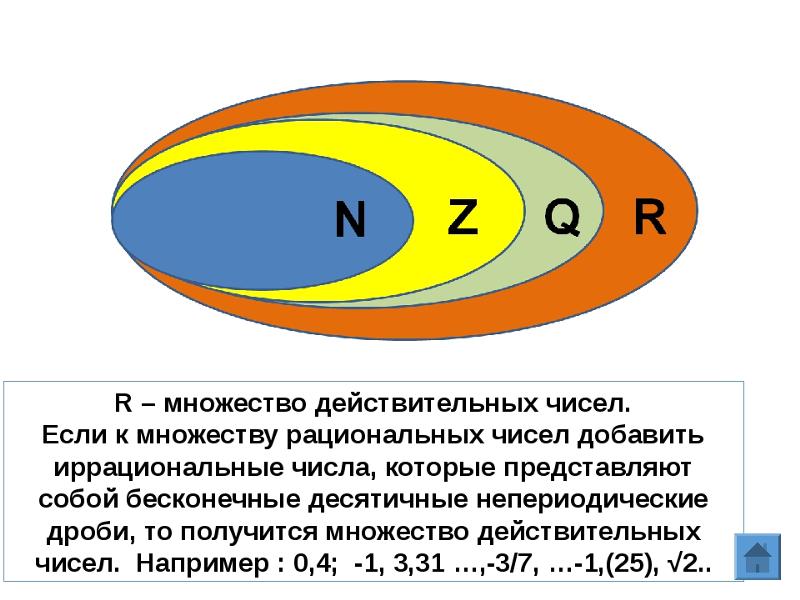 Что вам нужно это способ склеить числитель и знаменатель в составное число ценность.

Псевдокод для представления рациональное число с использованием вышеуказанного конструктора и селектора:

x,y:=8,3

рациональное(n,d)

число(x)/число(y)

— — вывод: 2.6666666666666665

Учебный материал, Примечания к лекциям, Задание, Справочник, Объяснение описания Wiki, краткая информация

12th Информатика: Глава 2: Абстракция данных: Представление абстрактного типа данных с использованием рациональных чисел |

Рациональные выражения

Рациональные выражения

Рациональные числа:

Грубо говоря, рациональное число — это выражение форма п/к где p и q — целые числа и кв. 0 . Что является «свободным» в этом определении, так это то, что два отдельные выражения p/q   и r/s может представлять одно и то же рациональное число. 1/Для например,   1/4 и 2/8 представляют одно и то же рациональное число.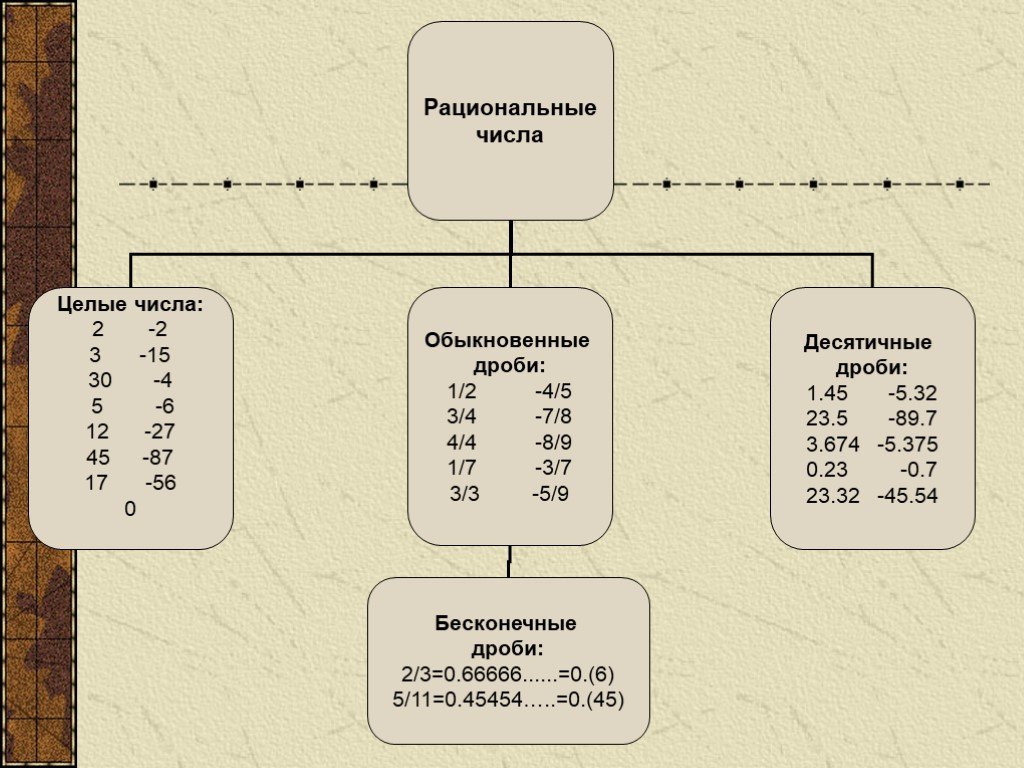 Эта эквивалентность отражается тот факт , если мы подумаем только о вовлеченном количестве, имея 1/4 пирога это то же самое, что иметь 2/8 пирога.

Выражения формы п/к где р и к являются целыми числами и q 0 часто называют дробями. Чего мы действительно хотим сказать, что рациональные числа являются абстрактными величинами, которые представлены по дробям.

Правило состоит в том, что дроби  p/q и r/s представляют один и тот же рациональный число (и пишем p/s = r/q ) тогда и только тогда, когда ps = rq как целые числа (то есть произведение целых чисел p и s равно произведению целых чисел r и q ). операции сложения, вычитания и умножения целых чисел используются для определения соответствующих операций над рациональными числами. Таким образом, мы определяем:

• p/q + r/s  =   (ps+ rq)/ номер
• p/q — r/s  =   (ps-rq)/ qs
• р/кв r/s  =   (pr)/(qs)

где в левой части уравнений + ,- и × обозначают операцию над рациональные числа, а в правой части уравнений они обозначают операции над целыми числами.

Мы также можем определить операцию сложения рациональных чисел для рациональные выражения p/q и р/с , где р0.

  р/к r/s  =   (ps)/(qr)

Важным свойством рациональных чисел является то, что любое выражение составлен из рациональных чисел с помощью сложения, вычитания , умножение и деление могут быть сокращены (упрощены) до рациональное число.

Учитывая любое целое число p , мы можем считать его таким же, как рациональное число  p/1 . Кроме того, определения сложения, вычитания и умножения рациональных чисел таковы, что они согласуются с определениями для тех операций над целыми числами, то есть

• p/1 + q/1 = (p+q)/1
• p/1 — q/1 = (p-q)/1
• стр/1 кв/1 = (пк)/1

Из-за этого принято говорить о целых числах, как если бы они были рациональными. и написать p вместо p/1 для рационального числа, соответствующего целому числу . стр . Технически это неверно, но, безусловно, удобно и хотя это может привести к концептуальным ошибкам, не привести к арифметическим ошибкам.

Рациональные выражения

Важным обобщением рационального числа является понятие рациональное выражение. Рациональное выражение — это выражение формы п/к где p и q являются полиномами и q\[Неравно] 0 . Говоря в широком смысле, все, что мы сказали выше 90 135 относительно целых и рациональных чисел можно перенести на многочлены. и рациональные выражения. В частности, мы можем использовать точно такое же правила определения равенства, сложения, вычитания, умножения и деление рациональных выражений, как мы делали это для рациональных чисел, но используя базовые операции сложения, вычитания, и умножение многочленов вместо этих операций над целыми числами. Стоит дать определение равенства рациональных выражений в деталях:

Даны два рациональных выражения  p/q и р/с мы говорим, что они равны, и запишем p/q = r/s , если и только если ps = rq в виде полиномов.

Интерпретация рациональных выражений:

Любое рациональное выражение можно интерпретировать как частичную функцию, принимающую целые числа в рациональные числа. Таким образом, x/y   можно интерпретировать как частичную функцию, принимающую каждая пара целых чисел, , к рациональное число p/q. Это функция является частичной, потому что если q=0 то p/q не представляет рационального количество! Давайте рассмотрим несколько более сложные случаи. За
пример, рациональные выражения 1/(x-1) и x/(x-5)   соответствует частичному функции, это потому, что 1/(x-1) не определено, когда x=1   и  x/(x-5) не определено, когда x=5 . Во многих случаях существование неопределенной точки очевидно из график функции, соответствующей рациональному выражению. Например, график 1/(х-1) это следующим образом

Однако в некоторых очень важных случаях пристрастность принадлежащий Функция
не очевидна на графике. Примером может служить рациональное
выражение (x ² -5x)/(x-5) . Функция, соответствующая этому выражению, не определена по адресу  . х=5 . В
, его соответствующая функция отличается от для
многочлен x   хотя может показаться, что мы могли бы аннулировать два
вхождений (x-5) . Тем не менее единственная разница между двумя функциями
в точке x=5 . Оба графики «похожи»

но график для (x ² -5x)/(x-5) имеет не хватает одного очка!.

Этот пример показывает, что два рациональных выражения могут быть «равные», но это не означает, что их соответствующие функции идентичны. Как мы увидим позже, отсюда следует, что два рациональных выражения могут быть равны , но все же иметь разные наборы решений (значения переменных, для которых соответствующая функция принимает значение 0). Однако будет так, что если два рациональных выражения равны, и их соответствующие функции определены для данного значение переменных, то соответствующие функции также будут быть равными для этих аргументов.