| 1 | Найти точное значение | sin(30) | |
| 2 | Найти точное значение | sin(45) | |
| 3 | Найти точное значение | sin(30 град. ) | |
| 4 | Найти точное значение | sin(60 град. ) | |
| 5 | Найти точное значение | tan(30 град. ) | |
| 6 | Найти точное значение | arcsin(-1) | |
| 7 | Найти точное значение | sin(pi/6) | |
| 8 | cos(pi/4) | ||
| 9 | Найти точное значение | sin(45 град. ) ) | |
| 10 | Найти точное значение | sin(pi/3) | |
| 11 | Найти точное значение | arctan(-1) | |
| 12 | Найти точное значение | cos(45 град. ) | |
| 13 | Найти точное значение | cos(30 град. ) | |
| 14 | Найти точное значение | tan(60) | |
| 15 | Найти точное значение | csc(45 град. ) | |
| 16 | Найти точное значение | tan(60 град. ) | |
| 17 | Найти точное значение | sec(30 град. ) ) | |
| 18 | Найти точное значение | cos(60 град. ) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | sin(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | tan(45 град. ) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 град. ) | |
| 25 | Найти точное значение | sec(45 град.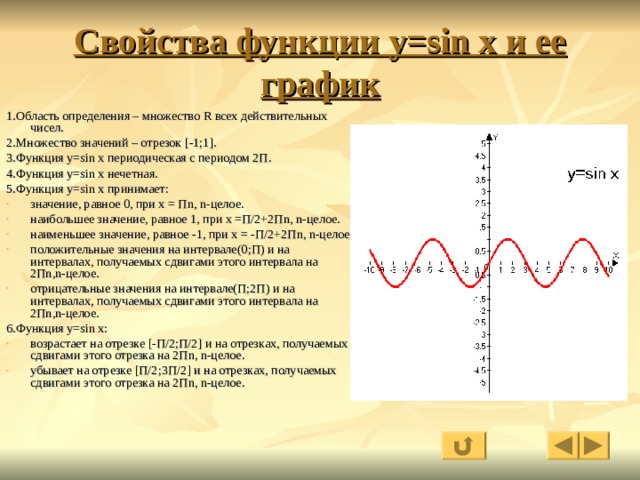 ) ) | |
| 26 | Найти точное значение | csc(30 град. ) | |
| 27 | Найти точное значение | sin(0) | |
| 28 | Найти точное значение | sin(120) | |
| 29 | Найти точное значение | cos(90) | |
| 30 | Преобразовать из радианов в градусы | pi/3 | |
| 31 | Найти точное значение | tan(30) | |
| 32 | Преобразовать из градусов в радианы | 45 | |
| 33 | Найти точное значение | cos(45) | |
| 34 | Упростить | sin(theta)^2+cos(theta)^2 | |
| 35 | Преобразовать из радианов в градусы | pi/6 | |
| 36 | Найти точное значение | cot(30 град.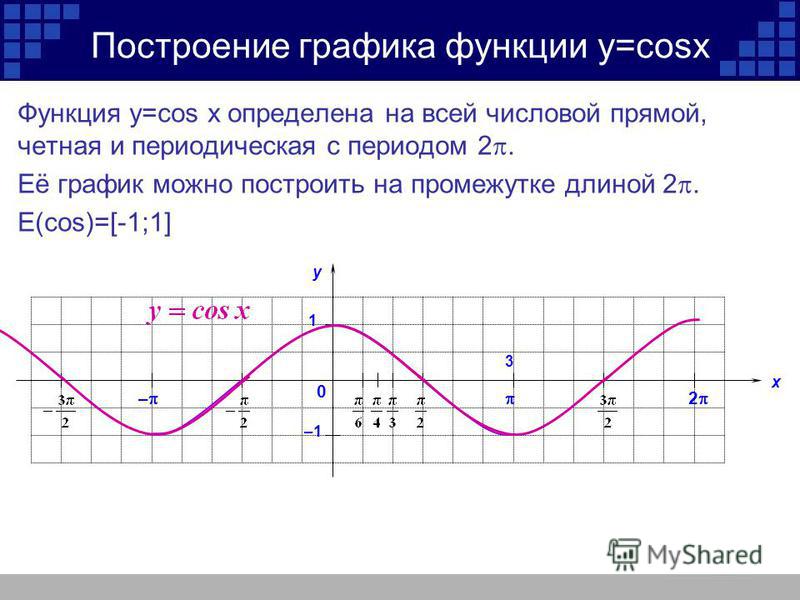 ) ) | |
| 37 | Найти точное значение | arccos(-1) | |
| 38 | Найти точное значение | arctan(0) | |
| 39 | Найти точное значение | cot(60 град. ) | |
| 40 | Преобразовать из градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2pi)/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | tan(pi/2) | |
| 45 | Найти точное значение | sin(300) | |
| 46 | Найти точное значение | cos(30) | |
| 47 | Найти точное значение | cos(60) | |
| 48 | Найти точное значение | cos(0) | |
| 49 | Найти точное значение | cos(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | sec(60 град.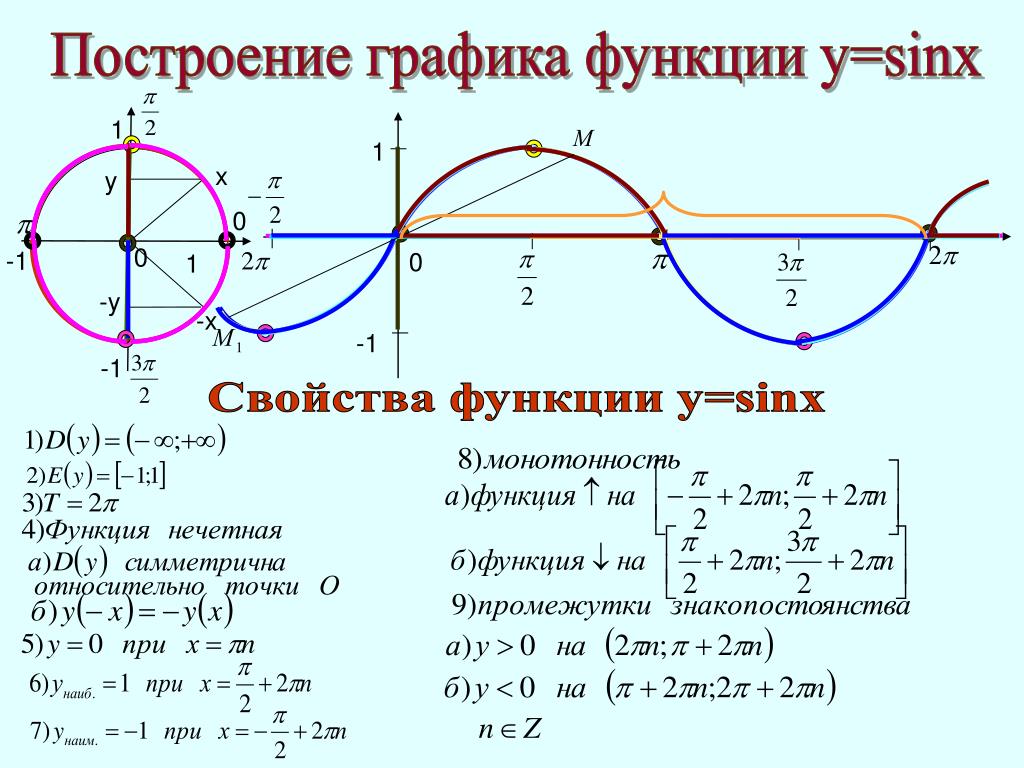 ) ) | |
| 53 | Найти точное значение | sin(300 град. ) | |
| 54 | Преобразовать из градусов в радианы | 135 | |
| 55 | Преобразовать из градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5pi)/6 | |
| 57 | Преобразовать из радианов в градусы | (5pi)/3 | |
| 58 | Преобразовать из градусов в радианы | 89 град. | |
| 59 | Преобразовать из градусов в радианы | 60 | |
| 60 | Найти точное значение | sin(135 град.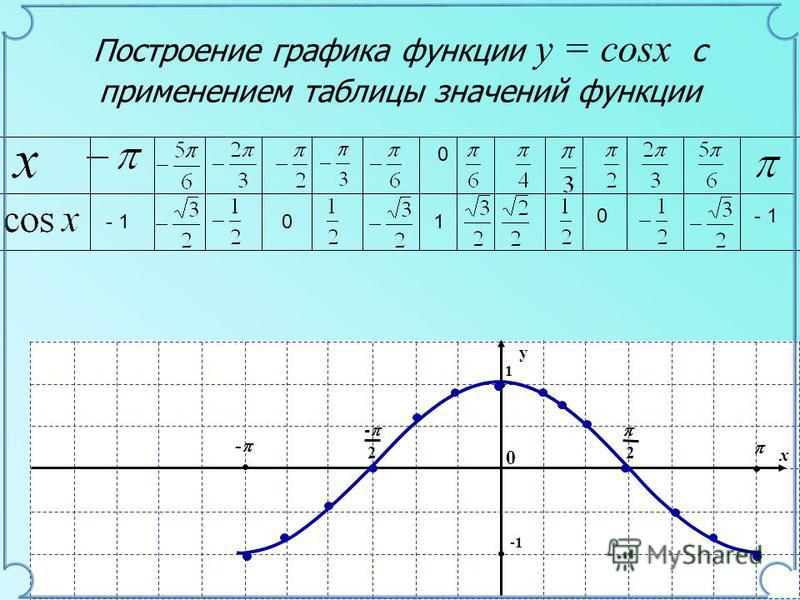 ) ) | |
| 61 | Найти точное значение | sin(150) | |
| 62 | Найти точное значение | sin(240 град. ) | |
| 63 | Найти точное значение | cot(45 град. ) | |
| 64 | Преобразовать из радианов в градусы | (5pi)/4 | |
| 65 | Найти точное значение | sin(225) | |
| 66 | Найти точное значение | sin(240) | |
| 67 | Найти точное значение | cos(150 град. ) | |
| 68 | Найти точное значение | tan(45) | |
| 69 | Вычислить | sin(30 град. ) ) | |
| 70 | Найти точное значение | sec(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | csc(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | tan((5pi)/3) | |
| 75 | Найти точное значение | tan(0) | |
| 76 | Вычислить | sin(60 град. ) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | arcsin(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | csc(45) | |
| 83 | Упростить | arctan( квадратный корень из 3) | |
| 84 | Найти точное значение | sin(135) | |
| 85 | Найти точное значение | sin(105) | |
| 86 | Найти точное значение | sin(150 град. ) ) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | tan((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | pi/4 | |
| 90 | Найти точное значение | sin(pi/2) | |
| 91 | Найти точное значение | sec(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | arcsin(0) | |
| 95 | sin(120 град. ) ) | ||
| 96 | Найти точное значение | tan((7pi)/6) | |
| 97 | Найти точное значение | cos(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразовать из градусов в радианы | 88 град. |
Практическая работа № 11
Тема: Тригонометрические функции их графики и свойства Цель
работы: закрепить
знания и умения студентов по освоению
свойств тригонометрических функций.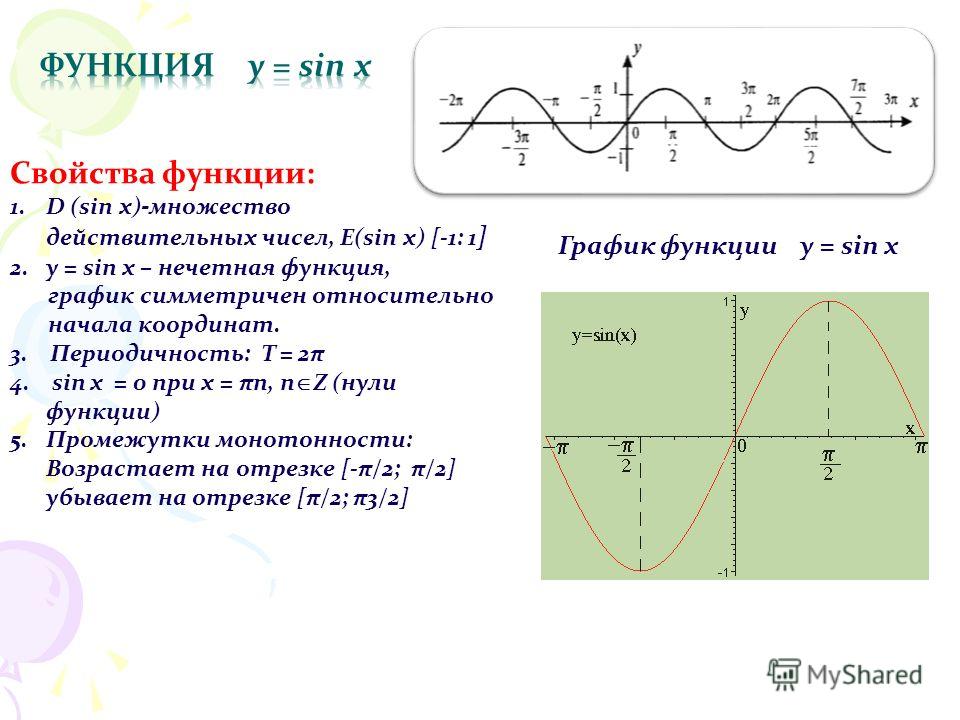
Теоритическое обоснование:
Функции y = sin x, y = cos x, y = mf(x), y = f(kx), y = tg x, y = ctg x
Функция y = sin x
Графиком функции является синусоида.
Полную неповторяющуюся часть синусоиды называют волной синусоиды.
Половину волны синусоиды называют полуволной синусоиды (или аркой). Свойства функции y = sin x:
1) Область определения функции – множество действительных чисел. 2) Область значений функции – отрезок [–1; 1] 3) Это нечетная функция. 4) Это непрерывная функция. 5) Координаты точек пересечения графика: — с осью абсцисс: (πn; 0), — с осью ординат: (0; 0). 6) На отрезке [-π/2; π/2] функция возрастает, на отрезке [π/2; 3π/2] – убывает. 7) На
промежутках [2πn; π + 2πn] функция принимает
положительные значения. 8) Промежутки возрастания функции: [-π/2 + 2πn; π/2 + 2πn]. Промежутки убывания функции: [π/2 + 2πn; 3π/2 + 2πn]. 9) Точки минимума функции: -π/2 + 2πn. Точки максимума функции: π/2 + 2πn 10) Функция ограничена сверху и снизу. Наименьшее значение функции –1, наибольшее значение 1. 11) Это периодическая функция с периодом 2π (Т = 2π) |
Для построения графика функции y = sin x удобно применять следующие масштабы:
— на листе в клетку за единицу отрезка примем длину в две клетки.
— на оси x отмерим длину π. При этом для удобства 3,14 представим в виде 3 – то есть без дроби. Тогда на листе в клетку π составит 6 клеток (трижды по 2 клетки). А каждая клетка получит свое закономерное имя (от первой до шестой): π/6, π/3, π/2, 2π/3, 5π/6, π. Это значения x.
— на оси
y отметим 1, включающий две клетки.
Составим таблицу значений функции, применяя наши значения x:
x | 0 | π — 6 | π — 3 | π — 2 | 2π — 3 | 5π — 6 | π |
y | 0 | 1 — 2 | √3 — 2 | 1 | √3 — 2 | 1 — 2 | 0 |
Далее
составим график. Получится полуволна,
наивысшая точка которой (π/2; 1).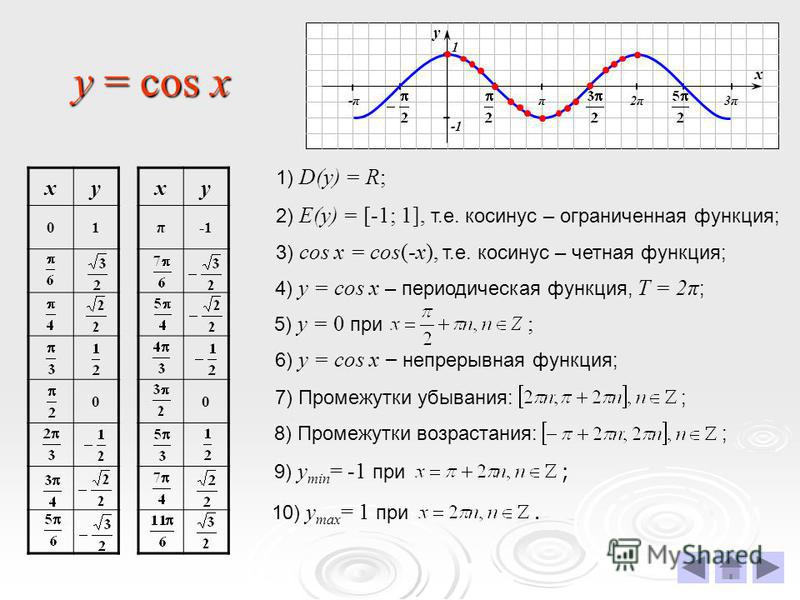 Это график
функции y = sin x на отрезке [0; π]. Добавим к построенному
графику симметричную полуволну
(симметричную относительно начала
координат, то есть на отрезке -π). Гребень
этой полуволны – под осью x с координатами
(-1; -1). В результате получится волна. Это
график функции y = sin x на отрезке [-π; π].
Это график
функции y = sin x на отрезке [0; π]. Добавим к построенному
графику симметричную полуволну
(симметричную относительно начала
координат, то есть на отрезке -π). Гребень
этой полуволны – под осью x с координатами
(-1; -1). В результате получится волна. Это
график функции y = sin x на отрезке [-π; π].
Можно продолжить волну, построив ее и на отрезке [π; 3π], [π; 5π], [π; 7π] и т.д. На всех этих отрезках график функции будет выглядеть так же, как на отрезке [-π; π]. Получится непрерывная волнистая линия с одинаковыми волнами.
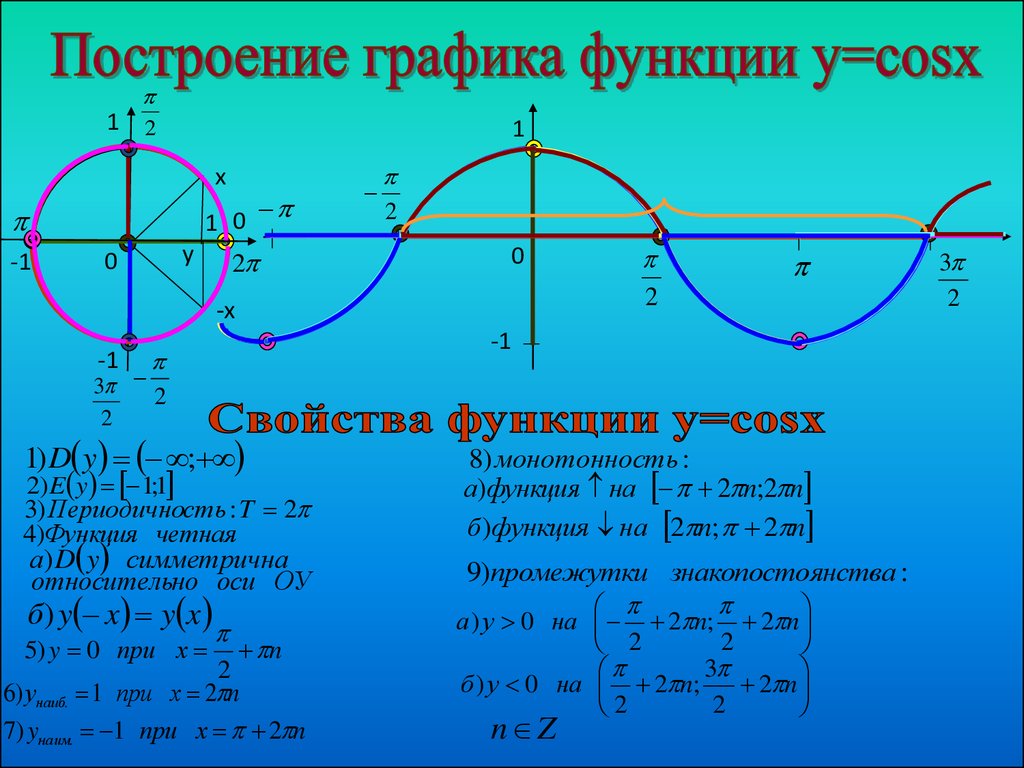
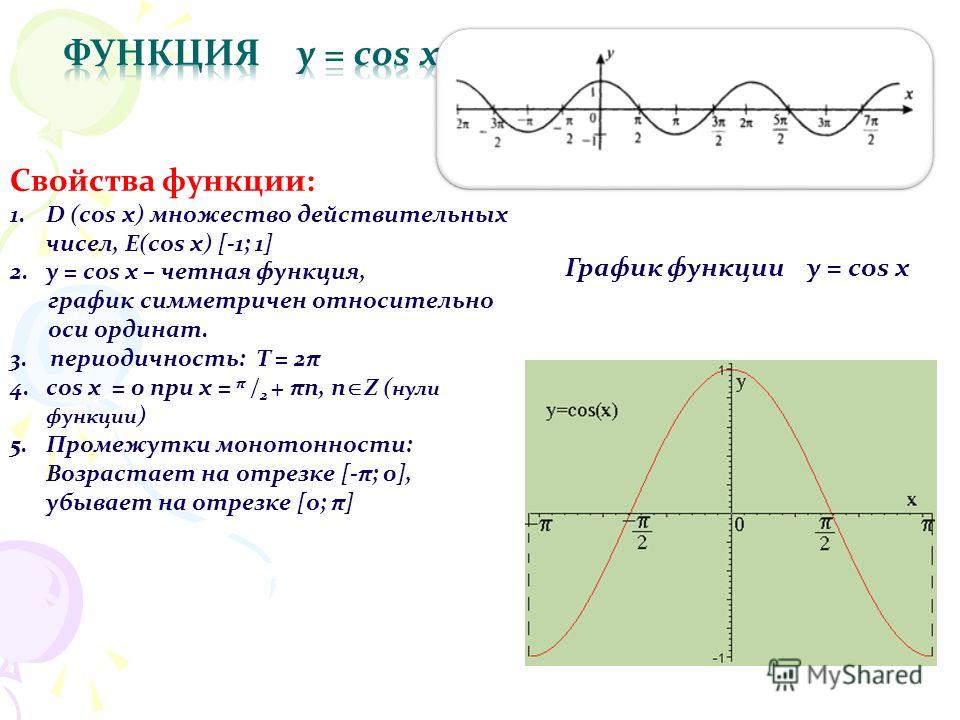
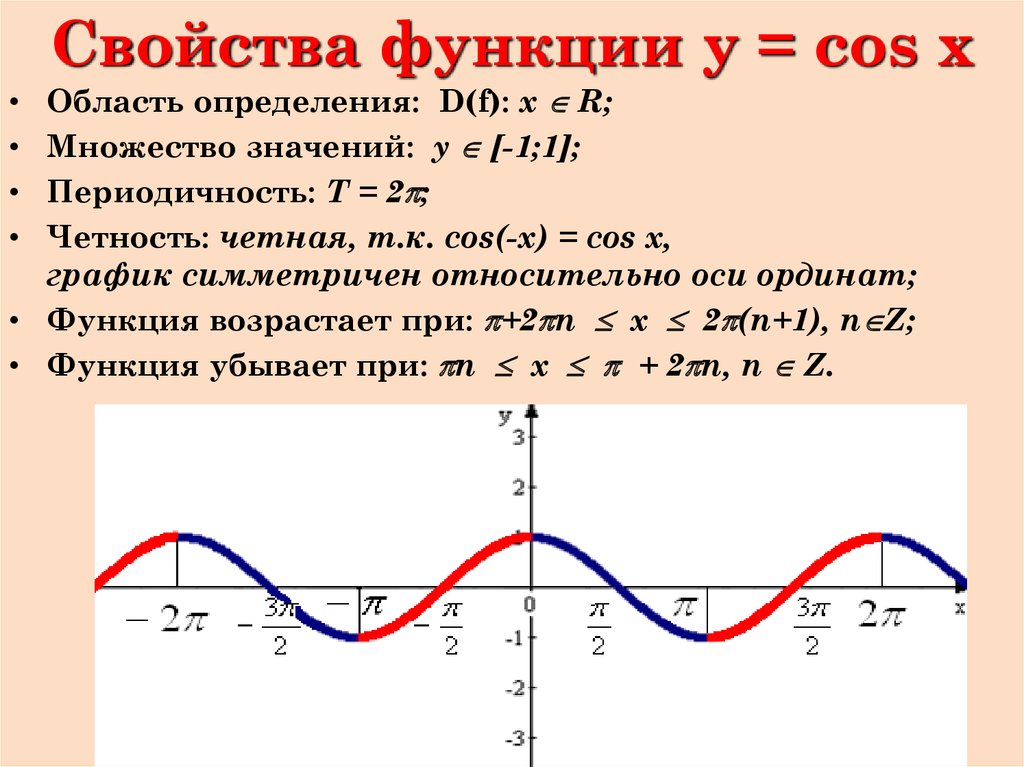
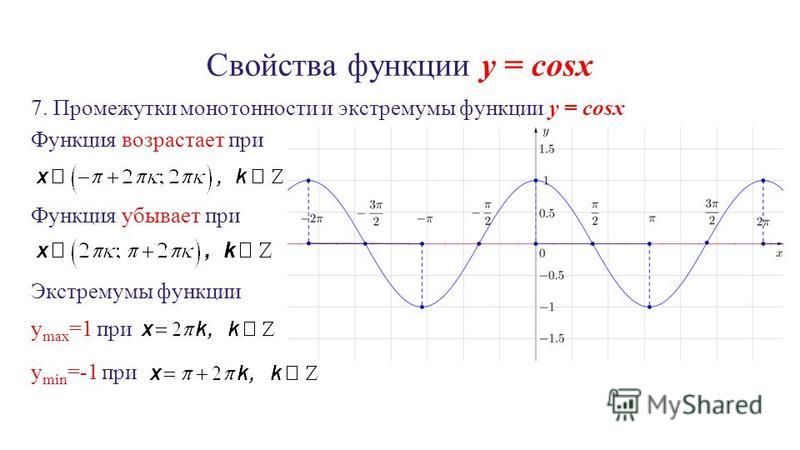
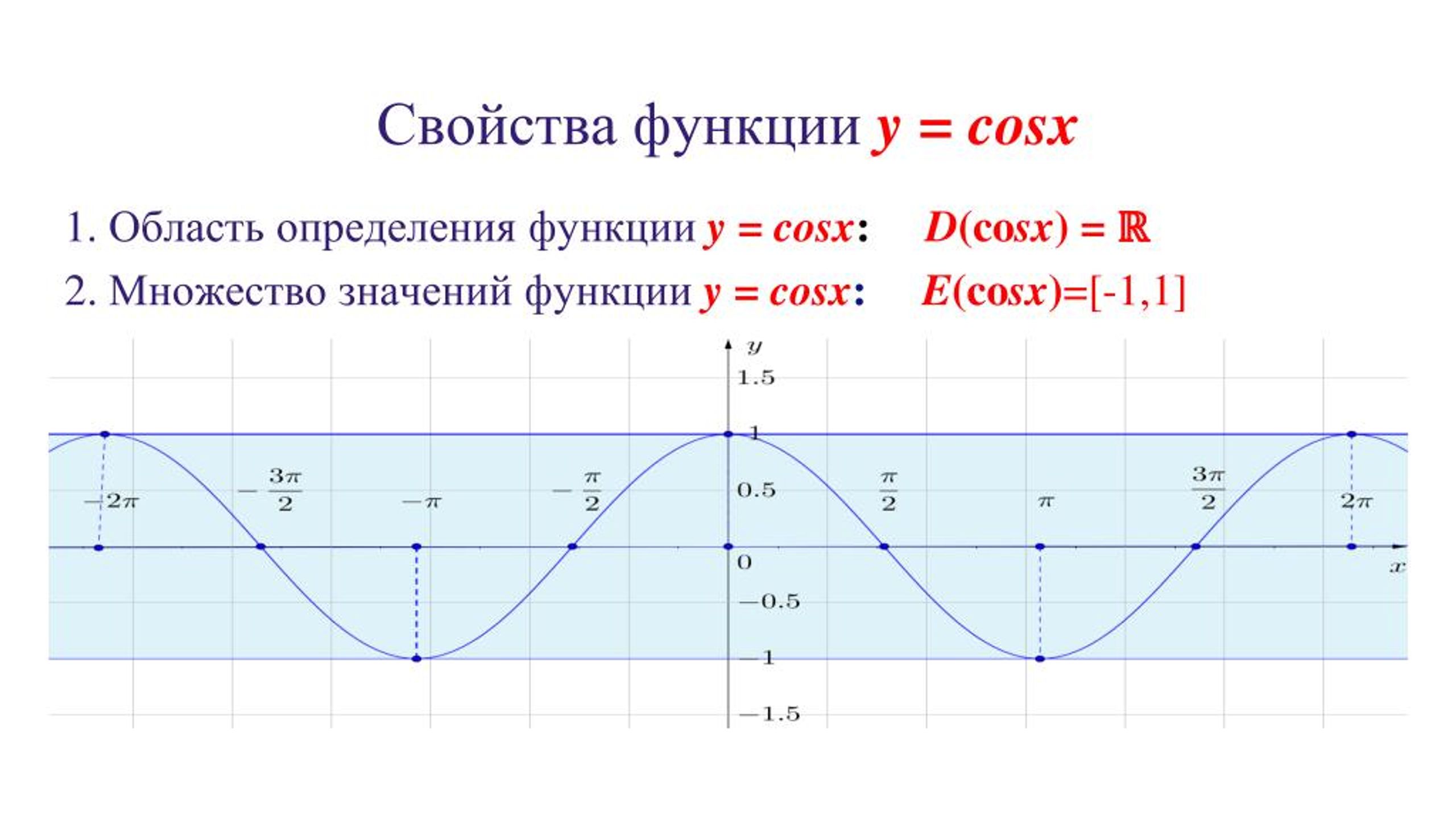
Функция y = cos x.
Графиком функции является синусоида (ее иногда называют косинусоидой).
Свойства функции y = cos x:
1) Область определения функции – множество действительных чисел. 2) Область значений функции – отрезок [–1; 1] 3) Это
четная функция. 4) Это непрерывная функция. 5) Координаты точек пересечения графика: — с осью абсцисс: (π/2 + πn; 0), — с осью ординат: (0;1). 6) На отрезке [0; π] функция убывает, на отрезке [π; 2π] – возрастает. 7) На промежутках [-π/2 + 2πn; π/2 + 2πn] функция принимает положительные значения. На промежутках [π/2 + 2πn; 3π/2 + 2πn] функция принимает отрицательные значения. 8) Промежутки возрастания: [-π + 2πn; 2πn]. Промежутки убывания: [2πn; π + 2πn]; 9) Точки минимума функции: π + 2πn. Точки максимума функции: 2πn. 10) Функция ограничена сверху и снизу. Наименьшее значение функции –1, наибольшее значение 1. 11) Это периодическая функция с периодом 2π (Т = 2π) |
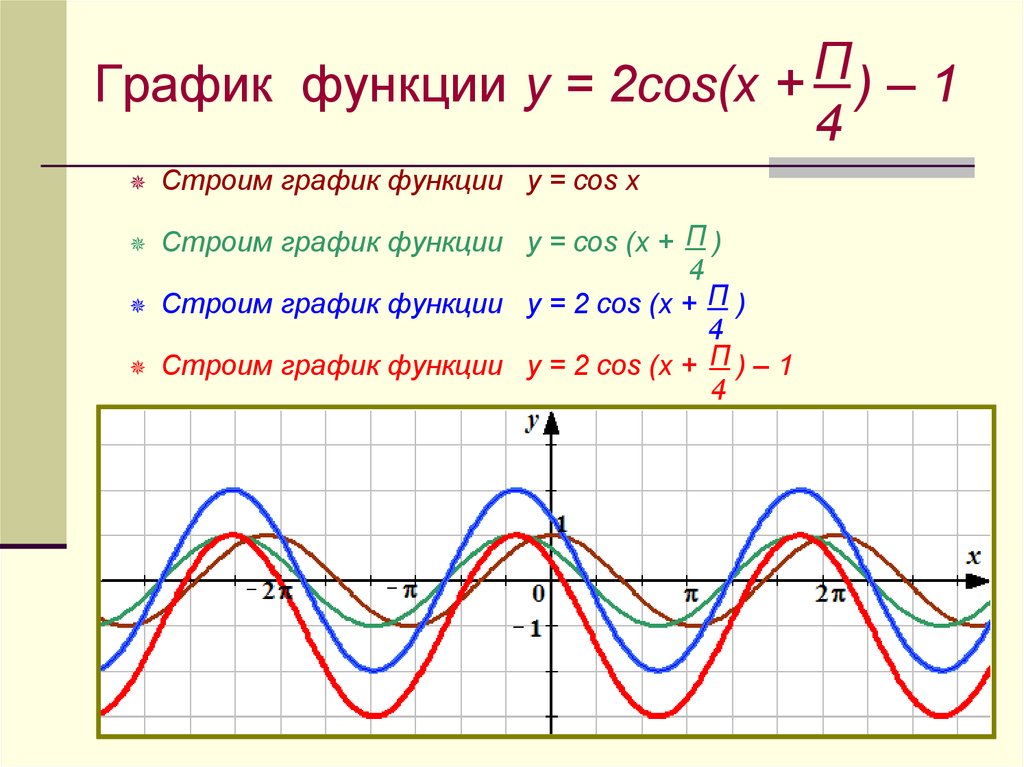
Функция y = mf(x).
Возьмем
предыдущую функцию y = cos x.
Как вы уже знаете, ее графиком является
синусоида.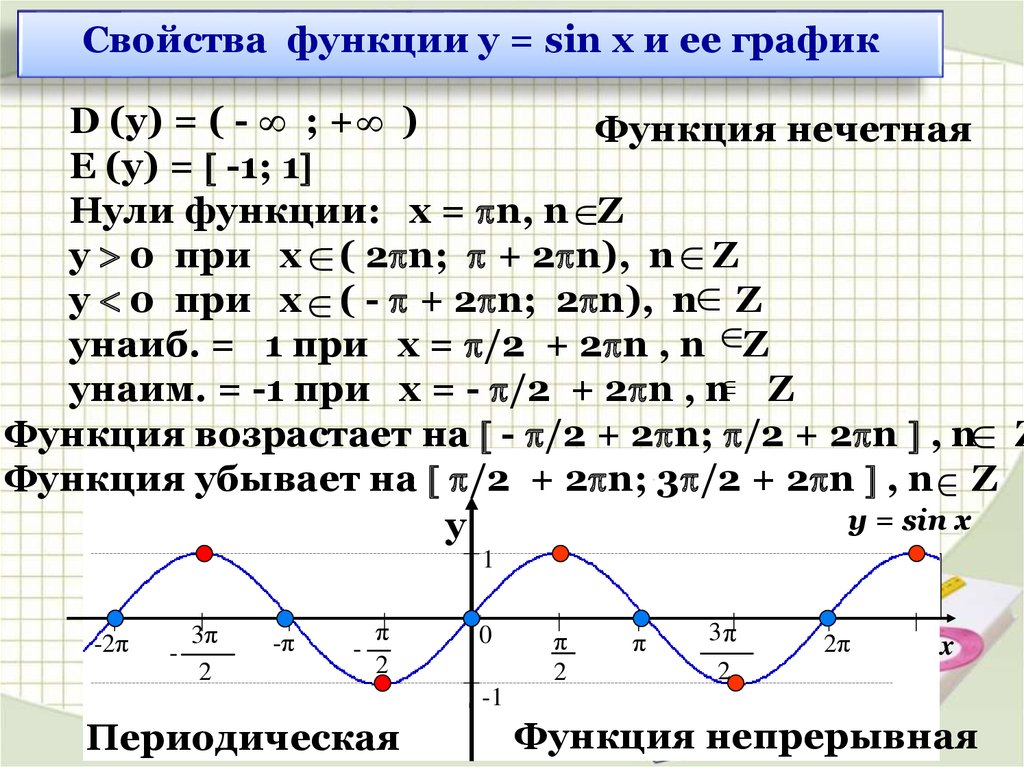 Если мы умножим косинус этой
функции на определенное число m, то волна
растянется от оси x (либо сожмется, в зависимости от величины
m).
Эта новая волна и будет графиком
функции y = mf(x), где m – любое действительное
число.
Если мы умножим косинус этой
функции на определенное число m, то волна
растянется от оси x (либо сожмется, в зависимости от величины
m).
Эта новая волна и будет графиком
функции y = mf(x), где m – любое действительное
число.
Таким образом, функция y = mf(x) – это привычная нам функция y = f(x), умноженная на m.
Если m < 1, то синусоида сжимается к оси x на коэффициент m. Если m > 1, то синусоида растягивается от оси x на коэффициент m.
Выполняя растяжение или сжатие, можно сначала построить лишь одну полуволну синусоиды, а затем уже достроить весь график.
Функция y = f(kx).
Если функция y = mf(x) приводит к растяжению синусоиды от оси x либо сжатию к оси x, то функция y = f(kx) приводит к растяжению от оси y либо сжатию к оси y.
Причем k – любое действительное число.
При 0
< k < 1 синусоида растягивается от оси y на коэффициент k.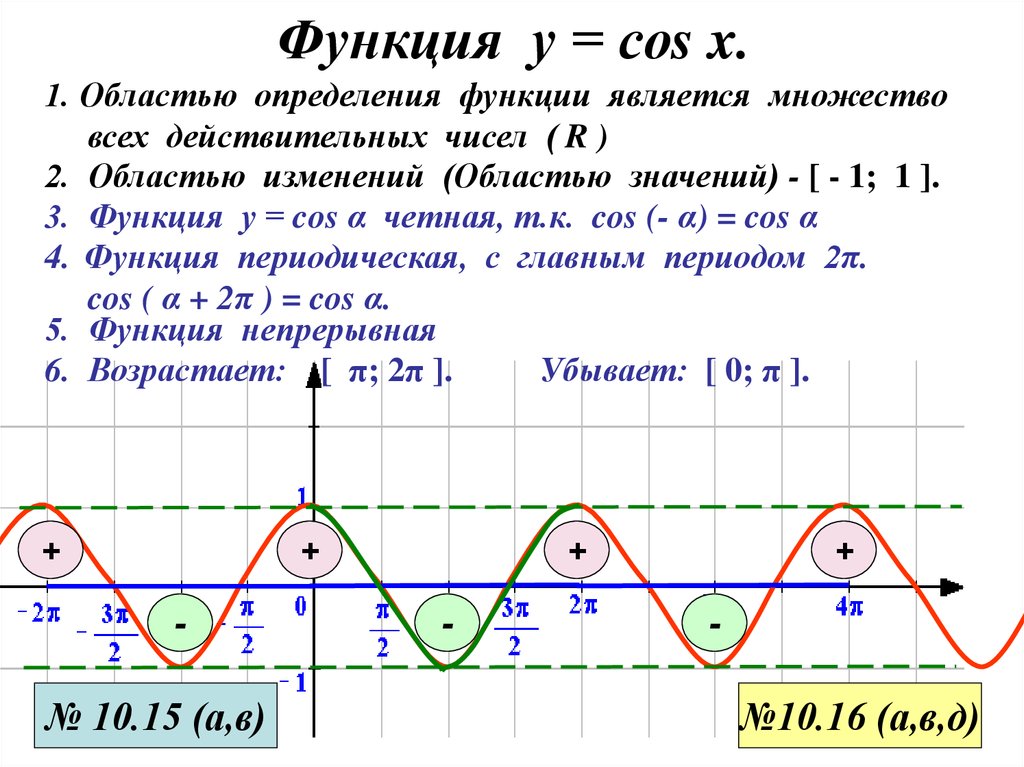 Если k > 1, то синусоида
сжимается к оси y на коэффициент k.
Если k > 1, то синусоида
сжимается к оси y на коэффициент k.
Составляя график этой функции, можно сначала построить одну полуволну синусоиды, а по ней достроить затем весь график.
Функция y = tg x.
Графиком функции y = tg x является тангенсоида.
Достаточно построить часть графика на промежутке от 0 до π/2, а затем можно симметрично продолжить ее на промежутке от 0 до 3π/2.
Свойства функции y = tg x:
1) Область определения функции – множество всех действительных чисел, кроме чисел вида x = π/2 + πk, где k – любое целое число. Это
означает, что на графике функции нет
точки, принадлежащей прямой x = π/2,
либо прямой x = 3π/2, либо прямой x = 5π/2, либо прямой x = –π/2 и т. 2) Область значений функции (–∞; +∞) 3) Это нечетная функция. 4) Это непрерывная функция на интервале (–π/2; π/2). 5) Это периодическая функция с основным периодом π (Т = π) 6) Функция возрастает на интервале (–π/2; π/2). 7) Функция не ограничена ни сверху, ни снизу. Не имеет ни наименьшего, ни наибольшего значений. |
Функция y = ctg x
Графиком функции y = ctg x также является тангенсоида (ее иногда называют котангенсоидой).
Свойства функции y = ctg x:
1) Область определения функции – множество всех действительных чисел, кроме чисел вида x = πk, где k – любое целое число. 2) Область значений функции (–∞; +∞) 3) Это
нечетная функция. 4) Это непрерывная функция. 5) Это периодическая функция с основным периодом π (Т = π) 6) Функция убывает в промежутке (πk; π + πk), где k – любое целое число. 7) Функция не ограничена ни сверху, ни снизу. Не имеет ни наименьшего, ни наибольшего значений. |
Текст задания:
Множество значений | ||
А1 | Определите множество значений функции: | 1) ;2) ;3) ;4) |
А2 | Найдите сумму целых значений функции | 1) 2) 3) 4) |
А3 | Укажите наибольшее целое значение функции | 1) 2) 3) 4) |
А4 | Определите множество значений функции: | 1) ;2) ;3) ;4) |
А5 | Найдите сумму целых значений функции | 1) 2) 3) 4) |
А6 | Укажите наименьшее целое значение функции | 1) 2) 3) 4) |
А7 | Определите множество значений функции: | 1) ;2) ;3) ;4) |
А8 | Найдите сумму целых значений функции | 1) 2) 3) 4) |
А9 | Укажите наибольшее целое значение функции | 1) 2) 3) 4) |
А10 | Определите множество значений функции: | 1) ;2) ;3) ;4) |
А11 | Найдите сумму целых значений функции | 1) 2) 3) 4) |
А12 | Укажите наименьшее целое значение функции | 1) 2) 3) 4) |
2.
 3: Функции синуса и косинуса
3: Функции синуса и косинуса- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 89289
- Мэтью Болкинс, Дэвид Остин и Стивен Шликер
- Государственный университет Гранд-Вэлли через ScholarWorks @ Государственный университет Гранд-Вэлли
Мотивирующие вопросы
- Что такое функции синуса и косинуса и как они возникают из точки, пересекающей единичный круг?
- Какими важными свойствами обладают функции синуса и косинуса?
- Как точно или приблизительно вычислить значения \(\sin(t)\) и \(\cos(t)\text{,}\)?
В разделе 2.1 мы видели, как отслеживание высоты точки, пересекающей окружность, генерирует периодическую функцию, например, в Рисунок 2.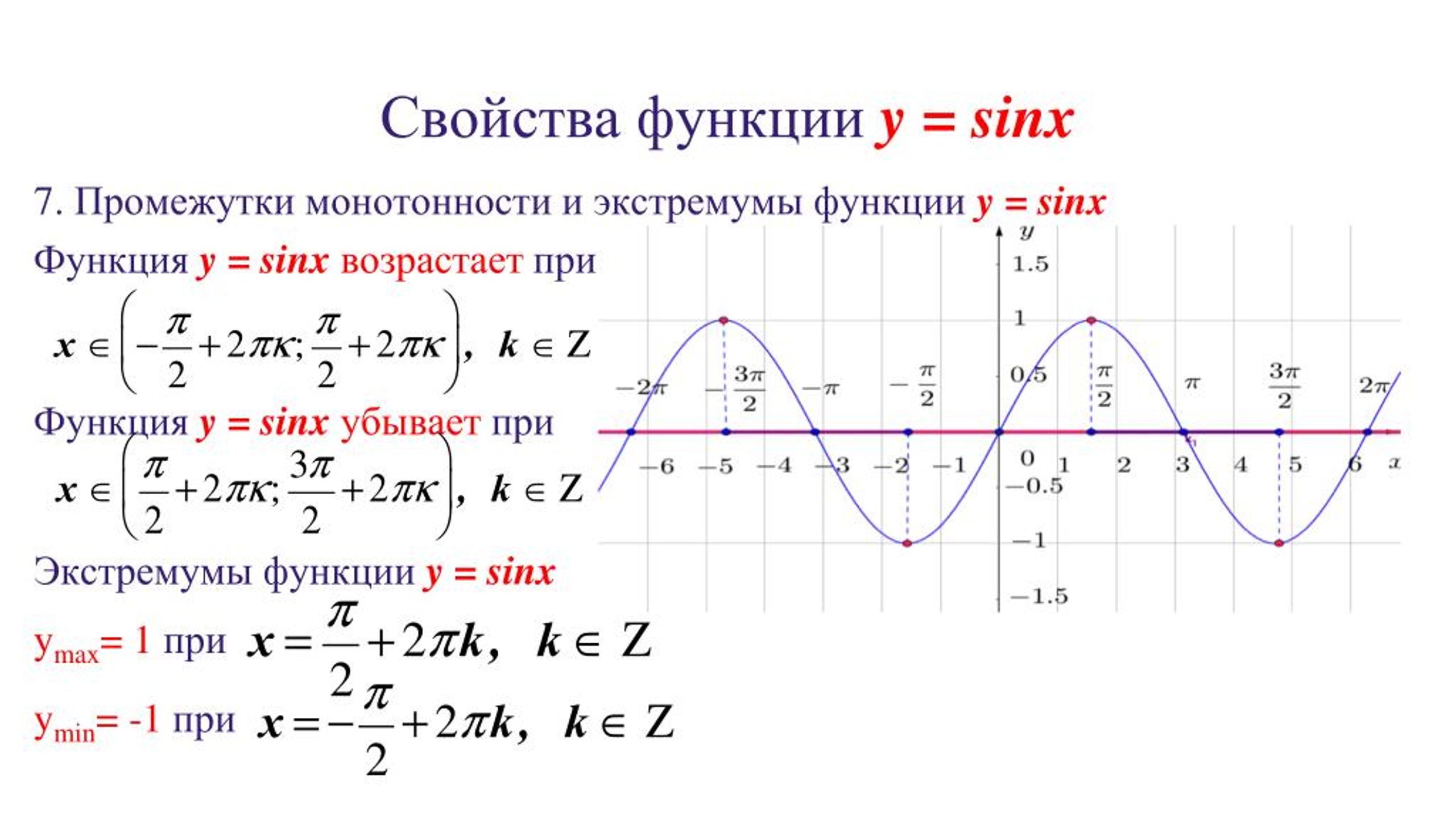 1.10. Затем в разделе 2.2 мы определили набор \(16\) особых точек на единичной окружности, как показано на Рис. \(\PageIndex{1}\)
1.10. Затем в разделе 2.2 мы определили набор \(16\) особых точек на единичной окружности, как показано на Рис. \(\PageIndex{1}\)
Вы также можете использовать файл Desmos по адресу http://gvsu.edu/s/0xt для обзора и изучения особых точек на единичной окружности.
Предварительный просмотр \(\PageIndex{1}\)
Если мы рассмотрим единичный круг на рисунке \(\PageIndex{1}\) , начните с \(t = 0\text{,}\) и пройдите круг против часовой стрелки, мы можем увидеть высоту, \(h\text{,}\) точки пересечения как функцию угла, \ (t\text{,}\) в радианах. Оттуда мы можем построить результирующие \((t,h)\) упорядоченные пары и соединить их для создания круговой функции, изображенной на рисунке \(\PageIndex{2}\) Рисунок
\(\PageIndex{2} \) График круговой функции, которая отслеживает высоту точки, пересекающей единичный круг.
- Каково точное значение \(f( \frac{\pi}{4} )\text{?}\) для \(f( \frac{\pi}{3} )\text{?}\ )
- Заполните следующую таблицу точными значениями \(h\), которые соответствуют указанным входам.
| \(т\) | \(0\) | \(\ гидроразрыва {\pi}{6}\) | \(\ гидроразрыва {\pi}{4}\) | \(\ гидроразрыва {\pi}{3}\) | \(\ гидроразрыва {\pi}{2}\) | \(\frac{2\pi}{3}\) | \(\frac{3\pi}{4}\) | \(\frac{5\pi}{6}\) | \(\пи\) |
| \(ч\) | |||||||||
| \(т\) | \(\пи\) | \(\frac{7\pi}{6}\) | \(\frac{5\pi}{4}\) | \(\frac{4\pi}{3}\) | \(\frac{3\pi}{2}\) | \(\frac{5\pi}{3}\) | \(\frac{7\pi}{4}\) | \(\frac{11\pi}{6}\) | \(2\пи\) |
| \(ч\) | |||||||||
3. Каково точное значение \(f( \frac{11\pi}{4} )\text{?}\) для \(f( \frac{14\pi}{3} ) \text{?}\)
Каково точное значение \(f( \frac{11\pi}{4} )\text{?}\) для \(f( \frac{14\pi}{3} ) \text{?}\)
4. Укажите четыре различных значения \(t\), для которых \(f(t) = -\frac{\sqrt{3}}{2}\text{.}\)
Определение функции синуса
Круговая функция, которая отслеживает высоту точки на единичной окружности, проходящей против часовой стрелки из \((1,0)\) как функцию соответствующего центрального угла (в радианах), является одной из наиболее важные функции в математике. Таким образом, мы даем функции имя: синус функция.
Определение \(\PageIndex{4}\): Word
Дан центральный угол в единичной окружности, который измеряет \(t\) радиан и пересекает окружность в точках \((1,0)\) и \ ((a,b)\text{,}\) как показано на рисунке \(\PageIndex{5}\) , мы определяем синус \(t\), обозначаемый \(\sin(t)\text {,}\) по правилу
\[ \sin(t) = b\text{.} \nonumber \]
Рисунок \(\PageIndex{5}\) Определение синуса угла \(t \text{. }\)
}\)Из-за соответствия между мерой угла в радианах и расстоянием, пройденным на единичной окружности, мы можем также думать о \(\sin(t)\) как об идентифицирующей \(y\)-координате точки после того, как он прошел \(t\) единиц против часовой стрелки по окружности от \((1,0)\text{.}\) Обратите внимание, что мы можем рассматривать синус отрицательных входных данных: например, \(\sin( -\frac{\pi}{2}) = -1\text{.}\)
Основываясь на нашей предыдущей работе с единичным кругом, мы знаем много различных точных значений функции синуса и суммируем их в Таблица \(\PageIndex{6}\)
| \(т\) | \(0\) | \(\ гидроразрыва {\pi}{6}\) | \(\ гидроразрыва {\pi}{4}\) | \(\ гидроразрыва {\pi}{3}\) | \(\frac{\pi}{2}\) | \(\frac{2\pi}{3}\) | \(\frac{3\pi}{4}\) | \(\frac{5\pi}{6}\) | \(\пи\) |
| \(\sin(t)\) | \(0\) | \(\ гидроразрыва{1}{2}\) | \(\ гидроразрыва {\ sqrt {2}} {2} \) | \(\ гидроразрыва {\ sqrt {3}} {2} \) | \(1\) | \(\ гидроразрыва {\ sqrt {3}} {2} \) | \(\ гидроразрыва {\ sqrt {2}} {2} \) | \(\ гидроразрыва{1}{2}\) | \(0\) |
| \(т\) | \(\пи\) | \(\frac{7\pi}{6}\) | \(\frac{5\pi}{4}\) | \(\frac{4\pi}{3}\) | \(\frac{3\pi}{2}\) | \(\frac{5\pi}{3}\) | \(\frac{7\pi}{4}\) | \(\frac{11\pi}{6}\) | \(2\пи\) |
| \(\sin(t)\) | \(0\) | \(-\frac{1}{2}\) | \(-\frac{\sqrt{2}}{2}\) | \(-\frac{\sqrt{3}}{2}\) | \(-1\) | \(-\frac{\sqrt{3}}{2}\) | \(-\frac{\sqrt{2}}{2}\) | \(-\frac{1}{2}\) | \(0\) |
Более того, если мы теперь нанесем эти точки обычным способом, как мы это делали в Preview Activity \(\PageIndex{1}\) , мы получим знакомую круговую волновую функцию, которая получается при отслеживании высоты точка, пересекающая окружность.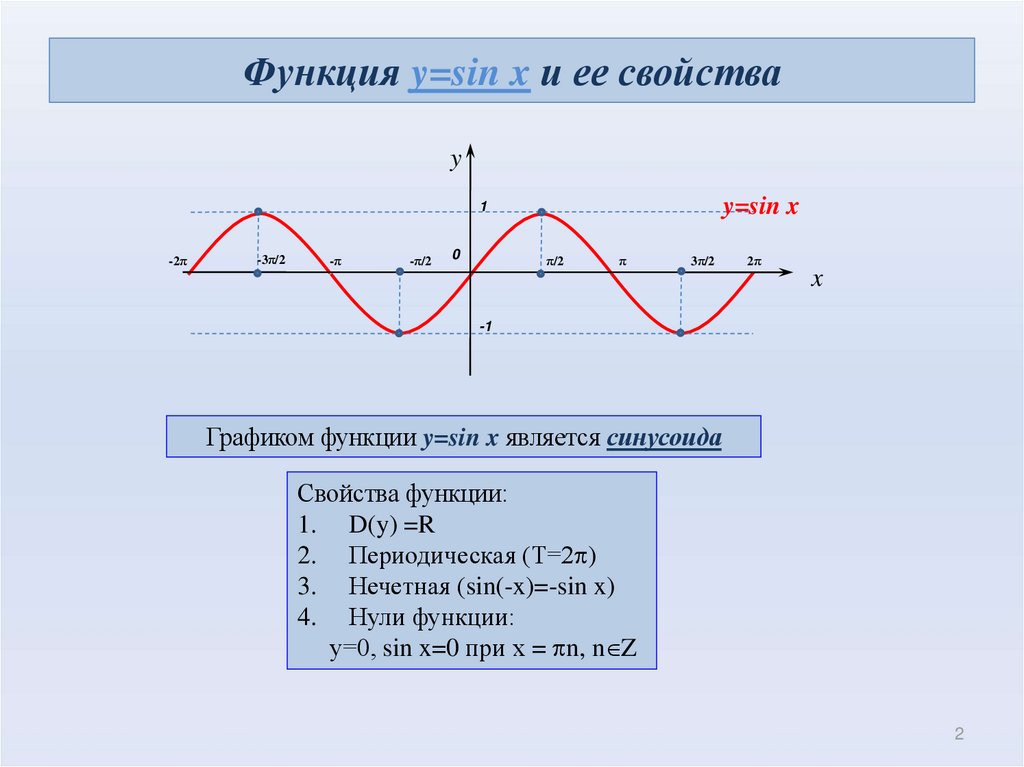 Мы часто называем график Figure \(\PageIndex{7}\) синусоидой .
Мы часто называем график Figure \(\PageIndex{7}\) синусоидой .
Определение функции косинуса
Для любого центрального угла в радианах \(t\) в единичной окружности с одной стороной, проходящей через точку \((1,0)\text{,}\), угол порождает единственную точку \((a, б)\), лежащий на окружности. Точно так же, как мы можем рассматривать \(y\)-координату как функцию \(t\text{,}\), \(x\)-координата также является функцией \(t\text{.}\) Поэтому мы даем следующее определение.
Определение \(\PageIndex{8}\)
Дан центральный угол в единичной окружности, измеряющий \(t\) радиан и пересекающий окружность в точках \((1,0)\) и \(( а,б)\текст{,}\) как показано на Рисунок \(\PageIndex{9}\) , мы определяем косинус \(t\), обозначаемый \(\cos(t)\text{,}\) по правилу
\[ \cos(t ) = a\text{.} \nonumber \]
Рисунок \(\PageIndex{9}\) Определение косинуса угла \(t\text{. }\)
}\)Опять же из-за соответствия между радианами мера угла и длины дуги вдоль единичной окружности, мы можем рассматривать значение \(\cos(t)\) как отслеживание \(x\)-координаты точки, пересекающей единичную окружность по часовой стрелке на расстоянии \( t\) единиц вдоль круга из \((1,0)\text{.}\) Теперь мы используем данные и информацию, которые мы получили о единичном круге, чтобы построить таблицу значений \(\cos(t) \), а также график кривой, которую он генерирует.
Activity \(\PageIndex{2}\)
Пусть \(k = g(t)\) будет функцией, которая отслеживает \(x\)-координату точки, пересекающей единичный круг против часовой стрелки от \(( 1,0)\text{.}\) То есть \(g(t) = \cos(t)\text{.}\) Используйте информацию, известную нам о единичном круге, которая представлена на рисунке \( \PageIndex{1}\) , чтобы ответить на следующие вопросы.
- Каково точное значение \(\cos(\frac{\pi}{6})\text{?}\) из \(\cos(\frac{5\pi}{6})\text{ ?}\) \(\cos(-\frac{\pi}{3})\text{?}\)
- Заполните следующую таблицу точными значениями \(k\), которые соответствуют указанным входам.

| \(т\) | \(0\) | \(\ гидроразрыва {\pi}{6}\) | \(\ гидроразрыва {\pi}{4}\) | \(\ гидроразрыва {\pi}{3}\) | \(\ гидроразрыва {\pi}{2}\) | \(\frac{2\pi}{3}\) | \(\frac{3\pi}{4}\) | \(\frac{5\pi}{6}\) | \(\пи\) |
| \(к\) | |||||||||
| \(т\) | \(\пи\) | \(\frac{7\pi}{6}\) | \(\frac{5\pi}{4}\) | \(\frac{4\pi}{3}\) | \(\frac{3\pi}{2}\) | \(\frac{5\pi}{3}\) | \(\frac{7\pi}{4}\) | \(\frac{11\pi}{6}\) | \(2\пи\) |
| \(к\) | |||||||||
3. На осях, указанных на рисунке \(\PageIndex{11}\) , нарисуйте точный график \(k = \cos(t)\text{.}\) Обозначьте точное местоположение несколько ключевых точек на кривой.
На осях, указанных на рисунке \(\PageIndex{11}\) , нарисуйте точный график \(k = \cos(t)\text{.}\) Обозначьте точное местоположение несколько ключевых точек на кривой.
Рисунок \(\PageIndex{11}\) Оси для построения \(k = \cos(t)\text{.}\)
4. Каково точное значение \(\cos( \frac{11\pi}{4} )\text{?}\) для \(\cos( \frac{14\pi}{3} )\ текст{?}\)
5. Укажите четыре различных значения \(t\), для которых \(\cos(t) = -\frac{\sqrt{3}}{2}\text{.}\)
6. Чем график \(k = \cos(t)\) отличается от графика \(h = \sin(t)\text{?}\) Чем графики похожи?
Когда мы работаем с функциями синуса и косинуса, всегда полезно помнить их определения в терминах единичной окружности и движения точки, пересекающей окружность. На http://gvsu.edu/s/0xe вы можете изучить и изучить полезный Desmos 9.0049, которая показывает, как это движение по кругу генерирует каждый из соответствующих графиков.
Свойства функций синуса и косинуса
Поскольку функция синуса является результатом отслеживания координаты \(y\) точки, пересекающей единичный круг, а функция косинуса — координаты \(x\), две функции имеют несколько общих свойств циклических функций.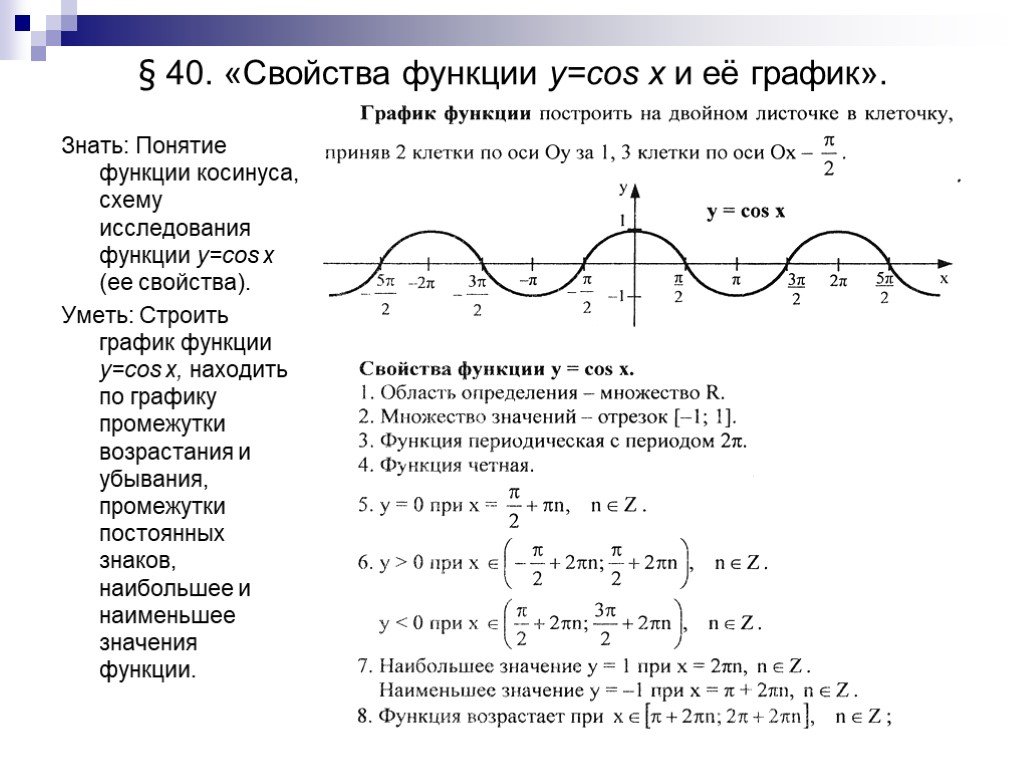
Свойства функций синуса и косинуса.
Для обоих \(f(t) = \sin(t)\) и \(g(t) = \cos(t)\text{,}\)
- домен функции — все действительные числа;
- диапазон функции: \([-1,1]\text{;}\)
- средняя линия функции равна \(y = 0\text{;}\)
- амплитуда функции равна \(a = 1\text{;}\)
- период функции равен \(p = 2\pi\text{.}\)
Также полезно сопоставить графики функций синуса и косинуса на одних и тех же координатных осях. Когда мы это делаем, как показано на рис. \(\PageIndex{2}\) , мы видим, что кривые можно рассматривать как горизонтальные переносы друг друга.
Рисунок \(\PageIndex{2}\) Графики функций синуса и косинуса.В частности, поскольку график синуса можно рассматривать как график косинуса, сдвинутый на \(\frac{\pi}{2}\) единиц вправо, отсюда следует, что для любого значения \(t\text{,}\ )
\[ \sin(t) = \cos(t-\frac{\pi}{2})\text{.} \nonumber \]
Аналогично, поскольку косинусоидальный график можно рассматривать как синусоидальный сдвинут влево,
\[ \cos(t) = \sin(t + \frac{\pi}{2})\text{. } \nonumber \] 92(t) = 1\text{.} \nonumber \]
} \nonumber \] 92(t) = 1\text{.} \nonumber \]
На графиках двух функций есть дополнительные тенденции и шаблоны, которые мы рассмотрим подробнее в следующем упражнении.
Упражнение \(\PageIndex{3}\)
Используйте Рисунок \(\PageIndex{12}\) , чтобы ответить на следующие вопросы.
- Приведите пример наибольшего из найденных интервалов, на котором \(f(t) = \sin(t)\) убывает.
- Приведите пример наибольшего интервала, который вы можете найти, на котором \(f(t) = \sin(t)\) убывает и вогнут вниз.
- Приведите пример наибольшего из найденных интервалов, на котором \(g(t) = \cos(t)\) возрастает.
- Приведите пример наибольшего интервала, который вы можете найти, на котором \(g(t) = \cos(t)\) возрастает и вогнут вверх.
- Без каких-либо вычислений, на каком интервале средняя скорость изменения \(g(t) = \cos(t)\) больше: \([\pi, \pi+0,1]\) или \([\ frac{3\pi}{2}, \frac{3\pi}{2} + 0.
 1]\text{?}\) Почему?
1]\text{?}\) Почему? - Как бы вы в целом охарактеризовали места на графиках синуса и косинуса, где функции возрастают или убывают быстрее всего?
- Думая с точки зрения единичного круга, для которого квадранты плоскости \(x\)-\(y\) \(\cos(t)\) отрицательны для угла \(t\), лежащего в этом квадрант?
Используя вычислительную технику
Мы установили, что знаем точное значение \(\sin(t)\) и \(\cos(t)\) для любого из \(t\)-значений в таблице 2.3. .6, а также для любых таких \(t \pm 2j\pi\text{,}\), где \(j\) — целое число, в силу периодичности функций. Но что, если мы хотим узнать \(\sin(1.35)\) или \(\cos(\frac{\pi}{5})\) или значения для других входных данных, которых нет в таблице?
Любое стандартное вычислительное устройство, такое как научный калькулятор, Desmos , Geogebra или WolframAlpha , имеет возможность вычислять функции синуса и косинуса при любом входном сигнале, который мы пожелаем. Поскольку ввод рассматривается как угол, каждое вычислительное устройство может учитывать угол в радианах или градусах. Всегда важно знать, какой тип ввода ожидает ваше устройство. Наше вычислительное устройство — Desmos 9.0049 . В Desmos вы можете изменить тип ввода между радианами и градусами, щелкнув значок гаечного ключа в правом верхнем углу и выбрав нужные единицы измерения. Радианная мера используется по умолчанию.
Всегда важно знать, какой тип ввода ожидает ваше устройство. Наше вычислительное устройство — Desmos 9.0049 . В Desmos вы можете изменить тип ввода между радианами и градусами, щелкнув значок гаечного ключа в правом верхнем углу и выбрав нужные единицы измерения. Радианная мера используется по умолчанию.
Чтобы вычислительное устройство могло вычислить синусоидальную и косинусную функции при любом желаемом значении, требуется основательная и сложная математика; алгоритмы включают идею исчисления, известную как бесконечный ряд. Несмотря на то, что ваше вычислительное устройство является мощным, полезно и важно понимать значение этих значений на единичной окружности и помнить специальные точки, для которых мы точно знаем выходные значения функций синуса и косинуса.
Activity \(\PageIndex{4}\)
По возможности точно ответьте на следующие вопросы. Если вы оцениваете значение, делайте это с точностью не менее \(5\) знаков после запятой.
- Координата \(x\) точки на единичной окружности, лежащей в третьем квадранте и координата \(y\) которой равна \(y = -\frac{3}{4}\text{.
 }\)
}\) - \(y\)-координата точки на единичной окружности, образованной центральным углом в стандартном положении, который измеряет \(t = 2\) радиан.
- \(x\)-координата точки на единичной окружности, образованной центральным углом в стандартном положении, который измеряет \(t = -3,05\) радиан.
- Значение \(\cos(t)\), где \(t\) — угол в квадранте II, удовлетворяющий условию \(\sin(t) = \frac{1}{2}\text{.}\)
- Значение \(\sin(t)\), где \(t\) — угол в квадранте III, для которого \(\cos(t) = -0,7\text{.}\)
- Средняя скорость изменения \(f(t) = \sin(t)\) на интервалах \([0,1,0,2]\) и \([0,8,0,9]\текст{.}\)
- Средняя скорость изменения \(g(t) = \cos(t)\) на интервалах \([0.1,0.2]\) и \([0.8,0.9]\text{.}\)
Резюме
- Функции синуса и косинуса являются результатом отслеживания \(y\)- и \(x\)-координат точки, пересекающей единичный круг против часовой стрелки от \((1,0)\text{.} \) Значением \(\sin(t)\) является \(y\)-координата точки, прошедшей \(t\) единиц по окружности из \((1,0)\) (или эквивалентно, что соответствует углу \(t\) радиан), а значение \(\cos(t)\) является \(x\)-координатой той же точки.

- Функции синуса и косинуса являются периодическими функциями, которые имеют одну и ту же область определения (множество всех действительных чисел), диапазон (интервал \([-1,1]\)), среднюю линию (\(y = 0\)) , амплитуда (\(a = 1\)) и период (\(P = 2\pi\)). Кроме того, функция синуса представляет собой горизонтальный сдвиг функции косинуса на \(\frac{\pi}{2}\) единиц вправо, поэтому \(\sin(t) = \cos(t-\frac{\ pi}{2})\) для любого значения \(t\text{.}\)
- Если \(t\) соответствует одному из известных нам специальных углов на единичной окружности (как на рис. 2.3.1), мы можем вычислить значения \(\sin(t)\) и \(\cos (т)\) точно. Для других значений \(t\text{,}\) мы можем использовать вычислительное устройство для оценки значения любой функции при данном входе; когда мы это делаем, мы должны позаботиться о том, в каких единицах мы вычисляем: в радианах или в градусах.
Упражнения
5.
Без использования вычислительного устройства определите точное значение каждой из следующих величин. 2(t)\)
2(t)\)
Эта страница под названием 2.3: Функции синуса и косинуса распространяется под лицензией CC BY-SA 4.0 и была создана, изменена и/или курирована Мэтью Болкинсом, Дэвидом Остином и Стивеном Шликером (ScholarWorks @Grand Valley State University) через исходный контент, отредактированный в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Автор
- Активное исчисление
- Лицензия
- CC BY-SA
- Версия лицензии
- 4,0
- Показать страницу TOC
- нет
- Теги
- источник@https://activecalculus.
 org/prelude
org/prelude
- источник@https://activecalculus.
Косинус: определения и примеры — Club Z! Tutoring
Косинус — это фундаментальная математическая функция, встречающаяся в различных областях математики, физики и техники. Это одна из трех основных тригонометрических функций, наряду с синусом и тангенсом, и обозначается символом «cos». Функция косинуса связывает отношение прилежащей стороны прямоугольного треугольника к гипотенузе. Он имеет множество приложений в таких областях, как геометрия, обработка сигналов и обработка изображений.
Функция косинуса определяется как отношение прилежащей стороны к гипотенузе прямоугольного треугольника. Это определение подразумевает, что функция косинуса принимает значения от -1 до 1 включительно. Функция косинуса может быть определена с помощью единичного круга, который представляет собой круг радиуса один с центром в начале координат на декартовой плоскости. Косинус угла? является координатой x точки на единичной окружности, полученной поворотом на угол ? против часовой стрелки от положительной оси x.
Одним из существенных свойств функции косинуса является ее периодичность. Функция косинуса повторяется через каждые 2? радианы или 360 градусов. Это свойство делает функцию косинуса полезной для описания периодических явлений, таких как колебания, волны и циклические процессы. Функция косинуса также является четной функцией, что означает, что cos(-?) = cos(?) для любого угла ?.
Функция косинуса имеет несколько фундаментальных тождеств, вытекающих из ее определения и свойств. Наиболее фундаментальным тождеством является тождество Пифагора, которое связывает функцию косинуса с функцией синуса и определяется как: 92(?) = 1
Это тождество получено из теоремы Пифагора, которая утверждает, что сумма квадратов смежных и противоположных сторон прямоугольного треугольника равна квадрату гипотенузы. Другим существенным тождеством является четно-нечетное тождество, которое связывает функцию косинуса с ее четностью и задается формулой: ось, которая является вертикальной осью, проходящей через начало координат.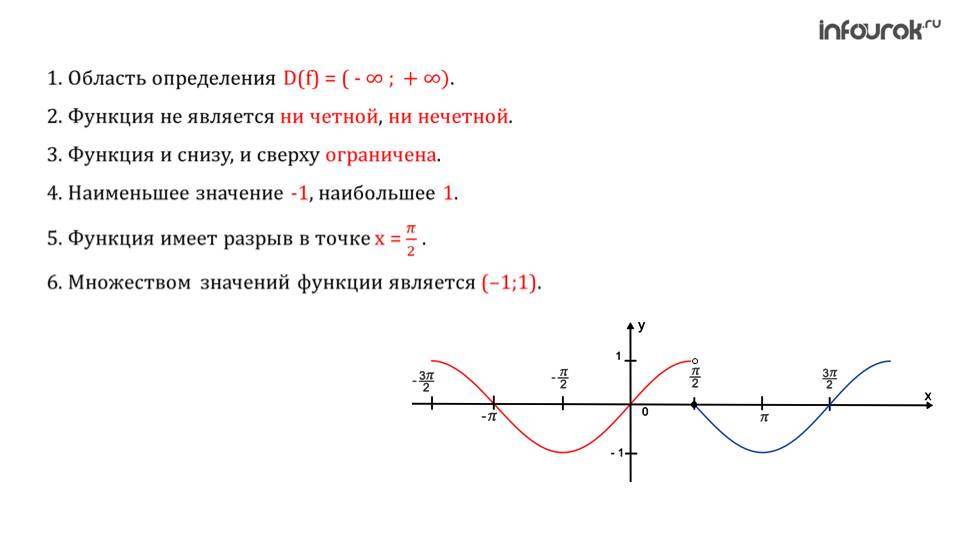
Функция косинуса имеет несколько применений в различных областях математики и естественных наук. В геометрии функция косинуса используется для нахождения длины прилежащей или противоположной стороны прямоугольного треугольника по гипотенузе и углу. Функция косинуса также используется для нахождения углов между двумя векторами в евклидовом пространстве, где скалярное произведение двух векторов выражается как произведение их величин и косинуса угла между ними.
При обработке сигналов функция косинуса используется для представления периодических сигналов, таких как звуковые волны, электрические сигналы и электромагнитные волны. Ряд Фурье, представляющий собой математический инструмент, используемый для представления периодических сигналов в виде суммы функций синуса и косинуса, основан на свойствах функции косинуса. Функция косинуса также используется в цифровой обработке сигналов для представления сигналов дискретного времени в виде суммы функций косинуса с разными частотами и амплитудами.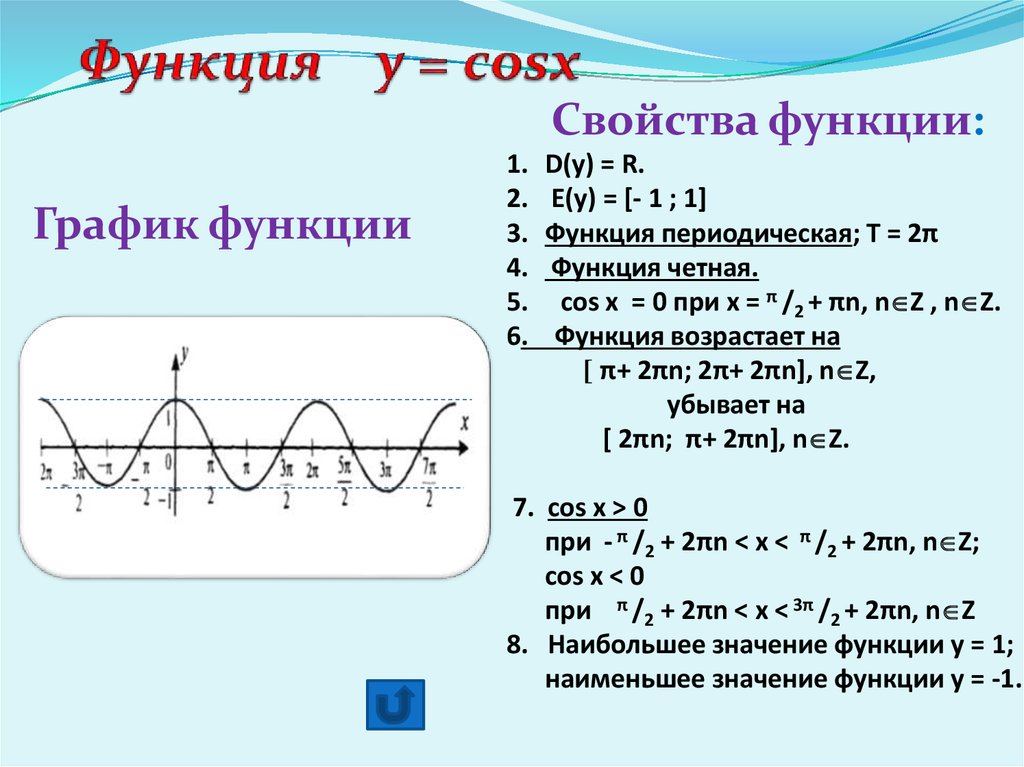
При обработке изображений функция косинуса используется в дискретном косинусном преобразовании (DCT) — математическом методе, используемом для сжатия и распаковки цифровых изображений. ДКП преобразует двумерное изображение в сумму косинусоидальных функций с разными частотами и амплитудами, где низкочастотные составляющие содержат большую часть энергии изображения, а высокочастотные составляющие — большую часть деталей. DCT широко используется в таких стандартах сжатия изображений и видео, как JPEG, MPEG и H.264.
В заключение, функция косинуса является фундаментальной математической функцией с многочисленными приложениями в различных областях математики, физики и техники. Это одна из основных тригонометрических функций, определяемая как отношение прилежащей стороны к гипотенузе прямоугольного треугольника.
Косинус угла определяется как отношение длины прилежащей стороны прямоугольного треугольника к гипотенузе. Другими словами, косинус — это функция, которая связывает угол с отношением двух сторон треугольника.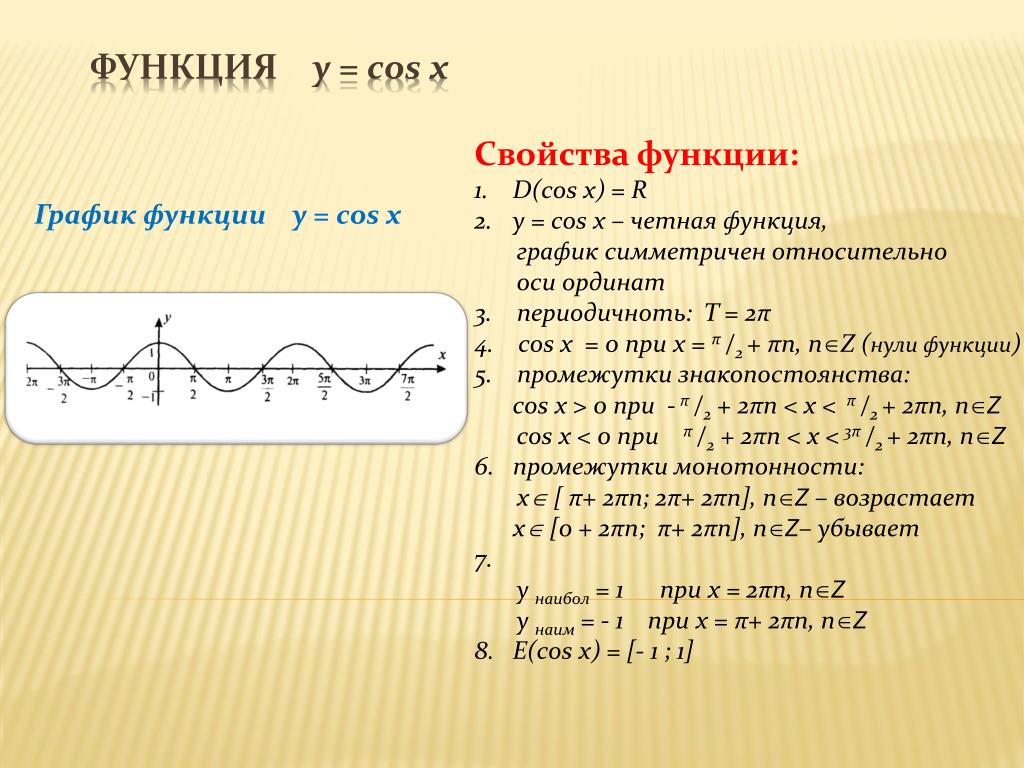

 На промежутках
[-π + 2πn; 2πn] функция принимает отрицательные
значения.
На промежутках
[-π + 2πn; 2πn] функция принимает отрицательные
значения.
 д.
д.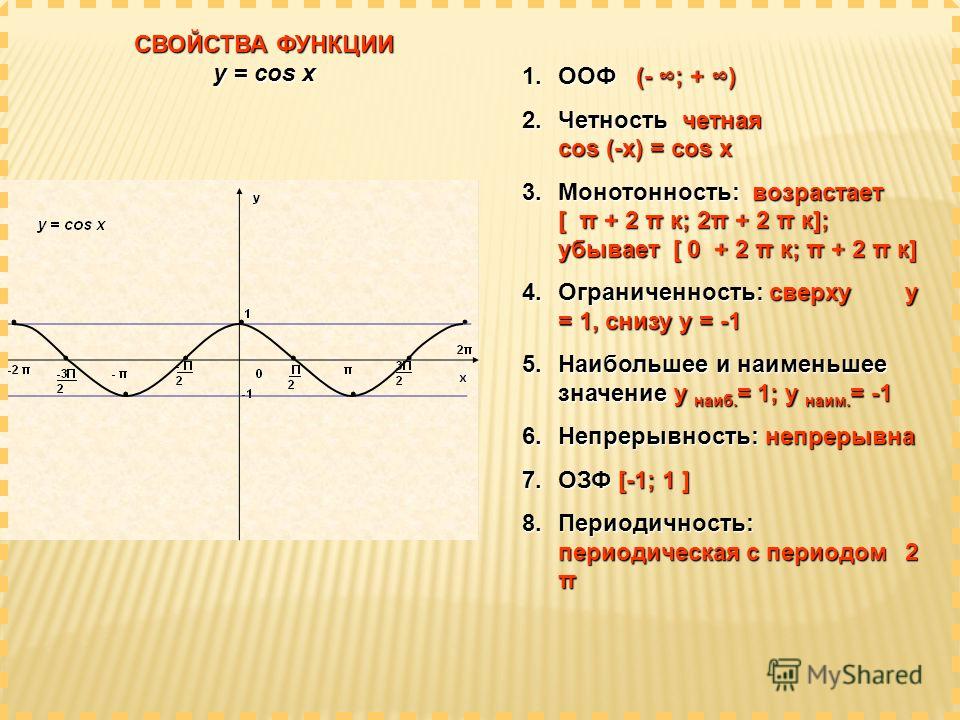
 1]\text{?}\) Почему?
1]\text{?}\) Почему?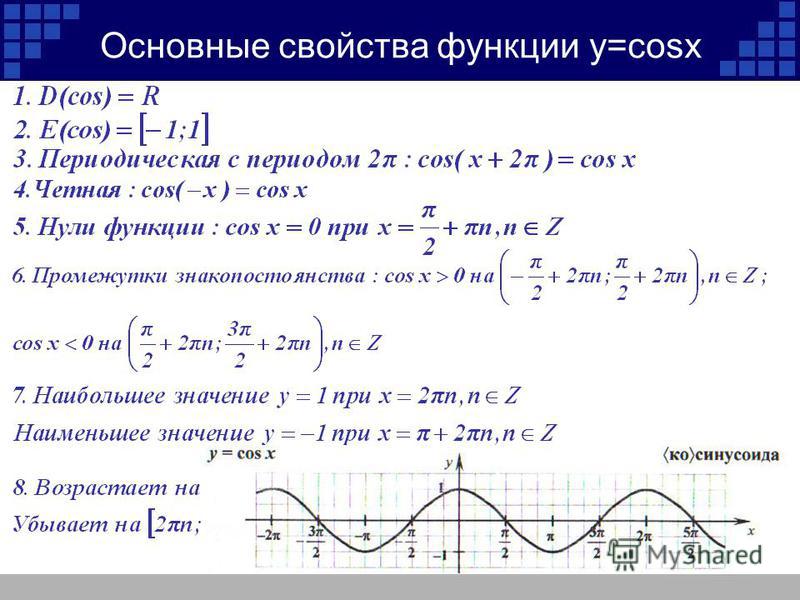 }\)
}\)
 org/prelude
org/prelude