Как доказать что число рациональное: Докажите, что число является рациональным. 4+√7 / (√7+1)∧2

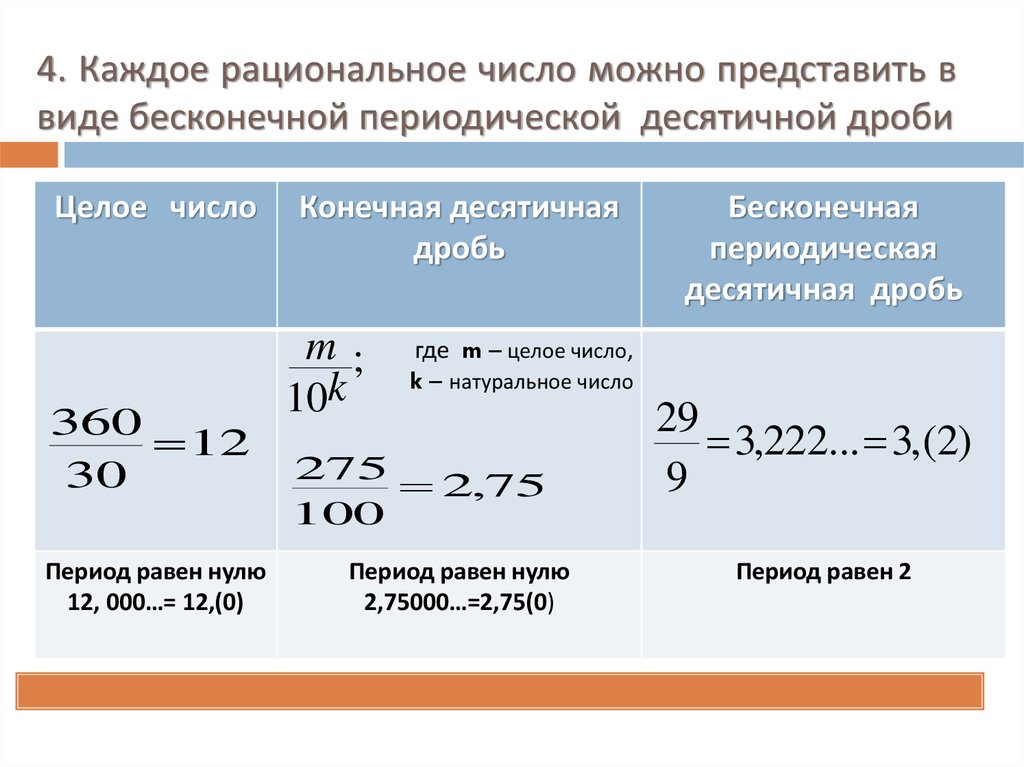
Числа рациональные и иррациональные

Числа рациональные и иррациональные

Айвен Нивен. Числа рациональные и иррациональные Эта книга посвящена одному из основных понятий математики — понятию действительного числа. Ученики старших классов (именно на них она в первую очередь и рассчитана) узнают из нее некоторые свойства чисел, о которых они раньше и не подозревали, и познакомятся с доказательствами теорем, принимаемых в школьном курсе алгебры на веру. Изложение очень простое и живое. Оно сопровождается рядом вопросов и задач, облегчающих активное усвоение материала. Автор книги — известный американский специалист по теории чисел. Оглавление От редактора Введение ГЛАВА I. Натуральные и целые числа § 1. Простые числа § 2. Единственность разложения на простые множители § 3. Целые числа § 4. Четные и нечетные целые числа § 5. Свойства замкнутости § 6. Замечания о природе доказательства ГЛАВА II. Рациональные числа § 1. Определение рациональных чисел § 2. Конечные и бесконечные десятичные дроби § 3. Различные сгюсобы формулировки и доказательства предложений § 4. Периодические десятичные дроби § 5. Всякую конечную десятичную дробь можно представить в виде периодической десятичной дроби § 6. Краткие выводы ГЛАВА III. Действительные числа § 1. Геометрическая точка зрения § 2. Десятичные представления § 3. Иррациональность числа V2 § 4. Иррациональность числа V3 § 5. Иррациональность чисел V6 и V2+V3 § 6. Слова, которыми мы пользуемся § 7. Приложение к геометрии § 8. Краткие выводы ГЛАВА IV. Иррациональные числа § 1. Свойства замкнутости § 2. Алгебраические уравнения § 3. Рациональные корни алгебраических уравнений § 4. Дальнейшие примеры § 5. Краткие выводы ГЛАВА V. Значения тригонометрических и логарифмической функций § 1. Иррациональные значения тригонометрических функций § 2. Одно общее правило § 3. Иррациональные значения десятичных логарифмов § 4. Трансцендентные числа § 5. Три знаменитые задачи на построение § 6. Дальнейший анализ числа V2 § 7. Краткие выводы ГЛАВА VI. Приближение иррациональных чисел рациональными § 1. Неравенства § 2. Приближение целыми числами § 3. Приближение рациональными числами § 4. Лучшие приближения § 5. Приближения с точностью до 1/n2 § 6. Ограничения точности приближений § 7. Краткие выводы ГЛАВА VII. Существование трансцендентных чисел § 1. Предварительные сведения из алгебры § 2. Один способ приближения числа а § 3. План доказательства § 4. Свойства многочленов § 5. Трансцендентность числа а § 6. Краткие выводы ПРИЛОЖЕНИЕ А. Доказательство бесконечности числа простых чисел ПРИЛОЖЕНИЕ Б. Доказательство основной теоремы арифметики ПРИЛОЖЕНИЕ В. Доказательство Кантора существования трансцендентных чисел ПРИЛОЖЕНИЕ Г. Доказательство иррациональности значений тригонометрических фуннций И. М. Яглом Ответы и указания к упражнениям ПРИЛОЖЕНИЕ В Литература

4. Множество рациональных чисел в дальнейшем будем обозначать буквой q. Остановимся на рассмотрении свойств этого множества.

Прежде всего отметим, что множество целых чисел Z является подмножеством множества рациональных чисел Q, то есть Z Ì Q.

Действительно, обозначим через С множество рациональных чисел вида . Таким образом, Î

С тогда и только тогда, когда среди дробей, эквивалентных , содержится дробь вида , так что ~ , или с = аd.

Очевидно, что = в том и только том случае, когда a = b. Результаты арифметических операций над элементами множества С не выводят нас из этого множества. Действительно,

+ = .

Аналогично:

× = и – = .

Если a b, то есть a = nb, где n Z, то

: = .

Отождествим рациональное число с целым числом a. Тогда множество С будет совпадать с множеством Z целых чисел. Операции сложения, умножения и вычитания определены в нем и обладают известными свойствами. В дальнейшем рациональное число обозначаем просто через

a и называем целым числом.

Из того, что Z Ì Q , следует бесконечность множества Q, а также отсутствие в нем наименьшего и наибольшего элементов.

Если разделить целое число а = на целое число b = ¹ 0, то получим a : b = : = . Следовательно, рациональное число есть частное целых чисел а и b ¹ 0. Но в таком случае дробь можно рассматривать как частное а : b и наоборот. Поэтому в дальнейшем рациональное число будем обозначать дробью и понимать как частное двух целых чисел а и b ¹ 0.

Приведенные выше правила арифметических действий над рациональными числами в новых обозначениях выглядят следующим образом:

+ = ; – = ;

× = ; : = .

Если даны две дроби и , то, используя основное свойство, можем записать: ~ и ~ . Очевидно, что дроби и имеют одинаковые знаменатели.

Процесс перехода от дробей и к эквивалентным им дробям и с одинаковыми знаменателями называется приведением дробей к общему знаменателю.

Если дроби и имеют одинаковые знаменатели, то их сумма и разность находятся по следующим правилам:

+ = ; – = .

Как уже отмечалось, всякая дробь может быть приведена к несократимой дроби с положительным знаменателем. Поэтому общность рассуждений не нарушится, если в дальнейшем всюду будем рассматривать только дроби с положительными знаменателями. Если , то дробь называется

правильной, если же , то неправильной.

Например, дроби являются правильными, а дроби – неправильными.

Теорема 12. Любое рациональное число единственным образом представимо в виде: = q + , где q – целое число, а – правильная несократимая дробь, то есть 0 ≤ с < d, НОД (с; d) = 1.

Доказательство существования. Прежде всего заметим, что считаем b > 0. Далее разделим а с остатком на b и получим а = bq + r, 0 < r < b. Тогда = q + . Пусть НОД(r, b) = k, тогда r = kc, b = kd, где НОД(с, d) = 1.

Сокращая дробь на k, получим = q + , что и дает требуемое представление.

Доказательство единственности. Пусть имеем два указанных представления рационального числа : = q₁ + и = q₂ + , здесь 0 ≤ с₁ < d₁, НОД (с₁; d₁) = 1, 0 ≤ с₂ < d₂, НОД (с₂; d₂) = 1. Тогда а = bq₁ + и а = bq₂ + . Так как а – целое число, bq₁ и bq₂ также целые числа, то и являются целыми числами. Кроме того, в силу единственности деления с остатком, можем записать равенства: bq₁ = bq₂ и = или q

₁ = q₂ и = .

Из последнего равенства можем записать: ; . Поскольку НОД (с₁; d₁) = 1 и НОД (с₂; d₂) = 1, то d₁ d₂ и d₂ d₁. Но d₁ > 0 и d₂ > 0, а значит, деление возможно только при условии d₁ = d₂. Отсюда имеем с₁ = с₂.

Итак, мы установили, что q₁ = q₂, d₁ = d₂, с₁ = с₂, то есть единственность доказана.

Рассмотрим примеры:.

Последнее равенство можно переписать иначе:

Числа вида и записываются, соответственно, и и называются смешанными числами.

Таким образом, любая неправильная дробь может быть единственным образом записана в виде смешанного числа.

Теорема 13. Если дроби и представляют одно и то же рациональное число, то произведения аb и cd имеют один и тот же знак или равны нулю одновременно.

Доказательство. Прежде всего, напомним, что эквивалентность дробей и означает справедливость равенства ad = bc. Рассмотрим два случая.

1. Пусть ab ¹ 0, тогда a ¹ 0. Кроме того, d ¹ 0 как знаменатель дроби. Следовательно, ad ¹ 0, но тогда из равенства ad = b

с следует, что bс ¹ 0, а так как b > 0, то с ¹ 0. Далее рассмотрим произведение (ab)(cd) = (ad) (bс) = (bс)² > 0, из которого следует, что ab и cd имеют одинаковые знаки.

2. Пусть теперь аb = 0, тогда a = 0, поскольку b ¹ 0 как знаменатель дроби. Но, в таком случае, из равенства ad = bс = 0 следует, что bс = 0, а поскольку b ¹ 0, имеем с = 0. Это означает, что cd= 0 и теорема доказана.

Определение 19. Рациональное число (b > 0) называется положительным, если a > 0, и отрицательными, если а < 0.

Поскольку произведение аb является целым числом, то оно удовлетворяет точно одному из условий: аb > 0; аb < 0; аb = 0. Но тогда, согласно теореме 13, для также выполняется точно одно из трех условий:

положительно; отрицательно; – нуль.

Множество положительных рациональных чисел будем обозначать символом Q₊, а множество отрицательных рациональных чисел – символом Q_–.Таким образом, Q = Q_ È {0} È Q₊.

Теорема 14. Сумма и произведение положительных рациональных чисел являются положительными рациональными числами.

Доказательство. Положительность чисел и означает выполнимость условий аb > 0 и cd > 0. Умножая обе части первого неравенства на d² > 0, а второго – на b² > 0 и складывая их, получим abd² + cdb² > 0. Последнее неравенство можно записать в виде (ad + bc)bd > 0, что означает положительность числа + = .

Аналогично из неравенств аb > 0 и cd > 0 следует, что (ab)(cd) = (ac)(bd) > 0. Последнее неравенство означает положительность числа · = , и справедливость теоремы доказана.

Определение 20. Говорят, что рациональное число меньше рационального числа , если существует положительное рациональное число такое, что выполняется равенство + = .

.

Если меньше , то говорят также, что больше и пишут: > .

Символы ≤ и ³ понимаются так же, как и во множестве целых неотрицательных чисел. Из данного определения вытекают важные следствия, выражающие правила сравнения дробей.

Следствие 1. .

Доказательство. Пусть < , тогда, по определению 20, существует положительное рациональное число такое, что выполняется равенство + = . По правилу сложения дробей , откуда следует, что and+bmd = bnc. Обе части последнего равенства разделим на число п ¹ 0. Полученное равенство ad + bd · = bc означает, что ad < bс, так как bd · > 0.

Справедливость обратного утверждения вытекает из того, что все преобразования, приведенные в первой части доказательства, выполнимы в обратном порядке. Таким образом, справедливость следствия можно считать доказанной.

Следствие 2. Если n Î N, то ,

то есть из двух дробей с одинаковыми положительна знаменателями меньше та, у которой меньше числитель.

Справедливость этого утверждения легко доказать, если учесть, что дроби всегда можно привести к общему знаменателю. А значит, общность не нарушится, если будем считать, что из неравенства следует существование положительного рационального числа , такого, что + = . Далее, по правилу сложения дробей, можем записать равенство . Откуда, учитывая определение равенства дробей, имеем а + т = b. Так как m > 0, то из последнего равенства следует, что а < b.

Аналогично доказывается справедливость обратного утверждения.

Определение 21. Рациональное число называется противоположным рациональному числу , если выполняется равенство + = 0.

Число, противоположное числу , будем обозначать – .

Аналогично определению 8 модуля целого числа можно сформулировать определение модуля рационального числа.

Теорема 15. Для любых , Î Q имеет место точно одно из трех соотношений: < ; = ; <.

Доказательство. Рассмотрим разность – . Она, как известно из теоремы 10, является числом рациональным и имеет вид . Согласно определению 19, рациональное число может быть числом положительным, равным нулю или отрицательным. По определению разности (17), можем записать равенство = + , из которого следуют 3 случая:

1. Если > 0, то, по определению 20, < .

2. Если = 0, то, по правилу сложения с нулем, = .

3. Если < 0, то рациональное число – > 0 или > 0. Далее рассмотрим разность – . Она выражается рациональным числом . Пользуясь определением разности, можем также записать равенство = + , из которого следует, что < , и справедливость теоремы доказана.

Теорема 16. Бинарное отношение «меньше» (больше) на множестве Q обладает свойством транзитивности:

.

Доказательство. Пользуясь определением 20 отношения «меньше», можем записать:

;

.

Из двух последних равенств имеем:

, или .

Поскольку , то, по определению отношения «меньше», можем записать, что < , и транзитивность доказана.

Аналогично можно доказать транзитивность отношения «больше».

Таким образом, рассмотренные отношения «меньше» и «больше» на множестве рациональных чисел Q обладают свойствами асимметричности, транзитивности и связности, а значит, являются отношениями строгого линейного порядка.

Итак, множество рациональных чисел Q является линейно упорядоченным.

Теорема 17. Между двумя различными числами из множества Q заключено бесконечно много чисел того же множества.

Доказательство. Рассмотрим два произвольно выбранных рациональных числа. Не нарушая общности рассуждений, представим эти числа дробями и , имеющими общий знаменатель. Для определенности положим, что < . Из последнего неравенства следует, что а < b. Рассмотрим рациональное число, представляемое дробью . Так как а < b, то 2а < а + b < 2b, a поскольку п > 0, можем записать , или .

Итак, мы показали, что между любыми двумя числами из множества Q заключено хотя бы одно число, также принадлежащее множеству Q.

Далее, рассматривая числа и , можно указать хотя бы одно рациональное число, заключенное между ними. Аналогично для чисел и . Продолжая описанный процесс, мы найдем между числами и бесконечно много различных чисел из множества Q.

Теорема 17 выражает свойство, называемое плотностью.

Теорема 18. Для любых двух рациональных чисел > 0 и у = найдется натуральное число п такое, что выполняется неравенство пх > у.

Доказательство. Рассмотрим два случая.

1. Если > , то достаточно взять п = 1, так как 1 · = > .

2. Если же 0 < ≤ , то по следствию 1 из определения 20 0 < ad ≤ bc. Во множестве целых чисел выполняется свойство Архимеда, то есть для положительных целых чисел ad и bс найдется натуральное число n такое, что nad > bc. Из последнего неравенства следует: n · = > . Теорема доказана.

Свойство множества рациональных чисел, выраженное теоремой 18, называется свойством Архимеда.

Таким образом установлено, что множество Q рациональных чисел обладает следующими свойствами: оно бесконечное, линейно упорядоченное, плотное, в нем нет наибольшего и наименьшего чисел и выполняется свойство Архимеда.

Кроме того, множество рациональных чисел Q образует числовое поле относительно операций сложения и умножения.

5. Рассмотрим прямую l и точку О на ней. Выберем отрезок е = ОА в качестве единицы измерения. Прямая l разбивается точкой О на два луча: положительный (правый) – тот, на котором находится точка А, и отрицательный (левый). Рациональному числу х = (n Î N) поставим в соответствие точку М = M (x) на прямой l по следующему правилу.

Разбиваем единичный отрезок е = ОА на n равных частей. Пусть e₁ = ОВ – одна из этих частей, так что е = пе₁. Последнее равенство будем также записывать в виде: .

O e₁B A M

e x

Рис. 4

Если m > 0, то откладываем отрезок e₁ от точки О вправо m раз. В результате получим точку М на положительном луче (рис. 4).

Если же m < 0 , то откладываем отрезок e₁ от точки О влево |m| раз. Точка М в этом случае будет лежать на отрицательном луче.

Найденную таким образом точку М поставим в соответствие числу х = . При этом число х = называем координатой точки М.

Отрезок ОМ будем считать направленным, то есть точка О считается началом этого отрезка, а точка М – его концом.

Два направленных отрезка ОМ и ОР называются равными (пишут ОМ = ОР) тогда и только тогда, когда равны их длины и совпадают направления. Учитывая это соглашение, можем записать: ОМ = m e₁. А поскольку e₁ = , то окончательно имеем ОМ = е. Последнее равенство надо понимать следующим образом: длина отрезка ОМ равна модулю числа ; отрезок ОМ направлен в ту же сторону, что и отрезок е = ОА, если > 0, и в сторону, противоположную е, если < 0.

Итак, каждому рациональному числу х = поставлена а соответствие точка М = М(х) прямой l. Отметим ряд свойств этого соответствия.

1) Каждому рациональному числу соответствует единственная точка на прямой l. Другими словами, если дробь х = несократима и М = М(х) – соответствующая ей точка, то дроби = , где р Î N, будет отвечать та же самая точка М прямой l. Действительно, пусть М^* – точка, отвечающая числу . Покажем, что точки М и М^* лежат на одном и том же луче прямой l, поскольку числа и имеют один и тот же знак.

Далее, для того чтобы найти точку М^*, соответствующую числу , следует разделить отрезок е на рп равных частей (или, что то же самое, отрезок е₁ = разделить еще на р равных частей) и полученный таким образом отрезок отложить от точки О раз в соответствующем направлении.

Но отрезок ОМ, построенный для дроби , представляет собой сумму отрезков, каждый из которых по длине равен отрезку е₁, а отрезок е₁, в свою очередь, есть сумма р отрезков, равных , а значит ОМ представляет собой сумму отрезков, равных по длине е₂. Так что точки М^* и М совпадают.

2) Различным рациональным числам соответствуют различные точки прямой l.

Рассмотрим два различных рациональных числа, представленных дробями х₁ = и х₂ = , где b > 0, d > 0. Поскольку ¹ , то ad ¹ bс. Покажем, что соответствующие им точки М₁ = М(х₁) и М₂ = М(х₂) на прямой l также различны.

Доказательство проведем методом от противного. Предположим, что М(х₁) = М(х₂) = М. Поскольку х₁ = – координата точки М, то, разбив единичный отрезок е на b равных частей, получим отрезок е₁ такой, что е = bе₁ и ОМ = aе₁. Аналогично, поскольку – координата той же самой точки М, найдем отрезок е₂, такой, что е = d е₂ и ОМ = се₂. Из равенств ОМ = ае₁ и ОМ = се₂ имеем: ае₁ = се₂. Умножая последнее равенство на bd ¹ 0, получим ad(bе₁) = cb(dе₂). Откуда, учитывая, что е = bе₁ и е = de₂, находим ade = cbe, что влечет за собой равенство ad = bс, а значит, = . Пришли к противоречию с условием ¹ . Требуемое доказано.

3) Целому числу k =отвечает та же самая точка М Î l, которая была поставлена ему в соответствие.

Действительно, поскольку знаменатель дроби равен единице, то откладываем единичный отрезок е целиком (не деля его на части) от раз от точки О вправо, если k > 0 , и влево, если k < 0. В результате получаем точку М, координатой которой будет число k.

Докажите или опровергните, что если r рационально и s рационально, то r + s должно быть рациональным и q не равно нулю. Все натуральные числа, целые числа, целые числа, дроби целых чисел и десятичные дроби (завершающие десятичные дроби и повторяющиеся десятичные дроби) являются подмножествами рациональных чисел. Иррациональное число определяется как число, которое не может быть выражено в виде дробей. Слово «рациональный» образовано от слова «рацио». Таким образом, мы можем заключить, что любое число, которое может быть выражено в виде дроби, где числитель является целым числом, а знаменатель является целым числом, отличным от нуля, тогда число называется рациональным числом. Некоторые примеры рациональных чисел: -5/6, -1/2, 0, 1/2, 2/5, 4/2 и т. д.

 

Как определить рациональное число?

Рациональное число может быть определено как любая дробь, имеющая ненулевой знаменатель. Пройдитесь по следующим характеристикам, чтобы определить, является ли число рациональным или нет.

• Если a можно выразить в виде p/q, где p и q — целые числа, а q не равно нулю, то число рационально.
• Все натуральные числа (N), целые числа (W), целые числа (Z), дроби целых чисел и десятичные дроби (конечные десятичные дроби и повторяющиеся десятичные дроби) являются подмножествами рациональных чисел.
• Рациональное число — это завершающееся или не завершающееся и повторяющееся десятичное число. Например, 3,6 или 4,181818 — рациональные числа.
• Если десятичная форма числа не повторяется или не завершается, то число называется иррациональным. Например, √7 равно 2,645751311064591…, что является иррациональным числом, поскольку его значение представляет собой неповторяющуюся десятичную дробь.

 

Рациональные и иррациональные числа

Рациональные числа	Иррациональные числа
Рациональное число — это число, которое может быть выражено в форме p/q, где p и q — целые числа, а q не равно нулю.	Иррациональное число определяется как число, которое не может быть выражено в виде дробей.
Рациональное число – это повторяющееся или завершающееся десятичное число. Например, 3,6 или 4,181818 — рациональные числа.	Если десятичная форма числа не повторяется или не завершается, то число называется иррациональным. Например, √7 — иррациональное число, значение которого равно 2,645751311064591…
Все натуральные числа (N), целые числа (W), целые числа (Z), дроби целых чисел и десятичные дроби (конечные десятичные дроби и повторяющиеся десятичные дроби). ) являются подмножествами рациональных чисел.	Набор иррациональных чисел является подмножеством действительных чисел, но представляет собой отдельный набор. Ни один из других наборов чисел не является подмножеством множества иррациональных чисел.

Докажите или опровергните, что если r рационально и s рационально, то r + s должно быть рациональным.

Решение:

Учитывая, что r и s являются рациональными числами.

Пусть r = a/b и s = m/n, где b, n ≠ 0

Теперь r + s = (a/b) + (m/n)

= (a×n + b× m)/bn

Мы знаем, что b, n ≠ 0. Итак, b × n ≠0.

Так как a, b, m и n являются целыми числами, то a×n и b×m также являются целыми числами.

Здесь (r + s) представлено в виде дроби с ненулевым знаменателем.

Мы знаем, что рациональное число — это число, которое может быть выражено в виде p/q, где p и q — целые числа, а q ≠ 0.

Итак, из определения рационального числа (r + s) является рациональным.

Отсюда доказано.

Решенные примеры для рациональных чисел

Пример 1. Какова десятичная форма рационального числа 6/24?

Решение:

Данное рациональное число 6/24 можно преобразовать в десятичное число, разделив числитель на знаменатель. Итак, разделив 6 на 24, мы получим 0,25. Следовательно, десятичное значение 6/24 равно 0,25.

Пример 2. Является ли √11 рациональным числом?

Решение:

Нет, √11 не рациональное число. Значение √11 равно 3,31662474… Это неповторяющаяся десятичная дробь. Итак, √11 — иррациональное число.

Пример 3: Определите рациональные числа среди следующих чисел: √8, 4/5, √11/3, -2/3, √9, 4,79583152331272…..

Решение:

4

5 Когда рациональное число упрощено, оно должно быть либо конечным, либо неконечным и повторяющимся десятичным числом. Здесь только 4/5, -2/3 и √9(√9 = 3) — рациональные числа среди данных чисел.

Пример 4: Из данных утверждений выберите правильное утверждение о рациональных числах.

а) Всякое ли целое число является рациональным?

б) Является ли «е» рациональным числом?

Решение:

а) Мы знаем, что целые числа являются подмножеством множества рациональных чисел. Итак, каждое целое число является рациональным числом. Итак, это утверждение верно.

b) Значение e равно 2,718281828459045… Это непрерывающееся и неповторяющееся десятичное число. Итак, е — иррациональное число. Следовательно, данное утверждение неверно.

Пример 5. Является ли π рациональным числом?

Решение:

Нет, π не является рациональным числом. Значение π равно 3,141592653589793238… Это непрерывающееся и неповторяющееся десятичное число. Итак, π — иррациональное число.

Часто задаваемые вопросы о рациональных числах

Вопрос 1: Что понимается под рациональным числом? Приведите несколько примеров рациональных чисел.

Ответ:

Рациональное число — это число, которое может быть выражено в виде p/q, где p и q — целые числа, а q не равно нулю. Набор рациональных чисел выражается буквой « Q ». Некоторые примеры рациональных чисел: -5/6, -1/2, 0, 1/2, 2/5, 4/2 и т. д.

Вопрос 2: Что такое иррациональные числа?

Ответ:

Иррациональное число определяется как число, которое не может быть выражено в виде дробей. Набор иррациональных чисел выражается как « Q ». Примерами иррациональных чисел являются √2, √3, √7, π, e и так далее.

Вопрос 3. Чем рациональное число отличается от иррационального?

Ответ:

Рациональное число — это число, которое можно представить в виде p/q, где p и q — целые числа, а q не равно нулю. Иррациональное число определяется как число, которое не может быть выражено в виде дробей. Рациональное число — это конечное десятичное число, а иррациональное число — бесконечное и неповторяющееся. Некоторые примеры рациональных чисел: -5/6, -1/2, 0, 1/2, 2/5, 4/2 и т. д., а примеры иррациональных чисел: √2, √3, π, e и т. д.

Вопрос 4. Является ли 0 рациональным числом?

Ответ:

Да, 0 — рациональное число, поскольку мы выражаем 0 как 0/1, 0/2, 0/3, 0/4 и т. д. Мы знаем, что рациональное число — это число, которое можно выразить в виде p/q, где p и q — целые числа, а q ≠ 0. 0 можно выразить в виде p/q в виде 0/1, где q ≠ 0. Мы можем заключить, что 0 — рациональное число.

Вопрос 5. Каким должен быть знаменатель рационального числа?

Ответ:

Мы знаем, что рациональное число — это число, которое может быть выражено в виде p/q, где p и q — целые числа, а q ≠ 0. Итак, знаменатель рационального числа может быть любым действительным числом, кроме нуля.

Центр изучения дискретной математики

Как нам поступить с , формирующим аргумента (доказательства)?

• Прямые доказательства : чтобы доказать импликацию $p \rightarrow q$, начните с предположения, что $p$ истинно, а затем докажите, что $q$ истинно при этом предположении.
• Косвенное доказательство : Напомним, что $p \rightarrow q \equiv \neg q \rightarrow \neg p$. Следовательно, чтобы доказать $p \rightarrow q$, мы могли бы вместо этого доказать $\neg q \rightarrow \neg p$, используя прямое доказательство: предположим $\neg q$ и докажем $\neg p$.
  • Докажите, что если $3n + 2$ нечетно, то $n$ нечетно.

    Вместо этого мы докажем, что если $n$ четно, то $3n + 2$ четно. Предположим, что $n$ четно; тогда $n = 2k$ для некоторого целого числа $k$. Таким образом, $3n + 2 = 3(2k) + 2 = 6k + 2 = 2(3k + 1)$, которое имеет форму $2k’$ для целого числа $k’$ и поэтому является четным.

  • Докажите, что сумма двух рациональных чисел рациональна.

    Попытаемся доказать это напрямую: если $r$ и $s$ — рациональные числа, то $r + s$ — рациональное число. Предположим, что $r$ и $s$ — рациональные числа. Тогда $r = a/b$ и $s = c/d$, где $a,b,c,d \in \mathbb{Z}$ и $b,d \neq 0$ по определению рациональных чисел. Теперь $r + s = (ad + bc)/bd$. Поскольку $a,b,c,d \in \mathbb{Z}$, $ad + bc$ и $bd$ оба являются целыми числами. Так как $b,d \neq 0$, то $bd \neq 0$. Следовательно, $r + s$ рационально. Прямое доказательство удалось! 92$ даже. Косвенное доказательство сработало!

• Бессмысленные/тривиальные доказательства : При попытке доказать, что $p \rightarrow q$ и $p$ ложны, утверждение следует автоматически.
• Доказательство от противного : Предположим, мы хотим доказать предложение $p$. Если вместо этого мы можем показать, что $\neg p \rightarrow F$ (то есть $\neg p$ приводит к противоречию), то $\neg p$ должно быть ложным. Таким образом, $p$ истинно. Заметим, что если мы хотим доказать $p \rightarrow q$ от противного, мы предполагаем $\neg(p \rightarrow q) \equiv \neg(\neg p \vee q) \equiv p \wedge \neg q$. 92$ четно, а значит, $b$ четно. Следовательно, и $a$, и $b$ четны, поэтому у них есть общий множитель $2$. Это противоречит предположению, что $a$ и $b$ не имеют общего делителя, поэтому наше предположение о рациональности $\sqrt{2}$ должно быть неверным. Следовательно, $\sqrt{2}$ иррационально.

Доказательство случаями : Чтобы доказать утверждение вида $(p_1 \vee p_2 \vee p_3 \vee \cdots) \rightarrow q$, мы можем вместо этого доказать $(p_1 \rightarrow q) \wedge (p_2 \rightarrow q) \wedge (p_3 \rightarrow q) \wedge \cdots$, так как логически эквивалентно исходному предложению.

• Докажите, что если $x$ и $y$ — вещественные числа, то $|xy| = |х||у|$.

  Мы можем рассмотреть следующие случаи:

  1. $x \ge 0$ и $y \ge 0$. Тогда $|ху| = xy = |x||y|$, поэтому утверждение верно.
  2. $x \ge 0$ и $y \lt 0$. Тогда $|у| = -y \gt 0$, поэтому $|xy| = x(-y) = |x||y|$, поэтому утверждение верно.
  3. $x \lt 0$ и $y \ge 0$. Тогда $|х| = -x \gt 0$, поэтому $|xy| = (-x)y = |x||y|$, поэтому утверждение верно.
  4. $x \lt 0$ и $y \lt 0$. Тогда $|х| = -x \gt 0$ и $|y| = -y \gt 0$, поэтому $|xy| = (-x)(-y) = |x||y|$, поэтому утверждение верно.

  Обратите внимание, что эти четыре случая охватывают все возможные варианты для $x$ и $y$. Поскольку утверждение выполняется в любом случае, оно должно быть верным для всех действительных чисел.

Доказательства эквивалентности : Чтобы доказать бикондиционал $p \leftrightarrow q$, докажите $(p \rightarrow q) \wedge (q \rightarrow p)$. Фраза «тогда и только тогда» указывает на то, что потребуется доказательство эквивалентности; распространенной ошибкой является доказательство $p \rightarrow q$, но не $q \rightarrow p$. 92)$, который имеет вид $2k’$ и поэтому является четным.

Доказательства существования : Чтобы доказать существование чего-либо, нужно доказать предложение $\exists x\;{P(x)}$. Такие доказательства могут быть либо конструктивными , когда находится $a$ такое, что $P(a)$ истинно, либо неконструктивными , когда мы доказываем $\exists x\;{P(x)}$ без нахождения $a$ такого, что $P(a)$ истинно.

• Докажите, что существует натуральное число, которое можно представить в виде суммы кубов двумя разными способами. 9{\sqrt{2}}$ и $y = \sqrt{2}$ удовлетворяют требованиям утверждения. Это пример неконструктивного доказательства существования, потому что мы не знаем, какая из этих пар обладает желаемым свойством, а только одна из них.

Доказательства уникальности : Чтобы доказать, что объект уникален, мы должны сначала доказать, что он существует. Предположим, что объект $x$. Чтобы показать, что оно уникально, мы затем доказываем, что если $y \neq x$, то $y$ не обладает этим свойством.

• Докажите, что если $p$ — целое число, то существует единственное целое число $q$ такое, что $p + q = 0$.

  Чтобы показать существование, положим $q = -p$ и заметим, что $p + q = p + (-p) = 0$. Теперь мы должны показать уникальность; мы делаем это, используя противоречие. Предположим, что $p + q = 0$ и $p + r = 0$ с $q \neq r$. Тогда $p + r = p + q$, а значит, $q = r$, противоречие.

Контрпримеры : Предыдущие методы доказательства показали, как доказать истинность утверждения. Чтобы доказать, что утверждение вида $\forall x\;P(x)$ ложно, нам нужно найти только одно $a$ такое, что $P(a)$ ложно. Такой $a$ называется контрпример .

• Покажите, что утверждение «каждое натуральное число есть сумма квадратов трех целых чисел» неверно.

  Нам просто нужно найти целое число, где это неверно. Для этого заметьте, что ясно, что три квадрата должны быть меньше, чем число. Рассмотрим целое число $7$; квадраты меньше $7$ равны $0$, $1$ и $4$. Мы можем исчерпывающе перепробовать все комбинации из трех этих квадратов. Нетрудно заметить, что никакая комбинация из трех этих чисел не дает 7$, поскольку у нас есть 4+1+1 = 6$ и 4+4 = 8$, и нет возможности прибавить или вычесть единицу. с любого из этих номеров. Следовательно, $7$ является контрпримером. 93+35$ нечетно. Следовательно, $x$ должно быть четным.

• Если $x$ рационально, то $1/x$ рационально.

  Это пример, когда вы должны обратить пристальное внимание на вселенную дискурса (в данном случае на рациональные числа). Обратите внимание, что $x=0$ — рациональное число, но $1/x$ не определено (и, следовательно, не является рациональным числом).

  Если ограничить $x$ ненулевыми рациональными числами, то верно утверждение: если $x$ рационально, то $x=a/b$ для некоторых целых чисел $a \neq 0$ и $b \neq 0 $, поэтому $1/x = b/a$ — рациональное число.

• Между любыми двумя рациональными числами находится рациональное число.

  Предположим, у нас есть два рациональных числа $x$ и $y$. Предположим, что $x \lt y$ (если это не так, просто поменяйте местами $x$ и $y$). Так как $x$ и $y$ рациональны, мы имеем $x = a/b$ и $y = c/d$ для некоторых целых чисел $a,b,c,d$. Нам нужно показать, что существует рациональное число $z$ такое, что $x \lt z \lt y$. Определите $z$ как: $$ z = \ frac {x + y} {2} = \ frac {\ frac {a} {b} + \ frac {c} {d}} {2} = \ frac {\ frac {ad + bc} {bd }}{2} = \frac{ad + bc}{2bd} $$

  Мы представили $z$ как отношение двух целых чисел, поэтому $z$ рационально. Нам еще нужно показать, что $z > x$ и $z \lt y$.

  No related posts.