Косинус угла 40: Косинус 40 равен чему? cos(40) = ?

36Risolvere per ?cos(x)=1/27Risolvere per xsin(x)=-1/28Преобразовать из градусов в радианы2259Risolvere per ?cos(x)=( квадратный корень из 2)/210Risolvere per xcos(x)=( квадратный корень из 3)/211Risolvere per xsin(x)=( квадратный корень из 3)/212Графикg(x)=3/4* корень пятой степени из x 13Найти центр и радиусx^2+y^2=914Преобразовать из градусов в радианы120 град. 2+n-72)=1/(n+9)

План урока «Основное тригонометрическое тождество»

Тема «Основное тригонометрическое тождество» вызывает у школьников недоумение и страх. 9 из 10 моих учеников во время подготовки к ОГЭ говорили о том, что тема трудная. Этот план урока поможет преподавателям математики зайти в сложную тему с уже известных и сделать синусы и косинусы следствием из знаний по темам «Теорема Пифагора» и «Подобие треугольников». В статье — 13 заданий для практики во время занятия и д/з.

Содержание:

• Цели урока
• Разминка
• Подводка к теме
• Определения
• Практическая часть
• Первое доказательство
• Практическая часть
• Основное тригонометрическое тождество
• Вывод новых формул
• Итоги урока
• Домашнее задание

Цели урока

1. связать стороны и углы в прямоугольном треугольнике;
2. изучить понятия синуса, косинуса, тангенса и котангенса;
3. научиться применять их на практике;
4. отработать навыки доказательств и вывода формул.

Разминка

Вспомните со школьником основные Пифагоровы тройки.

1. В прямоугольном треугольнике катеты равны 3 и 4. Чему равна гипотенуза?
2. В прямоугольном треугольнике катет равен 5, а гипотенуза — 13. Найдите второй катет.
3. В прямоугольном треугольнике катет равен 40, а гипотенуза — 41. Найдите второй катет.

В задании 2 и 3 используйте формулу разности квадратов, чтобы без сложных вычислений найти неизвестные элементы треугольников.

Подводка к теме

Перед изучением новой темы «Основное тригонометрическое тождество» актуализируйте знания по теме-предшественнику. Чтобы ввести тригонометрические функции, вспомните с учеником подобие треугольников.

Этапы подготовки:

Шаг 1. Рассмотрите пример двух подобных прямоугольных треугольников.

Шаг 2. Вспомните соотношения между сторонами.

Шаг 3. Докажите, что для подобных треугольников отношения соответствующих сторон равны.

Шаг 4. Обсудите с ребенком следующее: если изменить величину острого угла в прямоугольном треугольнике, изменятся длины сторон и соотношения между ними.

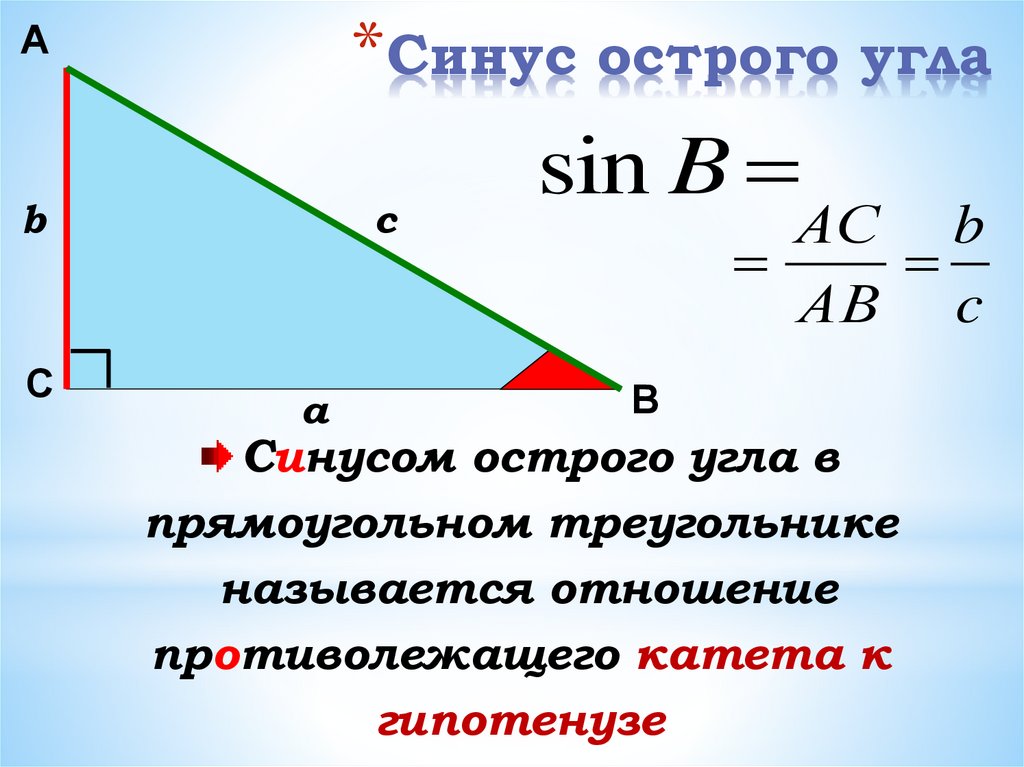
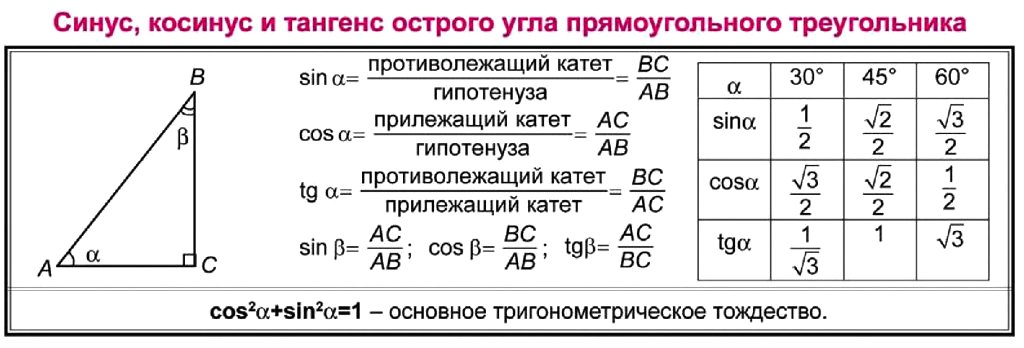
Определения

Соотношения из пункта выше требуют новых обозначений. Здесь на сцену и выходят синусы, косинусы, тангенсы и котангенсы, которые встают на место вопросов.

Упражнение. Для того же треугольника записать синус, косинус, тангенс и котангенс угла А.

Практическая часть

Задание 1. Найти тригонометрические функции острых углов в треугольниках со сторонами 3, 4, 5 и 6, 8, 10. 

Выводы из задания 1

1. Треугольники подобны. Значения тригонометрических функций совпадут.
2. Синус одного острого угла будет равен косинусу другого.

Задание 2. Найти пары равных функций.

Задание 3. Найти тригонометрические функции острых углов в треугольнике со сторонами 5, 12, 13.

Первое доказательство

Задание 4.

Практическая часть

Задание 5. Найти синус, косинус, тангенс большего острого угла прямоугольного треугольника с катетами 7 см и 24 см.

Основное тригонометрическое тождество

Школьник уже вспомнил, что длины сторон прямоугольного треугольника связаны теоремой Пифагора. Следовательно, тригонометрические функции тоже взаимосвязаны.

Задание 6. Доказать тождества, используя определения тригонометрических функций и теорему Пифагора.

Задание 7. Найти значения выражений.

sin² 40^° + cos² 40^° = …
cos² 89^° + sin² 89^° = …

Разберите вместе с учащимся следующий пример: в прямоугольном треугольнике АВC с острым углом А известно, что sin угла А = 0,8. Необходимо найти cos угла А.

Решение.

sin² угла А + cos² угла А = 1
cos² угла А = 1 − sin² угла А = 1 − 0,64 = …
cos² угла А = …

Задание 8.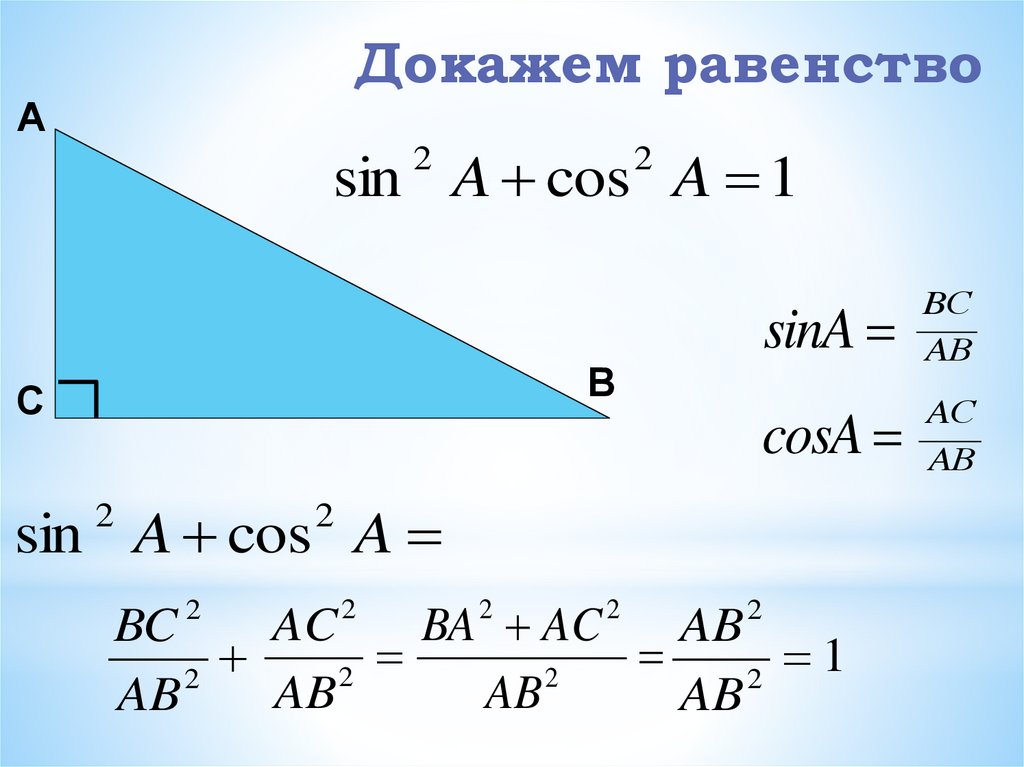 В прямоугольном треугольнике АВC угол С равен 90^°, cos угла А равен 0,96. Нужно найти sin угла А.

Задание 9. Найти котангенс острого угла прямоугольного треугольника, если косинус этого угла равен ³⁄_√10

Задание 10. Гипотенуза прямоугольного треугольника равна 20 см, а косинус одного из острых углов равен 0,8. Нужно найти катеты этого треугольника. Ответ записать в порядке возрастания через точку с запятой.

Вывод новых формул

Задание 11. Зная основное тригонометрическое тождество, совместно с учеником докажите следующую формулу.

Обсудите с учащимся, зачем эта формула нужна.

Задание 12. Найти синус, косинус и котангенс острого угла прямоугольного треугольника, если тангенс этого угла равен 7. В ответе соотнести значения.

Задание 13.

Итоги урока

Во время подведения итогов вспомните цели урока и обсудите с учеником, какие из них удалось достичь.

Примеры итогов, которые может озвучить школьник:

• научился связывать углы и стороны в прямоугольном треугольнике;
• изучил синусы, косинусы, тангенсы и котангенсы;
• сформулировал тригонометрические тождества;
• решил n задач;
• доказали n формул;
• закрепил знания по теореме Пифагора и подобным треугольникам.

Домашнее задание

Задание 1. Найти тригонометрические функции острых углов в треугольнике со сторонами 9, 40, 41. 

Задание 2. 

Задание 3.

Найти АВ, если известно, что в прямоугольном треугольнике АВС угол В = 90°, АС = 28, sin угла С равен ⁴⁄₇

Задание 4.

Задание 5. В прямоугольном треугольнике острые углы А и В. Известно, что sin угла А равен ⁵⁄₁₃

Нужно найти остальные значения.

Надеюсь, что план урока по теме «Основное тригонометрическое тождество» поможет сэкономить преподавателям время и силы, а ученикам преодолеть еще один барьер к успешной сдаче ОГЭ.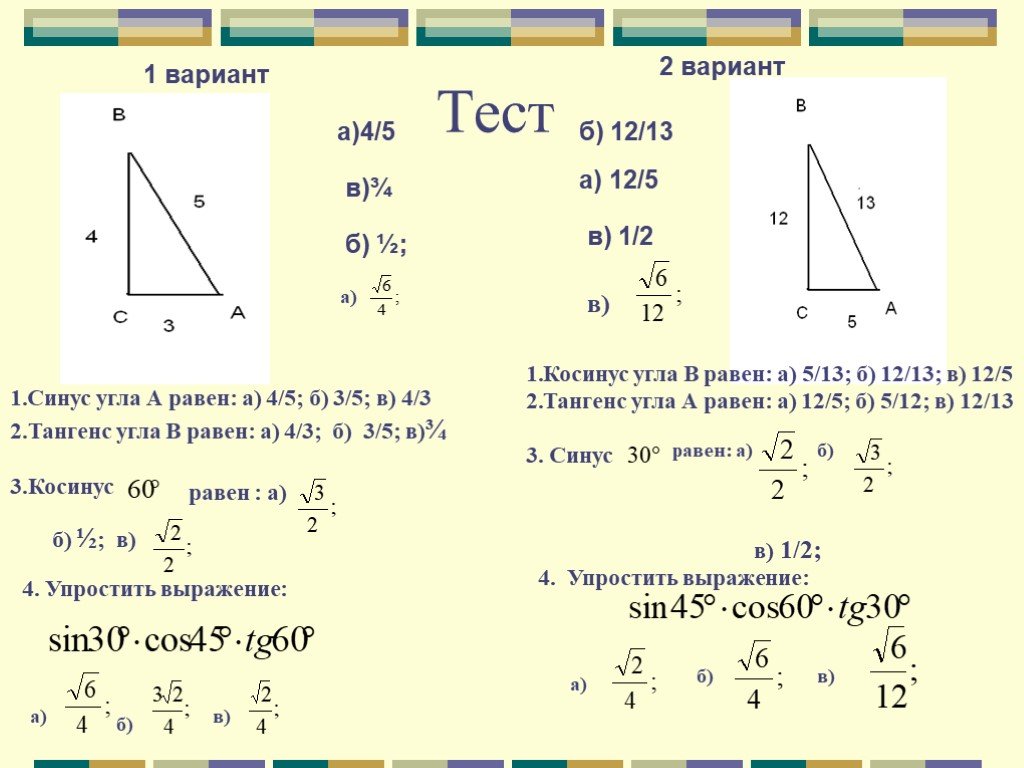 Какие еще темы тяжело даются вашим ученикам, напишите в комментариях!

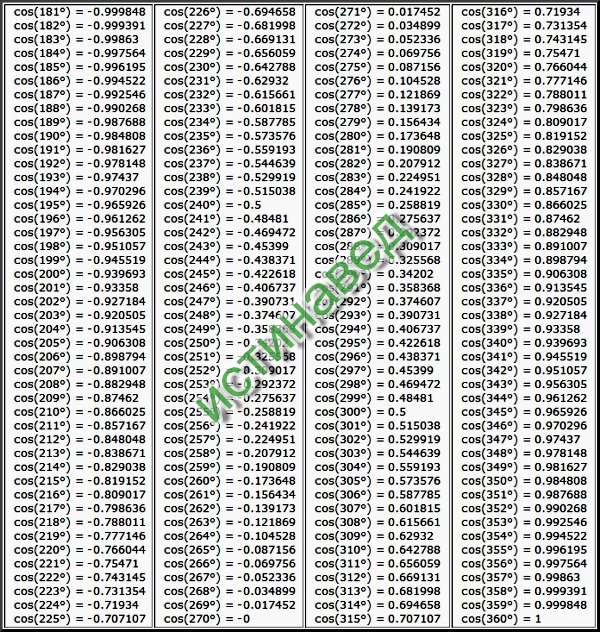
Cos 40 градусов — Найдите значение Cos 40 градусов

LearnPracticeDownload

Значение cos 40 градусов равно 0,7660444. . . . Cos 40 градусов в радианах записывается как cos (40° × π/180°), т. е. cos (2π/9) или cos (0,698131…). В этой статье мы обсудим способы нахождения значения cos 40 градусов на примерах.

• Cos 40°: 0,7660444. . .
• Cos (-40 градусов): 0,7660444. . .
• Cos 40° в радианах: cos (2π/9) или cos (0,6981317 . . .)

Каково значение Cos 40 градусов?

Значение cos 40 градусов в десятичной системе равно 0,766044443. . .. Cos 40 градусов также можно выразить с помощью эквивалента заданного угла (40 градусов) в радианах (0,69813 . . .)

Мы знаем, используя преобразование градусов в радианы, что θ в радианах = θ в градусах × (пи/ 180°)
⇒ 40 градусов = 40° × (π/180°) рад = 2π/9 или 0,6981. . .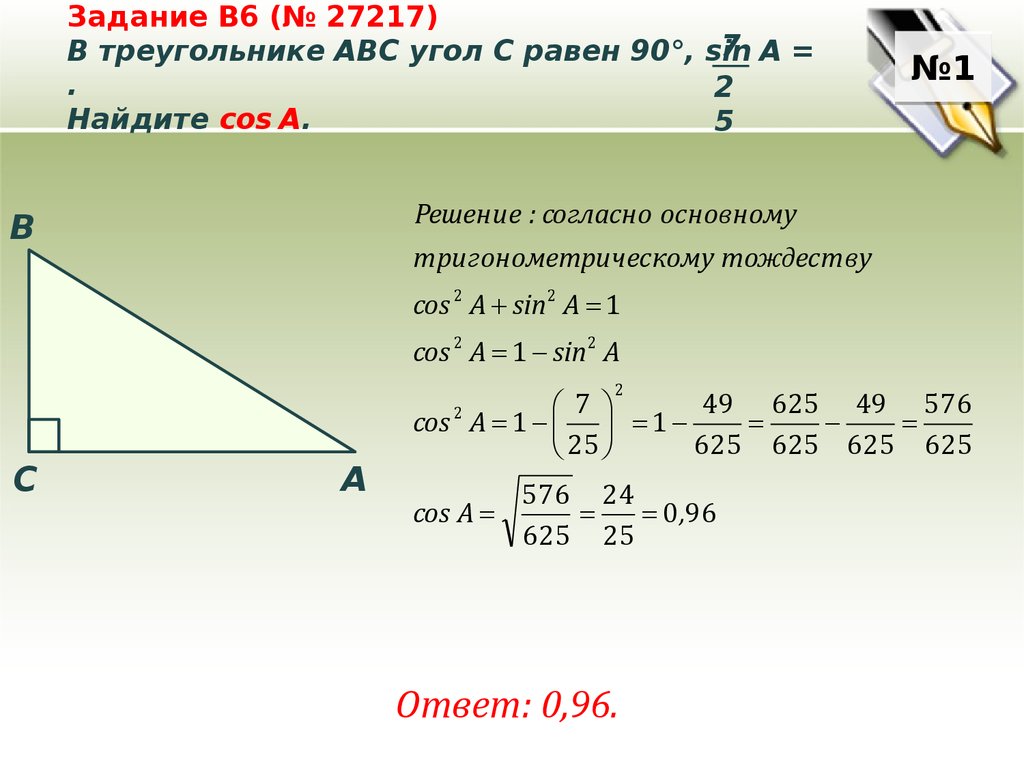
∴ cos 40° = cos (0,6981) = 0,7660444. . .

Объяснение:

Для cos 40 градусов угол 40° лежит между 0° и 90° (первый квадрант). Поскольку функция косинуса положительна в первом квадранте, значение cos 40° = 0,7660444. . .
Поскольку функция косинуса является периодической функцией, мы можем представить cos 40° как cos 40 градусов = cos(40° + n × 360°), n ∈ Z.
⇒ cos 40° = cos 400° = cos 760° и так далее.
Примечание: Поскольку косинус является четной функцией, значение cos(-40°) = cos(40°).

Методы определения значения косинуса 40 градусов

Функция косинуса положительна в 1-м квадранте. Значение cos 40° равно 0,76604. . .. Мы можем найти значение cos 40 градусов по:

• Используя Unit Circle
• Использование тригонометрических функций

Cos 40 градусов с помощью единичной окружности

Чтобы найти значение cos 40 градусов с помощью единичной окружности:

• Поверните ‘r’ против часовой стрелки, чтобы образовать угол 40° с положительной осью x.
• Cos 40 градусов равен координате x (0,766) точки пересечения (0,766, 0,6428) единичной окружности и r.

Следовательно, значение cos 40° = x = 0,766 (приблизительно)

Cos 40° в терминах тригонометрических функций

Используя формулы тригонометрии, мы можем представить cos 40 градусов как:

• ± √(1-sin² (40°))
• ± 1/√(1 + tan²(40°))
• ± кроватка 40°/√(1 + кроватка²(40°))
• ±√(косек²(40°) — 1)/косек 40°
• 1/сек 40°

Примечание: Поскольку 40° лежит в 1-м квадранте, окончательное значение cos 40° будет положительным.

Мы можем использовать тригонометрические тождества для представления cos 40° как

• -cos(180° — 40°) = -cos 140°
• -cos(180° + 40°) = -cos 220°
• sin(90° + 40°) = sin 130°
• sin(90° — 40°) = sin 50°

☛ Также проверьте:

• cos 21 градус
• , потому что 36 градусов
• потому что 2 градуса
• кос 33 градуса
• потому что 245 градусов
• потому что 83 градуса

Примеры использования Cos 40 градусов

1. Пример 1. Найдите значение 2 cos(40°)/3 sin(50°).

   Решение:

   Используя тригонометрические тождества, мы знаем, что cos(40°) = sin(90° — 40°) = sin 50°.
   ⇒ cos(40°) = sin(50°)
   ⇒ Значение 2 cos(40°)/3 sin(50°) = 2/3

2. Пример 2: Упростить: 9 (cos 40°/sin 130°)

   Решение:

   Мы знаем, что cos 40° = sin 130°
   ⇒ 9 cos 40°/sin 130° = 9 (cos 40°/cos 40°)
   = 9(1) = 9

3. Пример 3: Найдите значение cos 40°, если sec 40° равно 1,3054.

   Решение:

   Так как cos 40° = 1/сек 40°
   ⇒ cos 40° = 1/1,3054 = 0,766

перейти к слайдуперейти к слайдуперейти к слайду

 

Готовы увидеть мир глазами математика?

Математика лежит в основе всего, что мы делаем. Наслаждайтесь решением реальных математических задач на живых уроках и станьте экспертом во всем.

Забронируйте бесплатный пробный урок

Часто задаваемые вопросы о Cos 40 Degrees

Что такое Cos 40 Degrees?

Cos 40 градусов — значение тригонометрической функции косинуса для угла, равного 40 градусам. Значение cos 40° составляет 0,766 (приблизительно)

Каково значение Cos 40° в пересчете на Cosec 40°?

Поскольку функция косинуса может быть представлена ​​с помощью функции косеканса, мы можем записать cos 40° как [√(cosec²(40°) — 1)/cosec 40°]. Значение cosec 40° равно 1,55572.

Каково значение Cos 40 градусов по отношению к Cot 40°?

Мы можем представить функцию косинуса в терминах функции котангенса, используя тригонометрические тождества, cos 40° можно записать как cot 40°/√(1 + cot²(40°)). Здесь значение ctg 40° равно 1,19.175.

Как найти косинус 40° с точки зрения других тригонометрических функций?

Используя формулу тригонометрии, значение cos 40° может быть выражено через другие тригонометрические функции следующим образом:

• ± √(1-sin²(40°))
• ± 1/√(1 + tan²(40°))
• ± кроватка 40°/√(1 + кроватка²(40°))
• ± √(косек²(40°) — 1)/косек 40°
• 1/сек 40°

☛ Также проверьте: таблицу тригонометрии

Как найти значение Cos 40 градусов?

Значение cos 40 градусов можно рассчитать, построив угол 40° с осью x и затем найдя координаты соответствующей точки (0,766, 0,6428) на единичной окружности.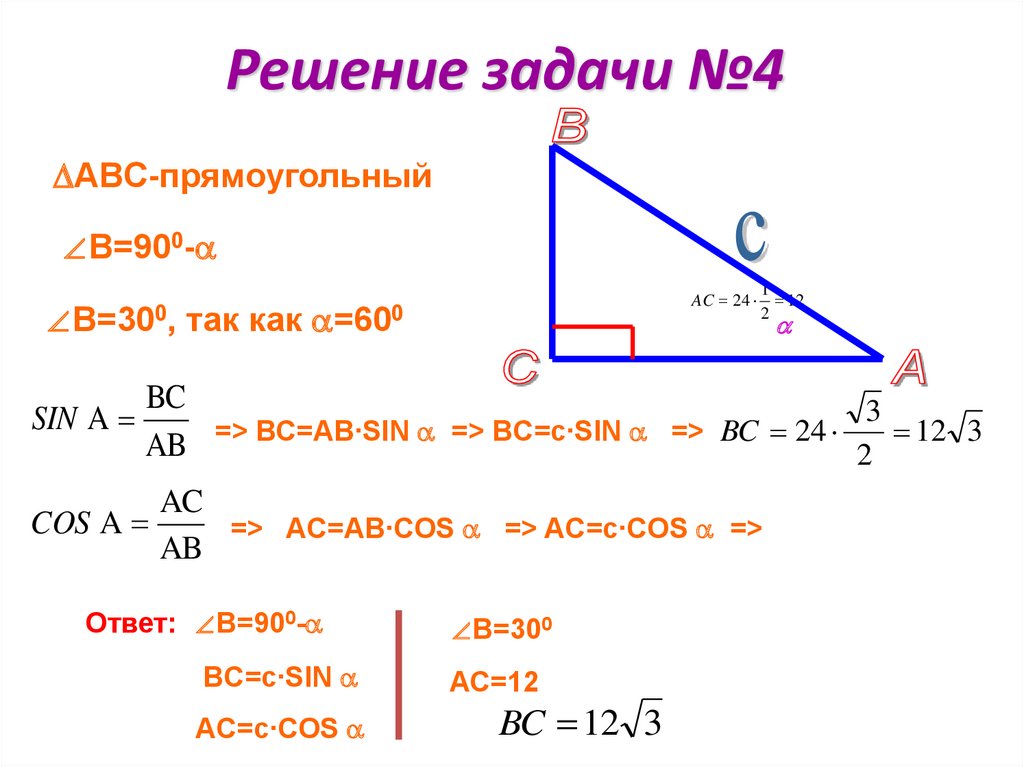 Значение cos 40° равно координате x (0,766). ∴ cos 40° = 0,766.

 

Скачать БЕСПЛАТНЫЕ учебные материалы

Тригонометрия

Рабочие листы по математике и
наглядная программа

Калькулятор — cos(40) — Solumaths

Cos, расчет онлайн

Резюме:

Тригонометрическая функция cos вычисляет cos угла в радианах, градусов или градианов.

cos online

---

Описание:

Калькулятор позволяет использовать большинство из тригонометрических функций , есть возможность вычислить косинус , синус и касательная угла через одноименные функции.

Косинус тригонометрической функции отметил потому что , позволяет вычислить косинус угла онлайн , можно использовать разные угловые единицы: градусы, грады и радианы, которые по умолчанию являются угловыми единицами.

1. Расчет косинуса

Вычисление косинуса угла в радианах

Калькулятор косинуса позволяет через функцию cos вычислить онлайн косинус угла в радианах, вы должны сначала выберите нужную единицу, нажав на кнопку параметров расчетного модуля. После этого можно приступать к расчетам.

Чтобы вычислить косинус онлайн от `pi/6`, введите cos(`pi/6`), после вычисления результат `sqrt(3)/2` возвращается.

Обратите внимание, что функция косинуса способна распознавать некоторые специальные углы и делать расчеты со специальными связанными значениями в точной форме.

Вычислить косинус угла в градусах

Чтобы вычислить косинус угла

в градусах, необходимо сначала выбрать нужную единицу измерения нажав на кнопку модуля расчета параметров. После этого можно приступать к вычислениям.

Чтобы вычислить косинус 90, введите cos(90). возвращает 0.

Вычисление косинуса угла в градусах

Для вычисления косинуса угла в градианах необходимо сначала выбрать нужную единицу измерения нажав на кнопку модуля расчета параметров. После этого можно приступать к вычислениям.

Чтобы вычислить косинус 50, введите cos(50), после вычисления возвращается результат `sqrt(2)/2`.

Обратите внимание, что функция косинуса способна распознавать некоторые специальные углы и выполнять исчисление со специальными ассоциированными точными значениями.

2. Специальные значения косинуса

Косинус допускает некоторые специальные значения, которые калькулятор может определить в точных формах. Вот список специальные значения косинуса

:
co (`pi/3`)/`-1`/«pi` s ) cos (`-3*pi/4`)

cos(`2*pi`)	`1`
cos(`pi`)	`-1`
cos(`pi/2`)	`0`
cos(`pi/4`)	`sqrt(2)
`1/2`
cos(`pi/6`)	`sqrt(3)/2`
cos(`2*pi/3`)	`-1/2`
cos(`3*pi/4`)	`-sqrt(2)/2`
cos(`5*pi/6`)	` -sqrt(3)/2`
cos(`0`)	`1`
cos(`-2*pi`)	`1`
cos(`-pi`)	`-1`
`0`
cos(`-pi/4`)	`sqrt(2)/2`
cos(`-pi/3`)	`1/2`
cos(`-pi/6`)	`sqrt(3)/2`
cos(`-2*pi/3`)	`-1/2`
`-sqrt(2)/2`
cos(`-5*pi/6`)	`-sqrt(3)/2`

3. Основные свойства

`AA x в RR, k в ZZ`,

• `cos(-x)= cos(x)`
• `cos(x+2*k*pi)=cos(x)`
• `cos(pi-x)=-cos(x) `
• `cos(pi+x)=-cos(x)`
• `cos(pi/2-x)=sin(x)`
• `cos(pi/2+x)=-sin(x) )`

Производная косинуса

Производная косинуса равна -sin(x).

Первообразная косинуса

Первообразная косинуса равна sin(x).

Свойства функции косинуса

Функция косинуса является четной функцией для каждого действительного x, `cos(-x)=cos(x)`. Следствием для кривой, представляющей функцию косинуса, является то, что она допускает ось ординат как ось симметрии.

Уравнение с косинусом

Калькулятор имеет решатель, который позволяет решать уравнение с косинусом формы cos(x)=a . Расчеты для получения результата детализированы, поэтому можно будет решать уравнения типа `cos(x)=1/2` или `2*cos(x)=sqrt(2)` с этапами расчета.

Синтаксис:

cos(x), где x — мера угла в градусах, радианах или градах.

---

Примеры:

cos(`0`), возвращает 1

---

Производный косинус:

Чтобы дифференцировать функцию косинуса онлайн, можно использовать калькулятор производной, который позволяет вычислить производную функции косинуса

производная от cos(x) является производной(`cos(x)`)=`-sin(x)`

---

Первообразная косинуса :

Калькулятор первообразной позволяет вычислить первообразную функции косинуса.

Первопроизводная cos(x) есть первопроизводная(`cos(x)`)=`sin(x)`

---

Предел косинуса :

Калькулятор предела позволяет вычислить пределы функции косинуса.

предел cos(x) is limit(`cos(x)`)

---

Обратная функция косинуса :

обратная функция косинуса это функция арккосинуса, отмеченная как arccos.

---

---

Графический косинус:

Графический калькулятор может отображать функцию косинуса в заданном интервале.

---

---

Свойство функции косинуса:

Функция косинуса является четной функцией.

---

Расчет онлайн с косинусом

См. также

Список связанных калькуляторов:

• Арккосинус : arccos. Функция arccos позволяет вычислять арккосинус числа. Функция arccos является обратной функцией функции косинуса.
• Арксинус : арксинус. Функция arcsin позволяет вычислить арксинус числа. Функция arcsin является обратной функцией функции синуса.
• Арктангенс: арктангенс. Функция арктангенса позволяет вычислить арктангенс числа. Функция арктангенса является обратной функцией функции тангенса.
• Тригонометрический калькулятор: simple_trig. Калькулятор, который использует тригонометрическую формулу для упрощения тригонометрического выражения.
• Косинус: cos. Кос-тригонометрическая функция вычисляет косинус угла в радианах, градусов или градианов.
• Косеканс: косеканс Тригонометрическая функция sec позволяет вычислить секанс угла, выраженного в радианах, градусах или градусах.
• Котангенс: котан. Тригонометрическая функция котана для вычисления котана угла в радианах, градусов или градианов.
• Тригонометрическое расширение: expand_trigo.

  No related posts.