Как обозначается площадь: какой буквой или знаком пишется параметр площади в математике
В жизни каждого человека по достижении 7-летнего возраста появляется необходимость обучаться в средней общеобразовательной школе. В этом заведении ученик получает базовые знания и навыки. В рамках учебной программы по математике школьники узнают, как обозначается площадь. Необходимо рассмотреть, какой буквой и единицей измерения необходимо это делать.
Содержание
Общие сведения
Изучение того, как и какой буквой обозначается общая площадь, необходимо начать с определения данного понятия в математике.
Под площадью понимается характеристика, имеющая числовое выражение. Ею описывается геометрическая фигура в двухмерном пространстве.
Объект, по отношению к которому возникает вопрос, как обозначить в письменном выражении площадь, может быть плоским или искривленным.Обозначение площади дает представление о размере и параметрах изучаемой площади.
В отдельных литературных источниках общая площадь встречается под названием квадратуры. Фигура, для которой возможно обозначить площадь, имеет наименование квадрируемой. Геометрические объекты, для которых значение площади в полученном решении оказалось одинаковым, встречаются под названием равновеликих.
Фигура, для которой возможно обозначить площадь, имеет наименование квадрируемой. Геометрические объекты, для которых значение площади в полученном решении оказалось одинаковым, встречаются под названием равновеликих.
Возможность определения площади и обозначения ее буквой появилась благодаря интегральному исчислению в математике. Общее представление о данном понятии было получено в результате формулирования теории меры множества. Постулаты, составляющие данную теорию, являются правдивыми для большинства объектов, изучаемых в геометрии.
Возможность практического измерения данной величины отмечается в результате использования планиметра и специальной палетки.
Важно! Основы геометрии: что это такое биссектриса треугольника
Площадь, обозначение которой становится доступным в результате ее числового выражения, характеризуется следующими параметрами:
- Положительная. В числе ее характеристик отсутствует понятие отрицательного значения.

- Аддитивная. Данный показатель относительно любого геометрического объекта определяется как суммированное значение объектов, образующих изучаемую фигуру при отсутствии внутренних ограничений.
- Инвариантная. Позволяет приравнивать площади фигур, которые в движении переходят друг в друга и полностью совпадают.
- Нормированная. Соответствует правилу, согласно которому 1 составляет площадь единичного квадрата.
- Монотонная. Параметр площади отдельной части геометрического объекта не превышает общую площадь всей изучаемой фигуры.
Знак площади, используемый в математике, появился в результате присвоения данного параметра для многоугольных геометрических объектов. Впоследствии перечень фигур, в отношении к площади которых использовалось обозначение буквой, увеличился на группу квадрируемых объектов.
Обратите внимание, к категории квадрируемой относится объект, поддающийся вписыванию в пределы многоугольника. Также достоверной является способность заключить многоугольник в данный квадрируемый объект.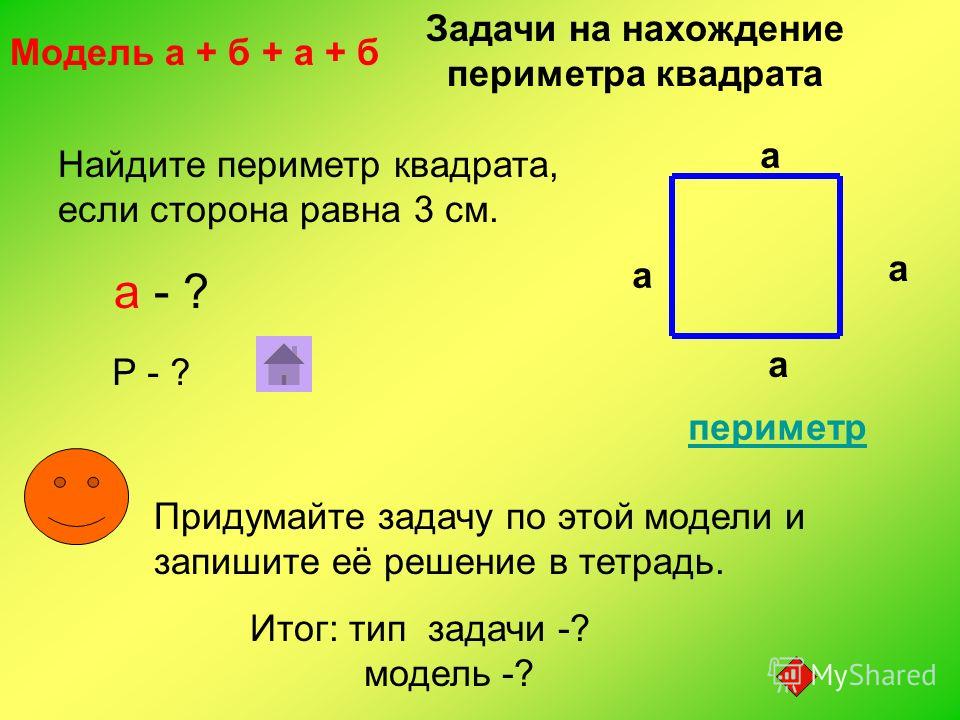
Познавательно! Как найти и чему будет равна длина окружности
Общее понимание категории позволяет ее трактовать в качестве числовой характеристики. При этом этот признак используется по отношению только к поверхности двухмерной, находящейся в пространстве трехмерном.
Для данного показателя присуща система измерения. Основными единицами, дающими представление о величине геометрического объекта, являются сантиметры, миллиметры, дециметры, метры, километры. В ряде источников встречается упоминание проведенных измерений в арах, гектарах. Отличительная особенность, свойственная для рассматриваемого показателя, возведение единиц измерения в квадрат.
Важно! Урок геометрии: как найти по формуле периметр треугольника
Варианты обозначения
Понятие используется не только в математике. Оно актуально и для физики.
Оно актуально и для физики.
В связи с разносторонностью применения возникает вопрос, какой буквой обозначается площадь.
В зависимости от дисциплины, в рамках которой применяется изучаемое понятие, становится очевидным ответ, какой буквой алфавита обозначают данную величину. Проститутки в Екатеринбурге intim66.ru
В таких науках, как физика и математика, используется знак латинского алфавита S. Данная буква имеет произношение {эс}.
Обратите внимание! Знаком S обозначают площадь таких фигур, как квадрат, треугольник, ромб, прямоугольник, круг.
Среди вопросов, занимающих умы студентов высших учебных заведений, присутствует тема: как обозначить данную величину нескольких геометрических объектов. В данном случае в письменном варианте применяются нижние индексы. Среди значений, используемых в индексной системе обозначений, присутствуют числа.
Примером выступает обозначение S1, S2, S3. Также считается допустимым применение сокращенных наименований геометрических объектов, по отношению к которым производится числовое измерение.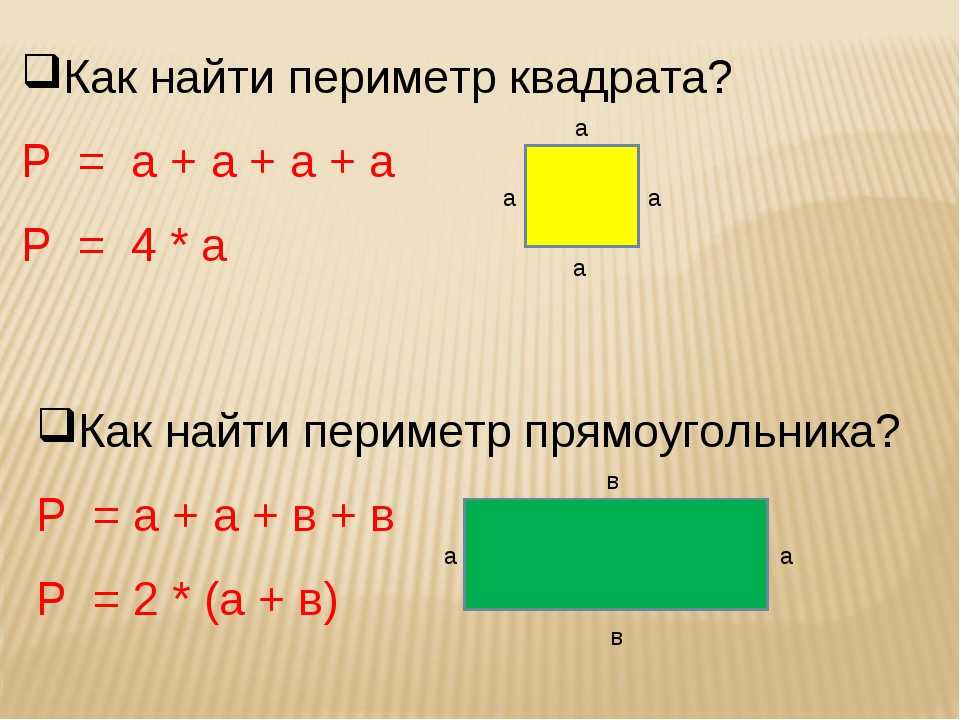 Так, при изучении треугольников для сокращенного названия используются наименования вершин, обозначенные латинскими буквами. В качестве примера могут быть SAOB, SCLE, SOME.
Так, при изучении треугольников для сокращенного названия используются наименования вершин, обозначенные латинскими буквами. В качестве примера могут быть SAOB, SCLE, SOME.
Интересно! Что значит вертикально и как выглядит вертикальная линия
Актуальным для учащихся является вопрос, как пишется в физике площадь. Следует отметить, что данным понятием характеризуется поперечное сечение. Считается допустимым использовать для уточненного обозначения нижний индекс. Сохраняется возможность написания простых чисел в индексной системе.
Вопрос, как пишется в строительной механике и сопромате данная величина, заставляет задуматься студентов. В данных дисциплинах под буквой латинского алфавита S подразумевается обозначение статического момента. Так выражается площадь по отношению к рассматриваемой оси. В качестве символа, обозначающего данный показатель, используется буква латинского алфавита A или F.
В качестве символа, обозначающего данный показатель, используется буква латинского алфавита A или F.
Полезное видео
Подведем итоги
Пространственное представление об изучаемом геометрическом объекте становится возможным благодаря площади. Обозначение данного показателя разнится в зависимости от выбранной дисциплины.
Вычисляем площадь квадрата: по стороне, диагонале, периметру
Площадь квадрата – базовое понятие, благодаря которому можно без проблем рассчитать расход материалов для ремонта, высчитать верные габариты мебели при замерах помещения, понять, сколько нужно удобрения и семян для высадки важных культур на огромном поле.
Приведенными формулами площади квадрата пользуются и строители, и мебельные производители, и представители сельского хозяйства.
Что такое квадрат?
Квадрат – правильный прямоугольник с равными сторонами. Каждый угол фигуры равен 90⁰. Квадрат относится к простым геометрическим фигурам, расположенным на плоскости. Найти площадь квадрата можно несколькими способами вычислений: по диагонали, по стороне, по периметру.
Каждый угол фигуры равен 90⁰. Квадрат относится к простым геометрическим фигурам, расположенным на плоскости. Найти площадь квадрата можно несколькими способами вычислений: по диагонали, по стороне, по периметру.
Формулы площади, примеры расчетов
Площадь простой фигуры – положительная величина, обладающая перечисленными ниже свойствами:
- Равные геометрические фигуры обладают равными площадями.
- В случае, если простая фигура разделена на несколько частей, ее общая площадь будет всегда равна сумме площадей всех элементов.
- Площадь квадрата всегда равна единице, если его сторона соответствует единице измерения.
По стороне
В геометрии площадь всегда обозначается как S, а маленькие латинские буквы (например, а и b) – это стороны простой фигуры.
В основе вычисления площади любого прямоугольника по стороне лежит простая формула:
Отсюда следует утверждение, что площадь квадрата равна квадрату его стороны.
Пример 1: Дан квадрат, сторона которого равна 5 см. Чему равна площадь?
Решение: S = 5² = 25 см
Пример 2: Сторона фигуры 3 см. Найдите площадь.
Решение: S = 3² = 9 см
По диагонали
Еще один вариант найти площадь – это произвести вычисления относительно диагонали фигуры (d). Правда, для этого нужно сперва найти длину самой диагонали. Известно, что диагональ делит квадрат на два равнобедренных треугольника. А значит, вычисления можно провести по известной теореме Пифагора, где катетами будут выступать стороны квадрата, а гипотенузой – собственно диагональ.
Расчет площади по диагонали производится по принципу: площадь квадрата равна квадрату длины диагонали (вычисленной по теореме Пифагора) и поделенному на два.
Пример: Дан квадрат, диагональ которого составляет 10 см. Как вычислить площадь?
Решение: Согласно формуле, приведенной выше, вычисления производятся так: S = 10²/2 = 100/2 = 50 cм²
По периметру
Периметр – сумма всех длин сторон квадрата. Обозначается периметр латинской буквой Р. Беря во внимание определение квадрата, получаем универсальную формулу расчета периметра для равностороннего четырехугольника: Р = 4а . То есть, периметр квадрата равен длине стороны, помноженной на четыре.
Обозначается периметр латинской буквой Р. Беря во внимание определение квадрата, получаем универсальную формулу расчета периметра для равностороннего четырехугольника: Р = 4а . То есть, периметр квадрата равен длине стороны, помноженной на четыре.
Вычисления площади квадрата относительно суммы всех сторон необходимо в том случае, если в задаче задано только значение периметра. Зная формулу вычисления периметра, очень легко найти площадь.
Если Р = 4а , то а = Р/4 . Далее уже нужно использовать формулу расчета площади по стороне.
Пример: Пусть будет дан квадрат с периметром 100 мм. Какова площадь?
Решение: Сторона квадрата будет равна 100/4 = 25 мм. Ну, а площадь квадрата дальше вычисляется по формуле, где площадь квадрата равна квадрату сторон. То есть, S = 25² = 625 мм²
Площадь квадрата вписанного в окружность
Этот вариант используется как следствие формулы, полученной ранее (расчет по диагонали). Согласно математическим данным, диаметр круга как раз и будет равен диагонали квадрата. Поэтому, чтобы оперативно рассчитать площадь равностороннего четырехугольника, достаточно будет знать диаметр круга. А далее используется уже известная формула: S = d²/2
Поэтому, чтобы оперативно рассчитать площадь равностороннего четырехугольника, достаточно будет знать диаметр круга. А далее используется уже известная формула: S = d²/2
Типовая задача: например, дана окружность с диагональю 8 см и в нее вписан квадрат. Какая площадь четырехугольника?
Видео урок
Формулы площади, прямоугольник, квадрат, треугольник и круг
Площадь — это пространство, занимаемое внутри любой фигуры. Это общая поверхность, покрытая периметром фигуры. Измеряется в квадратных единицах. Обычно он рассчитывается путем умножения основания фигуры на ее длину. Например, площадь комнаты равна произведению ее длины на ширину.
В этой статье мы узнаем о некоторых фигурах и их площадях, таких как площадь квадрата, площадь прямоугольника, площадь круга, площадь треугольника и другие.
Что такое площадь?
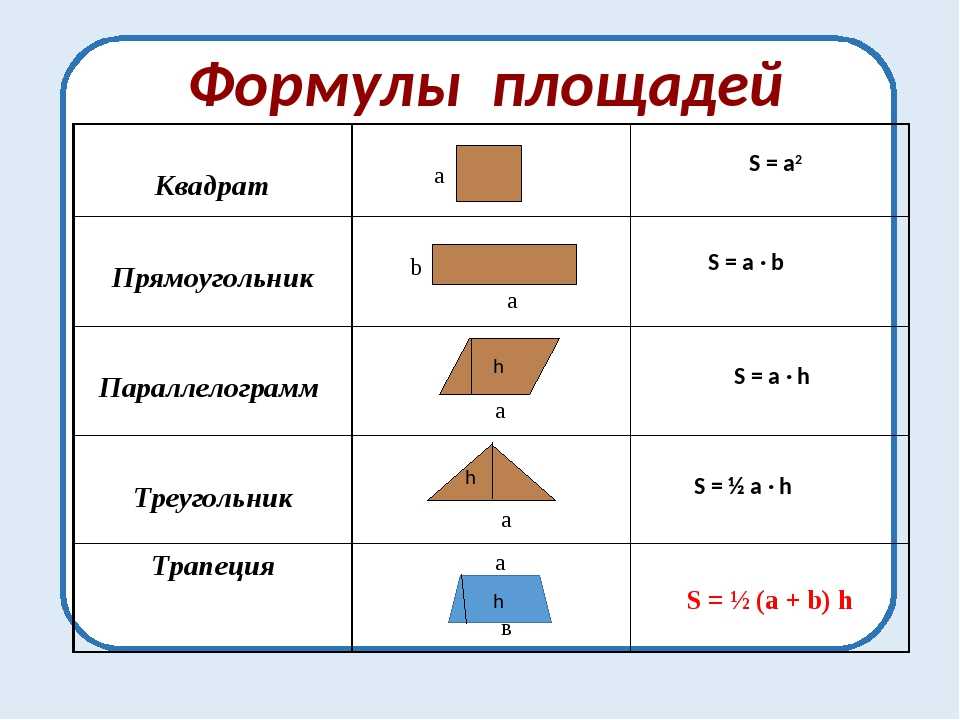
Площадь любой фигуры определяется как размер фигуры или поверхности или пространства, занимаемого фигурой в замкнутой области. Он рассчитывается для любых цифр и выражается в таких единицах, как м 2 , см 2 и т. д. Единицей площади всегда является квадратная единица. Обозначается буквой А. На приведенной ниже схеме показаны примеры геометрических фигур вместе с их площадью,
Площадь любой фигуры измеряется в единицах 2 или квадратных единиц. В то время как периметр фигуры измеряется в единицах, т. е. м, см и т. д.
Площадь фигуры используется для различных целей.
- Используется для расчета площади плитки, используемой при строительстве зданий.
- Используется для определения площади стен и пола.
- Используется в промышленности для производственных целей.
Прямоугольник
Прямоугольник – это двумерная фигура, которая является четырехугольником, т. е. имеет четыре стороны, противоположные стороны параллельны и равны. Все углы прямоугольника равны и их градус равен 9.0 градусов. Диагонали прямоугольника равны и являются перпендикулярными биссектрисами друг к другу.
е. имеет четыре стороны, противоположные стороны параллельны и равны. Все углы прямоугольника равны и их градус равен 9.0 градусов. Диагонали прямоугольника равны и являются перпендикулярными биссектрисами друг к другу.
**изображение
Формула прямоугольника:Формула для вычисления площади и периметра квадрата:
- Площадь прямоугольника (A) = l×b квадратных единиц
- Периметр Прямоугольник (P) = 2(l+b) единиц
, где
l длина прямоугольника
b ширина прямоугольника
Также проверьте:
Площадь прямоугольника
Квадрат
Квадрат — это двумерная фигура, которая является четырехугольником, т.е. имеет четыре стороны, его противоположные стороны параллельны, и все четыре стороны на площади равны. Все углы квадрата равны и их градусная мера равна 90 градусам. Диагонали квадрата равны и являются перпендикулярными биссектрисами друг к другу.
Диагонали квадрата равны и являются перпендикулярными биссектрисами друг к другу.
Площадь квадрата
Формула квадрата:Формула для вычисления площади и периметра квадрата: Квадрат(П) = 4а ед.
, где a — сторона квадрата.
Также проверьте:
Площадь квадрата
Треугольник
Треугольник — это простейший многоугольник, который получается путем соединения трех прямых линий. Как следует из названия, это многоугольник с тремя углами. Сумма длин всех сторон треугольника — это периметр треугольника, а пространство внутри периметра треугольника — это площадь треугольника.
Формула треугольника:
Формула для расчета площади и периметра треугольника составляет,
- Площадь треугольника (A) = 1/2 × BH. (a+b+c) единиц
, где
a, b и c — стороны квадрата.
h высота квадрата
Также проверьте:
Площадь треугольника
Круг
Круг — геометрическая фигура без прямой линии. Это геометрическое место точки, которая всегда находится на постоянном расстоянии от фиксированной точки. Фиксированная точка называется центром окружности, а фиксированное расстояние — радиусом окружности.
Формула круга:
Формула для вычисления площади и периметра круга:
- Площадь круга (A) = πr
- Периметр/длина окружности (C) = 2πr единиц
, где
r — радиус окружности
Также проверьте:
Площадь круга
Список формул
Список формул для площадей различных фигур:
Цифры | Формула | Переменные |
|---|---|---|
Прямоугольник | Площадь = l×b | l длина |
квадрат | Площадь = а 2 | а сторона квадрата |
треугольник | площадь = 1/2×bh | b основание |
Круг | Площадь = πr 2 | r — радиус окружности |
Трапеция | 9 0002 Площадь = 1/2×(a+b)h | а первая |
Эллипс | Площадь = πab малая ось |
Формулы площади Примеры
Пример 1: Найдите площадь прямоугольника с длиной 5 см и шириной 2 см.
Решение:
Пример 2. Найдите площадь квадратного парка со стороной 4 м.Дано,
Длина прямоугольника (l) = 5 см
Ширина прямоугольника (b) = 2 смПлощадь прямоугольника (A) = l × b 9 0003
А = 5 см × 2 см
= 10 см 2
Решение:
Пример 3: Найдите площадь треугольной пластины, высота которой 6 см, а основание 6 см.Дано,
Сторона квадрата (a) = 4 м
Площадь квадрата = a 2
10 = (4) 2 = 16 м 2Таким образом, площадь площадь парка составляет 16 м 2
Решение:
Пример 4: Найдите площадь круглого диска с радиусом 1,4 см.Дано,
Высота треугольника (h) = 6 см
Основание треугольника (b) = 8 смПлощадь треугольника (A) = 1/2(b × h)
A = 1/2(8 × 6)
= 48/2 = 24 см 2Площадь треугольной пластины 24 см 2

Решение:
Дано,
Радиус круга (r) = 1,4 см
Площадь круга (A) = πr 2
9 0002 А = π(1,4) 2
= 22/7(1,4)(1,4) = (4,4)(1,4)
= 6,16 см 2Площадь круглого диска 6,16 см 2 9 0003
Часто задаваемые вопросы о формулах площади
Q1: Что такое формулы площади?
Ответ:
Формулы площади — это формулы, которые используются для нахождения площади любой фигуры. Он используется для определения количества места, занимаемого фигурой. Как правило, площадь обозначается буквой «А». и измеряется в единицах 2 , т. е. см 2 , м 2 и т. д.
Q2: Какова формула площади для квадрата?
Ответ:
Формула площади квадрата — это формула для вычисления площади, занимаемой квадратом. Математическая формула для вычисления площади квадрата:
Площадь квадрата = (сторона) 2
Q3: Что такое формула площади для прямоугольника?
Ответ:
Формула площади прямоугольника — это формула для вычисления площади, занимаемой прямоугольником.
Математическая формула для вычисления площади прямоугольника:
Площадь прямоугольника = длина × ширина
Q4: Что такое формула площади для треугольника?
Ответ:
Формула площади треугольника — это формула для вычисления пространства, занимаемого треугольником. Математическая формула для вычисления площади треугольника:
Площадь треугольника = 1/2 (основание × высота)
Q5: Какова формула площади для круга?
Ответ:
Формула площади круга — это формула для вычисления пространства, занимаемого кругом. Математическая формула для вычисления площади круга:
Площадь круга = π (радиус) 2
Q6: Что такое формула площади для четырехугольника?
Ответ:
Формула площади четырехугольника — это формула для расчета пространства, занимаемого четырехугольником.
Математическая формула для вычисления площади четырехугольника:
Площадь четырехугольника = 1/2 × диагональ × сумма высот
что такое площадь квадрата 6 дюймов. на всех сторонах?
Алгебра
Элейн В.
спросил 29.10.13я не понимаю как вы находите площадь
Подписаться І 3
Подробнее
Отчет
2 ответа от опытных наставников
Лучший Новейшие Самый старыйАвтор: Лучшие новыеСамые старые
Рик С. ответил 06.11.13
Репетитор
4,8 (12)
Репетитор по математике – сертифицированный репетитор на уровне колледжа
См.
Смотрите таких репетиторов
Формула площади квадрата (длина х ширина) также обозначается как основание х высота. В частности, у квадрата все стороны равны, как указано, все четыре стороны равны 6 дюймам.
Площадь вычисляется как 6 дюймов x 6 дюймов = 36 квадратных дюймов = 36 дюймов 2
1 сторона. Формула будет выглядеть следующим образом: длина x ширина x 6, потому что у куба всего 6 сторон.
Площадь рассчитывается как 6 дюймов x 6 дюймов x 6 сторон = 36 дюймов 2 x 6 = 216 дюймов 2
90 002
Голосовать за 0 Понизить
Подробнее
Отчет
Вивиан Л. ответил 29.10.13
Репетитор
3 (1)Microsoft Word/Excel/Outlook, составление эссе, математика; Я ЛЮБЛЮ УЧИТЬ
Смотрите таких репетиторов
Смотрите таких репетиторов
Привет, Элейн;
Если это двумерный квадрат, то вы умножаете длину на ширину.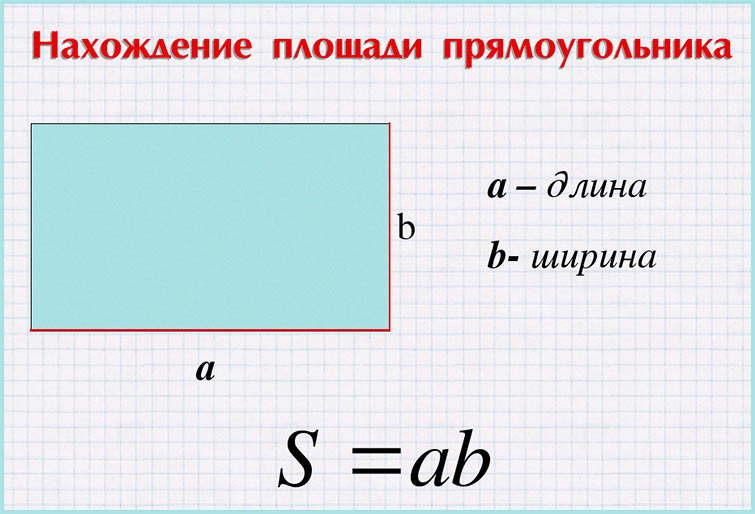



 Математическая формула для вычисления площади прямоугольника:
Математическая формула для вычисления площади прямоугольника: Математическая формула для вычисления площади четырехугольника:
Математическая формула для вычисления площади четырехугольника: