Период тригонометрических функций синус и косинус в градусах. В какой четверти угол поворота.
12+
3 месяца назад
Математика от Баканчиковой225 подписчиков
Тригонометрия 8-11 класс. Чему равен период синуса и косинуса? Как доказать, что период синуса и косинуса равен 360°? Как применять определение периода тригонометрических функций в решении задач? Сегодня мы ответим на эти вопросы. Если Вы не видели наши предыдущие уроки по теме: «Периодические функции», то обязательно посмотрите их, тогда этот урок будет Вам очень понятен. Вначале, мы напомним Вам, чему равен синус и косинус угла на единичной окружности. Затем докажем, что период синуса и косинуса равен 360°. Обратим Ваше внимание на то, чему равен наименьший положительный период синуса и косинуса. На примере пяти задач мы покажем Вам, как определять в какой четверти находится угол поворота тригонометрических функций синус и косинус, что позволит Вам легко понять тему «Формулы приведения».
В заключение Любовь Николаевна поделится своими рекомендациями и своим мнением о существующей системе оценки знаний учащихся, и к чему это приводит. Подробный план урока и ссылки на предыдущие уроки Вы можете найти в описании под видео.
00:00 Начало видео.
00:29 Чему равен период синуса?
06:03 Период косинуса равен периоду синуса.
07:31 Задача.
08:00 Задача 1а.
10:07 Задача 1б.
11:13 Задача 1в.
11:48 Задача 1г.
12:25 Задача 1д.
13:17 Рекомендации, советы и оценка ОГЭ и ЕГЭ Любовь Николаевны.
16:20 На следующем уроке …
Если Вы впервые на нашем канале или не смотрели наши предыдущие уроки, то рекомендуем Вам посмотреть следующие видео:
Периодичность функции. Определение периодической функции. Свойства функции. Алгебра 8-11 класс. https://rutube.ru/video/b25f67fb1e168fdb8b8f5cfddb654749/
Периодические функции в решении задач. Часть 1. Алгебра 8-11 класс. https://rutube.ru/video/e60e96860991be3329b8b4d08571c8c6/
Периодические функции в решении задач. Часть 2. Типовые задания и задачи ЕГЭ. Алгебра 7-11 класс.
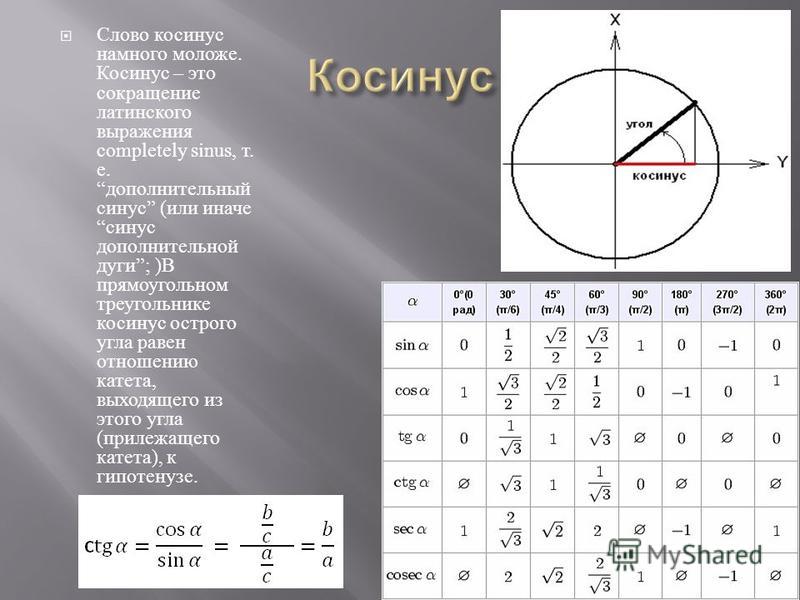
Cos Graph — Mathcracker.Com
Инструкции:
Используйте этот инструмент построения графиков для создания графика любой предоставленной вами функции косинуса с указанием всех этапов.
Пожалуйста, введите выражение cos, которое вы хотите вычислить, в поле формы ниже.
Подробнее об этом графовом калькуляторе cos
Этот калькулятор позволит вам построить график для любой функции косинуса, а также амплитуда, период и частота , показывая все шаги. Вам нужно предоставить действительную функцию, включающую функцию косинуса. Это может быть что-то тривиальное, например cos(x), или более сложное, например 2*cos(1/3 x + pi) — 4/5.
Как только вы укажете действительную функцию, включающую косинус, просто нажмите «Вычислить», чтобы получить результаты и все показанные этапы процесса.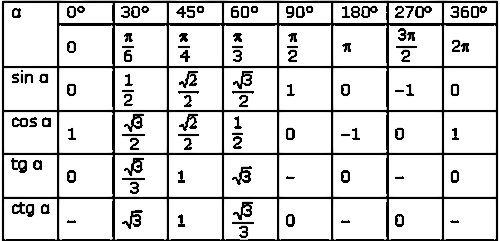
Косинус — это один тригонометрическая функция который имеет огромное количество применений в математике и физике. Он действительно часто используется также в геометрии, когда решение треугольников .
Как построить график cos?
Основной принцип построения графика любого типа функции заключается в том, чтобы прибегнуть к известной простой функции, для которой мы знаем ее график, а затем построить график, который мы хотим найти, на основе перевода и изменения масштаба этого простого графика.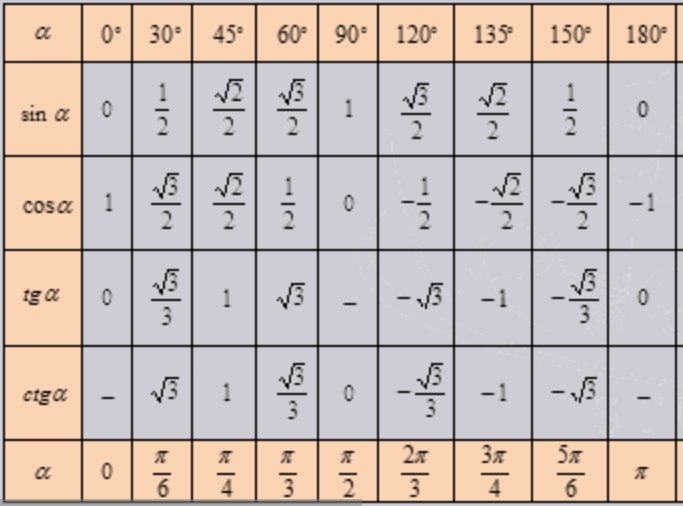
Для случая графика cos мы знаем, что простейшим выражением функции косинуса является f(x) = cos(x), график которой показан ниже:
Затем мы можем использовать этот базовый график для построения графиков более сложных функций cos, поскольку общая форма будет такой же, только ее можно потенциально перевести влево или вправо, вниз или вверх, и период также может потенциально меняться в зависимости от представленной функции.
Каковы этапы построения графика функции косинуса?
- Шаг 1 : Определите функцию cos, график которой вы хотите построить, в форме a*cos(bx+c)+d, если это возможно
- Шаг 2 : Значение a будет соответствовать амплитуда , d — единицы измерения, при этом основной график cos переводится вверх, а график смещается на -c/b вправо
-
Шаг 3
Действительно, только функции вида a*cos(bx+c)+d будут иметь четкое выражение для амплитуды, периода, частоты и трансляции, но это не единственные косинусные функции, которые можно представить.
2)\) — это cos-функция, но у нее нет периода или частоты, например.
График cos в сравнении с графиком sine?
Насколько похожи графики косинуса и синуса? Ну, довольно похожи. Во-первых, обратите внимание, что мы говорим об основных графиках косинуса и синуса, это sin(x) и cos(x).
Тогда график cos получается простым сдвигом графика синуса влево на \(\pi/2\) единиц. Таким образом, график cos и график синуса по сути одно и то же, за исключением перевода.
Cos график в градусах
Есть ли разница между графиком косинуса в радианах и графиком cos в градусах? Ну, есть разница в масштабе, так как cos завершает полный период в \(2\pi\) при измерении в радианах, и он завершает полный период в 360 градусах О
2)\), где мы все еще говорим, что у нас есть период
функция cos
.
Графики Cos, наряду с графиками синуса и тангенса, являются одними из наиболее распространенных тригонометрические графики с которыми вы обычно сталкиваетесь.
Пример: cos-график
Вычислите график : \(f(x) = \frac{1}{3} \cos\left( \frac{5}{4}x — \frac{5}{6}\right)\)
Отвечать: Предусмотрена следующая функция:
\[f(x) = \frac{1}{3} \cos\left( \frac{5}{4}x — \frac{5}{6}\right)\]
На основе аргумента переданной тригонометрической функции частота и период вычисляются следующим образом:
\[ \begin{array}{ccl} \text{Period} & = & \displaystyle\frac{2\pi}{\frac{5}{4}} \\\\ \\\\ & \approx & 5.
0265 \end{array}\]
а также
\[ \begin{array}{ccl} \text{Frequency} & = & \displaystyle\frac{\frac{5}{4}}{2\pi} \\\\ \\\\ & \approx & 0.1989 \end{array}\]
Поэтому, рассматривая представленную тригонометрическую функцию \(f(x) = \frac{1}{3} \cos\left( \frac{5}{4}x — \frac{5}{6}\right)\), получаем, что:
» Амплитуда в этом случае равна \(A = 1/3\).
» Фазовый сдвиг равен \(\displaystyle\frac{\frac{5}{6}}{\frac{5}{4}} = 0.6667\).
» Вертикальный сдвиг равен \( 0\).
Обобщая, для данной тригонометрической функции было найдено следующее
- Период = \(5.0265\)
- Частота = \(0.1989\)
- Амплитуда = \(1/3\)
- Фазовый сдвиг = \(0.6667\)
- Вертикальный сдвиг = \(\displaystyle 0\)
Ниже приведен соответствующий график
Пример: больше cos-графов
Является ли следующая функция периодической? \(f(x) = \frac{1}{3} \cos\left( \frac{5}{4}x^2 — \frac{5}{6}\right)\)
Отвечать:
Нет, это не так, из-за термина \(x^2\).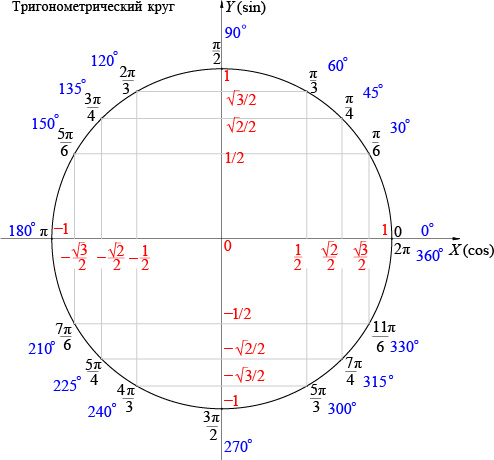
Пример: график косинуса
Вычислите график : \(f(x) = 2 \cos\left( \frac{5}{4}\left(x — \frac{7}{6}\right) + 1\right)\)
Отвечать: Обратите внимание, что полученное тригонометрическое выражение можно упростить следующим образом:
\( \displaystyle 2\cos\left(\frac{5}{4}\left(x-\frac{7}{6}\right)+1\right)\)
Путем расширения и упрощения терминов, допускающих упрощение
\( = \,\,\)
\(\displaystyle 2\cos\left(\frac{5}{4}x-\frac{11}{24}\right)\)
тогда функция, с которой мы будем работать, будет \(f(x) = 2\cos\left(\frac{5}{4}x-\frac{11}{24}\right)\).
Следовательно, на основе аргумента переданной тригонометрической функции частота и период вычисляются следующим образом:
\[ \begin{array}{ccl} \text{Period} & = & \displaystyle\frac{2\pi}{\frac{5}{4}} \\\\ \\\\ & \approx & 5.0265 \end{array}\]
а также
\[ \begin{array}{ccl} \text{Frequency} & = & \displaystyle\frac{\frac{5}{4}}{2\pi} \\\\ \\\\ & \approx & 0.1989 \end{array}\]
На основе предоставленной тригонометрической функции \(f(x) = 2 \cos\left( \frac{5}{4}\left(x — \frac{7}{6}\right) + 1\right)\) получаем, что:
» Амплитуда в этом случае равна \(A = 2\).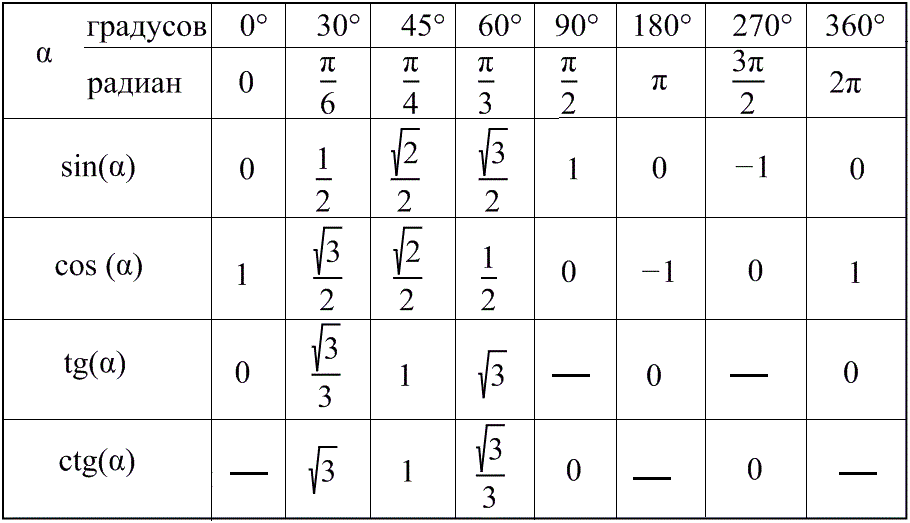
» Фазовый сдвиг равен \(\displaystyle\frac{\frac{11}{24}}{\frac{5}{4}} = 0.3667\).
» Вертикальный сдвиг равен \( 0\).
Обобщая, для данной тригонометрической функции было найдено следующее
- Период = \(5.0265\)
- Частота = \(0.1989\)
- Амплитуда = \(2\)
-
Фазовый сдвиг = \(0.
3667\)
- Вертикальный сдвиг = \(\displaystyle 0\)
3667\)
Ниже приведен соответствующий график
Больше калькуляторов по геометрии
Один из самых полезных, который вы можете найти, следующий
Калькулятор периода и частоты
, для которого вы задаете любую тригонометрическую функцию и получаете амплитуду, период и частоту.
Также, возможно, вас интересует оценка триггерных выражений или же построение графиков тригонометрических функций в целом.
Калькулятор — cos(2.8) — Solumaths
Cos, расчет онлайн
Итог:
Тригонометрическая функция cos вычисляет cos угла в радианах, градусов или градианов.
cos online
Описание:
Калькулятор позволяет использовать большинство из тригонометрических функций , есть возможность вычислить косинус ,
синус
и касательная
угла через одноименные функции.
Косинус тригонометрической функции отметил cos , позволяет вычислить косинус угла онлайн , можно использовать разные угловые единицы: градусы, грады и радианы, которые по умолчанию являются угловыми единицами.
- Расчет косинуса
- Специальные значения косинуса
- Основные свойства
Расчет косинуса угла в радианах
Калькулятор косинуса позволяет через функцию cos вычислить онлайн косинус угла в радианах, вы должны сначала выберите нужную единицу, нажав на кнопку параметров расчетного модуля. После этого можно приступать к расчетам.
Чтобы вычислить косинус онлайн от `pi/6`, введите cos(`pi/6`), после вычисления результат `sqrt(3)/2` возвращается.
Обратите внимание, что функция косинуса способна распознавать некоторые специальные углы и делать
расчеты со специальными связанными значениями в точной форме.
Вычислить косинус угла в градусах
Чтобы вычислить косинус угла в градусах, необходимо сначала выбрать нужную единицу измерения нажав на кнопку модуля расчета параметров. После этого можно приступать к вычислениям.
Чтобы вычислить косинус 90, введите cos(90). возвращает 0.
Вычислить косинус угла в градусах
Для вычисления косинуса угла в градианах необходимо сначала выбрать нужную единицу измерения нажав на кнопку модуля расчета параметров. После этого можно приступать к вычислениям.
Чтобы вычислить косинус 50, введите cos(50), после вычисления возвращается результат `sqrt(2)/2`.
Обратите внимание, что функция косинуса способна распознавать некоторые специальные углы и выполнять исчисление со специальными ассоциированными точными значениями.
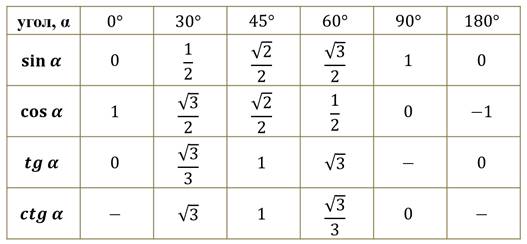
Косинус допускает некоторые специальные значения, которые калькулятор может определить в точных формах.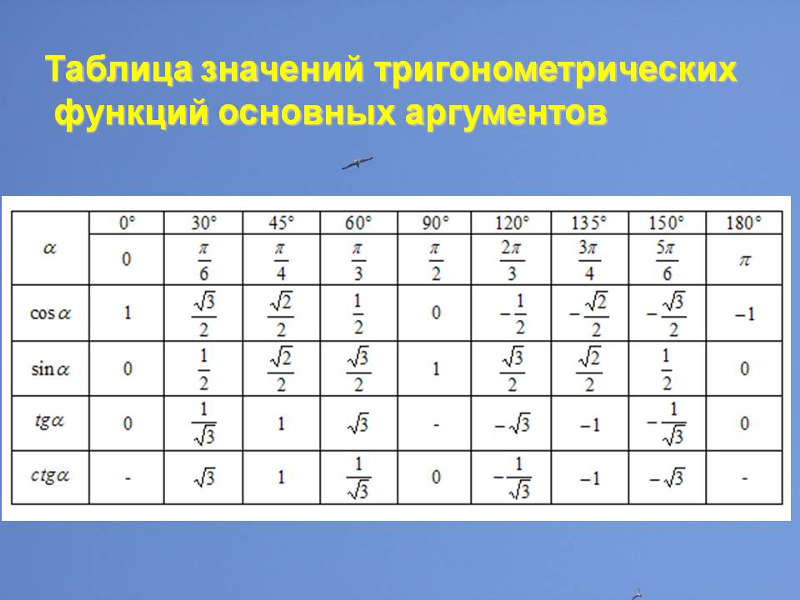
Вот список
специальные значения косинуса :
| cos(`2*pi`) | `1` | |
| cos(`pi`) | `-1` | |
| cos(`pi/2`) 70 7 7 7 90 90 90 90 | ||
| cos(`pi/4`) | `sqrt(2)/2` | |
| cos(`pi/3`) | `1/2` | |
| `sqrt(3)/2` | ||
| cos(`2*pi/3`) | `-1/2` | |
| cos(`3*pi/4`) | `-sqrt(2)/2` | |
| cos(`5*pi/6`) | `-sqrt(3)/2` | |
| cos(`0`) | `1` | `1` |
| cos(`-pi`) | `-1` | |
| cos(`pi/2`) | 7-7 `09` 90` | pi/4`)`sqrt(2)/2` |
| cos(`-pi/3`) | `1/2` | |
| cos(`-pi/6`) | `sqrt(3)/2` | |
| cos(`-2*pi/3`) | `-1/2` | |
| cos(`-3*pi/4`) | `-sqrt(2)/2` | |
| cos(`-5*pi/6`) | `-sqrt(3)/2` |
`AA x в RR, k в ZZ`,
- `cos(-x)= cos(x)`
- `cos(x+2*k*pi)=cos(x)`
- `cos(pi-x)=-cos(x) `
- `cos(pi+x)=-cos(x)`
- `cos(pi/2-x)=sin(x)`
- `cos(pi/2+x)=-sin(x) )`
Производная косинуса равна -sin(x).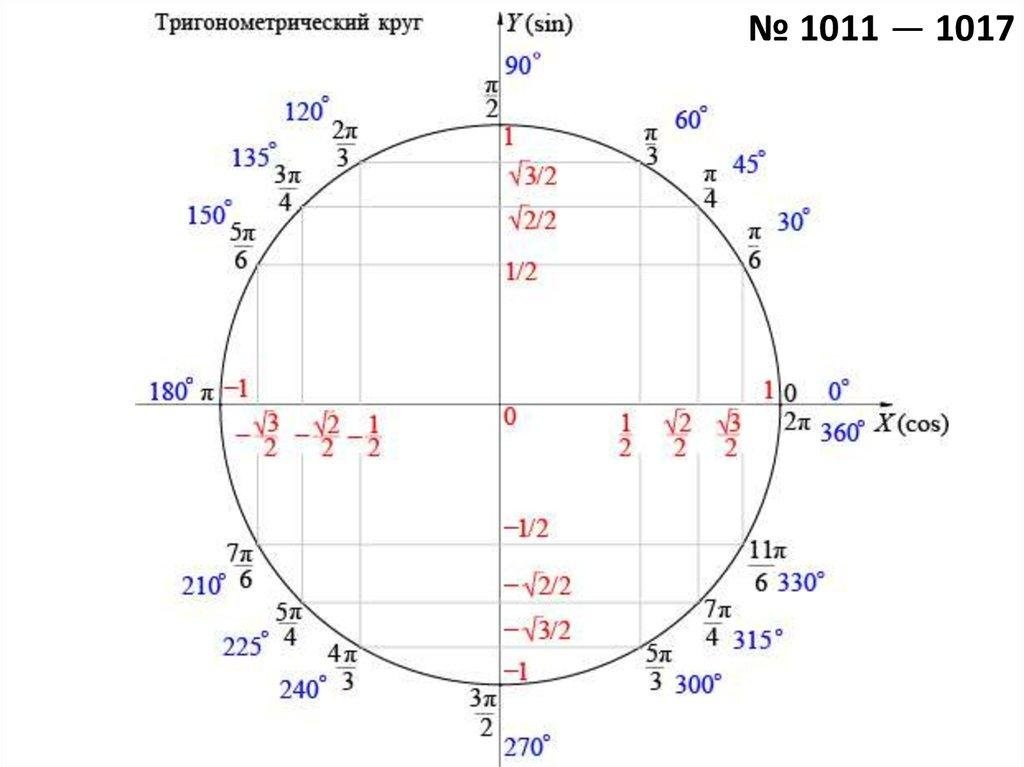
Первообразная косинуса равна sin(x).
Функция косинуса является четной функцией для каждого действительного x, `cos(-x)=cos(x)`. Следствием для кривой, представляющей функцию косинуса, является то, что она допускает ось ординат как ось симметрии.
Калькулятор имеет решатель, который позволяет решать уравнение с косинусом вида cos(x)=a . Расчеты для получения результата детализированы, поэтому можно будет решать уравнения типа `cos(x)=1/2` или `2*cos(x)=sqrt(2)` с этапами расчета.
Синтаксис:
cos(x), где x — мера угла в градусах, радианах или градах.
Примеры:
cos(`0`), возвращает 1
Производная косинус :
Чтобы дифференцировать функцию косинуса онлайн,
можно использовать калькулятор производной, который позволяет вычислить производную функции косинуса.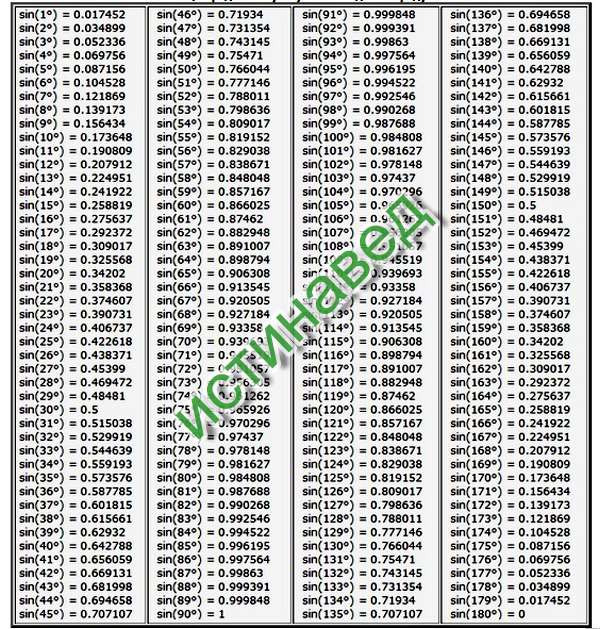
Первообразная косинуса :
Калькулятор первообразной позволяет вычислить первообразную функции косинуса.
Первопроизводная от cos(x) является первообразной(`cos(x)`)=`sin(x)`
Предельный косинус :
Калькулятор предела позволяет вычислить пределы функции косинуса.
предел cos(x) is limit(`cos(x)`)
Обратная функция косинуса :
обратная функция косинуса является функцией арккосинуса, отмеченной как arccos.
Графический косинус:
Графический калькулятор может отображать функцию косинуса в заданном интервале.
Свойство функции косинуса:
Функция косинуса является четной функцией.
Расчет онлайн с косинусом
См. также
Список связанных калькуляторов:
- Арккосинус : arccos. Функция arccos позволяет вычислять арккосинус числа.
Функция arccos является обратной функцией функции косинуса.
- Арксинус : арксинус. Функция arcsin позволяет вычислить арксинус числа. Функция arcsin является обратной функцией функции синуса.
- Арктангенс: арктангенс. Функция арктангенса позволяет вычислить арктангенс числа. Функция арктангенса является обратной функцией функции тангенса.
- Тригонометрический калькулятор: simple_trig. Калькулятор, который использует тригонометрическую формулу для упрощения тригонометрического выражения.
- Косинус: cos. Кос-тригонометрическая функция вычисляет косинус угла в радианах, градусов или градианов.
- Косеканс: косеканс Тригонометрическая функция sec позволяет вычислить секанс угла, выраженного в радианах, градусах или градусах.
- Котангенс : котан. Тригонометрическая функция котана для вычисления котана угла в радианах, градусов или градианов.
- Тригонометрическое расширение: expand_trigo. Калькулятор позволяет получить тригонометрическое разложение выражения.
- Тригонометрическая линеаризация : linearization_trigo. Калькулятор, позволяющий линеаризовать тригонометрическое выражение.
- Упростить калькулятор: упростить. Калькулятор, который может упростить алгебраическое выражение онлайн.
- Секанс : сек. Тригонометрическая функция sec позволяет вычислить секанс угла, выраженного в радианах, градусах или градусах.
- Синус : синус. Тригонометрическая функция sin для вычисления греха угла в радианах, градусов или градианов.
- Тангенс: коричневый. Тригонометрическая функция тангенса для вычисления тангенса угла в радианах, градусов или градианов.
Функция arccos позволяет вычислять арккосинус числа.
Функция arccos является обратной функцией функции косинуса.
Калькулятор позволяет получить тригонометрическое разложение выражения.
Калькулятор косинуса | Calculators.vip
Косинус для одних углов можно найти точные значения, а для других точную цифру определить сложно и можно вывести только приблизительное значение.
.
Поделитесь вычислением:
Найдите значение
X=SIN(A)X=COS(A)X=TAN(A)X=CTN(A)
A=ARC SIN(X)A= ARC COS (a) A = дуга TAN (x) a = дуга CTN (x)
Начальные данные
градуса
Radian
Рассчитайте
| 0 ° | 961 16.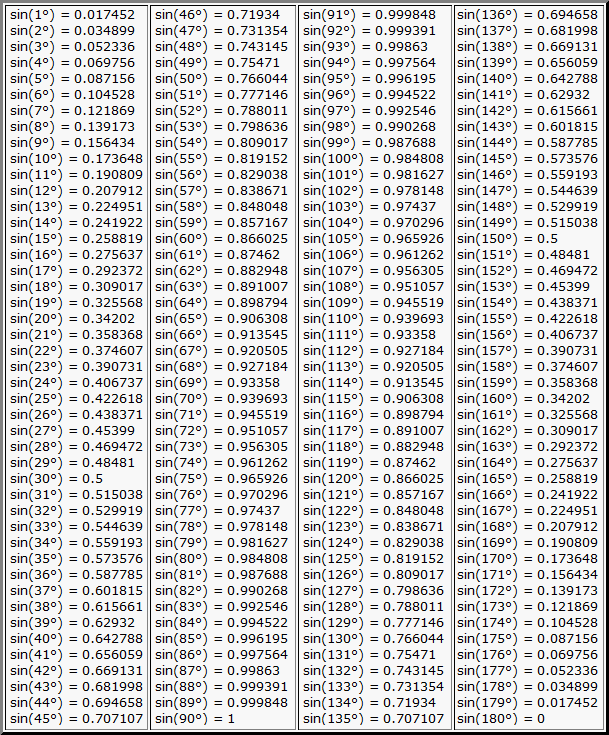 161261 16. 16 ° 160361 16 ° 160361 16. 16. 160361 16. до 31° | от 32° до 45° | ||||
|---|---|---|---|---|---|---|
| cos(0°) = 1 | cos(16°) = 0,961262 | COS (32 °) = 0,848048 | ||||
| COS (1 °) = 0,999848 | COS (17 °) = 0,956305 | COS (33 °) = 0,838677777777779976 COS (33 °) = 0,838677777777779976 | COS (33 °) = 0,8386777777777779976. | COS (18 °) = 0,951057 | COS (34 °) = 0,829038 | |
| COS (3 °) = 0,99863 | COS (19 °) = 0,945519 | COS (35.0917776 (351779. | 6 (351779.6.191776..191776.191776.191776.191776.191779776. | cos(4°) = 0,997564 | cos(20°) = 0,939693 | cos(36°) = 0,809017 |
| COS (5 °) = 0,996195 | COS (21 °) = 0,93358 | COS (37 °) = 0,798636 | ||||
| COS (6 °) = 0,994522 2 | COS (6 °) = 0,994522 2 | 9666666666666666666666666666666667666666667667667667676767. (38 °) = 0,788011|||||
| COS (7 °) = 0,992546 | COS (23 °) = 0,920505 | COS (39 °) = 0,777146 | ||||
| COS) = 0,777146 | ||||||
| COS) = 0,777146 | ||||||
| COS) = 0,777146 | ||||||
| COS) = 0,777146 | ||||||
| COS) = 0,777146 | ||||||
| COS) = 0,777146 | ||||||
COS).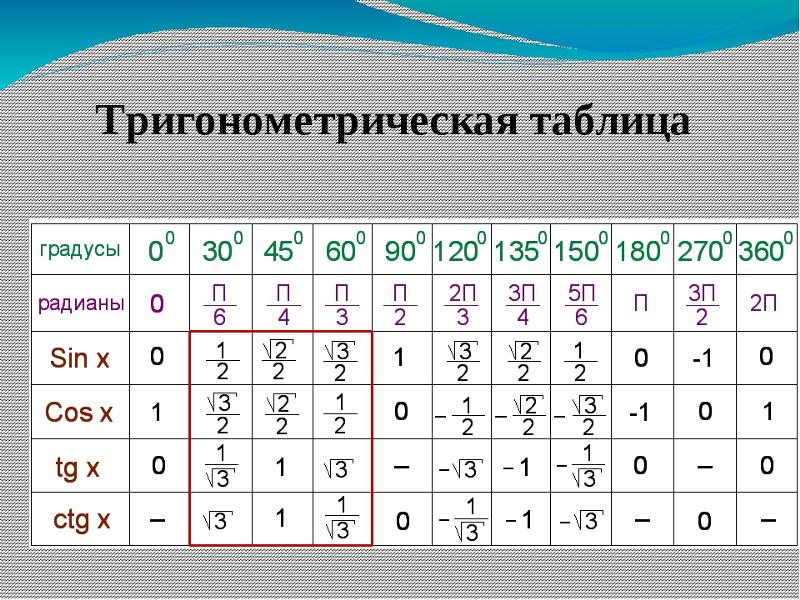 24°) = 0,913545 | cos(40°) = 0,766044 | |||||
| cos(9°) = 0,987688 | cos(25°) = 0, | 8COS (41 °) = 0,75471 | ||||
| COS (10 °) = 0,984808 | COS (26 °) = 0,898794 | COS (42 °) = 0,743145777 | COS (42 °) = 0,743145 | COS (42 °) = 0,743145777 | .COS (27 °) = 0,891007 | COS (43 °) = 0,731354 |
| COS (12 °) = 0,978148 | COS (28 °) = 0,82948 | 76666676 COS (28 °) = 0,82948766666666666666666666666666676.cos(13°) = 0,97437 | cos(29°) = 0,87462 | cos(45°) = 0,707107 | ||
| cos(14°) = 0.970296 | cos(30°) = 0.866025 | |||||
| cos(15°) = 0.965926 | cos(31°) = 0.857167 |
| 46 ° до 60 ° | 61 ° до 75 ° | 76 ° до 90 ° | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| COS (46 °) = 0,69658 | COS (611 °) = 0,48484688 | COS (611 °) = 0,48484688 | COS (611 °) = 0,4848888 | . | |||||||||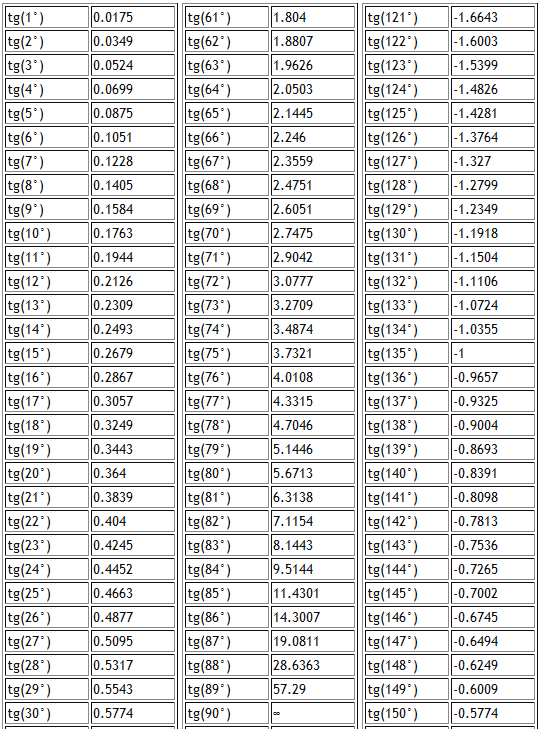
| cos(47°) = 0,681998 | cos(62°) = 0,469472 | COS (77 °) = 0,224951 | |||||||||||
| COS (48 °) = 0,669131 | COS (63 °) = 0,45399 | COS (78 °) = 0,207912 | COS (78 °) = 0,207912 | ||||||||||
| (78 °) = 0,207912 | (78 °) = 0,207912 | . cos (64 °) = 0,438371 | COS (79 °) = 0,190809 | ||||||||||
| COS (50 °) = 0,642788 | COS (65 °) = 0,422618 | COS (80776767676767676767676768 = 0,176767676767676767676767676767676767676767676767648 = 0,422618 | COS (65 °) = 0,422618. (51°) = 0,62932 | cos(66°) = 0,406737 | cos(81°) = 0,156434 | ||||||||
| cos(52°) = 0,615661 | COS (67 °) = 0,390731 | COS (82 °) = 0,139173 | |||||||||||
| COS (53 °) = 0,601815 | COS (68 °) = 0,374607777 | COS (68 °) = 0,374607777777777. |