Синус, косинус, тангенс, котангенс — 10 класс, урок и презентация
Дата публикации: .
Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания. Все материалы проверены антивирусной программой.
Скачать:Синус и косинус (PPTX)
Что будем изучать:
1. Определение синуса и косинуса.
2. Определение тангенса и котангенса.
3. Основное тригонометрическое тождество.
4. Таблица значений синуса, косинуса, тангенса, котангенса.
5. Основные свойства.
6. Синус и косинус в жизни.
7. Примеры и задачи.
Синус и косинус. Определения
Ребята, давайте отметим на числовой окружности точку $Р$. Посмотрите на рисунок, наша точка $Р$ соответствует некоторому числу $t$ числовой окружности, тогда абсциссу точки $Р$ будем называть косинусом числа $t$ и обозначать $cos(t)$, а ординату точки $Р$ назовем синусом
2=1$.Значения синуса, косинуса, тангенса, котангенса в четвертях окружности:
Значения синуса, косинуса, тангенса, котангенса в четвертях окружности:
Таблица значений синуса, косинуса, тангенса, котангенса
не сущ. – не существует значение, т.к. на 0 делить нельзя.
Основные свойства синуса и косинуса
Для любого числа $t$ справедливы равенства:
$sin(-t) = -sin(t)$.
$cos(- t) = cos(t)$.
$tg(- t) = -tg(t)$.
$ctg(- t) = -ctg(t)$.
$sin(t + 2π*k) = sin(t)$.
$cos(t +2π*k ) = cos(t)$.
$sin(t + π ) = -sin(t)$.
$cos(t +π ) = -cos(t)$.
$tg(t + π*k ) = tg(t)$.
$ctg(t +π*k ) = ctg(t)$.
$sin(t + \frac{π}{2}) = cos(t)$.
$cos(t + \frac{π}{2}) = -sin(t)$.
Синус и косинус в жизни
Для чего нужны синусы и косинусы в обычной жизни?
На практике синусы и косинусы применяются во всех инженерных специальностях, особенно в строительных. Их используют моряки и летчики в расчетах курса движения.
Не обходятся без синусов и косинусов геодезисты и даже путешественники. В географии эти понятия применяют для измерения расстояний между объектами и в спутниковых навигационных системах. Пример 1.
Вычислить синус и косинус $t$, при $t=\frac{53π}{4}$.
Решение:
Поскольку, числам $t$ и $t+2π*k$, $k$ – целое число, соответствует одна точка числовой окружности, то:
$\frac{53π}{4}=(12 + \frac{5}{4})*π = 12π + \frac{5π}{4}=\frac{5π}{4} + 2π*6$.
Воспользуемся свойством: $sin(t + 2π*k ) = sin(t)$, $cos(t +2π*k)= cos(t)$.
$sin(\frac{5π}{4} + 2π*6) = sin(\frac{5π}{4}) = sin(\frac{π}{4} + π)$.
$cos(\frac{5π}{4} + 2π*6) = cos(\frac{5π}{4})=cos(\frac{π}{4} + π)$.
Воспользуемся свойством: $sin(t + π ) = -sin(t)$, $cos(t+π) =-cos(t)$.
$sin(\frac{π}{4} + π)=-sin(\frac{π}{4})$.
$cos(\frac{π}{4} + π)=-cos(\frac{π}{4})$.
Из таблицы значений синуса и косинуса получаем: $sin(\frac{53π}{4})=-\frac{\sqrt{2}}{2}$; $cos(\frac{53π}{4})=-\frac{\sqrt{2}}{2}$.
Пример 2.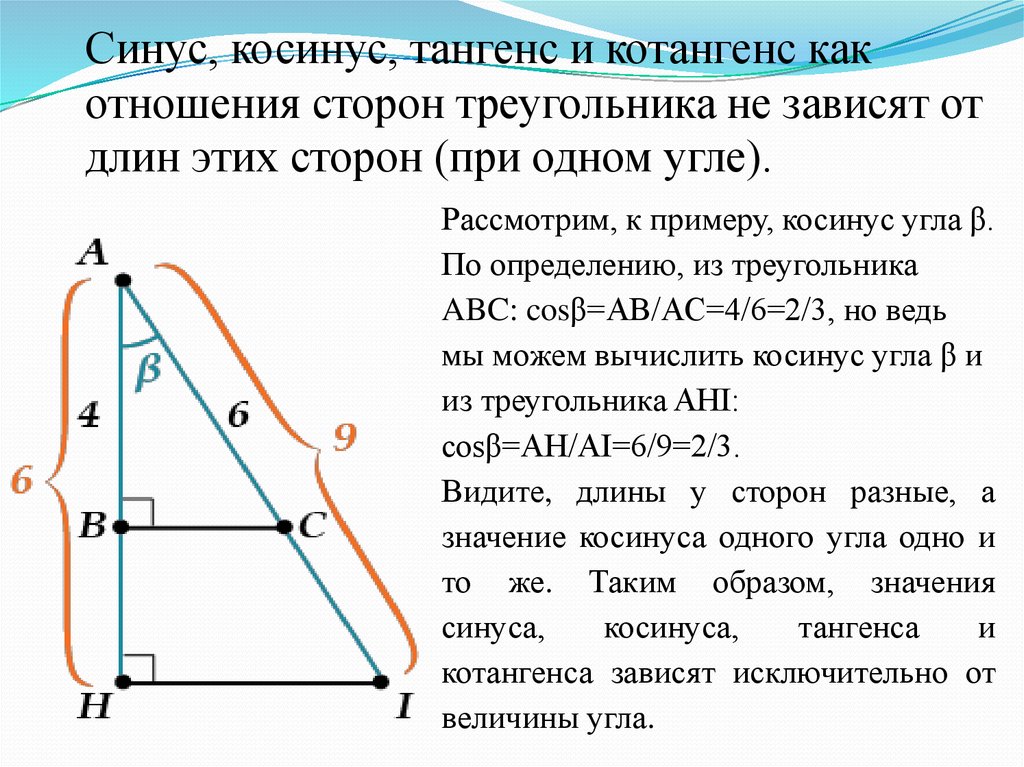
Вычислить синус и косинус $t$, при $t=-\frac{49π}{3}$.
Решение:
Поскольку, числам $t$ и $t+2π*k$, $k$ – целое число, соответствует одна точка числовой окружности, тогда:
$-\frac{49π}{3}=-(16 + \frac{1}{3})*π =-16π +(-\frac{π}{3}) = (-\frac{π}{3}) + 2π*(-8)$.
Воспользуемся свойством: $sin(t + 2π*k ) = sin(t)$, $cos(t +2π*k)= cos(t)$.
$sin(-\frac{π}{3} + 2π*(-8) )=sin(-\frac{π}{3} )$.
$cos(-\frac{π}{3} + 2π*(-8) )=cos(-\frac{π}{3} )$.
Воспользуемся свойством: $sin(- t) = -sin(t)$, $cos(- t) = cos(t)$.
$sin(-\frac{π}{3})=-sin(\frac{π}{3})$.
$cos(-\frac{π}{3})=cos(\frac{π}{3})$.
Из таблицы значений синуса и косинуса получаем: $sin(-\frac{49π}{3})=-\frac{\sqrt{3}}{2}$; $cos(-\frac{49π}{3})=\frac{1}{2}$.
Пример 3.
Решите уравнение и неравенство:
а) $sin(t)=\frac{\sqrt{3}}{2}$.
б) $sin(t)>\frac{\sqrt{3}}{2}$.
Решение:
$sin(t)$ – это ордината точки числовой окружности (из определения).
Значит на числовой окружности нужно найти точки с ординатой $\frac{\sqrt{3}}{2}$.
Пусть, это будут точки F и G. Определим, каким значениям $t$ соответствуют точки $F$ и $G$ на рисунке.
а) Точки $F$ и $G$ имеют координаты: $\frac{π}{3} +2 π*k$ и $\frac{2π}{3}+2 π*k$.
б) Точки, которые удовлетворяют неравенству $sin(t)>\frac{\sqrt{3}}{2}$, расположены на дуге FG.
Тогда: $\frac{π}{3} +2 π*k<t<\frac{2π}{3} +2 π*k$.
Ответ :
a) $t=\frac{π}{3}+2 π*k$ и $t= \frac{2π}{3} +2 π*k$.
б) $\frac{π}{3}+2 π*k<t<\frac{2π}{3} +2 π*k$.
Пример 4.
Решить уравнение и неравенство:
а) $cos(t)=\frac{1}{2}$.
Решение:
$cos(t)$ – это абсцисса точки числовой окружности (из определения).
Значит, на числовой окружности необходимо найти точки с абсциссой равной $\frac{1}{2}$. Пусть это будут точки F и G (см. рисунок). Надо определить, каким значениям $t$, они соответствуют.
а) Точки F и G имеют координаты: $-\frac{π}{3}+2π*k$ и $\frac{π}{3}+2π*k$.
б) Точки, которые удовлетворяют неравенству $cos(t)>\frac{1}{2}$, расположены на дуге FG.
Тогда: $-\frac{π}{3}+2π*k<t<\frac{π}{3}+2π*k$.
Ответ:
a) $-\frac{π}{3}+2π*k$ и $\frac{π}{3}+2π*k$.
б) $-\frac{π}{3}+2π*k<t<\frac{π}{3}+2π*k$.
Пример 5.
Вычислить тангенс и котангенс $t$, при: $t=-\frac{7π}{3}$.
Решение:
Числам $t$ и $t+2π*k$, где k – целое число, соответствует одна точка числовой окружности, тогда:
$-\frac{7π}{3} = -(2 + \frac{1}{3})*π = -2π +(-\frac{π}{3}) = (-\frac{π}{3}) + 2π$.
Воспользуемся свойством: $tg(x+ π*k) = tg(x)$, $ctg(x+π*k) = ctg(x)$.
$tg((-\frac{π}{3}) + 2π ) = tg(-\frac{π}{3})$.
$сtg((-\frac{π}{3}) + 2π ) = сtg(-\frac{π}{3})$.
Воспользуемся свойством: $tg(-x) = -tg(x)$, $ctg(-x) = -ctg(x)$.
$tg(-\frac{π}{3})=-tg(\frac{π}{3})$.
$сtg(-\frac{π}{3})=-сtg(\frac{π}{3})$.
Из таблицы значений получаем: $tg(-\frac{7π}{3}) =-tg(\frac{π}{3}) = -\sqrt{3}$.
$сtg(-\frac{7π}{3}) = -сtg(\frac{π}{3}) =-\frac{\sqrt{3}}{3}$.
Примеры для самостоятельного решения:
1) Вычислить синус и косинус $t$, при
а) $t=\frac{61π}{6}$,
б) $t= -\frac{52π}{3}$.
2) Решите уравнения:
a) $sin(t)=-\frac{1}{2}$;
б) $sin(t) >-\frac{1}{2}$;
в) $sin(t)
3) Решите уравнения:
a) $cos(t)=-\frac{1}{2}$;
б) $cos(t) >-\frac{1}{2}$;
а) $t= \frac{19π}{6}$;
б) $t=\frac{41π}{4}$.
§ 1. Синус, косинус, тангенс и котангенс любого угла и числа
Тригонометрия
Слово «тригонометрия» переводится на русский язык как измерение треугольника. И действительно, в начале это была наука о треугольниках. Да и ваше знакомство с тригонометрией началось с определения тригонометрических функций (синуса, косинуса, тангенса и котангенса) острого угла прямоугольного треугольника. Вспомним его.
Определение 1.
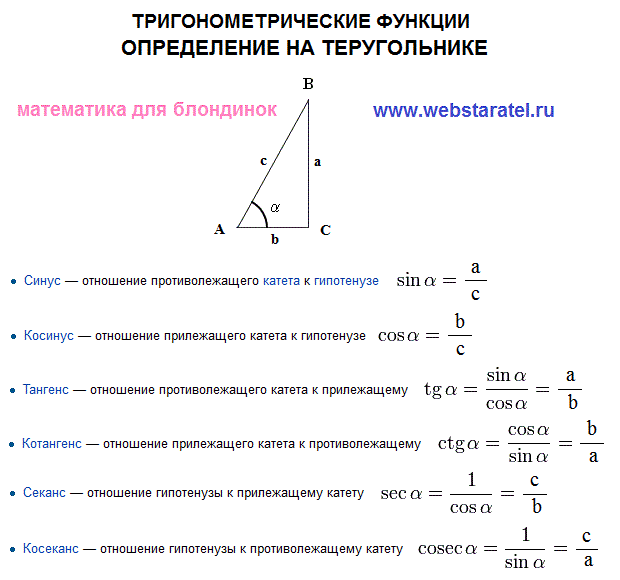
Чтобы найти синус, косинус, тангенс или
котангенс острого угла, нужно построить
прямоугольный треугольник, имеющий
данный острый угол, и найти отношение
соответствующих сторон. Именно: синус
равен отношению противолежащего катета
к гипотенузе; косинус равен отношению
прилежащего катета к гипотенузе; тангенс
равен отношению противолежащего катета
к прилежащему катету; котангенс равен
отношению прилежащего катета к
противолежащему катету.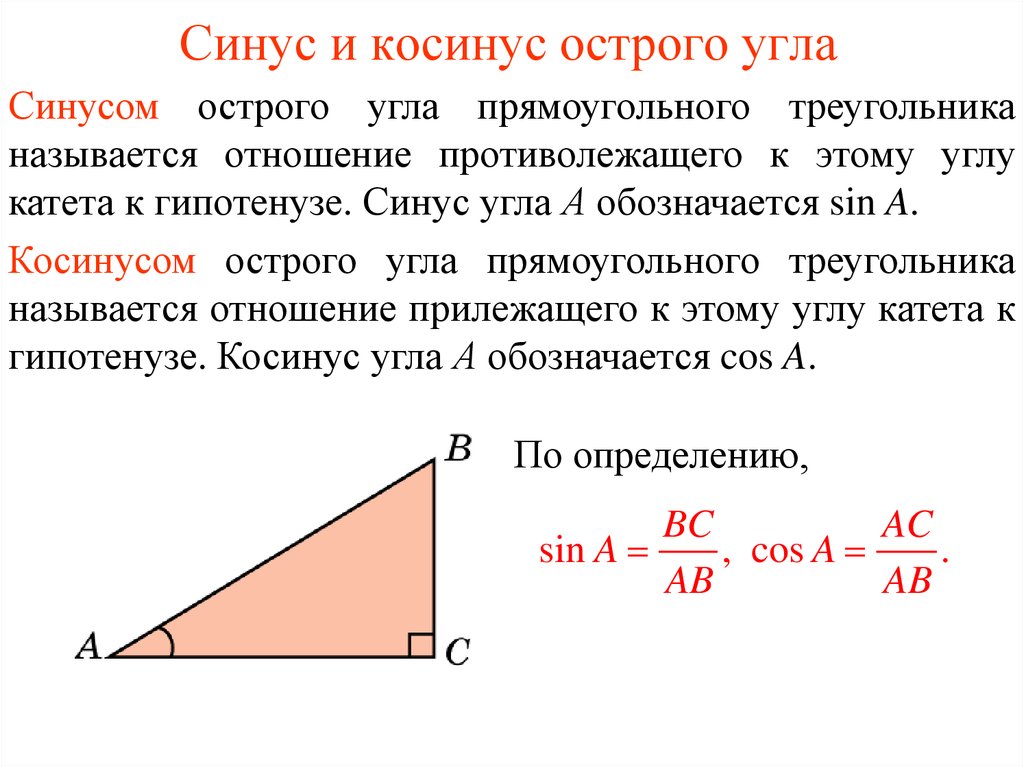
Задание 1. Начертите АВС с прямым углом С. Выразите в виде отношения сторон этого треугольника все тригонометрические функции углов A и В. Обратите внимание на их попарное равенство.
Задание 2. Докажите, что значение той или иной тригонометрической функции острого угла не зависит от выбора треугольника, а зависит только от величины угла.
Задание 3. Вспомните доказательство шести основных тригонометрических тождеств, основанное на только что приведенных определениях.
Задание 4. Пусть — острый угол. Выразите: а) tg через ctg; б) cos через sin; в) sin через
Задание 5.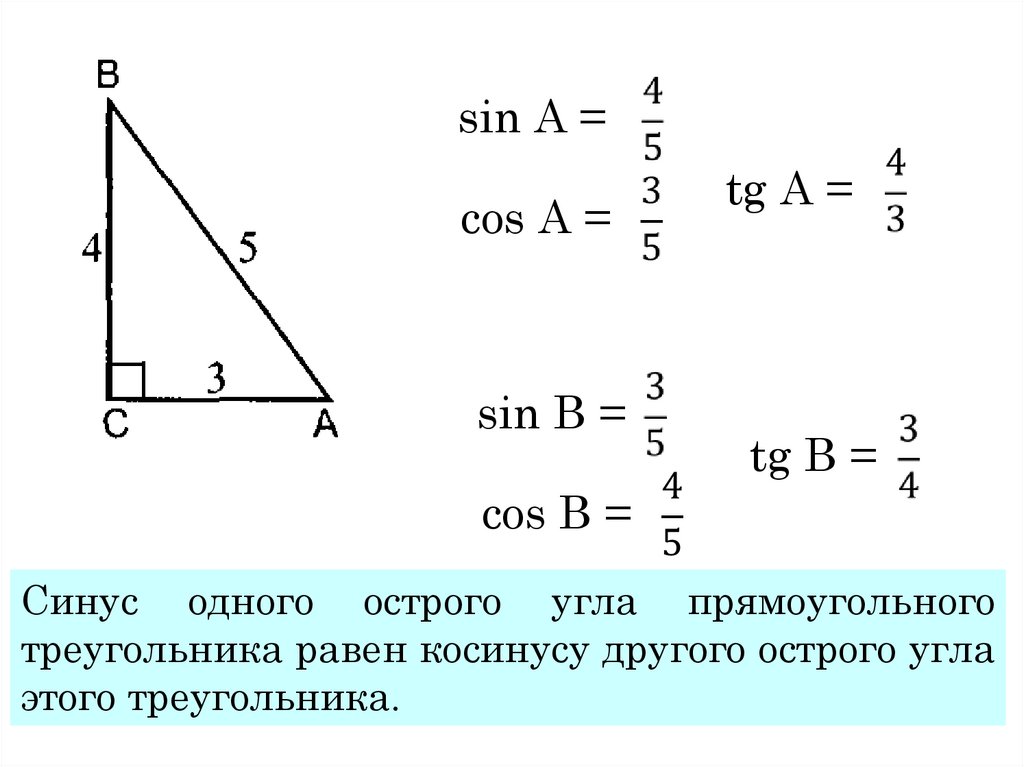
Вспомните
доказательство четырех формул приведения,
основанное на только что приведенных
определениях.
Задание 6. Используя таблицы в конце этого пособия, найдите значения следующих выражений: sin 80o, cos 56o, tg 72o, ctg 46o.
Задание 7. Докажите, что тригонометрические функции острого угла числа положительные, и при этом синус и косинус меньше 1.
Задание 8. Докажите, что тангенс и котангенс острого угла могут быть любыми положительными числами.
Докажите, что синус и косинус острого угла могут быть любыми положительными числами, меньшими 1. Задание 9. У
египетского треугольника АВС гипотенуза
АВ равна 5, катет ВС равен 4, катет АС
равен 3. Вычислите sin A, cos B, ctg A, tg B.
Сделайте чертеж.
Задание 10. Начертите равнобедренный прямоугольный треугольник. Обозначьте его катет через 1. Вычислите длину его гипотенузы. Как с помощью этого чертежа можно определить величины тригонометрических функций угла в 450?
Задание 11. Начертите прямоугольный треугольник с острыми углами в 30 и 60 градусов. Обозначьте его меньший катет через 1. Вычислите длину его гипотенузы и длину его большего катета. Как с помощью этого чертежа можно определить величины тригонометрических функций углов в 30
* * *
Следующим шагом в вашем ознакомлении с тригонометрией будет определение синуса, косинуса, тангенса и котангенса любого угла.
Под углом теперь
понимается уже не пара лучей, исходящих
из одной точки, а мера поворота луча
относительно некоторого начального
положения.
Поворот против часовой
стрелки считается положительными, а
поворот по часовой стрелке
отрицательным. Такой угол может содержать
любое число градусов, например, 1000о или
2000о.
Определение 2. Построим в прямоугольной системе координат окружность с центром в начале координат и с единичным радиусом – координатную окружность. Отложим от положительного направления оси абсцисс угол (если он положительный в направлении против часовой стрелки, а если отрицательный в направлении по часовой стрелке). Точку пересечения второй стороны угла с окружностью обозначим буквой А. Синусом отложенного угла называется ордината точки А, косинусом абсцисса точки А, тангенсом отложенного угла называется отношение его синуса к его косинусу, котангенсом отношение косинуса к синусу.
Задание 12. Выполнив
указанные построения, найдите значения
синуса, косинуса, тангенса и котангенса
угла 2250.
Задание 13. Докажите, что если углы отличаются друг от друга на целое число полных оборотов, то их синусы равны между собой, косинусы равны между собой, тангенсы равны между собой, котангенсы равны между собой:
sin( +360оn) = sin , cos ( + 360on) = cos , tg( + 360on) = tg, ctg( + 360on) = ctg, где n любое целое число: n Z.
Угол может измеряться не только в градусной мере. Большую ценность имеет радианная мера угла:
1 радиан — это
мера центрального угла, соответствующего
дуге, имеющей длину, равную радиусу
окружности; 1 радиан
57о;
1o
0,017 радиана.
Обозначение радианной меры указывать не принято. Запись sin 30 читается «синус угла в 30 радиан» (не путать с sin 30о!).
Задание 14. Вспомните, что такое число , и переведите в радианную меру: 360о, 90о, 45о, 60о.
Задание 15. Переведите в градусную меру: 2, , , 1,25.
Задание 16. Сделайте
себе справочную табличку по тригонометрии,
пользуясь черным, синим и красным
цветами. Начертите на клетчатой бумаге
прямоугольную систему координат: ось
абсцисс красного цвета, ось ординат
синего цвета, взяв единичный отрезок в 5 см (10 клеток).
Начертите черным цветом окружность с
центром в начале координат и радиусом
5 см. Ось абсцисс обозначьте не х, а cos x,
ось ординат не у, а sin x, соответственно красным и
синим цветом.
Все обозначения вдоль
осей и вдоль окружности делайте такими
же цветами.
Вдоль
окружности внутри нее отметьте градусные
меры углов: 0, 30, 45, 60, 90, 120, 135, 150, 180, 210, 225,
240, 270, 300, 315, 330, 360 градусов. Вне окружности
рядом с этими метками тоже черным цветом
надпишите радианные меры тех же углов.
Проецируя отмеченные на окружности
точки на оси координат, надпишите
соответствующим цветом значения синусов
и косинусов: 0,
,
,
,
1, , , , 1. На оси абсцисс вашего чертежа будут
отмечаться косинусы, а на оси ординат синусы углов.
Задание 17.
Потренируйтесь в работе со сделанной
таблицей: 1) переведите в радианную меру
315о ; 2) переведите в градусную меру
;
3) найдите sin 240о ; 4) найдите cos
;
5) найдите tg 150о;
6) найдите ctg
;
7) определите знак косинуса в IV четверти;
8) определите знак котангенса в III
четверти.
Задание 18. Определите, какие значения могут принимать sin x и cos x.
Задание 19. Определите, для каких углов не существует тангенс или котангенс.
Задание 20. Найдите корни уравнения 1) sin x = 1; 2) cos x = 1.
Задание 21. Проведите через точку (1;0) вертикальную прямую и постройте на ней координатную прямую с началом в точке (1;0), и положительным направлением вверх. Докажите, что эта прямая является линией тангенсов, найдя правило, по которому можно строить на ней тангенс любого угла из () числовой окружности.
Задание 22. Найдите с помощью линии тангенсов tg 0,25; tg ; tg 1,25; tg1,75.
Задание 23.
Проведите через точку (0;1) горизонтальную
прямую и постройте на ней координатную
прямую с началом в точке (0;1) и положительным
направлением вправо.
Докажите, что эта
прямая является линией котангенсов,
найдя правило, по которому можно строить
на ней котангенс любого угла из (0;π)
числовой окружности.
Задание 24. С помощью линии котангенсов найдите ctg 0,5; ctg 0,75; ctg (0,25).
Задача 1. Докажите, что sin(x) = sin x, cos(x) = cos x, tg(x) = tg x,
ctg(x) = ctg x. Укажите ОДЗ (область допустимых значений переменных) для каждой из этих формул.
Задача 2. Исходя из определения синуса и косинуса любого угла, докажите первое из основных тригонометрических тождеств. Укажите ОДЗ для этой формулы.
Задача 3. Докажите остальные пять основных тригонометрических тождеств. Укажите ОДЗ для каждой из этих формул.
* * *
Качественный
рывок, который мы сейчас совершим,
заключается в переходе от синуса,
косинуса, тангенса и котангенса любого угла к
синусу, косинусу, тангенсу и котангенсу
любого числа.
Это раскроет перед нами новые возможности.
Во-первых, станет возможным рассматривать композицию тригонометрических функций, например, такую, как sin cos x или sin (х2 + 5).
Задание 25. Объясните, почему до сих пор было нельзя рассматривать указанные функции.
Кроме, того, мы получаем возможность строить графики синуса, косинуса, тангенса и котангенса. До сих пор такой возможности у нас не было. В математике график строят в прямоугольной системе координат с одинаковыми координатными осями. Какая единица выбрана на оси абсцисс, такая должна быть и на оси ординат. А как можно построить график у = sin x, если х угол, а у число? Это физики могут строить графики, у которых на одной оси время в секундах, а на другой путь в метрах. Они так используют математический аппарат. Но в математике это не принято.
Определение 3.
Синусом (косинусом, тангенсом, котангенсом)
числа х называется синус (косинус, тангенс,
котангенс) угла в х радиан.
Задание 26. Найдите синус числа , косинус числа 1, тангенс числа 0.
Теперь мы можем считать синус, косинус, тангенс и котангенс функциями числового аргумента. Теперь для нас tg это не только тангенс развернутого угла, но и тангенс числа 3,14159… : tg tg 3,14.
Очень важно, что ранее выведенные формулы тригонометрии остаются верными и в новой ситуации. Докажем это.
По введенному определению, синус числа х равен синусу угла в х радиан, аналогично обстоит дело и с косинусом, тангенсом и котангенсом. Но если а равно b, то взяв верное утверждение, содержащее а, мы можем в любом месте заменить а на b, и утверждение останется верным (правило подстановки).
Возьмем любое
доказанное ранее утверждение относительно
синуса, косинуса, тангенса и котангенса
угла в а радиан и
заменим их на равные
им по определению синус, косинус, тангенс и котангенс
числа а.
Утверждение останется верным, ч.т.д.
Домашнее задание: Галицкий, Алгебра 8-9, глава 13, №№ 2, 4-9, 11-14, 17, 20, 27, 30, 31, 33, 36-43, 45-49, 51, 54, 57, 58, 60-62.
тригонометрических функций | Визуализируй это
Вы когда-нибудь задумывались, почему тригонометрические функции называются именно так?
являются?
Почему косинус называется «ко»синус, «косеканс» называется «ко»секанс и
«котангенс» называется «ко»тангенсом?
Имеют ли эти функции какое-либо значение вне треугольников?
Разве такие термины, как «секанс» и «касательная», не связаны с окружностями?
Старые братья:
Синус и косинус
Этимология: Слово «синус» происходит от латинского слова «синус».
что означает «бухта» или «складка». Это санскрит, арабский и персидский
версии происходят от греческого слова «хорде», что означает
тетива. В приведенной ниже визуализации, если мы представим, что ось X действует как зеркало, изображение станет
симметричный.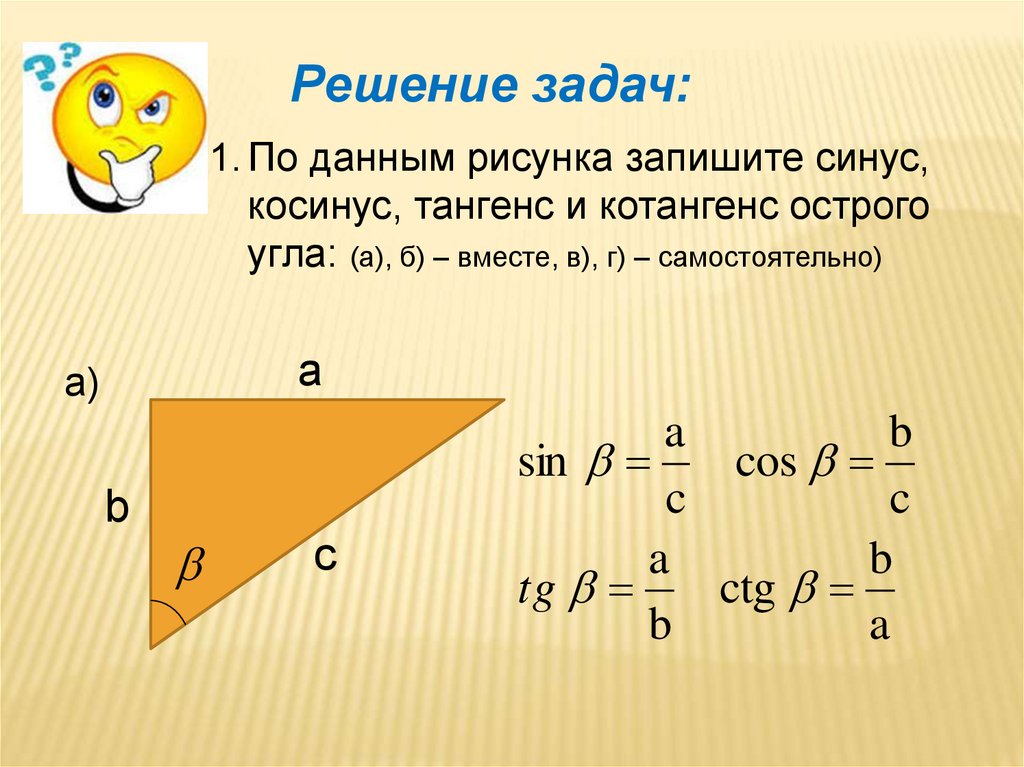
Отрезки OP и OP’ выглядят как тетивы лука, а перпендикуляры к оси X (их
длина равна 2sin(θ)) выглядит как лук
Визуализация: Рассмотрим единичный круг (круг радиуса 1). Рассмотрим линию, проведенную из начала координат O, которая образует угол θ с осью X в направлении против часовой стрелки. Эта линия пересекает окружности в точке P. Длина проекции отрезка OP на Ось Y равна синусу θ
Отрегулируйте угол с помощью следующего ползунка:
Или введите угол здесь:
92 = 1 для всех углов θ
Значение синусов и косинусов, кратных 90 градусам:
- Синус 0 градусов равен 0, так как прямая, совпадающая с осью X, не имеет проекции на ось Y
- Косинус 0 градусов равен 1, поскольку линия, проведенная внутри единичного круга и совпадающая с осью X, имеет проекция длины 1 на ось X
- Синус 90 градусов равен 1, так как линия, проведенная внутри единичного круга и совпадающая с осью Y, имеет проекция длины 1 на ось Y
- Косинус 90 градусов равен 0, так как прямая, совпадающая с осью Y, не имеет проекции на ось X
- Та же логика верна для 180 градусов и 270 градусов
- Эта визуализация также позволяет нам расширить определение тригонометрических функций за пределы 90 градусов, поскольку мы больше не ограничены треугольником
Знаки функций синуса и косинуса:
- Любой угол от 0 до 180 градусов имеет положительный синус, так как измеряется длина проекции на ось Y вдоль положительного направления Y
- Синус отрицательный для остальных углов, потому что длина проекции на ось Y измеряется вдоль отрицательное направление Y
- Любой угол от 0 до 90 градусов и от 270 до 360 градусов имеет положительный косинус, так как длина проекции на ось X измеряется вдоль положительного направления X
- Косинус отрицателен для остальных углов, поскольку длина проекции на ось X измеряется вдоль отрицательное направление X
Синус — нечетная функция: \[ \sin (-\theta) = — \sin (\theta) \]
- Рассмотрим угол θ, имеющий величину от 0 до 90 градусов
- Синус +θ всегда положителен, так как проекция на ось Y всегда вдоль положительной Y-направление
- Синус -θ всегда отрицательный, так как проекция на ось Y всегда вдоль отрицательной Y-направление
- Следовательно, sin(-θ) = -sin(θ): Синус является нечетной функцией
- То же верно и для угла θ, имеющего величину от 90 до 180 градусов: Sin(θ) равен всегда положительный, тогда как sin(-θ) всегда отрицательный
Косинус — четная функция: \[ \cos (-\тета) = \cos (\тета) \]
- Рассмотрим угол θ, имеющий величину от 0 до 90 градусов
- Косинус +θ всегда положителен, так как проекция на ось X всегда вдоль положительной Х-направление
- Косинус -θ всегда положителен, так как проекция на ось X всегда вдоль положительной X-направление
- Следовательно, cos(-θ) = cos(θ): косинус — четно-нечетная функция
- То же верно и для угла θ, имеющего величину от 90 до 180 градусов: Cos(θ) и cos(-θ) оба отрицательны
The Circle Grazers:
Тангенс и Котангенс
Этимология: Слово «тангенс» происходит от латинского глагола «tangere», что означает «касаться».
Визуализация: Рассмотрим тот же единичный круг с тем же отрезком OP. Рассмотрим касательную, проведенную к окружность в точке P. Длина между точкой P и точкой пересечения этой касательной с осью X равна касательной угла θ
Отрегулируйте угол с помощью следующего ползунка:
Или введите угол здесь:
Отношение между тангенсом и котангенсом:
Длина той же касательной, но от точки Р до ее точка пересечения с осью Y равна котангенсу θ
Вычеты
Значения тангенсов и котангенсов кратных 90 градусов
- Тангенс 0 градусов равен 0, так как точка P уже пересекает ось X
- Котангенс 0 градусов бесконечен, так как тангенс никогда не пересекается с осью Y
- Тангенс 90 градусов бесконечен, так как тангенс никогда не пересекается с осью X
- Котангенс 90 градусов равен 0, так как точка P уже пересекается с осью Y
- Та же логика верна для 180 градусов и 270 градусов
Внутренние преступники:
Секанс и Косеканс
Этимология: Слово «secant» происходит от французского глагола «secanter», что означает «резать».
Визуализация: Рассмотрим ту же единичную окружность с тем же отрезком OP и касательной, проведенной к окружность в точке P. Длина между началом координат и точкой пересечения касательной с осью X равна секанс θ
Отрегулируйте угол с помощью следующего ползунка:
Или введите угол здесь:
Связь между секансом и косекансом:
Расстояние между началом координат и точкой пересечения той же касательной с осью Y равно Косеканс θ 92 \тета\] Значения секанса и косеканса, кратных 90 градусам
- Секанс 0 градусов равен 1, так как точка P совпадает с осью X
- Косеканс 0 градусов бесконечен, так как касательная никогда не пересекается с осью Y
- Секанс 90 градусов бесконечен, так как касательная никогда не пересекается с осью X
- Косеканс 0 градусов равен 1, так как точка P совпадает с осью Y
- Та же логика справедлива для 180 градусов и 270 градусов
Разработано ChanRT | Разветвите меня на Github
Сколько существует триггерных функций?
Сколько существует основных тригонометрических функций? Я приведу аргументы для 1, 3, 6 и, по крайней мере, 12.
Ответ калькулятора: 3
Типичный калькулятор имеет три функции триггера, если они есть: синуса, косинуса и тангенса. Остальные три, которые вы можете видеть, — косеканс, секанс и котангенс — являются величинами, обратными синусу, косинусу и тангенсу соответственно. Разработчики калькуляторов ожидают, что вы нажмете клавишу косинуса, а затем клавишу обратной величины, например, если вам нужна секанс.
Ответ из учебника по математическому анализу: 6
Самый популярный ответ на количество основных триггерных функций может быть шесть. В отличие от разработчиков калькуляторов, авторы учебников по математическому анализу считают функции косеканса, секанса и котангенса достаточно полезными, чтобы оправдать их включение в качестве первоклассных триггерных функций.
Исторический ответ: не менее 12
Есть еще по крайней мере шесть тригонометрических функций, которые когда-то считались достойными упоминания. Это версин, гаверсин, коверсин, гаковерсин, экссекант и экссекант.
Все это можно выразить просто в терминах более знакомых триггерных функций. Например, versine(θ) = 2 sin 2 (θ/2) = 1 – cos(θ) и секущая(θ) = sec(θ) – 1.
Зачем так много функций? Исторически одним из основных применений тригонометрии была навигация, и некоторые широко используемые навигационные формулы формулируются проще всего в терминах этих архаичных названий функций. Например, закон гаверсинусов. Современные читатели могут спросить, почему бы просто не упростить все до синусов и косинусов. Но когда вы вычисляете вручную, используя таблицы, каждая именованная функция требует значительных усилий для оценки. Если таблица просто объединяет две общие операции в одну функцию, это может иметь смысл.
Эти имена функций имеют простой шаблон. Приставка «ха-» означает «половину», как и в слове «полпенни». Префикс «ex-» означает «вычесть 1». Приставка «со-» означает то же, что и всегда. (Подробнее об этом ниже.) Префикс «ver-» означает 1 минус кофункция.
Бессмысленное упражнение: сколько различных функций вы могли бы придумать, используя каждую комбинацию префиксов? Порядок префиксов может иметь значение в одних случаях, но не в других.
Минималистский ответ: 1
Противоположным историческому ответу был бы минималистский ответ. Нам не нужны секансы, косекансы и котангенсы, потому что они просто обратные величины синусов, косинусов и тангенсов. И нам даже не нужен тангенс, потому что tan(θ) = sin(θ)/cos(θ). Итак, мы остановились на синусе и косинусе, но нам на самом деле не нужен косинус, потому что cos(θ) = sin(π/2 – θ).
Немногие помнят, что «со» в косинусе означает «дополнение». Косинус угла θ – это синус дополнительного угла π/2 – θ. То же соотношение справедливо для секанса и косеканса, тангенса и котангенса и даже версина и каверсинуса.
Кстати, понимание этой взаимодополняющей связи облегчает запоминание правил исчисления. Пусть foo(θ) — функция, производная которой равна bar(θ). Тогда цепное правило говорит, что производная от foo(π/2 – θ) равна -bar(π/2 – θ). Другими словами, если производная от foo — это bar, то производная от cofoo — отрицательная cobar. Замените свою любимую триггерную функцию на «foo».