Косинусы углов: Синус, косинус угла треугольника

alexxlab / / Разное

Найдите косинусы углов §10 №32 ГДЗ Геометрия 7-9 класс Погорелов А.В. – Рамблер/класс

Найдите косинусы углов §10 №32 ГДЗ Геометрия 7-9 класс Погорелов А.В. – Рамблер/класс

Интересные вопросы

Школа

Подскажите, как бороться с грубым отношением одноклассников к моему ребенку?

Новости

Поделитесь, сколько вы потратили на подготовку ребенка к учебному году?

Школа

Объясните, это правда, что родители теперь будут информироваться о снижении успеваемости в школе?

Школа

Когда в 2018 году намечено проведение основного периода ЕГЭ?

Новости

Будет ли как-то улучшаться система проверки и организации итоговых сочинений?

Вузы

Подскажите, почему закрыли прием в Московский институт телевидения и радиовещания «Останкино»?

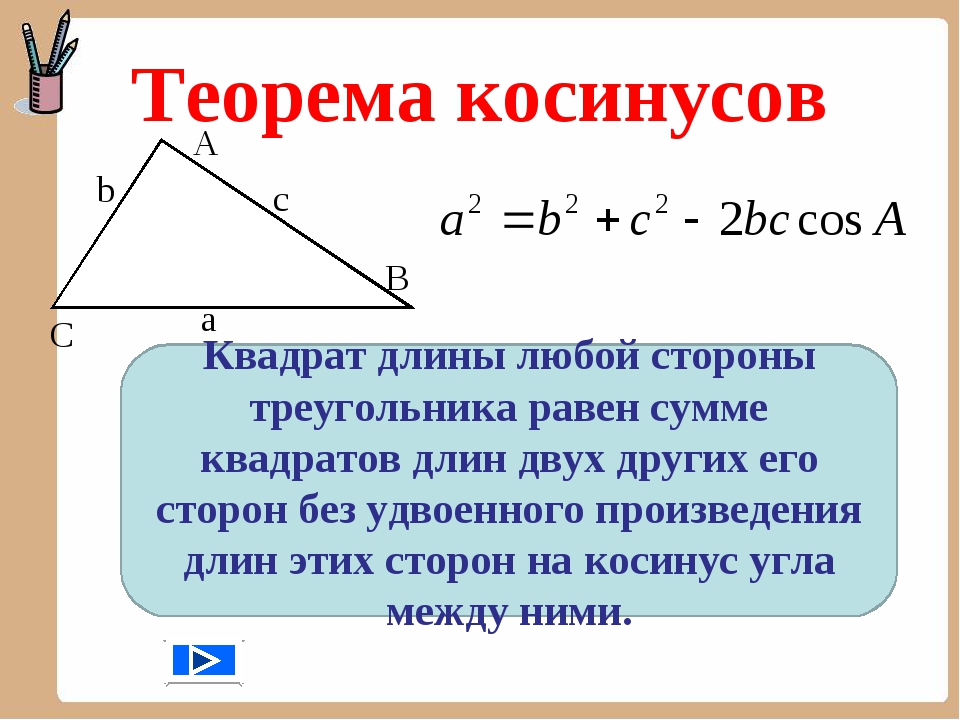
Даны вершины треугольника А (1; 1), В (4; 1), С (4; 5). Найдите косинусы углов треугольника.

ответы


cos C = 0,8.
Ответ: 0,6; 0; 0,8.
 

ваш ответ

Можно ввести 4000 cимволов

отправить

дежурный

Нажимая кнопку «отправить», вы принимаете условия  пользовательского соглашения

похожие темы

Экскурсии

Мякишев Г.Я.

Психология

Химия

похожие вопросы 5

Приготовление раствора сахара и расчёт его массовой доли в растворе. Химия. 8 класс. Габриелян. ГДЗ. Хим. практикум № 1. Практ. работа № 5.

Попробуйте провести следующий опыт. Приготовление раствора
сахара и расчёт его массовой доли в растворе.
Отмерьте мерным (Подробнее…)

ГДЗШкола8 классХимияГабриелян О.С.

Самостоятельная работа 19. Вариант 2. № 2 ГДЗ Геометрия 9 класс Зив Б.Г. Помогите доказать, используя параллельный перенос

Используя параллельный перенос, докажите, что углы при основании равнобедренной трапеции равны между собой.
 

ГДЗЭкзаменыГеометрия9 классЗив Б. Г.

ГДЗ Тема 21 Физика 7-9 класс А.В.Перышкин Задание №475 В обоих случаях поплавок плавает. В какую жидкость он погружается глубже?

Привет. Выручайте с ответом по физике…
Поплавок со свинцовым грузилом внизу опускают
сначала в воду, потом в масло. В обоих (Подробнее…)

ГДЗФизикаПерышкин А.В.Школа7 класс

ГДЗ Тема 21 Физика 7-9 класс А.В.Перышкин Задание №476 Изобразите силы, действующие на тело.

Привет всем! Нужен ваш совет, как отвечать…
Изобразите силы, действующие на тело, когда оно плавает на поверхности жидкости. (Подробнее…)

ГДЗФизикаПерышкин А.В.Школа7 класс

Не могу справиться с заданием, §8№26. Какой высоты должна быть….Геометрия 11 класс ГДЗ Погорелов

Не могу справиться с заданием, §8№26.
Сосуд имеет форму полушара радиуса R, дополненного ци-
линдром. Какой высоты должна (Подробнее. ..)

ГДЗ11 классГеометрияПогорелов А.В.

Mathway | Популярные задачи

1Найти точное значениеsin(30)
2Найти точное значениеsin(45)
3Найти точное значениеsin(30 град. )
4Найти точное значение
sin(60 град. )
5Найти точное значениеtan(30 град. )
6Найти точное значениеarcsin(-1)
7Найти точное значениеsin(pi/6)
8Найти точное значениеcos(pi/4)
9Найти точное значениеsin(45 град. )
10Найти точное значениеsin(pi/3)
11Найти точное значениеarctan(-1)
12Найти точное значениеcos(45 град. )
13Найти точное значениеcos(30 град. )
14Найти точное значениеtan(60)
15Найти точное значениеcsc(45 град. )
16Найти точное значениеtan(60 град. )
17Найти точное значениеsec(30 град.
)
18Найти точное значениеcos(60 град. )
19Найти точное значениеcos(150)
20Найти точное значениеsin(60)
21Найти точное значениеcos(pi/2)
22Найти точное значениеtan(45 град. )
23Найти точное значениеarctan(- квадратный корень из 3)
24Найти точное значениеcsc(60 град. )
25Найти точное значениеsec(45 град. )
26Найти точное значениеcsc(30 град. )
27Найти точное значениеsin(0)
28Найти точное значениеsin(120)
29Найти точное значениеcos(90)
30Преобразовать из радианов в градусы
pi/3
31Найти точное значениеtan(30)
32Преобразовать из градусов в радианы45
33Найти точное значениеcos(45)
34Упроститьsin(theta)^2+cos(theta)^2
35Преобразовать из радианов в градусыpi/6
36Найти точное значениеcot(30 град. )
37Найти точное значениеarccos(-1)
38Найти точное значениеarctan(0)
39Найти точное значениеcot(60 град. )
40Преобразовать из градусов в радианы30
41Преобразовать из радианов в градусы(2pi)/3
42Найти точное значениеsin((5pi)/3)
43Найти точное значениеsin((3pi)/4)
44Найти точное значениеtan(pi/2)
45Найти точное значениеsin(300)
46Найти точное значениеcos(30)
47Найти точное значениеcos(60)
48Найти точное значениеcos(0)
49Найти точное значениеcos(135)
50Найти точное значениеcos((5pi)/3)
51Найти точное значениеcos(210)
52Найти точное значениеsec(60 град. )
53Найти точное значениеsin(300 град. )
54Преобразовать из градусов в радианы135
55Преобразовать из градусов в радианы150
56Преобразовать из радианов в градусы(5pi)/6
57Преобразовать из радианов в градусы(5pi)/3
58Преобразовать из градусов в радианы89 град.
59Преобразовать из градусов в радианы60
60Найти точное значениеsin(135 град. )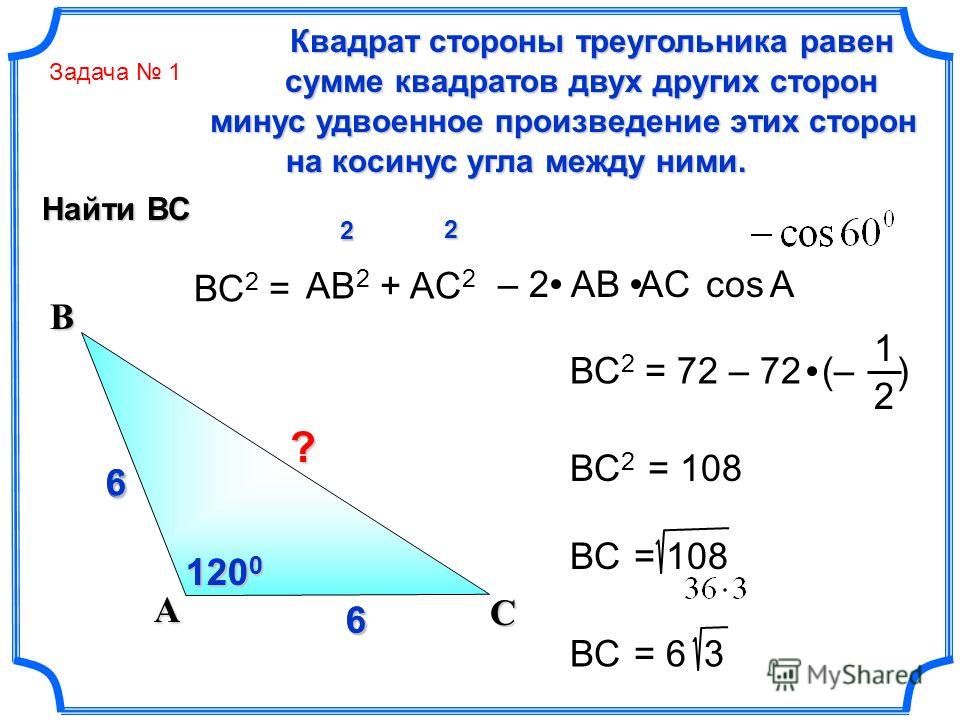
61Найти точное значениеsin(150)
62Найти точное значениеsin(240 град. )
63Найти точное значениеcot(45 град. )
64Преобразовать из радианов в градусы(5pi)/4
65Найти точное значениеsin(225)
66Найти точное значениеsin(240)
67Найти точное значениеcos(150 град. )
68Найти точное значениеtan(45)
69Вычислитьsin(30 град. )
70Найти точное значениеsec(0)
71Найти точное значениеcos((5pi)/6)
72Найти точное значениеcsc(30)
73Найти точное значениеarcsin(( квадратный корень из 2)/2)
74Найти точное значениеtan((5pi)/3)
75Найти точное значениеtan(0)
76Вычислитьsin(60 град. )
77Найти точное значениеarctan(-( квадратный корень из 3)/3)
78Преобразовать из радианов в градусы(3pi)/4
79Найти точное значениеsin((7pi)/4)
80Найти точное значениеarcsin(-1/2)
81Найти точное значениеsin((4pi)/3)
82Найти точное значениеcsc(45)
83Упроститьarctan( квадратный корень из 3)
84Найти точное значениеsin(135)
85Найти точное значениеsin(105)
86Найти точное значениеsin(150 град. )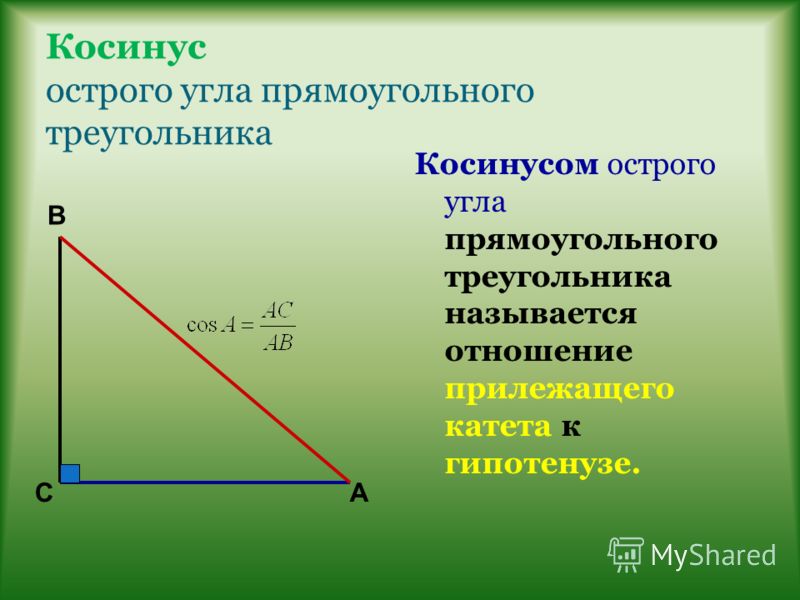
87Найти точное значениеsin((2pi)/3)
88Найти точное значениеtan((2pi)/3)
89Преобразовать из радианов в градусыpi/4
90Найти точное значениеsin(pi/2)
91Найти точное значениеsec(45)
92Найти точное значениеcos((5pi)/4)
93Найти точное значениеcos((7pi)/6)
94Найти точное значениеarcsin(0)
95		Найти точное значениеsin(120 град. )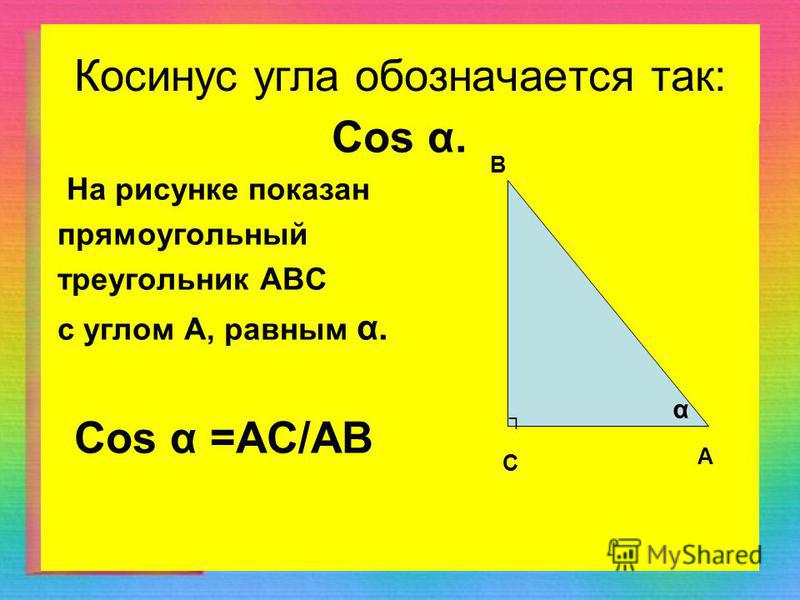
96Найти точное значениеtan((7pi)/6)
97Найти точное значениеcos(270)
98Найти точное значениеsin((7pi)/6)
99Найти точное значениеarcsin(-( квадратный корень из 2)/2)
100Преобразовать из градусов в радианы88 град.

Объяснение урока: Направляющие углы и направляющие косинусы

В этом объяснении мы научимся находить направляющие углы и направляющие косинусы для заданного вектора в пространстве.

Мы знаем, что в трехмерном координатном пространстве у нас есть 𝑥-, 𝑦- и 𝑧-оси. Они перпендикулярны друг другу, как показано на диаграмме ниже. Единица векторы ⃑𝑖, ⃑𝑗 и ⃑𝑘 действуют в 𝑥-, 𝑦- и 𝑧-направлениях соответственно.

Определение: углы направления

Для заданного вектора ⃑𝐴=𝐴,𝐴,𝐴 углы, которые этот вектор образует с осями 𝑥-, 𝑦- и 𝑧, равны 𝛼, 𝛽 , и 𝛾. Они известны как углы направления и записываются (𝛼,𝛽,𝛾).

Эти направляющие углы приводят нас к определению направляющих косинусов. Мы знаете, в прямоугольной тригонометрии косинус любого угла 𝜃 равен длина стороны, примыкающей к углу, деленная на длину гипотенузы: cosadjhyp𝜃=.

Определение: Направляющие косинусы

Направляющие косинусы представляют собой косинусы трех направляющих углов 𝛼, 𝛽 и 𝛾: Coscoscos𝛼 = 𝐴𝐴⃑𝐴⃑𝐴⃑𝐴⃑𝐴, 𝛽 = 𝐴𝐴⃑𝐴⃑𝐴⃑𝐴⃑𝐴, 𝛾 = 𝐴𝐴⃑𝐴⃑𝐴⃑𝐴. 

𝐴, 𝐴 и 𝐴 𝑥-, 𝑦- и и 𝑧-компоненты вектора ⃑𝐴, а ‖‖⃑𝐴‖‖ — величина или норма этого вектора, где ‖‖⃑𝐴‖‖=(𝐴)+𝐴+(𝐴).

Мы можем переставить три уравнения так, чтобы 𝛼 = 𝐴𝐴⃑𝐴⃑𝐴⃑𝐴⃑𝐴, 𝛽 = 𝐴𝐴𝐴⃑𝐴⃑𝐴⃑𝐴⃑𝐴, 𝛾 = 𝐴𝐴⃑𝐴⃑𝐴⃑𝐴 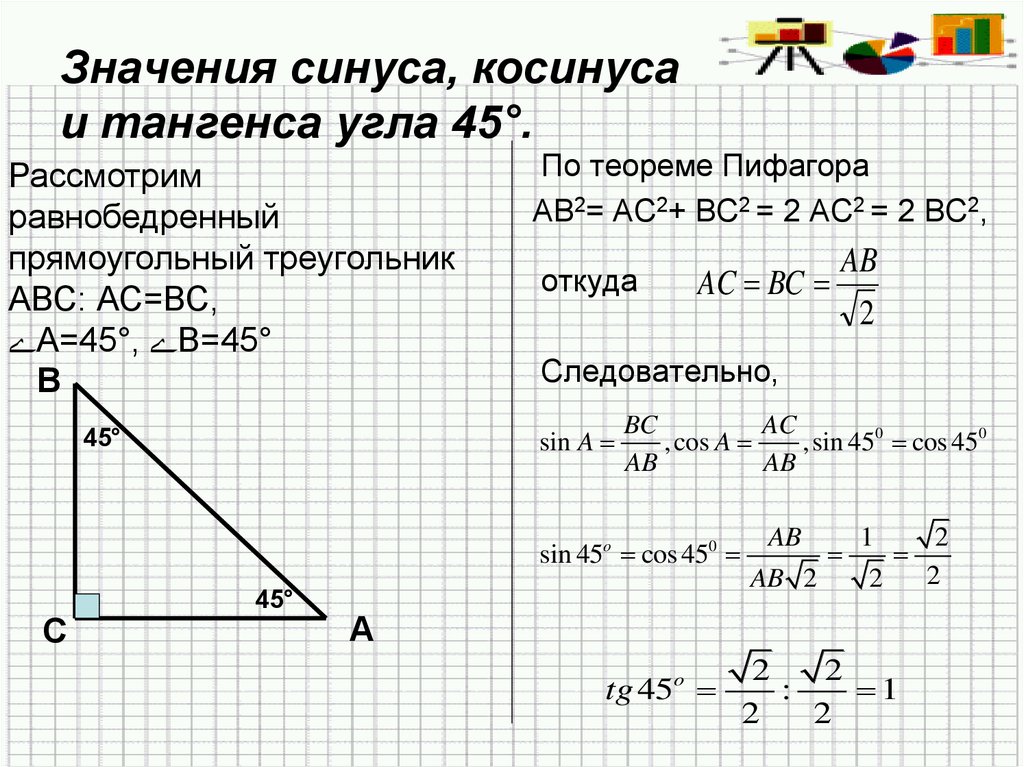. coscoscos

В нашем первом примере, мы продемонстрируем, как найти вектор ⃑𝐴, зная его направляющие углы и величину.

Пример 1. Нахождение вектора по его норме и направлению Углы

Найдите вектор ⃑𝐴, норма которого равна 41, а направляющие углы равны (135,120,60)∘∘∘.

Ответ

Норма вектора — это его величина или длина, а направляющие углы 𝛼, 𝛽 и 𝛾 — это углы между вектором и 𝑥-, 𝑦- и 𝑧-осями соответственно.

Используя формулы для направляющих косинусов, мы знаем, что для вектора ⃑𝐴=𝐴,𝐴,𝐴, coscoscos𝛼 = 𝐴𝐴⃑𝐴⃑𝐴⃑𝐴⃑𝐴, 𝛽 = 𝐴𝐴𝐴⃑𝐴⃑𝐴⃑𝐴, 𝛾 = 𝐴𝐴⃑𝐴⃑𝐴⃑𝐴⃑𝐴. следует: 𝐴 = ‖⃑𝐴⃑𝐴⃑𝐴⃑𝐴𝛼 = 41135 = −41√22, 𝐴 = ‖⃑𝐴⃑𝐴⃑𝐴⃑𝐴𝛽 = 41120 = −412, 𝐴 = ‖⃑𝐴⃑𝐴⃑𝐴⃑𝐴 = 4160 = 412.∘∘∘coscoscoscoscoscos

Следовательно, ⃑𝐴=−41√22,−412,412.

Прежде чем перейти к следующему примеру, рассмотрим формулу, связывающую направляющие косинусы.

Рассмотрим направление косинусов следующим образом: coscoscos𝛼=𝐴‖‖⃑𝐴‖‖,𝛽=𝐴‖‖⃑𝐴‖‖,𝛾=𝐴‖‖⃑𝐴‖‖.

Возведение в квадрат обеих частей этих трех уравнений дает нам Coscoscos𝛼 = (𝐴) ⃑𝐴⃑𝐴⃑𝐴, 𝛽 = 𝐴𝐴𝐴⃑𝐴⃑𝐴⃑𝐴, 𝛾 = (𝐴) ⃑𝐴⃑𝐴‖ .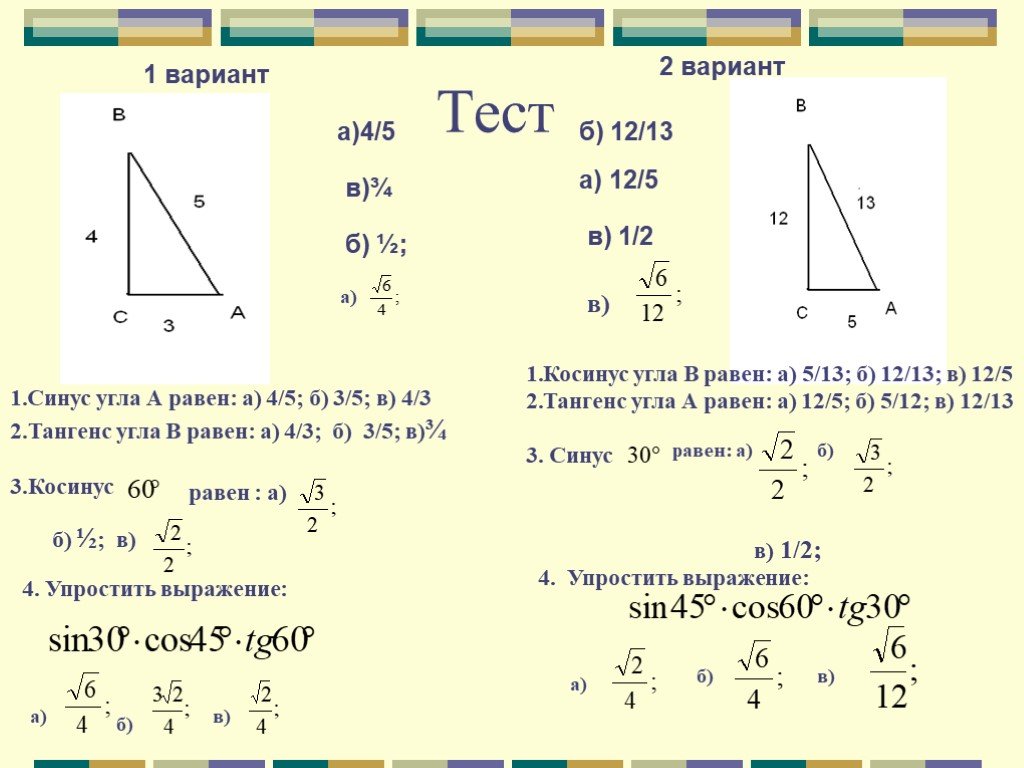

Складывая эти три уравнения, мы получаем coscoscos𝛼+𝛽+𝛾=(𝐴)+𝐴+(𝐴)‖‖⃑𝐴‖‖.

Мы также знаем, что ‖‖⃑𝐴‖‖=(𝐴)+𝐴+(𝐴).

Итак, ‖‖⃑𝐴‖‖=(𝐴)+𝐴+(𝐴).

Это означает, что правая часть уравнения равна 1.

Следовательно, coscoscos𝛼+𝛽+𝛾=1.

Формула: свойство направляющих косинусов трехмерного вектора

Если 𝛼, 𝛽 и 𝛾 — три угла направления, а cos𝛼 , cos𝛽 и cos𝛾 — соответствующие косинусы направления, то coscoscos𝛼+𝛽+𝛾=1.

Пример 2. Нахождение третьего направляющего угла вектора

Предположим, что 31∘, 65∘ и 𝜃 — это направляющие углы вектора. Что из следующего с точностью до сотой является 𝜃?

  1. 72.88∘
  2. 85.03∘
  3. 264.00∘
  4. 84.00∘

Ответ

, чтобы ответить на этот вопрос, мы будем использовать факт, что если три направления вектора 𝛼, и, и, и, и, и и, и, и, и, и, и, и, и, и, и, и, и, и, и, и, и, и, и, и, и, и, и, и, и, и, и, и, и, и, и, и, и, и, и и, и, и и, и, и мы будем использовать тот факт, что трех 𝛾, тогда coscoscos𝛼+𝛽+𝛾=1.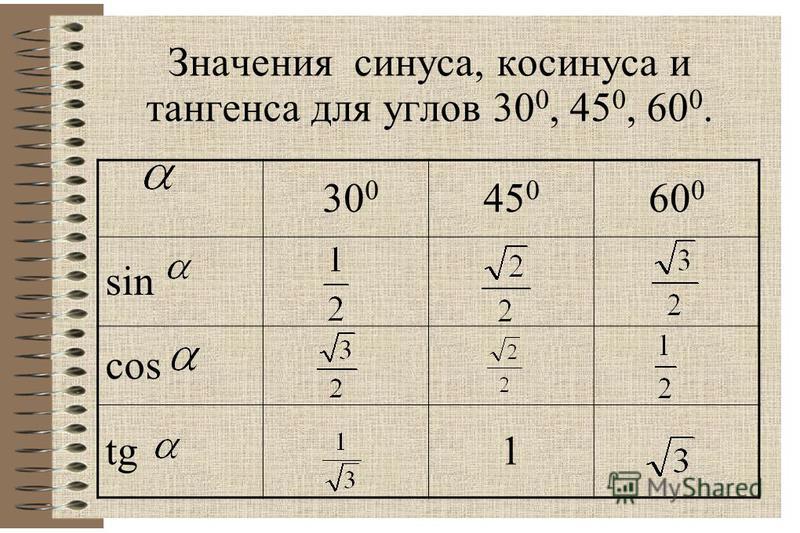

Если мы допустим 𝛼=31∘, 𝛽=65∘ и 𝛾=𝜃∘, то coscoscoscos∘∘31+65+𝜃=10,91334+𝜃≈1𝜃≈1−0,91334.

Извлекая квадратный корень из обеих частей нашего уравнения, cos𝜃≈0,29437.

Взяв арккосинус обеих сторон, 𝜃≈72,8797.∘

Итак, значение 𝜃 с точностью до сотой равно 72,88∘.

В следующем примере мы покажем, как вычислить направляющие косинусы вектора.

Пример 3. Нахождение направляющих косинусов вектора

Найдите направляющие косинусы вектора ⃑𝐴=(5,2,8).

Ответ

Для любого вектора ⃑𝐴 с компонентами 𝐴, 𝐴 и 𝐴 направляющие косинусы равны coscoscos𝛼=𝐴‖‖⃑𝐴‖‖,𝛽=𝐴‖‖⃑𝐴‖‖,𝛾=𝐴‖‖⃑𝐴‖‖, где ‖‖⃑𝐴‖‖=(𝐴)+𝐴+(𝐴).

Подставляя 𝐴=5, 𝐴=2 и 𝐴=8, имеем ‖‖⃑𝐴‖‖=(5)+(2)+(8)‖‖⃑𝐴‖‖=√93.

Следовательно, coscoscos𝛼=5√93,𝛽=2√93,𝛾=8√93.

Направляющие косинусы вектора ⃑𝐴 равны 5√93,2√93,8√93.

Пример 4. Нахождение углов направления вектора

Найдите направляющие углы вектора 212,21√22,212.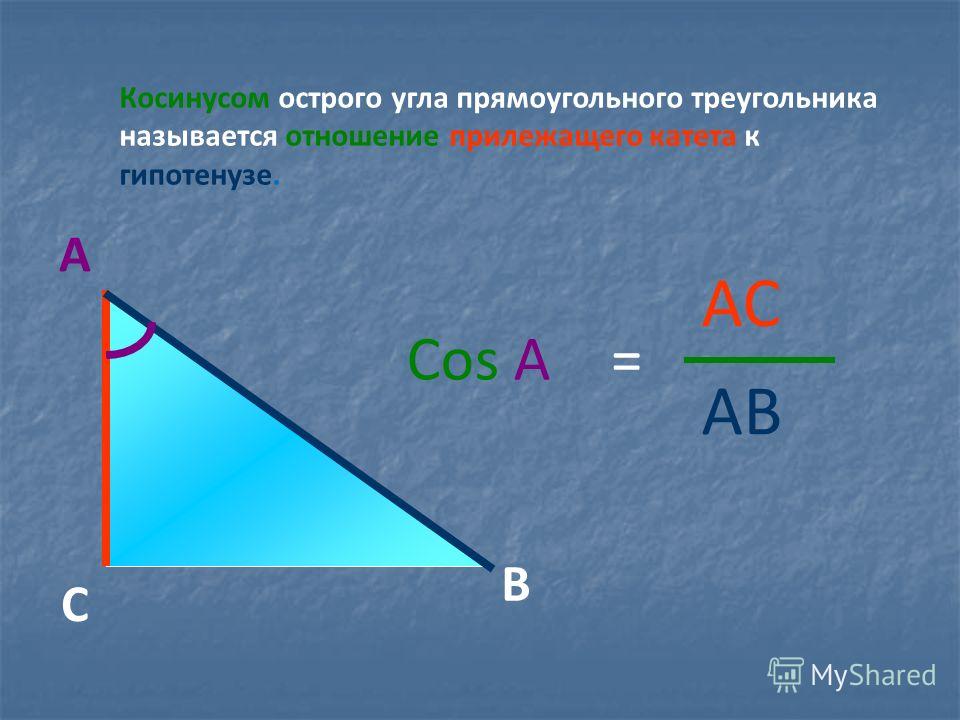

Ответ

Для любого вектора ⃑𝐴 с компонентами 𝐴, 𝐴 и 𝐴 направляющие косинусы равны coscoscos𝛼=𝐴‖‖⃑𝐴‖‖,𝛽=𝐴‖‖⃑𝐴‖‖,𝛾=𝐴‖‖⃑𝐴‖‖, где ‖‖⃑𝐴‖‖=(𝐴)+𝐴+(𝐴).

Подставляя 𝐴=212, 𝐴=21√22 и 𝐴=212, имеем ‖‖⃑𝐴‖‖=212+21√22+212‖‖⃑𝐴‖‖‖=√441‖‖⃑𝐴‖‖=21. 9003 coscoscos𝛼=21,𝛽=21,𝛾=21,√ которые упрощают до coscoscos𝛼=12,𝛽=√22,𝛾=12.

Взяв арккосинус обеих частей этих трех уравнений, 𝛼=60,𝛽=45,𝛾=60.∘∘∘

Углы направления вектора 212,21√22,212 равны (60,45,60)∘∘∘.

Пример 5. Нахождение углов направления вектора

Найдите меру углов направления вектора ⃑𝐹, представленного заданным цифра, скорректированная до одного десятичного знака.

Ответ

Начнем с того, что запишем вектор ⃑𝐹 в терминах его трех компонент, где мы определите 1 единицу как 1 см.

В 𝑥-направлении мы проходим 8 см, поэтому 𝑥-компонента равна 8. В 𝑦-направлении мы проходим 19см, поэтому 𝑦-компонента равна 19. В 𝑧-направлении мы проходим 9 см, поэтому 𝑧-компонента 9: ⃑𝐹=(8,19,9).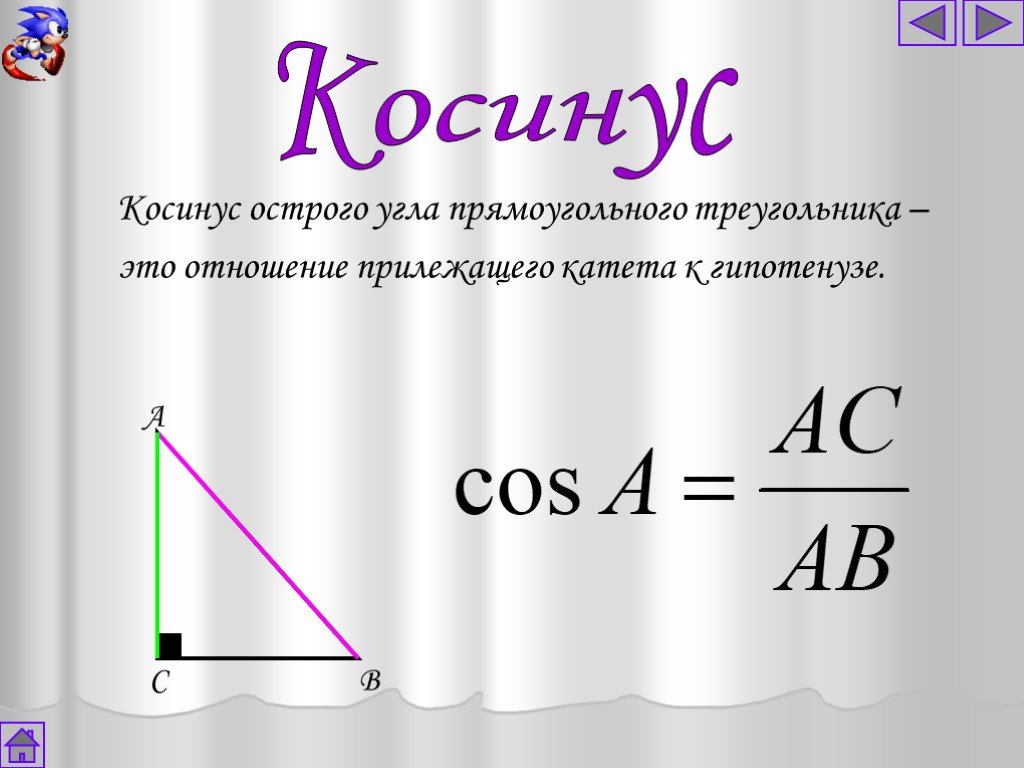

Величина вектора ‖‖⃑𝐹‖‖=(𝐹)+𝐹+(𝐹), где 𝐹, 𝐹 и 𝐹 — 𝑥-, 𝑦- и 𝑧-компоненты вектора ⃑𝐹: ‖‖⃑𝐹‖‖=(8)+(19)+(9)‖‖⃑𝐹‖‖=√506.

Дан любой вектор ⃑𝐹 с компонентами 𝐹, 𝐹 и 𝐹 и направляющими углами 𝜃, 𝜃 и 𝜃, 𝜃 = 𝐹𝐹⃑𝐹⃑𝐹⃑𝐹⃑𝐹𝜃 = 𝐹𝐹𝐹⃑𝐹⃑𝐹⃑𝐹𝜃 = 𝐹𝐹𝐹⃑𝐹⃑𝐹.coscoscos

Итак, 𝜃=8√506𝜃=69,2,𝜃=19√506𝜃=32,4, 𝜃=9√506𝜃=66,4.0003

Следовательно, направляющие углы вектора ⃑𝐹 равны 𝜃=69,2∘, 𝜃=32,4∘, 𝜃=66,4∘.

Мы закончим это объяснение повторением некоторых ключевых моментов.

Ключевые точки

  • Направляющие углы 𝛼, 𝛽 и 𝛾 — это углы между вектором и осями 𝑥-, 𝑦- и 𝑧 соответственно.
  • Косинусы направления представляют собой косинусы трех углов направления, 𝛼, 𝛽 и 𝛾, такой, что coscoscos𝛼=𝐴‖‖⃑𝐴‖‖,𝛽=𝐴‖‖⃑𝐴‖‖,𝛾=𝐴‖‖⃑𝐴‖‖.
  • Это означает, что 𝛼, и 𝛾 равны: 𝛼=𝐴‖‖⃑𝐴‖‖,𝛽=𝐴‖‖⃑𝐴‖‖,𝛾=𝐴‖‖⃑𝐴‖‖.coscoscos0062
  • Следующая формула связывает косинусы трех направлений: coscoscos𝛼+𝛽+𝛾=1.

2.

2: Закон косинусов
  1. Последнее обновление
  2. Сохранить как PDF
  • Идентификатор страницы
    3255 9\circ} = \dfrac{5}{\sin\;C} ,\nonumber \]

    , которое мы уже знали и в котором еще есть два неизвестных! Таким образом, эту задачу нельзя решить с помощью закона синусов.

    Чтобы решить треугольник в приведенном выше примере, мы можем использовать закон косинусов :

    Теорема \(\PageIndex{1}\): Закон косинусов

    Если треугольник имеет длины сторон \(a \), \(b \) и \(c \), противоположные углам \(A \) , \(B \) и \(C \) соответственно, то

    \[\begin{align} 92 — 2ab\;\cos\;C ~.\label{2.11} \\[4pt]
    \end{align} \nonumber \]

    Доказательство

    Чтобы доказать закон косинусов, пусть \(\triangle\ ,ABC \) — косой треугольник. Тогда \(\треугольник\,ABC\) может быть острым, как на рисунке \(\PageIndex{1a}\), или тупым, как на рисунке \(\PageIndex{1b}\). В каждом случае проведите высоту от вершины \(C \) до стороны \(\overline{AB} \). На рисунке \(\PageIndex{1a}\) высота делит \(\overline{AB} \) на два отрезка длины \(x \) и \(c-x \), а на рисунке \(\PageIndex{ 1b}\) высота продолжает сторону \(\overline{AB} \) на расстояние \(x \). Пусть \(h \) высота высоты. 92 ~-~ 2ca\;\cos\;B ~.\label{2.16} \]

    Итак, как для остроугольных, так и для тупоугольных треугольников мы доказали уравнение \ref{2.10} закона косинусов. Заметьте, что доказательство было для \(B\) острого и тупого. Аналогичными рассуждениями для \(A\) и \(C\) мы получаем две другие формулы.

    \(\square\)

    Обратите внимание, что мы не доказывали закон косинусов для прямоугольных треугольников, поскольку оказалось (см. упражнение 15), что все три формулы для этого случая сводятся к теореме Пифагора. Закон косинусов можно рассматривать как обобщение теоремы Пифагора.

    Кроме того, обратите внимание, что достаточно запомнить только одно из трех уравнений \ref{2.9}-\ref{2.11}, так как два других можно получить, «перебирая» буквы \(a \), \( b \) и \(c \), то есть заменить \(a \) на \(b \), заменить \(b \) на \(c \) и заменить \(c \) на \( a \) (аналогично для заглавных букв). Один цикл даст вам вторую формулу, а другой цикл даст вам третью.

    Угол между двумя сторонами треугольника часто называют включенным углом 9\цирк\; \)}\).

    Обратите внимание, что в примере \(\PageIndex{2}\) было только одно решение. Для случая 3 это будет всегда истинным: если даны две стороны и угол между ними, треугольник будет иметь ровно одно решение. Причина проста: при соединении двух отрезков в общей вершине для образования угла существует ровно один способ соединить их свободные концы с третьим отрезком, независимо от величины угла.

    Вам может быть интересно, почему мы использовали закон косинусов во второй раз в примере \(\PageIndex{2}\), чтобы найти угол \(B \). 2\), чтобы найти \(B\): 92}{2(3)(6)} ~=~ 1.139 ~,
    \nonumber \]

    что невозможно, так как \(| \cos\;A | \le 1 \). Таким образом, существует \(\fbox{нет решения}\).

    Мы могли бы избавить себя от некоторых усилий, если бы признали, что длина одной из сторон (\(c=6\)) больше суммы длин остальных сторон (\(a=2\) и \ (b=3\)), что (как показано на рисунке ниже) невозможно в треугольнике.

    Закон косинусов также можно использовать для решения треугольников в случае 2 (две стороны и один противоположный угол), хотя он используется для этой цели реже, чем закон синусов. Следующий пример дает представление о том, как это сделать. 9\circ ~,
    \nonumber \]

    , что близко к тому, что мы нашли раньше (небольшая разница из-за различного округления). Аналогично можно получить другой набор решений.

    Как и закон синусов, закон косинусов можно использовать для доказательства некоторых геометрических фактов, как в следующем примере.

    Пример \(\PageIndex{6}\): Диагонали параллелограмма

    Используйте закон косинусов, чтобы доказать, что сумма квадратов диагоналей любого параллелограмма равна сумме квадратов сторон.

    No related posts.

    • Добавить комментарий

    Ваш адрес email не будет опубликован. Обязательные поля помечены *