ОглавлениеПРЕДИСЛОВИЕАНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ § 1. Понятие о предмете аналитической геометрии § 2. Координаты § 3. Прямоугольная система координат § 4. Прямоугольные координаты § 5. Координатные углы § 6. Косоугольная система координат § 7. Уравнение линии § 8. Взаимное расположение линии и точки § 9.  § 10. Расстояние между двумя точками § 11. Деление отрезка в данном отношении § 11а. Деление отрезка пополам § 12. Определитель второго порядка § 13. Площадь треугольника § 14. Прямая линия; уравнение, разрешенное относительно ординаты (с угловым коэффициентом) § 15. Прямая, параллельная оси § 16. Общее уравнение прямой § 17. Построение прямой по ее уравнению § 18. Условие параллельности прямых § 19. Пересечение прямых § 20. Условие перпендикулярности двух прямых § 21. Угол между двумя прямыми § 22. Условие, при котором три точки лежат на одной прямой § 23. Уравнение прямой, проходящей через две точки § 24. Пучок прямых § 25. Уравнение прямой, проходящей через данную точку параллельно данной прямой § 26. Уравнение прямой, проходящей через данную точку перпендикулярно данной прямой § 27. Взаимное расположение прямой и пары точек § 28. Расстояние от точки до прямой § 29. Полярные параметры прямой § 30.  2+bx+c§ 51. Директрисы эллипса и гиперболы § 52. Общее определение эллипса, гиперболы и параболы § 53. Конические сечения § 54. Диаметры конического сечения § 55. Диаметры эллипса § 56. Диаметры гиперболы § 57. Диаметры параболы § 58. Линии второго порядка § 59. Запись общего уравнения второй степени § 60. Упрощение уравнения второй степени; общие замечания § 61. Предварительное преобразование уравнения второй степени § 62. Завершающее преобразование уравнения второй степени § 63. О приемах, облегчающих упрощение уравнения второй степени § 64. Признак распадения линий второго порядка § 65. Нахождение прямых, составляющих распадающуюся линию второго порядка § 66. Инварианты уравнения второй степени § 67. Три типа линий второго порядка § 68. Центральные и нецентральные линии второго порядка § 70. Упрощение уравнения центральной линии второго порядка § 71.  Равносторонняя гипербола как график уравнения y=k/x§ 72. Равносторонняя гипербола как график уравнения y=(mx+n)/(px+q) § 73. Полярные координаты § 74. Связь между полярными и прямоугольными координатами § 75. Архимедова спираль § 76. Полярное уравнение прямой § 77. Полярное уравнение конического сечения АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ § 78. Понятие о векторах и скалярах § 79. Вектор в геометрии § 80. Векторная алгебра § 81. Коллинеарные векторы § 82. Нуль-вектор § 83. Равенство векторов § 84. Приведение векторов к общему началу § 85. Противоположные векторы § 86. Сложение векторов § 87. Сумма нескольких векторов § 88. Вычитание векторов § 89. Умножение и деление вектора на число § 90. Взаимная связь коллинеарных векторов (деление вектора на вектор) § 91. Проекция точки на ось § 92. Проекция вектора на ось § 93. Основные теоремы о проекциях вектора § 94. Прямоугольная система координат в пространстве § 95.  Координаты точки§ 96. Координаты вектора § 97. Выражения вектора через компоненты и через координаты § 98. Действия над векторами, заданными своими координатами § 99. Выражение вектора через радиусы-векторы его начала и конца § 100. Длина вектора. Расстояние между двумя точками § 101. Угол между осью координат и вектором § 102. Признак коллинеарности (параллельности) векторов § 103. Деление отрезка в данном отношении § 104. Скалярное произведение двух векторов § 104а. Физический смысл скалярного произведения § 105. Свойства скалярного произведения § 106. Скалярные произведения основных векторов § 108. Условие перпендикулярности векторов § 109. Угол между векторами § 110. Правая и левая системы трех векторов § 111. Векторное произведение двух векторов § 112. Свойства векторного произведения § 113. Векторные произведения основных векторов § 114.  Выражение векторного произведения через координаты сомножителей§ 115. Компланарные векторы § 116. Смешанное произведение § 117. Свойства смешанного произведения § 118. Определитель третьего порядка § 119. Выражение смешанного произведения через координаты сомножителей § 120. Признак компланарности в координатной форме § 121. Объем параллелепипеда § 122. Двойное векторное произведение § 123. Уравнение плоскости § 124. Особые случаи положения плоскости относительно системы координат § 125. Условие параллельности плоскостей § 126. Условие перпендикулярности плоскостей § 127. Угол между двумя плоскостями § 128. Плоскость, проходящая через данную точку параллельно данной плоскости § 129. Плоскость, проходящая через три точки § 130. Отрезки на осях § 131. Уравнение плоскости в отрезках § 132. Плоскость, проходящая через две точки перпендикулярно данной плоскости § 133. Плоскость, проходящая через данную точку перпендикулярно двум плоскостям § 134.  Точка пересечения трех плоскостей§ 135. Взаимное расположение плоскости и пары точек § 136. Расстояние от точки до плоскости § 137. Полярные параметры плоскости § 138. Нормальное уравнение плоскости § 139. Приведение уравнения плоскости к нормальному виду § 140. Уравнения прямой в пространстве § 141. Условие, при котором два уравнения первой степени представляют прямую § 143. Направляющий вектор § 144. Углы между прямой и осями координат § 145. Угол между двумя прямыми § 146. Угол между прямой и плоскостью § 147. Условия параллельности и перпендикулярности прямой и плоскости § 148. Пучок плоскостей § 149. Проекции прямой на координатные плоскости § 150. Симметричные уравнения прямой § 151. Приведение уравнений прямой к симметричному виду § 152. Параметрические уравнения прямой § 153. Пересечение плоскости с прямой, заданной параметрически § 154. Уравнения прямой, проходящей через две данные точки § 155. 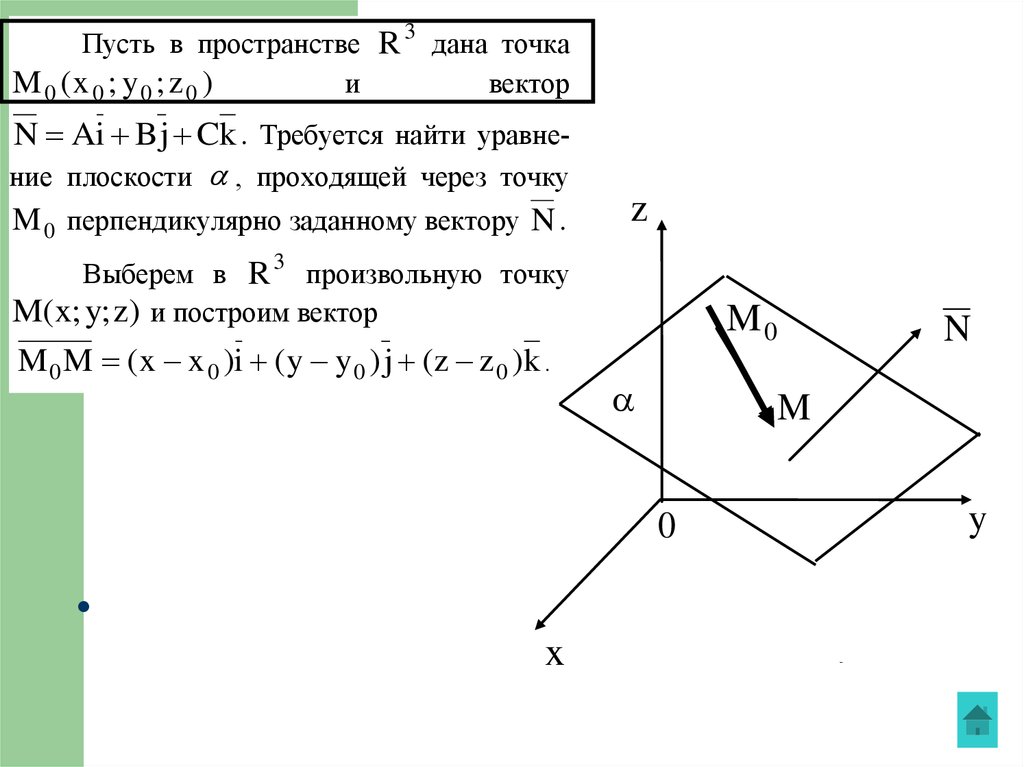 Уравнение плоскости, проходящей через данную точку перпендикулярно данной прямой§ 156. Уравнения прямой, проходящей через данную точку перпендикулярно данной плоскости § 157. Уравнение плоскости, проходящей через данную точку и данную прямую § 158. Уравнение плоскости, проходящей через данную точку и параллельной двум данным прямым § 159. Уравнение плоскости, проходящей через данную прямую и параллельной другой данной прямой § 160. Уравнение плоскости, проходящей через данную прямую и перпендикулярной данной плоскости § 161. Уравнения перпендикуляра, опущенного из данной точки на данную прямую § 162. Длина перпендикуляра, опущенного из данной точки на данную прямую § 163. Условие, при котором две прямые пересекаются или лежат в одной плоскости § 164. Уравнения общего перпендикуляра к двум данным прямым § 165. Кратчайшее расстояние между двумя прямыми § 165а. Правые и левые пары прямых § 166. Преобразование координат § 167. Уравнение поверхности § 168.  Цилиндрические поверхности, у которых образующие параллельны одной из осей координат§ 170. Проекция линии на координатную плоскость § 171. Алгебраические поверхности и их порядок § 172. Сфера § 173. Эллипсоид § 174. Однополостный гиперболоид § 175. Двуполостный гиперболоид § 176. Конус второго порядка § 177. Эллиптический параболоид § 178. Гиперболический параболоид § 179. Перечень поверхностей второго порядка § 180. Прямолинейные образующие поверхностей второго порядка § 181. Поверхности вращения § 182. Определители второго и третьего порядков § 183. Определители высших порядков § 184. Свойства определителей § 185. Практический прием вычисления определителей § 186. Применение определителей к исследованию и решению системы уравнений § 187. Два уравнения с двумя неизвестными § 188. Два уравнения с двумя неизвестными § 189. Однородная система двух уравнений с тремя неизвестными § 190. Два уравнения с двумя неизвестными§ 190а. Система n уравнений с n неизвестными ОСНОВНЫЕ ПОНЯТИЯ МАТЕМАТИЧЕСКОГО АНАЛИЗА § 192. Рациональные числа § 193. Действительные (вещественные) числа § 194. Числовая ось § 195. Переменные и постоянные величины § 196. Функция § 197. Способы задания функции § 198. Область определения функции § 199. Промежуток § 200. Классификация функций § 201. Основные элементарные функции § 202. Обозначение функции § 203. Предел последовательности § 204. Предел функции § 205. Определение предела функции § 206. Предел постоянной величины § 207. Бесконечно малая величина § 208. Бесконечно большая величина § 209. Связь между бесконечно большими и бесконечно малыми величинами § 210. Ограниченные величины § 211. Расширение понятия предепа § 212. Основные свойства бесконечно малых величин § 213. Основные теоремы о пределах § 214. Число е § 215. Предел sinx/x при x стремящемся к 0 Эквивалентные бесконечно малые величины§ 217. Сравнение бесконечно малых величин § 217а. Приращение переменной величины § 218. Непрерывность функции в точке § 219. Свойства функций, непрерывных в точке § 219а. Односторонний предел; скачок функции § 220. Непрерывность функции на замкнутом промежутке § 221. Свойства функций, непрерывных на замкнутом промежутке ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ § 223. Скорость § 224. Определение производной функции § 225. Касательная § 226. Производные некоторых простейших функций § 227. Свойства производной § 228. Дифференциал § 229. Механический смысл дифференциала § 230. Геометрический смысл дифференциала § 231. Дифференцируемые функции § 232. Дифференциалы некоторых простейших функций § 233. Свойства дифференциала § 234. Инвариантность выражения f'(x)dx § 235. Выражение производной через дифференциалы § 236. Функция от функции (сложная функция) § 237. Дифференциал сложной функции § 238. Производная сложной функции§ 239. Дифференцирование произведения § 240. Дифференцирование частного (дроби) § 241. Обратная функция § 242. Натуральные логарифмы § 243. Дифференцирование логарифмической функции § 244. Логарифмическое дифференцирование § 245. Дифференцирование показательной функции § 246. Дифференцирование тригонометрических функций § 247. Дифференцирование обратных тригонометрических функций § 247а. Некоторые поучительные примеры § 248. Дифференциал в приближенных вычислениях § 249. Применение дифференциала к оценке погрешности формул § 250. Дифференцирование неявных функций § 251. Параметрическое задание линии § 252. Параметрическое задание функции § 253. Циклоида § 254. Уравнение касательной к плоской линии § 254а. Касательные к кривым второго порядка § 255. Уравнение нормали § 256. Производные высших порядков § 257. Механический смысл второй производной § 258. Дифференциалы высших порядков § 259. Выражение высших производных через дифференциалы§ 260. Высшие производные функций, заданных параметрически § 261. Высшие производные неявных функций § 262. Правило Лейбница § 263. Теорема Ролля § 264. Теорема Лагранжа о среднем значении § 265. Формула конечных приращений § 266. Обобщенная теорема о среднем значении (Коши) § 267. Раскрытие неопределенности вида 0/0 § 268. Раскрытие неопределенности вида бесконесность на бесконечность § 269. Неопределенные выражения других видов § 270. Исторические сведения о формуле Тейлора § 271. Формула Тейлора § 272. Применение формулы Тейлора к вычислению значений функции § 273. Возрастание и убывание функции § 274. Признаки возрастания и убывания функции в точке § 274а. Признаки возрастания и убывания функции в промежутке § 275. Максимум и минимум § 276. Необходимое условие максимума и минимума § 277. Первое достаточное условие максимума и минимума § 278. Правило нахождения максимумов и минимумов § 279. Второе достаточное условие максимума и минимума§ 280. Нахождение наибольшего и наименьшего значений функции § 281. Выпуклость плоских кривых; точка перегиба § 282. Сторона вогнутости § 283. Правило для нахождения точек перегиба § 284. Асимптоты § 285. Нахождение асимптот, параллельных координатным осям § 286. Нахождение асимптот, не параллельных оси ординат § 287. Приемы построения графиков § 288. Решение уравнений. Общие замечания § 289. Решение уравнений. Способ хорд § 290. Решение уравнений. Способ касательных § 291. Комбинированный метод хорд и касательных ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ § 293. Первообразная функция § 294. Неопределенный интеграл § 295. Геометрический смысл интегрирования § 296. Вычисление постоянной интегрирования по начальным данным § 297. Свойства неопределенного интеграла § 298. Таблица интегралов § 299. Непосредственное интегрирование § 300. Способ подстановки (интегрирование через вспомогательную переменную) § 301. Интегрирование по частям§ 302. Интегрирование некоторых тригонометрических выражений § 303. Тригонометрические подстановки § 304. Рациональные функции § 304а. Исключение целой части § 305. О приемах интегрирования рациональных дробей § 306. Интегрирование простейших рациональных дробей § 307. Интегрирование рациональных функций (общий метод) § 308. О разложении многочлена на множители § 309. Об интегрируемости в элементарных функциях § 310. Некоторые интегралы, зависящие от радикалов § 311. Интеграл от биномиального дифференциала § 312. Интегралы вида … § 313. Интегралы вида S R(sinx, cosx)dx § 314. Определенный интеграл § 315. Свойства определенного интеграла § 316. Геометрический смысл определенного интеграла § 317. Механический смысл определенного интеграла § 318. Оценка определенного интеграла § 318а. Неравенство Буняковского § 319. Теорема о среднем интегрального исчисления § 320. Определенный интеграл как функция верхнего предела § 321. Дифференциал интеграла§ 322. Интеграл дифференциала. Формула Ньютона — Лейбница § 323. Вычисление определенного интеграла с помощью неопределенного § 324. Определенное интегрирование по частям § 325. Способ подстановки в определенном интеграле § 326. О несобственных интегралах § 327. Интегралы с бесконечными пределами § 328. Интеграл функции, имеющей разрыв § 329. О приближенном вычислении интеграла § 330. Формулы прямоугольников § 331. Формула трапеций § 332. Формула Симпсона (параболических трапеций) § 333. Площади фигур, отнесенных к прямоугольным координатам § 334. Схема применения определенного интеграла § 335. Площади фигур, отнесенных к полярным координатам § 336. Объем тела по поперечным сечениям § 337. Объем тела вращения § 338. Длина дуги плоской линии § 339. Дифференциал дуги § 340. Длина дуги и ее дифференциал в полярных координатах § 341. Площадь поверхности вращения ОСНОВНЫЕ СВЕДЕНИЯ О ПЛОСКИХ И ПРОСТРАНСТВЕННЫХ ЛИНИЯХ § 342. Кривизна§ 343. Центр, радиус и круг кривизны плоской линии § 344. Формулы для кривизны, радиуса и центра кривизны плоской линии § 345. Эволюта плоской линии § 346. Свойства эволюты плоской линии § 347. Развертка (эвольвента) плоской линии § 348. Параметрическое задание пространственной линии § 349. Винтовая линия § 350. Длина дуги пространственной линии § 351. Касательная к пространственной линии § 352. Нормальная плоскость § 353. Вектор-функция скалярного аргумента § 354. Предел вектор-функции § 355. Производная вектор-функции § 356. Дифференциал вектор-функции § 357. Свойства производной и дифференциала вектор-функции § 358. Соприкасающаяся плоскость § 359. Главная нормаль. Сопутствующий трехгранник § 360. Взаимное расположение линии и плоскости § 361. Основные векторы сопутствующего трехгранника § 362. Центр, ось и радиус кривизны пространственной линии § 363. Формулы для кривизны, радиуса и центра кривизны пространственной линии § 364. О знаке кривизны§ 365. Кручение РЯДЫ § 367. Определение ряда § 368. Сходящиеся и расходящиеся ряды § 369. Необходимое условие сходимости ряда § 370. Остаток ряда § 371. Простейшие действия над рядами § 372. Положительные ряды § 373. Сравнение положительных рядов § 374. Признак Даламбера для положительного ряда § 375. Интегральный признак сходимости § 376. Знакопеременный ряд. Признак Лейбница § 377. Абсолютная и условная сходимость § 378. Признак Даламбера для произвольного ряда § 379. Перестановка членов ряда § 380. Группировка членов ряда § 381. Умножение рядов § 382. Деление рядов § 383. Функциональный ряд § 384. Область сходимости функционального ряда § 385. О равномерной и неравномерной сходимости § 386. Определение равномерной и неравномерной сходимости § 387. Геометрический смысл равномерной и неравномерной сходимости § 388. Признак равномерной сходимости; правильные ряды § 389. Непрерывность суммы ряда § 390. Интегрирование рядов§ 391. Дифференцирование рядов § 392. Степенной ряд § 393. Промежуток и радиус сходимости степенного ряда § 394. Нахождение радиуса сходимости § 395. Область сходимости ряда, расположенного по степеням х – х0 § 396. Теорема Абеля § 397. Действия со степенными рядами § 398. Дифференцирование и интегрирование степенного ряда § 399. Ряд Тейлора § 400. Разложение функции в степенной ряд § 401. Разложение элементарных функций в степенные ряды § 402. Применение рядов к вычислению интегралов § 403. Гиперболические функции § 404. Обратные гиперболические функции § 405. Происхождение наименований гиперболических функций § 406. О комплексных числах § 407. Комплексная функция действительного аргумента § 408. Производная комплексной функции § 409. Возведение положительного числа в комплексную степень § 410. Формула Эйлера § 411. Тригонометрический ряд § 412. Исторические сведения о тригонометрических рядах § 413. Ортогональность системы функций cos nx, sin nx§ 414. Формулы Эйлера-Фурье § 415. Ряд Фурье § 416. Ряд Фурье для непрерывной функции § 417. Ряд Фурье для четной и нечетной функции § 418. Ряд Фурье для разрывной функции ДИФФЕРЕНЦИРОВАНИЕ И ИНТЕГРИРОВАНИЕ ФУНКЦИЙ НЕСКОЛЬКИХ АРГУМЕНТОВ § 420. Функция трех и большего числа аргументов § 421. Способы задания функций нескольких аргументов § 422. Предел функции нескольких аргументов § 424. Непрерывность функции нескольких аргументов § 425. Частные производные § 426. Геометрический смысл частных производных для случая двух аргументов § 427. Полное и частное приращения § 428. Частный дифференциал § 429. О выражении частной производной через дифференциал § 430. Полный дифференциал § 431. Геометрический смысл полного дифференциала (случай двух аргументов) § 432. Инвариантность выражения … полного дифференциала § 433. Техника дифференцирования § 434. Дифференцируемые функции § 435. Касательная плоскость и нормаль к поверхности§ 436. Уравнение касательной плоскости § 437. Уравнения нормали § 438. Дифференцирование сложной функции § 439. Замена прямоугольных координат полярными § 440. Формулы для производных сложной функции § 441. Полная производная § 442. Дифференцирование неявной функции нескольких переменных § 443. Частные производные высших порядков § 444. Полные дифференциалы высших порядков § 445. Техника повторного дифференцирования § 446. Условное обозначение дифференциалов § 447. Формула Тейлора для функции нескольких аргументов § 448. Экстремум (максимум и минимум) функции нескольких аргументов § 449. Правило нахождения экстремума § 450. Достаточные условия экстремума (случай двух аргументов) § 451. Двойной интеграл § 452. Геометрический смысл двойного интеграла § 453. Свойства двойного интеграла § 454. Оценка двойного интеграла § 455. Вычисление двойного интеграла (простейший случай) § 456. Вычисление двойного интеграла (общий случай)§ 457. Функция точки § 458. Выражение двойного интеграла через полярные координаты § 459. Площадь куска поверхности § 460. Тройной интеграл § 461. Вычисление тройного интеграла (простейший случай) § 462. Вычисление тройного интеграла (общий случай) § 463. Цилиндрические координаты § 464. Выражение тройного интеграла через цилиндрические координаты § 465. Сферические координаты § 466. Выражение тройного интеграла через сферические координаты § 467. Схема применения двойного и тройного интегралов § 468. Момент инерции § 471. Криволинейный интеграл § 472. Механический смысл криволинейного интеграла § 473. Вычисление криволинейного интеграла § 474. Формула Грина § 475. Условие, при котором криволинейный интеграл не зависит от пути § 476. Другая форма условия предыдущего параграфа ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ § 478. Уравнение первого порядка § 479. Геометрический смысл уравнения первого порядка § 480. Изоклины§ 481. Частное и общее решения уравнения первого порядка § 482. Уравнения с разделенными переменными § 483. Разделение переменных. Особое решение § 484. Уравнение в полных дифференциалах § 484а. Интегрирующий множитель § 485. Однородное уравнение § 486. Линейное уравнение первого порядка § 487. Уравнение Клеро § 488. Огибающая § 489. Об интегрируемости дифференциальных уравнений § 490. Приближенное интегрирование уравнений первого порядка по методу Эйлера § 491. Интегрирование дифференциальных уравнений с помощью рядов § 492. О составлении дифференциальных уравнений § 493. Уравнение второго порядка § 494. Уравнение n-го порядка § 495. Случаи понижения порядка § 496. Линейное уравнение второго порядка § 497. Линейное уравнение второго порядка с постоянными коэффициентами § 498. Линейное уравнение второго порядка с постоянными коэффициентами без правой части § 498а. Связь между случаями 1 и 3 § 498 § 499. Линейное уравнение второго порядка с постоянными коэффициентами с правой частью§ 500. Линейные уравнения любого порядка § 501. Метод вариации постоянных § 502. Системы дифференциальных уравнений. Линейные системы НЕКОТОРЫЕ ЗАМЕЧАТЕЛЬНЫЕ КРИВЫЕ § 503. Строфоида § 504. Циссоида Диокла § 505. Декартов лист § 506. Верзьера Аньези § 507. Конхоида Никомеда § 508. Улитка Паскаля; кардиоида § 509. Линия Кассини § 510. Лемниската Бернулли § 511. Архимедова спираль § 512. Эвольвента (развертка) круга § 513. Логарифмическая спираль § 514. Циклоиды § 515. Эпициклоиды и гипоциклоиды § 516. Трактриса § 517. Цепная линия |
Математический портал. Высшая математика. Математический анализ.
Литература: Сборник задач по математике. Часть 1. Под ред А. В. Ефимова, Б. П. Демидовича.
Существуют такие формы записи уравнения плоскости:
1) $Ax+By+Cz+D=0 -$ общее уравнение плоскости $P,$ где $\overline{N}=(A, B, C) -$ нормальный вектор плоскости $P. $
2) $A(x-x_0)+B(y-y_0)+C(z-z_0)=0 -$ уравнение плоскости $P,$ которая проходит через точку $M(x_0, y_0, z_0)$ перпендикулярно вектору $\overline{N}=(A, B, C).$ Вектор $\overline N$ называется нормальным вектором плоскости.
3) $\frac{x}{a}+\frac{y}{b}+\frac{z}{c}=1 -$ уравнение плоскости в отрезках на осях, где $a,$ $b$ и $c -$ величины отрезков, которые плоскость отсекает на осях координат.
4) $\begin{vmatrix}x-x_1&y-y_1&z-z_1\\x_2-x_1&y_2-y_1&z_2-z_1\\x_3-x_1&x_2-x_1&x_3-x_1\end{vmatrix}=0 — $ уравнение плоскости, которая проходит через три точки $A(x_1, y_1, z_1), B(x_2, y_2, z_2)$ и $C(x_3, y_3, z_3).$
5) $x\cos\alpha+y\cos\beta+z\cos\gamma-p=0 -$ нормальное уравнение плоскости, где $\cos\alpha, \cos\beta$ и $\cos\gamma -$ направляющие косинусы нормального вектора $\overline{N},$ направленного из начала координат в сторону плоскости, а $p>0 -$ расстояние от начала координат до плоскости. 2}}\right|.$$
{jumi[*3]}
Примеры:
2.180.
а) Заданы плоскость $P: -2x+y-z+1=0$ и точка $M(1, 1, 1).$ Написать уравнение плоскости $P’,$ проходящей через точку $M$ параллельно плоскости $P$ и вычислить расстояние $\rho(P, P’).$
Решение.
Так как п.лоскости $P$ и $P’$ параллельны, то нормальный вектор для плоскости $P$ будет также нормальным вектором для плоскости $P’.$ Из уравнения плоскости получаем $\overline{N}=(-2, 1, -1).$
Далее запишем уравнение плоскости по формуле (2): $A(x-x_0)+B(y-y_0)+C(z-z_0)=0 -$ уравнение плоскости, которая проходит через точку $M(x_0, y_0, z_0)$ перпендикулярно вектору $\overline{N}=(A, B, C).$
$-2(x-1)+(y-1)-(z-1)=0\Rightarrow -2x+y-z+2=0.$
Ответ: $-2x+y-z+2=0.$
2.181.
а) Написать уравнение плоскости $P’,$ проходящей через заданные точки $M_1(1, 2, 0)$ и $M_2(2, 1, 1)$ перпендикулярно заданной плоскости $P: -x+y-1=0. $
Решение.
Из уравнения плоскости $P,$ находим ее нормальный вектор $\overline{N}=(-1, 1, 0).$ Плоскость, перпендикулярная плоскости $P,$ параллельна ее нормальному вектору. Отсюда следует, что можно выбрать точку $M_3(x, y, z)\in P’$ такую, что что $\overline{M_1M_3}||\overline{N}.$
$\overline{M_1M_3}=(x-1, y-2, z).$
Условие коллинеарности векторов $\overline{M_1M_3}$ и $\overline{N}:$ $\frac{x_{M_1M_3}}{x_N}=\frac{y_{M_1M_3}}{y_N}=\frac{z_{M_1M_3}}{z_N}.$
Поскольку $z_N=0,$ то есть вектор $N\in XoY,$ то $z_{M_1M_3}=0.$
$\frac{x-1}{-1}=\frac{y-2}{1}.$ Пусть $x=2,$ тогда $y=1.$
Мы нашли точку $M_3=(2, 1, 0).$
Так как точка $M_1\in P’,$ то и $M_3\in P’.$ Запишем уравнение плоскости, которая проходит через три точки $M_1 (1, 2, 0), M_2(2, 1, 1)$ и $M_3(2, 1, 0).$
$\begin{vmatrix}x-1&y-2&z\\2-1&1-2&1\\2-1&1-2&0-0\end{vmatrix}=0 \Rightarrow $
$\begin{vmatrix}x-1&y-2&z\\1&-1&1\\1&-1&0\end{vmatrix}=0 \Rightarrow $
$(x-1)(-1)0+(-1)z+(y-2)-(-1)z-(-1)(x-1)-(y-2)0=0\Rightarrow$ $\Rightarrow-z+y-2+z+x-1=0\Rightarrow x+y-3=0. $
Ответ: $x+y-3=0.$
2.182.
а) Написать уравнение плоскости $P,$ проходящей через точку $M(1, 1, 1)$ параллельно векторам $a_1(0, 1, 2)$ и $a_2(-1, 0, 1).$
Решение.
Поскольку вектор $[a_1, a_2]$ перпендикулярен плоскости векторов $a_1$ и $a_2$ (см. векторное произведение), то он будет также перпендикулярен искомой плоскости. То есть вектор $[a_1, a_2]$ является нормальным для плоскости $P.$ Найдем этот вектор:
$[a_1, a_2]=\begin{vmatrix}i&j&k\\0&1&2\\-1&0&1\end{vmatrix}=i(1-0)-j(0+2)+k(0+1)=i-2j+k.$
Таким образом $\overline{N}=[a_1, a_2]=(1, -2, 1).$
Теперь можно найти уравнение плоскости $P,$ по формуле (2), как плоскости, проходящей через точку $M(1, 1, 1)$ перпендикулярно вектору $\overline N=(1, -2, 1):$
$1(x-1)-2(y-1)+1(z-1)=0\Rightarrow$
$x-2y+z=0.$
Ответ: $x-2y+z=0.$
2. 183.
а) Написать уравнение плоскости $P,$ проходящей через точки $M_1(1, 2, 0)$ и $M_2(2, 1, 1)$ параллельно вектору $a=(3, 0, 1).$
Решение.
Поскольку вектор $a$ параллелен плоскости $P,$ то для всякого вектора $\overline{M_1M_3},$ параллельного вектору $a,$ точка $M_3\in P.$
Пусть $M_3=(x, y, z).$ Тогда $\overline{M_1M_3}=(x-1, y-2, z).$ Так как $\overline{M_1M_3}||a,$ то $\frac{x_{M_1M_3}}{x_а}=\frac{y_{M_1M_3}}{y_а}=\frac{z_{M_1M_3}}{z_а}.$ $y_a=0,$ то есть вектор $a\in XoZ$ и всякий параллельный ему вектор так же будет принадлежать этой плоскости. Таким образом, $y_{M_1M_3}=y-2=0\Rightarrow y=2.$
Из условия параллельности векторов имеем $\frac{x-1}{3}=\frac{z}{1}.$ Пусть $x=4,$ тогда $z=1.$
Мы получили точку $M_3=(4, 2, 1).$
Запишем уравнение плоскости, которая проходит через три точки $M_1 (1, 2, 0), M_2(2, 1, 1)$ и $M_3(4, 2, 1).$
$\begin{vmatrix}x-1&y-2&z\\2-1&1-2&1\\4-1&2-2&1\end{vmatrix}=0 \Rightarrow $
$\begin{vmatrix}x-1&y-2&z\\1&-1&1\\3&0&1\end{vmatrix}=0 \Rightarrow $
$(x-1)(-1)1+1\cdot z\cdot 0+(y-2)3-3(-1)z-0\cdot 1\cdot(x-1)-1(y-2)1=0\Rightarrow$
$\Rightarrow -x+1+3y-6+3z-y+2=0\Rightarrow -x+2y+3z-3=0. $
Ответ: $-x+2y+3z-3=0.$
2.184.
а) Написать уравнение плоскости, проходящей через три заданные точки $M_1(1, 2,0),$ $M_2(2, 1, 1)$ и $M_3(3, 0, 1).$
Решение.
Воспользуемся формулой (4):
$\begin{vmatrix}x-1&y-2&z\\2-1&1-2&1\\3-1&0-2&1\end{vmatrix}=0 \Rightarrow $
$\begin{vmatrix}x-1&y-2&z\\1&-1&1\\2&-2&1\end{vmatrix}=0 \Rightarrow $
$(x-1)(-1)1+z(-2)+2(y-2)1-2(-1)z-(-2)(x-1)-1(y-2)1=0\Rightarrow$
$\Rightarrow -x+1+-2z+2y-4+2z+2x-2-y+2=0\Rightarrow x+y-3=0.$
Ответ: $x+y-3=0.$
{jumi[*4]}
Объяснение урока: Уравнения параллельных и перпендикулярных прямых
В этом объяснении мы научимся писать уравнение линии, параллельной или перпендикулярной другой прямой.
Существует множество полезных способов классификации прямых линий в зависимости от
на обстоятельства. Самое известное выражение прямой линии — использование
формула
| 𝑦=𝑚𝑥+𝑏, | (1) |
где мы построим этот график в плоскости 𝑥𝑦, где 𝑚 представляет наклон линии и 𝑏, представляющий 𝑦-перехват. Склон 𝑚 сообщает нам наклон линии, а 𝑦-перехват — это место, где она пересекает 𝑦-ось. Этих двух кусочков информации достаточно, чтобы все понять о прямой линии и построить ее в любой точке 𝑥𝑦-плоскости, и мы относиться к уравнению (1) как к форме «наклон-пересечение» прямая линия. Чаще всего при решении задачи с прямым строку, мы будем искать ответ в этом формате, где 𝑚 и 𝑏 рассчитываются как часть решения задачи.
Значение наклона 𝑚 определяет общее
«направление»
прямая линия. Читая слева направо, если 𝑚 положительно, то
склон идет
«в гору», а если 𝑚 отрицательно, то наклон идет
«спуск». Мы можем
продемонстрируйте это, проведя две прямые линии следующим образом:
𝑦=2𝑥+3𝑦=−12𝑥+3. и
Две линии имеют одинаковые 𝑦-пересечения, но наклоны с противоположные знаки. Эти две функции изображены на графике ниже, где 𝑦 отображается красным, а 𝑦 отображается зеленый. График 𝑦 движется «в гору», когда мы двигаться слева направо, что связано с положительным наклоном, тогда как 𝑦 движется «под гору» из-за отрицательного склон. Это фундаментальное свойство, относящееся к прямым линиям, и мы вернемся к этому позже, когда будем обсуждать перпендикулярные линии.
На данный момент стоит помнить, что форма наклона-пересечения
только один способ записать уравнение прямой линии, хотя это
самый распространенный. Как правило, нам может быть дано любое линейное уравнение как способ
классификация прямой линии, например 𝑥𝑦-плоскость
𝑎𝑥+𝑏𝑦=𝑘,
где 𝑎, 𝑏 и 𝑘
вещественные числа. Это выражение менее распространено, чем наклон-отрезок
форму уравнения (1), но, тем не менее,
совершенно действительный. Действительно, решая приведенное выше уравнение для 𝑦
даст традиционную форму пересечения наклона (при условии, что
𝑏≠0). Иногда нам будет дано уравнение
прямая линия в указанном выше формате, а не в форме пересечения наклона,
и ожидается, что мы будем работать с этим выражением изначально.
Есть два других способа написания прямой линии, которые особенно полезный. Предположим, нам сказали, что существует прямая линия, имеющая наклон 𝑚 и проходит через определенную точку (𝑥,𝑦). Тогда уравнение прямой линия с этими свойствами задается выражением 𝑦−𝑦=𝑚(𝑥−𝑥), которую, конечно, можно преобразовать в форму наклона и пересечения уравнение (1). Чтобы этот результат был непосредственно применим, наклон должен быть сначала известен, и есть много примеров, когда это будет случай, как мы увидим в остальной части этого объяснителя.
Окончательный результат наиболее актуален для обсуждения склона, так как он
выражает уравнение прямой, которая, как известно, проходит через
две точки (𝑥,𝑦) и
(𝑥,𝑦). В этом случае уравнение
прямая задается формулой
𝑦−𝑦𝑦−𝑦=𝑥−𝑥𝑥−𝑥.
В этом случае мы действительно решим переписать приведенное выше выражение в форма наклона-перехвата путем решения для 𝑦, так как это будет служить напоминанием о том, как мы можем вычислить наклон любой прямой линии из две точки, через которые проходит прямая. Предположим, мы должны были взять уравнение выше и умножьте обе части на (𝑦−𝑦). Это эффективно отменит это член в знаменателе левой части, что дает новый результат 𝑦−𝑦=(𝑦−𝑦)𝑥−𝑥𝑥−𝑥.
В качестве промежуточного шага мы можем немного подправить приведенное выше уравнение следующим образом: 𝑦−𝑦=𝑦−𝑦𝑥−𝑥(𝑥−𝑥).
Расширение правой части дает 𝑦−𝑦=𝑦−𝑦𝑥−𝑥𝑥−𝑦−𝑦𝑥−𝑥𝑥, а затем, наконец, решение для 𝑦 дает 𝑦=𝑦−𝑦𝑥−𝑥𝑥−𝑦−𝑦𝑥−𝑥𝑥+𝑦.
Это вряд ли самый аккуратный способ записи предыдущего уравнения, но он делает
позволяют нам сравнить его непосредственно с формой наклона-пересечения
прямой линии, как описано в уравнении (1). К
сравнивая 𝑥-члены между этим уравнением и тем,
непосредственно выше, мы находим, что мы можем записать наклон как
𝑚=𝑦−𝑦𝑥−𝑥,
что подтверждает то, что мы знаем о вычислении наклона прямой
прямой по двум точкам на прямой.
Эти результаты были включены в качестве напоминания об известных методах, которые мы можем использовать при работе с прямыми линиями, и мы будем использовать все эти на протяжении всего объяснителя как неотъемлемая часть нашей работы. Хотя мы будем дать некоторый план, работающий во многих примерах, обычно предполагается, что вы будет достаточно комфортно с этими методами, что многие этапы работы не должно быть слишком загадочным! Мы надеемся, что с этим моментом мы сейчас ввести первое из двух ключевых понятий этого эксплейнера: параллельный линии.
Определение: параллельные линии
Рассмотрим две прямые линии с наклонами 𝑚 и
𝑚. Эти две строки
параллельны, если 𝑚=𝑚 и прямые имеют разные
𝑦-перехваты. Если 𝑦-перехваты также
то же самое, то две строки идентичны.
Продемонстрируем это на примере. Предположим, что у нас была прямая строка, которая уже была записана в форме наклона и пересечения следующим образом: 𝑦=3𝑥−5.
Мы знаем, что уклон равен 3, а это значит, что уклон идет в гору, двигаясь слева направо. Кроме того, линия имеет 𝑦-перехват −5. Достаточно информация, позволяющая нам отобразить следующий сюжет.
Теперь предположим, что мы взяли вторую прямую, которая управляется уравнение 𝑦=3𝑥+1.
Ясно, что две прямые имеют одинаковый наклон, но разные 𝑦-перехваты. По нашему определению, приведенному выше, это означает, что две прямые параллельны друг другу, что можно увидеть, когда мы рисуем новая строка ниже зеленого цвета.
По определению параллелизма эти две линии никогда не пересекутся. Это можно наблюдать алгебраически, если попытаться решить одновременную
уравнения 𝑦=3𝑥−5 и
𝑦=3𝑥+1, что быстро приводит к математической ошибке.
Приведенная выше ситуация, вероятно, является самым простым обстоятельством для определения параллельны ли две прямые, потому что обе они написаны на наклон-пересечение, что означает, что мы можем напрямую сравнивать наклоны и 𝑦-перехваты. В следующих примерах мы увидим что мы должны больше работать и использовать многие результаты, которые были введены в этот объяснитель еще до того, как мы начали говорить о параллельных линиях.
Пример 1. Нахождение уравнения прямой, параллельной заданной прямой
Запишите в виде 𝑦=𝑚𝑥+𝑏 уравнение прямой через (−1,−1), параллельную прямой −6𝑥−𝑦+4=0.
Ответ
Начнем с преобразования уравнения −6𝑥−𝑦+4=0 в форму
стандартная форма наклон-пересечение. Это дает уравнение
𝑦=−6𝑥+4,
что означает, что наклон этой линии равен −6. Линия, которую мы
должен вычислить параллелен строке выше, что означает, что мы можем написать
наклон новой линии как 𝑚=−6. Нам также сообщают, что
новая линия должна проходить через точку (−1,−1), которая,
со знанием наклона достаточно, чтобы полностью классифицировать линию. Для
общая прямая с уклоном 𝑚, проходящая через
точка (𝑥,𝑦), мы можем использовать формулу
𝑦−𝑦=𝑚(𝑥−𝑥).
Подставляя в это уравнение 𝑚=−6 и (𝑥,𝑦)=(−1,−1), получаем 𝑦−(−1)=−6(𝑥−(−1)), который мы можем решить для 𝑦, чтобы найти 𝑦=−6𝑥−7.
Мы могли бы проверить, что эти линии параллельны, построив обе их, как мы сделали ниже. Первая строка выделена зеленым цветом, а вторая линия выделена красным цветом. Мы видим, что красная линия проходит через точку (−1,−1), которая нанесен фиолетовым цветом.
Не всегда необходимо чертить прямые линии или думать о них в любом случае
геометрическом смысле, если все, что нас интересует, это то, являются ли они
параллельно. Условия в приведенном выше определении являются алгебраическими условиями на
отношения между двумя склонами и двумя
𝑦-перехваты. Таким образом, построение прямых линий иногда может
рассматриваться как полезный метод, а не как необходимый шаг, хотя
Конечно, обычно хорошей практикой является набросок проблемы, чтобы
понять его полностью и помочь проверить любые результаты. В следующие два
примеров, мы ответим на вопросы, используя чисто алгебраические средства, а затем построим
график для проверки нашей работы.
Пример 2. Нахождение значений неизвестных коэффициентов в двух параллельных прямых Уравнения линий
Прямые линии 8𝑥+5𝑦=8 и 8𝑥+𝑎𝑦=−8 параллельны. Какова ценность 𝑎?
Ответ
Чтобы две прямые были параллельны, мы требуем, чтобы их два наклона были равный. Переставляя оба приведенных уравнения для 𝑦 даст два результата 𝑦=−85𝑥+85𝑦=−8𝑎𝑥−8𝑎.и
Два члена наклона будут равны, если 𝑎=5, что будет
также подразумевают, что 𝑦-перехваты будут разными
(тоже с обратным знаком). Это соответствует двум требованиям для прямого
линии должны быть параллельны, что означает, что вторая строка записывается полностью как
𝑦=−85𝑥−85.
Ниже мы начертили обе эти линии, чтобы продемонстрировать, что они параллельно, где первая линия окрашена в красный цвет, а вторая — в зеленый. Это подтверждает, что ответ 𝑎=5 правильный.
Пример 3. Нахождение уравнения прямой, параллельной другой заданной Линия
Найти в форме наклона–пересечения уравнение прохождения прямой через точку (3,1) и параллельно прямой, проходящей через две точки (1,−1) и (4,−3).
Ответ
Начнем с вычисления уравнения второй линии, чтобы мы могли найти наклон как часть этого процесса. Для прямой, проходящей через две точки (𝑥,𝑦) и (𝑥,𝑦), мы можем использовать формулу 𝑦−𝑦𝑦−𝑦=𝑥−𝑥𝑥−𝑥.
По установке (𝑥,𝑦)=(1,−1) и
(𝑥,𝑦)=(4,−3) в
уравнение выше, мы получаем
𝑦−(−1)−3−(−1)=𝑥−14−1.
Это немного упрощает −12(𝑦+1)=13(𝑥−1), который мы можем решить для 𝑦, чтобы найти 𝑦=−23𝑥−13.
Теперь, когда вторая строка была написана в наклоне-перехвате формы, мы видим, что наклон равен −23. Чтобы любая линия была параллельна этой линии, наклон должен быть то же самое, что означает, что 𝑚=−23.
Теперь, когда известен наклон новой линии, мы можем вспомнить формула прямой с известным наклоном 𝑚 который проходит через точку (𝑥,𝑦): 𝑦−𝑦=𝑚(𝑥−𝑥).
Взяв расчетный наклон 𝑚=−23 и заданная точка (𝑥,𝑦)=(3,1), мы подставляем оба из них в уравнение выше, чтобы получить 𝑦−1=−23(𝑥−3).
Решение для 𝑦 дает уравнение в форме пересечения наклона: 𝑦=−23𝑥+3.
Чтобы убедиться, что мы правильно выполнили расчеты, у нас есть
создал сюжет ниже. Две точки
(1,−1) и
(4,−3) показаны фиолетовым цветом, первый
линия, проходящая через эти две точки, отображается красным цветом. Смысл
(3,1) отображается черным цветом, а параллель
линия, проходящая через эту точку, показана зеленым цветом.
В предыдущих двух примерах мы видели, как нам нужна сильная понимание основных методов, которые могут быть использованы для получения уравнение прямой, в зависимости от того, какие два отрезка информация, которую нам изначально дают. В идеале это должен быть склон и 𝑦-перехват, который позволил бы линии быть записана непосредственно в форме наклона-перехвата. Обычно, однако это не так, и вместо этого нам дают информацию что требует от нас выполнения дополнительной работы, чтобы понять полную картину. Те же принципы будут верны, как мы переходим ко второй половине этого объяснения, чтобы сосредоточиться на перпендикулярные линии, где будем считать, что главные техники с использованием прямых линий полностью изучены.
Определение: перпендикулярные линии
Рассмотрим две прямые с наклонами 𝑚 и
𝑚. Эти две линии перпендикулярны (справа
углами друг к другу), если они имеют отношение
𝑚=−1𝑚. Эта связь часто выражается
эквивалентная форма 𝑚𝑚=−1, означающая, что произведение наклонов
должно быть −1. Две перпендикулярные прямые встретятся ровно один раз.
Чтобы проиллюстрировать эту идею, мы вернемся к двум линиям, которые мы дал в самом начале этого объяснения. Они были определены как 𝑦=2𝑥+3𝑦=−12𝑥+3.и
Мы заметили, что наклон первой линии был положительным, что означает, что она пошла «в гору», и что уклон второй линии был отрицательный, что означает, что он пошел «по наклонной». Напоминаю, когда На графике две линии выглядят следующим образом.
Чего мы еще не сказали, так это того, что визуально эти две линии
кажутся перпендикулярными друг другу, сходятся под прямым углом
в точке (0,3), что тоже бывает
быть 𝑦-перехватом. Если наклон первого
линия записывается как 𝑚=2 и наклон
вторая строка как 𝑚=−12, то мы находим
что они подчиняются заданному соотношению
𝑚=−1𝑚. Тогда, по нашим
определение, эти прямые перпендикулярны.
Если две прямые перпендикулярны, то 𝑚=−1𝑚, что означает, что два наклона должны иметь противоположный друг другу знак. Следовательно, если 𝑚 положительно, то 𝑚 должно быть отрицательное, и наоборот. Геометрически говоря, если первая линия в гору, то вторая (перпендикулярная) линия идет под гору, и наоборот наоборот Это геометрическое понимание обеспечивает метод проверки перпендикулярны ли две данные прямые. Следует отметить, однако, что две линии, имеющие наклоны с противоположными знаками, не означает, что они перпендикулярны. Например, если одна линия имела наклон 10 000 а другой имел наклон −10000, то эти точно не будет перпендикулярно!
Обратите внимание, что, в отличие от критериев для параллельных прямых, для перпендикулярных
прямых нет условий на 𝑦-перехваты
задействованы две линии. На самом деле, это совершенно не имеет значения, когда
решение о том, перпендикулярны ли две прямые, зависит только от
два наклона соответствующих линий. Мы действительно можем доказать, что два
перпендикулярные линии всегда будут пересекаться. Предположим, мы взяли два
перпендикулярные прямые с двумя разными 𝑦-перехватами
но с соотношением между наклонами
𝑚=−1𝑚. Мы могли бы взять две строки в
наклон-пересечение, как показано ниже:
𝑦=𝑚𝑥+𝑐𝑦=−1𝑚𝑥+𝑐.и
Мы можем решить как для 𝑥, так и для 𝑦 найдите, где эти две линии встречаются друг с другом, сначала установив 𝑚𝑥+𝑐=−1𝑚𝑥+𝑐.
Приведение членов наклона к левой части и 𝑦-перехват члена в правой части дает 𝑚+1𝑚𝑥=𝑐−𝑐, которую мы решили записать в эквивалентной форме 𝑚+1𝑚𝑥=𝑐−𝑐.
Решение для 𝑥 дает 𝑥=𝑚(𝑐−𝑐)𝑚+1.
Важным моментом является то, что мы всегда можем вычислить
𝑥-координата места встречи, независимо от
значения 𝑐 или 𝑐, хотя мы
следует опасаться, что мы не можем допустить, чтобы наклон любой линии был равен нулю,
иначе исходное отношение
𝑚=−1𝑚 будет недействительным. К
подставив указанное выше значение для 𝑥 в уравнение
𝑦=𝑚𝑥+𝑐, мы найдем
(после пропуска некоторой работы), что
𝑦=𝑐+𝑐𝑚𝑚+1,
означает, что у нас всегда есть выражение для
𝑦-координата места встречи.
На данный момент это все, что нам нужно понять о перпендикулярные линии, и мы теперь продолжим с некоторыми примерами этого тип.
Пример 4. Определение условия перпендикулярности двух прямых Используя их Уравнения
Если прямые 𝑦=𝑎𝑥+𝑏 и 𝑦=𝑐𝑥+𝑑 перпендикулярны, какая из следующие произведения равны −1?
- 𝑏 и 𝑐
- 𝑏 и 𝑑
- 𝑎 и 𝑑
- 𝑎 и 𝑐
Ответ
Предположим, что существуют две перпендикулярные линии с наклонами 𝑚 и 𝑚. Затем, по определение, эти наклоны должны быть в отношениях 𝑚=−1𝑚. В качестве альтернативы мы можем выразить это в виде 𝑚𝑚=−1.
Теперь, когда это альтернативное выражение установлено, мы видим
что две заданные строки записаны в наклоне-перехвате
форма. Следовательно, наклоны равны соответственно 𝑎 и
𝑐. Чтобы эти прямые были перпендикулярны,
требуют, чтобы 𝑎=−1𝑐, или,
альтернативно, что 𝑎𝑐=−1. Следовательно
произведение 𝑎 и 𝑐
равно −1, что соответствует варианту D выше.
Сейчас мы приведем два последних примера, которые потребуют от нас также понимать критерии перпендикулярности двух прямых как и все различные формулы для прямых линий, которые мы дали в начало этого пояснителя. Для обоих примеров выполним работать алгебраически, а затем построить графики прямых линии в качестве подтверждающего шага. Учитывая, что мы всегда будем говорить относительно перпендикулярных линий, мы ожидаем наблюдать поведение что мы отмечали ранее: если одна линия имеет положительный наклон, то другой будет иметь отрицательный наклон (и наоборот), а это означает, что одна линия всегда будет идти в гору, а другая всегда будет идти вниз.
Пример 5.
Нахождение уравнения прямой, перпендикулярной другой
Заданная линияНайти в форме наклона–отрезка уравнение прямой перпендикуляр к 𝑦=2𝑥−4, который проходит через точка 𝐴(3,−3).
Ответ
Нам удобно дать первую строку в форма наклона-перехвата, что означает, что мы можем напрямую считывать наклон как 𝑚=2. Чтобы любая другая строка была перпендикуляр, два наклона должны подчиняться соотношению 𝑚=−1𝑚, что дает наклон второй линии как 𝑚=−12. Мы решим записать это как 𝑚=−12.
Уравнение прямой с наклоном 𝑚, которое проходит через точку (𝑥,𝑦) данный 𝑦−𝑦=𝑚(𝑥−𝑥).
Подставляем 𝑚=−12 и (𝑥,𝑦)=(3,−3) в это выражение, давая 𝑦−(−3)=−12(𝑥−3).
Перестановка и решение для 𝑦 дает уравнение в форме наклона-перехвата: 𝑦=−12𝑥−32.
На приведенном ниже графике первая линия отмечена красным цветом, а
вторая, перпендикулярная линия зеленого цвета. Как видим, две строки
кажутся перпендикулярными, а вторая линия проходит через
точка (3,−3), как показано черным цветом. Два наклона имеют противоположные знаки, что также отражено в
диаграмма.
Пример 6. Определение в форме наклона–пересечения уравнения Линия, заданная перпендикуляром Линия
Определить в форме наклона–отрезка уравнение прямой проходящей через 𝐴(13,−7) и перпендикулярной прямой, проходящей через 𝐵(8,−9) и 𝐶(−8,10).
Ответ
Сначала вычислим наклон прямой линии, которая проходит через точки 𝐵 и 𝐶. Наклон прямой через две точки (𝑥,𝑦) и (𝑥,𝑦) выглядит следующим образом: 𝑚=𝑦−𝑦𝑥−𝑥.
Подставляем значения (𝑥,𝑦)=(8,−9) и (𝑥,𝑦)=(−8,10) в это уравнение, дающее 𝑚=10−(−9)−8−8=−1916.
Установив этот результат, мы теперь заинтересованы в
найти уравнение прямой линии, которая
перпендикулярно исходной прямой, проходя через
точка 𝐴(13,−7). Если наклон второй линии
𝑚, тогда у нас должны быть отношения
𝑚=−1𝑚, что дает
𝑚=−1=1619. мы напишем
это проще, как 𝑚=1619. Теперь мы можем найти
уравнение этой прямой, вспомнив, что уравнение для
прямая с известным наклоном, проходящая через точку
(𝑥,𝑦) задается
формула
𝑦−𝑦=𝑚(𝑥−𝑥).
Теперь подставим 𝑚=1619 и (𝑥,𝑦)=(13,−7) в это уравнение дает 𝑦−(−7)=1619(𝑥−13).
Решение этого уравнения относительно 𝑦 дает форму наклона и точки пересечения 𝑦=1619𝑥−34119.
Ниже мы начертили исходную прямую красным цветом, и это проходит через две точки 𝐵 и 𝐶, которые нанесены фиолетовым цветом. Вторая линия выделена зеленым цветом, а это явно перпендикулярно красной линии, тоже проходящей через заданную точку 𝐴.
Ключевые точки
- Форма наклона и точки пересечения прямой определяется выражением
𝑦=𝑚𝑥+𝑏, где 𝑚 — наклон
а 𝑏 — это 𝑦-перехват.
- Уравнение с наклоном 𝑚, которое проходит через точка (𝑥,𝑦) может быть записана как 𝑦−𝑦=𝑚(𝑥−𝑥), что может быть перестроены в форму наклона-перехвата.
- Уравнение прямой через две точки (𝑥,𝑦) и (𝑥,𝑦) можно записать как 𝑦−𝑦𝑦−𝑦=𝑥−𝑥𝑥−𝑥, который также можно преобразовать в форму наклона и пересечения.
- Проведите две прямые с наклонами 𝑚 и 𝑚. Эти прямые параллельны, если 𝑚=𝑚 (и два 𝑦-перехвата разные).
- Если мы имеем отношение 𝑚=−1𝑚, то две прямые перпендикулярны и гарантировано что они встретятся друг с другом. Это отношение иногда записывается в виде 𝑚𝑚=−1.
линий в координатной плоскости | Геометрия | Параллельные и перпендикулярные линии
Популярные учебные пособия
Линии на координатной плоскостиКак написать уравнение прямой в форме пересечения наклона, если у вас есть две точки?
Пытаетесь написать уравнение в форме пересечения наклона? Есть две точки на вашей линии? Вам нужно будет найти свой наклон и y-перехват.
Посмотрите этот урок и узнайте, что нужно сделать, чтобы написать уравнение в форме пересечения наклона!Как написать уравнение линии в форме пересечения наклона, если у вас есть одна точка и параллельная линия?
Хотите найти форму пересечения наклона линии, когда вам дана точка на этой линии и другая линия, параллельная этой линии? Помните, параллельные прямые имеют одинаковый наклон. Если вы сможете найти наклон этой параллельной линии, вы получите наклон своей линии! В этом уроке вы увидите, как найти наклон вашей линии и использовать этот наклон вместе с заданной точкой, чтобы написать уравнение для линии в форме пересечения наклона. Взглянем!
Как написать уравнение линии в форме пересечения наклона, если у вас есть одна точка и перпендикулярная линия?
Хотите найти форму пересечения наклона линии, когда вам дана точка на этой линии и другая линия, перпендикулярная этой линии? Помните, что перпендикулярные линии имеют наклоны, противоположные друг другу.
В этом уроке вы увидите, как найти наклон, используя наклон перпендикулярной линии. Затем используйте этот наклон и заданную точку, чтобы написать уравнение для линии в форме пересечения наклона. Проверьте это!Как представить уравнение в стандартной форме в форме пересечения наклона или наклона точки?
Хотите попрактиковаться в преобразовании уравнения прямой в различные формы? Тогда этот урок создан для вас! Следуйте инструкциям, поскольку этот учебник покажет вам, как взять линейное уравнение из стандартной формы и преобразовать его в форму пересечения наклона и форму точки-наклона.
Как перевести уравнение в форме точки-наклона в стандартную форму или форму пересечения наклона?
Хотите попрактиковаться в преобразовании уравнения прямой в различные формы? Тогда этот урок создан для вас! Следуйте инструкциям, поскольку этот учебник покажет вам, как взять линейное уравнение из формы точка-наклон и преобразовать его в стандартную форму и форму с пересечением наклона.
Как написать уравнение для вертикальной линии?
Пытаетесь найти уравнение вертикальной линии, проходящей через заданную точку? Помните, что вертикальные линии имеют только значение «x» и не имеют значения «y». Следуйте этому руководству, чтобы увидеть, как использовать предоставленную информацию для написания уравнения вертикальной линии.
Как написать уравнение для горизонтальной линии?
Пытаетесь найти уравнение горизонтальной линии, проходящей через заданную точку? Помните, что вертикальные линии имеют только значение «y» и не имеют значения «x». Следуйте этому руководству, чтобы увидеть, как использовать предоставленную информацию для написания уравнения горизонтальной линии.
Как нарисовать вертикальную линию?
Чтобы изобразить вертикальную линию, проходящую через заданную точку, сначала начертите эту точку. Затем нарисуйте прямую линию вверх и вниз, проходящую через точку, и все готово! Чтобы увидеть этот процесс в действии, посмотрите этот урок!
Как нарисовать горизонтальную линию?
Чтобы изобразить горизонтальную линию, проходящую через заданную точку, сначала начертите эту точку.
Затем нарисуйте прямую линию слева и справа, которая проходит через точку, и все готово! Чтобы увидеть этот процесс в действии, посмотрите этот урок!Как нарисовать линию, если известны наклон и точка пересечения?
Пытаетесь построить линию с заданным наклоном и точкой пересечения с осью Y? Думаете, вам нужно сначала найти уравнение? Подумайте еще раз! В этом руководстве вы увидите, как использовать заданный наклон и точку пересечения по оси Y для построения графика линии.
Как написать уравнение прямой в форме точка-наклон, если у вас есть наклон и одна точка?
Пытаетесь написать уравнение в форме точка-наклон? Нашли точку на линии и наклоне? Правильно подставьте эти значения в форму точки-наклона линии, и вы получите ответ! Посмотрите этот урок, чтобы узнать все подробности!
Как написать уравнение прямой в форме точка-наклон, если у вас есть две точки?
Пытаетесь написать уравнение в форме точка-наклон? Есть две точки, но нет наклона? Вам нужно будет использовать эти точки, чтобы сначала найти уклон.
Посмотрите этот урок и узнайте, что нужно сделать, чтобы написать уравнение в форме точка-наклон!Как написать уравнение линии в форме пересечения наклона, если у вас есть наклон и пересечение Y?
Хотите написать уравнение в форме пересечения наклона? У вас уже есть наклон и точка пересечения по оси Y? Идеальный! Просто правильно подставьте эти значения в уравнение, и все готово! Узнайте, как в этом уроке.
Что такое форма линейного уравнения в виде точки и наклона?
Когда вы изучаете линейные уравнения, вы обязательно столкнетесь с формой линии точка-наклон. Эта форма весьма полезна при создании уравнения линии, если вам задан наклон и точка на линии. Посмотрите этот урок и узнайте о форме линии точка-наклон!
Что такое форма пересечения наклона линейного уравнения?
Когда вы изучаете линейные уравнения, вы обязательно столкнетесь с формой линии точка-наклон.