Котангенс половинного угла формула: Формулы тригонометрических функции двойного и половинного угла – онлайн-тренажер для подготовки к ЕНТ, итоговой аттестации и ВОУД

2}\alpha — 1}}\normalsize\).

Формулы половинного угла

1. Синус половинного угла: \(sin \large\frac{\alpha }{2}\normalsize = \pm \sqrt {\large\frac{{1 — cos \alpha }}{2}\normalsize}\). Примечание: Знак перед корнем выбирается в зависимости от квадранта, в который попадает угол \(\frac{\alpha}2\) в левой части. Данное правило справедливо также для других формул, приведенных ниже.
2. Косинус половинного угла: \(cos \large\frac{\alpha }{2}\normalsize = \pm \sqrt {\large\frac{{1 + cos \alpha }}{2}\normalsize}\).
3. Тангенс половинного угла: \(tg \large\frac{\alpha }{2}\normalsize = \pm \sqrt {\large\frac{{1 — cos \alpha }\normalsize}{{1 + cos \alpha }}} = \large\frac{{sin \alpha }}{{1 + cos \alpha }}\normalsize = \large\frac{{1 — cos \alpha }}{{sin \alpha }}\normalsize \).
4. Котангенс половинного угла: \(ctg \large\frac{\alpha }{2}\normalsize = \pm \sqrt {\large\frac{{1 + cos \alpha }\normalsize}{{1 — cos \alpha }}} = \large\frac{{sin \alpha }}{{1 — cos \alpha }}\normalsize = \large\frac{{1 + cos \alpha }}{{sin \alpha }}\normalsize\). 2\frac{α}2+cosα\)

5. Упростите.

   \( 1 – 8sin2x · cos2x\)

6. Упростите выражение.

   \(\frac{1-cos2x+sin2x}{1+cos2x+sin2x}\)

7. Упростите выражение.

   \(\frac{sin4x}{1+cos4x}\cdot \frac{cos2x}{1+cos2x}\)

8. Упростите выражение.

   \(\frac{cos2\alpha}{1-sin2\alpha}-\frac{1+tg\alpha}{1-tg\alpha}\)

9. Най­ди­те \(sin(\frac{7\pi}2-\alpha), если \ sin\alpha=0,8 \ и \ \alpha \in(\frac{\pi}2; \pi)\). 2\frac{\alpha}2}\)

Сообщить об ошибке

Обязательные

Математическая грамотность

Грамотность чтения

История Казахстана

Предметы по профилю

Биология

Химия

Английский язык

Французский язык

География

Немецкий язык

Информатика

Основы права

Русская литература

Математика

Физика

Русский язык

Всемирная история

Укажите предмет *

Скопируйте и вставьте вопрос задания *

Опишите подробнее найденную ошибку в задании *

Прикрепите скриншот

Объем файла не должен превышать 1МБ

Казахский

Русский

Обратите внимание! По выбранным Вами предметам ГРАНТЫ не предоставлены. В AlmaU, Университете Нархоз и Каспийском Университете представлены специальности, где профильными предметами являются математика, физика, география, иностранный язык, Человек. Общество. Право, всемирная история, биология, химия и творческий экзамен.

1. Скачайте приложение iTest, используя QR-код или строку поиска в AppStore или Play Market

2. Авторизуйтесь в приложении и готовьтесь к экзаменам вместе с нами

Формулы половинного угла в тригонометрии, синус и косинус половинного угла, вывод формул половинного угла

Формулы половинного угла (аргумента) представляют собой противоположность формулам двойного угла , так как они выражают синус, косинус, тангенс и котангенс угла α2 при помощи тригонометрических функций угла α. В статье раскрыты формулы половинного угла и добавлены их доказательства с примерами решений.

Список формул половинного угла

Стандартные формулы половинного угла:

sin2α2=1-cosα2cos2α2=1+cosα2tg2α2=1-cosα1+cosαctg2α2=1+cosα1-cosα

Формулы для sin и cos половинного угла справедливы при любом значении заданного угла α.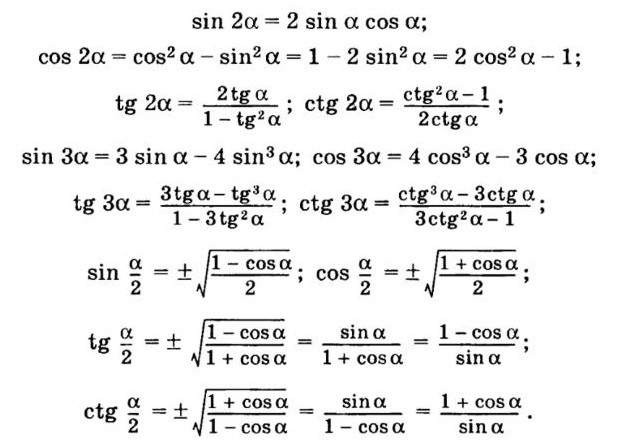 Формулу для tg любого угла αопределяет tgα2, значение угла α≠π+2π·z при z равном любому целому числу ( выражение 1+cosα с таким же значением α не должно принимать значение 0). Формула ctg угла считается справедливой для любого угла α, где половинный угол имеет место быть, α≠2π·z.

Самые значимые формулы половинного угла для квадратов тригонометрических функций выводятся через положительное или отрицательное значение арифметического квадратного корня. Имеем формулы половинного угла:

sinα2=±1-cosα2, cosα2=±1+cosα2, tgα2=±1-cosα1+cosα, ctgα2=±1+cosα1-cosα

Знак «-» указывает, что тригонометрическая функция принадлежит определенной четверти угла α2.

Применим формулы на практике.

Доказательство формул половинного угла

Доказательство формул половинного угла основывается на формулах cos двойного угла cosα=1-2·sin2α2 и cosα=2·cos2α2-1. Упростив первое выражение по sin2α2, получим саму формулу половинного угла sin2α2=1-cosα2, второе выражение по cos2α2 получим cos2α2=1+cosα2.

Чтобы доказать формулы половинного угла для tg и ctg угла α2, необходимо применить основные тригонометрические тождества tgα2=sinα2cosα2 и ctgα2=cosα2sinα2, к ним необходимо добавить формулы половинного угла cos и sin, которые доказали выше. При подстановке получим выражения, имеющие вид:

tg2α2=sin2α2cos2α2=1-cosα21+cosα2=1-cosα1+cosα;ctg2α2=cos2α2sin2α2=1-cosα21+cosα2=1+cosα1-cosα;

Все формулы половинного угла были доказаны.

Примеры использования

Покажем применение формул половинного угла при решении примера.

Пример 1

Известно, что cos30°=32. Необходимо вычислить значение cos 15 градусов, используя формулы половинного угла.

Решение

Данный пример рассматривает применение формулы половинного угла для косинуса, имеющей вид cos2α2=1+cosα2.

Следуя из условия, подставляем числовые значения и получаем: cos215°=1+cos30°2=1+322=2+34. После получения значения косинуса 15 градусов, необходимо найти само значение косинуса. Для этого вспомним, что угол в 15 градусов принадлежит первой четверти. Там косинус угла имеет положительное значение ( чтобы вспомнить знаки тригонометрических функций, необходимо повторить

теорию знаков синуса, косинуса, тангенса и котангенса по четвертям). Следуя из вышесказанного, имеем cos215°=2+34, тогда cos 15°=2+34=2+32. Ответ: cos 15°=2+32.

Применяя формулу половинного угла, стоит учитывать тот факт, что угол может быть не явного вида α2 и α, а потребует дальнейшего приведения к стандартному виду. Главное условие – нахождение аргумента в правой части формул половинного угла было в 2 раза больше, чем в левой. Иначе применение формулы будет невозможно.

Если формула позволит записывать данное равенство таким образом sin27α=1-cos14α2 или sin2 5α17=1-cos10α172, то формула будет применима.

Для правильного преобразования и применения формул половинного аргумента необходимо досконально изучить свойства тригонометрических функций. Не любое выражение поддается такому преобразованию в тригонометрии.

Необходимо внимательно следить за значениями углов тригонометрических функций и их нахождение в четвертях для определения знака для выражения.

Все формулы половинного угла в тригонометрии:

 

 

Автор: Ирина Мальцевская

Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта

Cot Half Angle Formula — GeeksforGeeks

Тригонометрия — это раздел математики, который использует тригонометрические соотношения для определения углов и неполных сторон треугольника. Тригонометрические отношения, такие как синус, косинус, тангенс, котангенс, секанс и косеканс, используются для исследования этой области математики. Это исследование того, как связаны стороны и углы прямоугольного треугольника. Тригонометрия состоит из слов «Тригонон» и «Метрон», которые обозначают треугольник и измерение соответственно. Применение уравнений и тождеств, основанных на этой связи, облегчает оценку неизвестных размеров прямоугольного треугольника.

Котангенс Тригонометрическое отношение

Отношение длин любых двух сторон прямоугольного треугольника называется тригонометрическим отношением. В тригонометрии эти соотношения связывают отношение сторон прямоугольного треугольника к углу. Отношение котангенса выражается как отношение длины прилежащей стороны угла к длине противолежащей стороны. Обозначается символом кроватка.

 

Если θ — угол между основанием и гипотенузой прямоугольного треугольника, то

cot θ = Основание/Перпендикуляр = cos θ/sin θ

Здесь основание – сторона, примыкающая к углу, а перпендикуляр – сторона, противоположная ему.

Cot Половина угла (Cot θ /2) Формула

В тригонометрии формулы половинного угла обычно представляются как θ/2, где θ — угол. Уравнения половинного угла используются для определения точных значений тригонометрических соотношений стандартных углов, таких как 30°, 45° и 60°. Мы можем получить значения отношений для сложных углов, таких как 22,5° (половина 45°) или 15° (половина 30°), используя значения отношений для этих обычных углов. Котангенс половинного угла обозначается аббревиатурой cot θ/2. Это тригонометрическая функция, которая возвращает значение функции кроватки для половины угла. Период функции кроватка θ равен π, а период кроватки θ/2 равен 2π.

 

cot θ/2 = √((1 + cos θ)/(1 – cos θ))

Вычисление

Формула синуса и косинуса.

Мы знаем, что sin θ/2 = ±√((1 – cos θ) / 2).

Найдите cos θ/2, используя тождество sin ² θ + cos ² θ = 1.

cos θ/2 = √(1 – (√((1 – cos θ) / 2)) ² )

cos θ/2 = √(1 – ((1 – cos θ)/ 2))

cos θ/2 = √((2 – 1 + cos θ)/ 2)

cos θ/2 = √((1 + cos θ)/ 2)

Кроме того, мы знаем cot θ/2 = cos (θ/2)/sin (θ/2).

Получаем

ctg θ/2 = √((1 + cos θ)/ 2)/ √((1 – cos θ)/ 2)

ctg θ/2 = √((1 + cos θ )/(1 – cos θ))

Отсюда выводится формула для коэффициента половин котангенса.

Примеры задач

Задача 1. Если cos θ = 3/5, найти значение ctg θ/2 по формуле половинного угла.

Решение:

Имеем, cos θ = 3/5.

По формуле получаем

ctg θ/2 = √((1 + cos θ)/(1 – cos θ))

= √((1 + (3/5))/ (1 – ( 3/5)))

= √((8/5)/ (2/5))

= √4

= 2

Задача 2. Если cos θ = 12/13, найти значение кроватки θ/2 по формуле половинного угла.

Решение:

Имеем, cos θ = 12/13.

Используя формулу получаем,

кроватка θ/2 = √((1 + cos θ)/(1 – cos θ))

= √((1 + (12/13))/ (1 – (12/13))

= √((25/13)/ (1/13))

= √25

= 5

-угловая формула.

Решение:

Итак, sin θ = 8/17.

Найдите значение cos θ по формуле sin ² θ + cos ² θ = 1.

cos θ = √(1 – (64/289)))

= √(225/289)

= 15/17

По формуле получаем = √((1 + (15/17))/ (1 – (15/17)))

= √((32/17)/ (2/17))

= √16

= 4

Задача 4. Если sec θ = 5/4, найти значение ctg θ/2 по формуле половинного угла.

Решение:

Имеем, сек θ = 5/4.

Используя cos θ = 1/сек θ, мы получаем cos θ = 4/5.

По формуле получаем

cot θ/2 = √((1 + cos θ)/(1 – cos θ))

= √((1 + (4/5))/ (1 – ( 4/5)))

= √((9/5)/ (1/5))

= √9

= 3

Задача 5. Если тангенс θ = 12/5, найти значение кроватки θ/2 по формуле половинного угла.

Решение:

Имеем тангенс θ = 12/5.

Очевидно, cos θ = 5/√(12 ² + 5 ² ) = 5/13

Используя формулу, получаем,

кроватка θ/2 = √((1 + cos θ)/(1 – cos θ))

= √((1 + (5/13))/ (1 – (5/13))

= √((18/13)/ (8/5))

= √(18/8)

= √(9/4)

= 3/2

Задача 6. Если кроватка θ = 8/15, найдите значение cot θ/2 по формуле половинного угла.

Решение:

Имеем, кроватка θ = 8/15.

Очевидно, cos θ = 8/√(8 ² + 15 ² ) = 8/17

Используя формулу, получаем,

кроватка θ/2 = √((1 + cos θ)/(1 – cos θ))

= √((1 + (8/17))/ (1 – (8/17))

= √((25/17)/ (9/17))

= √(25/9)

= 5/3

Задача 7. Найти значение cot 15° по формуле половинного угла .

Решение:

Нам нужно найти значение кроватки 15°.

Возьмем θ/2 = 15°

=> θ = 30°

Используя формулу половины угла, которую мы имеем,

ctg θ/2 = √((1 + cos θ)/(1 – cos θ )) 92}\frac{\alpha }{2} = \frac{{1 — \cos \alpha}}{2},\;\; \Стрелка вправо\влево| {\ грех \ гидроразрыва {\ альфа} {2}} \ справа | = \ sqrt {\ frac {{1 — \ cos \ alpha}} {2}} , \; \; \Rightarrow \sin \frac{\alpha}}{2} = \pm \sqrt {\frac{{1 — \cos\alpha}}{2}} .\]

Мы получили тождество синуса половины угла:

\[\sin \frac{\alpha}{2} = \pm\sqrt{\frac{1 — \cos\alpha}{2}}\]

Знак \(\pm\) в начале правой части означает, что квадратный корень может быть положительным или отрицательным — в зависимости от квадранта, в котором угол \(\frac{\alpha }{2}\) ложь. 92}\frac{\alpha }{2} = \frac{{1 + \cos \alpha}}{2},\;\; \Стрелка вправо\влево| {\ cos \ frac {\ alpha {2}} \ right | = \ sqrt {\ frac {{1 + \ cos \ alpha}} {2}}, \; \; \Rightarrow \cos\frac{\alpha}{2} = \pm \sqrt {\frac{{1 + \cos\alpha}}{2}} . \]

Следовательно,

\[\cos \frac{\alpha}{2} = \pm\sqrt{\frac{1 + \cos\alpha}{2}}\]

Знак зависит от квадранта, в котором находится \(\frac{\alpha }{2}\).

Тангенс половины угла

Теперь мы можем вывести формулу для вычисления \(\tan \frac{\alpha}{2}.\) Используя приведенные выше тождества, мы получаем 92}\frac{\alpha}{2}}} = \frac{{1 — \cos \alpha}}{{1 + \cos \alpha}}.\]

Следовательно,

\[\tan \frac{\alpha}{2} = \pm\sqrt{\frac{1 — \cos\alpha}{1 + \cos\alpha}}\]

, где знак \(\pm\) зависит от того, в какие квадранты окружности попадает угол \(\frac{\alpha}{2}\).

Мы также можем получить выражение для \(\tan \frac{\alpha }{2}\), не извлекая квадратный корень.

Умножение числителя и знаменателя в правой части формулы 92}\frac{\alpha} {2}}} = \frac{{\sin\alpha}}{{1 + \cos\alpha}},\]

то есть

\[\tan \frac{\alpha}{2} = \frac{\sin\alpha}{1 + \cos\alpha}\]

Аналогично, умножая числитель и знаменатель на \({\sin\frac{\alpha}{2}},\), мы можем получить тождество тангенса половинного угла в форме

\[\tan \ frac{\ alpha} {2} = \ frac {{\ sin \ frac {\ alpha} {2}}} {{\ cos \ frac {\ alpha} {2}}} = \ frac {{2\sin\frac{\alpha}{2}\sin\frac{\alpha}{2}}}{{2\sin\frac{\alpha}{2}\cos\frac{\alpha}{ 2}}} = \ frac {{2 {{\ sin } ^ 2} \ frac {\ alpha {2}}} {{\ sin \ alpha}} = \ frac {{1 — \ cos \ alpha }} {{\ грех \ альфа}}, \]

или

\[\tan \frac{\alpha}{2} = \frac{1 — \cos\alpha}{\sin\alpha}\]

Котангенс половинного угла

По определению,

\[\cot \frac{\alpha }{2} = \frac{1}{{\tan \frac{\alpha }{2}}}.

No related posts.