Текст задания:
Вычислите логарифмы с использованием следующих формул: и
1)
2)
3)
4)
5)
6)
7)
8)
9)
10)
11)
12)
13)
Задачи на основное логарифмическое тождество:
1)
2)
3)
4)
5)
6)
7)
8)
9)
10)
11)
12)
13)
14)
15)
16)
17)
Задачи на формулу перехода к новому основанию
1)
2)
3)
4)
5)
6)
7)
8)
9)
Раздел 3. Основы тригонометрии. Функции, их свойства и графики.
Уравнения и неравенства
Самостоятельная работа № 6
Тема: Формулы половинного аргумента
Цель: закрепить
знания и умения студентов применять
основные тригонометрические формулы.
Теоритическое обоснование:
Формулы половинного аргумента
Синус половинного угла
Примечание: Знак перед корнем выбирается в зависимости от квадранта, в который попадает угол α/2 в левой части. Данное правило справедливо также для других формул, приведенных ниже.
Косинус половинного угла
Тангенс половинного угла
Котангенс половинного угла
Выражение синуса через тангенс половинного угла
Выражение косинуса через тангенс половинного угла
Выражение тангенса через тангенс половинного угла
Выражение котангенса через тангенс половинного угла
Текст задания:
1. Доказать
тождества :
Доказать
тождества :
а). 1 + 2 cos 2α + cos 4α = 4 cos2 α cos 2α.
б). 1 — 2 cos 3α + cos 6α = — 4 sin2 3α/2 • cos 3α.
в). 1 + sin α = 2cos2 (π/4 — α/2).
г). 1— sin α = 2sin2 (π/4 — α/2).
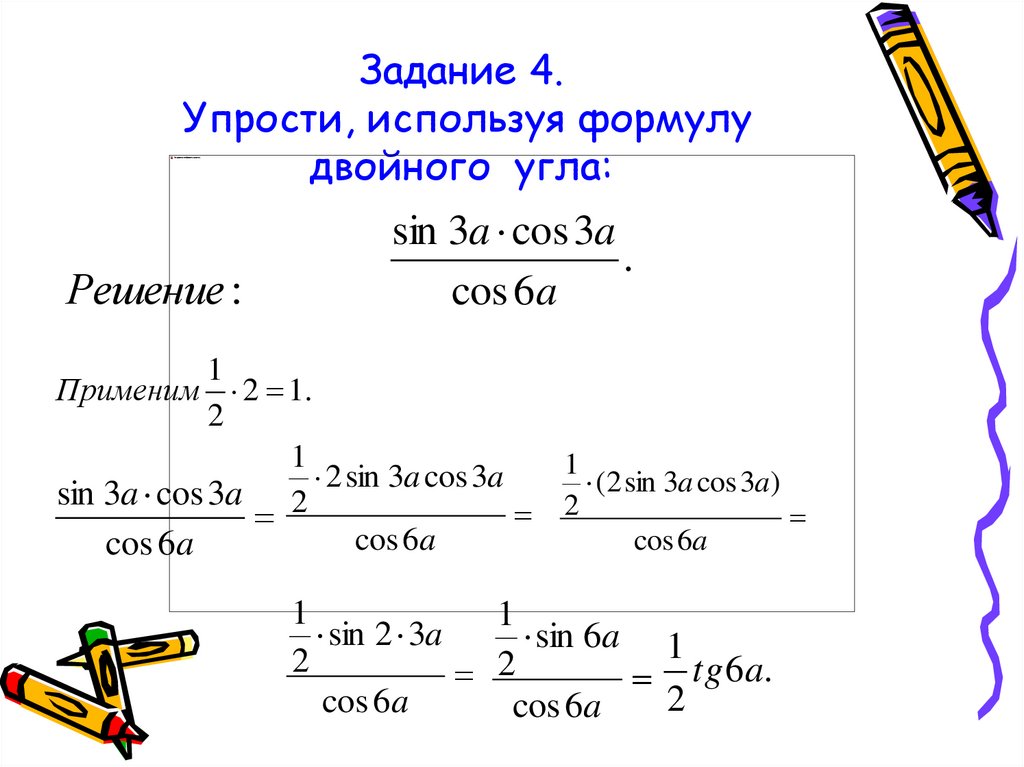
2. Упростить выражение
3. Найти sin α, cos α и tg α, если известно, что cos 2α = —0,6.
4. Найти sin α/2, cos α/2 и tg α/2, если известно, что | cos α | = 0,6, причем угол α, оканчивается во 2-й четверти,
5. Найти tg α, если sin 2α = 1/3
6. Вычислить:
а). sin ( 1/2 arccos 0,8 ). в). tg [ 1/2 arcsin (— 0,8 )]
б). cos ( 1/2 arcsin 0,6 ) г). tg [ 1/2 arctg (— 0,75 )]
Самостоятельная работа № 7
Тема: Преобразование тригонометрических выражений
Цель: закрепить
знания и умения студентов по освоению
свойств тригонометрических функций.
Теоритическое обоснование:
Формулы приведения:
Текст задания:
1. Найти значение выражения , если известно, что tg α = 1/3
2. Найти значение выражения , если известно, что котангенс угла α не определен.
3. Найти значение выражения , если известно, что ctg α = ½
4. Упростить выражения:
5. Доказать тождества:
Самостоятельная работа № 8
Тема: Решение тригонометрических неравенств (синус, косинус).
Цель: закрепить знания и умения студентов по освоению методов решения тригонометрических неравенств.
Теоритическое обоснование:
Утверждение 1. Множество решений неравенства sinx > a, есть
R, если a < -1;
(arcsina + 2pk; p — arcsina + 2pk), если -1 ≤ a < 1;
Пустое множество, если a ≥ 1.

Утверждение 2. Множество решений неравенства sinx <
R, если a > 1;
(-p — arcsina + 2pk; arcsina + 2pk), если -1 < a ≤ 1;
Пустое множество, если a ≤ -1.
Утверждение 3. Множество решений неравенства cosx > a, есть
R, если a < -1;
(2pk — arccosa; 2pk + arccosa), если -1 ≤ a < 1;
Пустое множество, если a ≥ 1.
Утверждение 4. Множество решений неравенства cosx < a, есть
R, если a > 1;
(2pk + arccosa; 2p(k + 1) — arccosa), если -1 < a ≤ 1;
Пустое множество, если a ≤ -1.
2\frac{23π}{12}-\sqrt{27}=\sqrt{108}\)\( \frac{1+\cos\frac{2\cdot 23π}{12}}{2}\)\(-\sqrt{27}=\sqrt{108}\)\(\frac{1+\cos\frac{23π}{6}}{2}\)\(-\sqrt{27}=\)…
\(\frac{23π}{6}=\frac{24π-π}{6}=\frac{24π}{6}-\frac{π}{6}=4π-\frac{π}{6}\).Попали в самое большое из трех стандартных значений косинуса: \(\frac{1}{2}\), \(\frac{\sqrt{2}}{2}\), \(\frac{\sqrt{3}}{2}\). Значит \(\cos\frac{23π}{6}=\frac{\sqrt{3}}{2}\).
…\(=\sqrt{108}\)\(\frac{1+\frac{\sqrt{3}}{2}}{2}\)\(-\sqrt{27}=\sqrt{27\cdot 4}\)\(\frac{1+\frac{\sqrt{3}}{2}}{2}\)\(-\sqrt{27}=2\sqrt{27}\cdot\)\(\frac{1+\frac{\sqrt{3}}{2}}{2}\)\(-\sqrt{27}=\sqrt{27}(1+\frac{\sqrt{3}}{2})-\sqrt{27}=\)
\(=\sqrt{27}+\frac{\sqrt{27\cdot 3}}{2}-\sqrt{27}=\frac{\sqrt{81}}{2}=\frac{9}{2}=4,5\).Это решение не самое простое из всех возможных (наиболее легкое приведено в статье «формулы двойного угла»), но до него легче всего догадаться, если знаешь формулу половинного угла.
 2\frac{7π}{8}\).
2\frac{7π}{8}\).\(=\sqrt{32}-\sqrt{128}\)\(\frac{1-\cos\frac{7π}{4}}{2}\)\(=\)
Вычислим косинус с помощью формулы приведения. Для этого сначала преобразуем \(\frac{7π}{4}\):
\(\frac{7π}{4}=\frac{8π-π}{4}=\frac{8π}{4}-\frac{π}{4}=2π-\frac{π}{4}\)
\(=\sqrt{32}-\sqrt{128}\)\(\frac{1-\cos(2π-\frac{π}{4})}{2}\)\(=\)
Теперь применим к косинусу формулу приведения:
-
\((2π-\frac{π}{4})\) – это четвертая четверть, косинус в ней положителен. Значит, знак перед косинусом останется прежним.
-
\(2π\) — находится на «горизонтали» — функция остается прежней.

\(\cos(2π-\frac{π}{4})=\cos\frac{π}{4}\).
\(=\sqrt{32}-\sqrt{128}\)\(\frac{1-\cos\frac{π}{4}}{2}\)\(=\)
\(\cos\frac{π}{4}=\frac{\sqrt{2}}{2}\).
\(=\sqrt{32}-\sqrt{128}\)\(\frac{1-\frac{\sqrt{2}}{2}}{2}\)\(=\)
Домножим числитель и знаменатель дроби на \(2\), чтоб избавиться от «трехэтажности».
\(=\sqrt{32}-\sqrt{128}\)\(\frac{2-\sqrt{2}}{4}\)\(=\)
Игнорировать корни больше невозможно. Вынесем из \(\sqrt{128}\) четверку, чтоб она сократилась со знаменателем:
\(\sqrt{128}=\sqrt{16\cdot 8}=4\sqrt{8}\)
\(=\sqrt{32}-4\sqrt{8}\)\(\frac{2-\sqrt{2}}{4}\)\(=\)
Сократим четверки.

\(=\sqrt{32}-\sqrt{8}(2-\sqrt{2})=\)
Раскроем скобки.
\(=\sqrt{32}-2\sqrt{8}+\sqrt{16}=\)
Занесем \(2\) под корень и вычислим \(\sqrt{16}\).
\(=\sqrt{32}-\sqrt{32}+4=4\).
Ответ: \(4\).
Смотрите также:
Формулы тригонометрии с примерамиЧто такое полуугловые тождества?
Обновлено 7 декабря 2020 г.
Автор Lisa Maloney
Как и в алгебре, когда вы начинаете изучать тригонометрию, вы накапливаете наборы формул, которые можно использовать для решения задач.
 Одним из таких наборов являются тождества половинного угла, которые можно использовать для двух целей. Один из них заключается в преобразовании тригонометрических функций ( θ /2) в функции в терминах более знакомого (и более простого) θ . Другой заключается в том, чтобы найти фактическое значение тригонометрических функций числа 9.0007 θ , когда θ можно выразить как половину более привычного угла.
Одним из таких наборов являются тождества половинного угла, которые можно использовать для двух целей. Один из них заключается в преобразовании тригонометрических функций ( θ /2) в функции в терминах более знакомого (и более простого) θ . Другой заключается в том, чтобы найти фактическое значение тригонометрических функций числа 9.0007 θ , когда θ можно выразить как половину более привычного угла.Обзор тождеств половинных углов
Во многих учебниках по математике перечисляются четыре основных тождества половинных углов. Но, применяя смесь алгебры и тригонометрии, эти уравнения можно преобразовать в ряд полезных форм. Вам не обязательно запоминать все это (если только ваш учитель не настаивает), но вы должны, по крайней мере, понимать, как их использовать:
Идентификация половинного угла для синуса
\sin\bigg(\frac{θ}{2}\bigg) = ±\sqrt{\frac{1 — \cosθ}{2}}
Половина угла для косинуса
\cos\bigg(\frac{θ}{2}\bigg) = ±\sqrt{\frac{1 + \cosθ}{2}}
Полуугольные тождества для касательной
\tan \ bigg (\ frac {θ} {2} \ bigg) = ± \ sqrt {\ frac {1 — \ cos θ} {1 + \ cos θ}} \\ \, \\ \ tan \ bigg (\ frac {θ} {2}\bigg) = \frac{\sinθ}{1 + \cosθ} \\ \,\\ \tan\bigg(\frac{θ}{2}\bigg) = \frac{1 — \cosθ} {\sinθ} \\ \,\\ \tan\bigg(\frac{θ}{2}\bigg) = \cscθ — \cotθ
Полуугольные тождества для котангенса \\ \,\\ \cot\bigg(\frac{θ}{2}\bigg) = \frac{\sinθ}{1 — \cosθ} \\ \,\\ \cot\bigg(\frac{θ {2}\bigg) = \frac{1 + \cosθ}{\sinθ} \\ \,\\ \cot\bigg(\frac{θ}{2}\bigg) = \cscθ + \cotθ
Пример использования тождеств половинного угла
Так как же использовать тождества половинного угла? Первый шаг — признать, что вы имеете дело с углом, который составляет половину более знакомого угла.

- Квадрант I: все тригонометрические функции
- Квадрант II: только синус и косеканс
- Квадрант III: только тангенс и котангенс
- Квадрант IV: только косинус и секанс в этом случае ваш угол θ представляет собой 30 градусов, которые попадают в квадрант I, вы знаете, что значение синуса, которое он возвращает, будет положительным. Таким образом, вы можете опустить знак ± и просто вычислить:
\sin(15) = \sqrt{\frac{1 — \cos(30)}{2}}
Подставить знакомое известное значение cos(30). В этом случае используйте точные значения (в отличие от десятичных приближений из таблицы):
\sin(15) = \sqrt{\frac{1 — \sqrt{3/2}}{2}}
Далее , упростите правую часть уравнения, чтобы найти значение sin(15).
 Начните с умножения выражения под радикалом на 2/2, что даст вам:
Начните с умножения выражения под радикалом на 2/2, что даст вам:\sin(15) = \sqrt{\frac{2(1 — \sqrt{3/2})}{4}}
Это упрощается до:
\sin(15) = \sqrt{\frac{2 — \sqrt{3}}{4}}
Затем можно извлечь квадратный корень из 4:
\sin(15) = \frac{1}{2}\sqrt{2 — \sqrt{3}}
В большинстве случаев это примерно равно насколько вы упростите. Хотя результат может быть не очень красивым, вы перевели синус незнакомого угла в точную величину.
представьте, что вас попросили найти синус угла 15 градусов. Это не тот угол, для которого большинство студентов запоминают значения триггерных функций. Но если вы примете 15 градусов равным θ/2, а затем найдете θ, вы обнаружите, что: , является более привычным углом, здесь будет полезно использовать формулу половинного угла.
Поскольку вас попросили найти синус, на самом деле есть только одна формула половинного угла на выбор:
\sin\bigg(\frac{θ}{2}\bigg) = ±\sqrt{\frac{1 — \cosθ}{2}}
Подставляя в θ /2 = 15 градусов и θ = 30 градусов дает вам:
\sin(15) = ±\sqrt{\frac{1 — \cos(30)}{2}}
Если вас попросили найти касательную или котангенс, оба из которых наполовину умножают способы выражения своей половинной идентичности угла, вы просто выбираете версию, которая выглядит проще всего для работы.
Знак ± в начале некоторых половинных тождеств означает, что рассматриваемый корень может быть положительным или отрицательным.
 Вы можете разрешить эту неоднозначность, используя свои знания о тригонометрических функциях в квадрантах. Вот краткий обзор того, какие триггерные функции возвращают положительные значения, в которых квадранты:
Вы можете разрешить эту неоднозначность, используя свои знания о тригонометрических функциях в квадрантах. Вот краткий обзор того, какие триггерные функции возвращают положительные значения, в которых квадранты:Формулы половинного угла — Примеры | Тождества половинного угла
Мы изучаем формулы половинного угла (или тождества половинного угла) в тригонометрии. Формулы половинного угла можно получить, используя формулы двойного угла. Как известно, формулы двойного угла можно вывести, используя формулы суммы и разности углов тригонометрии. Полууглы в формулах половинного угла обычно обозначаются как θ/2, x/2, A/2 и т. д., а половинный угол представляет собой дольный угол. Формулы половинного угла используются для нахождения точных значений тригонометрических соотношений таких углов, как 22,5° (что составляет половину стандартного угла 45°), 15° (что составляет половину стандартного угла 30°) и т.

Давайте рассмотрим формулы половинного угла вместе с их доказательствами и несколькими решенными примерами.
1. Что такое формулы половинного угла? 2. Полуугольные тождества 3. Вывод формул половинного угла с использованием формул двойного угла 4. Полуугольная формула защиты от греха 5. Формула половинного угла для вычисления Cos 6. Формула полуугла получения загара 7. Формула половинного угла с использованием полупериметра 8. Часто задаваемые вопросы о Half Angle Formula Что такое формулы половинного угла?
В этом разделе мы увидим формулы половинного угла для sin, cos и tan. Мы знаем значения тригонометрических функций (sin, cos, tan, cot, sec, cosec) для таких углов, как 0°, 30°, 45°, 60° и 9°.
 0° из тригонометрической таблицы. Но чтобы узнать точные значения sin 22,5°, tan 15° и т. д., формулы половинного угла чрезвычайно полезны. Кроме того, они помогают доказать несколько тригонометрических тождеств. У нас есть формулы половинного угла, полученные из формул двойного угла, и они выражаются через половинные углы, например θ/2, x/2, A/2 и т. д. Вот список важных формул половинного угла:
0° из тригонометрической таблицы. Но чтобы узнать точные значения sin 22,5°, tan 15° и т. д., формулы половинного угла чрезвычайно полезны. Кроме того, они помогают доказать несколько тригонометрических тождеств. У нас есть формулы половинного угла, полученные из формул двойного угла, и они выражаются через половинные углы, например θ/2, x/2, A/2 и т. д. Вот список важных формул половинного угла:Полуугольные удостоверения
Вот популярные тождества половины угла , которые мы используем при решении многих задач тригонометрии, следующие:
- Формула половинного угла sin: sin A/2 = ±√[(1 — cos A) / 2]
- Формула половинного угла для cos: cos A/2 = ±√[(1 + cos A) / 2]
- Формула половины угла tan: tan A/2 = ±√[1 — cos A] / [1 + cos A] (или) sin A / (1 + cos A) (или) (1 — cos A) / грех А
Вывод формул половинного угла с использованием формул двойного угла
Чтобы вывести приведенные выше формулы, сначала выведем следующие формулы половинного угла.
 Формулы двойного угла основаны на двойных углах, таких как 2θ, 2A, 2x и т. д. Мы знаем, что формулы двойного угла для sin, cos и tan равны
Формулы двойного угла основаны на двойных углах, таких как 2θ, 2A, 2x и т. д. Мы знаем, что формулы двойного угла для sin, cos и tan равны- sin 2x = 2 sin x cos x .
- cos 2x = cos 2 x — sin 2 x (или)
= 1 — 2 sin 2 х (или)
= 2 cos 2 х — 1 - тангенс 2x = 2 тангенс х / (1 — тангенс 2 х)
Если мы заменим x на A/2 в обеих частях каждого уравнения формулы двойного угла, мы получим половинные тождества углов (поскольку 2x = 2(A/2) = A).
- sin A = 2 sin(A/2) cos(A/2)
- cos A = cos 2 (A/2) — sin 2 (A/2) (или)
= 1 — 2 sin 2 (A/2) (или)
= 2 cos 2 (А/2) — 1 - tan A = 2 tan (A/2) / (1 — tan 2 (A/2))
Мы также можем вывести одну формулу половины угла, используя другую формулу половины угла. Например, только из формулы cos A мы можем вывести 3 важных тождества полууглов для sin, cos и tan, которые упомянуты в первом разделе.
 Вот доказательство формулы половинного угла.
Вот доказательство формулы половинного угла.Полуугольная формула защиты от греха
Теперь докажем формулу половины угла для синуса. Используя одну из приведенных выше формул для cos A, мы имеем
cos A = 1 — 2 sin 2 (A/2)
Отсюда
2 sin 2 (A/2) = 1 — cos A
sin 2 (A/2) = (1 — cos A) / 2
sin (A/2) = ±√[(1 — cos A) / 2]
Формула половинного угла для производного Cos
Теперь докажем формулу половины угла для функции косинуса. Используя одну из приведенных выше формул cos A,
cos A = 2 cos 2 (A/2) — 1
Отсюда
2 cos 2 (A/2) = 1 + cos A
cos 2 (A/2) = (1 + cos A) / 2
cos (A/2) = ±√[(1 + cos A) / 2]
Формула получения загара с половинным углом
Мы знаем, что tan (A/2) = [sin (A/2)] / [cos (A/2)]
Из формул половинного угла sin и cos
tan (A/2) = [±√(1 — cos A)/2] / [±√(1 + cos A)/2]
= ±√[(1 — cos A) / (1 + cos A)]
Это является одной из формул загара (A/2).
 Выведем две другие формулы, рационализировав здесь знаменатель.
Выведем две другие формулы, рационализировав здесь знаменатель.тангенс (A/2) = ±√[(1 — cos A) / (1 + cos A)] × √[(1 — cos A) / (1 — cos A)]
= √[(1 — cos A) 2 / (1 — cos 2 A)]
= √[(1 — cos A) 2 / sin 2 A]
= (1 — cos A) / sin A
Это вторая формула тангенса (A/2). Чтобы вывести другую формулу, давайте умножим и разделим приведенную выше формулу на (1 + cos A). Тогда мы получаем
тангенс (A/2) = [(1 — cos A) / sin A] × [(1 + cos A) / (1 + cos A)]
= (1 — cos 2 A) / [sin A (1 + cos A)]
= sin 2 A / [sin A (1 + cos A)]
= sin A / ( 1 + cos A)
Таким образом, tan (A/2) = ±√[(1 — cos A) / (1 + cos A)] = (1 — cos A) / sin A = sin A / (1 + cos А).
Формула половинного угла с использованием полупериметра
В этом разделе мы увидим формулы половинного угла с использованием полупериметра.
 т. е. это формулы половины угла через стороны треугольника. Рассмотрим треугольник ABC, где AB = c, BC = a и CA = b.
т. е. это формулы половины угла через стороны треугольника. Рассмотрим треугольник ABC, где AB = c, BC = a и CA = b.Давайте выведем здесь одну из этих формул. Мы знаем, что полупериметр треугольника равен s = (a + b + c)/2. Отсюда имеем 2s = a + b + c. Из одной из приведенных выше формул
cos A = 2 cos²(A/2) — 1 (или)
2 cos²(A/2) = 1 + cos A
Теперь, используя закон косинусов,
2 cos 2 (A/2) = 1 + [ (b 2 + c 2 — a 2 ) / (2bc) ]
2 cos 2 (A/2) = [2bc + b² + c² — a²] / [2bc]
2 cos 2 (A/2) = [ (b + c)² — a²] / [2bc] [с использованием формулы (a+b)²]
2 cos 2 (A/2) = [ (b + c + a) (b + c — a) ] / [2bc] [Используя формулу a² — b²]
2 cos 2 (A/2) = [ 2s (2s — 2a) ] / [ 2bc] [As 2s = a + b + c]
2 cos 2 (A/2) = [ 2s (s — a) ] / [bc]
cos 2 (A/2) = [ s(s — a) ] / [bc]
cos (A/2) = √[ s (s — a) ] / [bc]
Мы получили формулу полуугла для косинуса угла A/2 .
 Точно так же мы можем получить другие тождества половинного угла косинуса, используя полупериметр. Другая формула синусов половинного угла может быть получена с использованием полупериметра.
Точно так же мы можем получить другие тождества половинного угла косинуса, используя полупериметр. Другая формула синусов половинного угла может быть получена с использованием полупериметра.sin 2 (A/2) = (1 − cos A)/2
= (1/2)[1−(b 2 +c 2 −a 2 )/2bc] (Используя закон косинусов)
= (1/2)(a 2 −(b−c) 2 )/2bc
= (1/2)(a + b − c)(a + c − b)/2bc
= (1/2){(a + b + c) − 2c}{(a + b + c) − 2b}/2bc
= (1/2)(2s − 2c )(2s − 2b)/2bc
= (s − b)(s − c)/bc
⇒ sin (A/2) = √[(s − b)(s − c)/bc]
Точно так же мы можем вывести другие формулы половинного угла синуса. Формулы половинного угла для функции тангенса можно вывести по формуле tan (A/2) = sin (A/2)/cos (A/2).
☛ Связанные темы:
- Формулы углов
- Тригонометрические функции
- Тригонометрические уравнения
Часто задаваемые вопросы о Half Angle Formula
Что такое формулы половинного угла в тригонометрии?
Формулы половинного угла дают значения половинных углов, таких как A/2, x/2 и т.
 д. тригонометрических соотношений. Формулы половинного угла для sin, cos и tan:
д. тригонометрических соотношений. Формулы половинного угла для sin, cos и tan:- sin A/2 = ±√[(1 — cos A) / 2]
- cos A/2 = ±√[(1 + cos A) / 2]
- tan A/2 = ±√[1 — cos A] / [1 + cos A]
Что такое формула половинного угла для греха?
Формула половины угла для sin в тригонометрии: sin A/2 = ±√[(1 — cos A) / 2]. У нас есть другая формула половинного угла греха в терминах полупериметра. Если a, b и c — стороны треугольника, а A, B и C — соответствующие им противоположные углы, то sin A/2 = √[(s — b) (s — c)/bc].
Что такое формула половинного угла для косинуса?
Формула половинного угла для cos: cos A/2 = ±√[(1 + cos A)/2]. У нас есть еще одна формула половинного угла cos через полупериметр. Если a, b и c — стороны треугольника, а A, B и C — соответствующие им противоположные углы, то cos (A/2) = √[s (s — a)/bc].
Что такое формула половинного угла для касательной?
Формула половины угла тангенса: tan (A/2) = ±√[1 — cos A] / [1 + cos A] = (1 — cos A) / sin A = sin A / (1 + cos A ).
 У нас есть еще одна формула половинного угла тангенса в терминах полупериметра. Если a, b и c — стороны треугольника, а A, B и C — соответствующие им противоположные углы, то sin A/2 = √[(s — b) (s — c)] / [s(s) — а)].
У нас есть еще одна формула половинного угла тангенса в терминах полупериметра. Если a, b и c — стороны треугольника, а A, B и C — соответствующие им противоположные углы, то sin A/2 = √[(s — b) (s — c)] / [s(s) — а)].Зачем использовать формулы половинного угла?
Мы используем формулы половины угла для нахождения тригонометрических отношений половин стандартных углов, например, мы можем найти тригонометрические отношения углов, таких как 15°, 22,5° и т. д., используя тождества половинного угла. Их можно использовать для доказательства различных тригонометрических тождеств. Они также используются при решении интегралов.
Как вывести формулу половинного угла для Cos?
Используя формулу двойного угла для cos,
cos 2x = 2cos 2 x — 1
Заменив x на (A/2), мы получим
cos A = 2 cos 2 (A/2) — 1
Мы решим это для cos (A/2) .
2 cos 2 (A/2) = 1 + cos A
cos 2 (A/2) = (1 + cos A) / 2
cos A/2 = ±√(1 + cos A) / 2
Что такое tan 15°, используя тождества половинного угла?
Используя тождество половинного угла tan,
tan (A/2) = (1 — cos A) / sin A
Замена A = 30°,
тангенс (30°/2) = (1 — cos 30°) / sin 30°
= [1 — (√3/2)] / (1/2) (из таблицы триггеров)
= [ (2 — √3) / 2] / (1/2)
= 2 — √3
Следовательно, тангенс 15° = 2 — √3.

-



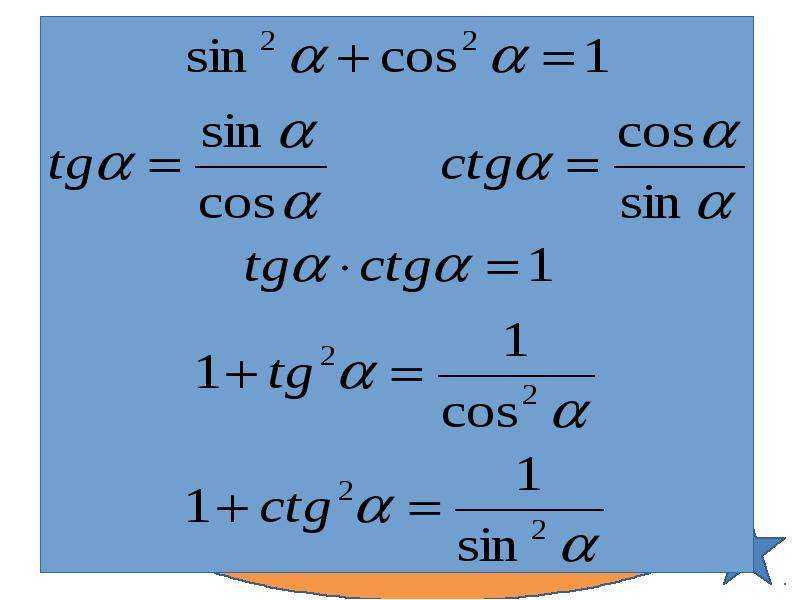

 Одним из таких наборов являются тождества половинного угла, которые можно использовать для двух целей. Один из них заключается в преобразовании тригонометрических функций ( θ /2) в функции в терминах более знакомого (и более простого) θ . Другой заключается в том, чтобы найти фактическое значение тригонометрических функций числа 9.0007 θ , когда θ можно выразить как половину более привычного угла.
Одним из таких наборов являются тождества половинного угла, которые можно использовать для двух целей. Один из них заключается в преобразовании тригонометрических функций ( θ /2) в функции в терминах более знакомого (и более простого) θ . Другой заключается в том, чтобы найти фактическое значение тригонометрических функций числа 9.0007 θ , когда θ можно выразить как половину более привычного угла.
 Вы можете разрешить эту неоднозначность, используя свои знания о тригонометрических функциях в квадрантах. Вот краткий обзор того, какие триггерные функции возвращают положительные значения, в которых квадранты:
Вы можете разрешить эту неоднозначность, используя свои знания о тригонометрических функциях в квадрантах. Вот краткий обзор того, какие триггерные функции возвращают положительные значения, в которых квадранты: Начните с умножения выражения под радикалом на 2/2, что даст вам:
Начните с умножения выражения под радикалом на 2/2, что даст вам:
 0° из тригонометрической таблицы. Но чтобы узнать точные значения sin 22,5°, tan 15° и т. д., формулы половинного угла чрезвычайно полезны. Кроме того, они помогают доказать несколько тригонометрических тождеств. У нас есть формулы половинного угла, полученные из формул двойного угла, и они выражаются через половинные углы, например θ/2, x/2, A/2 и т. д. Вот список важных формул половинного угла:
0° из тригонометрической таблицы. Но чтобы узнать точные значения sin 22,5°, tan 15° и т. д., формулы половинного угла чрезвычайно полезны. Кроме того, они помогают доказать несколько тригонометрических тождеств. У нас есть формулы половинного угла, полученные из формул двойного угла, и они выражаются через половинные углы, например θ/2, x/2, A/2 и т. д. Вот список важных формул половинного угла: Формулы двойного угла основаны на двойных углах, таких как 2θ, 2A, 2x и т. д. Мы знаем, что формулы двойного угла для sin, cos и tan равны
Формулы двойного угла основаны на двойных углах, таких как 2θ, 2A, 2x и т. д. Мы знаем, что формулы двойного угла для sin, cos и tan равны Вот доказательство формулы половинного угла.
Вот доказательство формулы половинного угла.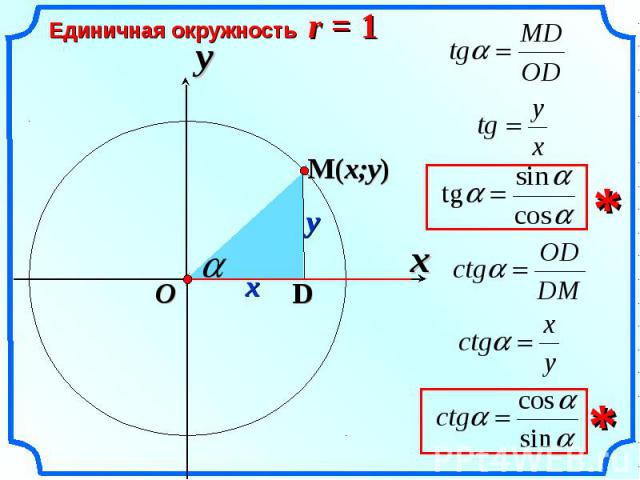 Выведем две другие формулы, рационализировав здесь знаменатель.
Выведем две другие формулы, рационализировав здесь знаменатель. т. е. это формулы половины угла через стороны треугольника. Рассмотрим треугольник ABC, где AB = c, BC = a и CA = b.
т. е. это формулы половины угла через стороны треугольника. Рассмотрим треугольник ABC, где AB = c, BC = a и CA = b. Точно так же мы можем получить другие тождества половинного угла косинуса, используя полупериметр. Другая формула синусов половинного угла может быть получена с использованием полупериметра.
Точно так же мы можем получить другие тождества половинного угла косинуса, используя полупериметр. Другая формула синусов половинного угла может быть получена с использованием полупериметра. д. тригонометрических соотношений. Формулы половинного угла для sin, cos и tan:
д. тригонометрических соотношений. Формулы половинного угла для sin, cos и tan: У нас есть еще одна формула половинного угла тангенса в терминах полупериметра. Если a, b и c — стороны треугольника, а A, B и C — соответствующие им противоположные углы, то sin A/2 = √[(s — b) (s — c)] / [s(s) — а)].
У нас есть еще одна формула половинного угла тангенса в терминах полупериметра. Если a, b и c — стороны треугольника, а A, B и C — соответствующие им противоположные углы, то sin A/2 = √[(s — b) (s — c)] / [s(s) — а)].