2. Линейная функция. Первый урок
Здравствуйте уважаемые родители и обучающиеся! Откройте ваши тетради для классных работ и запишите тему урока: «Линейная функция, ее график и свойства» Откройте страницу учебника 163, положите учебник перед собой. Приступим к изучению материала… Сегодня мы поговорим о конкретных видах функции. Линейных функциях. Почему они называются линейными? Обратимся к словарю: Конечно, нас интересует геометрический смысл этого слова. Линейная функция потому называется линейной, потому что ее график задает линию — одну сплошную прямую… Давайте рассмотрим практический пример линейной функции. Пример: Представим, что едет машина легковая с постоянной скоростью 100 км/ч. а грузовая со скоростью 60 км/ч. Скорость машин не меняется, а время идет. Проходит час, два, три, четыре… Машины еще в пути…Сколько они проехали?.. Давайте изобразим траекторию ее движения… У нас есть две величины: Расстояние (S) и t (время). Зависимость очевидна. Дольше едешь — дальше будешь! Неправда ли? Составим таблицу значений: Мы получили значения по времени и расстоянию в течение 5 часов для легкового и грузового автомобилей. Теперь можем перейти к графическому изображению, то есть графику функций: S = 60t и S=100t. За ось y ( зависимые переменные) обозначаем значения расстояния, за ось x (независимые переменные) обозначим время t. И построим графики в координатной плоскости: Что мы видим в качестве графика — прямую! А какие формулы нам дали график — прямую??? Формулы вида: S = 60t и S=100t!!! Получается, что формулы определенного вида дают определенные функции. Да. И мы сейчас с этим разберемся! Записываем определение:
В колонке «Функция» (см рисунок выше) вы видите что они разные, но все они задают прямую, только под разным наклоном. 1 функция: у=5x+3. Рассмотрим алгоритм ( правило построения линейной функции): 1 шаг. Это линейная функция. Почему? Потому что она представляет собой формулу y=kx+b, где к=5, b=3. 2 шаг. Согласно правилу, для построения линейной функции нужны две точки. Где их взять? И как? Легко. Вам нужно составить таблицу значений из двух чисел, которые вы сами захотите, но так, чтобы легко было их высчитать для построения самого графика. Как видите, я взял независимые переменные x=0, x=1. Почему я так сделал? Я бы мог взять x=4334, но не стал…. Мне нужно получить всего лишь две точки, чтобы их соединить прямой. Зачем мне составлять сложные координаты. Я возьму такие, которые дают хорошие удобные числа. 3 шаг. Мы готовы построить график. Для этого обращаемся к координатной плоскости. Строим точки с координатами: (0; 3) и (3;8) и соединяем прямой. Получаем график линейной функции — прямую!!! Смотрите рисунок. Давайте потренируемся в построении линейной функции. Я взял несколько линейных функций для эксперимента. Давайте обсудим: Что в этих функциях одинакового? Мы видим, что у нее одинаковый коэффициент k=2. Значит графики одинаково будут построены? Как вы считаете? Смотрите на рисунок, на формулу и графики… Что делает расположение графиков именно такими при одинаковом коэффициенте k=2? Меняет дело другой коэффициент b. Запомните: коэффициент b в функции y=кx+b отвечает за точку пересечения графика с осью y. Проверьте это утверждение, глядя на рисунок… С коэффициентом b в функции вида y=kx+b разобрались. Посмотрите на функцию, где коэффициент b отсутствует. То есть функция изменить немного вид: y=kx. Это не означает, что она перестала быть линейной, она просто будет проходить всегда через начало координат!!! Так как b отвечает за точку пересечения с осью y, а y =о! Давайте проиллюстрируем!!! Слева функции, справа — их исполнение! Что их объединяет? Только то, что они линейные и проходят через одну точку — через начало координат, поскольку коэффициент b у них отсутствует, как видите сами.
Запомните: Если коэффициент b в функции y=кx+b отсутствует, то функция проходит через начало координат — (0;0). Функция вида y=кx называется прямой пропорциональной зависимостью. (стр 165 читайте)!!! В линейной функции y=кx+b , коэффициент k тоже имеет свою роль. Его называют коэффициентом наклона. Запишем правило: Другими словами: если прямая при пересечении с осью x образует: ——тупой угол: k<0 ——острый угол: k>0 Проведем опыт: Рассмотрим несколько линейных функции: y=-2x+1; y=5x+3; Первая функция: Вторая функция: Вот мы и разобрали значение коэффициентов. Ну, а пара чисел x и y — переменные, независимая и зависимая. Если вам необходимо больше информации: жмите сюда Давайте посмотрим видео и подытожим все, что мы сказали выше: Решение задач на линейную функцию y=кx+b Сегодня мы рассмотрим с вами задачи: № 857 Смотрим решение и пробуем работать самостоятельно: |
Линейная функция y=kx+b определение и её график
- Определение линейной функции
- График линейной функции
- Примеры
Определение линейной функции
Рассмотрим движение машины по прямой со скоростью 50 км/ч, но не из начальной точки.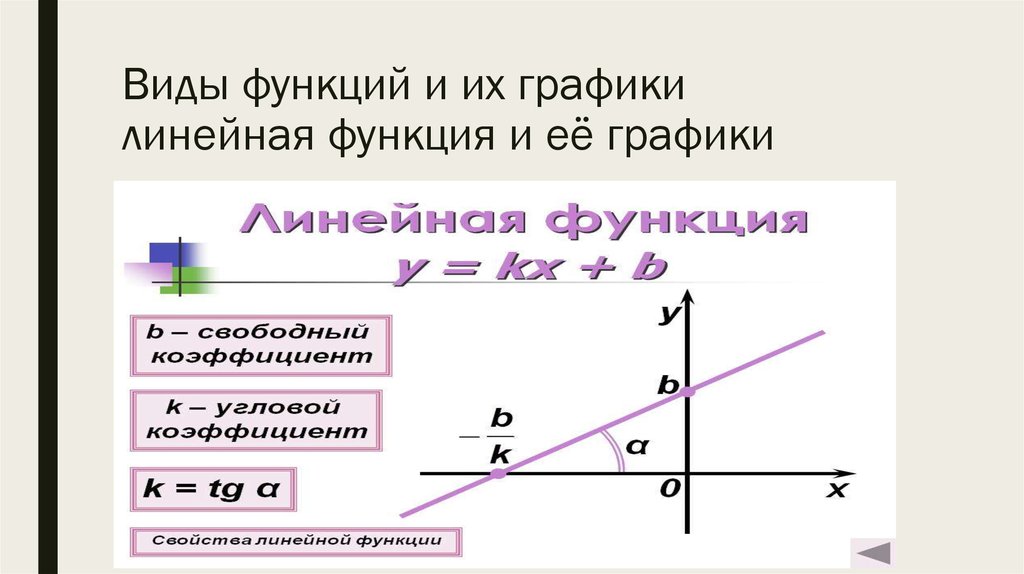 Допустим, что мы уже находимся на расстоянии 20 км от начала координат и будем удаляться. Тогда зависимость расстояния до начала координат от времени s = 50t+20. От прямой пропорциональности s = 50t эту формулу отличает дополнительное слагаемое, связанное с ненулевыми начальными условиями.
Допустим, что мы уже находимся на расстоянии 20 км от начала координат и будем удаляться. Тогда зависимость расстояния до начала координат от времени s = 50t+20. От прямой пропорциональности s = 50t эту формулу отличает дополнительное слагаемое, связанное с ненулевыми начальными условиями.
Если обобщить формулы, описывающие подобные зависимости, то получаем:
Прямая пропорциональность y = kx является частным случаем линейной функции y = kx+b, при k $\neq$ 0 и b = 0.
График линейной функции
Графиком линейной функции является прямая.
Согласно аксиоме планиметрии, через любые две точки можно провести прямую и притом только одну. Значит, положение прямой на плоскости полностью определяется двумя точками . Получаем:
Например: построим график функции y = 2x+1
$k = 2 \gt 0$ – функция возрастает
b=1 – функция пресекает ось Y в точке (0;1)
Примеры
Пример 1.Постройте графики линейных функций. Укажите, возрастает или убывает функция. Найдите точку её пересечения с осью Y.
Найдите точку её пересечения с осью Y.
а) y = x+2
$k = 1 \gt 0$ – функция возрастает
b = 2 точка пересечения с осью Y (0;2)
б) y = x-1
$k = 1 \gt 0$ – функция возрастает
b = -1 точка пересечения с осью Y (0;-1)
в) $y = \frac{1}{2} x+3$
$k = \frac{1}{2} \gt 0$ – функция возрастает
b = 3 точка пересечения с осью Y (0;3)
г) y = -x-1
$k = -1 \lt 0$ – функция убывает
b = -1 точка пересечения с осью Y (0;-1)
д) y = -2x+3
$k = -2 \lt 0$ – функция убывает
b = 3 точка пересечения с осью Y (0;3)
е) $y = — \frac{1}{3} x$
$k = -\frac{1}{3} \lt 0$ – функция убывает
b = 1 точка пересечения с осью Y (0;1)
ж) y = 1
Прямая, параллельная оси Х и проходящая через точку (0;1)
k = 0 функция постоянна
b = 1 точка пересечения с осью Y (0;1)
з) y = -5
Прямая, параллельная оси Х и проходящая через точку (0;-5)
k = 0 функция постоянна
b = -5 точка пересечения с осью Y (0;-5)
Пример 2.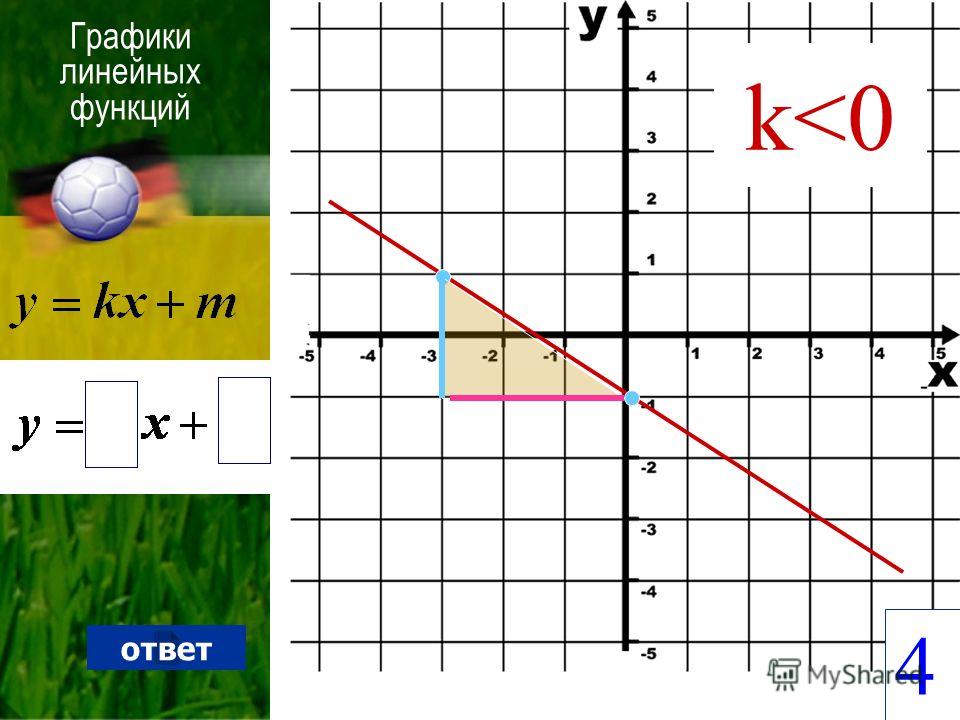 График линейной функции y=kx-3 проходит через точку A(-1;0,5). Найдите k.
График линейной функции y=kx-3 проходит через точку A(-1;0,5). Найдите k.
Подставляем в формулу функции координаты точки A:
$0,5 = k \cdot (-1)-3$
k=-0,5-3=-3,5
Ответ:-3,5
Пример 3*.Найдите уравнение прямой, проходящей через точки A(2;4)и B(-1;1)
Угловой коэффициент:
$$k = \frac{Y_B-Y_A}{X_B-X_A} = \frac{-1-2}{1-4} = 1$$
Уравнение имеет вид y = x+b.
Подставляем координаты A:
$$4 = 2+b \Rightarrow b = 2 $$
Искомое уравнение: y = x+2
Что такое линейная функция? Как решить линейную функцию?|Mathhelp
18 декабря 2017 г.
Автор: StudyGate
Теги: Помощь по алгебре, Помощь с домашним заданием
Что такое линейная функция? Как решить линейную функцию?
Если вы ранее научились решать линейные уравнения, вы готовы перейти к решению линейных функций . Они очень похожи, и в процессе также используются простые шаги, поэтому, если вы решаете линейных уравнений во сне, функции будут на одном дыхании!
Шаг 1: Определите, что вы действительно смотрите на линейную функцию.
Если вы еще не знали, линейная функция всегда будет начинаться с f(x) =, за которой следует остальная часть уравнения. Это достаточно легко запомнить, так как f означает функцию
Шаг 2: Замените значения переменными в соответствии с инструкциями.
Когда вы впервые познакомитесь с линейными функциями , вам, скорее всего, дадут значение для замены вашей переменной. Другие функции попросят вас найти уравнение линии, а затем решить соответствующую функцию. В любом случае замените значения, которые вам даны для решения, для вашей переменной.
Шаг 3: Решите свою переменную и проверьте свою работу.
Решите функцию так же, как линейное уравнение ; изолируйте свою переменную, сделайте все, что вы делали с одной частью уравнения, с другой, и упростите свои термины до их наименьших значений.
Если этот процесс не так прост, как вы думали, сделайте шаг назад и освежите свою память с помощью домашнего задания по уравнениям. Ничего страшного, если вам нужно больше практики. Как только вы освоите линейные уравнения, решение линейных функций станет для вас самым простым занятием!
Список категорий
- Карьерные советы (10)
- Образование (17)
- Справка по английскому языку (1)
- Инновации (7)
- Справка по математике (7)
- Онлайн-обучение (52)
- Онлайн-репетиторство (55)
- Советы по исследованиям (3)
- Научная помощь (4)
- Делать заметки (8)
- Технология (3)
- Советы родителям (37)
- Советы студентам (71)
- Подготовка к испытаниям (10)
- советов для достижения успеха (27)
- Советы репетиторам (18)
- Блоги репетиторов (3)
- Советы по обучению (23)
- Репетиторы (20)
- Без рубрики (6)
Популярные теги
Справка по алгебре карьерный совет Справка по химии колледж образование Советы по образованию для родителей Финляндия Веселье Будущее образования Справка по геометрии домашнее задание Помощь с домашним заданием как выбрать колледж информация для учителей Инновации младший год обучение Лайфхаки Справка по математике Онлайн обучение Онлайн-репетиторство Вакансии онлайн-репетитора Советы для родителей общественный колледж Риверсайд Руководство StudyGate Учебные привычки Советы по учебе Технологии Советы по подготовке к экзамену Советы для студентов Советы репетиторам Советы по обучению Калифорнийский университет Риверсайд
График наклона/пересечения и пересечения | Hatsudy
После изучения определений и понятий прямой пропорциональности и обратной пропорциональности в математике следующим шагом в изучении являются линейные функции.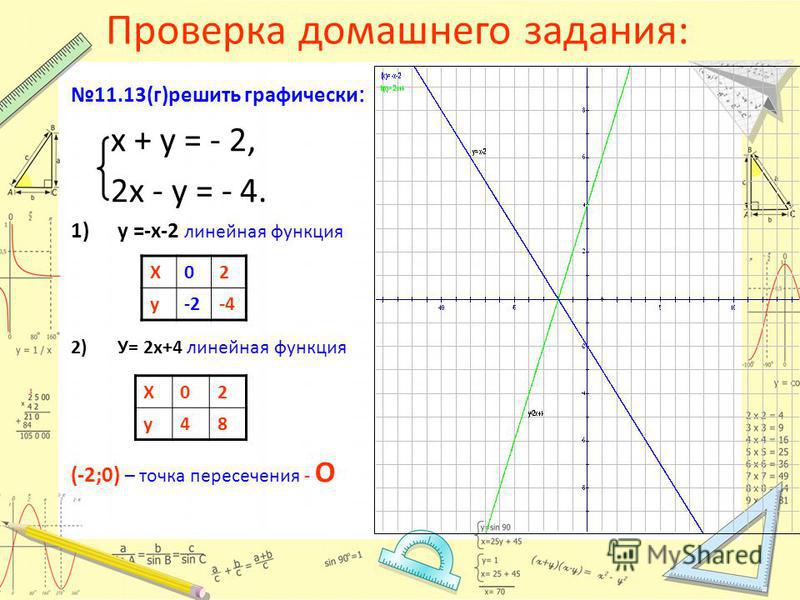 Подобно графику прямой пропорциональности, это линейные функции, в которых при увеличении значения $x$ значение $y$ увеличивается в том же отношении.
Подобно графику прямой пропорциональности, это линейные функции, в которых при увеличении значения $x$ значение $y$ увеличивается в том же отношении.
В линейных функциях есть два понятия: наклон и точка пересечения. В зависимости от значений наклона и точки пересечения форма графика будет меняться. Линейные функции также требуют, чтобы мы рисовали графики и составляли из них линейные уравнения.
Во многих задачах требуется точка пересечения, и в таких случаях точку пересечения можно найти с помощью уравнений.
Концепция линейных функций почти такая же, как и у прямых пропорций. Поэтому в повседневной жизни мы часто используем расчеты линейных функций. Итак, мы объясним, как решать задачи с линейными функциями.
Содержание
- 1 Линейные функции являются специальными пропорциями
- 1.1 Линейные функции имеют наклон и точку пересечения, что дает формулу $y=ax+b$
- 2 Как нарисовать график линейной функции
- 2.
 1 Скорость изменения: как нарисовать график, включающий дроби
1 Скорость изменения: как нарисовать график, включающий дроби
- 2.
- 3 Найти уравнение для линейной функции по отрезку и координатам
- 3.1 Найти уравнение для a Линейная функция на основе графика
- 3.2 Вычисление уравнения линейной функции с помощью системы уравнений
- 4 Как найти координаты пересечения с помощью линейных функций
- 5 Упражнения: графики линейных функций и текстовые задачи
- 6 Создание и решение уравнений для линейных функций
Линейные функции — это специальные пропорции
С пропорциями связано много вещей. По этой причине мы часто используем пропорции в нашей повседневной жизни. Еще одна концепция, которая также важна в нашей повседневной жизни, — это линейные функции. Пропорции и линейные функции похожи, и все мы используем линейные функции в повседневной жизни.
Например, мы используем линейные функции, когда думаем о наших повседневных расходах. Это расчет линейной функции для определения того, сколько вы можете тратить каждый день на основе ваших текущих сбережений.
Формула пропорциональности: $y=ax$. Например, если вы получаете пособие в размере 20 долларов США в месяц и вообще не тратите денег, ваши сбережения через $x$ месяцев будут выражены следующим уравнением.
- $y=20x$
Если вы откладываете деньги с нуля, уравнение будет таким же линейным. С другой стороны, если у вас уже есть сбережения, вы должны учитывать сумму сбережений.
Например, если у вас уже есть сбережения в размере $50, общая сумма сбережений через $x$ месяцев будет следующей.
- $y=20x+50$
В реальной жизни принято начинать с определенной точки, а не с нуля. В линейных функциях мы создаем уравнение, которое учитывает это.
Давайте думать о линейных функциях как о частном случае пропорциональности. Линейная функция — это пропорция, которая начинается не с нуля, а с определенной точки.
Линейные функции имеют наклон и точку пересечения, что приводит к формуле $y=ax+b$
Формула прямой зависимости: $y=ax$. С другой стороны, формула линейной функции $y=ax+b$. Чтобы начать с определенной точки, мы добавляем $+b$ к пропорциональной формуле.
С другой стороны, формула линейной функции $y=ax+b$. Чтобы начать с определенной точки, мы добавляем $+b$ к пропорциональной формуле.
$b$ — это значение при $x=0$. В предыдущем примере у вас уже было сбережений 50 долларов. Следовательно, $b=50$.
В линейных функциях $a$ в $y=ax+b$ называется наклоном. Кроме того, $b$ называется перехватом. Запомните эти слова, потому что задачи линейной функции часто требуют значения наклона и точки пересечения.
Например, предположим, что у нас есть уравнение $y=-2x-5$. В этом случае наклон равен -2. Кроме того, перехват -5. Уравнение почти такое же, как и прямая пропорция, поэтому концепция несложная. Просто убедитесь, что вы помните слова.
-Некоторые проблемы имеют область применения
Математика — это то, что мы учимся применять в повседневной жизни. Поэтому некоторые математические задачи имеют переменную область определения.
Предположим, вы хотите наполнить водой семейный бассейн. Однако количество воды, которое может находиться в бассейне, фиксировано. Нельзя наливать в бассейн бесконечное количество воды.
Однако количество воды, которое может находиться в бассейне, фиксировано. Нельзя наливать в бассейн бесконечное количество воды.
Следовательно, можно определить диапазон $x$. Это называется домен. Кроме того, из-за домена $x$ можно определить диапазон $y$.
Как нарисовать график линейной функции
Изучая линейные функции, вы также должны понимать, как рисовать графики. Как построить график линейной функции?
Линейная функция имеет свойство. То есть график $y=ax+b$ всегда проходит через координату $(0,b)$. Например, подставим $x=0$. Результат следующий.
$y=a×0+b$
$y=b$
Таким образом, когда $x=0$, $y=b$. Поскольку он проходит через координату $(0,b)$, координата, пересекающая ось $y$, всегда равна $b$.
Итак, рисуя график линейной функции, сначала сосредоточьтесь на точке пересечения. Например, граф $y=-2x+3$ будет графом, проходящим через координату $(0,3)$.
Затем найдите координату $y$, подставив свое любимое число в $x$.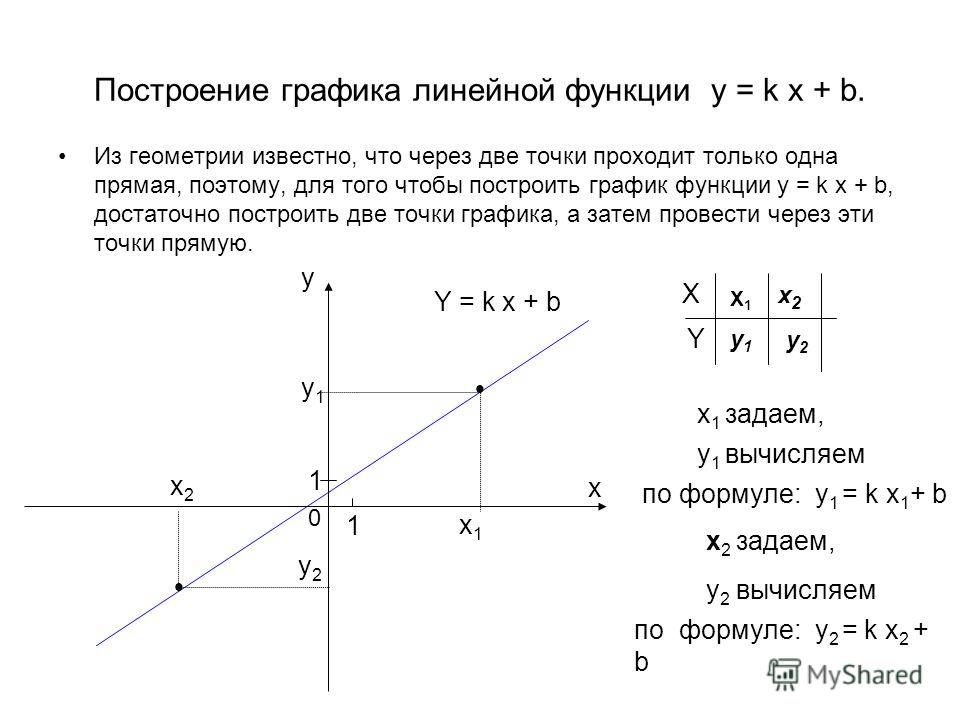 Например, в графе $y=-2x+3$, если $x=1$, то $y=1$. Другими словами, он проходит через координату $(1,1)$. Затем соедините две точки $(0,3)$ и $(1,1)$ прямой линией.
Например, в графе $y=-2x+3$, если $x=1$, то $y=1$. Другими словами, он проходит через координату $(1,1)$. Затем соедините две точки $(0,3)$ и $(1,1)$ прямой линией.
График $y=-2x+3$ — это прямая, проходящая через две точки $(0,3)$ и $(1,1)$. Вы можете подставить любое число в $x$: 1, 2, 3 и т. д., чтобы получить координаты. Предпочтительно использовать числа, которые легко вычислить.
Линейная функция представляет собой пропорциональный линейный график. Поскольку график всегда представляет собой прямую линию, вы можете нарисовать график линейной функции, соединив две координаты. Ниже приводится краткое описание того, как нарисовать график.
- Найдите точку пересечения, $(0,b)$.
- Подставьте число вместо $x$ и получите любые координаты.
- Соедините две координаты прямой линией
В таком порядке мы можем нарисовать прямую линию линейной функции на графике.
-Чем больше уклон, тем круче он становится
Насколько увеличивается или уменьшается координата $y$, сильно зависит от уклона. Если значение наклона $a$ велико, то график, естественно, станет более крутым. Когда значение наклона $a$ мало, наклон графика становится пологим.
Если значение наклона $a$ велико, то график, естественно, станет более крутым. Когда значение наклона $a$ мало, наклон графика становится пологим.
Кроме того, если наклон является положительным числом, график будет представлять собой прямую линию, восходящую вправо. С другой стороны, если наклон является отрицательным числом, график будет представлять собой прямую линию, направленную вниз вправо.
Убедитесь, что понимаете это свойство графика линейной функции.
Скорость изменения: как построить график с дробями
В линейных функциях вас могут спросить о скорости изменения. Какова скорость изменения? Поймите, что скорость изменения — это наклон линейной функции. Скорость изменения и наклон — это одно и то же. Поэтому, когда вас спросят о скорости изменения в задаче о линейной функции, попробуйте ответить на вопрос о наклоне.
Скорость изменения — это величина изменения значения $y$ по мере увеличения числа $x$. Например, для линейной функции с $y=2x+3$, когда $x$ увеличивается от 0 до 2, $y$ увеличивается от 3 до 7.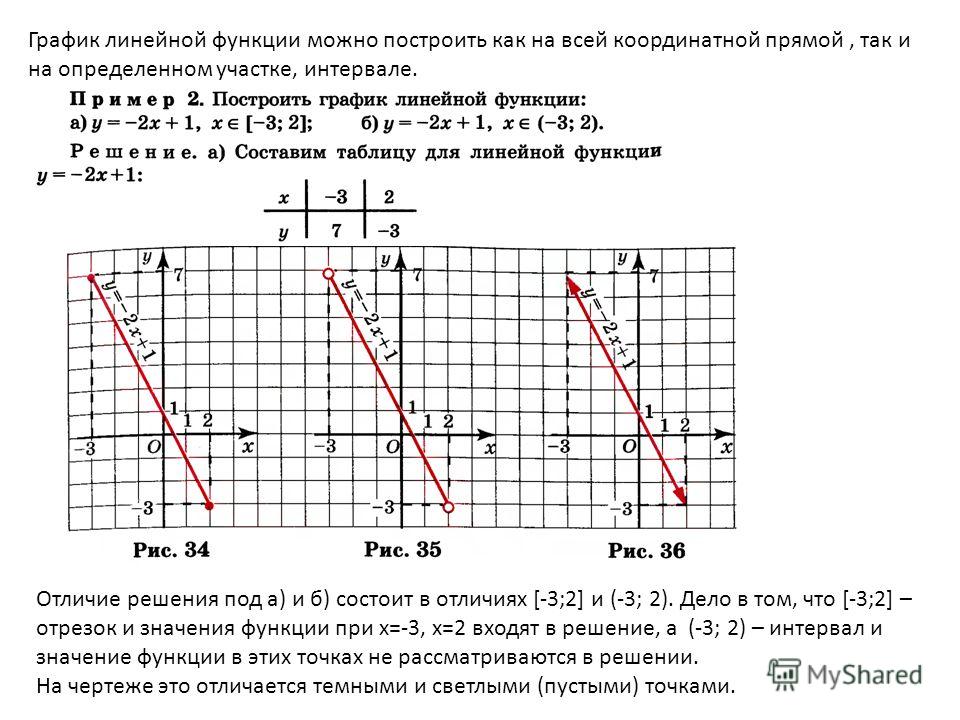 Когда $x$ увеличивается на 2, $y$ увеличивается на 4, поэтому скорость изменения (наклон) равна 2,9.0003
Когда $x$ увеличивается на 2, $y$ увеличивается на 4, поэтому скорость изменения (наклон) равна 2,9.0003
Наклон можно получить из суммы изменения числа $x$ и $y$. Таким образом, даже если мы не знаем наклон линейной функции, мы можем вычислить наклон (скорость изменения) из таблицы или графика.
Скорость изменения можно рассчитать по следующей формуле.
Глядя на одну только формулу, это кажется сложным. Кроме того, вы можете подумать, что вам нужно запомнить эту формулу. Однако скорость изменения линейной функции имеет то же значение, что и наклон. Вам не нужно запоминать формулу, потому что вы можете просто получить наклон.
Например, какой будет формула для следующего графика?
У многих людей возникают проблемы с построением линейных функций с дробями и поиском уравнения. Однако, даже если наклон линейной функции представляет собой дробь, мы все равно можем решить проблему, если поймем скорость изменения.
Если мы сосредоточимся на оси $y$, мы сможем найти точку пересечения.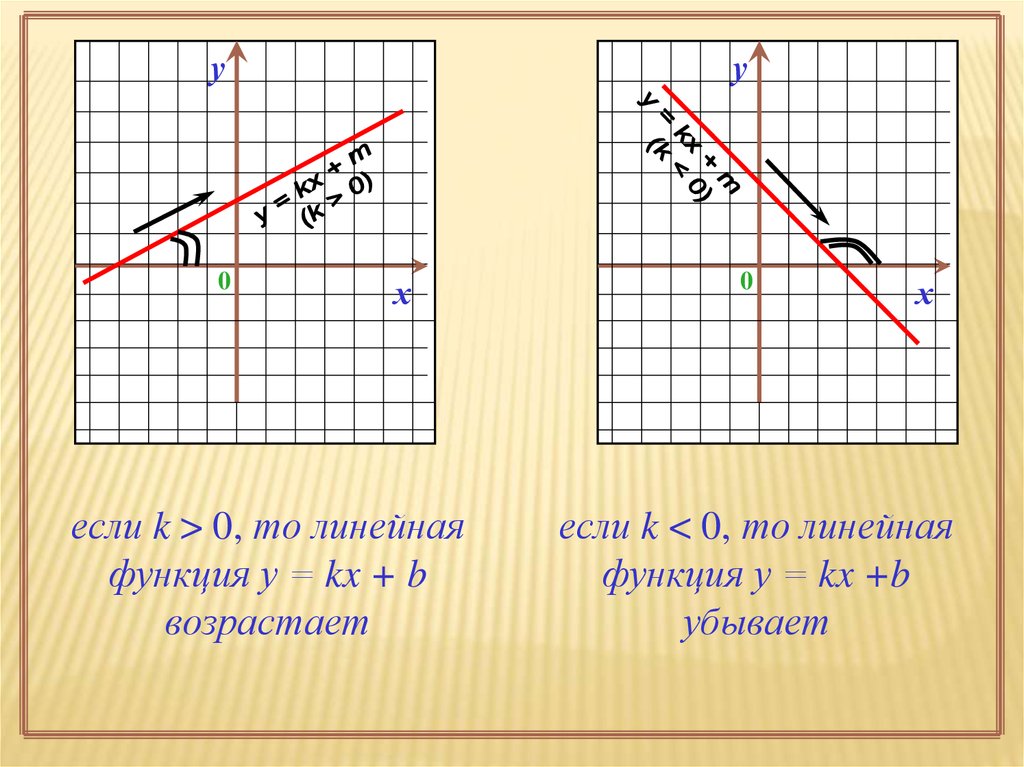 Итак, на графике выше $b=2$. Далее, давайте рассчитаем скорость изменения, чтобы получить наклон.
Итак, на графике выше $b=2$. Далее, давайте рассчитаем скорость изменения, чтобы получить наклон.
Если мы проверим координаты графика, то сможем найти определенные числа в следующих координатах.
- $(4,5)$
- $(0,2)$
- $(-4,-1)$
Если мы проверим эти координаты, то увидим, что значение $x$ равно увеличилось на 4, а значение $y$ увеличилось на 3. Результат следующий.
Следовательно, скорость изменения равна $\displaystyle\frac{3}{4}$. Нам не нужно запоминать формулу, чтобы получить скорость изменения; нам просто нужно получить наклон, чтобы удовлетворить условию пропорциональности.
Формула пропорциональности: $y=ax$. При увеличении значения $x$ на 4 значение $y$ увеличивается на 3. Подставляя число в формулу, получаем $4=3a$. Вычисление дает нам $a=\displaystyle\frac{3}{4}$, что дает нам наклон. Другими словами, линейная функция для графика представляет собой следующее уравнение.
- $y=\displaystyle\frac{3}{4}x+2$
В качестве альтернативы мы можем применить координаты к формуле линейной функции, чтобы получить наклон. Из графика мы уже знаем, что $b=2$. Поскольку мы знаем точку пересечения, уравнение на графике имеет вид $y=ax+2$. Затем подставьте координаты $(4,5)$ или $(-4,-1)$.
Из графика мы уже знаем, что $b=2$. Поскольку мы знаем точку пересечения, уравнение на графике имеет вид $y=ax+2$. Затем подставьте координаты $(4,5)$ или $(-4,-1)$.
Например, замена $(-4,-1)$ приведет к следующему результату.
$-1=-4a+2$
$4a=2+1$
$4a=3$
$a=\displaystyle\frac{3}{4}$
Таким образом, мы можно получить наклон из формулы линейной функции. Вам не нужно запоминать формулу скорости изменения. Если вы постараетесь запомнить много формул, вы их забудете. Итак, постарайтесь запомнить только самые важные формулы и получить ответ.
-Построение графика из уравнения линейной функции
Мы обсудили, как получить выражение из графика. С другой стороны, как нам нарисовать график?
Тот же способ построения графика линейной функции. Даже если наклон представляет собой дробь, вы можете построить график, используя скорость изменения. Например, как бы вы построили график следующего выражения?
- $y=-\displaystyle\frac{2}{3}x+2$
Точка пересечения равна 2, поэтому она проходит через $(0,2)$. Кроме того, если $x$ увеличивается на 3, $y$ уменьшается на 2. Другими словами, если $x=3$, $y=0$. Поскольку прямая проходит через $(3,0)$, мы можем нарисовать следующий график.
Кроме того, если $x$ увеличивается на 3, $y$ уменьшается на 2. Другими словами, если $x=3$, $y=0$. Поскольку прямая проходит через $(3,0)$, мы можем нарисовать следующий график.
Как упоминалось ранее, линейная функция завершается путем соединения двух координат прямой линией. Даже если наклон представляет собой дробь, способ построения графика остается прежним.
Найти уравнение для линейной функции по отрезку и координатам
В задачах о линейной функции нам может понадобиться найти выражение для линейной функции по графику или координатам. Как найти уравнение линейной функции? Есть несколько способов сделать это; самый простой способ — найти линейное уравнение по отрезку и координатам.
В некоторых задачах значение перехвата уже известно. В этом случае мы можем заменить значение $b$.
Также, если мы знаем координаты, мы знаем значения $x$ и $y$. Линейная функция — это функция, в которой значение $y$ однозначно определяется подстановкой $x$. Мы можем найти значение $y$, подставив любой $x$. Поэтому при подстановке координат можно получить наклон.
Мы можем найти значение $y$, подставив любой $x$. Поэтому при подстановке координат можно получить наклон.
Например, каково выражение для линейной функции в следующем случае?
- Точка пересечения равна 1: $b=1$
- Переход через координату $(2,2)$
Поскольку точка пересечения равна 1, уравнение $y=ax+1$. А так как он проходит через координату $(2,2)$, подставим $x=2$ и $y=2$. Получаем следующее.
$2=2a+1$
$-2a=1-2$
$-2a=-1$
$a=\displaystyle\frac{1}{2}$
Наклон $a =\displaystyle\frac{1}{2}$. Следовательно, выражение линейного уравнения равно $y=\displaystyle\frac{1}{2}x+1$.
Из условия задачи мы уже знаем, что точка пересечения равна 1. Напротив, нам не известен наклон линейной функции. Таким образом, мы можем подставить координаты и получить наклон.
Найдите уравнение для линейной функции на графике
Кроме того, нам может понадобиться найти выражение для линейной функции на графике. При чтении графика проверьте точки пересечения и координаты графика. Например, каковы точки пересечения и координаты следующего графика?
При чтении графика проверьте точки пересечения и координаты графика. Например, каковы точки пересечения и координаты следующего графика?
Проверяем $y$-координату, точка пересечения равна 1. Так же из графика можно подставлять любые координаты. Неважно, какие координаты вы подставите. Однако в математике нам нужно использовать простые координаты, чтобы избежать просчетов. Итак, в данном случае мы будем использовать координату $(1,-1)$.
На графике точка пересечения равна 1, поэтому выражение линейной функции равно $y=ax+1$. Также эта линейная функция проходит через координату $(1,-1)$. Итак, давайте подставим $x=1$ и $y=-1$. Расчет следующий.
$-1=a+1$
$-a=1+1$
$-a=2$
$a=-2$
Наклон равен -2, поэтому мы получаем уравнение $ у=-2x+1$. Даже если нам нужно найти точку пересечения и координаты по графику, способ получения уравнения линейной функции тот же.
Обратите внимание, что можно также рассчитать $a$ по скорости изменения при чтении графика. На предыдущем графике, как показано ниже, при каждом увеличении значения $x$ значение $y$ увеличивается на -2. Следовательно, мы видим, что скорость изменения равна -2.
На предыдущем графике, как показано ниже, при каждом увеличении значения $x$ значение $y$ увеличивается на -2. Следовательно, мы видим, что скорость изменения равна -2.
Скорость изменения такая же, как и наклон. Из точки пересечения и наклона мы видим, что уравнение имеет вид $y=-2x+1$.
Вычисление уравнения линейной функции с помощью системы уравнений
С другой стороны, бывают случаи, когда нам не представлен график, и мы не знаем точки пересечения. Все, что мы знаем, это две координаты. Например, мы знаем только следующие две координаты:
- $(-6,-7)$
- $(3,-1)$
Как придумать выражение для линейной функции? В этом случае мы можем использовать системы линейных уравнений (или одновременных уравнений), чтобы получить уравнение линейной функции. Даже если есть два неизвестных числа, мы можем найти число, составив два уравнения, то есть систему уравнений.
Если мы подставим $(-6,-7)$ и $(3,-1)$ в $y=ax+b$, получим следующее.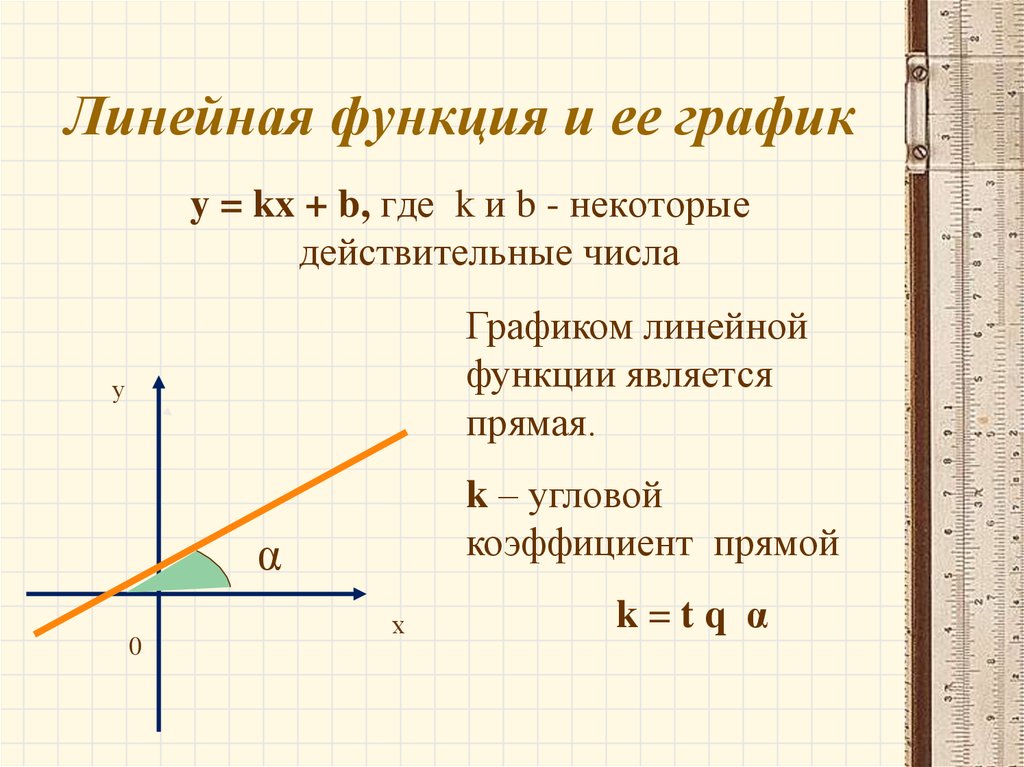
$\begin{eqnarray} \left\{\begin{array}{l}-7=-6a+b\\-1=3a+b\end{array}\right.\end{eqnarray}$
Давайте решим это с помощью одновременных уравнений. Результат следующий.
$\begin{array}{r}-7=-6a+b\\\underline{-)\phantom{0}-1=3a+b}\\-6=-9a\\a=\displaystyle \frac{2}{3}\end{array}$
Системы линейных уравнений дают нам $a=\displaystyle\frac{2}{3}$. И, решив одновременные уравнения, подставив $a=\displaystyle\frac{2}{3}$, мы можем вычислить $b=-3$.
Например, замена $(3,-1)$ приводит к следующему.
$-1=3×\displaystyle\frac{2}{3}+b$
$-1=2+b$
$b=-3$
Следовательно, $y=\displaystyle\frac{2}{3}x-3$. Даже если график не представлен, если мы знаем две координаты, мы все равно можем найти линейную функцию, используя систему линейных уравнений.
Как найти координаты пересечения с помощью линейных функций
Пересечение — одна из сложных задач линейных функций; нас часто просят найти точку пересечения двух линейных функций.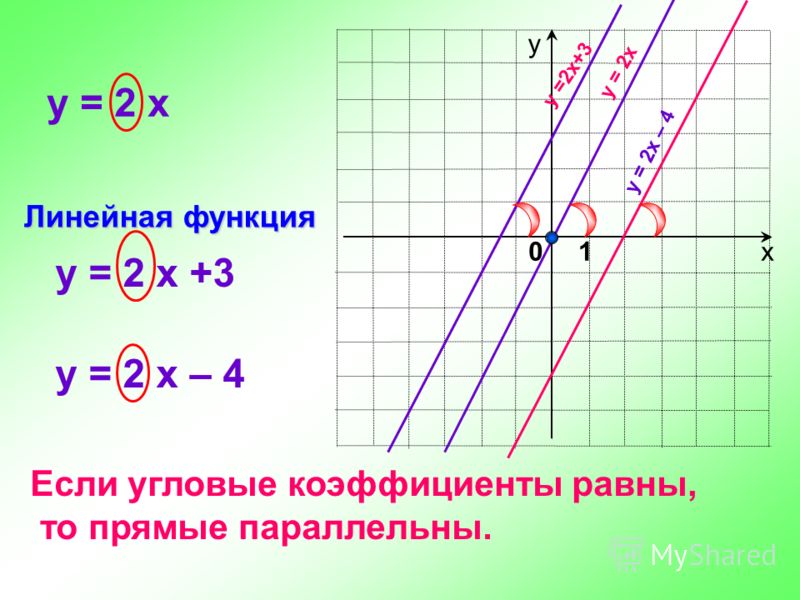 Как найти точку пересечения?
Как найти точку пересечения?
Например, попробуйте найти точку пересечения P следующих двух выражений.
- $y=-2x-2$
- $y=x+2$
Совместное уравнение дает значение, которое удовлетворяет двум уравнениям. Давайте решим следующую систему уравнений, используя $y=-2x-2$ и $y=x+2$. Тогда мы можем найти точку пересечения.
$\begin{eqnarray} \left\{\begin{array}{l}y=-2x-2\\y=x+2\end{array}\right.\end{eqnarray}$
Почему Можем ли мы найти пересечение, используя систему линейных уравнений? Использование одновременных уравнений означает то же самое, что нахождение значений $x$ и $y$, удовлетворяющих условиям $y=-2x-2$ и $y=x+2$. Вычисление $x$ и $y$, удовлетворяющих двум уравнениям, аналогично нахождению точки пересечения.
Как упоминалось выше, даже если у нас есть два неизвестных числа, мы все равно можем найти число, используя одновременные уравнения. Когда мы решаем одновременные уравнения, мы получаем следующее.
$\begin{array}{r}y=-2x-2\\\underline{-)\phantom{0}\phantom{0}y=x+2}\\0=-3x-4\\ 3x=-4\\x=-\displaystyle\frac{4}{3}\end{array}$
Затем подставьте $x=-\displaystyle\frac{4}{3}$.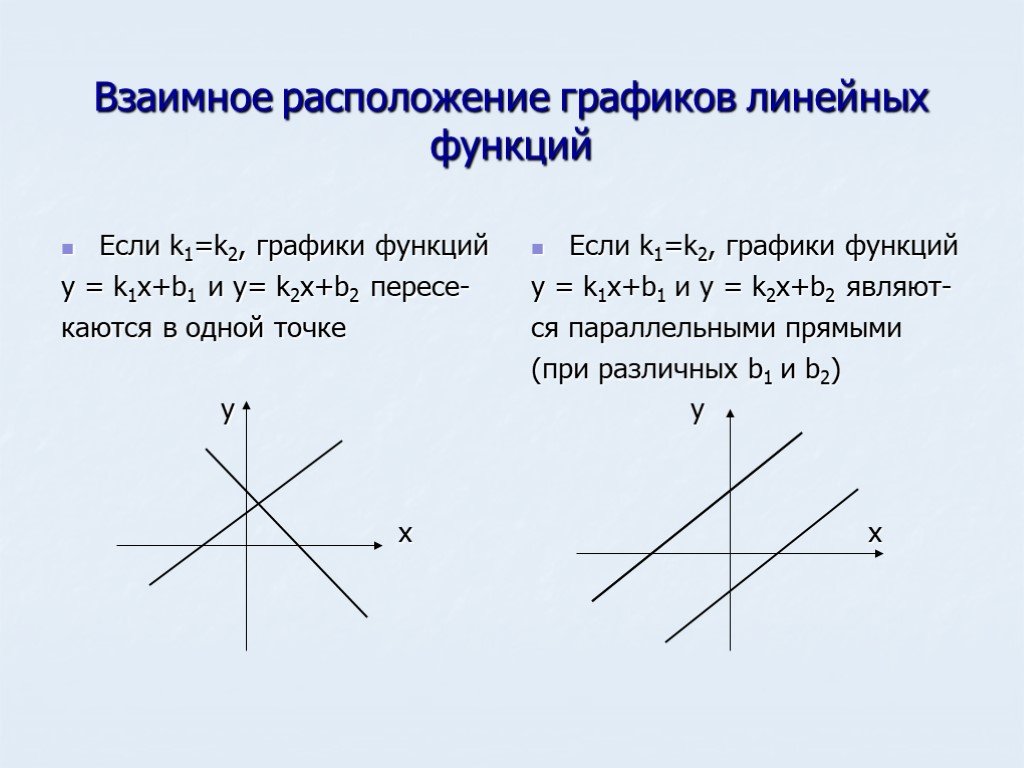 Например, если мы подставим $y=x+2$, то получим следующее.
Например, если мы подставим $y=x+2$, то получим следующее.
$y=-\displaystyle\frac{4}{3}+2$
$y=-\displaystyle\frac{4}{3}+\displaystyle\frac{6}{3}$
$y=\displaystyle\frac{2}{3}$
Таким образом, мы знаем, что координата точки P равна $\left(-\displaystyle\frac{4}{3},\displaystyle\frac{2}{3}\right)$.
Упражнения: графики линейных функций и текстовые задачи
Q1: Решите следующие задачи.
- Найти уравнение для линейной функции (1)
- Найти уравнение для линейной функции (2)
- Найдите пересечение (1) и (2)
A1: Ответы.
(а)
Нам нужно найти линейное уравнение из графика. Итак, давайте сосредоточимся на перехвате. В уравнении (1) точка пересечения равна 4. Следовательно, $b=4$.
Кроме того, (1) проходит через координату $(1,2)$. Поэтому подставим $y=ax+4$. Получаем следующее.
$2=a+4$
$a=-2$
Мы нашли, что наклон равен -2. Следовательно, уравнение (1) равно $y=-2x+4$.
Следовательно, уравнение (1) равно $y=-2x+4$.
(b)
Глядя на график, мы не можем найти точку пересечения (2). Итак, вычислим уравнение (2) по двум координатам. Выберите любую из (2) координат. Например, (2) проходит через следующие координаты.
- $(2,3)$
- $(5,4)$
Далее вычислим наклон и точку пересечения, используя систему уравнений. Подставляя в формулу $y=ax+b$, получаем следующее.
$\begin{eqnarray} \left\{\begin{array}{l}3=2a+b\\4=5a+b\end{array}\right.\end{eqnarray}$
Решая одновременные уравнения, получаем следующее.
$\begin{array}{r}3=2a+b\\\underline{-)\phantom{0}4=5a+b}\\-1=–3a\\a=\displaystyle\frac{ 1}{3}\end{array}$
Замена $a=\displaystyle\frac{1}{3}$ на $3=2a+b$ дает следующее.
$3=2×\displaystyle\frac{1}{3}+b$
$\displaystyle\frac{9}{3}=\displaystyle\frac{2}{3}+b$
$b =\displaystyle\frac{7}{3}$
Следовательно, уравнение в (2) имеет вид $y=\displaystyle\frac{1}{3}x+\displaystyle\frac{7}{3}$.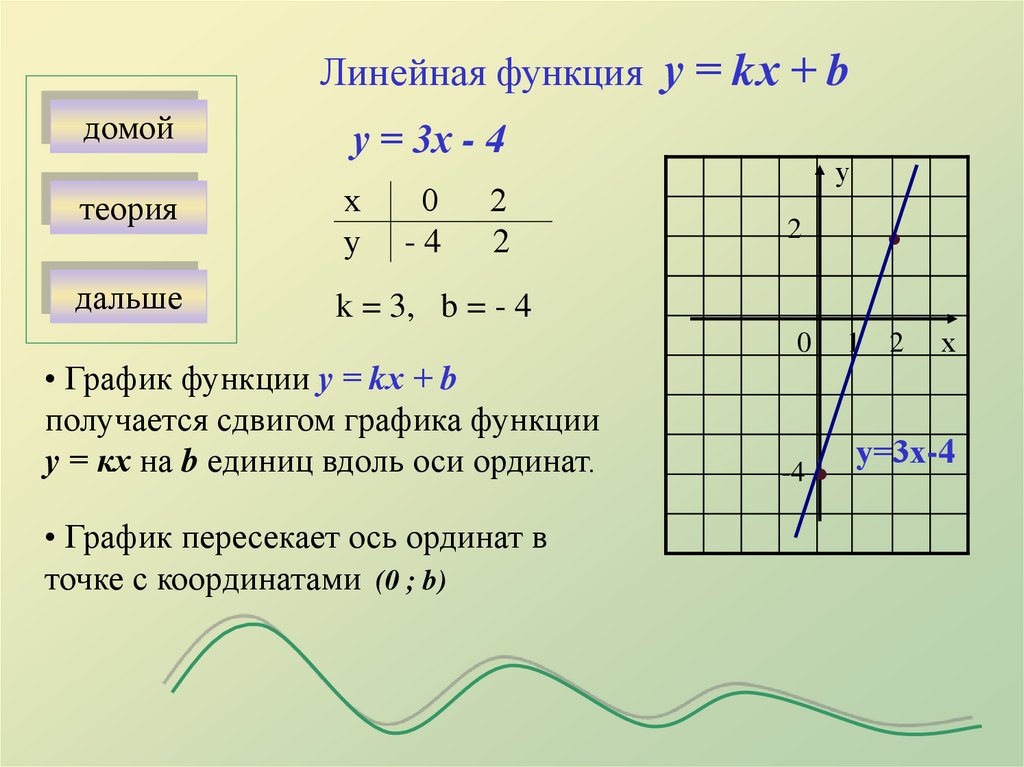
(c)
Чтобы получить пересечение двух уравнений, решите одновременные уравнения. Теперь, когда у нас есть линейные функции (1) и (2), мы можем использовать эти два уравнения для создания следующей системы уравнений.
$\begin{eqnarray} \left\{\begin{array}{l}y=-2x+4\\y=\displaystyle\frac{1}{3}x+\displaystyle\frac{7}{3 }\end{array}\right.\end{eqnarray}$
Методом подстановки получаем следующее.
$-2x+4=\displaystyle\frac{1}{3}x+\displaystyle\frac{7}{3}$
$(-2x+4)\textcolor{red}{×3}=\left(\displaystyle\frac{1}{3}x+\displaystyle\frac{7}{3}\right)\textcolor{red }{×3}$
$-6x+12=x+7$
$-6x-x=7-12$
$-7x=-5$
$x=\displaystyle\frac{5 {7}$
Затем замените $x=\displaystyle\frac{5}{7}$ на $y=-2x+4$. Результат следующий.
$y=-2×\displaystyle\frac{5}{7}+4$
$y=-\displaystyle\frac{10}{7}+\displaystyle\frac{28}{7}$
$y=\displaystyle\frac{18}{7}$
Таким образом, точка пересечения (1) и (2) может быть вычислена как $\left(\displaystyle\frac{5}{7},\displaystyle\frac{18}{7}\right)$.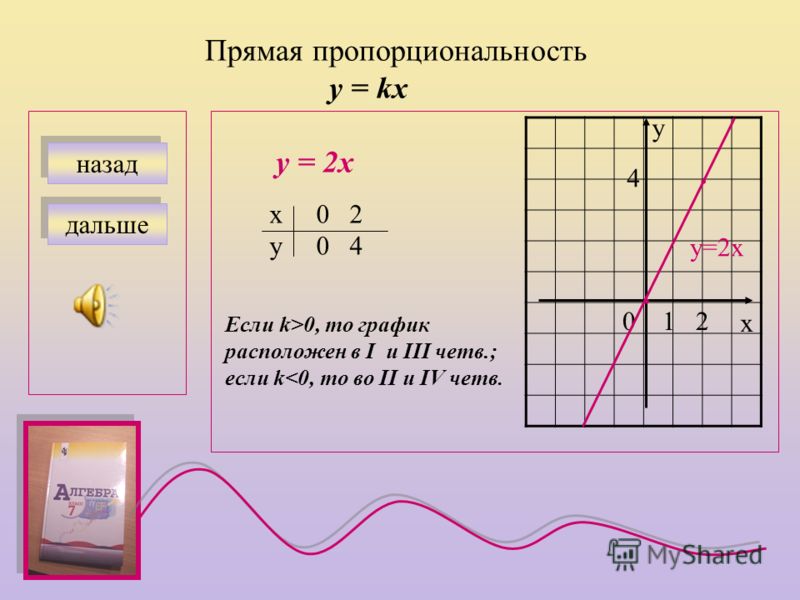
Q2: Решите следующие проблемы.
Существует треугольник AB=10 см, BC=6 см и ∠ABC=90°. Точка P начинается в точке A, проходит через точку B со скоростью 1 см/сек и попадает в точку C. Площадь △APC через $x$ секунд после выхода точки P из точки A равна $y$ см 2 .
- Рассчитайте площадь △APC через 8 секунд.
- Используйте знак неравенства, чтобы выразить домен $x$ и домен $y$.
- Когда точка P находится на BC, выразите отношение между $x$ и $y$.
A2: Ответы.
(а)
Через 8 секунд длина точки доступа составляет 8 см. Это означает, что горизонтальная длина треугольника равна 8 см. С другой стороны, длина по вертикали равна 6 см. Формула площади треугольника выглядит следующим образом.
- Площадь треугольника = Ширина × Высота × $\displaystyle\frac{1}{2}$
Следовательно, площадь треугольника такова.
- $8×6×\displaystyle\frac{1}{2}=24$
Ответ: 24 см 2 .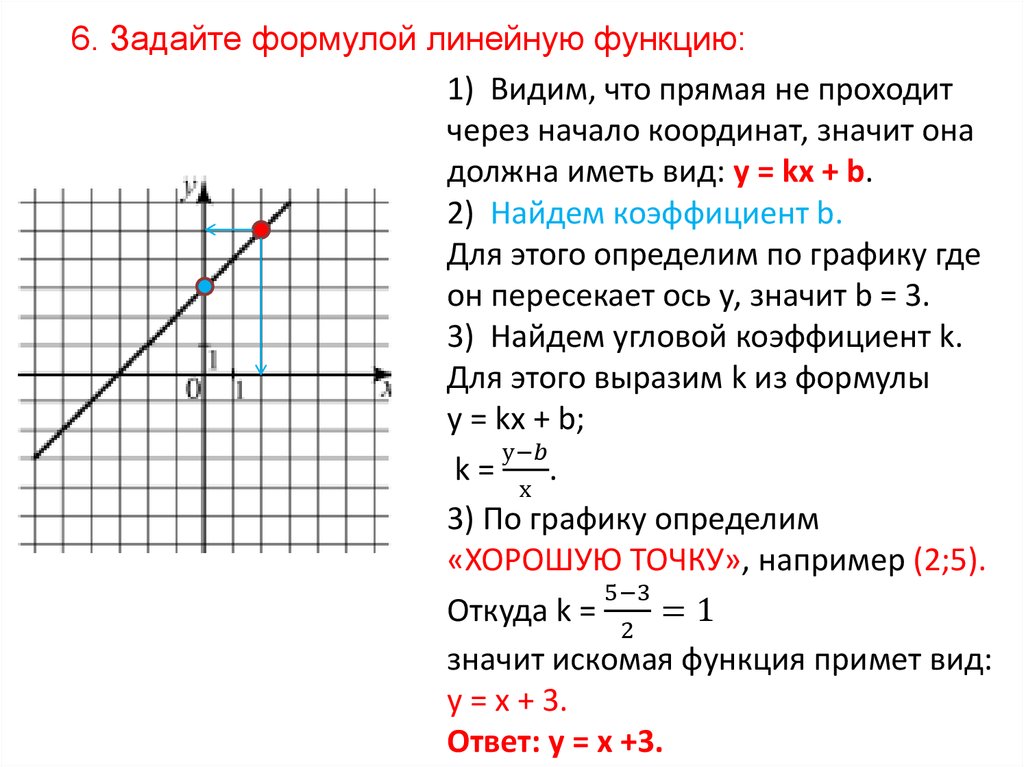
(б)
Общая длина АВ и ВС 16 см. Поскольку точка P перемещается со скоростью 1 см в секунду, она достигает точки C через 16 секунд. Поэтому область определения $x$ такова.
- $0≤x≤16$
С другой стороны, что касается площади △APC, площадь △APC становится наибольшей, когда точка P достигает точки B. Это происходит потому, что точка P движется по BC, площадь △APC становится меньше. Кроме того, площадь △ABC выглядит следующим образом.
- $10×6×\displaystyle\frac{1}{2}=30$
Следовательно, область определения $y$ такова.
- $0≤y≤30$
(c)
Когда точка P находится на BC, горизонтальная длина фиксируется на уровне 10 см. С другой стороны, вертикальная длина варьируется. Если мы сможем найти вертикальную длину (длину CP), мы сможем составить уравнение, выражающее площадь △APC.
Как определить длину CP? Трудно мыслить в терминах треугольника. Итак, давайте рассмотрим длину CP на следующей прямой.
Итак, давайте рассмотрим длину CP на следующей прямой.
Длина АС 16 см. А поскольку он движется со скоростью 1 см в секунду, длина точки доступа через $x$ секунд составляет $x$ см. Итак, длина CP равна $(16-x)$.
Длина по горизонтали составляет 10 см, а по вертикали — $(16-x)$ см. Следовательно, площадь △APC выглядит следующим образом.
$y=10×(16-x)×\displaystyle\frac{1}{2}$
$y=5×(16-x)$
$y=-5x+80$
Создать и Решение уравнений для линейных функций
Поле, похожее на прямую пропорцию, представляет собой линейные функции. Думайте о линейных функциях в математике как о частном случае пропорций.
Есть так много ситуаций, когда нам приходится использовать линейные функции для выполнения вычислений. Например, когда вы рассчитываете свои будущие сбережения, вы используете линейные функции. При расчете нам нужно найти наклон и точку пересечения, чтобы создать уравнение.
Также в линейных функциях есть много задач, использующих графики.

 .
. 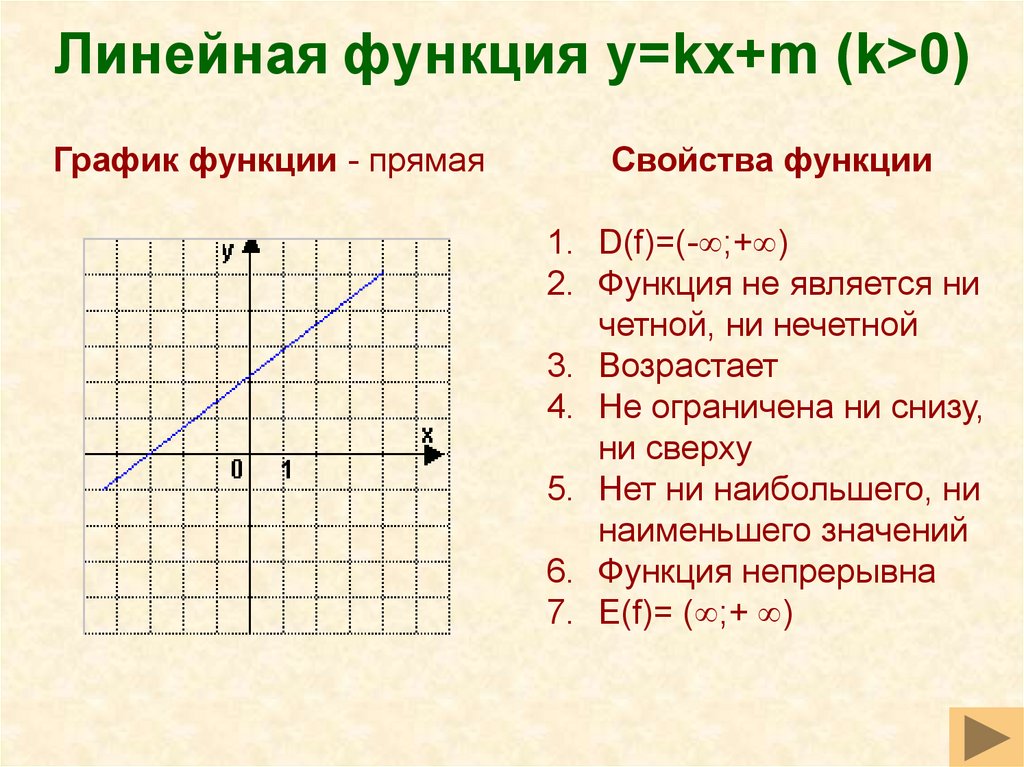 Давайте убедимся, построим каждую функцию:
Давайте убедимся, построим каждую функцию:
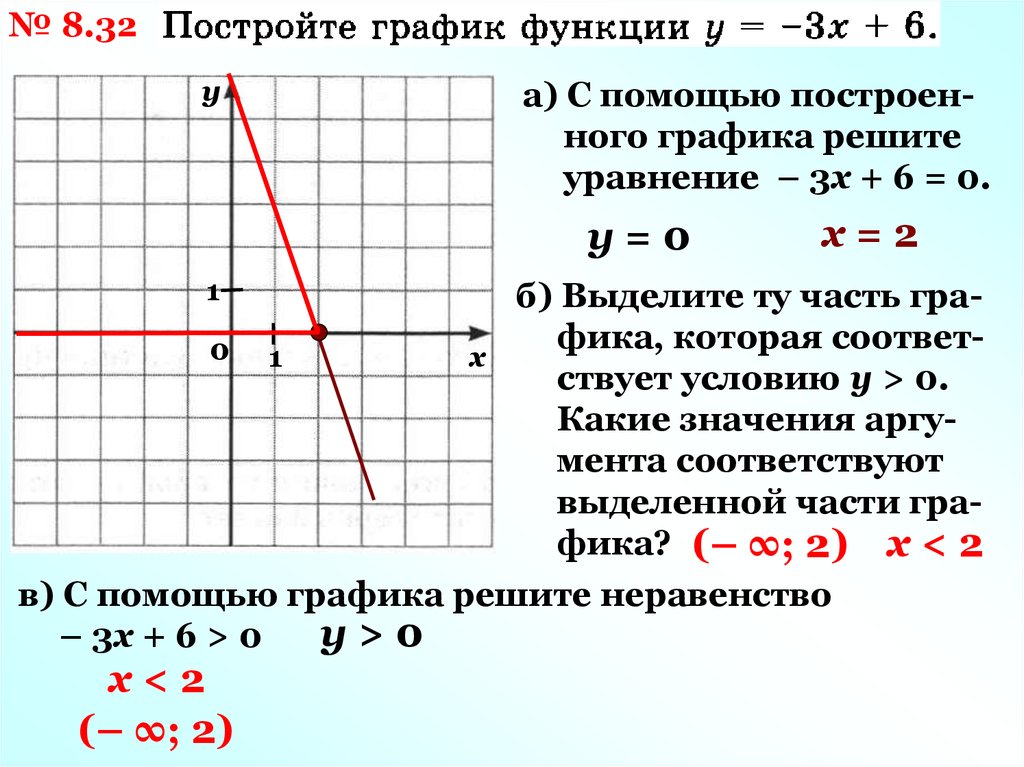 ..
..  Это мы обсуждали с вами уже.
Это мы обсуждали с вами уже.  1 Скорость изменения: как нарисовать график, включающий дроби
1 Скорость изменения: как нарисовать график, включающий дроби