Признак делимости на 9: примеры, доказательство
В данной статье будет дана формулировка признака делимости на 9 с его доказательством. Заключительным этапом будет приведение примера делимости на 9 с разным значением переменной.
Признак делимости на 9, примеры
Рассмотрим сам признак делимости на 9: когда сумма цифр целого числа делится на 9, тогда само число также делится на 9; когда сумма цифр не делится на 9, тогда очевидно, что и число не будет делиться на 9.
Для того, чтобы использовать данный признак делимости, необходимо разбираться в сложении натуральных чисел. Известно, что из простых натуральных чисел существует только число 9, которое способно поделиться на 9 без остатка, то есть подходит под выше написанное определение.
Пример 1Определить, какие из приведенных чисел 621, −32 112, 222, −331 поделятся на 9 без остатка.
Решение
Для решения задания необходимо перейти к вычислению сумм каждого из предложенных чисел. Получаем, что 6+2+1=9, 3+2+1+1+2=9, 2+2+2=8 и 3+3+1=7.
Видно, что только 9 поделится на 9, а 8 и 7 нет. Отсюда имеем, что 621 и -32112 поделятся на 9 а 222 и -331 не поделятся.
Ответ: 621 и −32 112.
Бывают случаи, когда сумма цифр является трехзначным числом. Когда имеем число 945, то сумма его цифр – это 18, а сумма цифр 999888777666555 равняется 105. Тогда для установления делимости на 9 нужно применять правило несколько раз.
Определить, делится ли число 876 505 998 872 на 9.
Решение
Необходимо воспользоваться признаком делимости на 9. Переходим к вычислению суммы цифр заданного числа. Тогда получим, что 8+7+6+5+0+5+9+9+8+8+7+2=74. Чтобы определить, будет ли делиться 74 на 9,нужно найти сумму цифр. Тогда получаем, что 7+4=11, а 1+1=2. Отсюда следует, что 2 не поделится на 9. То есть число 74 на 9 не делится.
Ответ: не делится.
Чтобы проверить, будет делиться число на 9 или нет, нужно произвести деление на 9. Применение признака делимости на 9 и непосредственное деление на 9 занимает практически одно и то же время.
Доказательство признака делимости на 9
Чтобы доказать признак делимости на 9, нужно использовать дополнительные результаты.
Когда разложим по рядам любое натуральное число а, правила умножения натурального числа на 10, 100, 1000 позволяет представить все при помощи записи a=an·10n+an−1·10n−1+…+a2·102+a1·10+a0, где an, an−1, …, a0являются цифрами, записанных слева направо. Имеем, что 10=9+1, 100=99+1=11·9+1, 1 000=999+1=111·9+1, …, тогда число а можно представить в виде a=an·11…1·9+1+…+a2·11·9+1+a1·(1·9+1)+a0.
Нужно преобразовать выражения до вида a=9·11…1·an+…+11·a2+1·a1+an+…+a2+a1+a0.
Отсюда получаем, что сумма an+…+a2+a1+a0 является суммой всех цифр, входящих в состав числа а. Чтобы запись была краткой, запишем a=9·11…1·an+…+11·a2+1·a1+A. Данное преобразование числа а применяется при доказательстве признака делимости на 9.
Используем 2 свойства делимости:
- для возможности деления а на b нужно производить деление модуля а на модуль b;
- при возможности деления на число b всего выражения a=s+t очевидно, что и все выражение поделится на b.
Рассмотрим само доказательство признака делимости на 9 вместе с необходимыми и достаточными условиями.
Теорема 1Для того, чтобы целое число а делилось на 9 без остатка, необходимо и достаточно, что и сумма цифр числа а делилась на 9.
Доказательство 1При а=0 теорема очевидна. Если а отлично от нуля, а его модуль – это натуральное число, тогда представим его в виде суммы вида a=9·11…1·an+…+11·a2+1·a1+A, что и было представлено задолго до написания теоремы. Выражение 9·11…1·an+…+11·a2+1·a1 имеет множитель 9, а сумма скобок – это натуральное число при любых an, an−1, …, a1. Видно, что свойство делимости подходит для выражения. Необходимо доказать, что сумма всех цифр (A) делится на 9, тогда и само число разделится на 9.
Если A делится на 9, тогда по равенству a=9·11…1·an+…+11·a2+1·a1+A и по второму указанному перед теоремой свойству имеем, что и модуль а будет делиться на 9. Получим, что и само число а будет делиться на 9. Достаточное свойство доказано.
Доказательство необходимого свойства включает в себя деление на 9 числа а при делении суммы всех цифр числа а.
Когда а будет делиться на 9, тогда и модуль числа разделится на 9. Это возможно благодаря первому свойству делимости. Из a=9·11…1·an+…+11·a2+1·a1+A и второго свойства видно, что A поделится на 9 без остатка. Необходимое свойство доказано.
Другие случаи делимости на 9
Рассмотрим примеры решения примеров с доказательством делимости на 9, когда имеется буквенное выражение.
Пример 3Будет ли выражение 10n−1 делиться на 9 при натуральном n?
Решение
Видим, что . То есть сумма цифр числа равняется 9n, а 9n делится на 9 без остатка. Значит, что выражение соответствует признаку делимости при любом значении n.
Ответ: делится.
Имеются случаи, когда делимость на 9 нельзя определить при помощи деления на 9. Тогда выражение представляется в виде произведения нескольких множителей, где один из них делится на 9.
Рассмотрим два таких способа. Решим примеры с помощью бинома Ньютона.
Определить, делится ли выражение 4n+6n-1 на 9 при любом значении n.
Решение
Представляем 4 в виде 3+1, используем формулу бинома Ньютона и получим:
4n+6n-1=3+1n+6n-1==Cn0·3n+Cn1·3n-1·1+…+Cnn-2·32·1n-1+Cnn-1·3·n-1+Cnn·1n++6n-1==3n+Cn1·3n-1+…+Cnn-2·32+n·3+1+6n-1==3n+Cn1·3n-1+…+Cnn-2·32+9n
Когда n=1, получаем, что 4n+6n-1=41+6·1-1=9. Очевидно, что 9 делится на 9. Когда значение n больше 1, тогда видно, что сумма 3n+Cn1·3n-1+…+Cnn-2·32+9n может быть упрощена при помощи выноса 9 за скобки. Получим выражение вида 9·3n-2+Cn1·3n-3+…+Cnn-2·30+n. Очевидно, что произведение поделится на 9, а значение выражения в скобке удовлетворяет условию n>1 и является натуральным числом. Отсюда имеем, что 4n+6n-1 делится на 9 при любых натуральных значениях n.
Ответ: делится.
Если исходное выражение c n переменной в виде многочлена, тогда используется такой способ.
При доказательстве n=9·m, n=9·m+1, …, n=9·m+8, где m является целым числом, а исходное выражение делится на 9, тогда очевидно, что делимость будет доказана при любом значении n.
Доказать, что n6-8n4+16n2 будет делиться на 9 при любом значении n.
Решение
Чтобы удобней было вычислять, нужно выражение n6-8n4+16n2 разложить на множители. тогда получим, что
n6-8n4+16n2=n2·(n4-8n2+16)=n2·(n2-4)2==n2·(n-2)2·(n+2)2
Пусть m будет целым числом. Отсюда имеем, что n=9·m даст выражение вида n2·(n-2)2·(n+2)2=(9m)2·(9m-2)2·(9m+2)2. Так как имеется множитель 9, то очевидно, что выражение поделится на 9.
Если выражение вида n=9·m+1, то получим, что
n2·(n-2)2·(n+2)2=(9m+1)2·(9m-1)2·(9m+3)2==9m+12·9m-12·9·3m+12
Данное произведение поделится на 9, так как есть множитель 9. Таким же образом проверяется выражение вида n2·(n-2)2·(n+2)2 при n=9·m+2, n=9·m+3, …, n=9·m+8
Отсюда видно, что делимость на 9 доказана, значит, выражение делится на 9 при любом значении n.
Рассмотрим пример при помощи метода математической индукции.
Пример 6Доказать, что выражение 4n+6n-1 делится на 9 при любом значении n.
Решение
Чтобы доказать делимость на 9, необходимо использовать формулу математической индукции.
Когда n=1, то выражение 4n+6n-1 равняется 9, значит и делится на 9. Если предположить, что n=k, тогда выражение запишется так 4k+6k-1. Оно тоже делится на 9.
По предыдущему шагу понятно, что 4n+6n-1 будет делиться на число 9 при n=k+1.
Получаем, что
4k-1+6·(k+1)-1==4·4k+6k+5==4·(4k+6k-1)-18k+9==4·(4k+6k-1)-9·(2k-1)
Тогда из разности вида 4·4k+6k-1 видно, что она делится на 9. Предыдущий шаг показал, что 4k+6k-1 делится на 9 также, как и 9·(2k-1). Отсюда получаем, что вся разность поделится на 9. Можно говорить о том, что выражение 4n+6n-1 при n=k+1 будет делиться на 9.
Данное задание было решено при помощи метода математической индукции. Получили в результате, что заданное выражение поделится на 9 при любом целом значении n.
ПРИЗНАКИ ДЕЛИМОСТИ чисел, кратность чисел с примерами
Признаки делимости чисел на 2, 3, 4, 5, 6, 8, 9, 10, 11, 25 и другие числа полезно знать для быстрого решения задач на Цифровую запись числа. Вместо того, чтобы делить одно число на другое, достаточно проверить ряд признаков, на основании которых можно однозначно определить, делится ли одно число на другое нацело (кратно ли оно) или нет.
Основные признаки делимости
Приведем основные признаки делимости чисел:
- Признак делимости числа на «2»
Число делится нацело на 2, если число является четным (последняя цифра равна 0, 2, 4, 6 или 8)
Пример: Число 1256 кратно 2, поскольку оно заканчивается на 6. А число 49603 не делится нацело на 2, поскольку оно заканчивается на 3. - Признак делимости числа на «3»
Число делится нацело на 3, если сумма его цифр делится на 3
Пример: Число 4761 делится на 3 нацело, поскольку сумма его цифр равна 18 и она делится на 3. А число 143 не кратно 3, поскольку сумма его цифр равна 8 и она не делится на 3. - Признак делимости числа на «4»
Число делится нацело на 4, если последние две цифры числа равны нулю или число, составленное из двух последних цифр, делится на 4
Пример: Число 2344 кратно 4, поскольку 44 / 4 = 11. А число 3951 не делится нацело на 4, поскольку 51 на 4 не делится. - Признак делимости числа на «5»
Число делится нацело на 5, если последняя цифра числа равна 0 или 5
Пример: Число 5830 делится нацело на 5, поскольку оно заканчивается на 0. А число 4921 не делится на 5 нацело, поскольку оно заканчивается на 1. - Признак делимости числа на «6»
Число делится нацело на 6, если оно делится нацело на 2 и на 3
Пример: Число 3504 кратно 6, поскольку оно заканчивается на 4 (признак делимости на 2) и сумма цифр числа равна 12 и она делится на 3 (признак делимости на 3). А число 5432 на 6 нацело не делится, хотя число заканчивается на 2 (соблюдается признак делимости на 2), однако сумма цифр равна 14 и она не делится на 3 нацело. - Признак делимости числа на «8»
Число делится нацело на 8, если три последние цифры числа равны нулю или число, составленное из трех последних цифр числа, делится на 8
Пример: Число 93112 делится нацело на 8, поскольку число 112 / 8 = 14. А число 9212 не кратно 8, поскольку 212 не делится на 8. - Признак делимости числа на «9»
Число делится нацело на 9, если сумма его цифр делится на 9
Пример: Число 2916 кратно 9, поскольку сумма цифр равна 18 и она делится на 9. А число 831 не делится на 9 нацело, поскольку сумма цифр числа равна 12 и она не делится на 9. - Признак делимости числа на «10»
Число делится нацело на 10, если оно заканчивается на 0
Пример: Число 39590 делится на 10 нацело, поскольку оно заканчивается на 0. А число 5964 не делится на 10 нацело, поскольку оно заканчивается не на 0. - Признак делимости числа на «11»
Число делится нацело на 11, если сумма цифр, стоящих на нечетных местах, равна сумме цифр, стоящих на четных местах или суммы должны отличаться на 11
Пример: Число 3762 делится нацело на 11, поскольку 3 + 6 = 7 + 2 = 9. А число 2374 на 11 не делится, поскольку 2 + 7 = 9, а 3 + 4 = 7. - Признак делимости числа на «25»
Число делится нацело на 25, если оно заканчивается на 00, 25, 50 или 75
Пример: Число 4950 кратно 25, поскольку оно заканчивается на 50. А 4935 не делится на 25, поскольку заканчивается на 35.
А число 143 не кратно 3, поскольку сумма его цифр равна 8 и она не делится на 3.
А число 2374 на 11 не делится, поскольку 2 + 7 = 9, а 3 + 4 = 7.Признаки делимости на составное число
Чтобы узнать, делится ли заданное число на составное, нужно разложить это составное число на взаимно простые множители, признаки делимости которых известны. Взаимно простые числа — это числа, не имеющие общих делителей кроме 1. Например, число делится нацело на 15, если оно делится нацело на 3 и на 5.
Рассмотрим другой пример составного делителя: число делится нацело на 18, если оно делится нацело на 2 и 9. В данном случае нельзя раскладывать 18 на 3 и 6, поскольку они не являются взаимно простыми, так как имеют общий делитель 3. Убедимся в этом на примере.
Число 456 делится на 3, так как сумма его цифр равна 15, и делится на 6, так как оно делится и на 3 и на 2.
Но если разделить 456 на 18 вручную, то получится остаток. Если же для числа 456 проверять признаки делимости на 2 и 9, сразу же видно, что оно делится на 2, но не делится на 9, так как сумма цифр числа равна 15 и она не делится на 9.
Обратите внимание на рисунок ниже, что поведение функции на каждом из отрезков x отличается.
Поведение графика на пересечении x можно определить, изучив кратность нуля.
Точка пересечения x [латекс]х=-3[/латекс] является решением уравнения [латекс]\влево(х+3\вправо)=0[/латекс]. Граф проходит непосредственно через точку пересечения x в точке [latex]x=-3[/latex]. Фактор является линейным (имеет степень 1), поэтому поведение вблизи точки пересечения похоже на поведение линии; он проходит прямо через перехват. Мы называем это одиночным нулем, потому что ноль соответствует одному фактору функции. 9{2}=\left(x — 2\right)\left(x — 2\right)[/latex]
Множитель повторяется, то есть множитель [латекс]\left(x — 2\right) [/latex] появляется дважды.
{ 3}[/латекс]. Мы называем это тройным нулем или нулем с кратностью 3,9.0011
Для нулей с четной кратностью графики касаются или касаются оси x при этих значениях x. Для нулей с нечетной кратностью графики пересекают или пересекают ось x при этих значениях x. См. приведенные ниже графики для примеров графиков полиномиальных функций с кратностью 1, 2 и 3. но для каждой увеличивающейся четной степени график будет казаться более плоским по мере приближения и выхода из 9{p}[/latex], поведение вблизи точки пересечения x h определяется степенью p . Мы говорим, что [latex]x=h[/latex] является нулем кратности p .
График полиномиальной функции будет касаться оси x нулями с четными кратностями. График будет пересекать ось x по нулям с нечетной кратностью.
Сумма кратностей является степенью полиномиальной функции.
Как: Имея график полиномиальной функции степени [latex]n[/latex], определите нули и их кратности.
- Если график пересекает ось x и кажется почти линейным на пересечении, это один ноль.
- Если график касается оси x и отскакивает от оси, это нуль с четной кратностью.
- Если график пересекает ось x в нуле, это ноль с нечетной кратностью.
- Сумма кратностей равна степени п .
Пример: определение нулей и их кратностей
Используйте график функции степени 6 для определения нулей функции и их возможных кратностей.
Показать раствор
Попробуйте
Используйте график функции степени 5, чтобы определить нули функции и их кратности.
Показать раствор
Определение конечного поведения
Как мы уже узнали, поведение графа 9{n — 1}+…+{a}_{1}x+{a}_{0}[/latex]
в конечном счете либо возрастет, либо упадет, как x безгранично возрастает, и будет либо расти, либо падать, как x неограниченно уменьшается.
{п}[/латекс], является четной степенной функцией, поскольку x увеличивается или уменьшается без ограничений, [латекс]f\left(x\right)[/латекс] увеличивается без ограничений. Когда ведущий член представляет собой нечетную степенную функцию, поскольку x убывает неограниченно, [латекс]f\left(x\right)[/латекс] также неограниченно уменьшается; поскольку x увеличивается без ограничений, [латекс]f\left(x\right)[/latex] также увеличивается без ограничений. Если ведущий член отрицательный, он изменит направление конечного поведения. В таблице ниже представлены все четыре случая.
| Четная степень | Нечетная степень |
|---|---|
Попробуйте
Внесите свой вклад!
У вас есть идеи по улучшению этого контента? Мы будем признательны за ваш вклад.
Улучшить эту страницуПодробнее
Полиномиальные графики: нули и их кратности
End Behavior»Flexing»»Bumps»Graphing
Purplemath
Вещественные (то есть некомплексные) нули многочлена соответствуют x -пересечений графика этого многочлена.
Таким образом, мы можем найти информацию о количестве действительных нулей полинома, глядя на график, и, наоборот, мы можем сказать, сколько раз график будет касаться или пересекать ось x , глядя на нули полинома. полиномиальный (или в факторизованной форме полинома).
Ноль имеет «кратность», которая относится к числу раз, которое связанный с ним множитель встречается в многочлене. Например, квадратичный ( x + 3)( x — 2) имеет нули x = -3 и x = 2, каждый из которых встречается один раз. Многочлен одиннадцатой степени ( x + 3) 4 ( x — 2) 7 имеет те же нули, что и квадратный, но в этом случае решение x = -3 имеет кратность 4 потому что множитель ( x + 3) встречается четыре раза (то есть множитель возводится в четвертую степень), а решение x = 2 имеет кратность 7, поскольку множитель ( x − 2) встречается семь раз.
Содержимое продолжается ниже
MathHelp.
comНули функции (и, да, «нули» — правильный способ написания множественного числа от «ноль») — это решения линейных множителей, которые они мне дали. . Решение каждого фактора дает мне:
x + 5 = 0 ⇒ x = -5
x + 2 = 0 ⇒ x = -2
x = -2
x = х = 1
х − 5 = 0 ⇒ x = 5
Кратность каждого нуля — это количество раз, когда встречается соответствующий ему множитель. Другими словами, множественности — это мощности. (Для множителя x — 5 понятная мощность равна 1.) Тогда мой ответ:
x = -5 с кратностью 3
x = -2 с кратностью 4
x = 1 с кратностью кратность 2
x = 5 с кратностью 1
Смысл кратностей в графическом представлении состоит в том, что любые множители, встречающиеся четное число раз (то есть любые нули, встречающиеся дважды, четыре раза, шесть раз и т. д. ) являются квадратами, поэтому они не меняют знак.
Квадраты всегда положительны. Это означает, что x -пересечение, соответствующее нулю четной кратности, не может пересекать ось x , потому что ноль не может заставить график изменить знак с положительного (выше оси x ) на отрицательный (ниже оси x ) или наоборот.
Практический результат заключается в том, что нуль четной кратности заставляет график едва касаться оси x , а затем поворачивает его обратно в исходное положение. Вы можете увидеть это на следующих графиках:
у = ( х + 6)( х — 7)
х = -6 раз
х = 7 раз
у = ( 9 х ) 01 х х − 7) 2
x = -6 один раз
x = 7 дважды
y = ( x + 6) 7 9 0 9 0 9 199 2 7)
х = −6 дважды
x = 7 один раз
y = ( x + 6) 2 ( x − 7) 2
x = -6 дважды
x = 7 дважды
= 7, но кратность нуля определяет, пересечет ли график ось x в этом нуле или вместо этого повернется в обратном направлении.
Если ноль имел кратность 1, график пересекал ось x в нуле; если ноль был кратности 2, граф просто «поцеловал» x -ось, прежде чем вернуться туда, откуда пришла.
Любой ноль, соответствующий множитель которого встречается парами (то есть два раза, или четыре раза, или шесть раз и т. д.), «отскочит» от оси x и вернется в исходное положение. Любой нуль, соответствующий множитель которого встречается нечетное количество раз (то есть один раз, или три раза, или пять раз и т. д.), пересечет ось x . Полиномиальные нули с четной и нечетной кратностью будут всегда вести себя таким образом.
На графике видно, что нули находятся при x = −15, x = -10, x = -5, x = 0, x 9010, = 9 = 15, так как график касается или пересекает ось x в этих точках. (По крайней мере, я предполагаю, что график пересекается именно в этих точках, поскольку упражнение не дает мне точных значений.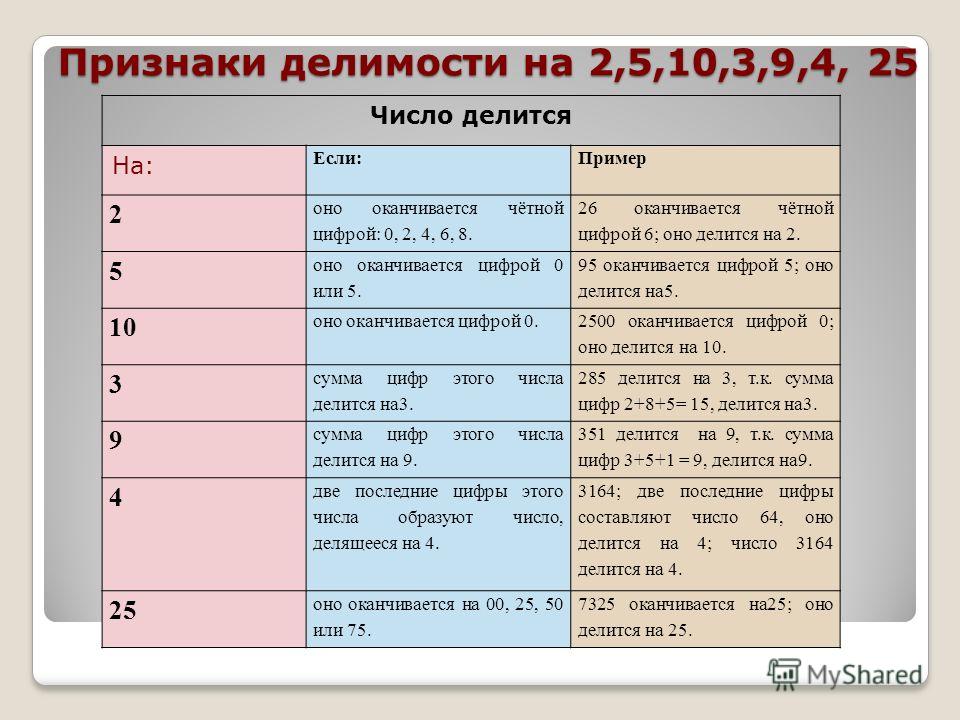
Когда я делаю предположения по картинке, мне приходится делать определенные предположения.)
Поскольку график просто касается x = -10 и x = 10, то эти нули должны встречаться четное количество раз. Остальные нули должны встречаться нечетное количество раз. Нули нечетной кратности могут встречаться только один раз, а могут встречаться три, пять и более раз каждый; по графику не скажешь. (По крайней мере, нет способа отличить от — мы узнаем об этом подробнее на следующей странице.) И нули четной кратности могут встречаться четыре, шесть или более раз каждый; Я не могу сказать, глядя.
Но если я суммирую минимальную кратность каждого, я должен получить степень, потому что в противном случае эта задача потребует больше информации, чем я могу дать. У меня есть четыре нуля нечетной кратности (при x = -15, x = -5, x = 0 и x = 15) и два нуля четной кратности (при x = -10 и x = 10).