Разложение по векторам: Разложение вектора по векторам

Координаты вектора. Разложение вектора по двум неколлинеарным векторам 9 класс онлайн-подготовка на Ростелеком Лицей |

Тема 5: Метод координат

• Видео
• Тренажер
• Теория

Заметили ошибку?

 

Координаты вектора. Разложение вектора по двум неколлинеарным векторам.

Если векторы a⃗ и b⃗ коллинеарны и a⃗≠0⃗, то существует такое число k, что b⃗=ka⃗.

Пусть a⃗ и b⃗ – два данных вектора. Если вектор p представлен в виде p⃗=xa⃗+yb⃗, где x и y – некоторые числа, то говорят, что вектор p⃗ разложен по векторам a⃗ и b⃗. Числа x и y называются коэффициентами разложения.

Теорема

На плоскости любой вектор можно разложить по двум данным неколлинеарным векторам, причем коэффициенты разложения определяются единственным образом.

Напомню, что для задания прямоугольной системы координат нужно провести две взаимно перпендикулярные прямые, на каждой из них выбрать направление (оно обозначается стрелкой) и выбрать единицу измерения отрезков.

При выбранной единице измерения отрезков длина каждого отрезка выражается положительным числом.

В дальнейшем под длиной отрезка мы будем понимать это число.

 

 

Отложим от начала координат O единичные векторы (т.е. векторы, длины которых равны единице) i⃗ и j⃗ так, чтобы направление вектора i⃗совпало с напралением оси Ox, а направление вектора j⃗ – с направлением оси Oy. Векторы i⃗ и j⃗ назовем координатными векторами.

Координатные векторы не коллинеарны, поэтому любой вектор p⃗ можно разложить по координатным векторам, т.е. представить в виде p⃗=xi⃗+yj⃗, причем коэффициенты разложения (числа x и y) определяются единственным образом. Коэффициенты разложения вектора p⃗ по координатным векторамназываются координатными векторами

p⃗ в данной системе координат. Координаты вектора будем записывать в фигурных скобках после обозначения вектора: p⃗{x;y}.

Так как нулевой вектор можно представить в виде 0⃗=0.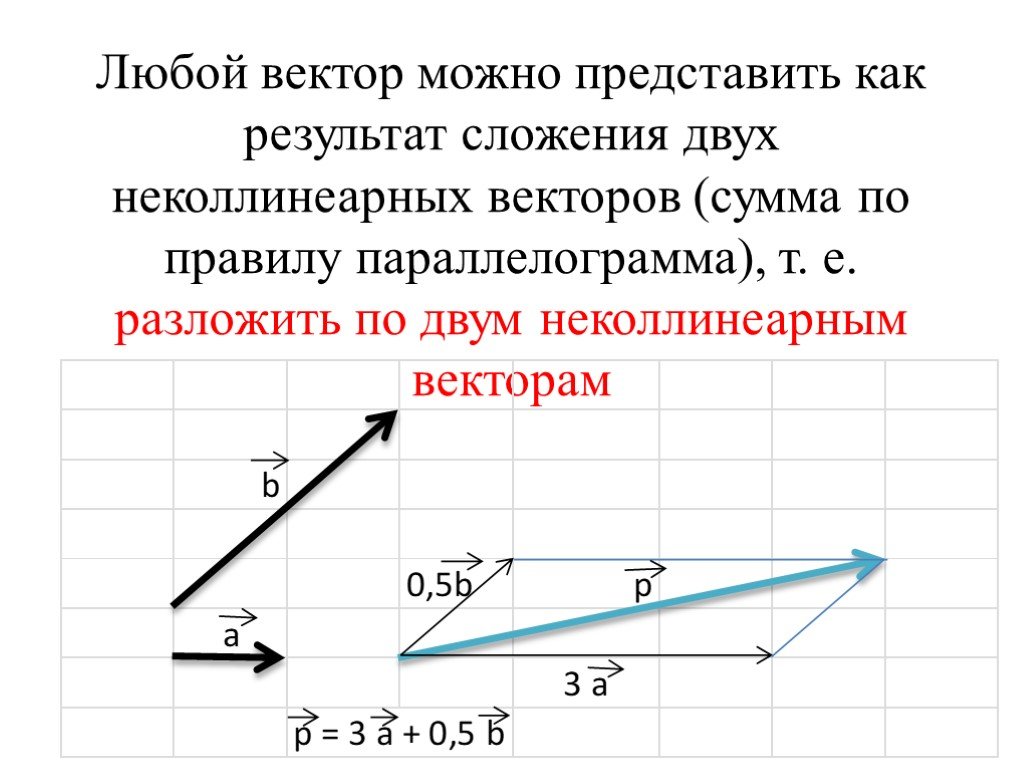 i⃗+0^.j⃗, то его координаты равны нулю: 0⃗{0;0}. Если векторы a⃗=x1i⃗+y1j⃗ и b⃗=x₂i⃗+y₂j⃗ равны, то x₁ = x₂ и y₁ = y₃. Таким образом, координаты равных векторов соответственно равны.

Рассмотрим правила, позволяющие по координатам векторов находить координаты их суммы, разности и произведения вектора на число.

1. Каждая координата суммы двух или более векторов равна сумме соответствующих координат этих векторов.

   Докажем это утверждение для двух векторов. Рассмотрим векторы a{x1;y1} и b{x2;y2}. Так как a⃗=x1i⃗+y1j⃗ и b ⃗=x2i⃗ +y2j⃗ ,то, пользуясь свойствами сложения векторов и умножения вектора на число, получим:

   a⃗+b⃗=x₁i⃗+y₁j⃗+x₂i⃗+y₂j⃗=(x₁+x₂)i⃗+(y₁+y₂)j⃗ .

   Следовательно, что координаты вектора a⃗+b⃗ равны {x1+x2;y1+y2}.

   Аналогично доказывается следующее утверждение:

2. Каждая координата разности двух или более векторов равна разности соответствующих координат этих векторов.

   Иными словами, если a⃗{x₁;y₁} и b⃗{x₂;y₂} – данные векторы, то вектор a⃗–b⃗ имеет координаты {x1-x2;y1-y2}.

3. Каждая координата произведения вектора на число равна произведению соответствующей координаты вектора на это число.

   В самом деле, пусть вектор a⃗ имеет координаты {x;y}. Найдем координаты вектора ka⃗, гдеk – произвольное число. Так как a⃗=xi⃗+yj⃗, то kxi⃗+kyj⃗. Отсюда следует, что координаты вектора ka⃗ равны {kx;ky}.

   Рассмотренные правила позволяют определить координаты любого вектора, представленного в виде алгебраической суммы данных векторов с известными координатами.

   Найти координаты вектора a⃗+b⃗,если a⃗{3;2},b⃗{2;5}

   Чтобы найти координаты вектора суммы, надо сложить соответствующие координаты данных векторов, получим:

   a⃗+b⃗ имеет координаты {3 + 2; 2 + 5}, то есть {5; 7}

   Найти координаты вектора 2a⃗, если a⃗{3;2}

   Значит, вектор 2a⃗ имеет координаты {2 ⋅ 3; 2 ⋅ 2}, то есть {6;4}

Итак, сегодня мы узнали, что любой вектор можно разложить по двум неколлинеарным векторам, ввели понятие координат вектора и рассмотрели правила, позволяющие находить координаты суммы, разности векторов, и произведения вектора на число.

А в следующий раз мы найдем связь между координатами вектора и координатами его начала и конца.

Заметили ошибку?

Расскажите нам об ошибке, и мы ее исправим.

Разложение вектора по двум неколлинеарным векторам

Вы узнаете в этой статье что значит разложить вектор по двум неколлинеарным векторам.

Представление вектора \vec{c} в виде \vec{c}=x \vec{a}+y \vec{b}, где векторы \vec{a} и \vec{b} являются неколлинеарными векторами, называется разложением вектора по двум неколлинеарным векторам.

Теорема (о разложении вектора по двум неколлинеарным векторам)

Теорема. Любой вектор с можно единственным образом представить в виде \vec{c}=x \vec{a}+y \vec{b}, где \vec{a} и \vec{b} — неколлинеарные векторы, х и у — числа.

Коллинеарные вектора \vec{m} и \vec{n} — это такие вектора, где один из векторов параллелен другому и связан с ним соотношением

\vec{m}=k\vec{n}

Доказательство:

Пусть даны векторы \vec{c}=\overrightarrow{AB}, \vec{a} и \vec{b}. Проведем через точки A и B прямые, параллельные векторам \vec{a} и \vec{b}, и обозначим точку C их пересечения. Тогда \overrightarrow{AB}=\overrightarrow{AC}+\overrightarrow{CB}.

К теореме о разложении вектора по двум коллинеарным векторам

Так как векторы \vec{a} и \overrightarrow{AC} коллинеарные, то существует такое число х, что \overrightarrow{AC} =х\vec{a}. Векторы \vec{b} и \overrightarrow{CB} тоже коллинеарные, следовательно, существует такое число у, что \overrightarrow{CB} =y\vec{b}.

Таким образом, \vec{c}=x \vec{a}+y \vec{b}.

Докажем единственность такого представления вектора с способом от противного. Допустим, что имеется другое разложение вектора, например, такое:

\vec{c}=n \vec{a}+m \vec{b}, тогда два разложения вектора \vec{c} можно приравнять:
n \vec{a}+m \vec{b}=x \vec{a}+y \vec{b} (если равны левые части равенств, то равны и правые).

Перенесем все в левую часть равенства:

n \vec{a}+m \vec{b}-x \vec{a}-y \vec{b}=0
(n-x)\vec{a}+(m-y) \vec{b}=0
\displaystyle \vec{a}=\frac{y-m}{n-x} \vec{b}

То есть векторы \vec{a} и \vec{b} получаются коллинеарными. А у нас условие — векторы \vec{a} и \vec{b} — неколлинеарные вектора.

Таким образом, возможно только единственно возможное представление вектора \vec{c} в виде \vec{c}=x \vec{a}+y \vec{b}, где векторы \vec{a} и \vec{b} являются неколлинеарными векторами.

Теорема доказана.

Если вектор \vec{c} коллинеарен какому-либо из векторов \vec{a} и \vec{b}, то либо число x, либо число y равно нулю.

Базис векторов и разложение вектора по базису

В декартовой системе координат Oxy вектор с координатами (x, y) можно разложить по единичным векторам \vec{e_1}(1;0) и \vec{e_2}(0;1).

Тогда, например, вектор \vec{c}(3; -1) можно представить в виде разложения:

\vec{c}=x \vec{e_1}+y \vec{e_2}=3 \vec{e_1}-1 \vec{e_2}

Действительно:

\begin{cases} 3=3 \cdot 1+(-1)\cdot 0, \\ — 1=3 \cdot 0+(-1)\cdot 1. \end{cases}

Система векторов, по которым можно разложить вектор с коэффициентами разложения равными его координатам, называется базисом вектора. Вектора базиса всегда не коллинеарные. Координаты вектора будут верны только в отношении данного базиса.

Однако, это не отменяет тот факт, что вектор можно разложить и по другим векторам, то есть по новому базису. Тогда говорят о переходе к новому базису векторов.

Обычно в декартовой системе координат базисные векторы на плоскости обозначают так: \vec{i}(1;0) и \vec{j}(0;1).

В пространственной декартовой системе координат базис векторов будет: \vec{i}(1; 0; 0), \vec{j}(0;1; 0), \vec{k}(0;0;1)

В то же время на любых векторах можно построить свою систему отсчета, тогда данные вектора будут считаться базисом этой системы и в этой системе можно найти координаты любого вектора. То есть любой вектор можно разложить по базису, конечно, если при этом базисные вектора не являются коллинеарными.

Примеры разложения вектора

Пример 1. Разложить вектор \vec{c}(0; 1) по двум векторам \vec{a}(3; 6) и \vec{b}(4; 9).

Решение:

Для разложения вектора \vec{c} запишем:

\vec{c}=x \vec{a}+y \vec{b}

Нам нужно найти коэффициенты разложения x и y, для этого разложим каждую координату вектора \vec{c}:

• Для абсциссы: 0=x \cdot 3+y \cdot 4
• Для ординаты: 1=x \cdot 6+y \cdot 9

Получаем систему из двух уравнений с двумя неизвестными, которую решаем:

\begin{cases} 3x+4y=0, \\ 6x+9y=1. \end{cases}

Решая, получаем: \displaystyle x=\frac{-4}{3} и y=1
И разложение вектора \vec{c} будет иметь вид: \displaystyle \vec{c}=-\frac{4}{3} \vec{a}+\vec{b}

Пример 2. Найти координаты вектора \vec{a} в базисе, если известно разложение вектора по базису \vec{e_1} и \vec{e_2}:

\vec{a}=7 \vec{e_1}+5 \vec{e_2}

Решение: Координаты вектора в базисе векторов \vec{e_1} и \vec{e_2} будут равны коэффициентам разложения, то есть \vec{a}(7; 5)

Ответ: \vec{a}(7; 5)

Пример 3. Разложить вектор \vec{b}(1; 2) по базису \vec{e_1}(2; 3) и \vec{e_2}(2; 5).

Решение:

Запишем разложение вектора по базису:

\vec{b}=b_1 \vec{e_1}+b_2 \vec{e_2}

Получим систему уравнений:

\begin{cases} 1=2b_1+4b_2, \\ 2=2b_1+5b_2. \end{cases}

От второго уравнения системы отнимем первое, получим:

\begin{cases} 1=b_2, \\ 2=2b_1+5b_2. \end{cases}

Тогда:

\begin{cases} b_2=1, \\ b_1=-1,5. \end{cases}

И разложение вектора будет иметь вид: \vec{b}=-1,5 \vec{e_1}+\vec{e_2}

Векторная декомпозиция | Brilliant Math & Science Wiki

Каждый вектор можно рассматривать как сумму двух или более других векторов.

Рассмотрим три вектора на рисунке выше. Поскольку \( \overrightarrow{AC} \) состоит из \( \overrightarrow{AB}\) и \( \overrightarrow{BC} ,\), устанавливается следующее выражение:

\[ \overrightarrow{AC} = \ overrightarrow{AB} + \overrightarrow{BC} . \]

Векторное разложение — это общий процесс разбиения одного вектора на два или более векторов, которые в сумме составляют исходный вектор. Векторы

компонентов , на которые разлагается исходный вектор, выбираются на основе конкретных деталей рассматриваемой проблемы.

Учитывая точки \(O=(0,0,0), A=(1,0,0), B=(0,1,0), C=(0,0,1), \) и \( D=(3,4,5) ,\) каково значение \(a+b+c,\), где \( a, b, \) и \( c \) удовлетворяют следующему уравнению:

\[ \overrightarrow{OD} = a\cdot\overrightarrow{OA}+b\cdot\overrightarrow{OB}+c\cdot\overrightarrow{OC}? \]

---

У нас есть

\[ \begin{массив} &\overrightarrow {OD} = (3,4,5), &\overrightarrow {OA} = (1,0,0), &\overrightarrow {OB} = (0,1, 0), &\overrightarrow {OC} = (0,0,1).\end{массив} \]

Затем

\[ \begin{выравнивание} \overrightarrow{OD} &= a\cdot\overrightarrow{OA}+b\cdot\overrightarrow{OB}+c\cdot\overrightarrow{OC} \\ (3,4,5) &= а(1,0,0) + б(0,1,0) + с(0,0,1) \\ &= (а,0,0) + (0,b,0) + (0,0,с) \\ &= (а,б,в) \\\\ \Стрелка вправо a &= 3, b = 4, c = 5.

\end{выравнивание} \]

Следовательно, \(a+b+c = 3+4+5 = 12.\) \(_\квадрат \)

Обратите внимание, что \(\overrightarrow{OD}\) был разложен на три вектора, параллельных трем координатным осям. Также обратите внимание, что векторы \(\overrightarrow{OA},\overrightarrow{OB},\) и \(\overrightarrow{OC}\) являются единичными векторами координатного пространства.

Если \(\vec{a} = (1,1,0), \vec{b} = (1,0,1)\) и \(\vec{c} = (0,1,1),\ ) как можно \( \vec{d} = (5,6,7) \) выразить с помощью \( \vec{a}, \vec{b}\) и \( \vec{c}? \)

---

Пусть \( \vec{d}= x \vec{a} + y \vec{b} + z \vec{c} .\) Тогда мы имеем

\[ \begin{выравнивание} \vec{d} &= x \vec{a} + y \vec{b} + z\vec{c} \\ (5,6,7) &= х(1,1,0) + у(1,0,1) + z(0,1,1) \\ &= (х+у, х+z, у+z), \end{выравнивание} \]

что подразумевает

\[ \begin{выравнивание} х+у &= 5 \\ х+г &= 6 \\ у+г &= 7 \\\\ \Стрелка вправо x=2, y&=3, z=4. \end{выравнивание} \]

Следовательно,

\[ \vec{d} = 2 \vec{a} + 3 \vec{b} + 4 \vec{c}. \ _\square\]

Если векторы \(\vec{a} = (3,-2,-4)\) и \(\vec{b} = (x+1,8,2y)\) параллельны, каково значение \(х+у?\)

---

Так как \( \vec{a}\) и \( \vec{b} \) параллельны, некоторое действительное число \(m\), которое удовлетворяет \( \vec{b} = m \vec{a} \) существует. Таким образом,

\[ \begin{выравнивание} \vec{b} &= m\vec{a} \\ (x+1, 8, 2y) &= m(3,-2,-4) \\ &= (3м, -2м, -4м), \end{выравнивание} \]

что подразумевает

\[ \begin{выравнивание} х+1 &= 3м\\ 8&=-2м\\ 2г&= -4м \\\\ \Стрелка вправо m&= -4, x=-13, y=8. \end{выравнивание} \]

Следовательно, \( x+y = -13+8=-5. \ _ \квадрат \)

Координаты точек \(A,B,\) и \(C\) равны \((1,3), (4,1),\) и \((7,5),\) соответственно. Если \(\overrightarrow{PA} + \overrightarrow{PB} + \overrightarrow{PC}=\overrightarrow{0}, \), каковы координаты точки \(P?\)

---

Пусть вектор положения точки \(P\) равен \(\overrightarrow{OP}=(x,y). \) Тогда мы имеем

\[ \begin{выравнивание} \overrightarrow{PA} &= (1-x,3-y) \\ \overrightarrow{PB} &= (4-x,1-y) \\ \overrightarrow{PC} &= (7-x, 5-y). \end{выравнивание} \]

Так как нам дано \( \overrightarrow{PA} + \overrightarrow{PB} + \overrightarrow{PC} = \overrightarrow{0} ,\), мы имеем

\[ \begin{выравнивание} \overrightarrow{PA} + \overrightarrow{PB} + \overrightarrow{PC} &= \overrightarrow{0} \\ (1-x,3-y)+ (4-x,1-y)+(7-x, 5-y) &= (0,0) \\ (12-3x, 9-3y) &= (0,0) \\\\ \Стрелка вправо x&= 4, y= 3. \end{выравнивание} \]

Таким образом, координаты точки \(P\) равны \( P=(4,3). \) \(_\квадрат\)

Если векторы \( \vec{a} = (1,-2)\) и \( \vec{b} = (4,-5)\) удовлетворяют \( \vec{a}=\vec{x} + \vec{y}\) и \(\vec{b}= \vec{x} -2\vec{y},\) что такое \(\vec{x}-\vec{y}?\)

---

У нас есть

\[ \begin{выравнивание} \vec{x} + \vec{y} &= \vec{a} \\ \vec{x} -2\vec{y} &= \vec{b} \\ \стрелка вправо \vec{x} &= \frac{1}{3} \big(2 \vec{a} + \vec{b} \big), \\ \vec{y} &= \frac{1}{3} \big( \vec{a} — \vec{b}\big). \end{выравнивание} \]

Следовательно, \( \vec{x} — \vec{y} \) равно

\[ \begin{выравнивание} \vec{x} — \vec{y} &= \frac{1}{3} \big(2 \vec{a} + \vec{b}\big) — \frac{1}{3} \big ( \vec{a} — \vec{b}\big) \\ &= \frac{1}{3} \big( \vec{a}+2\vec{b} \big) \\ &= \frac{1}{3} \vec{a} + \frac{2}{3} \vec{b} \\ &= \left( \frac{1}{3}, -\frac{2}{3} \right) + \left( \frac{8}{3}, -\frac{10}{3}\right ) \\ &= (3, -4).\ _\квадрат \конец{выравнивание} \]

Одно обычно полезное разложение — с компонентами, которые лежат параллельно каждой из осей координат.

На рисунке выше показано разложение вектора в трехмерном пространстве. Обратите внимание, что красный вектор можно разложить на три зеленых вектора, которые параллельны трем осям координат. Таким образом, \( \overrightarrow{OD} \) состоит из трех векторов \( \overrightarrow{OA}, \overrightarrow{OB} \) и \( \overrightarrow{OC}.\) Поэтому соответствует следующее выражение:

\[ \overrightarrow{OD} = \overrightarrow{OA} + \overrightarrow{OB} + \overrightarrow{OC} . \]

Можно определить единичные векторы, указывающие на каждую из положительных осей координат, следующим образом:

\[ \begin{align} \hat{x} &= (1, 0, 0) \\ \шляпа{у} &= (0, 1, 0) \\ \шляпа{г} &= (0, 0, 1). \end{align} \]

Отсюда следует, что для любого вектора \( \vec{V} = (v_x, v_y, v_z) \) выполняется

\[ \vec{V} = v_x \hat{ x} + v_y \шляпа{y} + v_z \шляпа{z}. \]

Таким образом, часто встречаются векторы, записанные в терминах единичных векторов \( \hat{x} \), \( \hat{y} \) и \( \hat{z} \). Альтернативная запись использует \( \hat{i} = \hat{x} \) , \( \hat{j} = \hat{y} \) и \(\hat{k} = \hat{z} \).

Например, вектор \( (-1, 2, 3) \) может быть выражен как \( -\hat{x} + 2 \hat{y} + 3 \hat{z} \).

Обратите внимание, что единичные векторы координат ортонормированы. То есть, \( \hat{x} \cdot \hat{x} = \hat{y} \cdot \hat{y} = \hat{z} \cdot \hat{z} = 1 \) и \(\шляпа{x} \cdot \шляпа{y} = \шляпа{y} \cdot \шляпа{z} = \шляпа{x} \cdot \шляпа{z} = 0 \).

Когда два вектора \( \vec{V}= (v_x, v_y, v_z)\) и \( \vec{W} = (w_x, w_y, w_z) \) добавляются,

\[ \vec{V }+\vec{W} = (v_x \шляпа{x} + v_y \шляпа{y} + v_z \шляпа{z}) + (w_x \шляпа{x} + w_y \шляпа{y} + w_z \шляпа{ z}) = (v_x + w_x) \hat{x} + (v_y + w_y) \hat{y} + (v_z + w_z) \hat{z}, \]

, что то же самое, что и \( ( v_x + w_x, v_y + w_y, v_z + w_z)\). Точно так же, если взять скалярное произведение \( \vec{V} \cdot \vec{W} \), получится

\[ \begin{align} \vec{V} \cdot \vec{W} &= (v_x \hat{x} + v_y \hat{y} + v_z \hat{z}) \cdot (w_x \hat{x} + w_y \hat{ у} + w_z \шляпа{г}) \\ &= v_x w_x \шляпа{x} \cdot \шляпа{x} + v_y w_y \шляпа{y} \cdot \шляпа{y} + v_z w_z \шляпа{z} \cdot \шляпа{z} \\ &= v_x w_x + v_y w_y + v_z w_z, \end{выравнивание} \]

как и ожидалось.

Разложение вектора на компоненты

Главная > Математика > Предварительное исчисление > Разложение вектора на компоненты

Во многих приложениях необходимо разложить вектор на сумму двух перпендикулярных компонент вектора. Это верно для многих физических приложений, связанных с силой, работой и другими векторными величинами. Перпендикулярные векторы имеют скалярное произведение нуля и называются ортогональными векторами .

На рис. 1 показаны векторы u и v с вектором u , разложенным на ортогональные компоненты w ₁ и w ₂ .

Вектор u теперь можно записать как u = w ₁ + w ₂ , где w ₁ параллелен вектору v , а w ₁ перпендикулярен/ортогон al to w ₂ . Компонента вектора w ₁ также называется проекцией вектора u на вектор v , proj _v u .

Проект _v u можно рассчитать следующим образом:

ПРОЕКЦИЯ U НА V:

Пусть u и v — ненулевые векторы:

projv u=[u· vv2]v

Как только компонент вектора proj _v u найден, поскольку u = w ₁ + w ₂ , компонент вектора w ₂ может быть найден путем вычитания w ₁ от до .

w ₂ = u — w ₁

Рассмотрим несколько примеров.

Для работы этих примеров требуется использование различных векторных правил. Если вы не знакомы с правилом, перейдите в соответствующую тему для ознакомления.

Пример 1: Пусть u=〈-2,2〉 и v=〈3,5〉. Запишите вектор u как сумму двух ортогональных векторов, один из которых является проекцией u на v.

Шаг 1: Найдите проект v u . projvu=[u·v∥v∥2]v=w1	projvu=[u·v∥v∥2]v projvu=[(−2·3)+(2·5)32+522]〈3,5〉 projvu=[−6+10342]〈3,5〉 projvu=[434]〈3,5〉=[217]〈3,5〉 projvu=〈617,1017〉
Шаг 2: Найдите ортогональный компонент. ш 2 = и — ш 1	ш 2 = и — ш 1 w2=〈−2,2〉−〈617,1017〉 w2=〈(−2−617), (2−1017)〉 w2=〈−4017,2417〉
Шаг 3: Запишите вектор как сумму двух ортогональных векторов. и = ш 1 + ш 2	ты = ш 1 + ш 2 и=〈617,1017〉+〈−4017,2417〉

Пример 2. Для заданных векторов u=〈1,3〉 и v=〈-4,5〉 запишите u как сумму двух ортогональных векторов, один из которых является проекцией u на v.

Шаг 1: Найдите проект v u . projvu=[u·v∥v∥2]v=w1	projvu=[u·v∥v∥2]v projvu=[(1·−4)+(3·5)(−4)2+522]〈−4,5〉 projvu=[−4+15412]〈−4,5〉 projvu=[1141]〈−4,5〉 projvu=〈−4441,5541〉
Шаг 2: Найдите ортогональный компонент. ш 2 = и — ш 1	ш 2 = и — ш 1 w2=〈1,3〉−〈−4441,5541〉 w2=〈(1+4441), (3−5541)〉 w2=〈8541,6841〉
Шаг 3: Запишите вектор как сумму двух ортогональных векторов. No related posts. Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт