Косинус 120 градусов таблица: Косинус 120 | Треугольники

Mathway | Популярные задачи

1	Найти точное значение	sin(30)
2	Найти точное значение	sin(45)
3	Найти точное значение	sin(30 град. )
4	Найти точное значение	sin(60 град. )
5	Найти точное значение	tan(30 град. )
6	Найти точное значение	arcsin(-1)
7	Найти точное значение	sin(pi/6)
8	Найти точное значение	cos(pi/4)
9	Найти точное значение	sin(45 град. )
10	Найти точное значение	sin(pi/3)
11	Найти точное значение	arctan(-1)
12	Найти точное значение	cos(45 град. )
13	Найти точное значение	cos(30 град. )
14	Найти точное значение	tan(60)
15	Найти точное значение	csc(45 град. )
16	Найти точное значение	tan(60 град. )
17	Найти точное значение	sec(30 град. )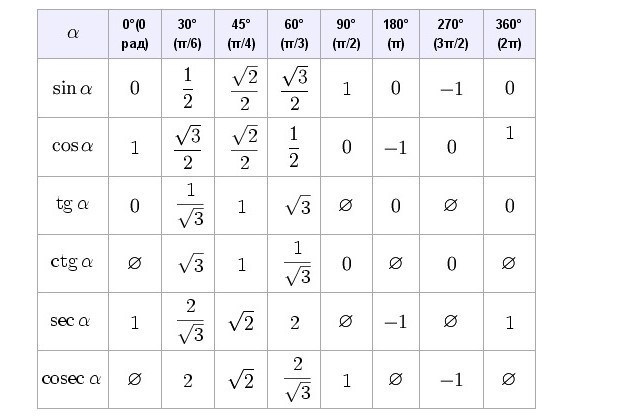
18	Найти точное значение	cos(60 град. )
19	Найти точное значение	cos(150)
20	Найти точное значение	sin(60)
21	Найти точное значение	cos(pi/2)
22	Найти точное значение	tan(45 град. )
23	Найти точное значение	arctan(- квадратный корень из 3)
24	Найти точное значение	csc(60 град. )
25	Найти точное значение	sec(45 град. )
26	Найти точное значение	csc(30 град. )
27	Найти точное значение	sin(0)
28	Найти точное значение	sin(120)
29	Найти точное значение	cos(90)
30	Преобразовать из радианов в градусы	pi/3
31	Найти точное значение	tan(30)
32	Преобразовать из градусов в радианы	45
33	Найти точное значение	cos(45)
34	Упростить	sin(theta)^2+cos(theta)^2
35	Преобразовать из радианов в градусы	pi/6
36	Найти точное значение	cot(30 град. )
37	Найти точное значение	arccos(-1)
38	Найти точное значение	arctan(0)
39	Найти точное значение	cot(60 град. )
40	Преобразовать из градусов в радианы	30
41	Преобразовать из радианов в градусы	(2pi)/3
42	Найти точное значение	sin((5pi)/3)
43	Найти точное значение	sin((3pi)/4)
44	Найти точное значение	tan(pi/2)
45	Найти точное значение	sin(300)
46	Найти точное значение	cos(30)
47	Найти точное значение	cos(60)
48	Найти точное значение	cos(0)
49	Найти точное значение	cos(135)
50	Найти точное значение	cos((5pi)/3)
51	Найти точное значение	cos(210)
52	Найти точное значение	sec(60 град. )
53	Найти точное значение	sin(300 град. )
54	Преобразовать из градусов в радианы	135
55	Преобразовать из градусов в радианы	150
56	Преобразовать из радианов в градусы	(5pi)/6
57	Преобразовать из радианов в градусы	(5pi)/3
58	Преобразовать из градусов в радианы	89 град.
59	Преобразовать из градусов в радианы	60
60	Найти точное значение	sin(135 град. )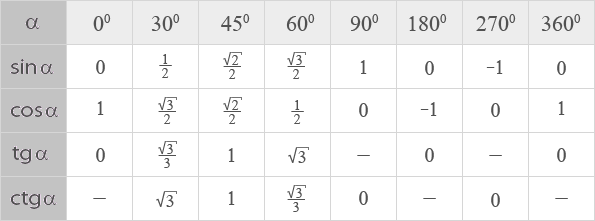
61	Найти точное значение	sin(150)
62	Найти точное значение	sin(240 град. )
63	Найти точное значение	cot(45 град. )
64	Преобразовать из радианов в градусы	(5pi)/4
65	Найти точное значение	sin(225)
66	Найти точное значение	sin(240)
67	Найти точное значение	cos(150 град. )
68	Найти точное значение	tan(45)
69	Вычислить	sin(30 град. )
70	Найти точное значение	sec(0)
71	Найти точное значение	cos((5pi)/6)
72	Найти точное значение	csc(30)
73	Найти точное значение	arcsin(( квадратный корень из 2)/2)
74	Найти точное значение	tan((5pi)/3)
75	Найти точное значение	tan(0)
76	Вычислить	sin(60 град. )
77	Найти точное значение	arctan(-( квадратный корень из 3)/3)
78	Преобразовать из радианов в градусы	(3pi)/4
79	Найти точное значение	sin((7pi)/4)
80	Найти точное значение	arcsin(-1/2)
81	Найти точное значение	sin((4pi)/3)
82	Найти точное значение	csc(45)
83	Упростить	arctan( квадратный корень из 3)
84	Найти точное значение	sin(135)
85	Найти точное значение	sin(105)
86	Найти точное значение	sin(150 град. )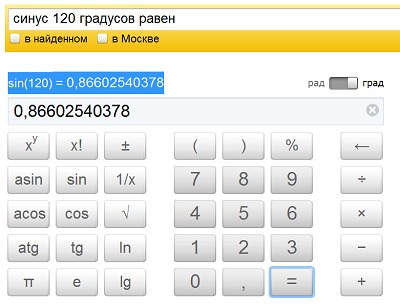
87	Найти точное значение	sin((2pi)/3)
88	Найти точное значение	tan((2pi)/3)
89	Преобразовать из радианов в градусы	pi/4
90	Найти точное значение	sin(pi/2)
91	Найти точное значение	sec(45)
92	Найти точное значение	cos((5pi)/4)
93	Найти точное значение	cos((7pi)/6)
94	Найти точное значение	arcsin(0)
95	Найти точное значение	sin(120 град. )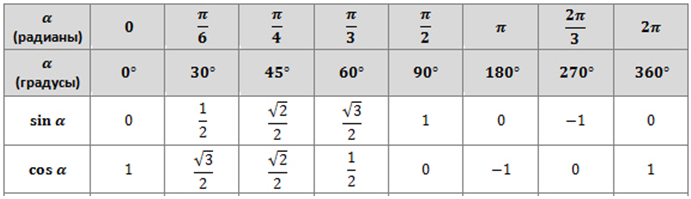
96	Найти точное значение	tan((7pi)/6)
97	Найти точное значение	cos(270)
98	Найти точное значение	sin((7pi)/6)
99	Найти точное значение	arcsin(-( квадратный корень из 2)/2)
100	Преобразовать из градусов в радианы	88 град.

А синуса график волна за волной…(с) Всякие задачки на…

А синуса график волна за волной…(с)

Всякие задачки на сообразительность — это прекрасно. Но хорошо можно понять и школьника, которому они совершенно не интересны — поскольку весьма далеки от реальности и непонятно, зачем вообще нужны. Если это спорт такой — так ведь есть множество всяческих видов спорта, гораздо более азартных.

У школьной математики в Израиле (а, наверное, и во многих других странах, я просто не знаком с ситуацией) есть одна очень неприятная проблема. Математика изучается очень многими в отрыве от её истории и её применения. Именно потому, что изучение естественных наук необязательно, а, значит, учитель и не может на них ссылаться в процессе объяснения материала. Разумеется, и ученик вполне вправе рассуждать о математике, как о некоторых хитрых абстракциях. Навыдумывали мол, а  мне учить. То, что математические понятия не выдуманы в башнях мудрецами от скуки и безделья, а возникли для описания реальных природных процессов, далеко не всегда удаётся понять в школе.

«Если бы я был директором» — никогда бы не излагал многие разделы математики в отрыве от их применения. Например, в физике, как минимум.

Классический пример такой оторванности от практики — тригонометрические функции. На 3 единицы изучают их, как отношения сторон в прямоугольном треугольнике. И всё. А потом откуда-то возникают «незаконные» синусы и косинусы тупых углов, поскольку теоремы синусов и теорема косинусов работают и для тупоугольных треугольников.

Всё началось с подобия и теоремы Фалеса. Из неё следует, что удобным способом описания угла может быть описание его в виде, например, отношения катета и гипотенузы прямоугольного треугольника с таким углом. Поскольку прямоугольные треугольники с одинаковым острым углом подобны , их стороны пропорциональны и отношения соответствующих сторон (при заданном угле) не зависят от длин сторон треугольников.

sin(A) = a/c  ;   cos(A) = b/c  ;  tan(A) = a/b   при этом ( 90 >А>0 ) градусов

Потом появились таблицы значений синуса, косинуса и тангенса в зависимости от размера угла. Самые простенькие таблицы можно составить самостоятельно — используя транспортир и линейку, измеряя углы и стороны нарисованного прямоугольного треугльника. Более точные — требуют вычислений, о которых пока говорить рано.

А при появлении компьютера эти вычисления были переданы ему. Осталось только набрать значение угла, найти кнопку и нажать её.

А зачем это всё людям потребовалось в своё время? А вот представим, что мы осаждаем древнюю крепость на равнине. надо изготовить осадные лестницы, а для этого надо знать высоту крепостной стены. Близко к ней нас не подпустят и верёвкой измерить никак не получится. Но таблица тангенсов углов может помочь.  Сначала расположимся на достаточном удалении от крепости, чтобы лучники врага не подстрелили. Измерим угол, под которым видна верхняя часть стены. Затем разведчик подползёт по направлению к крепости поближе, измеряя при этом расстояние, которое он проползёт. И вновь измерит угол, под которыи видна стена. Понятно, что расстояний до стены (x и y) мы не знаем.

1/tan(A)= x/h       1/tan(B)= y/h   1/tan(A) — 1/tan(B) = (x-y)/h

h = (tan(A) * tan(B))*( x-y) / ( tan(B) — tan(A))

где  h — высота крепостной стены,  ( x-y) — расстояние, которое прополз разведчик.

Всё это, разумеется, будет измерено в полевых условиях не очень точно, но тут главное — не сделать лестницу слишком короткой. Однако и слишком длинной её делать нельзя — она может не выдержать собственного веса, не говоря уже о тех, кто будет по ней лезть.

Конечно, это один, и не самый важный. пример того, как люди могли использовать тригонометрические функции. Таких примеров тьма — и в строительстве, и в геодезии, и в астрономии. Самые точные и подробные таблицы были у астрономов.

«Незаконные» синусы и косинусы.

Наберём на калькуляторе 150 градусов. Нажмём кнопку «sin» . Результат = 0.5

Откуда он взялся?

Рассмотрим теорему синусов. Если выводить её через равенство выражений для площади треугольника,  то можно записать

AB*AC*sin(A) = AB*BC*sin(B)=BC*AC*sin(C), откуда, разделив каждую из частей равенста на AB*AC*BC и получим выражение для теоремы синусов. Но в данном случае нам интересно, а что же делать, если один из углов — тупой?

Чтоб теорема осталось справедливой, и чтоб выражение для площади треугольника осталось справедливым, надо доопределить понятие синуса угла. Например, в выражении удвоенной площади треугольника AB*AC*sin(A) выражение AВ*sin(A) — это высота, опущенная на AС. Если положить, что и в тупоугольном треугольнике это тоже должна быть высота, только опущенная уже на продолжение АС, то выражение для площади треугольника и теорема синусов станут справедливыми для любого треугольника вообще. Определим поэтому синус тупого угла равным синусу острого угла, смежного с ним.  sin(A)=sin(180 — A)

Поэтому синус 150 градусов = синусу 30 градусов и равен 0.5.

Аналогичные рассуждения при выводе теоремы косинусов, которая должна быть справедлива и для тупоугольного треугольника, приводят к доопределению косинуса тупого угла как отрицательного косинуса угла, смежного с ним.

cos(A)= -cos(180 — A)   ;       cos(120) =-cos(60) =-0.5

Обобщённое понятие угла.

Пока речь шла только о треугольниках. ничего большего и не требовалось. Но человек продолжал изобретать различного рода механизмы. В том числе и связанные с вращением. И тут понятия угла в пределах 0-180 градусов оказалось явно недостаточно. Но не было никаких проблем расширить понятия синуса и косинуса для любого угла и при этом сохранить все свойства этих понятий, выведенные для треугольников.

Рассмотрим окружность единичного радиуса с центром в начале координат Х-У

Если углом называть угол между осью Х и единичным радиусом, отсчитывая его против часовой стрелки от положительного направления оси Х, то в пределах 0-180 градусов для синуса угла можно принять проекцию единичного вектора на ось У, а для косинуса — проекцию на ось Х. Это совпадёт с предыдущими определениями синуса и косинуса. данными для треугольников. А вот дальше — это уже расширение определения. Зачем оно нужно?

Прежде, чем ответить на такой вопрос, рассмотрим, как будет выглядеть график функции (зависимости) синуса от угла. Кстати, при равномерном вращении радиус-вектора угол поворота будет пропорционален времени, поэтому очень часто, рассматривая различного рода физические процессы, связанные с равномерным вращением, используют не угол поворота. а время.

Разумеется, совершив полный оборот, радиус-вектор вернётся в исходную точку, и дальше всё повторится. Поэтому функция периодическая, с периодом 360 градусов.

Как оказалось, такая функция идеально подходит не только для описания вращательного  движения механизмов, придуманных человеком, но и для огромного количества особых природных процессов, называемых колебательными процессами.

Самый простой классический пример такого процесса — колебание груза на пружинке. К сожалению, чтобы объяснить, почему это так, необходимо иметь некоторое представление о физике и механике. Например, о том, что в широких пределах изменения её длины, пружинка действует на груз с силой, пропорциональной отклонению от положения равновесия, что в свою очередь, определяется упругими свойствами металла в определённых пределах нагрузки.

И поэтому второй закон Ньютона запишется для груза на пружинке, как

-КX(t) = m * X«(t)   где к — коэффициент упругости пружины,  X(t) — смещение груза от положения равновесия, а X«(t) — ускорение груза (вторая производная от смешения по времени).

Из дальнейшего изучения функции sin(t) и её производных выяснится, что её вторая производная = -sin(t), т.е. она идеально подходит (после подбора соответствующих констант) в качестве решения приведенного дифференциального уравнения.

Кроме того, изучая на физике поведение вращающейся в магнитном поле проводящей ток рамки, можно обнаружить, что возникающий ток в рамке будет синусоидально зависеть от угла поворота рамки. А это означает, что турбины генерируют переменный ток, также описываемый синусоидой. Выходит, что вся электротехника использует в описании тригонометрические функции.
И волны на море удивительным образом похожи на синусоиду. Да-да — волновые процессы (не только на море, но и вообще)тоже описываются тригонометрическими функциями.

Так что появление тригонометрических функций не было капризом сумасшедших математиков. Эти функции были спрятаны в природе. Математики их просто обнаружили.

Tags: тригонометрия

Значение cos 120 в градусах и радианах с решенными примерами 3}\right)\) или cos (2,0943951).

Это тригонометрическое отношение, которое символизирует функцию во втором квадранте. Так как значение косинуса отрицательно во втором квадранте, то cos 120 будет иметь отрицательное значение. Тригонометрическая функция – это функция, которая связывает углы прямоугольного треугольника с отношением его сторон. В тригонометрии мы имеем дело с 6 тригонометрическими функциями, а именно синус, косинус, тангенс, котангенс, секанс, косеканс и т. д.

Что такое значение Cos 120?

Значение cos 120 градусов равно -0,5 или -1/2, а значение cos 120 в радианах равно \(\cos \left(\frac{2\pi }{3}\right)\) или cos (2,0943951 ). Всякий раз, когда значение любого угла должно быть указано в радианах, нам нужно умножить его на \(\frac{\pi}{180}\).

Используя ту же процедуру, мы можем записать cos 120 как \(\cos \\left(120\times \frac{\pi }{180}\right)\). Это равно \(\cos\left(\frac{2\pi }{3}\right)\).

Итак, мы можем написать, что \(\cos \ \left(\frac{2\pi }{3}\right)=-\frac{1}{2}\)

Когда дело доходит до выражения значения cos 120 в различных формах, мы можем записать его как:

Cos 120 в десятичных дробях = -0,5

Cos 120 в дробях = -1/2

Cos 120 в радианах = \( \cos\left(\frac{2\pi }{3}\right)\) или cos (2,0943951).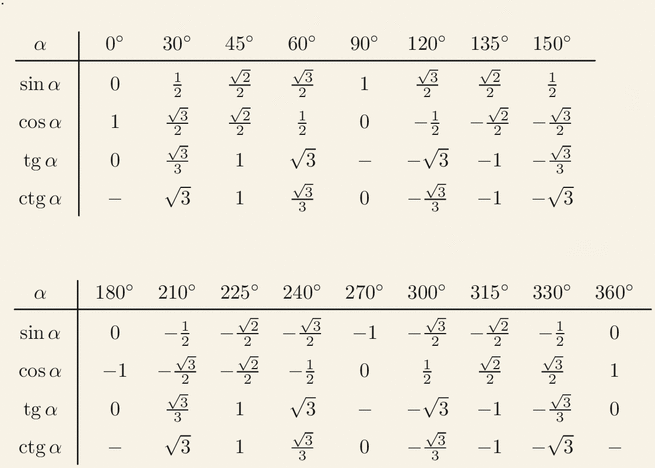

Мы видели, что значение cos 120 отрицательно. Это потому, что мы знаем, что 120 градусов лежат между 90 и 180 градусами, которые находятся во втором квадранте.

Значение косинуса отрицательно во втором квадранте, таким образом, значение косинуса 120 = -0,5

Также отметим, что функция косинуса является четной функцией, а это значит, что cos 120 градусов = cos (-120) градусов.

Как найти значение Cos 120 градусов?

Мы можем найти значение cos 120 градусов двумя способами:

1. значение Cos 120 градусов с помощью единичного круга
2. значение Cos 120 градусов с помощью тригонометрических тождеств

Единичный круг

Чтобы найти значение Cos 120 градусов, используя единичный круг, мы должны:

• Поверните букву «r» против часовой стрелки так, чтобы она образовала угол 120 градусов с положительной осью x.
• Значение cos 120 берется из координаты x точки пересечения r с единичным кругом, то есть (-0,5, 0,866).

Таким образом, значение cos 120 градусов = -0,5

Как найти значение Cos 120 градусов с помощью тригонометрических тождеств

Cos 120 градусов можно представить с помощью тригонометрических функций. Некоторые из распространенных представлений упомянуты ниже: 92120-1}}{{cosec}120}\)

\(\cos 120=\frac{1}{\sec 120}\)

Поскольку cos 120 лежит во втором квадранте, значение cos 120 градусы всегда будут отрицательными.

Некоторые из общих тригонометрических тождеств, которые представляют cos 120 градусов: \cos 300\)

\(\sin (90+120)=\sin 210\)

\(\sin (90-120)=\sin (-30)\)

Таблица тригонометрических значений

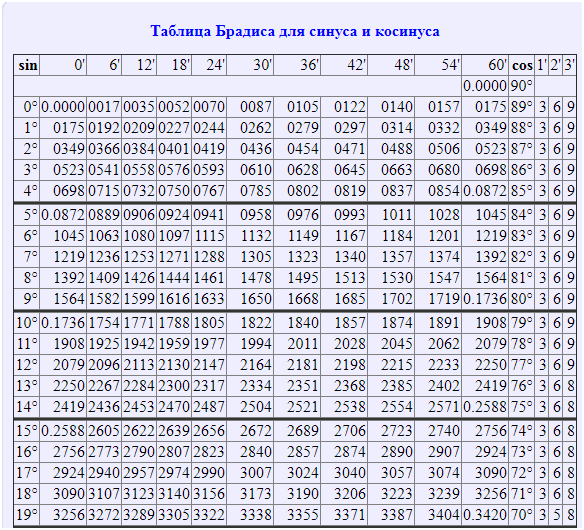
Angles (In Degrees)

0

30

45

60

90

120

150

180

210

270

300

330

360

Angles (In Radians)

0

π/6

π/4

π/3

π/2

2π/3

5π/6

π

7π/ 6

3π/2

5π/3

11π/6

2π

SIN

0

1/2

1/√2

A /2

0

-1/2

-1

-√3/2

-1/2

0

cos

1

√3/2

1/√ 2

1/2

0

-1/2

-√3/2

-1

-√3/2

0

1/2

√3/2

1

TAN

0

1/√3

1

√3

ac —

0

√1/3

∞

-√3

-1/√3

0

cot

∞

√3

1

1/√3

0

-1/√3

-√3

∞

√3

0

-1/√3

-A -1

-2/√3

-2

∞

sec

1

2/√3

√2

2

∞

-2

-2/√ 3

-1

-2/√3

∞

2

-2/√3

1

Периодичность функции косинуса

В тригонометрии функция косинуса является периодической функцией.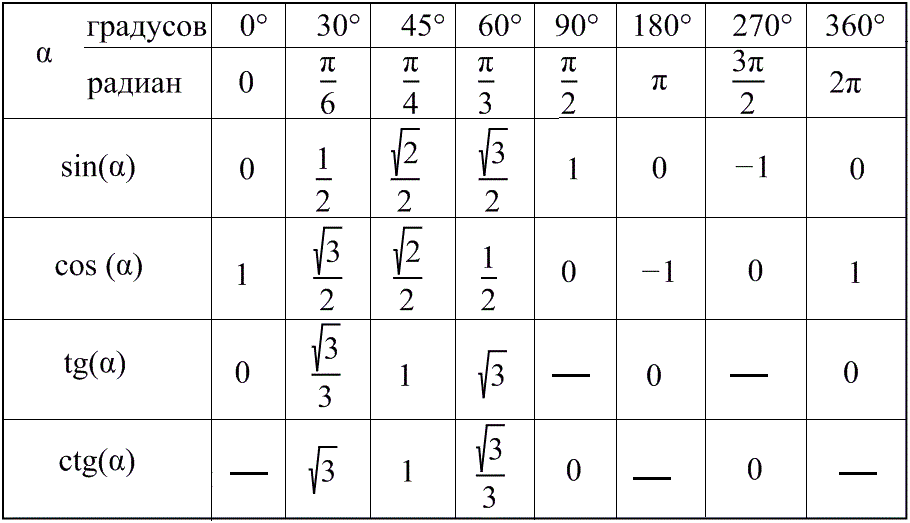 Это означает, что функция повторяется через фиксированный интервал в обоих направлениях. Любая функция косинуса может быть графически представлена ​​следующим образом:

При внимательном рассмотрении графика можно заметить, что график и функция повторяются после интервала от 0 до \(2\pi\). Когда нам нужно определить период любого графика, мы принимаем во внимание интервал значений x функции, где цикл графика повторяется в любом направлении.

Таким образом, мы можем заключить, что для общей функции косинуса периодичность равна \(2\pi\).

Решенные Примеры значения Cos 120

Пример 1: Найдите значение \(\frac{2\cos 120}{3\sin \left(-30\right)}\).

Ответ 1: Нам нужно найти значение:

\(\frac{2\cos 120}{3\sin \left(-30\right)}\)

Мы знаем, что \(\ cos 120=\sin \left(90-120\right)\)

Следовательно, \(\cos 120=\sin \left(-30\right)\) 92120=0,25\)

Мы надеемся, что приведенная выше статья поможет вам понять и подготовиться к экзамену. Оставайтесь с нами в приложении Testbook, чтобы получать больше обновлений по связанным с математикой темам и другим подобным предметам. Кроме того, обратитесь к серии тестов, доступных для проверки ваших знаний по нескольким экзаменам.

Часто задаваемые вопросы о значении cos 120

В.1 Как найти значение cos 120?

Ans.1 Значение cos 120 может быть найдено с использованием двух методов: единичного круга и тригонометрических тождеств.

Q.2 Каковы sin и cos 120 градусов?

Ответ 2 Значение sin 120 равно \(\frac{\sqrt{3}}{2}\), а значение cos 120 равно -1/2.

В.3. Чему равен косинус числа 120 в радианах?

Ответ 3 Значение косинуса 120 в радианах записывается как cos \(\frac{2\pi }{3}\).

Q.4 Что такое значение cos 120?

Ответ 4 Значение cos 120 градусов равно -0,5 или -1/2, а значение cos 120 в радианах равно \(\cos \left(\frac{2\pi }{3}\right )\) или cos (2. 092120-1}}{{cosec}120}\)
\(\cos 120=\frac{1}{\sec 120}\)

Скачать публикацию в формате PDF

Мэтуэй | Популярные задачи

92

1	Найдите точное значение	грех(30)
2	Найдите точное значение	грех(45)
3	Найдите точное значение	грех(30 градусов)
4	Найдите точное значение	грех(60 градусов)
5	Найдите точное значение	загар (30 градусов)
6	Найдите точное значение	угловой синус(-1)
7	Найдите точное значение	грех(пи/6)
8	Найдите точное значение	cos(pi/4)
9	Найдите точное значение	грех(45 градусов)
10	Найдите точное значение	грех(пи/3)
11	Найдите точное значение	арктан(-1)
12	Найдите точное значение	cos(45 градусов)
13	Найдите точное значение	cos(30 градусов)
14	Найдите точное значение	желтовато-коричневый(60)
15	Найдите точное значение	csc(45 градусов)
16	Найдите точное значение	загар (60 градусов)
17	Найдите точное значение	сек(30 градусов)
18	Найдите точное значение	cos(60 градусов)
19	Найдите точное значение	соз(150)
20	Найдите точное значение	грех(60)
21	Найдите точное значение	cos(pi/2)
22	Найдите точное значение	загар (45 градусов)
23	Найдите точное значение	arctan(- квадратный корень из 3)
24	Найдите точное значение	csc(60 градусов)
25	Найдите точное значение	сек (45 градусов)
26	Найдите точное значение	csc(30 градусов)
27	Найдите точное значение	грех(0)
28	Найдите точное значение	грех(120)
29	Найдите точное значение	соз(90)
30	Преобразовать из радианов в градусы	пи/3
31	Найдите точное значение	желтовато-коричневый(30)
35	Преобразовать из радианов в градусы	пи/6
36	Найдите точное значение	детская кроватка(30 градусов)
37	Найдите точное значение	арккос(-1)
38	Найдите точное значение	арктан(0)
39	Найдите точное значение	детская кроватка(60 градусов)
40	Преобразование градусов в радианы	30
41	Преобразовать из радианов в градусы	(2 шт. No related posts. Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт