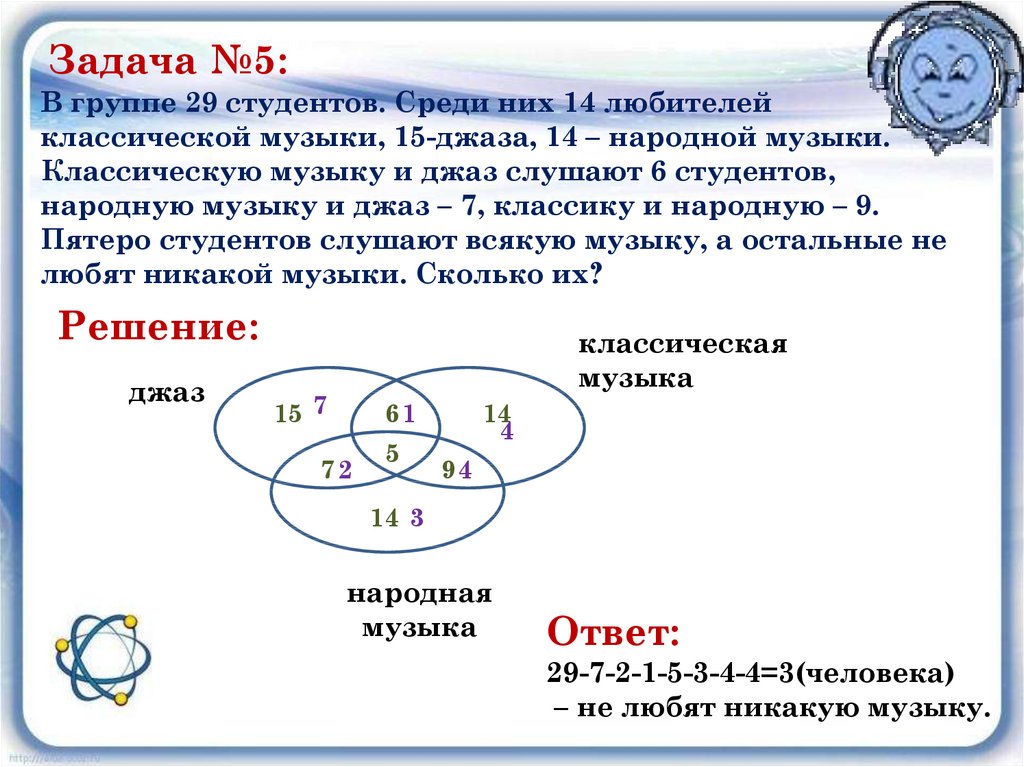
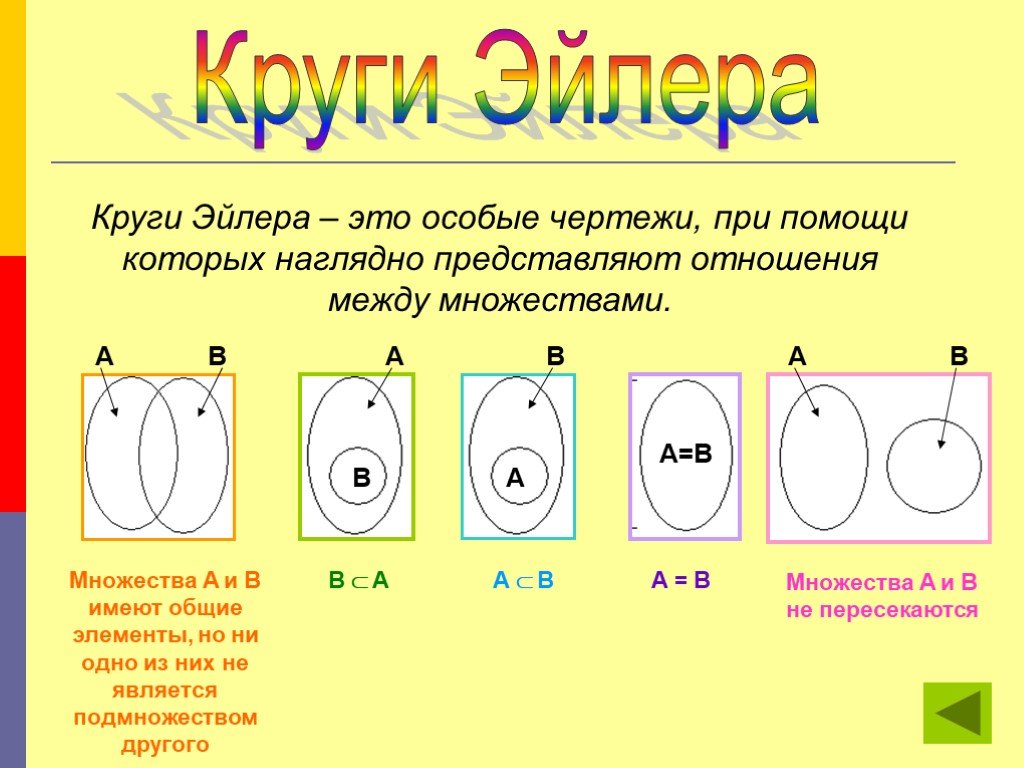
Множества на кругах Эйлера-Венна — презентация онлайн
Похожие презентации:
Круги Эйлера в решении задач
Множества и операции над ними. Решение задач с помощью кругов Эйлера
Множество. Элементы множества. Изображение множеств. 5 класс
Множества и операции над множествами
Элементы теории множеств. Понятие множества
Понятие множества. Способы задания множеств. Операции над множествами
Множества. Круги Эйлера
Элементы теории множеств.Понятие множества
Элементы и множества. Операции над множествами и их свойства
Теория множеств
Множество
геометрических фигур
Множество
четных однозначных чисел
— элемент множества геометрических фигур
— элемент множества четных однозначных чисел
знак называется включением (можно сравнить со знаком )
A
A
B
Например:
• Множество цифр:
0;1;2;3;4;5;6;7;8;9
• Множество букв русского алфавита
Предметы, из которых состоит
множество, называются его
Например:
1).
 Цифра 6 – элемент множества цифр.
Цифра 6 – элемент множества цифр.2). Буква Л – элемент множества букв
русского алфавита
Для обозначения множеств используют большие
буквы латинского алфавита или фигурные скобки,
внутри которых записывают элементы
множества(при этом порядок элементов не имеет
значения).
Например:
1). А— множество цифр: А={0;1;2;3;4;5;6;7;8;9}.
2). W— множество букв русского алфавита:
W={А;Б;В;Г;Д;Е;Ж;З;И;Й;К;Л;М;Н;О;П;Р;С;Т;У;Ф;Х;
Ц;Ч;Ш;Щ; Ь;Ы;Ъ;Э;Ю;Я }
Для обозначения элементов множества
используют малые буквы латинского алфавита
Например:
1). f = 6 – элемент множества цифр
2). а = Р – элемент множества букв русского
алфавита
Принадлежность предмета данному множеству
обозначается
Непринадлежность – символом
Например:
1). f = 6 ; 6 є А, где А— множество цифр.
2). К є W, где W— множество букв русского
алфавита
Множество может быть:
• 1). Конечное :
Например: А— множество цифр
• 2). Бесконечное:
Например: N – множество натуральных чисел
3).
 Пустое:
Пустое:ø- множество, в котором нет ни одного элемента
Например: X – множество решений уравнения
õ 25
2
Первый способ: перечислительный
A={1; 2; 3; 4; 5}
Второй способ: описательный – множество
выделяется из всевозможных других тем или
иным свойством
A={Х/ — первые пять натуральных чисел}
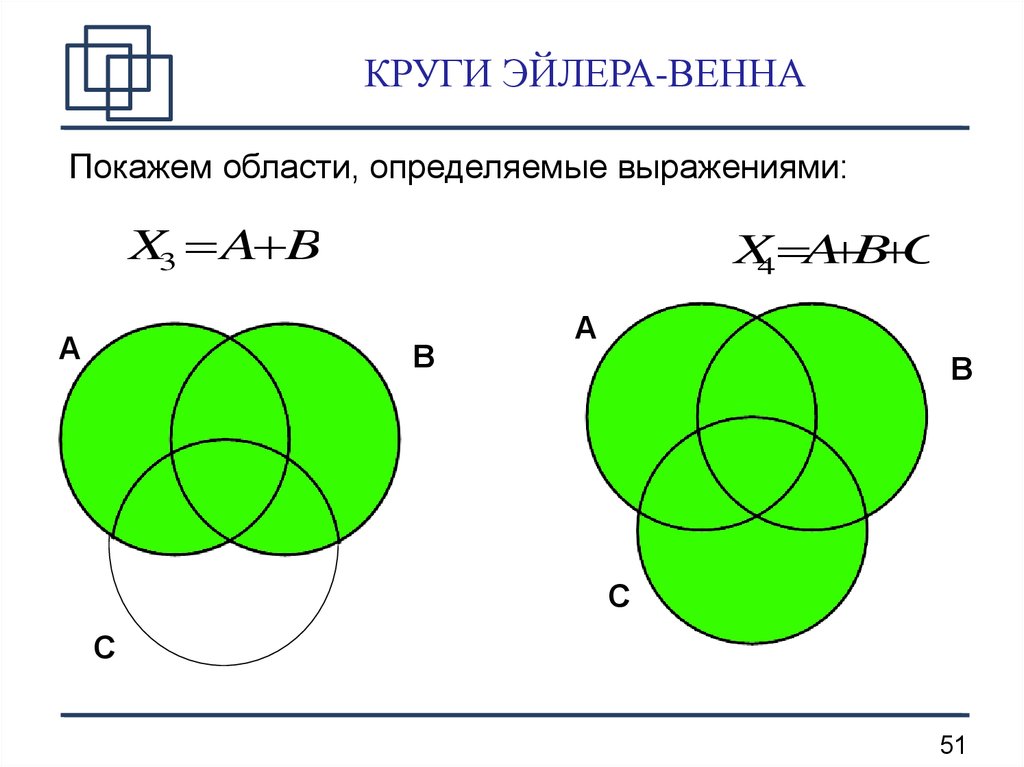
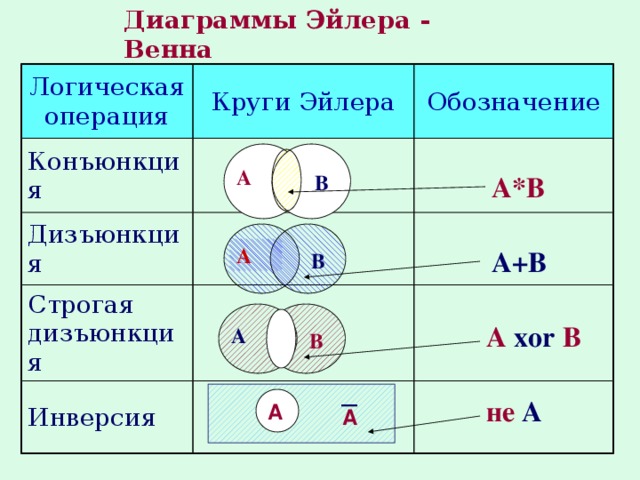
Объединение множеств
Объединением (суммой) множеств А и В называется
множество тех элементов, каждый из которых принадлежит
хотя бы одному из множеств А или В .
A B x x A x B
A, B
А U В=А
A
A
АUВ
АUВ
B
А
В
1. Объединение A B = х / х А или х В
множества
пересекаются
множества не
пересекаются
одно множество является
подмножеством другого
A
A
A
B
B
А В
А В
B
А В=А
Пересечение множеств
A B x x A x B
A, B
А В= А
A
A
А В= Ø
B
А
В
2. Пересечение A B = х / х А и х В
множества
пересекаются
В
А В
множества не
пересекаются
одно множество является
подмножеством другого
множества A B
А
В
А В=
А
В
А В=В
Разность множеств
• Разностью множеств А и В называется
множество, которое содержит все элементы
А, не входящие в В.
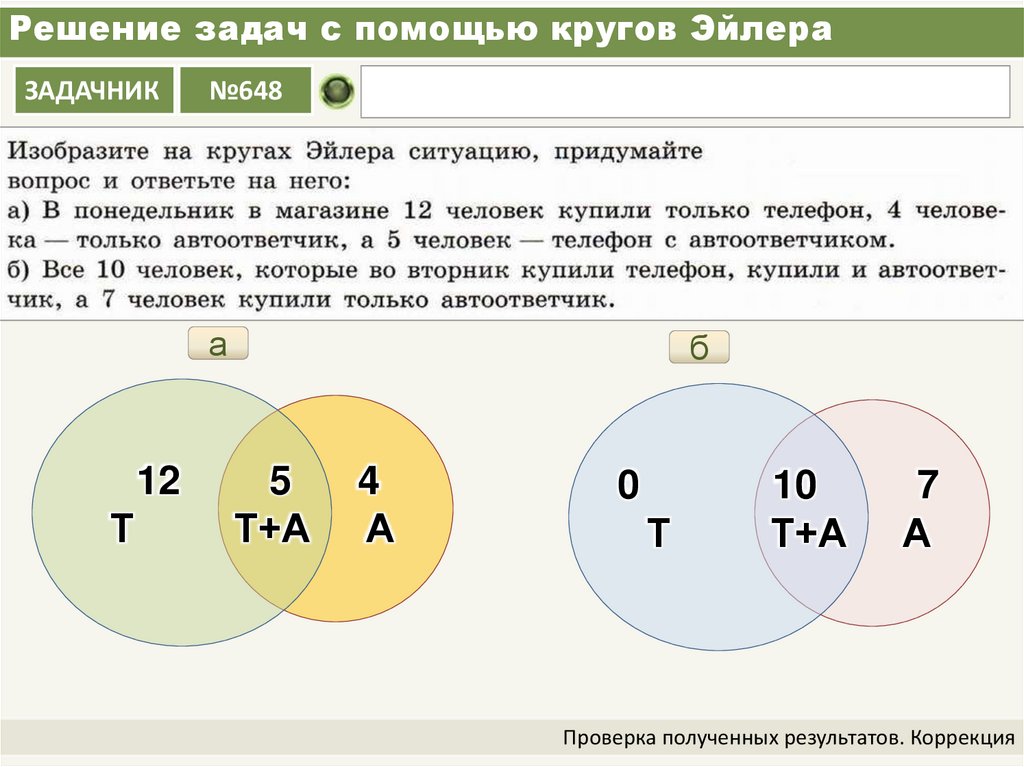 A \ B x x A x B
A \ B x x A x B Если А=В, то A\B = ø
A
A
A
В
А \ В
А \ В
А \ В= А
B
А
В
3. Разность A \ B = х / х А и х В
множества
пересекаются
А
множества не
пересекаются
одно множество является
подмножеством другого
множества A B
А
В
А\В
А
В
В
А \ В=А
А\В
Разбиение множества
• Разбиением множества А называется
семейство Аi , i I непустых и различных
подмножеств А, таких, что объединение Аi
равно А и Аi∩Aj=ø.
Множества Аi называются классами
разбиения.
Разбиением А={1, 2, 3, 4} является множество
B={{1}, {2, 3}, {4}} или С={{1}, {2, 3, 4}}
Универсальное множество
• Если все рассматриваемые в ходе какого –
либо рассуждения множества являются
подмножествами некоторого множества U,
то множество называется универсальным
множеством (универсум).
Например множество действительных чисел
для арифметики является универсумом.
Мощность множества
• Число элементов конечного множества А
называется мощностью множества и обозначается
|А|.
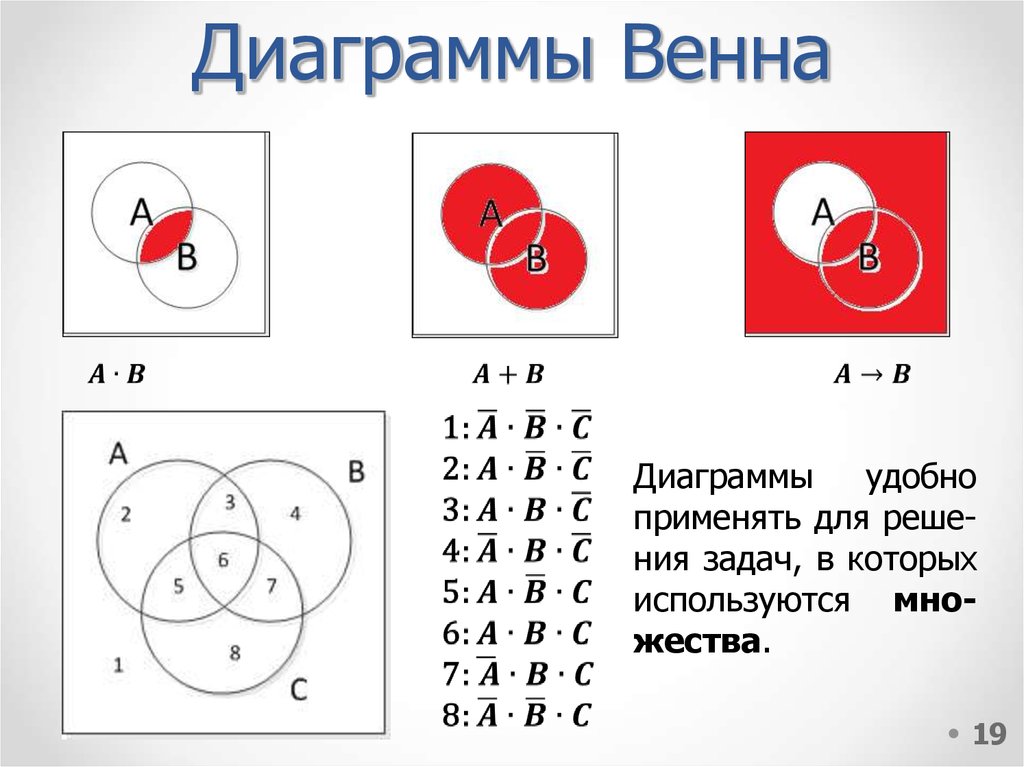
• Если между элементами двух различных множеств
А и В можно установить взаимно однозначное
называются эквивалентными или равномощными.
Записывается А≈В.
Например множество натуральных чисел и четных
чисел равномощные
• Множество называется счетным,
элементы которого можно поставить во
взаимно-однозначное соответствие со
всеми числами натурального ряда.
Пример Множество целых чисел,
множество нечетных чисел.
О множествах, эквивалентных множеству
всех действительных чисел,
принадлежащих интервалу [0,1],
говорят, что они имеют мощность
континуума. (continuumнепрерывное).
Леонард Эйлер, крупнейший математик
XVIII века, родился в Швейцарии. Эйлер
принадлежит к числу гениев, чьё творчество
стало достоянием всего человечества. До сих
пор во всех странах изучают тригонометрию
и логарифмы в том виде, какой придал им
Эйлер.
Он оставил важнейшие труды по самым
различным отраслям математики, механики,
физики, астрономии и по ряду прикладных
наук.
Трудно
даже
перечислить
все
отрасли, в которых
трудился
великий
учёный.
Леонард Эйлер написал более 850 научных работ. В
одной из них и появились круги. А впервые он их
использовал в письмах к немецкой принцессе. Эйлер
писал тогда, что «круги очень подходят для того, чтобы
облегчить наши размышления».
Позднее
аналогичный
прием
использовал ученый Джон Венн —
британский логик и философ; основные
труды в области логики классов; и этот
приём назвали «диаграммы Венна»,
который используется во многих областях:
теория множеств, теория вероятностей,
логика, статистика, компьютерные науки.
При решении целого ряда задач Леонард Эйлер
использовал идею изображения множеств с помощью кругов,
и они получили название «круги Эйлера».
Этот метод даёт более наглядное представление о
отношений в логических задачах.
Множество всех действительных чисел
Эйлер изобразил с помощью этих кругов:
N-множество натуральных чисел,
Z – множество целых чисел,
Q – множество рациональных чисел,
R – множество вех действительных чисел.

R
Q
5/6
-0,25
Z
-36
0
-7
N
5
1
9
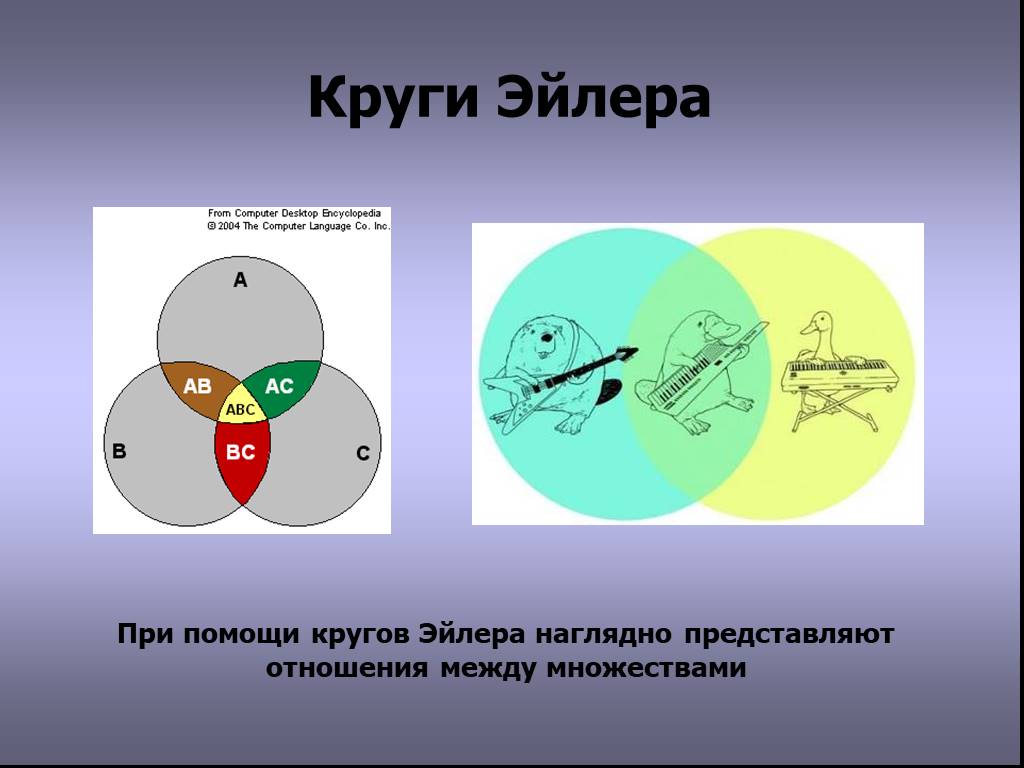
Круги ЭЙЛЕРА —
геометрические схемы, с
помощью которых можно
изобразить отношения между
подмножествами, для
наглядного представления.
Наряду с кругами в подобных
задачах применяют
прямоугольники и другие фигуры.
А∪В-?
Натуральные числа
Простые
числа
2
А
Четные
числа
В
А∩В-?
D
C
естественные
социальные
технические
гуманитарные
философия
Примеры кругов Эйлера-Венна
Игрушка
Кукла
Заводная
игрушка
Заводной
автомобиль
Пистолет
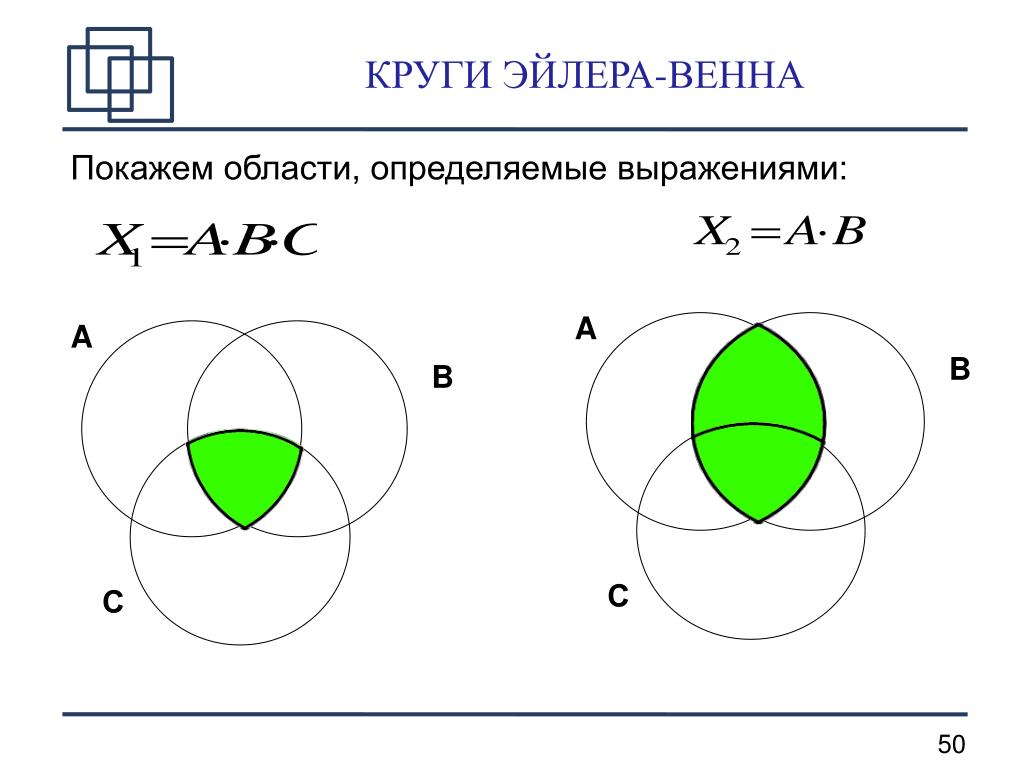
Даны множества A={1; 3; 6; 8}, В={2; 4; 6; 8}.
Найти объединение, пересечение и разность
множеств А и В: A∪B, A∩B, A∖B, B∖A — ?
Очевидно, что объединение двух данных
множеств A∪B={1; 2; 3; 4; 6; 8}, их пересечение
A∩B={6; 8}, а разности A∖B={1; 3} и В∖А={2; 4}
А
1
3
6
8
В
2
4
Так эти
множества
можно
представить на
кругах.
В магазин «Мир музыки» пришло 35 покупателей.
Из них 20 человек купили новый диск певицы
Максим, 11 – диск Земфиры, 10 человек не купили ни
одного диска. Сколько человек купили диски и
Максим, и Земфиры?
Изобразим эти множества
на кругах Эйлера.
11
20
диски
Максим
35
диски
Земфиры
Теперь посчитаем: Всего внутри большого круга 35
По условию задачи 20 покупателей купили новый диск
певицы Максим, следовательно, 25 – 20 = 5 покупателей
купили только диск Земфиры. А в задаче сказано, что 11
покупателей купили диск Земфиры, значит 11 – 5 = 6
покупателей купили диски и Максим, и Земфиры:
не купили
диски
6
диски
Максим
10
5
диски
Земфиры
Ответ: 6 покупателей купили диски и Максим, и Земфиры
Использованные Интернет-ресурсы:
1. http://mat.1september.ru Газета «Математика» Издательского дома
«Первое сентября»
2.
 http://www.math.ru Math.ru: Математика и образование
http://www.math.ru Math.ru: Математика и образование3. http://festival.1september.ru/articles/635933/
4. https://znanija.com/task/3231925
5. https://yandex.ru/images/search?textstype=image&lr=43&noreask=1&p
arent-reqid=1483952074037160-1110803268472871449321762-sas13418&source=wiz
English Русский Правила
виды, примеры задач и решение, для дошкольников, для школьников
Пожаловаться
Содержание:
Виды кругов Эйлера
Где применяются круги Эйлера
Для дошкольников
Пример
Для школьников
Применение на уроках математики
Применение на уроках русского языка
Видео
Круги Эйлера – это простая диаграмма, с помощью которой можно показать отношения между общим и его частями. Она также помогает увидеть логические цепочки между явлениями и понятиями.
Метод Эйлера применяют для упрощения решения задач во многих областях: от математики до менеджмента. Он помогает находить ответы с помощью наглядных логических цепочек.
Он помогает находить ответы с помощью наглядных логических цепочек.
Леонард Эйлер (1707-1783) – швейцарский математик, физик, механик и философ. Долгое время (более 30 лет) проработал в Петербургской Академии Наук. Внес большой вклад в становление российской науки.
Расскажем, что собой представляют круги Эйлера и как их применяют в разных сферах.
Виды кругов Эйлера
Круги Эйлера помогают увидеть логические цепочки между явлениями и понятиями и используются во множестве сфер.Эйлер выделил шесть типов соотношений между понятиями, которые выразил в соответствующих схемах.
- Равнозначные. Два одинаковых круга. Например, А.С.Пушкин = автор повести «Капитанская дочка».
- Пересекающиеся. Часть одного круга частично совпадает с частью другого (человек может быть одновременно и футболистом, и поэтом).
- Подчиненные.
 Один маленький круг внутри большого (корова относится к классу млекопитающих).
Один маленький круг внутри большого (корова относится к классу млекопитающих). - Соподчиненные. Несколько одинаковых по размеру маленьких кругов внутри большого (яблоко, груша, персик – фрукты).
- Противоречащие. Разделенный пополам круг, каждая часть которого не имеет ничего общего с другой. Например, две конкурирующие между собой компании, производящие автомобили.
- Противоположные. Две части круга, между которыми есть свободное пространство. В отличие от предыдущей группы, между ними нет конфликта (холодное и горячее).
В сложной логической задаче иногда может встречаться сразу несколько видов таких схем.
Где применяются круги Эйлера
Круги Эйлера широко используются во многих упражнениях на развитие мышления и логики. Сам ученый применял этот метод для решения сложных математических задач, поскольку схематичное изображение простых фигур позволяет упрощать рассуждения и наглядно демонстрировать возможные пути решения.
Сегодня круги Эйлера широко используют в своей работе:
- математики;
- экономисты;
- маркетологи;
- менеджеры и др.
Основное преимущество данного метода – его универсальность. Он подойдет и для развития мышления у детей, и для решения сложных математических (и не только!) задач.
Для дошкольников
Соподчиненные круги Эйлера отлично подойдут для обучения в детском саду, так как с их помощью можно наглядно объяснить расположение множеств относительно друг другаКруги Эйлера применяют для обучения детей уже в старшей группе детского сада. С их помощью легко наглядно объяснить малышам все варианты расположения множеств относительно друг друга.
Пример
Воспитатель просит детей разложить карточки по двум категориям:
- предметы красного цвета;
- транспорт.
На пересечении этих двух «кругов» окажется красная машинка, так как она подходит под оба требования.
Результат: в игровой форме дошкольники учатся находить изображения, обладающие одним или несколькими отличительными признаками.
Подобные занятия способствуют развитию у детей нестандартного мышления и помогают концентрировать внимание. С их помощью малыши учатся логически рассуждать, сравнивать и делать выводы.
Для школьников
Задачи с использованием кругов Эйлера встречаются и в школьной программе. Некоторые из них включены в ОГЭ и ЕГЭ.
Применение на уроках математики
Задача. В школьной и городской библиотеке зарегистрировано 35 учеников. Из них 25 ребят постоянно посещают школьную, а 20 – городскую библиотеку. Требуется найти количество тех детей, которые являются читателями:
- обеих библиотек;
- только городской или только школьной библиотеки.
Решение
Круги Эйлера используют во время уроков математики. Фото: https://4brain.ru/
Фото: https://4brain.ru/1. Определим, сколько школьников посещает обе библиотеки:
(25 + 20) – 35 = 10 (человек).
2. Из них только в городскую библиотеку ходят:
35 – 25 = 10 (человек).
3. А только в школьную библиотеку предпочитают ходить:
35 – 20 = 15 (человек).
Применение на уроках русского языка
Круги Эйлера используют при разных видах разбора предложения, чтобы найти общие и схожие черты в их строении.
Например, при морфологическом разборе ученики сравнивают слова одной и той же части речи (или разных частей), которые имеют общие морфологические признаки. В этом случае графическая схема быстрее помогает детям научиться различать похожие лингвистические обороты.
Круги Эйлера способствуют развитию и тренировке зрительной памяти. С их помощью ученики лучше запоминают, а также усваивают прочитанный и увиденный материал.
Круги Эйлера широко применяются во многих сферах, помогают справляться с нестандартными задачами. Например, определиться с будущей профессией или планами на выходные. Попробуйте и вы применить этот метод к решению своих повседневных вопросов!
Видео
Список литературы
- Круги Эйлера, сайт.
- Использование кругов Эйлера на занятиях по развитию логического мышления у дошкольников, сайт.
- Круги Эйлера: почему один раз увидеть лучше, чем сто раз услышать, сайт.
- Использование Кругов Эйлера в русском языке, сайт
Фото: © Depositphotos
РубрикаОбучение
Новая эра: ученые создали искусственный интеллект, который заменяет учителей при проверке ЕГЭ
Игры на английском языке для детей: 12 идей, как изучать его весело
Кто сказал, что ангелов не существует? Просто на Земле их называют «мама»
Комментарии
Узнавай и участвуй
Клубы на Бэби.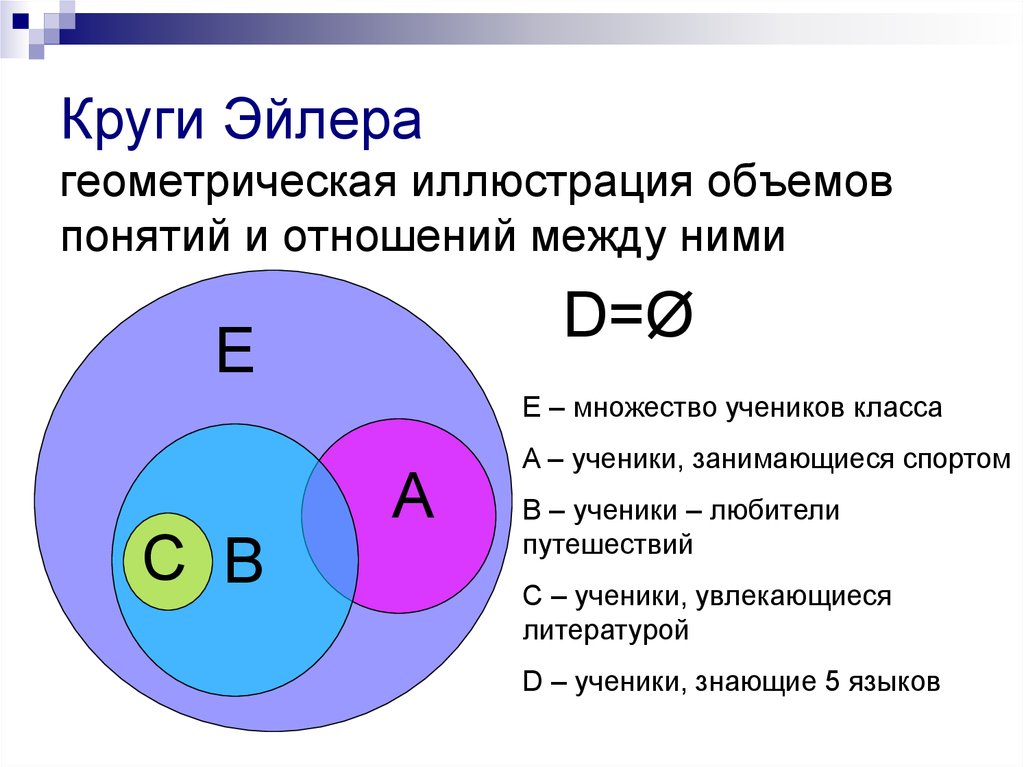 ру — это кладезь полезной информации
ру — это кладезь полезной информации
Биострахование – ценнейший подарок к рождению ребенкаCovid-19 этой осеньюКак совместить воспитание ребенка и работуЧто делать, если ребенок хочет стать стилистом?Астма у детей — на что обратить вниманиеОбучение в Нетологии со скидкой до 75% для мамШкольные экскурсии — учимся в путешествияхОцените состояние иммунитета вашего ребенкаОнлайн приёмная психолога — для мам часто болеющих детейПочему ребенок часто болеет?30 шагов к сильному иммунитету!Счастье — когда все здоровы!Инфекционист о прививкахИгра: соберите аптечку для ребенкаПервая помощь при ОРВИПервая аптечка для малыша
Галерея диаграмм Эйлера и Венна
Галерея диаграмм Эйлера и Веннаlibrary(eulerr)
Эта виньетка служит галереей для диаграмм Эйлера и демонстрацией различных доступных вариантов настройки.
Равномерные пересечения
uniform_intersections <- euler(c("A" = 10, "B" = 10, "C" = 10,
"А&В" = 4, "А&В" = 4, "В&В" = 4,
"А&В&С" = 2))
сюжет (uniform_intersections) Непересекающиеся множества
disjoint_sets <- euler(c(A = 1, B = 1, C = 1))
сюжет (непересекающиеся_множества,
labels = c("Том", "Грег", "Альберта"),
ребра = список(lty = 1:3)) Множество, содержащееся в пересечении двух множеств
полностью_содержащее <- euler(c("A" = 15, "B" = 15, "C" = 0 ,
«А и В» = 3, «А и С» = 0, «В и С» = 0,
"А&В&С" = 3))
сюжет (полностью_содержащий,
labels = list(col = c("белый", "черный", "черный")),
края = список (столбец = «белый», lex = 2),
fills = c("черный", "голубой", "оранжевый")) Два множества пересекаются внутри третьего
intersecting_inside <- euler(c("A" = 15, "B" = 0, "C" = 0,
«А и В» = 3, «А и С» = 3, «В и С» = 0,
"А&В&С" = 2))
сюжет (intersecting_inside,
заполняет = список (заполняет = c ("лавандаblush3",
"голубой2",
"светлый лосось",
"",
"",
"",
"слива2")),
легенда = список (сторона = "право")) Сложный набор (для кружков!)
one_contained <- euler(c("A" = 7, B = 6, C = 0,
«А&В» = 0, «А&В» = 1, «В&В» = 1,
"А&В&С" = 2),
форма = "эллипс")
сюжет (one_contained,
количество = список(тип = "процент")) Матрешка
Наборы пересекаются внутри других наборов.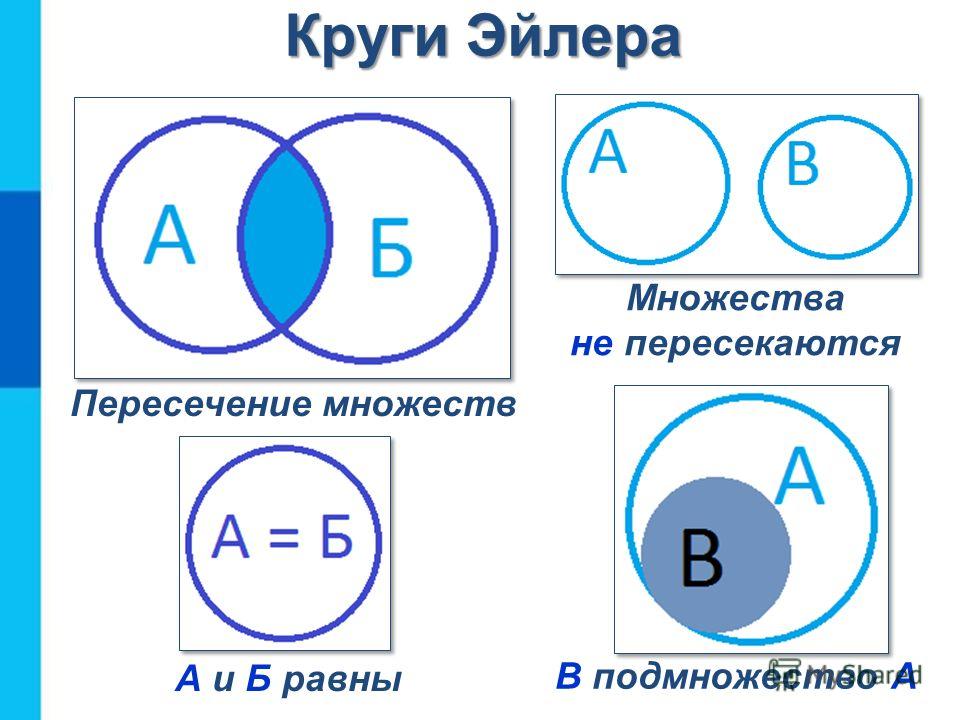 Этот пример также иллюстрирует, как алгоритм автоматической корректировки этикетки (позаимствованный из отличного ggrepel пакет) работает.
Этот пример также иллюстрирует, как алгоритм автоматической корректировки этикетки (позаимствованный из отличного ggrepel пакет) работает.
russian_doll <- euler(c("A" = 15, "B" = 0, C = 0,
«А и В» = 10, «А и С» = 0, «В и С» = 0,
"А&В&С" = 5))
сюжет(русская_кукла,
метки = с(
"Длинная и сложная\nэтикетка, которую, скорее всего, придется отклонить",
"Еще одна очень\nдлинная этикетка, которая\nвероятно будет\nнарушать\nдругие этикетки",
"Зрелище перед нами\nбыло поистине величественным")
) Связь набора Уилкинсона
Это установленное отношение взято из Wilkinson et al. Лучше всего работает с эллипсами.
Уилкинсон <- euler(c(A = 4, B = 6, C = 3, D = 2, E = 7, F = 3,
"A&B" = 2, "A&F" = 2, "B&C" = 2, "B&D" = 1,
"Б&Ф" = 2, "К&Д" = 1, "Д&Э" = 1, "Э&Ф" = 1,
"A&B&F" = 1, "B&C&D" = 1),
форма = "эллипс")
сюжет (Уилкинсон,
метки = список (семейство шрифтов = "с засечками"),
края = список (lty = 3),
количество = список (тип = "процент",
шрифт = 3)) Набор генов
гены <- euler(c("SE" = 13, "Лечить" = 28, "Анти-КПК" = 101, "DAS28" = 91,
«SE&Treat» = 1, «SE&DAS28» = 14, «Treat&Anti-CCP» = 6,
"SE&Анти-КПК&DAS28" = 1))
сюжет (гены,
количество = список (тип = c ("проценты", "числа"))) Три множества, пересекающиеся внутри четвертого
three_inside_fourth <- euler(c ("A" = 30,
"A&B" = 3, "A&C" = 3, "A&D" = 3,
"A&B&C" = 2, "A&B&D" = 2, "A&C&D" = 2,
"А&В&С&D" = 1))
участок (три_внутри_четвертого) Комбинация eulerAPE
Комбинация из статьи eulerAPE.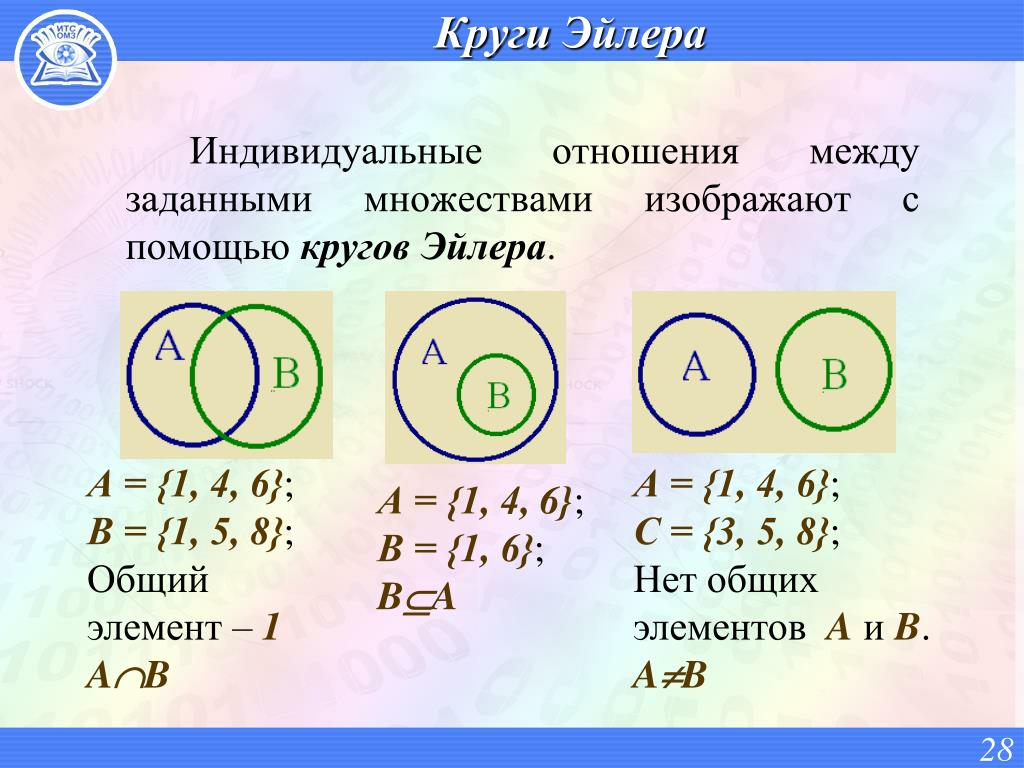
eulerape <- euler(c("a" = 3491, "b" = 3409, "c" = 3503,
"a&b" = 120, "a&c" = 114, "b&c" = 132,
"a&b&c" = 126),
форма = "эллипс",
управление = список (экстраопт = ЛОЖЬ))
plot(eulerape) Четыре равномерных взаимодействия
uniform <- euler(c("A" = 10, "B" = 10, "C" = 10, "D" = 10,
"A&B" = 3, "A&C" = 3, "A&D" = 0, "B&C" = 0, "B&D" = 3, "C&D" = 3,
"A&B&C" = 1, "A&B&D" = 1, "A&C&D" = 1, "B&C&D" = 1,
"А&В&С&D" = 1))
сюжет (униформа, метки = список (метки = c ("Фродо", "Сэм", "Веселый", "Пиппин")),
шрифт = 1:4,
цвет = 1:4,
cex = seq(1, 1.5, length.out = 4))) Две окружности, полностью пересекающиеся
two_overlapping <- euler(c("A" = 0, "B" = 0, "A&B" = 10))
сюжет (два_перекрытия) Диаграммы Эйлера и Венна: они не только для развлечения Диаграммы Венна и Эйлера (произносится как «майлер») невероятно популярны в Интернете как забавные диаграммы.
 Они предлагают простой способ изображения понятий теории множеств.
Они предлагают простой способ изображения понятий теории множеств.Итак, в чем разница между ними? Почему они смешные? Полезны ли они для реальных данных?
Оба типа диаграмм используются для отображения понятий из теории множеств:
Union – Комбинация двух множеств. На диаграммах Венна и Эйлера.
Перекресток – Входит в оба набора. На диаграммах Венна и Эйлера.
Разность – Все, кроме пересечения двух множеств. На диаграммах Венна и Эйлера.
Относительное дополнение – В одном наборе, а не в другом. На диаграммах Венна и Эйлера.
Абсолютное дополнение – Все, чего нет в другом наборе. Только на диаграммах Эйлера.
Подмножество — Набор, полностью содержащийся в другом наборе. Только на диаграммах Эйлера.
Непересекающиеся – Два множества, не имеющие общих элементов. Только на диаграммах Эйлера.
Только на диаграммах Эйлера.
Все диаграммы Венна являются диаграммами Эйлера, но не все диаграммы Эйлера являются диаграммами Венна. Диаграммы Эйлера имеют только те комбинации пересечений, которые действительно существуют в реальном мире. Диаграммы Венна представляют все гипотетически возможные логические отношения между категориями.
Диаграммы Венна по определению должны отображать все возможные комбинации пересечений, что создает некоторые интересные проблемы с компоновкой.
Когда есть три круга, показывается каждое пересечение, но как только вы доберетесь до четырех категорий, круги не работают.
Эллипсы могут работать до пяти категорий, но помимо пяти странные формы должны использоваться для вплетения и выхода из всех комбинаций пересечений.
Пять уже довольно сложно читать, но как только эти странные формы вступают в игру, чтение диаграмм становится почти невозможным, а текстовые описания взаимосвязей часто легче понять.
Это подводит нас к тому, почему так много забавных диаграмм.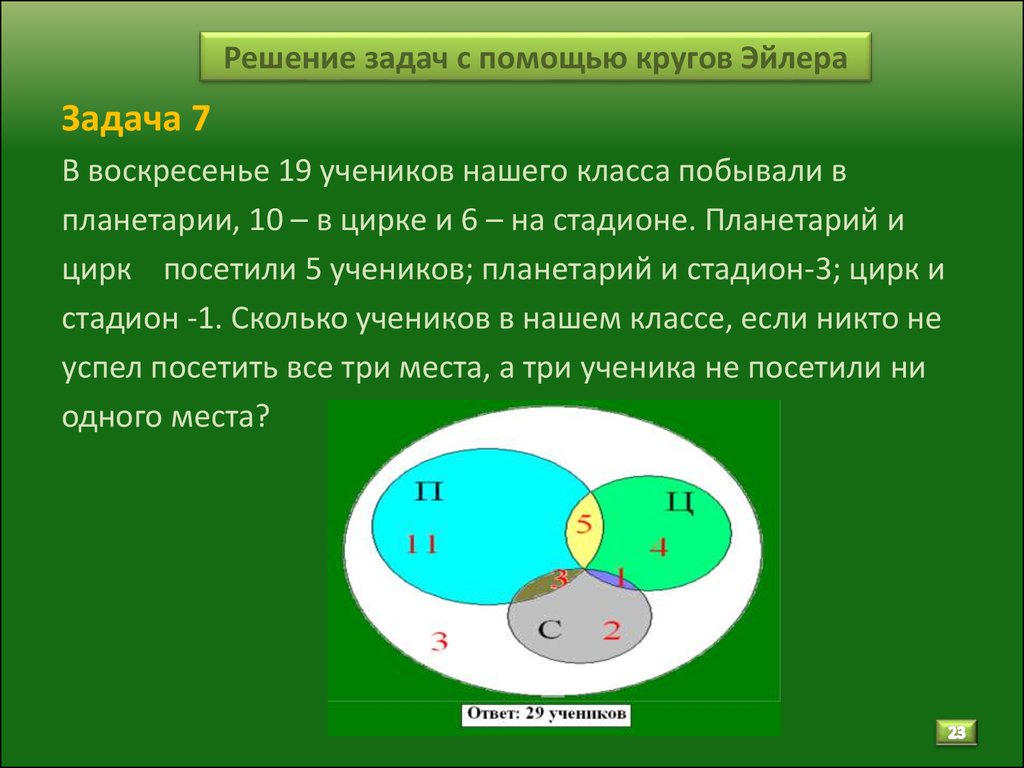
Диаграмма Венна для позвоночных и беспозвоночных, которую мы показали вам ранее, предполагает, что некоторые животные могут одновременно иметь позвоночник и не иметь позвоночника.
Хотя это может быть и не смешно, любой, кто посещал уроки естествознания в шестом классе, скажет вам, что это довольно глупо. С лучшей темой указание на отношения, которые не существуют, может быть довольно забавным.
Некоторые диаграммы достигают юмора, помещая что-то в категорию, которой оно не принадлежит, или в категорию, в которую вы обычно не ожидаете его попадания. Некоторая творческая маркировка (как на диаграмме Эйлера ниже) тоже всегда помогает.
Мы знаем, что диаграммы Эйлера могут быть забавными, но могут ли они быть полезными?
Некоторые диаграммы содержат количественную информацию, используя площадь каждой части диаграммы.
Одним из хороших примеров этого является Глобальная карта социальных сетей 2011 от Global Web Index. Сами по себе диаграммы Эйлера, подобные этой, дают вам довольно хорошее общее представление о задействованных значениях.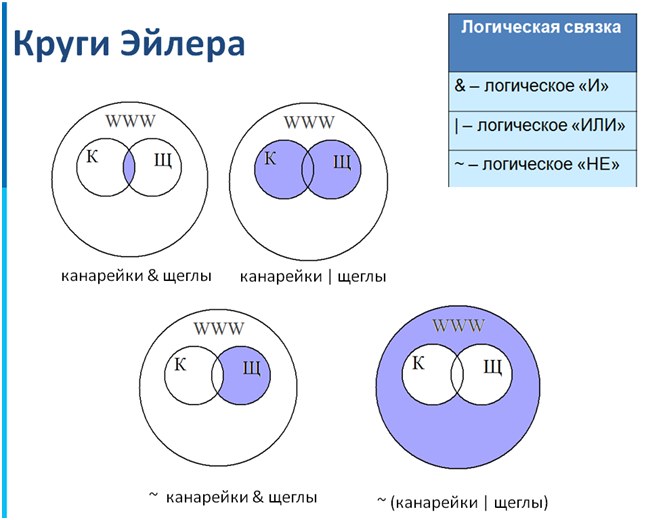

 Один маленький круг внутри большого (корова относится к классу млекопитающих).
Один маленький круг внутри большого (корова относится к классу млекопитающих).