Площадь куба: онлайн калькулятор, формулы, примеры решений
Фигура {$ main.figures[data.figure] $}
Рассчитываем {$ main.types[data.type] $}
Введите 1 величину
Сторона A
Диагональ фигуры (D)
Диагональ грани (d)
Введите 1 величину
Радиус (r)
Диаметр (d)
Введите 3 величины
Сторона A
Сторона B
Сторона C
Диагональ фигуры (d)
Введите 2 величины (радиус и диаметр основания приняты за одну величину)
Высота (h)
Образующая конуса (s)
Радиус (r)
Диаметр (d)
Введите H и 1 величину
Высота (h)
Радиус (r)
Диаметр (d)
Введите 3 величины
Количество сторон (n)
Высота (h)
Сторона a
Количество сторон (n)
Введите 2 величины
Сторона основания (a)
Высота (h)
Длина бокового ребра (s)
Угол (α)
Между стороной и плоскостью основания
{$ main.
Результат расчёта
- Объём: {$ result.v|number:4 $}
- Площать: {$ result.s|number:4 $}
- Площать: {$ result.s $}
Куб — это правильный шестигранник, каждая грань которого является квадратом. Кубические фигуры часто встречаются в реальной жизни, поэтому на работе или в быту вам может понадобиться вычислить объем или площадь поверхности объекта, который имеет форму кубика.
Геометрия куба
Куб или правильный гексаэдр — это частный случай шестигранной прямоугольной призмы, все грани которой представляют собой квадраты. Кроме того, куб — это и частный случай прямоугольного параллелепипеда, у которого длина, ширина и высота абсолютно равны. Куб — уникальная фигура, существующая в разных многомерных пространствах. К примеру, нульмерный куб — это точка, одномерный — отрезок, двухмерный — квадрат, а четырехмерный — тессеракт. В нашем родном трехмерном пространстве куб встречается повсеместно, к примеру, в форме детских кубиков, рафинированного сахара, картонных коробок, газетных киосков или предметов интерьера.
К примеру, нульмерный куб — это точка, одномерный — отрезок, двухмерный — квадрат, а четырехмерный — тессеракт. В нашем родном трехмерном пространстве куб встречается повсеместно, к примеру, в форме детских кубиков, рафинированного сахара, картонных коробок, газетных киосков или предметов интерьера.
Кубы широко используются в программировании, аналитике, научных изысканиях и прочих высоких материях. Идеальная форма геометрической фигуры позволяет при помощи разномерных кубов выражать массивы данных, измерять объемы или визуализировать данные. Кубические фигуры часто встречаются в реальности и абстрактных задачах, поэтому вам может понадобиться рассчитать объем или площадь поверхности кубика для решения самых разных проблем.
Площадь поверхности куба
Площадь кубической фигуры — это сумма площадей всех граней. Каждая грань куба — это квадрат. Площадь квадрата, то есть одной грани, определяется по простой формуле как:
Sg = a2
Куб — это гексаэдр, то есть шестигранник.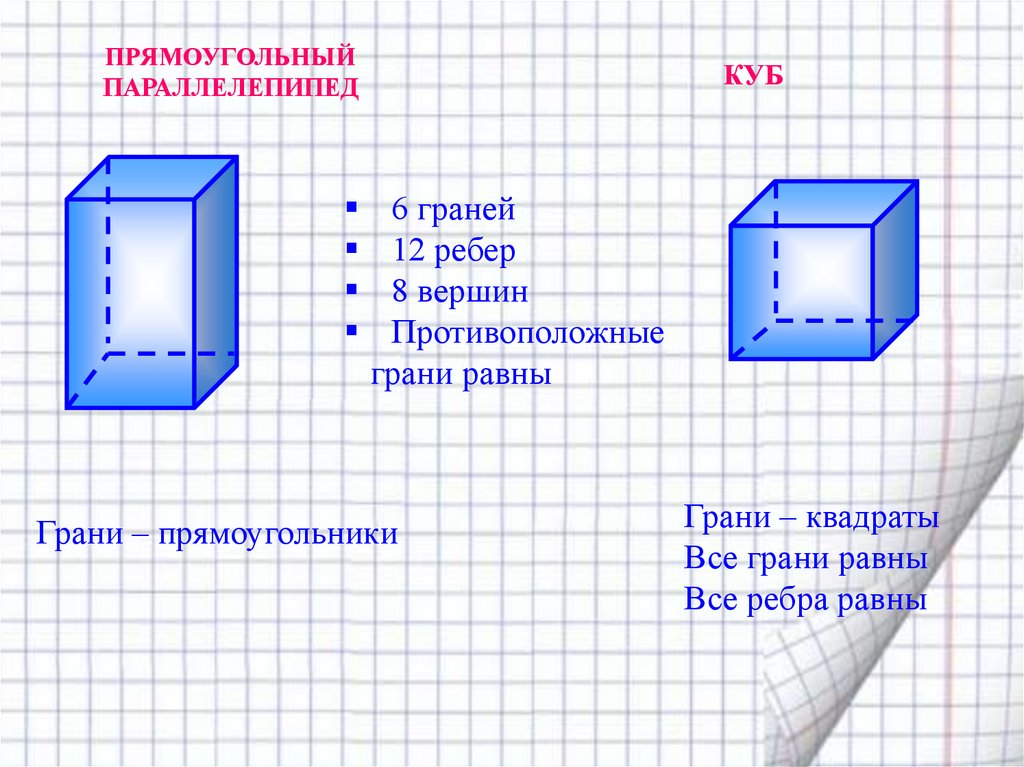 Таким образом, площадь поверхности кубической фигуры представляет собой сумму шести квадратов:
Таким образом, площадь поверхности кубической фигуры представляет собой сумму шести квадратов:
S = 6 Sg = 6 a2
Определить площадь куба можно не только при помощи длины его ребра: для расчета площади поверхности вы можете использовать диагональ самого куба или диагональ одной грани.
Диагональ куба — это отрезок, который находится внутри пространства куба и соединяет две противоположные вершины. Проведенная диагональ разделяет куб на два прямоугольных треугольника. Согласно теореме Пифагора квадрат ребра куба равен одной трети от квадрата диагонали D, следовательно, формула площади полной поверхности приобретает вид:
S = 2 D2
Площадь поверхности куба легко определить и с помощью диагонали одной грани. Площадь квадрата через диагональ равна:
S = 0,5 d2.
Так как у куба 6 граней, общая площадь поверхности составит сумму шести граней куба, то есть:
S = 6 × 0,5 d2 = 3 d2
Таким образом, чтобы определить площадь поверхности кубической фигуры вам достаточно ввести в форму-онлайн калькулятора всего один параметр на выбор:
- длину ребра;
- диагональ куба;
- диагональ квадрата.

Рассмотрим примеры использования данных формул в реальной жизни.
Примеры из жизни
Ящик
Представьте, что вы хотите соорудить из листов ДСП ящик для хранения инструментов в форме куба. Вы знаете, что он отлично впишется в пространство на чердаке высотой 50 см. Сколько же квадратных метров ДСП вам понадобится для создания такого контейнера? Зная высоту, равную a = 0,5 м вы можете легко подсчитать площадь общей поверхности куба, введя данный параметр в онлайн-калькулятор. Вы получите ответ в виде:
S = 1,5
Таким образом, вам понадобится всего 1,5 квадратных метра ДСП для создания ящика для инструментов. Зная всего один параметр, вы без труда порежете листы на грани куба и соорудите нужную конструкцию.
Контейнер
Допустим, вы хотите обработать антикоррозионным покрытием грузовые контейнеры, которые имеют кубическую форму. Для правильного расчета параметров покрытия вам необходимо знать площадь обрабатываемой поверхности. Вы знаете, что диагональ грани стандартного контейнера равняется d = 3 м. Зная этот параметр, вы легко рассчитаете площадь кубической поверхности, которая равна
Зная этот параметр, вы легко рассчитаете площадь кубической поверхности, которая равна
S = 18
Зная общую площадь покрытия, вы без проблем определите необходимое количество антикоррозионной жидкости.
Заключение
Куб встречается в реальной жизни не так часто, как призматические фигуры или параллелепипеды, однако в любом случае вам может понадобиться удобный калькулятор, при помощи которого вы определите площадь полной поверхности кубического объекта. Наш сервис поможет решить вам бытовые, производственные или школьные задачи мгновенно и без ошибок.
Закон квадрата-куба | это… Что такое Закон квадрата-куба?
Закон квадрата — куба представляет собой принцип, применяемый в технике и биомеханике, и базируется на математическом пересчете размеров. Он был впервые продемонстрирован в 1638 г. Галилео Галилеем в «Discorsi e Dimostrazioni Matematiche, intorno a due nuove scienze («Беседы и математические доказательства двух новых наук»), 1638»;. Он гласит
Когда объект подвергается пропорциональному увеличению размеров, его новый объем будет пропорционален кубу множителя, а новая площадь его поверхности пропорциональна квадрату множителя.
где v1 — объем исходного объекта, v2 — новый объем, — линейный размер исходного объекта, а — новый линейный размер. Заметьте, что не имеет значения, какой линейный размер используется.
где A1 — площадь поверхности исходного объекта, а A2 — новая площадь поверхности.
Например, куб с длиной стороны 1 метр имеет плошадь поверхности 6 м² и объем 1 м³. Если длину стороны удвоить, площадь его поверхности увеличится до 24 м², а его объем увеличится до 8 м³. Этот принцип применим ко всем телам.
Содержание
|
Применения
Техника
Если физический объект увеличить в размерах при сохранении неизменной плотности материала, из которого он изготовлен, его масса увеличится в третьей степени, в то время как площадь его поверхности — только в квадрате масштабного множителя. Это должно означать, что в том случае, если увеличенному в размерах объекту сообщить то же ускорение, что и оригиналу, на поверхность увеличившегося объекта будет действовать большее давление
Это должно означать, что в том случае, если увеличенному в размерах объекту сообщить то же ускорение, что и оригиналу, на поверхность увеличившегося объекта будет действовать большее давление
Давайте рассмотрим простой пример — тело массой = M имеет ускорение = a и площадь поверхности = A , на которую действует ускоряющая сила.
Сила, вызванная ускорением: F = M*a, а давление на поверхность T = F/A = M*a/A
Теперь рассмотрим объект, размеры которого умножены на коэффициент = x так, чтобы его новая масса M’ = x3*M, а поверхность, на которую действует сила, имеет новую площадь, A’ = x2*A.
Новая сила, вызванная ускорением F’ = x³*M*a и
Результирующее давление на поверхность
T' = F'/A'
= x3*M*a/(x2*A)
= x*(M*a/A)
= x*T
Таким образом, при простом увеличении размеров объекта с сохранением того же самого материала конструкции (плотности), и при же самом ускорении, давление, производимое им на повехность, увеличится во столько же раз. Это показывает, что способность сопротивляться напряжению у объекта снизится и он станет более склонен к разрушению в процессе ускорения.
Это показывает, что способность сопротивляться напряжению у объекта снизится и он станет более склонен к разрушению в процессе ускорения.
Это и есть объяснение тому, почему большие транспортные средства плохо выдерживают испытания на разрушения при столкновениях и почему есть пределы высоты строительства высотных зданий. Аналогично, чем больше размер объекта, тем меньше другие объекты окажут сопротивление движению, вызывая его замедление
Биомеханика
Если размеры животного значительно увеличить, его мускульная сила серьезно уменьшится, так как поперечное сечение его мускулов увеличится пропорционально площади коэффициента масштабирования, в то время как его масса увеличится пропорционально кубу коэффициента масштабирования. В результате этого сердечно-сосудистые функции сильно ограничатся. Для летающих животных, если их увеличить в размерах, их нагрузка на крылья должна возрасти, и поэтому им, чтобы совершать такой же взлет, придется лететь быстрее,. Это будет нелегко ввиду того, что сила мускулов станет меньше. Это также объясняет, почему шмель может иметь большой размер тела относительно размаха его крыльев, что невозможно для большего летающего животного. Для животных малых размеров сопротивление воздуха на единицу массы также выше, что объясняет, отчего маленькое насекомое, такое, как муравей не погибнет, падая с любой высоты, а экипаж танка, также как и слон, не сможет выжить при падении с высоты в одну милю
Это также объясняет, почему шмель может иметь большой размер тела относительно размаха его крыльев, что невозможно для большего летающего животного. Для животных малых размеров сопротивление воздуха на единицу массы также выше, что объясняет, отчего маленькое насекомое, такое, как муравей не погибнет, падая с любой высоты, а экипаж танка, также как и слон, не сможет выжить при падении с высоты в одну милю
По этой причине гигантские насекомые, пауки и другие животные, показываемые в фильмах ужасов — нереальны, поскольку такие крутые размеры вызвали бы их разрушение. Исключением являются гигантские водные животные, поскольку вода способна поддерживать такие огромные существа.
Данная статья статья представляет собой несколько доработанный перевод статьи из английской Википедии
Square-Cube Law
См. также
Биомеханика
Allometric law (англ.)
On Being the Right Size (англ.)
Ссылки
Wayne Throop. «Sauropods, Elephants, Weightlifters: Miscellaneous Issues» (англ.
«World Builders: The Limits to Animal Size — Size to Volume Ratio». (англ.)
Michael C. LaBarbera. «The Biology of B-Movie Monsters»(англ.)
Калькулятор куба x³
Базовый калькулятор
Поделись этим калькулятором и страницей
Калькулятор Использование
Найдите значение числа n в кубе. Введите положительные или отрицательные целые числа или десятичные числа или научную нотацию E.
Кубирование отрицательных чисел
При кубировании отрицательных чисел ответ всегда будет отрицательным. В этом калькуляторе вам не нужно использовать круглые скобки при вводе, потому что вы все равно получите правильный ответ, хотя вы должны знать, что ниже показано, как ваши вводы на самом деле интерпретируются калькулятором.
- -2³ означает -(2 × 2 × 2) = -8
- -(2)³ означает -(2 × 2 × 2) = -8
- (-2)³ означает (-2 × -2 × -2) = -8
Когда выражение степени записывается с положительным значением, таким как 4³, большинству легко понять, что это означает 4 × 4 × 4 = 64
отрицательное значение без круглых скобок означает неоднозначность. Для разных людей это имеет разное значение.
Для разных людей это имеет разное значение.
Различные возможные интерпретации -4³:
1. минус (4 в кубе) или -(4)³ = -(4 × 4 × 4) = -64
2. (минус 4) в кубе или (-4 )³ = (-4 × -4 × -4) = -64
Используйте круглые скобки, чтобы четко указать, какое вычисление вы действительно хотите выполнить. Скобки не изменяют ваши результаты, когда показатель степени нечетен, например, 3, но они имеют явное значение, когда показатель степени четен, например, 2. Калькулятор площади для -4²
Куб
Число n в кубе записывается как n³ и n³ = n × n × n. Если n — целое число, то n³ — совершенный куб.
Например, 3 в кубе записывается как 3³ и 3³ = 3 × 3 × 3 = 27. 27 — совершенный куб.
Числа от 0 до 10 в кубе и полученные в результате идеальные кубы
- 0 в кубе равно 0³ = 0 × 0 × 0 = 0
- 1 куб равен 1³ = 1 × 1 × 1 = 1
- 2 в кубе равно 2³ = 2 × 2 × 2 = 8
- 3 в кубе равно 3³ = 3 × 3 × 3 = 27
- 4 в кубе равно 4³ = 4 × 4 × 4 = 64
- 5 в кубе равно 5³ = 5 × 5 × 5 = 125
- 6 в кубе равно 6³ = 6 × 6 × 6 = 216
- 7 в кубе равно 7³ = 7 × 7 × 7 = 343
- 8 в кубе равно 8³ = 8 × 8 × 8 = 512
- 9 в кубе равно 9³ = 9 × 9 × 9 = 729
- 10 в кубе равно 10³ = 10 × 10 × 10 = 1000
Дополнительные показания
Википедия «Куб (алгебра)» по адресу
https://en.
Википедия «Куб» по адресу https://en.wikipedia.org/wiki/Куб
Подписаться на калькуляторSoup:
Решение уравнений с квадратами и кубами — Концепция
Многие формулы для расчета объемов (формулы объема призмы, объема цилиндров, объема конусов и объема пирамид) требуют решение уравнений с квадратными корнями или кубическими корнями. Чтобы решить эти уравнения, мы используем многие из тех же принципов, которые мы изучили при решении уравнений с квадратными корнями в алгебре, таких как выделение неизвестной переменной и упрощение.
квадратный корень кубический корень
В геометрии вы будете решать задачи с квадратными и кубическими корнями. Итак, мы рассмотрим здесь 3 быстрые задачи.
Первое уравнение с одной переменной r и r возводится в квадрат.

Давайте посмотрим еще два. Вот следующий. х в кубе равно 27. Что ж, чтобы отменить кубирование чего-либо, я возьму не квадратный, а кубический корень. Таким образом, кубический корень из x в кубе будет равен x. Я должен проделать ту же операцию с другой стороны, и кубический корень из 27 будет равен 3. Теперь, если мы вернемся к нашей первой задаче, мы заметим кое-что, что я мог бы сказать, что это было положительно или минус 2, умноженный на квадратный корень из 5. Поскольку мы занимаемся геометрией и почти всегда говорим о расстояниях, мы почти всегда будем брать положительный корень. Потому что 2 умножить на квадратный корень из 5, умноженный на 20, и если я возьму отрицательное значение, умноженное само на себя, мы также получим 20. Так что тут может быть два ответа. Однако, если мы вернемся к этому кубическому корню, если я сказал, что х может быть -3, давайте просто кратко взглянем на это. -3 куб. -3 раза -3 равно 9. Итак, у меня будет 9 раз -3, что равно -27. Так что обратите внимание, что с кубическим корнем вы получите только один ответ.
 Отрицательный не будет одним из ваших ответов.
Отрицательный не будет одним из ваших ответов. Последнее, что мы собираемся рассмотреть, это то, что вы будете решать, когда будете говорить об объеме сферы. Чтобы изолировать здесь r, сначала возьмем обратную величину четырех третей. Итак, я собираюсь умножить обе части на три четверти. Значит, три четверти умножить на 823. Я введу это в свой калькулятор. Три четверти умножить на 823 — это 617,25. Итак, что мы сделали, так это выделили число пи, умноженное на r в кубе. Я пока не умею извлекать кубический корень, поэтому я собираюсь разделить обе части на число Пи. Итак, теперь я собираюсь получить еще одну десятичную дробь, я собираюсь разделить ее на число пи и получить 19.6.5 округлим. 196,5 равно r в кубе.
Теперь, когда у нас есть только r в кубе, мы можем взять кубический корень и выделить r. Итак, мы возьмем кубический корень из обеих сторон, и я скажу, что кубический корень из нашего куба равен r, и в моем калькуляторе я напечатаю, если ваш учитель еще не показал вам способ вы вводите это, вы собираетесь ввести 196,5, а затем сказать, чтобы он увеличил его до дроби.


