Учебное пособие по линейной алгебре
Учебное пособие по линейной алгебре
ОглавлениеГлава I. ЛИНЕЙНЫЕ ПРОСТРАНСТВА§ 2. ПРОСТЕЙШИЕ СВОЙСТВА ЛИНЕЙНЫХ ПРОСТРАНСТВ § 3. ЛИНЕЙНАЯ ЗАВИСИМОСТЬ ВЕКТОРОВ § 4. БАЗИС ЛИНЕЙНОГО ПРОСТРАНСТВА. КООРДИНАТЫ ВЕКТОРА ОТНОСИТЕЛЬНО БАЗИСА § 5. РАЗМЕРНОСТЬ ЛИНЕЙНОГО ПРОСТРАНСТВА § 6. ИЗОМОРФИЗМ ЛИНЕЙНЫХ ПРОСТРАНСТВ § 7. ПРЕОБРАЗОВАНИЕ КООРДИНАТ ВЕКТОРА ПРИ ИЗМЕНЕНИИ БАЗИСА  ПОДПРОСТРАНСТВА ЛИНЕЙНОГО ПРОСТРАНСТВА§ 9. ЛИНЕЙНАЯ ОБОЛОЧКА ИЛИ ПОДПРОСТРАНСТВО, НАТЯНУТОЕ НА ДАННУЮ СИСТЕМУ ВЕКТОРОВ § 10. ФУНДАМЕНТАЛЬНАЯ СИСТЕМА РЕШЕНИЙ ОДНОРОДНОЙ СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ § 11. ЛИНЕЙНОЕ МНОГООБРАЗИЕ. ЛИНЕЙНОЕ МНОГООБРАЗИЕ РЕШЕНИЙ СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ Глава II. ЛИНЕЙНЫЕ ПРЕОБРАЗОВАНИЯ § 12. ПОНЯТИЕ ЛИНЕЙНОГО ПРЕОБРАЗОВАНИЯ. ПРЕДСТАВЛЕНИЕ ЛИНЕЙНОГО ПРЕОБРАЗОВАНИЯ МАТРИЦЕЙ § 13. ПРИМЕРЫ ЛИНЕЙНЫХ ПРЕОБРАЗОВАНИЙ § 14. СВЯЗЬ МЕЖДУ МАТРИЦАМИ ЛИНЕЙНОГО ПРЕОБРАЗОВАНИЯ В РАЗЛИЧНЫХ БАЗИСАХ § 15. ДЕЙСТВИЯ НАД ЛИНЕЙНЫМИ ПРЕОБРАЗОВАНИЯМИ И МАТРИЦАМИ. КОЛЬЦО ЛИНЕЙНЫХ ПРЕОБРАЗОВАНИЙ И КОЛЬЦО МАТРИЦ § 16. ОБРАТНОЕ ПРЕОБРАЗОВАНИЕ. ВЫРОЖДЕННЫЕ И НЕВЫРОЖДЕННЫЕ ПРЕОБРАЗОВАНИЯ. РАНГ И ЯДРО ЛИНЕЙНОГО ПРЕОБРАЗОВАНИЯ § 17. ОБ ИНВАРИАНТНЫХ ПОДПРОСТРАНСТВАХ И ИНДУЦИРОВАННЫХ ПРЕОБРАЗОВАНИЯХ § 18. СОБСТВЕННЫЕ ВЕКТОРЫ И СОБСТВЕННЫЕ ЗНАЧЕНИЯ ЛИНЕЙНОГО ПРЕОБРАЗОВАНИЯ § 19. ХАРАКТЕРИСТИЧЕСКИЙ МНОГОЧЛЕН МАТРИЦЫ И ЛИНЕЙНОГО ПРЕОБРАЗОВАНИЯ. СУЩЕСТВОВАНИЕ СОБСТВЕННЫХ ВЕКТОРОВ § 20.  О ПРИВЕДЕНИИ МАТРИЦЫ ЛИНЕЙНОГО ПРЕОБРАЗОВАНИЯ К ДИАГОНАЛЬНОЙ ФОРМЕ§ 21. О СОБСТВЕННЫХ ВЕКТОРАХ ЛИНЕЙНОГО ПРЕОБРАЗОВАНИЯ С СИММЕТРИЧЕСКОЙ МАТРИЦЕЙ Глава III. ЕВКЛИДОВЫ ПРОСТРАНСТВА § 22. ПОНЯТИЕ ЕВКЛИДОВА ПРОСТРАНСТВА. ПРИМЕРЫ § 23. ДЛИНА ВЕКТОРА. УГОЛ МЕЖДУ ВЕКТОРАМИ. НЕРАВЕНСТВО КОШИ—БУНЯКОВСКОГО § 24. ПОНЯТИЕ МЕТРИЧЕСКОГО ПРОСТРАНСТВА § 25. ОРТОГОНАЛЬНОСТЬ ВЕКТОРОВ. ОРТОНОРМИРОВАННЫЙ БАЗИС. ОРТОГОНАЛЬНО-ДОПОЛНИТЕЛЬНОЕ ПОДПРОСТРАНСТВО § 26. ИЗОМОРФИЗМ ЕВКЛИДОВЫХ ПРОСТРАНСТВ § 27. ОРТОГОНАЛЬНЫЕ МАТРИЦЫ § 28. ОРТОГОНАЛЬНЫЕ ПРЕОБРАЗОВАНИЯ ЕВКЛИДОВА ПРОСТРАНСТВА § 29. СИММЕТРИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ ЕВКЛИДОВА ПРОСТРАНСТВА § 30. ПРЕДСТАВЛЕНИЕ НЕВЫРОЖДЕННОГО ЛИНЕЙНОГО ПРЕОБРАЗОВАНИЯ ЕВКЛИДОВА ПРОСТРАНСТВА В ВИДЕ ПРОИЗВЕДЕНИЯ ОРТОГОНАЛЬНОГО ПРЕОБРАЗОВАНИЯ НА СИММЕТРИЧЕСКОЕ Глава IV. КВАДРАТИЧНЫЕ ФОРМЫ § 32. ПОНЯТИЕ КВАДРАТИЧНОЙ ФОРМЫ § 33.  ПРЕОБРАЗОВАНИЕ МАТРИЦЫ КВАДРАТИЧНОЙ ФОРМЫ ПРИ ЛИНЕЙНОЙ ЗАМЕНЕ ПЕРЕМЕННЫХ. КАНОНИЧЕСКИЙ ВИД КВАДРАТИЧНОЙ ФОРМЫ§ 34. ОРТОГОНАЛЬНОЕ ПРЕОБРАЗОВАНИЕ КВАДРАТИЧНОЙ ФОРМЫ К КАНОНИЧЕСКОМУ ВИДУ § 35. НАХОЖДЕНИЕ ОРТОГОНАЛЬНОГО ПРЕОБРАЗОВАНИЯ, ПРИВОДЯЩЕГО ВЕЩЕСТВЕННУЮ КВАДРАТИЧНУЮ ФОРМУ К КАНОНИЧЕСКОМУ ВИДУ § 36. МЕТОД ЛАГРАНЖА ПРИВЕДЕНИЯ КВАДРАТИЧНОЙ ФОРМЫ К КАНОНИЧЕСКОМУ ВИДУ § 37. ЗАКОН ИНЕРЦИИ КВАДРАТИЧНЫХ ФОРМ § 38. ЭКВИВАЛЕНТНОСТЬ ВЕЩЕСТВЕННЫХ КВАДРАТИЧНЫХ ФОРМ § 39. ПРИВЕДЕНИЕ ОБЩЕГО УРАВНЕНИЯ ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА К КАНОНИЧЕСКОМУ ВИДУ |
§ 3. Канонический вид квадратичной формы
Мы уже говорили о том, что в каждом базисе линейного пространства квадратичная форма задается однородным многочленом второй степени, который называется видом данной квадратичной формы. Каноническим
видом квадратичной формы называется такой
ее вид, в котором коэффициенты при
произведениях разноименных переменных
равны 0, т.
е. при .
Нормальным видом действительной квадратичной формы называется такой ее канонический вид, в котором отличные от нуля коэффициенты при квадратах равны 1 или –1. Все отличные от нуля коэффициенты при квадратах нормального вида комплексной квадратичной формы равны 1.
Теорема 5.6. Для любой квадратичной формы, заданной на линейном пространстве в существует базис, в котором эта квадратичная форма имеет канонический вид, и существует базис, в котором она имеет нормальный вид.
Или другая формулировка этой же теоремы:
Для любой квадратичной формы от n переменных существует линейное невырожденное преобразование переменных, приводящее ее к каноническому виду, и существует линейное невырожденное преобразование переменных, приводящее ее к нормальному виду.
Теорему
5.6 мы докажем позже, а сейчас на примере
покажем, как привести квадратичную
форму к каноническому виду методом,
который называется методом Лагранжа или выделения полных квадратов.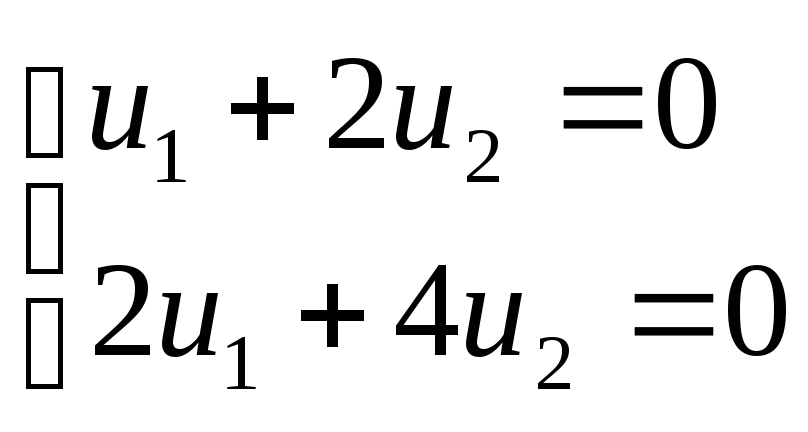
Он
заключается в следующем: выбираем
переменную, коэффициент при квадрате
которой отличен от 0, и выделяем полный
квадрат, включающий в себя все слагаемые
с этой переменной. С этой целью записываем
перед скобкой число, обратное выбранному
коэффициенту, а в скобках – половину
производной по выбранной переменной.
За скобками остается квадратичная
форма, количество переменных которой
уже на единицу меньше, с которой поступаем
также. После конечного числа шагов
получаем канонический вид.
Пример. ▼
где . Матрица этого линейного преобразования запишется так:
.
Как видим, она невырождена, значит, и преобразование переменных является невырожденным. Вводя обозначения
,
получаем
нормальный вид квадратичной формы: .
▲
Замечания. 1. На самом деле при применении метода Лагранжа получаем не прямое преобразование, приводящее квадратичную форму к каноническому виду, а обратное, т. е. преобразование, которое выражает не старые переменные через новые, а наоборот.
2. Если все коэффициенты при квадратах исходной квадратичной формы равны нулю, а отличен от нуля, например, коэффициент при произведении , применим вначале следующее преобразование: Матрица этого преобразования выглядит так:
.
Очевидно, она невырождена, и поэтому, соответствующее преобразование переменных также будет невырожденным.
Заметим, что канонический вид квадратичной формы определяется неоднозначно, тем не менее, имеет место
Теорема
5.7 (закон
инерции). Все канонические виды одной квадратичной
формы на действительном линейном
пространстве имеют одинаковое число
положительных коэффициентов и одинаковое
число отрицательных коэффициентов.
Нормальный вид квадратичной формы
определяется однозначно с точностью
до порядка следования коэффициентов.
►Доказательство достаточно провести для нормального вида.
Пусть в базисе линейного пространства квадратичная форма имеет вид
, (5.21)
а в базисе – вид
. (5.22)
Так как , то достаточно показать, что . Предположим, что это не так. Пусть, например, . Обозначим
, .
Так как а , то сумма не прямая, поэтому , следовательно, . Так как , то из (5.21) видно, что Но так как , то из (5.22) видно, видно, что Итак, мы пришли к противоречию. Таким образом, . Аналогично доказывается, что , значит, .◄
Замечание. Для квадратичных форм на комплексном
линейном пространстве нормальный вид,
очевидно, определяется однозначно, так
как количество отличных от нуля
коэффициентов совпадает с рангом
квадратичной формы.
$$ H = \left( \начать{массив}{рррр} 0 и 1 и 0 и 0 \\ 1 и 0 и 2 и 0 \\ 0&2&0&-3\ 0 & 0 & — 3 & 0 \\ \конец{массив} \верно) $$
============================================
$$ E_{1} = \left( \начать{массив}{рррр} 1 и 0 и 0 и 0 \\ 1 и 1 и 0 и 0 \\ 0 и 0 и 1 и 0 \\ 0 и 0 и 0 и 1 \\ \конец{массив} \верно) $$ $$ P_{1} = \left( \начать{массив}{рррр} 1 и 0 и 0 и 0 \\ 1 и 1 и 0 и 0 \\ 0 и 0 и 1 и 0 \\ 0 и 0 и 0 и 1 \\ \конец{массив} \верно) , \; \; \; Q_{1} = \влево( \начать{массив}{рррр} 1 и 0 и 0 и 0 \\ — 1&1&0&0\ 0 и 0 и 1 и 0 \\ 0 и 0 и 0 и 1 \\ \конец{массив} \верно) , \; \; \; D_{1} = \влево( \начать{массив}{рррр} 2 и 1 и 2 и 0 \\ 1 и 0 и 2 и 0 \\ 2 & 2 & 0 & — 3 \\ 0 & 0 & — 3 & 0 \\ \конец{массив} \верно) $$
============================================
$$ E_{2} = \left( \начать{массив}{рррр} 1 & — \frac{ 1 }{ 2 } & 0 & 0 \\ 0 и 1 и 0 и 0 \\ 0 и 0 и 1 и 0 \\ 0 и 0 и 0 и 1 \\ \конец{массив} \верно) $$ $$ P_{2} = \слева( \начать{массив}{рррр} 1 & — \frac{ 1 }{ 2 } & 0 & 0 \\ 1 & \ frac { 1 }{ 2 } & 0 & 0 \\ 0 и 0 и 1 и 0 \\ 0 и 0 и 0 и 1 \\ \конец{массив} \верно) , \; \; \; Q_{2} = \влево( \начать{массив}{рррр} \ frac { 1 }{ 2 } & \ frac { 1 }{ 2 } & 0 & 0 \\ — 1&1&0&0\ 0 и 0 и 1 и 0 \\ 0 и 0 и 0 и 1 \\ \конец{массив} \верно) , \; \; \; D_{2} = \влево( \начать{массив}{рррр} 2 и 0 и 2 и 0 \\ 0 & — \frac{ 1 }{ 2 } & 1 & 0 \\ 2 & 1 & 0 & — 3 \\ 0 & 0 & — 3 & 0 \\ \конец{массив} \верно) $$
============================================
$$ E_{3} = \влево( \начать{массив}{рррр} 1 и 0 & — 1 и 0 \\ 0 и 1 и 0 и 0 \\ 0 и 0 и 1 и 0 \\ 0 и 0 и 0 и 1 \\ \конец{массив} \верно) $$ $$ P_{3} = \влево( \начать{массив}{рррр} 1 & — \frac{ 1 }{ 2 } & — 1 & 0 \\ 1 & \frac{ 1 }{ 2 } & — 1 & 0 \\ 0 и 0 и 1 и 0 \\ 0 и 0 и 0 и 1 \\ \конец{массив} \верно) , \; \; \; Q_{3} = \влево( \начать{массив}{рррр} \ frac { 1 }{ 2 } & \ frac { 1 }{ 2 } & 1 & 0 \\ — 1&1&0&0\ 0 и 0 и 1 и 0 \\ 0 и 0 и 0 и 1 \\ \конец{массив} \верно) , \; \; \; D_{3} = \влево( \начать{массив}{рррр} 2 и 0 и 0 и 0 \\ 0 & — \frac{ 1 }{ 2 } & 1 & 0 \\ 0 & 1 & — 2 & — 3 \\ 0 & 0 & — 3 & 0 \\ \конец{массив} \верно) $$
============================================
$$ E_{4} = \влево( \начать{массив}{рррр} 1 и 0 и 0 и 0 \\ 0 и 1 и 2 и 0 \\ 0 и 0 и 1 и 0 \\ 0 и 0 и 0 и 1 \\ \конец{массив} \верно) $$ $$ P_{4} = \слева( \начать{массив}{рррр} 1 & — \frac{ 1 }{ 2 } & — 2 & 0 \\ 1 & \ frac { 1 }{ 2 } & 0 & 0 \\ 0 и 0 и 1 и 0 \\ 0 и 0 и 0 и 1 \\ \конец{массив} \верно) , \; \; \; Q_{4} = \влево( \начать{массив}{рррр} \ frac { 1 }{ 2 } & \ frac { 1 }{ 2 } & 1 & 0 \\ — 1 & 1 & — 2 & 0 \\ 0 и 0 и 1 и 0 \\ 0 и 0 и 0 и 1 \\ \конец{массив} \верно) , \; \; \; D_{4} = \влево( \начать{массив}{рррр} 2 и 0 и 0 и 0 \\ 0 & — \frac{ 1 }{ 2 } & 0 & 0 \\ 0 & 0 & 0 & — 3 \\ 0 & 0 & — 3 & 0 \\ \конец{массив} \верно) $$
============================================
$$ E_{5} = \влево( \начать{массив}{рррр} 1 и 0 и 0 и 0 \\ 0 и 1 и 0 и 0 \\ 0 и 0 и 1 и 0 \\ 0 и 0 и 1 и 1 \\ \конец{массив} \верно) $$ $$ P_{5} = \влево( \начать{массив}{рррр} 1 & — \frac{ 1 }{ 2 } & — 2 & 0 \\ 1 & \ frac { 1 }{ 2 } & 0 & 0 \\ 0 и 0 и 1 и 0 \\ 0 и 0 и 1 и 1 \\ \конец{массив} \верно) , \; \; \; Q_{5} = \влево( \начать{массив}{рррр} \ frac { 1 }{ 2 } & \ frac { 1 }{ 2 } & 1 & 0 \\ — 1 & 1 & — 2 & 0 \\ 0 и 0 и 1 и 0 \\ 0 и 0 & — 1 и 1 \\ \конец{массив} \верно) , \; \; \; D_{5} = \влево( \начать{массив}{рррр} 2 и 0 и 0 и 0 \\ 0 & — \frac{ 1 }{ 2 } & 0 & 0 \\ 0 & 0 & — 6 & — 3 \\ 0 & 0 & — 3 & 0 \\ \конец{массив} \верно) $$
============================================
$$ E_{6} = \влево(
\начать{массив}{рррр}
1 и 0 и 0 и 0 \\
0 и 1 и 0 и 0 \\
0 & 0 & 1 & — \ frac { 1 }{ 2 } \\
0 и 0 и 0 и 1 \\
\конец{массив}
\верно)
$$
$$ P_{6} = \влево(
\начать{массив}{рррр}
1 & — \frac{ 1 }{ 2 } & — 2 & 1 \\
1 & \ frac { 1 }{ 2 } & 0 & 0 \\
0 & 0 & 1 & — \ frac { 1 }{ 2 } \\
0 & 0 & 1 & \ frac { 1 }{ 2 } \\
\конец{массив}
\верно)
, \; \; \; Q_{6} = \влево(
\начать{массив}{рррр}
\ frac { 1 }{ 2 } & \ frac { 1 }{ 2 } & 1 & 0 \\
— 1 & 1 & — 2 & 0 \\
0 & 0 & \ frac { 1 }{ 2 } & \ frac { 1 }{ 2 } \\
0 и 0 & — 1 и 1 \\
\конец{массив}
\верно)
, \; \; \; D_{6} = \влево(
\начать{массив}{рррр}
2 и 0 и 0 и 0 \\
0 & — \frac{ 1 }{ 2 } & 0 & 0 \\
0 & 0 & — 6 & 0 \\
0 & 0 & 0 & \ frac { 3 }{ 2 } \\
\конец{массив}
\верно)
$$ 9Т Н Р = D $$
$$\слева(
\начать{массив}{рррр}
1 и 1 и 0 и 0 \\
— \ frac { 1 }{ 2 } & \ frac { 1 }{ 2 } & 0 & 0 \\
— 2&0&1&1\
1 & 0 & — \ frac { 1 }{ 2 } & \ frac { 1 }{ 2 } \\
\конец{массив}
\верно)
\левый(
\начать{массив}{рррр}
0 и 1 и 0 и 0 \\
1 и 0 и 2 и 0 \\
0&2&0&-3\
0 & 0 & — 3 & 0 \\
\конец{массив}
\верно)
\левый(
\начать{массив}{рррр}
1 & — \frac{ 1 }{ 2 } & — 2 & 1 \\
1 & \ frac { 1 }{ 2 } & 0 & 0 \\
0 & 0 & 1 & — \ frac { 1 }{ 2 } \\
0 & 0 & 1 & \ frac { 1 }{ 2 } \\
\конец{массив}
\верно)
= \слева(
\начать{массив}{рррр}
2 и 0 и 0 и 0 \\
0 & — \frac{ 1 }{ 2 } & 0 & 0 \\
0 & 0 & — 6 & 0 \\
0 & 0 & 0 & \ frac { 3 }{ 2 } \\
\конец{массив}
\верно)
$$
$$ Q^T D Q = H $$
$$\слева(
\начать{массив}{рррр}
\frac{ 1 }{ 2 } & — 1 & 0 & 0 \\
\ frac { 1 }{ 2 } & 1 & 0 & 0 \\
1 & — 2 & \frac{ 1 }{ 2 } & — 1 \\
0 & 0 & \ frac { 1 }{ 2 } & 1 \\
\конец{массив}
\верно)
\левый(
\начать{массив}{рррр}
2 и 0 и 0 и 0 \\
0 & — \frac{ 1 }{ 2 } & 0 & 0 \\
0 & 0 & — 6 & 0 \\
0 & 0 & 0 & \ frac { 3 }{ 2 } \\
\конец{массив}
\верно)
\левый(
\начать{массив}{рррр}
\ frac { 1 }{ 2 } & \ frac { 1 }{ 2 } & 1 & 0 \\
— 1 & 1 & — 2 & 0 \\
0 & 0 & \ frac { 1 }{ 2 } & \ frac { 1 }{ 2 } \\
0 и 0 & — 1 и 1 \\
\конец{массив}
\верно)
= \слева(
\начать{массив}{рррр}
0 и 1 и 0 и 0 \\
1 и 0 и 2 и 0 \\
0&2&0&-3\
0 & 0 & — 3 & 0 \\
\конец{массив}
\верно)
$$ 92=3\Big(y-\frac{1}{4}\Big)$$
ясно дает понять, что мы имеем дело с параболическим цилиндром, но нам нужна (метрическая) каноническая форма, мы должны сделать что-то большее.
2+2pY=0
$$
где $\lambda$ и $p$ отличны от $0$, а $\lambda$ положительна ($2$ в $2p$ просто позволяет избежать дробей).
В самом деле, если $B’$ и $A’$ — матрицы матрицы $F$, т.е.
$$
B’=\left( \begin{matrix}\lambda & 0 & 0 & 0\\ 0 & 0 & 0 & p\\ 0 & 0 & 0 & 0\\ 0 & p & 0 & 1\ end{matrix } \верно)
$$
и
$$
A’=\left( \begin{matrix}\lambda & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{matrix} \right)
$$
тогда инерция $B’$ равна $(2,1)$, а инерция $A$ равна $(1,0)$, как и следовало ожидать.
Мы также знаем, что есть четыре инварианта относительно переноса и поворота системы координат, а именно, если квадрика имеет полную матрицу
$$
\mathcal{B}=\left( \begin{matrix} a_{11} & a_{12} & a_{13} & a_{14}\\ a_{11} & a_{22} & a_{23} & a_{24} \\ a_{13} & a_{23} & a_{33} & a_{34} \\ a_{14} & a_{24} & a_{34} & a_{44} \end{matrix } \верно)
$$
то величины $\det(B)$, $\det(A)$, $\mathrm{tr}(A)$ и
$$
I_2=\det\left( \begin{matrix} a_{11} & a_{12}\\ a_{11} & a_{22} \end{matrix} \right)+\det\left( \begin{matrix } a_{22} & a_{23}\\ a_{23} & a_{33} \end{matrix} \right)+\det\left( \begin{matrix} a_{33} & a_{13}\ \ a_{13} & a_{11} \end{matrix} \right)
$$
не меняются при переносах и вращениях.