4.2 Предел функции в точке. Два определения и их эквивалентность
Определение 4.7 (предел функции по Коши). Точка $b \in \overline{\mathbb {R}}$ называется пределом функции $f\colon E \to \mathbb {R}$ в точке $a \in \overline{\mathbb {R}}$, если $a$ — предельная точка множества $E$ и
$$\forall \varepsilon > 0\ \exists \delta > 0\ \forall x \in B_\delta ‘(a) \cap E\colon f(x) \in B_\varepsilon (b).$$
Пишут: $\lim \limits _{E \ni x \to a} = b$ или $f(x)\to b$ при $E \ni x \to a$.
В частности, если $a, b\in \mathbb {R}$, то определение 4.7 можно переписать следующим образом:
Определение 4.8. Число $b \in \mathbb {R}$ называется пределом функции $f\colon E \to \mathbb {R}$ в точке $a \in \mathbb {R}$, если $a$ — предельная точка $E$ и
$$\forall \varepsilon > 0\ \exists \delta > 0\ \forall x \in E\colon (0 < |x — a| < \delta \Rightarrow |f(x) — b| < \varepsilon ).$$
Замечание. (Геометрический смысл). Пусть $f\colon E \to \mathbb {R}$, $a$ — предельная точка $E$. Тогда $b = \lim \limits _{E \ni x \to a} \Leftrightarrow $ $\forall B_\varepsilon (b)\ \exists B_\delta ‘(a)\colon f(B_\delta ‘(a) \cap E) \subset B_\varepsilon (b)$.
(Геометрический смысл). Пусть $f\colon E \to \mathbb {R}$, $a$ — предельная точка $E$. Тогда $b = \lim \limits _{E \ni x \to a} \Leftrightarrow $ $\forall B_\varepsilon (b)\ \exists B_\delta ‘(a)\colon f(B_\delta ‘(a) \cap E) \subset B_\varepsilon (b)$.
Определение 4.9 (предел функции по Гейне). Точка $b \in \overline{\mathbb {R}}$ называется пределом функции $f\colon E \to \mathbb {R}$ в точке $a \in \overline{\mathbb {R}}$, если $a$ — предельная точка множества $E$ и
$$\forall \{ x_ n\} , x_ n \in E \backslash \{ a\} \ (\lim \limits _{n\to \infty }x_ n = a \Rightarrow \lim \limits _{n\to \infty }f(x_ n) = b).$$
Теорема 4.1. Определения предела функции по Коши и по Гейне эквивалентны.
$\blacktriangle $ ($\Rightarrow $) Докажем, что если $\lim \limits _{E \ni x \to a} f(x) = b$ по Коши, то $\lim \limits _{E \ni x \to a} = b$ по Гейне.
Итак, пусть $f\colon E \to \mathbb {R}, a$ — предельная точка $E$ и $\forall \varepsilon > 0\ \exists \delta > 0\ \forall x \in B_\delta ‘(a) \cap E \colon f(x) \in B_\varepsilon (b)\ (*)$.
Пусть $\{ x_ n\} , x_ n \in E \backslash \{ a\} , x_ n \to a$. Покажем, что $f(x_ n) \to b$. Т.к. $x_ n \to a$, то
$\exists N\ \forall n > N\colon x_ n \in B_\delta (a)$. Т.к. $x_ n \in E \backslash \{ a\} $, то $\forall n > N\colon x_ n \in B_\delta ‘(a) \cap E \stackrel{\mbox{по ($*$)}}{\Rightarrow }$ $ f(x_ n) \in B_\varepsilon (b)$.
Получаем: $\forall \varepsilon > 0\ \exists N\ \forall n > N\colon f(x_ n) \in B_\varepsilon (b)$, т.е. $\lim \limits _{n\to \infty }f(x_ n) = b$. Определение по Гейне выполняется.
($\Leftarrow $) Пусть определение по Коши не выполняется. В начале обоих определений формируются некоторые одинаковые требования, естественно, что не выполнение их в одном определении означает их невыполнение во втором определении. Поэтому пусть $f\colon E \to \mathbb {R}$ и $a$ — предельная точка множества $E$, но определение по Коши не выполняется, т.е.
$$\exists \varepsilon > 0\ \forall \delta > 0\ \exists x \in B_\delta ‘(a) \cap E\colon f(x) \not\in B_\varepsilon (b).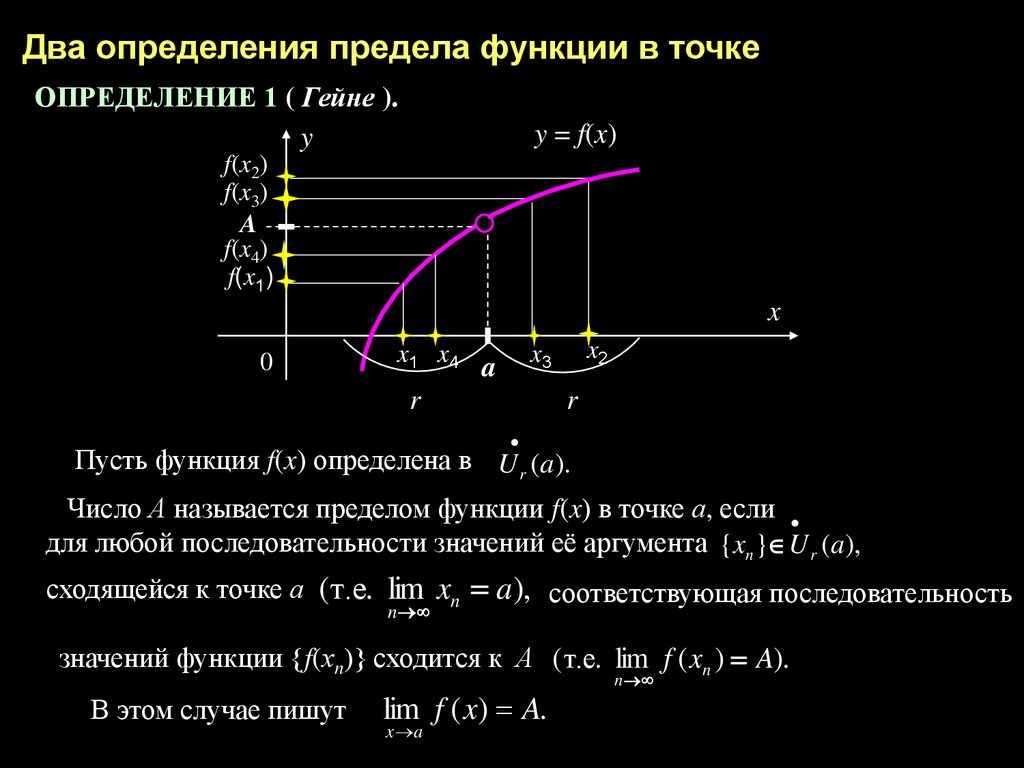 $$
$$
Возьмем последовательность чисел $\delta _ n = \frac1n$ и построим соответствующую последовательность точек $x_ n \in B_{\delta _ n}'(a) \cap E\colon f(x_ n) \not\in B_\varepsilon (b)$. Итак, $x_ n \in E \backslash \{ a\} $ и $x_ n \to a\ (\mbox{т.к. }\delta _ n \to 0)$, но
$f(x_ n) \not\in B_\varepsilon (b) \Rightarrow b \not= \lim \limits _{n\to \infty }f(x_ n)$. Определение по Гейне не выполняется. $\blacksquare $
Замечание. Т.к. определения по Коши и по Гейне эквивалентны, то в дальнейшем будем говорить просто, что функция $f\colon E \to \mathbb {R}$ имеет предел в точке $a$, равный $b$. Если $a$ — внутренняя точка множества $E \cup \{ a\} $, то пишут $\lim \limits _{x\to a} f(x) = b$ (опуская указание на множество $E$).
Пример: Пусть $a, b \in \mathbb {R}$. Расписать на языке $\varepsilon $-$\delta $:
$\lim \limits _{x\to +\infty } f(x) = b \Leftrightarrow \forall \varepsilon >0\ \exists \delta >0\ \forall x\ (x > \frac1\delta \Rightarrow |f(x) — b| < \varepsilon )$.
$\lim \limits _{x \to a} f(x) = -\infty \Leftrightarrow \forall \varepsilon > 0\ \exists \delta > 0\ \forall x\ (0 < |x — a| < \delta \Rightarrow f(x) < -\frac1\varepsilon )$.
Пример: Доказать, что $\lim \limits _{x\to +\infty } \frac{\sin x}{x} = 0$.
$\blacktriangle $ $\forall \varepsilon > 0\ \exists \delta = \varepsilon \ \forall x\ (x > \frac1\delta \Rightarrow \left|\frac{\sin x}x\right| \leqslant \frac1x < \varepsilon ) \Leftrightarrow \lim \limits _{x\to +\infty } \frac{\sin x}x = 0.$ $\blacksquare $
Левосторонний и правосторонний пределы функции в точке
Естественные науки / Математический анализ функции одной переменной / Левосторонний и правосторонний пределы функции в точке
Переходим к рассмотрению односторонних пределов функции в точке x0, при которых переменная x «движется» к x0 слева (левосторонний предел) или справа (правосторонний предел). Нам потребуется понятие полуокрестности.
Нам потребуется понятие полуокрестности.
Пусть d > 0. Интервал (a, x0) называется левой полуокрестностью точки x0, интервал (x0 – d, x0) – левой d-полуокрестностью точки x0. Интервалы (x0, b), (x0, x0 + d) называются, соответственно,
Пусть f(x0) определена в левой полуокрестности точки x0.
Число b называется левосторонним пределом функции f(x) в точке x0 (обозначение: f(x) = b), если для любого e > 0 найдется d > 0, такое, что для всех значений x, принадлежащих левой d-полуокрестности (x0 – d, x0), выполняется неравенство: |f(x) – b| < e.
Символическиf(x) = b означает: «e>0$d > 0 «x(x0 – d < x < x0 ® | f(x) – b | < e) (см. рис. 1.8).
Аналогично, число b называется правосторонним пределом функции f(x) в точке x0 (обозначение: f(x) = b), если для любого e > 0 найдется d > 0, такое, что для
всех значений x, принадлежащих правой d-полуокрестности (x0, x0 + d), выполняется неравенство: | f(x) – b | < e (см. рис. 1.9).
Символическиf(x) = b означает: «e >0 $d >0 «x(x0 < x < x0 + d ® |f(x) – b| < e).
Пример 3.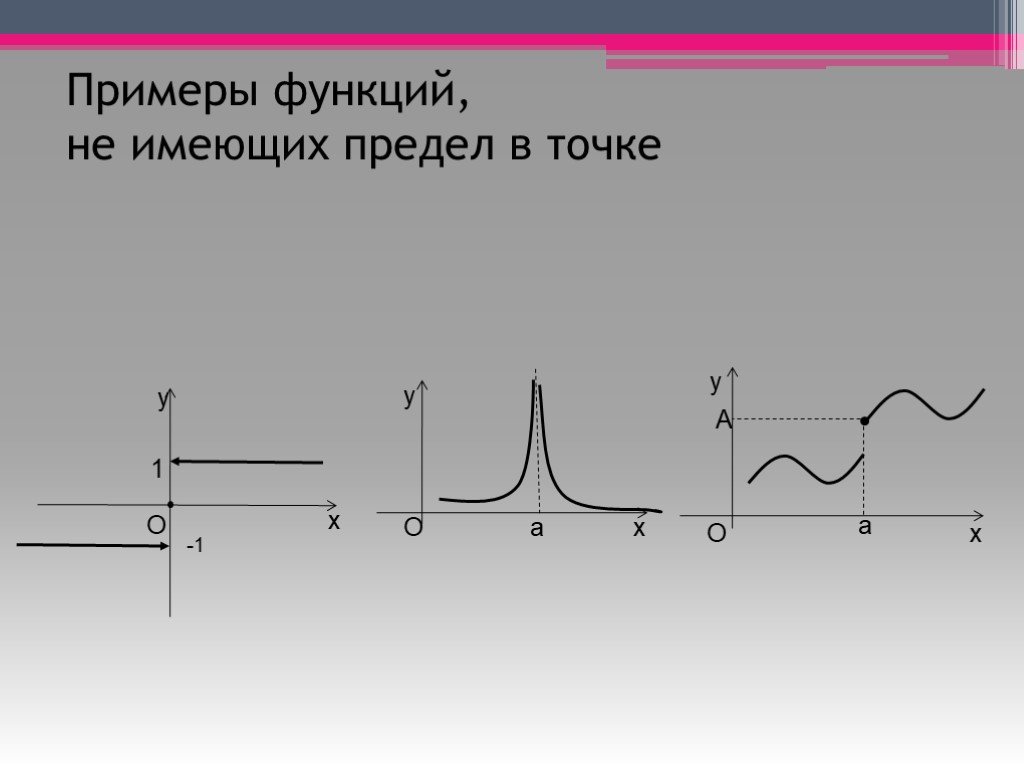
Функция f(x) задана равенством (рис. 1.10):
f(x) = .
Найти f(x) и f(x).
Решение. Покажем, что f(x) = 1, а f(x) = 3.
Рассмотрим значения x < 1, тогда f(x) = 2x – 1 и | f(x) – 1| = |2x – 1 – 1| = 2|x – 1|. Зафиксируем малое e > 0. Подсчитаем: | f(x) – 1| < e Û 2 |x – 1| < e Û |x – 1| < . Так как x < 1, то f(x) – 1| < e, если 1 – < x < 1, следовательно, d = . Итак, если 1 – < x < 1, то | f(x) – 1| < e, т.е. f(x) = 1.
Рассмотрим значения x > 1, тогда f(x) = 4 – x.
| f(x) – 3| = |2 – x – 3| = |1 – x|. Отсюда | f(x) – 1| < e Û |1 – x| < e, т.е. | f(x) – 1 | < e для x Î (1, 1 + e). Значит, f(x) = 3.
Очевидно, если f(x) = b, то f(x) = b и f(x) = b.
Верно и обратное, если f(x) = f(x) = b, то f(x) = b.
Если же правосторонний предел функции в точке x0 не равен левостороннему пределу функции в точке x0, то f(x) = b не существует. Так, в примере 3 функция f(x) не имеет предела в точке x0.
исчисление — Разница между значением функции в точке и ее пределом в этой точке?
спросил
Изменено 1 год, 7 месяцев назад
Просмотрено 2к раз
$\begingroup$
Будучи старшеклассником, я понимаю основное теоретическое различие между ними, например, предел — это то, к чему приближается функция, когда вход приближается к чему-то (но никогда не равен ему), или как она ведет себя вблизи этой точки и т. {0}$ и т. д. Для Примера
{0}$ и т. д. Для Примера
Оба хорошо определены, но все же разные. Что означает это различие в подобных случаях?
- исчисление
- пределы
- непрерывность
$\endgroup$
6
$\begingroup$
Определение предела $f(x)$ при $x=x_0$ рассматривает поведение $f$ по мере приближения к $x_0$, но фактически не рассматривает значение по адресу $x_0$.
Например, если у вас есть функция $$f(x) = \begin{case}0, &x\neq 0\\1, &x=0\end{cases}$$ тогда $f(0)=1$, но $\lim_{x\to 0} f(x) = 0.$
Для непрерывных функций $f(x_0) = \lim_{x\to x_0} f (х)$. (То, что пределы функции существуют и равны простому вычислению функции, в конце концов является определением непрерывности.) Многие учебники оценивают пределы, подставляя $x_0$, когда рассматриваемая функция «очевидно» непрерывна в $ х_0$. Большинство функций, с которыми вы сталкиваетесь «в дикой природе», непрерывны почти везде, включая многочлены, рациональные функции, триггерные функции и композиции, составленные из этих частей. Чтобы быть полностью строгим, вы должны доказать, что конкретная функция непрерывна, прежде чем подключаться к ней для оценки предела, но на практике, когда вы станете более опытными и удобными, вы начнете пропускать этот шаг.
Большинство функций, с которыми вы сталкиваетесь «в дикой природе», непрерывны почти везде, включая многочлены, рациональные функции, триггерные функции и композиции, составленные из этих частей. Чтобы быть полностью строгим, вы должны доказать, что конкретная функция непрерывна, прежде чем подключаться к ней для оценки предела, но на практике, когда вы станете более опытными и удобными, вы начнете пропускать этот шаг.
Причина, по которой неопределенные формы, такие как $\frac{0}{0}$, так сильно подчеркиваются, заключается в том, что они являются одним из наиболее распространенных случаев, когда непрерывность функции не очевидна, и где тщательный анализ с использованием определения пределов иногда необходимы.
$\endgroup$
$\begingroup$
Уловка, которую использует ваш учебник, заключается в следующем:
Действительнозначная функция $f:D \rightarrow \mathbb{R}$ в области $D \subseteq \mathbb{R}$ непрерывна в $c \in \mathbb{R}$, если $\lim_{x \rightarrow c} f(x) = f(c)$.
Таким образом, в учебнике в основном говорится: «Мы знаем, что эта функция $ f(x) = \frac{4x+3}{x-2} $ непрерывна при $x = 4$, поэтому мы можем просто взять $\lim_{ x \rightarrow 4} f(x) = f(4). $»
Но подождите минутку! Откуда мы знаем, что функция $ f(x) = \frac{4x+3}{x-2} $ непрерывна в точке $x = 4$??? Чтобы показать, что $ f(x) = \frac{4x+3}{x-2} $ непрерывна в точке $x = 4$, не нужно ли сначала показать, что $\lim_{x \rightarrow 4} f(x) = f(4) $????
Итак, в учебнике для решения этой задачи более или менее используется круговая логика. Но для многих практических целей мы знаем из предыдущего опыта, где общие функции являются непрерывными/прерывистыми. Если мы знаем, что функция непрерывна в точке предела, мы можем использовать простую замену.
Более строгое доказательство того, что $\lim_{x \rightarrow 4} \frac{4x+3}{x-2} = \frac{19}{2}$, выглядит следующим образом:
Пусть $\epsilon > 0$. Выберите $\delta = \min\{\frac{2}{11}\epsilon , 1\}$ и пусть $\vert x — 4 \vert < \delta$.
Тогда $\vert f(x) — \frac{19}{2}\vert = \vert\frac{4x+3}{x-2} — \frac{19}{2}\vert = \ vert \frac{-11x+44}{2x-4} \vert = 11 \vert x-4 \vert \vert \frac{1}{2x-4} \vert$.
Обратите внимание, что $ \frac{1}{6} \le \vert \frac{1}{2x-4} \vert \le \frac{1}{2}$, поэтому
$ 11 \vert x-4 \vert \vert \frac{1}{2x-4} \vert \le \frac{11}{2} \vert x-4 \vert < \frac{11}{2 }\дельта\ле\эпсилон $. Следовательно, $\lim_{x \rightarrow 4} \frac{4x+3}{x-2} = \frac{19}{2}$. $\square$
Вы бы узнали, что это вводный курс колледжа по реальному анализу, но для вводного курса исчисления HS это немного излишне. Они хотят, чтобы вы получили представление об ограничениях, прежде чем вдаваться в строгость (если вы когда-нибудь это сделаете). Для многих прикладных STEM-профессий базовых понятий пределов более чем достаточно.
$\endgroup$
AC Понятие лимита
\(\require{marginnote}\newcommand{\dollar}{\$} \DeclareMathOperator{\erf}{erf} \DeclareMathOperator{\arctanh}{arctanh} \новая команда{\lt}{<} \новая команда{\gt}{>} \newcommand{\amp}{&} \)
¶Мотивирующие вопросы
Что такое математическое понятие предела и какую роль играют пределы в изучении функций?
Что означает обозначение \(\lim_{x \to a} f(x) = L\text{?}\)
Как определить значение предела функции в точке?
Как мы используем среднюю скорость для вычисления мгновенной скорости?
Функции лежат в основе математики: функция — это процесс или правило, связывающее каждый отдельный вход ровно с одним соответствующим выходом.
Функции особенно важны в исчислении, поскольку они часто моделируют важные явления — местоположение движущегося объекта в данный момент времени, скорость, с которой автомобиль расходует бензин при определенной скорости, реакцию больного на величину дозы лекарства — и исчисление можно использовать для изучения того, как эти выходные величины изменяются в ответ на изменения входной переменной. Более того, размышления о таких понятиях, как средняя и мгновенная скорость, естественным образом ведут нас от исходной функции к родственной, иногда более сложной функции. В качестве одного из примеров этого подумайте о падающем мяче, функция положения которого задается \(s(t) = 64 — 16t^2\) и средней скорости мяча на интервале \([1,x]\text {. }\) Заметьте, что 92}{x-1}\) сообщает нам среднюю скорость мяча на интервале от \(t = 1\) до \(t = x\text{,}\), и если нас интересует мгновенная скорость мяча, когда \(t = 1\text{,}\) мы хотели бы знать, что происходит с \(g(x)\) по мере того, как \(x\) становится все ближе и ближе к \(1\text{ .}\) При этом \(g(1)\) не определено, так как приводит к частному \(0/0\text{.}\)
}\) Заметьте, что 92}{x-1}\) сообщает нам среднюю скорость мяча на интервале от \(t = 1\) до \(t = x\text{,}\), и если нас интересует мгновенная скорость мяча, когда \(t = 1\text{,}\) мы хотели бы знать, что происходит с \(g(x)\) по мере того, как \(x\) становится все ближе и ближе к \(1\text{ .}\) При этом \(g(1)\) не определено, так как приводит к частному \(0/0\text{.}\)
Вот тут-то и появляется идея ограничения . Используя предел, мы сможем позволить \(x\) быть сколь угодно близким, но не равным, к \(1\) и полностью понять поведение \(g(x)\) вблизи этого значения. Далее мы разработаем ключевой язык, нотацию и концептуальное понимание, а сейчас рассмотрим предварительное задание, в котором используется графическая интерпретация функции для изучения точек на графике, в которых происходит интересное поведение.
Предварительный просмотр 1.2.1
Предположим, что \(g\) является функцией, представленной на графике ниже. Используйте график, чтобы ответить на каждый из следующих вопросов.
Определить значения \(g(-2)\text{,}\) \(g(-1)\text{,}\) \(g(0)\text{,}\) \(g (1)\text{,}\) и \(g(2)\text{,}\), если они определены. Если значение функции не определено, объясните, какой признак графика вам об этом говорит.
Для каждого из значений \(a = -1\text{,}\) \(a = 0\text{,}\) и \(a = 2\text{,}\) завершите следующее предложение: «По мере того, как \(x\) становится все ближе и ближе (но не равно) к \(a\text{,}\), \(g(x)\) становится настолько близким, насколько мы хотим».
Что происходит, когда \(x\) становится все ближе и ближе (но не равно) к \(a = 1\text{?}\) Подходит ли функция \(g(x)\) так близко, как нам хотелось бы к единому значению?
Рисунок 1.2.1 График \(y = g(x)\) для предварительного просмотра 1.2.1.
Подраздел 1.2.1 Понятие предела
Пределы можно рассматривать как способ изучения тенденции или тренда функции, когда входная переменная приближается к фиксированному значению или даже когда входная переменная неограниченно увеличивается или уменьшается. Мы откладываем изучение последней идеи до тех пор, пока в ходе курса у нас не появятся некоторые полезные инструменты исчисления для понимания конечного поведения функций. Здесь мы сосредоточимся на том, что значит сказать, что «функция \(f\) имеет предел \(L\), когда \(x\) приближается к \(a\text{.}\)». Для начала мы думаем о недавний пример.
Мы откладываем изучение последней идеи до тех пор, пока в ходе курса у нас не появятся некоторые полезные инструменты исчисления для понимания конечного поведения функций. Здесь мы сосредоточимся на том, что значит сказать, что «функция \(f\) имеет предел \(L\), когда \(x\) приближается к \(a\text{.}\)». Для начала мы думаем о недавний пример.
В предварительном упражнении 1.2.1 мы увидели, что для заданной функции \(g\text{,}\) по мере того, как \(x\) становится все ближе и ближе (но не равно) к 0, \(g(x)\ ) максимально приближается к значению 4. Поначалу это может показаться нелогичным, поскольку значение \(g(0)\) равно \(1\text{,}\), а не \(4\text{ .}\) По самому своему определению пределы учитывают поведение функции , сколь угодно близкое к фиксированному входу, но значение функции при фиксированном входе не имеет значения. Более формально 1 Далее следует не то, что математики считают формальным определением предела. Чтобы быть абсолютно точным, необходимо дать количественную оценку того, что значит сказать «настолько близко к \(L\), насколько нам нравится», и «достаточно близко к \(a\text{. }\)». Этого можно достичь с помощью то, что традиционно называют определением пределов эпсилон-дельта. Представленного здесь определения достаточно для целей данного текста. Скажем следующее.
}\)». Этого можно достичь с помощью то, что традиционно называют определением пределов эпсилон-дельта. Представленного здесь определения достаточно для целей данного текста. Скажем следующее.
Определение 1.2.2
Для функции \(f\text{,}\) с фиксированным входом \(x = a\text{,}\) и действительным числом \(L\text{,}\) мы говорим, что \(f\) имеет предел \(L\), поскольку \(x\) приближается к \(a\) , и напишите
\begin{уравнение*} \lim_{x \to a} f(x) = L \end{уравнение*}
при условии, что мы можем сделать \(f(x)\) как можно более близким к \(L\), взяв \(x\) достаточно близко (но не равным) к \(a\text{.}\) Если мы не можем сделать \(f(x)\) настолько близким к одному значению, насколько нам хотелось бы, поскольку \(x\) приближается к \(a\text{,}\), то мы говорим, что \(f\) делает не имеет предела, когда \(x\) приближается к \(a\text{.}\)
Для функции \(g\), изображенной на рисунке 1.2.1, мы можем сделать следующие наблюдения:
\begin{уравнение*} \lim_{x \to -1} g(x) = 3, \ \lim_{x \to 0} g(x) = 4, \\text{and} \ \lim_{x \to 2} g(x ) = 1\текст{,} \end{уравнение*}
, но \(g\) не имеет предела как \(x \to 1\text{.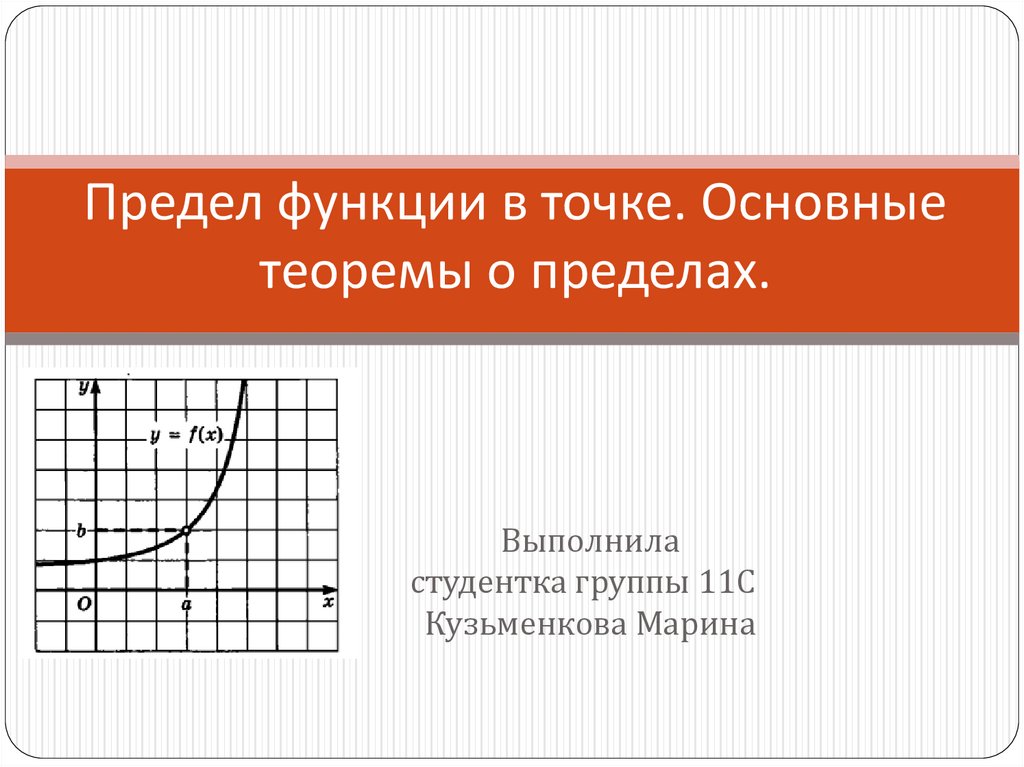 }\) При графической работе достаточно спросить, приближается ли функция к одному значению с каждой стороны фиксированного входа, а понимая, что значение функции прямо на фиксированном входе не имеет значения. Это рассуждение объясняет значения первых трех установленных пределов. В такой ситуации, как скачок графика \(g\) в точке \(x = 1\text{,}\), проблема в том, что если мы приближаемся к \(x = 1\) слева, значения функции стремится приблизиться к 3, как нам хотелось бы, но если мы приблизимся к \(x = 1\) справа, значения функции будут настолько близки к 2, насколько нам хотелось бы, и не существует единого числа, которое все значения этих функций приближаются. Вот почему предел \(g\) не существует при \(x = 1\text{.}\)
}\) При графической работе достаточно спросить, приближается ли функция к одному значению с каждой стороны фиксированного входа, а понимая, что значение функции прямо на фиксированном входе не имеет значения. Это рассуждение объясняет значения первых трех установленных пределов. В такой ситуации, как скачок графика \(g\) в точке \(x = 1\text{,}\), проблема в том, что если мы приближаемся к \(x = 1\) слева, значения функции стремится приблизиться к 3, как нам хотелось бы, но если мы приблизимся к \(x = 1\) справа, значения функции будут настолько близки к 2, насколько нам хотелось бы, и не существует единого числа, которое все значения этих функций приближаются. Вот почему предел \(g\) не существует при \(x = 1\text{.}\)
Для любой функции \(f\text{,}\) обычно существует три способа ответить на вопрос «имеет ли \(f\) предел в точке \(x = a\text{,}\), и если да, каков предел?» Во-первых, рассуждайте графически, как мы только что сделали с примером из предварительного просмотра 1. 2.1. Если у нас есть формула для \(f(x)\text{,}\), то есть две дополнительные возможности: (1) оценить функцию на последовательности входных данных, приближающихся к \(a\) с обеих сторон, обычно используя некоторые разновидность вычислительной технологии и спросите, приближается ли последовательность выходных данных к одному значению; (2) использовать алгебраическую форму функции, чтобы понять тенденцию ее выходных данных по мере того, как входные значения приближаются к \(a\text{.}\). Первый подход дает только приблизительное значение предела, в то время как последний может часто используется для точного определения предела. Следующий пример демонстрирует оба этих подхода, а также использует графики соответствующих функций для подтверждения наших выводов. 92}{x+2}\text{;}\) \(a = -1\text{,}\) \(a = -2\)
2.1. Если у нас есть формула для \(f(x)\text{,}\), то есть две дополнительные возможности: (1) оценить функцию на последовательности входных данных, приближающихся к \(a\) с обеих сторон, обычно используя некоторые разновидность вычислительной технологии и спросите, приближается ли последовательность выходных данных к одному значению; (2) использовать алгебраическую форму функции, чтобы понять тенденцию ее выходных данных по мере того, как входные значения приближаются к \(a\text{.}\). Первый подход дает только приблизительное значение предела, в то время как последний может часто используется для точного определения предела. Следующий пример демонстрирует оба этих подхода, а также использует графики соответствующих функций для подтверждения наших выводов. 92}{x+2}\text{;}\) \(a = -1\text{,}\) \(a = -2\)
Решение
Сначала построим график \(f\) вместе с таблицами значений рядом \(a = -1\) и \(a = -2\text{. }\)
}\)
| \ (х\) | \(ф(х)\) |
| \(-0,9\) | \(2.9\) |
| \(-0,99\) | \(2.99\) |
| \(-0,999\) | \(2.999\) |
| \(-0,9999\) | \(2,9999\) |
| \(-1.1\) | \(3.1\) |
| \(-1.01\) | \(3.01\) |
| \(-1,001\) | \(3.001\) |
| \(-1.0001\) | \(3.0001\) |
| \(х\) | \(ф(х)\) |
| \(-1,9\) | \(3.9\) |
| \(-1,99\) | \(3.99\) |
| \(-1,999\) | \(3.999\) |
| \(-1,9999\) | \(3,9999\) |
| \(-2.1\) | \(4.1\) |
| \(-2.01\) | \(4.01\) |
| \(-2.001\) | \(4.001\) |
| \(-2.0001\) | \(4. 0001\) 0001\) |
Таблица 1.2.4 Таблица значений \(f\) вблизи \(x=-1\text{.}\) Таблица 1.2.5 Таблица значений \(f\) вблизи \(x=-2\ text{.}\)Рисунок 1.2.6 График \(f(x)\) на \([-4,2]\text{.}\) 92) = 0\text{,}\) и \((x+2) \to (-2 + 2) = 0\text{,}\), так что \(x \to -2\text{,} \) числитель \(f\) стремится к 0, а знаменатель стремится к 0. Мы называем \(0/0\) неопределенной формой и вернемся к нескольким важным вопросам, связанным с такими величинами, позже в курсе. А пока мы просто наблюдаем, что это говорит нам о том, что есть еще какая-то работа. Из таблицы 1.2.5 и рисунка 1.2.6 видно, что \(f\) должен иметь предел \(4\) в точке \(x = -2\text{.}\). Чтобы алгебраически понять, почему это случае, давайте работать непосредственно с формой \(f(x)\text{.}\) Обратите внимание, что 92}{х+2}\\ = \amp \lim_{x \to -2} \frac{(2-x)(2+x)}{x+2}\text{.} \end{align*}
На этом этапе важно отметить, что поскольку мы берем предел как \(x \to -2\text{,}\), мы рассматриваем значения \(x\), которые близко, но не равно \(-2\text{. }\). x}{x+2}\) имеет значение 1 для каждого возможного значения \(x\text{.}\) Таким образом, мы можем упростить последнее вышеприведенное выражение и теперь находим, что
}\). x}{x+2}\) имеет значение 1 для каждого возможного значения \(x\text{.}\) Таким образом, мы можем упростить последнее вышеприведенное выражение и теперь находим, что
\begin{уравнение*} \lim_{x \to -2} f(x) = \lim_{x \to -2} 2-x\text{.} \end{equation*}
Поскольку \(2-x\) является просто линейной функцией, этот предел теперь легко определить, и его значение явно равно \(4\text{.}\) Таким образом, из нескольких точек мы видели, что \(\lim_{x \to -2} f(x) = 4\text{.}\)
Далее мы обращаемся к функции \(g\text{,}\) и построить две таблицы и график.
| \(х\) | \(г(х)\) |
| \(2,9\) | \(0,84864\) |
| \(2,99\) | \(0,86428\) |
| \(2,999\) | \(0,86585\) |
| \(2,9999\) | \(0,86601\) |
| \(3.1\) | \(0,88351\) |
| \(3.01\) | \(0,86777\) |
| \(3.001\) | \(0,86620\) |
\(3. 0001\) 0001\) | \(0,86604\) |
| \(х\) | \(г(х)\) |
| \(-0,1\) | \(0\) |
| \(-0,01\) | \(0\) |
| \(-0,001\) | \(0\) |
| \(-0,0001\) | \(0\) |
| \(0,1\) | \(0\) |
| \(0,01\) | \(0\) |
| \(0,001\) | \(0\) |
| \(0,0001\) | \(0\) |
Таблица 1.2.7 Таблица значений \(g\) рядом с \(x=3\text{.}\) Таблица 1.2.8 Таблица значений \(g\) рядом с \(x=0\text{ .}\)Рисунок 1.2.9 График \(g(x)\) на \([-4,4]\text{.}\)
Во-первых, как \(x \to 3\text{,} \) из данных (и графика) видно, что функция приближается примерно к \(0,866025\text{.}\). Чтобы быть точным, мы должны использовать тот факт, что \(\frac{\pi}{x} \to \frac{\pi}{3}\text{,}\), и, таким образом, мы находим, что \(g(x) = \sin(\frac{\pi}{x}) \to \sin(\frac {\pi}{3})\) как \(x \to 3\text{. }\) Точное значение \(\sin(\frac{\pi}{3})\) равно \(\frac {\sqrt{3}}{2}\text{,}\), что приблизительно равно 0,8660254038. Таким образом, мы видим, что
}\) Точное значение \(\sin(\frac{\pi}{3})\) равно \(\frac {\sqrt{3}}{2}\text{,}\), что приблизительно равно 0,8660254038. Таким образом, мы видим, что
\begin{уравнение*} \lim_{x \to 3} g(x) = \frac{\sqrt{3}}{2}\text{.} \end{equation*}
Поскольку \(x \to 0\text{,}\) мы наблюдаем, что \(\frac{\pi}{x}\) не ведет себя элементарно. Когда \(x\) положителен и приближается к нулю, мы делим на все меньшие и меньшие положительные значения, и \(\frac{\pi}{x}\) неограниченно возрастает. Когда \(x\) отрицательно и приближается к нулю, \(\frac{\pi}{x}\) неограниченно уменьшается. В этом смысле, когда мы приближаемся к \(x = 0\text{,}\), входные параметры синуса быстро растут, и это приводит к диким колебаниям на графике \(g\text{.}\ ) Поучительно построить график функции \(g(x) = \sin\left(\frac{\pi}{x}\right)\) с помощью графической утилиты, а затем увеличить \(x = 0 \text{.}\) Это показывает, что функция никогда не достигает единственного значения вблизи начала координат, и предполагает, что \(g\) не имеет предела в \(x = 0\text{. }\) 9k \pi}{3}\right) = \frac{\sqrt{3}}{2} \приблизительно 0,866025\text{.}
\end{equation*}
}\) 9k \pi}{3}\right) = \frac{\sqrt{3}}{2} \приблизительно 0,866025\text{.}
\end{equation*}
Эта последовательность данных предполагает, что значение предела равно \(\frac{\sqrt{3}}{2}\text{.}\) Очевидно, что функция не может иметь два разных значения для предела, и это показывает, что \(g\) не имеет предела, поскольку \(x \to 0\text{.}\)
Важный урок, который можно извлечь из примера 1.2.3, заключается в том, что таблицы могут вводить в заблуждение при определении значение лимита. Хотя таблица значений полезна для исследования возможного значения предела, мы также должны использовать другие инструменты для подтверждения значения, если мы думаем, что таблица предполагает существование предела. 93 — 8}{х}\)
На этом заканчивается довольно длинное введение в понятие пределов. Важно помнить, что наше основное побуждение к рассмотрению пределов функций проистекает из нашего интереса к изучению скорости изменения функции. С этой целью мы завершаем этот раздел, возвращаясь к нашей предыдущей работе со средней и мгновенной скоростью и подчеркивая роль, которая ограничивает игру.
С этой целью мы завершаем этот раздел, возвращаясь к нашей предыдущей работе со средней и мгновенной скоростью и подчеркивая роль, которая ограничивает игру.
Подраздел 1.2.2 Мгновенная скорость
Предположим, что у нас есть движущийся объект, положение которого в момент времени \(t\) задано функцией \(s\text{.}\). Мы знаем, что средняя скорость объекта на интервале времени \([a, b]\) равно \(AV_{[a,b]} = \frac{s(b)-s(a)}{b-a}\text{.}\) Определим мгновенную скорость при \(a \) быть пределом средней скорости, когда \(b\) приближается к \(a\text{.}\). Обратите внимание, что при \(b \to a\text{,}\) длина временного интервала становится короче и короче (всегда включая \(a\)). В разделе 1.3 мы введем полезное сокращенное обозначение для представления мгновенной скорости изменения. Сейчас мы будем писать \(IV_{t=a}\) для мгновенной скорости в точке \(t = a\text{,}\) и, таким образом,
\begin{уравнение*}
IV_{t=a} = \lim_{b \to a} AV_{[a,b]} = \lim_{b \to a} \frac{s(b)-s(a)}{b-a}\text {. }
\end{уравнение*}
}
\end{уравнение*}
Эквивалентно, если мы думаем об изменяющемся значении \(b\) как о форме \(b = a + h\text{,}\), где \(h\) — некоторое небольшое число, тогда мы можем вместо этого написать
\begin{уравнение*} IV_{t=a} = \lim_{h \to 0} AV_{[a,a+h]} = \lim_{h \to 0} \frac{s(a+h)-s(a)}{ ч}\текст{.} \end{уравнение*}
Опять же, самая важная идея здесь заключается в том, что для вычисления мгновенной скорости мы берем предел средних скоростей по мере сокращения временного интервала. Два разных занятия дают возможность глубже изучить эти идеи и роль ограничений. 92\text{,}\) где \(s\) измеряется в метрах, а \(t\) измеряется в минутах.
Определите наиболее упрощенное выражение для средней скорости объекта на интервале \([3, 3+h]\text{,}\), где \(h \gt 0\text{.}\)
Определите среднюю скорость объекта на отрезке \([3,3.2]\text{.}\) Укажите в ответе единицы.
- Определите мгновенную скорость объекта, когда \(t = 3\text{.
 }\) Включите единицы измерения в свой ответ.
}\) Включите единицы измерения в свой ответ.
В заключительном задании этого раздела вам предлагается провести некоторые связи между средней скоростью, мгновенной скоростью и наклонами определенных линий.
Мероприятие 1.2.4
Для движущегося объекта, положение которого \(s\) в момент времени \(t\) указано на графике ниже, ответьте на каждый из следующих вопросов. Предположим, что \(s\) измеряется в футах, а \(t\) измеряется в секундах.
- Используйте график для оценки средней скорости объекта на каждом из следующих интервалов: \([0.5,1]\text{,}\) \([1.5,2.5]\text{,}\) \( [0,5]\text{.}\) Нарисуйте каждую линию, наклон которой представляет собой среднюю скорость, которую вы ищете.
- Как можно использовать средние скорости или наклоны линий для оценки мгновенной скорости объекта в фиксированный момент времени?
- Используйте график для оценки мгновенной скорости объекта при \(t = 2\text{.}\) Должна ли эта мгновенная скорость при \(t = 2\) быть больше или меньше средней скорости при \([1.
 5 ,2.5]\), которые вы вычислили в (а)? Почему?
5 ,2.5]\), которые вы вычислили в (а)? Почему?
Рисунок 1.2.10 График функции положения \(y = s(t)\) в Упражнении 1.2.4.
Подраздел 1.2.3 Резюме
Ограничения позволяют нам исследовать тенденции в поведении функции вблизи определенной точки. В частности, при установлении предела в заданной точке возникает вопрос, имеют ли ближайшие значения функции возможность приблизиться к определенному фиксированному значению.
Когда мы пишем \(\lim_{x \to a} f(x) = L\text{,}\), мы читаем это как говорящее «предел \(f\) по мере того, как \(x\) приближается \ (a\) равно \(L\text{,}\)», и это означает, что мы можем сделать значение \(f(x)\) как можно более близким к \(L\), взяв \(x \) достаточно близко (но не равно) к \(a\text{.}\)
Если мы хотим знать \(\lim_{x \to a} f(x)\) для заданного значения \(a\) и известной функции \(f\text{,}\), мы можем оценить это значение из графика \(f\) или путем создания таблицы значений функций, которые являются результатом последовательности \(x\)-значений, которые все ближе и ближе к \(a\text{.
 }\) Если мы нужно точное значение предела, нам нужно поработать с функцией алгебраически и посмотреть, сможем ли мы использовать знакомые свойства известных базовых функций, чтобы понять, как различные части формулы для \(f\) изменяются при \(x \to а\текст{.}\)
}\) Если мы нужно точное значение предела, нам нужно поработать с функцией алгебраически и посмотреть, сможем ли мы использовать знакомые свойства известных базовых функций, чтобы понять, как различные части формулы для \(f\) изменяются при \(x \to а\текст{.}\)Мгновенная скорость движущегося объекта в фиксированное время определяется путем определения предела средних скоростей объекта за все более и более короткие интервалы времени, каждый из которых содержит интересующее время.
Подраздел Упражнения
¶1 Пределы на кусочном графе
2 Численная оценка предела
3 Пределы для кусочной формулы
4 Оценка предела алгебраически
5
-4}\текст{.}\)
6
Пусть \(g(x) = -\frac{|x+3|}{x+3}\text{.}\)
- Каков домен \(g\text{?}\)
- Используйте последовательность значений рядом с \(a = -3\), чтобы оценить значение \(\lim_{x \to -3} g(x)\text{,}\), если вы считаете, что предел существует.
 Если вы считаете, что предела не существует, объясните, почему.
Если вы считаете, что предела не существует, объясните, почему. - Используйте алгебру, чтобы упростить выражение \(\frac{|x+3|}{x+3}\) и, следовательно, работать над точным вычислением \(\lim_{x \to -3} g(x)\), если он существует, или объяснить, как ваша работа показывает, что предела не существует. Обсудите, как ваши выводы соотносятся с вашими результатами в (b). (Подсказка: \(|a| = a\) всякий раз, когда \(a \ge 0\text{,}\), но \(|a| = -a\) всякий раз, когда \(a \lt 0\text{.}\ ))
- Верно или неверно: \(g(-3) = -1\text{.}\) Почему?
- Верно или неверно: \(-\frac{|x+3|}{x+3} = -1\text{.}\) Почему? Как это равенство связано с вашей работой выше с функцией \(g\text{?}\)
- На основе всей вашей работы выше, постройте точный размеченный график \(y = g(x)\) на интервале \([-4,-2]\text{,}\) и напишите предложение, которое объясняет, что вы теперь знаете о \(\lim_{x \to -3} g(x)\text{.}\)
7
Для каждого из следующих запросов нарисуйте график на предоставленных осях функции, которая имеет указанные свойства.

 }\) Включите единицы измерения в свой ответ.
}\) Включите единицы измерения в свой ответ. 5 ,2.5]\), которые вы вычислили в (а)? Почему?
5 ,2.5]\), которые вы вычислили в (а)? Почему?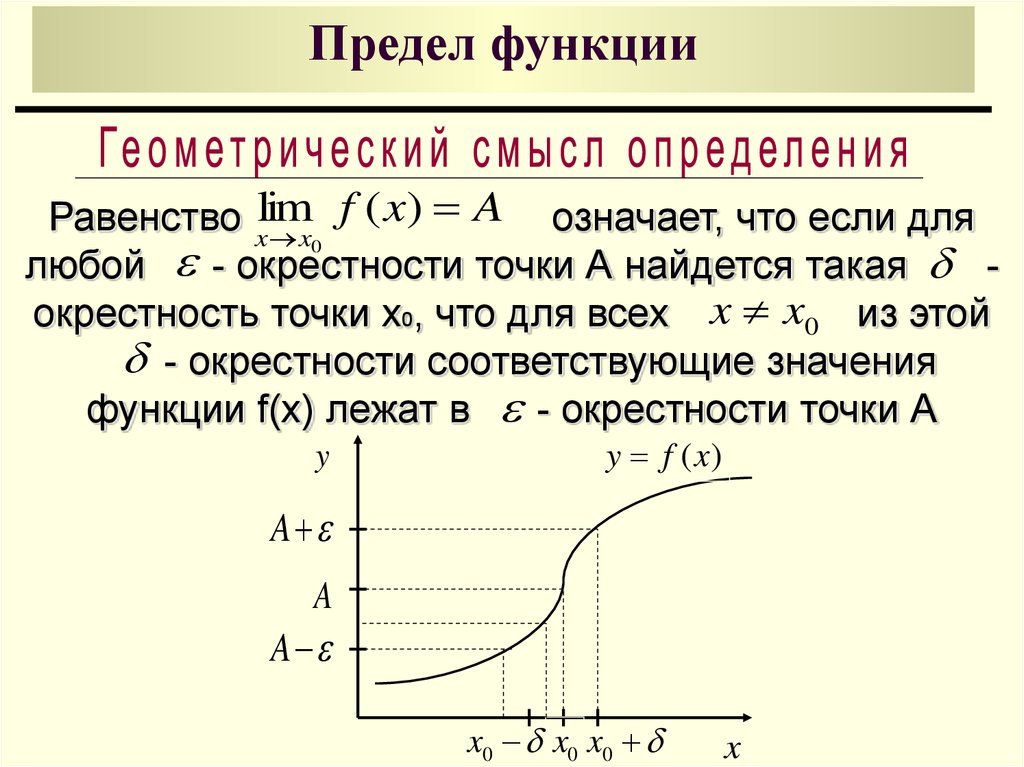 }\) Если мы нужно точное значение предела, нам нужно поработать с функцией алгебраически и посмотреть, сможем ли мы использовать знакомые свойства известных базовых функций, чтобы понять, как различные части формулы для \(f\) изменяются при \(x \to а\текст{.}\)
}\) Если мы нужно точное значение предела, нам нужно поработать с функцией алгебраически и посмотреть, сможем ли мы использовать знакомые свойства известных базовых функций, чтобы понять, как различные части формулы для \(f\) изменяются при \(x \to а\текст{.}\) Если вы считаете, что предела не существует, объясните, почему.
Если вы считаете, что предела не существует, объясните, почему.