Квадратное уравнение через дискриминант: Онлайн калькулятор. Решение квадратных уравнений

2
D1>0, значит, уравнение имеет 2 корня
x1,2= k +/ квадратный корень из D1)/a
x1= (-(-12) +9)/3=21/3=7
x2= (-(-12) -9)/3=3/3=1

Оценили на сколько легче решение?;)
Спасибо за внимание, желаю Вам успехов в учебе =)

• В нашем случае в уравнениях D и D1 были >0 и мы получили по 2 корня. Если бы было D=0 и D1=0, то мы получили бы по одному корню, а если бы было D
• Через корень дискриминанта (D1) можно решать только те уравнения, в которых член b четный(!)

Прежде чем мы узнаем, как найти дискриминант квадратного уравнения вида ax2+bx+c=0 и как найти корни данного уравнения, нам необходимо вспомнить определение квадратного уравнения. Уравнение, которое имеет вид ax 2 + bx + c = 0 (где a,b и c — любые числа, также надо помнить, что a ≠ 0) является квадратным. Все квадратные уравнения мы разделим на три разряда:

1. те, у которых нет корней;
2. имеется один корень в уравнении;
3. есть два корня.

Для того чтобы определить количество корней в уравнении нам необходим дискриминант.

Как найти дискриминант. Формула

Нам дано: ax 2 + bx + c = 0.

Формула дискриминанта: D = b 2 — 4ac .

Как найти корни дискриминанта

По знаку дискриминанта определяется количество корней:

1. D = 0, у уравнения один корень;
2. D > 0, у уравнения два корня.

Корни у квадратного уравнения находятся по следующей формуле:

X1= -b + √D/2а; X2= -b + √D/2a.

Если D = 0, то Вы можете смело использовать любую из представленных формул. У Вас получится одинаковый ответ в любом случае. А если получается так, что D > 0, то тогда Вам не придется ничего считать, так как корней уравнение не имеет.

Надо сказать, что находить дискриминант — это не так уж сложно, если знать формулы и внимательно осуществлять подсчеты. Иногда возникают ошибки при подстановке отрицательных чисел в формулу (нужно помнить, что минус на минус дает плюс). Будьте внимательны, и все получится!

Квадратные уравнения изучают в 8 классе, поэтому ничего сложного здесь нет. Умение решать их совершенно необходимо.

Квадратное уравнение — это уравнение вида ax 2 + bx + c = 0, где коэффициенты a , b и c — произвольные числа, причем a ≠ 0.

Прежде, чем изучать конкретные методы решения, заметим, что все квадратные уравнения можно условно разделить на три класса:

1. Не имеют корней;
2. Имеют ровно один корень;
3. Имеют два различных корня.

В этом состоит важное отличие квадратных уравнений от линейных, где корень всегда существует и единственен. Как определить, сколько корней имеет уравнение? Для этого существует замечательная вещь — дискриминант .

Дискриминант

Пусть дано квадратное уравнение ax 2 + bx + c = 0. Тогда дискриминант — это просто число D = b 2 − 4ac .

Эту формулу надо знать наизусть. Откуда она берется — сейчас неважно. Важно другое: по знаку дискриминанта можно определить, сколько корней имеет квадратное уравнение.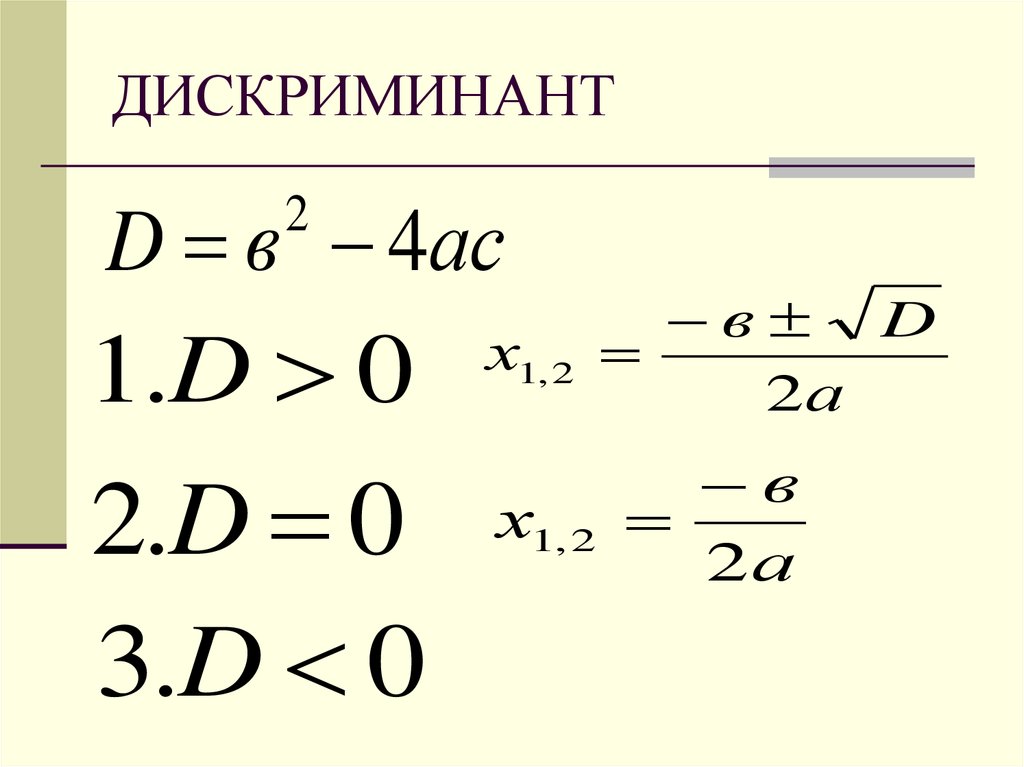 А именно:

1. Если D
2. Если D = 0, есть ровно один корень;
3. Если D > 0, корней будет два.

Обратите внимание: дискриминант указывает на количество корней, а вовсе не на их знаки, как почему-то многие считают. Взгляните на примеры — и сами все поймете:

Задача. Сколько корней имеют квадратные уравнения:

1. x 2 − 8x + 12 = 0;
2. 5x 2 + 3x + 7 = 0;
3. x 2 − 6x + 9 = 0.

Выпишем коэффициенты для первого уравнения и найдем дискриминант:
a = 1, b = −8, c = 12;
D = (−8) 2 − 4 · 1 · 12 = 64 − 48 = 16

Итак, дискриминант положительный, поэтому уравнение имеет два различных корня. Аналогично разбираем второе уравнение:

a = 5; b = 3; c = 7;
D = 3 2 − 4 · 5 · 7 = 9 − 140 = −131.

Дискриминант отрицательный, корней нет. Осталось последнее уравнение:
a = 1; b = −6; c = 9;
D = (−6) 2 − 4 · 1 · 9 = 36 − 36 = 0.

Дискриминант равен нулю — корень будет один.

Обратите внимание, что для каждого уравнения были выписаны коэффициенты. Да, это долго, да, это нудно — зато вы не перепутаете коэффициенты и не допустите глупых ошибок. Выбирайте сами: скорость или качество.

Кстати, если «набить руку», через некоторое время уже не потребуется выписывать все коэффициенты. Такие операции вы будете выполнять в голове. Большинство людей начинают делать так где-то после 50-70 решенных уравнений — в общем, не так и много.

Корни квадратного уравнения

Теперь перейдем, собственно, к решению. Если дискриминант D > 0, корни можно найти по формулам:

Основная формула корней квадратного уравнения

Когда D = 0, можно использовать любую из этих формул — получится одно и то же число, которое и будет ответом. Наконец, если D

1. x 2 − 2x − 3 = 0;
2. 15 − 2x − x 2 = 0;
3. x 2 + 12x + 36 = 0.

Первое уравнение:
x 2 − 2x − 3 = 0 ⇒ a = 1; b = −2; c = −3;
D = (−2) 2 − 4 · 1 · (−3) = 16.

D > 0 ⇒ уравнение имеет два корня. Найдем их:

Второе уравнение:
15 − 2x − x 2 = 0 ⇒ a = −1; b = −2; c = 15;
D = (−2) 2 − 4 · (−1) · 15 = 64.

D > 0 ⇒ уравнение снова имеет два корня. Найдем их

\[\begin{align} & {{x}_{1}}=\frac{2+\sqrt{64}}{2\cdot \left(-1 \right)}=-5; \\ & {{x}_{2}}=\frac{2-\sqrt{64}}{2\cdot \left(-1 \right)}=3. \\ \end{align}\]

Наконец, третье уравнение:
x 2 + 12x + 36 = 0 ⇒ a = 1; b = 12; c = 36;

D = 12 2 − 4 · 1 · 36 = 0.

D = 0 ⇒ уравнение имеет один корень. Можно использовать любую формулу. Например, первую:

Как видно из примеров, все очень просто. Если знать формулы и уметь считать, проблем не будет. Чаще всего ошибки возникают при подстановке в формулу отрицательных коэффициентов. Здесь опять же поможет прием, описанный выше: смотрите на формулу буквально, расписывайте каждый шаг — и очень скоро избавитесь от ошибок.

Неполные квадратные уравнения

Бывает, что квадратное уравнение несколько отличается от того, что дано в определении. Например:

1. x 2 + 9x = 0;
2. x 2 − 16 = 0.

Несложно заметить, что в этих уравнениях отсутствует одно из слагаемых. Такие квадратные уравнения решаются даже легче, чем стандартные: в них даже не потребуется считать дискриминант. Итак, введем новое понятие:

Уравнение ax 2 + bx + c = 0 называется неполным квадратным уравнением, если b = 0 или c = 0, т.е. коэффициент при переменной x или свободный элемент равен нулю.

Разумеется, возможен совсем тяжелый случай, когда оба этих коэффициента равны нулю: b = c = 0. В этом случае уравнение принимает вид ax 2 = 0. Очевидно, такое уравнение имеет единственный корень: x = 0.

Рассмотрим остальные случаи. Пусть b = 0, тогда получим неполное квадратное уравнение вида ax 2 + c = 0. Немного преобразуем его:

Поскольку арифметический квадратный корень существует только из неотрицательного числа, последнее равенство имеет смысл исключительно при (−c /a ) ≥ 0. Вывод:

1. Если в неполном квадратном уравнении вида ax 2 + c = 0 выполнено неравенство (−c /a ) ≥ 0, корней будет два. Формула дана выше;
2. Если же (−c /a )

Как видите, дискриминант не потребовался — в неполных квадратных уравнениях вообще нет сложных вычислений. На самом деле даже необязательно помнить неравенство (−c /a ) ≥ 0. Достаточно выразить величину x 2 и посмотреть, что стоит с другой стороны от знака равенства. Если там положительное число — корней будет два. Если отрицательное — корней не будет вообще.

Теперь разберемся с уравнениями вида ax 2 + bx = 0, в которых свободный элемент равен нулю. Тут все просто: корней всегда будет два. Достаточно разложить многочлен на множители:

Вынесение общего множителя за скобку

Произведение равно нулю, когда хотя бы один из множителей равен нулю. Отсюда находятся корни. В заключение разберем несколько таких уравнений:

Задача. Решить квадратные уравнения:

1. x 2 − 7x = 0;
2. 5x 2 + 30 = 0;
3. 4x 2 − 9 = 0.

x 2 − 7x = 0 ⇒ x · (x − 7) = 0 ⇒ x 1 = 0; x 2 = −(−7)/1 = 7.

5x 2 + 30 = 0 ⇒ 5x 2 = −30 ⇒ x 2 = −6. Корней нет, т.к. квадрат не может быть равен отрицательному числу.

4x 2 − 9 = 0 ⇒ 4x 2 = 9 ⇒ x 2 = 9/4 ⇒ x 1 = 3/2 = 1,5; x 2 = −1,5.

Квадратное уравнение

Главная » АЛГЕБРА » Квадратное уравнение

АЛГЕБРА

Автор Ольга Викторовна Опубликовано 05.06.2021

Квадратное уравнение – важное уравнение не только в школьном курсе алгебры. Квадратное уравнение часто используется в геометрии при расчете. Поэтому знать формулы корней квадратного уравнения, чтобы решать его быстрее, нужно всем.

Содержание

Определение квадратного уравнения

Квадратное уравнение – это уравнение вида , где – переменная, , , – некоторые числа, причем . В квадратном уравнении коэффициент называют первым коэффициентом, – вторым коэффициентом, – свободным членом.

Формула корней

Формула корней квадратного уравнения имеет вид:

Выражение называется дискриминантом квадратного уравнения и обозначается буквой .

Влияние дискриминанта на корни квадратного уравнения

Максимальное количество корней квадратного уравнения равно степени уравнения. Квадратное уравнение имеет вторую степень переменной, поэтому и должно иметь два корня. Однако возможны случаи совпадения корней, тогда формально говорят, что “уравнение имеет один корень”, хотя правильнее говорить – “уравнение имеет одно значение переменной”, или “корни уравнения совпадают и равны…” Есть еще вариант, что уравнение не имеет действительных корней или не имеет действительных решений. Узнать о том – решается квадратное уравнение и сколько имеет корней можно вычислив дискриминант.

1. Если , то существует только одно значение переменной, удовлетворяющее уравнению . Однако условились говорить, что в этом случае квадратное уравнение имеет два равных действительных корня, а само число называют корнем кратности два.
2. Если , то квадратное уравнение не имеет действительных корней.
3. Если , то квадратное уравнение имеет два различных действительных корня.

Приведенное квадратное уравнение

Пусть дано квадратное уравнение . Так как , то, разделив обе части уравнения на , получим уравнение

. Считая, что и , получим уравнение , в котором первый коэффициент равен 1. Это уравнение называется приведенным.

Формула корней приведенного квадратного уравнения имеет вид:

Неполные квадратные уравнения

Уравнения вида   ,   и называются квадратными уравнениями.

Биквадратное уравнение

Уравнение вида   называется биквадратным уравнением. Оно решается с помощью замены переменной по формуле и приводится к квадратному уравнению .

Примеры решения квадратного уравнения

Уравнение 1

Решите уравнение

Решение:Найдем дискриминант , .

Найдем корни уравнения по формуле корней квадратного уравнения:

.

Отсюда

,       .

Ответ: ,  .

Уравнение 2

Решите уравнение .

Решение: находим дискриминант , . Применим формулу корней квадратного уравнения:

. Тогда

, .

Ответ: ,  .

Уравнение 3

Решите уравнение .

Решение: найдем дискриминант

, . Так как дискриминант отрицателен, то уравнение не имеет корней.

Ответ: нет корней.

Уравнение 4

Решите уравнение

Решение: находим дискриминант

, . Применим формулу корней квадратного уравнения

.

Отсюда

,

Таким образом, уравнение имеет единственный корень .

Ответ:

Уравнение 5

Решите квадратное уравнение

Решение: Применим формулу корней для приведенного квадратного уравнения: . Отсюда ,  .

Ответ: ,  .

( 3 оценки, среднее 3.67 из 5 )

Поделиться с друзьями

Видео-вопрос: Использование знака дискриминанта для определения числа комплексных корней квадратного уравнения

Стенограмма видео

Сколько недействительных корней будет иметь квадратное уравнение, если его дискриминант отрицателен?

Прежде чем мы сможем ответить на этот вопрос, давайте начнем с определения некоторых ключевых терминов. Квадратное уравнение имеет вид 𝑎𝑥 в квадрате плюс 𝑏𝑥 плюс 𝑐 равно нулю. В этом примере мы будем думать исключительно о значениях 𝑎, 𝑏 и 𝑐, которые являются действительными числами. Но для любого квадратного уравнения 𝑎 не может быть равно нулю. Корнями этого квадратного уравнения являются решения или значения 𝑥, которые удовлетворяют 𝑎𝑥 в квадрате плюс 𝑏𝑥 плюс 𝑐 равно нулю. И затем вопрос спрашивает нас, сколько невещественных корней будет у него, если дискриминант отрицательный.

Итак, что мы подразумеваем под дискриминантом? Что ж, чтобы ответить на это, вспомним квадратную формулу. Это говорит нам о том, что решения уравнения 𝑎𝑥 в квадрате плюс 𝑏𝑥 плюс 𝑐 равно нулю: 𝑥 равно отрицательному 𝑏 плюс или минус квадратный корень из 𝑏 в квадрате минус четыре 𝑎𝑐 по всем двум 𝑎. Дискриминант — это выражение внутри квадратного корня. Мы используем Δ для его представления, и это 𝑏 в квадрате минус четыре 𝑎𝑐.

Отсюда следует, что если дискриминант, если 𝑏 в квадрате минус четыре 𝑎𝑐, положителен, когда мы извлекаем квадратный корень, мы получаем действительное решение. И, в частности, если дискриминант положителен, квадратный корень является ненулевым действительным числом. Это означает, что когда у нас есть положительный дискриминант, у квадратного уравнения есть два действительных решения. Другими словами, есть два действительных корня. Однако, если дискриминант равен нулю, мы берем квадратный корень из нуля, который равен нулю. Это означает, что наши решения 𝑎𝑥 в квадрате плюс 𝑏𝑥 плюс 𝑐 равно нулю просто отрицательные 𝑏 более двух 𝑎. Итак, это на самом деле одно решение. Итак, когда дискриминант равен нулю, мы получаем один действительный корень.

А если дискриминант отрицательный, как в этом вопросе? Что ж, если оно отрицательное, мы извлекаем квадратный корень из отрицательного числа, что дает нам мнимое решение. Это означает, что на самом деле нет никаких реальных корней. Вместо этого мы получаем комплексные корни. Но сколько комплексных корней мы получим? Что ж, давайте предположим, что когда мы берем квадратный корень из 𝑏 в квадрате минус четыре 𝑎𝑐, мы получаем некоторое значение 𝑑, умноженное на 𝑖, где 𝑑 — константа, действительная константа, а 𝑖 — мнимое число, которое является решением уравнения 𝑖 квадрат равен минус единице.

В этом случае решения нашего квадратного уравнения: 𝑥 равно отрицательному 𝑏 плюс или минус 𝑑𝑖 по двум 𝑎. Мы можем разделить это на два разных решения 𝑥 sub one и 𝑥 sub two. Это не настоящие, а сложные решения квадратного уравнения. Они отрицательны 𝑏 плюс 𝑑𝑖 больше двух 𝑎 и минус 𝑏 минус 𝑑𝑖 больше двух 𝑎 соответственно. Мы видим, что есть два комплексных решения квадратного уравнения, хотя дискриминант отрицательный.

Итак, ответ — два. Квадратное уравнение будет иметь два невещественных корня, если его дискриминант отрицателен.

9.4: Руководство по решению квадратных уравнений и приложений

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

18385

• Аноним
• LibreTexts 9{2}−10x+30=0\).

  Решение :

  Начнем с идентификации a , b и c . Здесь

  Подставляем эти значения в дискриминант и упрощаем.

  Поскольку дискриминант отрицателен, мы заключаем, что реальных решений нет.

  Ответ :

  Нет действительного решения

  Если мы воспользуемся квадратичной формулой из предыдущего примера, мы обнаружим, что отрицательное подкоренное число останавливает процесс упрощения и показывает, что действительного решения нет. 9{2}-10x+1=0\)

  Решение :

  Здесь

  Подставим эти значения в дискриминант:

  Поскольку дискриминант положительный, мы можем заключить, что существует два действительных решения.

  Ответ :

  Два действительных решения

  Если мы используем квадратичную формулу в предыдущем примере, мы обнаружим, что положительное подкоренное в квадратной формуле приводит к двум действительным решениям.

  Двумя действительными решениями являются \(\frac{5-3 \sqrt{2}}{7}\) и \(\frac{5+3 \sqrt{2}}{7}\). Обратите внимание, что эти решения иррациональны; мы можем приблизить значения на калькуляторе. 9{2}-7x-4=0\)

  Решение :

  В этом примере

  Подставьте эти значения в дискриминант и упростите.

  Поскольку дискриминант положителен, мы заключаем, что существует два действительных решения. Кроме того, поскольку дискриминант представляет собой полный квадрат, мы получаем два рациональных решения.

  Ответ :

  Два действительных решения

  Мы могли бы решить предыдущее квадратное уравнение, используя квадратную формулу следующим образом:

  \(\begin{array}{lll}{x=\frac{7-9}{4}} & {\text {или}} &{x=\frac{7+9}{4}} \ \ {x=\frac{-2}{4}} && {x=\frac{16}{4}} \\ {x=-\frac{1}{2}} && {x=4}\end {массив}\)

  Примечание

  Если дискриминант представляет собой полный квадрат, то мы могли бы разложить исходное уравнение на множители.

  \(\begin{array}{rlr}{2 x+1} & {=0} & {\text {или}} & {x-4=0} \\ {2 x} & {=-1 } & {} & {x=4} \\ {x} & {=-\frac{1}{2}}\end{array}\)

  Учитывая особое условие, когда дискриминант равен 0, мы получаем только одно решение, двойной корень. 9{2}-6x+1=0\)

  Решение :

  Здесь a=9, b=−6 и c=1, и мы имеем

  Поскольку дискриминант равен 0, мы заключаем, что существует только одно действительное решение, двойной корень.

  Ответ :

  Одно действительное решение

  Так как 0 является полным квадратом, мы можем решить приведенное выше уравнение, разложив его на множители.

  \(\begin{array}{rrr}{3 x-1=0} & {\text {или} \quad 3 x-1=0} \\ {3 x=1} & {3 x=1 } \\ {x=\frac{1}{3}} & {x=\frac{1}{3}}\end{массив}\) 9{2}-6x-7=0\)

  Решение :

  Начните с идентификации a , b и c коэффициента каждого члена. Здесь

  Подставим эти значения в дискриминант и упростим.

  Так как дискриминант положительный, а не полный квадрат, используйте квадратичную формулу и ожидайте два действительных решения.

  Ответ :

  Решения: \(=\frac{1 \pm 2 \sqrt{2}}{3}\)

  Пример \(\PageIndex{8}\)

  Решите:

  \(4 x(x-2)=-7\)

  Решение :

  Начните с перезаписи квадратного уравнения в стандартной форме.

  Здесь

  Подставляем эти значения в дискриминант и упрощаем.

  Поскольку дискриминант отрицателен, решения не являются действительными числами.

  Ответ :

  Нет действительного решения

  Пример \(\PageIndex{9}\)

  Решить: 9{2}+2x-7=2x-3\)

  Ответ

  \(\pm\frac{2 \sqrt{5}}{5}\)

  Приложения, использующие квадратные уравнения

  В этом разделе алгебраические установки обычно состоят из квадратного уравнения, решения которого могут не быть целыми числами.

  Пример \(\PageIndex{10}\)

  Высота треугольника на 2 дюйма меньше, чем удвоенная длина его основания. Если общая площадь треугольника 11 квадратных дюймов, то найти длины основания и высоты. Округлить ответы до сотых

  Решение :

  Рисунок \(\PageIndex{1}\)Рисунок \(\PageIndex{2}\)

  Используйте формулу \(A=\frac{1}{2}bh\) и тот факт, что площадь составляет 11 квадратных дюймов, чтобы составить алгебраическое уравнение. {2}-x-11}\конец{массив}\)

  Используйте коэффициенты a = 1, b = −1 и c = −11, чтобы определить тип решения.

  Поскольку дискриминант положительный, ожидайте два действительных решения.

  В этой задаче игнорируйте отрицательное решение и рассматривайте только положительное решение.

  \(x=\frac{1+3 \sqrt{5}}{2}\)

  Обратно подставьте, чтобы найти высоту.

  Ответ :

  Размеры основания \(\frac{-1+3 \sqrt{5}}{2}\приблизительно 3,85\) дюймов, а высота \(-1+3 \sqrt{5} \приблизительно 5,71\) дюймов.

  Пример \(\PageIndex{11}\)

  Сумма квадратов двух последовательных натуральных чисел равна 481. Найдите целые числа.

  Решение :

  Пусть n представляет первое положительное целое число.

  Пусть n+1 представляет следующее положительное целое число.

  Алгебраическая установка следующая:

  Рисунок \(\PageIndex{3}\)

  Перепишите квадратное уравнение в стандартной форме.

  Когда коэффициенты велики, иногда проще использовать квадратичную формулу вместо того, чтобы пытаться разложить ее на множители. В этом случае a=1 , b=1 и c=-240 . Подставляем в квадратную формулу и упрощаем.

  \(\begin{array}{ll}{n=\frac{-1-31}{2}} & {n=\frac{-1+31}{2}} \\ {n=\frac {-32}{2}} & {n=\frac{30}{2}} \\ {n=-16} & {n=15}\end{массив}\)

  Поскольку проблема требует положительного числа, игнорируем отрицательное решение и выбираем n = 15.

  \(\begin{aligned} n+1 &=\color{OliveGreen}{15}\color{black}{+}1 \\ & =16 \end{выровнено}\) 9{2}-4ac\). Если дискриминант отрицателен, то решения недействительны. Если дискриминант положительный, то решения действительны. Если дискриминант равен 0, то есть только одно решение — двойной корень.

• Выберите подходящий метод решения квадратного уравнения на основе значения его дискриминанта. Хотя квадратичная формула решает любое квадратное уравнение, это может быть не самый эффективный метод.
• При решении задач используйте ключевые слова и фразы, чтобы составить алгебраическое уравнение, моделирующее задачу. В этом разделе установка обычно включает квадратное уравнение. 9{2}−6t+1=0\)

Ответить

1. −8, действительного решения нет

3. 25, два действительных раствора

5. −72, действительного решения нет

7. 1, два действительных раствора

9. −1, действительного решения нет

11. 20, два действительных раствора

13. 0, одно действительное решение

Упражнение \(\PageIndex{4}\) решение

Выберите подходящий метод для решения следующего. 9{2}=4(3t−1)\)

• \(5t(5t−6)=−9\)
• \((х+1)(х+7)=3\)
• \((х-5)(х+7)=14\)

Ответить

1. \(-1, 3\)

3. \(-\frac{2}{3} , 1\)

5. Нет реального решения

7. \(-\frac{1}{5} , 0\)

9. Нет реального решения

11. \(-1\pm\sqrt{5}\)

13. \(\frac{5}{2}\)

15. \(2\pm\sqrt{5}\)

17. Нет реального решения

19. \(\pm\frac{2 \sqrt{5}}{5}\)

21. \(\frac{1}{2}, 4\)

23. \(0, \frac{1}{18}\)

25. Нет реального решения

27. \(\frac{-1\pm\sqrt{6}}{2}\)

29. Нет реального решения

31. \(-\frac{1}{2}, \frac{1}{3}\)

33.\(\frac{2}{3}\)

35. \(-4\pm 2\sqrt{3}\)

Упражнение \(\PageIndex{5}\) число приложений проблемы

Составьте алгебраическое уравнение и решите с его помощью следующее.

1. Положительное действительное число на 2 меньше другого. Если к квадрату меньшего прибавить в 4 раза больше, получится 49. Найдите числа.
2. Положительное действительное число на 1 больше, чем другое. Если из квадрата большего вычесть удвоенное меньшее, получится 4. Найдите числа.
3. Положительное действительное число на 6 меньше другого. Если сумма квадратов двух чисел равна 38, то найдите числа.
4. Положительное действительное число на 1 больше, чем в два раза. Если 4 раза меньшее число вычесть из квадрата большего, то получится 21. Найдите числа.

Ответить

1. \(3\sqrt{5}\) и \(3\sqrt{5}-2)

3. \(\sqrt{10\pm 3\)

Упражнение \(\PageIndex{6}\) приложения задачи по геометрии

Округлите свои ответы до сотых.

1. Площадь прямоугольника 60 квадратных дюймов. Если длина в 3 раза больше ширины, то найдите размеры прямоугольника.
2. Площадь прямоугольника 6 квадратных футов. Найдите размеры прямоугольника, если его длина на 2 м больше ширины.
3. Площадь прямоугольника 27 квадратных метров. Если длина на 6 м меньше ширины в 3 раза, то найдите размеры прямоугольника.
4. Площадь треугольника равна 48 квадратных дюймов. Если основание в 2 раза больше высоты, то найдите длину основания.
5. Площадь треугольника 14 квадратных футов. Если основание на 4 фута больше высоты в 2 раза, то найдите длину основания и высоту.
6. Площадь треугольника 8 квадратных метров. Если основание на 4 метра меньше высоты, то найти длину основания и высоту.
7. Периметр прямоугольника равен 54 сантиметрам, а площадь 180 квадратных сантиметров. Найдите размеры прямоугольника.
8. Периметр прямоугольника равен 50 дюймов, а площадь 126 квадратных дюймов. Найдите размеры прямоугольника.
9. Джордж успешно ухаживает за садом размером 6 на 8 метров. В следующем сезоне он планирует удвоить площадь посадки, увеличив ширину и высоту на одинаковую величину. На сколько он должен увеличить длину и ширину?
10. Вокруг сада размером 6 на 8 футов должна быть построена единая кирпичная ограда. Если общая площадь сада, включая бордюр, должна быть 100 квадратных футов, то найдите ширину кирпичного бордюра.

Ответить

1. Длина: 13,42 дюйма; ширина: 4,47 дюйма

3. Длина: 6,48 метра; ширина: 4,16 метра

5. Высота: 2,87 фута; база: 9,74 фута

7. Длина: 15 см; ширина: 12 сантиметров

9. 2,85 метра

Упражнение \(\PageIndex{7}\) Применение теоремы Пифагора

1. Если стороны квадрата измеряются \(\sqrt{106}\) единицами, то найдите длину диагонали.
2. Если диагональ квадрата равна \(\sqrt{310}\) единиц, найдите длину каждой стороны.
3. Диагональ прямоугольника равна \(\sqrt{63}\) дюймам. Найдите размеры прямоугольника, если его ширина на 4 см меньше длины.
4. Диагональ прямоугольника равна \(\sqrt{23}\) дюймам. Найдите размеры прямоугольника, если его ширина на 2 см меньше длины.
5. Верх 20-футовой лестницы, прислоненной к зданию, достигает высоты 18 футов. На каком расстоянии основание лестницы от стены? Округлите до сотых.
6. Для безопасного использования лестницы основание должно располагаться примерно на 1/4 длины лестницы от стены. Если безопасно использовать 20-футовую лестницу, то какой высоты по отношению к зданию будет достигать вершина лестницы? Округлите до сотых.
7. Диагональ телевизионного монитора составляет 32 дюйма. Если монитор имеет соотношение сторон 3:2, то определите его длину и ширину. Округлите до сотых.
8. Диагональ телевизионного монитора составляет 52 дюйма. Если на мониторе 16:9соотношение сторон, затем определить его длину и ширину. Округлите до сотых.

Ответить

1. \(\sqrt{203}\) единиц

3. Длина: \(2+\sqrt{52}\) дюймов; ширина: \(−2+\sqrt{52}\) дюймов

5. \(2\sqrt{19} \примерно 8,72\) футов

7. Длина: 26,63 дюйма; ширина: 17,75 дюйма

Упражнение \(\PageIndex{8}\) бизнес-задачи приложений

1. Прибыль в долларах от работы сборочной линии, ежедневно производящей нестандартную униформу, определяется функцией \(P(t)=−40t^{2 }+9{2}\).

   No related posts.