Квадратные неравенства решение: Квадратные неравенства, решение, примеры, графический метод, тесты

{2}+b \times y+c<0\]

В выражении a,b,c – простые числа, y не равно нулю, вместо знака ˂ может стоять любой знак, выражающий неравенство.

Во многих источниках по математике можно встретить квадратные неравенства под наименованием «неравенства второй степени». Это легко пояснить. Левая часть приведенного выражения присутствует многочлен второй степени в виде квадратного трехчлена:

a×y2+b×y+c

Многие называют такие неравенства квадратичными, но это неправильно, так как квадратичными в математике принято называть функции. Они имеют вид:

\[x=a \times y 2+b \times y+c\]

Чтобы можно было легко понять разницу, лучше на примере рассмотреть, что такое квадратные неравенства системы уравнений.

Пример:

3×y²+1×y+14>0

В приведенном примере в качества a цифра 3, в качестве b число 1, в качестве c число 14.

В качестве простых чисел могут быть и положительные, и отрицательные числа, дроби, и т.

{2}-8 \geq 0\]

Содержание

Как решать квадратные неравенства

Есть несколько методов решения неравенств квадратных уравнений:

Графический.
Методом интервалов.
Посредством выделения квадратного двучлена из левой части выражения.

Рассмотрим подробнее особенности применения каждого метода.

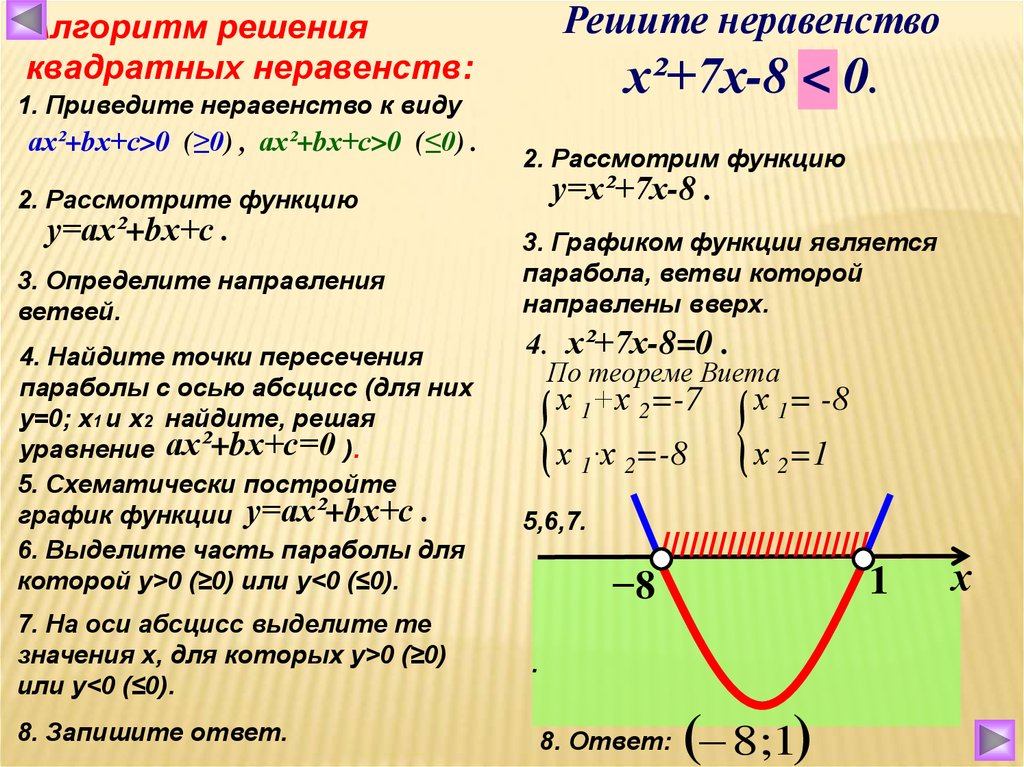
Графический метод решения квадратных неравенств

Метод заключается в выполнении анализа и изучения графика квадратичной функции.

x=a×y²+b×y+c для квадратных неравенств типа a×y2+b×y+c<0.

В качестве решения квадратного неравенства выступают интервалы, на которых эта функция принимает или положительное, или отрицательное значение.

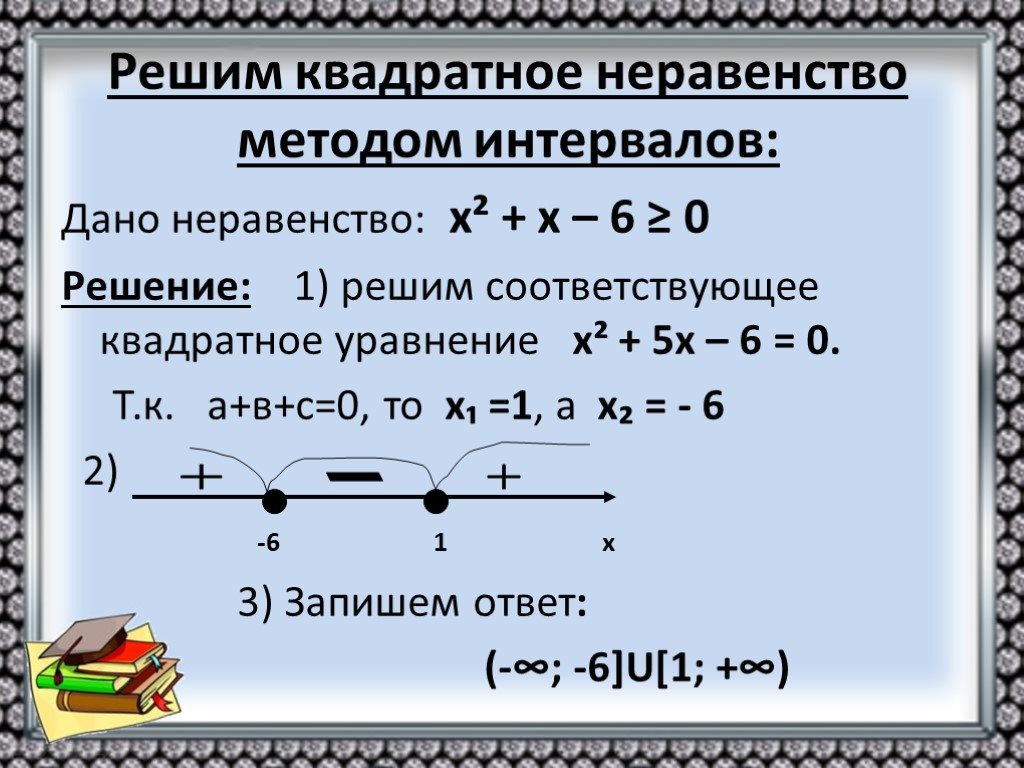
Метод интервалов

Еще один метод, как решить квадратное неравенство – метод интервалов, при условии, что в выражении только одна переменная. Этот способ актуален и используется для решения практически всех видов неравенств, а не только квадратных. Способ состоит в том, чтобы определить знаки интервалов, на которые делится координатная ось нулями трехчлена:

a×y²+b×y+c,

если таковые имеют место быть.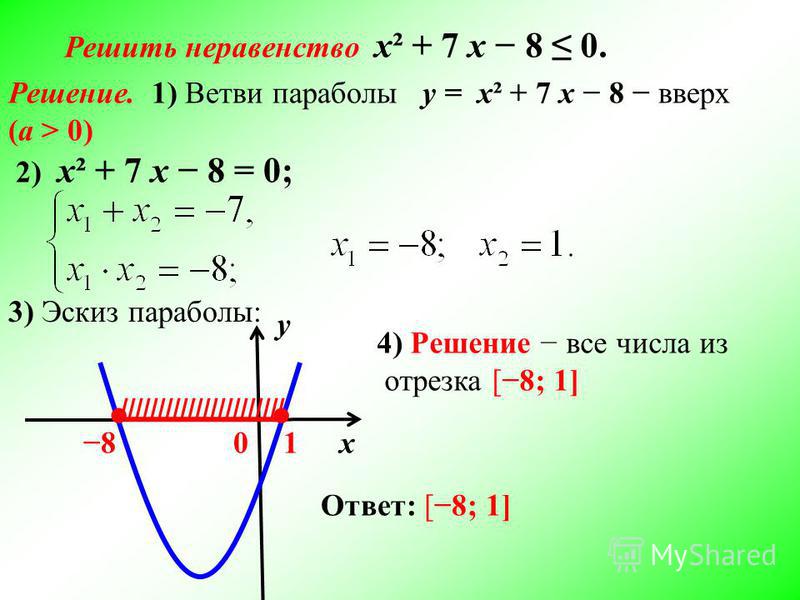

Для квадратного неравенства, имеющего вид a×y²+b×y+c<0, ответом будут интервалы со знаком минуса.

Для квадратного неравенства, имеющего вид a×y2+b×y+c>0, ответом будут интервалы со знаком плюс.

Если решение квадратных неравенств предполагает поиск ответа нестрогого неравенства, то решением будет интервал, на котором расположены точки, идентичные нулям трехчлена.

Нет времени решать самому?

Наши эксперты помогут!

Контрольная

| от 300 ₽ |

Реферат

| от 500 ₽ |

Курсовая

| от 1 000 ₽ |

Выделение квадрата двучлена

Чтобы выделить квадрат двучлена из левой части выражения, потребуется выполнить равнозначное преобразование, после чего можно будет решать равносильное неравенство, имеющее вид:

\[(x-y) 2<z\]

Вместо знака ˂ может встречаться любой другой, кроме знака равенства (>,≥, ≤).

В неравенствах такого плана y и z – любые числовые значения.

Неравенства, которые сводятся к квадратным

К квадратному можно привести любое другое неравенство с помощью равносильного преобразования.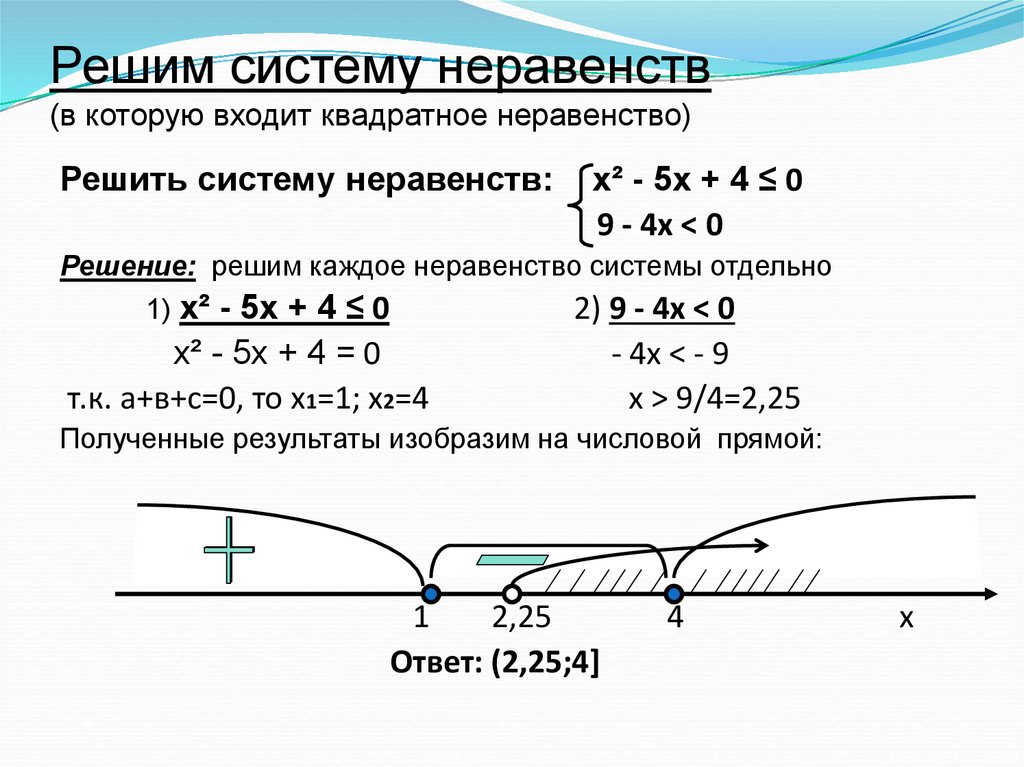 {2}+x+\frac{1}{4} \leq 0 \)

Решение.

Для данного неравенства \(\ \mathrm{a}=1>0 \), \(\ \mathrm{D}=\mathrm{o} \)и корень соответствующего уравнения \(\ x_{0}=-\frac{1}{2} \) . В этом случае квадратичная функция принимает только неотрицательные значения. Поэтому это неравенство имеет единственное решение \(\ x=-\frac{1}{2} \)

Ответ

\(\ x=-\frac{1}{2} \)

Физика

166

Реклама и PR

Педагогика

Психология

Социология

Астрономия

Биология

Культурология

Экология

Право и юриспруденция

Политология

Экономика

Финансы

История

Философия

Информатика

Право

Информационные технологии

Экономическая теория

Менеджент

719

Математика

338

Химия

Микро- и макроэкономика

Медицина

Государственное и муниципальное управление

География

542

Информационная безопасность

Аудит

Безопасность жизнедеятельности

Архитектура и строительство

Банковское дело

Рынок ценных бумаг

Менеджмент организации

Маркетинг

238

Кредит

Инвестиции

Журналистика

Конфликтология

Этика

Формулы дифференцирования Бесконечная убывающая геометрическая прогрессия и ее формулы Формула n-го члена геометрической прогрессии Формула n-го члена арифметической прогрессии Формула знаменателя геометрической прогрессии

Узнать цену работы

Узнай цену

своей работы

Имя

Выбрать тип работыЧасть дипломаДипломнаяКурсоваяКонтрольнаяРешение задачРефератНаучно — исследовательскаяОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерскаяНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация в ВАКПубликация в ScopusДиплом MBAПовышение оригинальностиКопирайтингДругое

Принимаю Политику конфиденциальности

Подпишись на рассылку, чтобы не пропустить информацию об акциях

Как решать и строить графики квадратных неравенств (6 случаев) – JDM Educational

Решение квадратных уравнений и построение графиков – это одно, но квадратные неравенства добавляют еще один уровень работы. Однако, если у вас есть метод, вы можете решить эти проблемы без особых проблем.

Итак, как решать квадратные неравенства и строить графики? Чтобы решить квадратное неравенство, сначала приведите его к стандартной форме. Затем определите случай, в котором вы находитесь, и найдите нули квадратного числа. Затем начертите соответствующую параболу из квадратичной. Наконец, заштрихуйте соответствующую область на графике на основе знаков и символа неравенства.

Конечно, некоторые случаи легче решить и построить график, чем другие, но есть способ решить любую задачу.

В этой статье мы более подробно рассмотрим этапы решения и графического отображения квадратных неравенств. Мы уделим особое внимание возможным случаям для наборов решений и тому, что делать в каждой ситуации.

Начнем.

Как решить и построить график квадратного неравенства

Если вы хотите решить и построить график квадратного неравенства, вам нужно выполнить 7 шагов.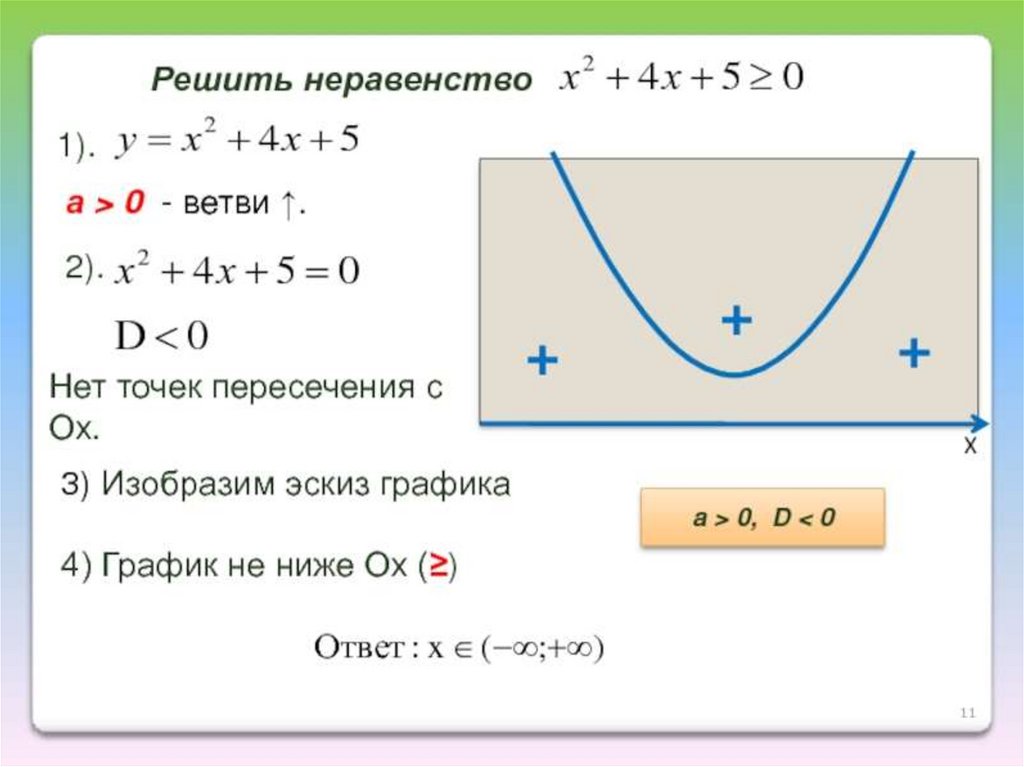 Выполняя их в таком порядке, вы ничего не пропустите:

1. Привести квадратное неравенство к стандартному виду с а > 0.
2. Найти значение v _y (координата y вершины параболы).
3. Используйте v _y, чтобы определить вариант решения.
4. Найдите нули квадратного числа.
5. Запишите множество решений квадратного неравенства.
6. Постройте график параболы, соответствующей квадратичной.
7. Заштрихуйте соответствующую область на графике, исходя из знака неравенства.

Сначала мы объясним каждый из этих шагов более подробно. Затем мы рассмотрим несколько примеров, чтобы все стало ясно.

1. Преобразование квадратного неравенства в стандартную форму с > 0

Стандартная форма просто означает, что одна сторона неравенства равна нулю. Для этого потребуется только вычитание.

Как найти формулу выражения…

Включите JavaScript

Как найти формулу экспоненциальной функции

Однако мы хотим сделать дополнительный шаг и сделать > 0 (то есть положительный коэффициент для x ² ). Иногда это будет быстрее с умножением на -1, что потребует от нас переключения направления символа неравенства.

Например, допустим, у нас есть квадратное неравенство -2x ² + 3x + 4 > 5. Чтобы преобразовать в стандартную форму с > 0:

-2x ² + 3x + 4 > 5 [исходное неравенство]
-2x ² + 3x + 4 – 5 > 5 – 5 [вычесть 5 с обеих сторон]
6 + 9005 -2x 9 -2x 9 – 1 > 0
-1(-2x ² + 3x – 1) < 0 [умножить обе стороны на -1 и поменять направление символа неравенства]
2x ² – 3x + 3x < 0

Теперь наше квадратное неравенство имеет стандартный вид, одна сторона которого равна нулю.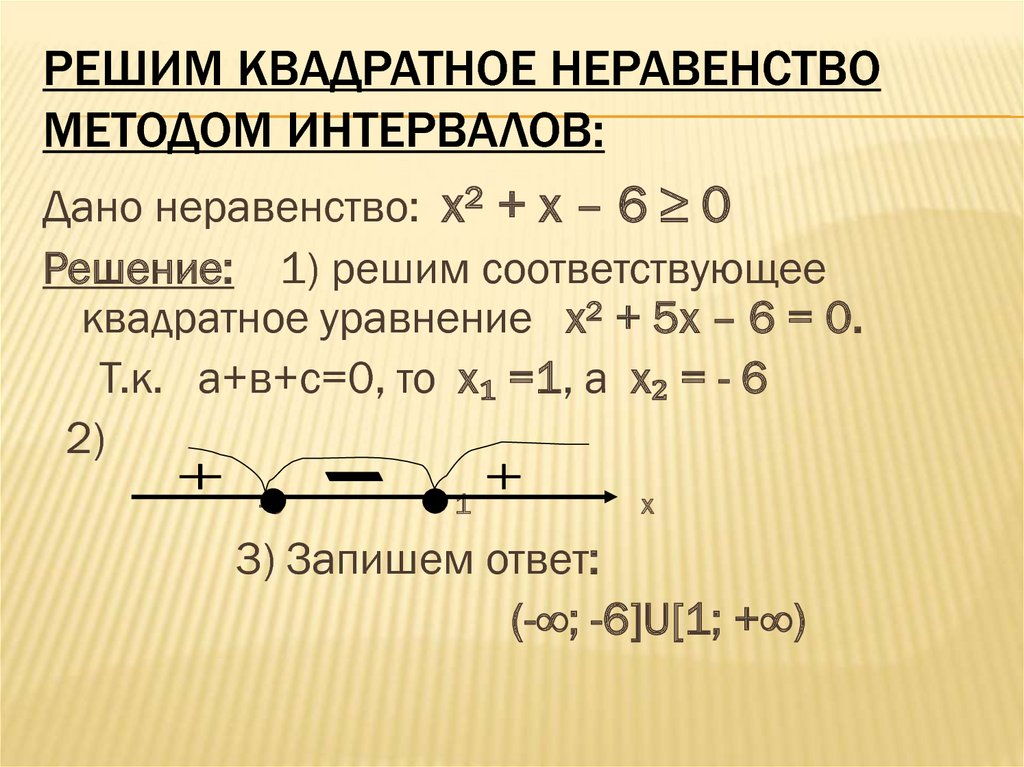 У нас также есть a > 0 (поскольку a = 2), что облегчает нашу работу на следующих шагах.

2. Найдите значение V

_y (координата y вершины параболы)

Помните, что для квадратичного f(x) = ax ² + bx + c мы можем изобразить соответствующее парабола. Эта парабола имеет вершину с координатами (V _x, V _Y), где:

V _x = -B / 2A
V _Y = (4AC – B 9005 2 666. ) / 4a

Итак, чтобы найти v _y (координата y вершины), все, что нам нужно сделать, это подставить a, b и c в v _y , формула координаты y вершины параболы.

Например, вернемся к приведенному ранее к стандартному виду неравенству:

2x ² — 3x + 1 < 0 C = 1.
Заменить их в формулу V _Y Придает нам:
V _Y = (4AC — B ²) / 4A
V _Y = (4 (2 (2 )(1) – (-3) ²) / 4 (2)
V _Y = (8 -9) / 8
V _y = -1 / 8
Итак, координата Y вершины вершины. параболы -1/8.
3. Используйте v
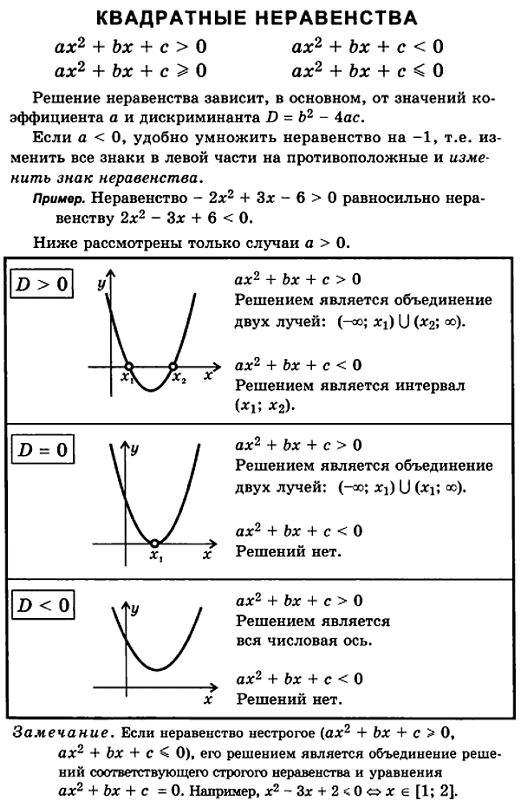
_y, чтобы определить случай для решений
Существует 6 вариантов решения квадратного неравенства, в зависимости от знака v _y и направления символа неравенства:
Случай 1: v
_г > 0
В этом случае координата y вершины положительна (она выше оси x). Поскольку a > 0, парабола открывается вверх, что означает, что парабола всегда выше оси x, а квадратичная функция f(x) всегда положительна.
Для v _y > 0 возможны следующие 4 подслучая:
f(x) > 0: каждое значение x в области является решением.
f(x) >= 0: каждое значение x в домене является решением.
f(x) < 0: решения нет.
f(x) <= 0: решения нет.
Случай 2: v
_y = 0
В этом случае координата y вершины положительна (она лежит на оси x). Поскольку a > 0, парабола открывается вверх, что означает, что парабола всегда находится на оси x или над ней, а квадратичная функция f(x) всегда положительна или равна нулю.
Для v _y = 0 возможны следующие 4 подслучая:
f(x) > 0: каждое значение x в области является решением, за исключением v _x , x-координата вершины.
f(x) >= 0: каждое значение x в домене является решением.
f(x) < 0: решения нет.
f(x) <= 0: единственным решением является v _x , x-координата вершины.
Случай 3: v
_y < 0
В этом случае координата y вершины отрицательна (ниже оси x). Поскольку a > 0, парабола открывается вверх, что означает, что парабола иногда находится над осью x, иногда ниже оси x, а иногда пересекает ось x (именно здесь мы находим нули).
Итак, f(x) может принимать положительные, отрицательные или нулевые значения. На самом деле f(x) имеет в этом случае два нуля, r и s (r < s).
Для v _y < 0 возможны следующие 4 подслучая:
f(x) > 0: некоторые значения x в области являются решениями: x < r и x > s.
f(x) >= 0: некоторые значения x в области являются решениями: x <= r и x >= s.
f(x) < 0: некоторые значения x в области являются решениями: r < x < s.
f(x) <= 0: некоторые значения x в области являются решениями: r <= x <= s.
Продолжая наш предыдущий пример, мы видим, что v _y = -1/8 помещает нас в случай 3, v _y < 0. Мы также имеем f(x) < 0, то есть 3 ^рд поддел.
Это означает, что некоторые значения x в области являются решениями: значения x между нулями квадратного числа.
В следующей таблице приведены случаи для v _y , знак неравенства и решения квадратного неравенства.
>=2 0 (5 x
Cases Case 1
v _y > 0 Case 2
v _y = 0 Case 3
v _y < 0
f(x) > 0 все x все x
кроме
v _x x < r
и
x > s
)0324 Все x All x x <= R
и
x> = S
F (x) <0 None 240324. ) <= 0 нет v _x r<=x<=s
квадратного неравенства при а > 0.
4. Найдите нули квадратного неравенства
Вы можете найти нули квадратного числа несколькими способами. Один из способов состоит в том, чтобы разложить квадратное число на множители и приравнять множители к нулю.
Другой способ — использовать квадратичную формулу. Это самый универсальный метод, так как он даст нам нули любого квадратичного числа (как бы трудно его ни было разложить на множители!)
Имея нули квадратного числа (назовем их r и s), мы можем записать решение устанавливает для неравенства, а затем переходите к построению графика параболы и затенению соответствующих областей.
В нашем предыдущем примере квадратное выражение равно f(x) = 2x ² – 3x + 1, где a = 2, b = -3 и c = 1.
Используя квадратичную формулу (на рисунке ниже) , находим:
Квадратичная формула.
r = 1/2 и s = 1 являются решениями квадратного уравнения (обратите внимание, что r < s).
5. Запишите набор решений квадратного неравенства
Теперь, когда у нас есть случай и нули, мы можем записать набор решений квадратного неравенства.
Следуя предыдущему примеру, вспомните, что мы были в Случае 3 (v _y < 0) и подслучай 3 (f(x) < 0).
Это означает, что наш набор решений равен r < x < s или ½ < x < 1. Мы также можем записать этот набор в виде (1/2, 1).
Помните, что открытая скобка означает, что конечная точка не включена в набор.
6. Постройте график параболы, соответствующей квадратному
Теперь мы построим график параболы, используя следующий тип кривой:
сплошная кривая для инклюзивных неравенств (символы >= или <=)
пунктирная кривая для строгих неравенств (символы > или <)
Возвращаясь к нашему примеру, допустим, мы хотим построить график y < f(x). В этом случае мы будем использовать пунктирную линию для построения параболы.
Мы знаем, что нули равны r = 1/2 и s = 1. Мы также знаем, что вершина находится в точке (v _x , v _y ), или (3/4, -1/8 ).
Если мы нанесем эти три точки, чтобы начать наш график, мы можем сделать набросок в форме параболы, которая пересекает все три точки.
График f(x) = 2x ² – 3x + 1 показан ниже (нарисован пунктирной линией).
График f(x) = 2x ² – 3x + 1, нарисованный пунктирной линией.
7. Закрасьте соответствующую область графика на основе знака неравенства
Чтобы закрасить соответствующую область, мы закрасим выше или ниже кривой в зависимости от знака неравенства:
Для y > f(x) > 0 или y >= f(x), мы заштриховываем над кривой параболы.
Для y < f(x) или y <= f(x) мы заштриховываем ниже кривой параболы.
Возвращаясь к нашему предыдущему примеру, если мы хотим построить график y < f(x), мы захотим закрасить нижнюю часть кривой.
График y < 2x ² – 3x + 1, нарисованный пунктирной линией и заштрихованный ниже.
Пример: решение и построение квадратного неравенства
Теперь давайте пройдемся по шагам, чтобы решить и построить график квадратного неравенства 2x ² + 6x — 12 > 8. Мы будем делать это шаг за шагом.
Шаг 1 — преобразовать в стандартную форму с > 0.
Мы можем просто вычесть 8 с обеих сторон, чтобы получить:
2x ² + 6x – 20 > 0 Шаг
9005 равен 4 найти v _y = (4ac – b ² ) / 4a:
v _y = (4ac – b ² ) / 4a
v _y = (4(-20) – 6 ² ) / 4(2)
v _y = (-160 – 36) / 8
v _y = -24,5
Шаг 3 — использовать v
_y для определения варианта решения.
Поскольку v _y < 0, мы находимся в случае 3. Поскольку f(x) > 0, мы находимся в подслучае 1. Решениями являются x < r и x > s.
Шаг 4 — найти нули квадратного уравнения.
После использования квадратной формулы с a = 2, b = 6 и c = -20 мы получаем r = -5 и s = 2.
Шаг 5 — записать набор решений квадратного неравенства.
Имеем x < r и x > s, или x < -5 и x > 2,
Шаг 6 состоит в построении параболы, соответствующей квадратичной функции f(x) = 2x
² + 6x – 12.
Мы используем пунктирную кривую, так как имеем строгое неравенство (символ >).
График f(x) = 2x ² + 6x – 20, нарисованный в виде пунктирной кривой.
Шаг 7 заключается в затенении соответствующей области.
Если у нас есть неравенство y > f(x), то мы хотим закрасить выше кривой.
График y > 2x ² + 6x – 20, нарисованный пунктирной линией и заштрихованный сверху.
Заключение
Теперь вы знаете, как решать и изображать квадратные неравенства. Надеюсь, этот метод сделает вещи немного проще для понимания и немного менее громоздкими.
Подробнее о неравенствах без решений можно узнать в моей статье здесь.
Подробнее о сложных неравенствах можно узнать здесь.
Надеюсь, эта статья оказалась вам полезной. Если это так, пожалуйста, поделитесь ею с теми, кто может использовать эту информацию.
Не забудьте подписаться на мой канал YouTube и получать обновления о новых математических видео!
Подпишитесь на наш канал на YouTube!
~Джонатон
Решение линейных и квадратных неравенств с помощью программы Step-by-Step Math Problem Solver графика большего числа на числовой прямой. Эти отношения порядка можно выразить с помощью следующих символов:
> означает «больше чем».
≤ означает «меньше или равно»
≥ означает «больше или равно».
Например,
«1 меньше 3» можно записать как 1
«7 меньше 9» можно записать как 7
«-3 больше, чем -5» можно записать как -3 > -5.
«2 меньше или равно x» можно записать как 2 ≤ x.
«4 больше или равно y» можно записать как 4 ≥ y.
Утверждения, содержащие любой из вышеуказанных символов, называются неравенствами. Неравенства типа
1 Говорят, что
имеют один и тот же порядок или один и тот же смысл, потому что левый элемент меньше правого в каждом случае. Говорят, что неравенства типа
7 -5

имеют противоположный порядок или противоположный смысл, потому что в одном случае левое слагаемое меньше правого, а в другом случае левое слагаемое больше правый член.
СВОЙСТВА НЕРАВЕНСТВ
В разделе 3.1 мы видели, что уравнение первой степени с одной переменной имеет только одно решение. Но неравенство первой степени имеет бесконечное число решений. Например, графики бесконечного числа целочисленных решений неравенства x > 3 показаны на рис. 3.1.
Иногда невозможно определить решения данного неравенства просто путем проверки. Но, используя следующие свойства, мы можем составить эквивалентные неравенства (неравенства с одинаковыми решениями), в которых решение очевидно при проверке.
1. Если к каждому члену неравенства прибавить или вычесть одно и то же выражение, результатом будет эквивалентное неравенство в том же порядке.

Символами,
а
— эквивалентные неравенства.
Пример 1 а. Потому что 3
3 + 4
б. Если х
х + 2
в. Если 4
4 + (-2)
2. Если каждый элемент неравенства умножить или разделить на одно и то же положительное число, результатом будет эквивалентное неравенство в том же порядке.
В символах
эквивалентны неравенствам.
Пример 2 а. Потому что 2 0,
2(5)
б. Если 3x
в. Если 5 0, то
5(z)
3. Если каждый член неравенства умножить или разделить на одно и то же отрицательное число, результатом будет эквивалентное неравенство в обратном порядке.
В символах
эквивалентны неравенствам.
Пример 3 а. Потому что 3
3(-2) > 5(-2) или -6 >-10
б.
Если -3x
в. Если 2
2(у) > х(у) или 2у > ху
Три вышеуказанных свойства применимы также к неравенствам вида a > b, а также к
РЕШЕНИЕ НЕРАВЕНСТВ
Теперь давайте посмотрим, как эти три свойства могут помочь нам решить неравенства.
Пример 4 Решите , где x — целое число.
Решение Умножив каждый член на 2 (положительное число), мы получим
Затем, разделив каждый член на 3, получим
График этого неравенства:
В приведенном выше примере все неравенства были в одном порядке, потому что мы применили только Свойство 2 выше. Теперь рассмотрим следующее неравенство.
Пример 5 Решите — 3x + 1 > 7, где x — целое число.
Решение Прибавляя — 1 к каждому члену, получаем
-3x + 1 + (-1) > 7 + (-1)
-3x > 6
Теперь применим свойство 3 и разделим каждый член на -3 . В этом случае мы должны изменить порядок неравенства.
При решении текстовых задач, связанных с неравенствами, мы следуем шести шагам, описанным на стр.
115, за исключением того, что слово уравнение будет заменено словом неравенство.
РЕЗЮМЕ ГЛАВЫ
Символические версии словесных предложений называются уравнениями . Уравнения, в которых переменная имеет показатель степени 1, являются уравнениями первой степени . Значение переменной, для которого уравнение верно, называется решением уравнения.
Уравнения, имеющие одинаковые решения, называются эквивалентными уравнениями . Уравнение, решение которого не очевидно при проверке, можно преобразовать в эквивалентное уравнение, решение которого очевидно. Мы делаем это, применяя одно или несколько из следующих свойств:

эквивалентны уравнениям. По симметричному свойству равенства члены уравнения можно менять местами без изменения знака. Таким образом,

, если a = b, то b = a
Мы можем решить фолумулу, подставив известные значения в формулу и найдя неизвестную переменную. Мы также можем решить для данной переменной с точки зрения других переменных.
Мы можем использовать следующие свойства для записи эквивалентных неравенств:

Мы должны обратить неравенство всякий раз, когда мы умножаем или делим оба члена неравенства на отрицательное число.
ПЕРЕВОД СЛОВЕСНЫХ ПРЕДЛОЖЕНИЙ
Большинство задач, связанных с практическим применением математики, выражаются словами. Прежде чем мы сможем решить такие задачи, мы должны перевести словесные предложения в математические уравнения. Затем мы можем использовать методы предыдущих разделов для решения уравнений.
В этом разделе мы будем заниматься только написанием алгебраических выражений и уравнений. В следующих разделах мы фактически будем решать уравнения.

В разделах 1.2 и 1.3 мы связывали определенные словосочетания с определенными математическими операциями:
«Сумма», «умноженная на», «плюс», «больше чем», «добавить», «превышает» и « превышено на» может быть связано с дополнением.
«Отнять», «меньше», «уменьшить на», «вычесть из», «вычесть», «вычесть из», «меньше» и «разность» могут быть связаны с вычитанием.
«Умножение», «умножение», «дважды (два раза)», «от» и «произведение» могут быть связаны с умножением.
«Деление на» и «частное от» могут быть связаны с делением.
Мы можем перевести эти словосочетания в алгебраические выражения, как показано в следующих примерах.
Пример 1
Точно так же мы можем преобразовать словесные предложения в уравнения.
Пример 2
Распространенные ошибки: При переводе такой фразы, как «a вычитается из b», важен порядок. Надо писать
б — а, а не а — б
, так как a вычитается из b. Например, чтобы перевести
«Если из 4-кратного целого числа вычесть семь, получится 17»,
мы представляем целое число символом, скажем, x, а затем записываем предложение следующим образом.
ПРИЛОЖЕНИЯ
В последнем разделе мы переводили словесные предложения в уравнения. Сейчас мы будем решать различные словесные задачи. Предлагаются следующие шаги.
Чтобы решить задачу со словами:
Представьте каждую величину, которую вы хотите найти, в виде словосочетания.
Представьте каждую величину из шага 1 в терминах одной переменной.
Если применимо, сделайте эскиз или таблицу и укажите все количества.
Напишите уравнение, представляющее словесное предложение, связывающее известные и неизвестные величины.
Решите полученное уравнение.
Используя результат шага 5, ответьте на исходный вопрос.
На практике мы обычно объединяем шаги 1 и 2.
Выполните шесть шагов, перечисленных выше, чтобы решить следующую задачу со словами.
Сумма определенного числа и 9 равна четырехкратному числу. Какой номер?
Решение
Шаги 1-2 Сначала мы записываем то, что хотим найти (число), в виде словосочетания. Затем мы используем переменную для представления этого числа.
Число: x
Шаг 3 Скетч в этой задаче неприменим.
Шаг 4. Запишем уравнение, связывающее известные и неизвестные величины.
x + 9 — 4x
Шаг 5 Теперь решим полученное уравнение.
x + 9 — x = 4x — x
9 = 3x
3 = x
Шаг 6 Число равно 3. Последовательные целые числа — это целые числа, которые отличаются на 1 или -1. Например, 3 и 4 — это последовательные целые числа, а -2 и -1 — последовательные целые числа. Если x представляет собой целое число, то следующее последовательное целое число представляется как x + 1.
Последовательные четные целые числа — это четные целые числа, отличающиеся на 2 или -2. Например, 6 и 8 — последовательные четные целые числа, а -4 и -2 — последовательные четные целые числа. Если x представляет собой четное целое число, то следующее последовательное четное целое число представляется как x + 2.
Последовательные нечетные целые числа — это нечетные целые числа, отличающиеся на 2 или -2. Например, 5 и 7 — последовательные нечетные целые числа, а -3 и -1 — последовательные нечетные целые числа. Если x представляет собой нечетное целое число, то следующее последовательное нечетное целое число представляется как x + 2.
Пример 2 Выполните шесть шагов, перечисленных на стр. 115, чтобы решить следующую задачу со словами.
Сумма двух последовательных нечетных целых чисел равна 12. Что это за числа?
Решение
Шаги 1-2 Сначала мы запишем то, что мы хотим найти (целые числа), в виде фраз из двух слов.
Затем мы используем переменную для представления целых чисел. Меньшее нечетное целое: x
Следующее последовательное нечетное целое: x + 2
Шаг 3 Скетч неприменим в этой задаче.
Шаг 4 Далее мы пишем уравнение, связывающее известные и неизвестные величины.
x + (x + 2) = 12
Шаг 5 Теперь решим полученное уравнение.
x + x + 2 = 12
2x + 2 = 12
2x = 10
x = 5
Шаг 6. Целые числа равны 5 и 5 + 2 или 7.
В следующем примере полезен эскиз.
Пример 3 Выполните шесть шагов, перечисленных на стр.
No related posts.