Метод половинного деления (метод дихотомии)
Данный метод описывает алгоритм нахождение корней (нулей) функции. Чтобы найти минимум целевой функции методом дихотомии используйте этот калькулятор.
Считаем, что отделение корней произведено и на интервале [a,b] расположен один корень, который необходимо уточнить с погрешностью ε.Итак, имеем f(a)f(b)<0. Метод дихотомии заключается в следующем. Определяем половину отрезка c=½(a+b) и вычисляем f(c). Проверяем следующие условия
1. Если |f(c)| < ε, то c – корень. Здесь ε — заданная точность.
2. Если f(c)f(a)<0, то корень лежит в интервале [a,c].
3. Если f(c)f(b)<0, то корень лежит на отрезке[c,b].
Продолжая процесс половинного деления в выбранных подынтервалов, можно дойти до сколь угодно малого отрезка, содержащего корень ξ.
Так как за каждую итерацию интервал, где расположен корень уменьшается в два раза, то через n итераций интервал будет равен:
В качестве корня ξ. возьмем =½(bn+an). Тогда погрешность определения корня будет равна (bn – an)/2. Если выполняется условие
(bn–an)/2<ε, то процесс поиска заканчивается и ε=½(bn+an).
см. более подробный алгоритм метода бисекции.
Теорема 2. Итерационный процесс половинного деления сходится к искомому корню ξ с любой наперед заданной точностью ε.
Доказательство: Рассмотрим последовательность чисел ξi являющихся приближением корня на i-ом шаге.
ξi=½(bi+ai), i=0,1,…
где a0=a; b0=b; ai;bi — границы подынтервалов, в которых f(ai)f(bi)<0. Рассмотрим разности
|ξ1— ξ0
Имеем |ξ1-ξ0|=½(b1+a1-b0-a0).
Так как всегда имеем либо b1=b0, a1=½(b0+a0), либо a1=a0, b1=½(a0+b0), поэтому , если, b1=b0либо , если a1=a0.
Повторяя аналогичные рассуждения и учитывая, что всегда выполняется соотношение либо bi=bi-1, ai=½(bi-1+ai-1), либо bi=½(bi-1+ai-1), ai=ai-1. Получим
;
;
, где a0=a, b0=b.
Отсюда видно, что какое бы малое число ε>0 мы ни задали, всегда можно найти такое
Графически метод дихотомии выглядит следующим образом
|f(c)|≤δ f(a)f(c)<0 f(b)f(c)<0
Сходимость метода дихотомии линейная с коэффициентом α=0,5. Покажем это.
Если в качестве xn брать an, то из формулы (6) мы можем записать , .
Отсюда следует .
Отметим, что за 10 итераций (n=10) интервал уменьшается в 210 = 1024 ≈ 103 раз. За 20 итераций (n=2) уменьшается в 220 ≈ 106 раз.
Перейти к онлайн решению своей задачи
Скачать решение
Методом дихотомии также можно находить и минимальное и максимальное значения функции. Для этого необходимо найти производную функции и приравнять ее нулю.
Пример №1. Найти экстремум функции: y=5x 2-4x+1 методом дихотомии, если ε=0.1, а исходный интервал [0,10].
- Решение
- Видео решение
Находим производную функции: y ‘ = 10x-4. Найдем нули функции методом дихотомии: y’=0.
Поскольку F(0)*F(10)Итерация 1.
Находим середину отрезка: c = (0 + 10)/2 = 5
F(x) = 46
F(c) = -4
Поскольку F(c)•F(a) < 0, то b=5
Итерация 2.
Находим середину отрезка: c = (0 + 5)/2 = 2.
5
F(x) = 21
F(c) = 46
Поскольку F(c)•F(a) < 0, то b=2.5
Итерация 3.
Находим середину отрезка: c = (0 + 2.5)/2 = 1.25
F(x) = 8.5
F(c) = 21
Поскольку F(c)•F(a) < 0, то b=1.25
Итерация 4.
Находим середину отрезка: c = (0 + 1.25)/2 = 0.625
F(x) = 2.25
Поскольку F(c)•F(a) < 0, то b=0.625
Остальные расчеты сведем в таблицу.
| N | c | a | b | f(c) | f(x) | ε |
| 1 | 5 | 10 | 5 | -4 | 46 | 5 |
| 2 | 2.5 | 5 | 2.5 | 46 | 21 | 2. 5 |
| 3 | 1.25 | 2.5 | 1.25 | 21 | 8.5 | 1.25 |
| 4 | 0.625 | 1.25 | 0.625 | 8.5 | 2.25 | 0.625 |
| 5 | 0.3125 | 0.625 | 0.3125 | 2.25 | -0.875 | 0.3125 |
| 6 | 0.4688 | 0.625 | 0.4688 | -0.875 | 0.6875 | 0.1563 |
x=(0.3125+0.46875)/2 = 0.3906
Ответ:x=0.3906; F(x) = 0.
6875
Количество итераций, N = 6
Параметр сходимости
На отрезке [0,10] функция имеет экстремум x=0.3906.
Пример №2. Методом дихотомического поиска найдите максимумы функций, пологая, что Δ=0,05.
f(x) = x*cos(x), 0 ≤x≤ π
Пример №3. Методом бисекции найти решение нелинейного уравнения на отрезке [a,b] с точностью ε = 10-2. Выбрав полученное решение в качестве начального приближения, найти решение уравнения методом простой итерации с точностью ε = 10-4. Для метода простой итерации обосновать сходимость и оценить достаточное для достижения заданной точности число итераций.
sqrt(t)+x2 = 10, a = 2.6, b = 3
Найдем корни уравнения:
Используем для этого Метод половинного деления (метод дихотомии)..
Считаем, что отделение корней произведено и на интервале [a,b] расположен один корень, который необходимо уточнить с погрешностью ε.
Итак, имеем f(a)f(b)Определяем половину отрезка c=1/2(a+b) и вычисляем f(c). Проверяем следующие условия:
1. Если |f(c)| 2. Если f(c)f(a)3. Если f(c)f(b)Продолжая процесс половинного деления в выбранных подынтервалов, можно дойти до сколь угодно малого отрезка, содержащего корень ξ.
Так как за каждую итерацию интервал, где расположен корень уменьшается в два раза, то через n итераций интервал будет равен:
bn-an=1/2n(b-a)
В качестве корня ξ. возьмем 1/2(an+bn). Тогда погрешность определения корня будет равна (bn – an)/2. Если выполняется условие:
(bn – an)/2 то процесс поиска заканчивается и ξ = 1/2(an+bn).
Решение.
Поскольку F(2.6)*F(3)Итерация 1.
Находим середину отрезка: c = (2.6 + 3)/2 = 2.8
F(c) = -1.628
Поскольку F(c)•F(x) > 0, то a=2.
8Итерация 2.
Находим середину отрезка: c = (2.8 + 3)/2 = 2.9
F(x) = 0.113
F(c) = -0.487
Поскольку F(c)•F(x) Итерация 3.
Находим середину отрезка: c = (2.8 + 2.9)/2 = 2.85
F(x) = -0.189
F(c) = 0.113
Поскольку F(c)•F(x) Итерация 4.
Находим середину отрезка: c = (2.8 + 2.85)/2 = 2.825
F(x) = -0.339
F(c) = -0.189
Поскольку F(c)•F(x) > 0, то a=2.825
Остальные расчеты сведем в таблицу.
| N | c | a | b | f(c) | f(x) |
| 1 | 2.6 | 3 | 2.8 | -1.6275 | -0.4867 |
| 2 | 2.8 | 3 | 2.9 | -0.4867 | 0.1129 |
| 3 | 2. 8 | 2.9 | 2.85 | 0.1129 | -0.1893 |
| 4 | 2.8 | 2.85 | 2.825 | -0.1893 | -0.3386 |
| 5 | 2.825 | 2.85 | 2.8375 | -0.3386 | -0.2641 |
| 6 | 2.8375 | 2.85 | -0.2641 | -0.2267 |
Решение было получено и оформлено с помощью сервиса Метод Ньютона онлайн
Пример №2. Локализовать корень нелинейного уравнения f(x) = 0 и найти его методом бисекции с точностью ε1 = 0,01. Выбрав полученное решение в качестве начального приближения, найти решение уравнения методом простой итерации с точностью ε2 = 0,0001.
Для метода простой итерации обосновать сходимость и оценить достаточное для достижения заданной точности ε2 число итераций.
Онлайн калькулятор: Метод бисекции
Калькулятор, который находит приближенное решение уравнения методом бисекции или методом деления отрезка пополам. Небольшая теория под калькулятором.
Метод бисекции
Уравнение
Начальное приближение x0
Начальное приближение x1
Критерий останова (погрешность)
Критерий останова (тип)
Приращение x
Отличие функции от нуля
Точность вычисления
Знаков после запятой: 4
Формула
Файл очень большой, при загрузке и создании может наблюдаться торможение браузера.
Метод бисекции
Существует довольно очевидная теорема: «Если непрерывная функция на концах некоторого интервала имеет значения разных знаков, то внутри этого интервала у нее есть корень (как минимум, один, но может быть и несколько)».
На базе этой теоремы построено несколько методов численного нахождения приближенного значения корня функции. Обобщенно все эти методы называются методами дихотомии, т. е. методами деления отрезка на две части (необязательно равные).
Здесь уже были рассмотрены Метод хорд и Метод секущих, теперь дошла очередь и до самого простого метода дихотомии, называемого методом бисекции, или методом деления отрезка пополам. Как следует из названия, именно в этом методе отрезок делится каждый раз на две равные части. Середина отрезка считается следующим приближением значения корня. Вычисляется значение функции в этой точке, и, если критерий останова не достигнут, выбирается новый интервал. Интервал выбирается таким образом, чтобы на его концах значения функции по прежнему имели разный знак, то есть чтобы он по прежнему содержал корень. Такой подход обеспечивает гарантированную сходимость метода независимо от сложности функции — и это весьма важное свойство. Недостатком метода является то же самое — метод никогда не сойдется быстрее, т.
е. сходимость метода всегда равна сходимости в наихудшем случае.
Итерационная формула проста:
Метод бисекции является двухшаговым, то есть новое приближение определяется двумя предыдущими итерациями. Поэтому необходимо задавать два начальных приближения корня.
Метод требует, чтобы начальные точки были выбраны по разные стороны от корня (то есть корень содержался в выбранном интервале).
В качестве критерия останова берут один из следующих:
— значение функции на данной итерации стало меньше заданого ε.
— изменение хk в результате итерации стало меньше заданого ε. Поскольку интервал на каждом шаге уменьшается в два раза, вместо проверки x можно рассчитать количество требуемых итераций.
Подробнее: Метод бисекции.
Алгебра анализ Математика метод бисекции метод деления отрезка пополам метод дихотомии решение уравнений уравнение уравнения Численные методы
Калькулятор дробей
Этот калькулятор дробей выполняет базовые и расширенные операции с дробями, выражения с дробями в сочетании с целыми, десятичными и смешанными числами.
Он также показывает подробную пошаговую информацию о процедуре расчета дроби. Калькулятор помогает найти значение из операций с несколькими дробями. Решайте задачи с двумя, тремя и более дробями и числами в одном выражении.
Правила выражения с дробями:
Дроби — используйте косую черту для деления числителя на знаменатель, т.е. для пятисотых введите 5/100 . Если вы используете смешанные числа, оставьте пробел между целой и дробной частями.
Смешанные числа (смешанные числа или дроби) сохраняют один пробел между целым числом и дробью
и используют косую черту для ввода дробей, например, 1 2/3 . Пример отрицательной смешанной дроби: -5 1/2 .
Поскольку косая черта одновременно является знаком дробной строки и деления, используйте двоеточие (:) в качестве оператора деления дробей, т. е. 1/2 : 1/3 .
Decimals (десятичные числа) вводятся с десятичной точкой . и они автоматически преобразуются в дроби — т.
е. 1,45 .
Математические символы
| Символ | Название символа | Значение символа | Пример | ||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| + | плюс | дополнение | 1/2 + 1/3 | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| — | знак минус | вычитание | 1 1/2 — 2/3 | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| * | звездочка | умножение | 2/3 * 3/4 | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| × | знак умножения | умножение | 2 /3 × 5/6 | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| : | знак деления | деление | 1/2 : 3 | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| / | деление косая черта | деление | 1/3 / 5 1/2 • сложение дробей и смешанных чисел: 8/5 + 6 2/7 • деление целых чисел и дробей: 5 ÷ 1/2 • сложные дроби: 5/8 : 2 2/3 • десятичная дробь: 0,625 • Преобразование дроби в десятичную: 1/4 • Преобразование дроби в процент: 1/8 % • сравнение дробей: 1/4 2/3 • умножение дроби на целое число: 6 * 3/4 • квадратный корень дроби: sqrt(1/16) • уменьшение или упрощение дроби (упрощение) — деление числителя и знаменателя дроби на одно и то же ненулевое число — эквивалентная дробь: 4/22 • выражение со скобками: 1/3 * (1/2 — 3 3/8) • составная дробь: 3/4 от 5/7 • кратные дроби: 2/3 от 3/5 • разделить, чтобы найти частное: 3/5 ÷ 2/3 Калькулятор следует известным правилам для порядка операций .
другие математические задачи »
Множество и делительные номера в Excel01Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel для Интернета Excel 2021 Excel 2021 для Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel 2010 Excel 2007 Excel для Mac 2011 Дополнительно…Меньше Умножать и делить в Excel легко, но для этого нужно создать простую формулу. Умножение чиселДопустим, вы хотите выяснить, сколько воды в бутылках вам нужно для конференции с клиентами (общее количество участников × 4 дня × 3 бутылки в день) или компенсацию командировочных расходов (общее количество миль × 0,46). Существует несколько способов умножения чисел. Умножение чисел в ячейкеДля выполнения этой задачи используйте * (звездочка) арифметический оператор. Например, если ввести в ячейку =5*10 , ячейка отобразит результат 50 . Умножить столбец чисел на постоянное число Предположим, вы хотите умножить каждую ячейку в столбце из семи чисел на число, содержащееся в другой ячейке.
Умножение чисел в разных ячейках по формулеВы можете использовать функцию ПРОИЗВЕД для умножения чисел, ячеек и диапазонов. Вы можете использовать любую комбинацию до 255 номеров или ссылок на ячейки в функции PRODUCT . Например, формула =ПРОИЗВЕД(A2,A4:A15,12,E3:E5,150,G4,h5:J6) умножает две отдельные ячейки (A2 и G4), два числа (12 и 150) и три диапазоны (A4:A15, E3:E5 и h5:J6). Разделить числа Допустим, вы хотите узнать, сколько человеко-часов ушло на завершение проекта (общее количество часов проекта ÷ общее количество людей в проекте) или фактическое количество миль на галлон во время вашей недавней поездки по пересеченной местности (общее количество миль ÷ общее количество галлонов). Разделить числа в ячейкеДля выполнения этой задачи используйте арифметический оператор / (косая черта). Например, если ввести в ячейку = 10/5 , ячейка отобразит 2 . Важно: Не забудьте ввести знак равенства ( = ) в ячейку, прежде чем вводить числа и / .оператор; в противном случае Excel будет интерпретировать введенный вами текст как дату. Например, если вы введете 7/30, Excel может отобразить в ячейке 30 июля. Или, если вы введете 12/36, Excel сначала преобразует это значение в 1/12/1936 и отобразит в ячейке 1 декабря. Примечание. В Excel нет функции РАЗДЕЛИТЬ . Разделение чисел с использованием ссылок на ячейки Вместо того, чтобы вводить числа непосредственно в формулу, вы можете использовать ссылки на ячейки, такие как A2 и A3, для ссылки на числа, которые вы хотите разделить и разделить. Пример: Пример будет легче понять, если вы скопируете его на пустой лист. Пример копирования
Разделить столбец чисел на постоянное число Предположим, вы хотите разделить каждую ячейку в столбце из семи чисел на число, которое содержится в другой ячейке.
 |
Наиболее распространенные мнемоники для запоминания этого порядка операций: 
Запишите дробь.
Есть четыре курицы. Какую часть животных составляют куры? Выразите ответ дробью в простейшей форме.
Просто помните, что все формулы в Excel начинаются со знака равенства (=), и вы можете использовать панель формул для их создания.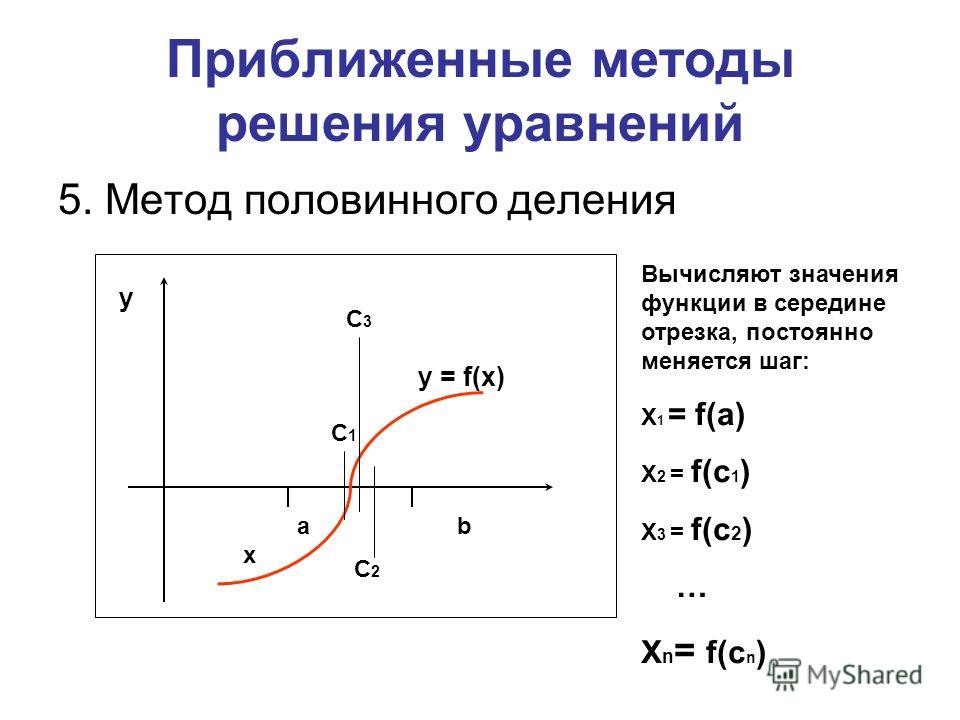
В этом примере число, на которое вы хотите умножить, равно 3, содержащемуся в ячейке C2.
Есть несколько способов деления чисел.
В этом примере нужно разделить число 3, содержащееся в ячейке C2.