Неполные квадратные уравнения. Примеры и решение
- Решение неполных квадратных уравнений
Неполное квадратное уравнение – это уравнение вида
ax2 + bx + c = 0,
в котором хотя бы один из коэффициентов b или c равен нулю. Следовательно, неполное квадратное уравнение может иметь вид:
| ax2 + bx = 0, | если c = 0; |
| ax2 + c = 0, | если b = 0; |
| ax2 = 0, | если b = 0 и c = 0. |
Чтобы решить уравнение вида ax2 + bx = 0, надо разложить левую часть уравнения на множители, вынеся x за скобки:
x(ax + b) = 0.
Произведение может быть равно нулю только в том случае, если один из множителей равен нулю, значит:
x = 0 или ax + b = 0.
Чтобы ax + b было равно нулю, нужно, чтобы
| x = — | b | . |
| a |
Следовательно, уравнение ax2 + bx = 0 имеет два корня:
| x1 = 0 и x2 = — | b | . |
| a |
Неполные квадратные уравнения вида ax2 + bx = 0, где b ≠ 0, решаются разложением левой части на множители. Такие уравнения всегда имеют два корня, один из которых равен нулю.
Пример 1. Решите уравнение:
a2 — 12a = 0.
Решение:
| a2 — 12a = 0 | |
| a(a — 12) = 0 | |
| a1 = 0 | a — 12 = 0 |
| a2 = 12 | |
Пример 2.
Решите уравнение:
7x2 = x.
Решение:
| 7x2 = x | |
| 7x2 — x = 0 | |
| x(7x — 1) = 0 |
| x1 = 0 | 7x — 1 = 0 | |||
| 7x = 1 | ||||
|
Чтобы решить уравнение вида ax2 + c = 0, надо перенести свободный член уравнения c в правую часть:
| c | . | |
| a |
В этом случае уравнение не будет иметь корней, так как квадратный корень нельзя извлечь из отрицательного числа.
Если данное неполное уравнение будет иметь вид x2 — c = 0, то сначала опять переносим свободный член в правую часть и получаем:
x2 = c.
В этом случае уравнение будет иметь два противоположных корня:
x1 = +√c , x2 = -√c .
Неполное квадратное уравнение вида ax2 + c = 0, где c ≠ 0, либо не имеет корней, либо имеет два корня, которые являются противоположными числами.
Пример 1. Решите уравнение:
24 = 2y2.
Решение:
| 24 = 2y2 | |
| 24 — 2y2 = 0 | |
| -2y2 = -24 | |
| y2 = 12 | |
| y1 = +√12 | y2 = -√12 |
Пример 2.
Решите уравнение:
b2 — 16 = 0.
Решение:
| b2 — 16 = 0 | |
| b2 = 16 | |
| b1 = 4 | b2 = -4 |
Уравнение вида ax2 = 0 всегда имеет только один корень: x = 0. Так как a ≠ 0, то из ax2 = 0 следует, что x2 = 0, значит, и x = 0. Любое другое значение
Квадратные уравнения — подготовка к ЕГЭ по Математике
Квадратное уравнение – уравнение вида , где
Числа называются коэффициентами квадратного уравнения.
Квадратное уравнение может иметь два действительных корня, один действительный корень или ни одного.
Количество корней квадратного уравнения зависит от знака выражения, которое называется дискриминант.
Дискриминант квадратного уравнения: .
Если > 0, квадратное уравнение имеет два корня: и .
Если = 0, квадратное уравнение имеет единственный корень .
Если < 0, квадратное уравнение не имеет действительных корней.
Чтобы решать квадратные уравнения, надо уметь:
- правильно определять коэффициенты квадратного уравнения;
- находить дискриминант и определять количество корней;
- находить корни уравнения по формуле.
1)
Коэффициентом является числа: .
2)
В этом уравнении коэффициенты – это числа:
Обратите внимание на слагаемые и : x — это не коэффициент, а переменная.
3)
А в этом уравнееии нужно быть внимательными, потому что коэффициенты — дробные числа:
Квадратные уравнения вида , в которых коэффициент , называются приведенными.
Запишем несколько квадратных уравнений и проверим, сколько корней они имеют.
Задача 1.
Решение:
В этом уравнении , , .
Дискриминант уравнения равен > 0. Уравнение имеет два корня.
Задача 2.
Решение:
В этом уравнении .
Дискриминант уравнения равен . Уравнение имеет единственный корень.
Заметим, что в левой части уравнения находится выражение, которое называют полным квадратом. В самом деле, . Мы применили формулу сокращенного умножения.
Уравнение имеет единственный корень .
Задача 3.
Решение:
В этом уравнении .
Дискриминант уравнения равен < 0. Корней нет.
Задача 4. Решим уравнение:
Решение:
Дискриминант уравнения равен > 0.
Уравнение имеет два корня.
Корни уравнения:
Задача 5. Решим уравнение:
Решение:
Дискриминант положительный, поэтому уравнение имеет два корня:
Рассмотрим другой пример.
Задача 6.
Дискриминант положительный, уравнение имеет два корня.
Находим их по формуле корней квадратного уравнения:
Что делать в том случае, если корень из дискриминанта не является целым числом? Тогда корни квадратного уравнения будут записаны выражением, в котором содержится квадратный корень. Такие выражения называются иррациональными.
Задача 7. Решим уравнение:
Решение:
Обратите внимание, что слагаемые в правой части записаны не в том порядке, в котором они указаны в общем виде квадратного уравнения. Поэтому, прежде чем начать решать, перепишем уравнение в следующем виде:
Найдем дискриминант: Уравнение имеет один корень:
Задача 8. И еще одно уравнение:
Решение:
Найдем дискриминант
Дискриминант отрицательный, поэтому квадратное уравнение не имеет корней.
Так и запишем в ответе: корней нет.
Теорема Виета
Полезная теорема для решения квадратных уравнений – теорема Виета.
Если и – корни уравнения , то , .
Теорему Виета удобно использовать, когда коэффициент при равен 1, то есть квадратное уравнение приведенное.
Например,
Коэффициенты этого уравнения . Значит, сумма корней и равна 5, а произведение корней равно 6. Эти два числа подобрать нетрудно, потому что
Тогда
Теорема Виета помогает проверить, правильно ли мы решили квадратное уравнение.
Например, в нашем уравнении сумма корней равна , а произведение корней равно .
Квадратное уравнение можно решить несколькими способами. Можно вычислять дискриминант, или воспользоваться теоремой Виета, а иногда можно просто угадать один из корней. Или оба корня.
Неполные квадратные уравнения
Квадратное уравнение, в котором один из коэффициентов b или с (или они оба) равны нулю, называется неполным. В таких случаях искать дискриминант не обязательно. Можно решить проще.
Задача 9. Рассмотрим уравнение: .
Решение:
В этом уравнении и . Очевидно, – единственный корень уравнения.
Задача 10. Рассмотрим квадратное уравнение: . Здесь , а другие коэффициенты нулю не равны.
Решение:
Проще всего разложить левую часть уравнения на множители по формуле разности квадратов. Получим:
Произведение двух множителей равно нулю тогда и только тогда, когда хотя бы один из них равен нулю.
Значит, или
Вот похожее уравнение: .
Поскольку , уравнение можно записать в виде:
Отсюда или
.
Пусть теперь не равно нулю и .
Задача 11. Рассмотрим квадратное уравнение: .
Левую часть уравнения можно разложить на множители, вынеся за скобки. Получим:
.
Произведение двух множителей равно нулю тогда и только тогда, когда хотя бы один из них равен нулю.
Значит, или .
Задача 12. Решим уравнение: .
Разложить по формуле разности квадрата не получится, тогда попробуем перенести слагаемое 4 в правую часть уравнения.
.
Мы знаем, что нет такого действительного числа, квадрат которого был бы отрицательным числом.
Значит, уравнение не имеет действительных корней.
Напомним, что решить уравнение – значит найти все его корни или доказать, что их нет.
Разложение квадратного трехчлена на множители
.
Здесь и – корни квадратного уравнения .
Запомните эту формулу. Она необходима для решения квадратичных и дробно-рациональных неравенств.
Например, уравнение
.
Его корни
,
.
.
Полезные лайфхаки для решения квадратных уравнений.
1) Намного проще решать квадратное уравнение, если коэффициент , который умножается на , положителен. Кажется, что это мелочь, да? Но сколько ошибок на ЕГЭ возникает из-за того, что старшеклассник игнорирует эту «мелочь».
Например, уравнение
.
Намного проще умножить его на – 1, чтобы коэффициент стал положительным. Получим:
.
Дискриминант этого уравнения равен
.
Корни уравнения: .
2)Прежде чем решать квадратное уравнение, посмотрите на него внимательно.
Может быть, можно сократить обе его части на какое-нибудь не равное нулю число?
Вот, например, уравнение .
Разделим все коэффициенты этого квадратного уравнения на 5. Получим .
Уравнение упростилось. Остается решить его.
Или такое уравнение.
Задача 13. .
Можно сразу посчитать дискриминант и корни. А можно заметить, что все коэффициенты и делятся на 17. Поделив обе части уравнения на 17, получим:
.
Здесь можно и не считать дискриминант, а сразу угадать первый корень: . А второй корень легко находится по теореме Виета.
3)Работать с дробными коэффициентами неудобно. Например, уравнение
.
Вы уже догадались, что надо сделать. Умножить обе части уравнения на 100! Получим:
.
Корни этого уравнения равны 1 и -6.
Задача 14. Решим уравнение:
Умножим обе части уравнения на 2. Получим:
.
Теперь решение этого квадратного уравнения можно осуществить с помощью любого уже известного нам способа.
Корни этого уравнения -11 и -1.
Смотри также: Квадратичная функция
Обзор различных методов решения квадратного уравнения — Концепция
Решение квадратных уравнений может быть трудным, но, к счастью, есть несколько различных методов, которые мы можем использовать в зависимости от того, какой тип квадратного уравнения мы пытаемся решить. Четыре метода решения квадратного уравнения — это разложение на множители с использованием квадратных корней, завершение квадрата и квадратной формулы.
факторинг свойство квадратного корня завершение квадрата квадратичная формула плюсы минусы сравнение
Итак, о чем я хочу поговорить, так это об обзоре всех различных способов решения квадратного уравнения.
Под этим я подразумеваю любую форму: ax² плюс bx плюс c. Итак, у нас есть четыре разных способа, как нам удобно. У нас есть разложение на множители, квадратный корень, завершение квадрата и квадратичная формула. Мы можем использовать эти методы в разное время, и я хочу просто поговорить о том, когда мы можем их использовать, почему они хороши и почему они плохи. Так что я просто пройдусь по ряду и расскажу о каждом из них. «Проверка» означает плюсы, а «минус» — минусы. Факторинг, как правило, является самым быстрым и простым способом решения чего-либо, если оно поддается факторингу. Часто мы имеем дело с квадратным числом, которое нельзя разложить на множители, поэтому разложение на множители нам не поможет. Так что это быстро и просто, когда это удобно, но не всегда факторизуемо. Так быстро и просто, но не всегда применимо.
Следующее, о чем мы поговорим, это свойство квадратного корня. Это когда у нас что-то в квадрате. Итак, за: это здорово, когда вы решаете что-то в квадрате. Единственная проблема в том, что это не всегда та ситуация, с которой мы имеем дело.
Каждый раз, когда у вас есть термин X или что-то в этом роде, мы не сможем его использовать. Так что это не всегда квадратный термин. Это здорово, когда это применимо, но это не всегда так. На самом деле это не так уж и часто.
Завершение квадрата. Самое замечательное в завершении квадрата то, что мы всегда можем это сделать. Никогда не будет времени, когда вы не сможете завершить квадрат. Но крушение в том, что это может стать уродливым. Если вы имеете дело с коэффициентом или нечетным средним членом или чем-то подобным, вы собираетесь ввести дроби. Это не всегда будет самая приятная ситуация.
Наконец, квадратичная формула. Это здорово, опять же, потому что вы всегда можете его использовать. А минусы, это зависит от человека. Если вы используете квадратные корни, что некоторым людям не всегда нравится, вам также всегда нужно использовать квадратные корни. Обычно это не так просто, как некоторые из этих других методов, я бы сказал, что заполнение квадрата немного проще, но это то, что вы должны помнить.
Таким образом, вы должны помнить формулу, и это может стать некрасивым.
Итак, это четыре разных способа, плюсы и минусы, а также некоторые вещи, о которых следует подумать, когда вы решаете проблему. На самом деле я не собираюсь ничего решать за вас. Я только что сделал небольшую диаграмму, чтобы вы знали, какие ресурсы у вас есть, а также плюсы и минусы каждого из них.
Как решать квадратные уравнения? Решение квадратных уравнений
Прежде чем перейти к решению квадратных уравнений, давайте вспомним несколько фактов о квадратных уравнениях. Слово «квадратный» произошло от слова «квадрат» и означает «квадрат». Это означает, что в квадратном уравнении есть переменная, возведенная в степень 2 как член наибольшей степени. Стандартная форма квадратного уравнения задается уравнением ax 2 + bx + c = 0, где a ≠ 0. Мы знаем, что любое значение (значения) x, которое удовлетворяет уравнению, известно как решение (или) корень уравнения и процесс нахождения значений x, удовлетворяющих уравнению ax 2 + bx + c = 0 известен как решение квадратных уравнений.
Существуют различные методы решения квадратных уравнений. Но самым популярным методом является решение квадратных уравнений методом факторизации. Давайте подробно изучим все методы здесь вместе с несколькими решенными примерами.
| 1. | Как решать квадратные уравнения? |
| 2. | Решение квадратичных уравнений с помощью факторинга |
| 3. | Решение квадратных уравнений путем заполнения квадрата |
| 4. | Решение квадратичных уравнений с помощью графика |
| 5. | Решение квадратных уравнений по квадратичной формуле |
| 6. | Часто задаваемые вопросы о решении квадратных уравнений |
Как решать квадратные уравнения?
Решение квадратных уравнений означает нахождение значения (или) значений переменной, удовлетворяющих уравнению.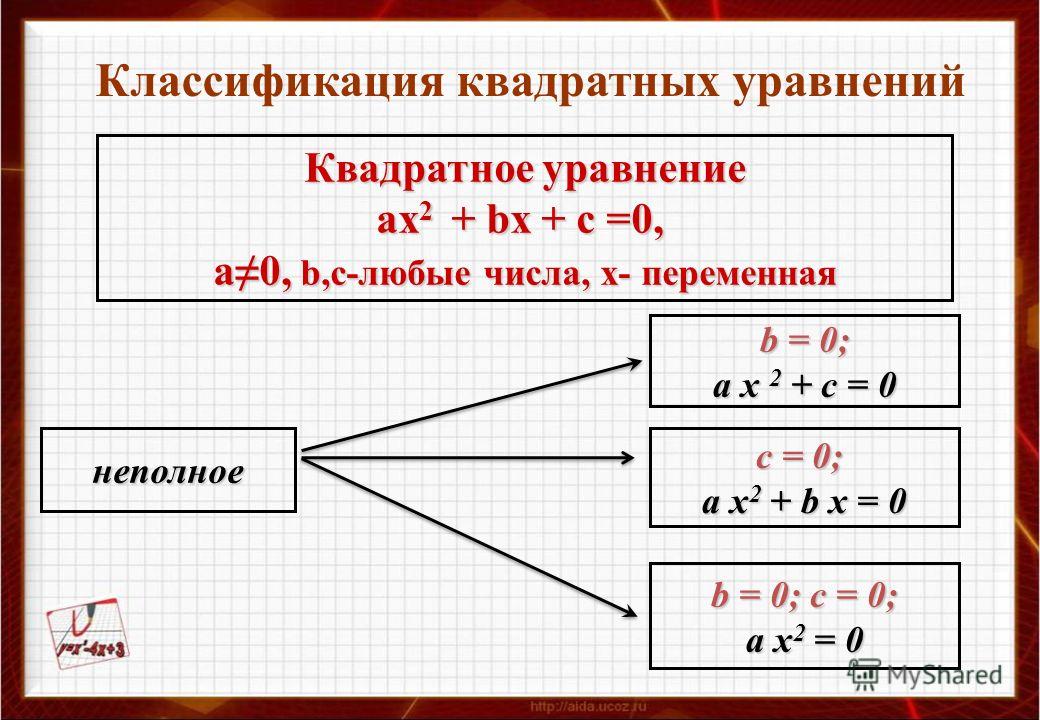
Значение (я), которые удовлетворяют квадратному уравнению, известны как его корни (или) решения (или) нули. Поскольку степень квадратного уравнения равна 2, оно может иметь максимум 2 корня. Например, легко увидеть, что x = 1 и x = 2 удовлетворяют квадратному уравнению x 2 — 3x + 2 = 0 (можно подставить каждое из значений в это уравнение и проверить). Таким образом, x = 1 и x = 2 являются корнями x 2 — 3x + 2 = 0. Но как их найти, если они не заданы? Существуют различные способы решения квадратных уравнений.
- Решение квадратных уравнений методом факторизации
- Решение квадратных уравнений путем заполнения квадрата
- Решение квадратных уравнений с помощью графика
- Решение квадратных уравнений по квадратной формуле
Помимо этих методов, существуют и другие методы, которые используются только в особых случаях (когда в квадратном уравнении отсутствуют члены), как описано ниже.
Решение квадратных уравнений отсутствует b
В квадратном уравнении ax 2 + bx + c = 0, если член с b отсутствует, уравнение принимает вид ax 2 + c = 0.
Это можно решить, извлекая квадратный корень из обеих частей. Процесс поясняется примерами ниже.
- x 2 — 4 = 0 ⇒ x 2 = 4 ⇒ x = ±√4 ⇒ x = ± 2
Таким образом, корни уравнения равны 2 и -2. - x 2 + 49 = 0 ⇒ x 2 = -49 ⇒ x = ±√(-49) ⇒ x = ± 7i
Таким образом, корни уравнения равны 7i и -7i.
(обратите внимание, что это мнимые (или) комплексные числа).
Решение квадратных уравнений отсутствует c
В квадратном уравнении ax 2 + bx + c = 0, если член с c отсутствует, уравнение принимает вид ax 2 + bx = 0. Для решения этого типа уравнения , мы просто выносим x из левой части, устанавливаем каждый из множителей равным нулю и решаем. Процесс поясняется примерами ниже.
- х 2 — 5х = 0 ⇒ х (х — 5) = 0 ⇒ х = 0; х — 5 = 0 ⇒ х = 0; х = 5
Таким образом, корни уравнения равны 0 и 5. - х 2 + 21х = 0 ⇒ х (х + 21) = 0 ⇒ х = 0; х + 21 = 0 ⇒ х = 0; х = -21
Таким образом, корни уравнения равны 0 и -11.
Теперь мы изучим методы решения квадратных уравнений в каждом из вышеупомянутых методов.
Решение квадратичных уравнений с помощью факторинга
Решение квадратичных уравнений с помощью факторизации — один из известных методов, используемых для решения квадратных уравнений. Пошаговый процесс решения квадратных уравнений факторингом объясняется вместе с примером.
- Шаг — 1: Приведите уравнение к стандартной форме. т. е. получить все члены с одной стороны (обычно с левой стороны) уравнения так, что другая сторона равна 0,
- Шаг — 2: Фактор квадратного выражения. Если вы хотите узнать, как разложить квадратное выражение на множители, нажмите здесь.
- Шаг — 3: По нулевому свойству произведения установите каждый из факторов равными нулю.
- Шаг — 4: Решите каждое из приведенных выше уравнений.
Пример: Решите квадратное уравнение x 2 — 3x + 2 = 0, разложив его на множители.
Решение:
Разлагая на множители левую часть, получаем (x — 1) (x — 2) = 0.
Тогда x — 1 = 0 (или) x — 2 = 0
что дает x = 1 (или) x = 2.
Таким образом, решения квадратного уравнения x 2 — 3x + 2 = 0 равны 1 и 2. Этот метод применим только тогда, когда квадратное выражение факторизуемо. Если это НЕ факторизуемо, то мы можем использовать один из других методов, как описано ниже. Подобно квадратным уравнениям, у нас есть решения для линейных уравнений, которые используются для решения задач линейного программирования.
Решение квадратных уравнений путем заполнения квадрата
Завершение квадрата означает запись квадратного выражения ax 2 + bx + c в форме a (x — h) 2 + k (которая также известна как вершинная форма), где h = -b/2a и «k» можно получить, подставив x = h в ax 2 + bx + c. Пошаговый процесс решения квадратных уравнений путем заполнения квадрата объясняется вместе с примером.
- Шаг — 1: Приведите уравнение к стандартной форме.
- Шаг — 2: Заполните квадрат с левой стороны. Если вы хотите узнать, как заполнить квадрат, нажмите здесь.
- Шаг — 3: Решите это для x (По пути нам придется извлечь квадратный корень с обеих сторон).
Пример: Решите 2x 2 + 8x = -3, заполнив квадрат.
Решение:
Данное уравнение в стандартной форме имеет вид 2x 2 + 8x + 3 = 0. Заполнив квадрат в левой части, получим 2 (x + 2) 2 — 5 = 0. Теперь решая его относительно x,
Добавление 5 с обеих сторон,
2 (х + 2) 2 = 5
Разделив обе части на 2,
(х + 2) 2 = 5/2
Извлекая квадратный корень с обеих сторон,
х + 2 = √(5/2) = √5/√2 · √2/√2 = √10/2
Вычитание 2 с обеих сторон,
х = -2 ± (√10/2) = (-4 ± √10) / 2
Таким образом, корнями квадратного уравнения 2x 2 + 8x = -3 являются (-4 + √10)/2 и (-4 — √10)/2.
Решение квадратичных уравнений с помощью графика
Для решения квадратного уравнения путем построения графика сначала нужно построить квадратное выражение (когда уравнение имеет стандартную форму) либо вручную, либо с помощью графического калькулятора. Тогда точки пересечения графика (точки, в которых график пересекает ось x) являются не чем иным, как корнями квадратного уравнения. Вот шаги, чтобы решить квадратные уравнения с помощью графика.
- Шаг — 1: Войдите в стандартную форму.
- Шаг — 2: Нарисуйте квадратное выражение (которое находится слева).
- Шаг — 3: Определите точки пересечения по оси x.
- Шаг — 4: Координаты абсцисс точек пересечения абсцисс являются не чем иным, как корнями квадратного уравнения.
Пример: Решите квадратное уравнение 3x 2 + 5 = 11x с помощью графика.
Решение:
Преобразование данного уравнения в стандартный вид, вычитание 11x с обеих сторон, 3x 2 — 11x + 5 = 0. Теперь нарисуйте квадратное выражение. Нарисуйте график квадратичной функции y = 3x 2 — 11x + 5 либо вручную, либо с помощью графического калькулятора (GDC) и определите точки пересечения x. Его график равен
Таким образом, решения квадратного уравнения 3x 2 + 5 = 11x равны 0,532 и 3,135.
Из приведенного выше примера видно, что графический метод решения квадратных уравнений может не давать точных решений (т. е. давать только десятичные приближения корней, если они иррациональны). т. е., если мы решим то же уравнение с помощью дополнения квадрата, мы получим x = (11 + √61) / 6 и x = (11 — √61) / 6. Но мы не можем получить эти точные корни графическим методом.
Что делать, если график вообще не пересекает ось X? Это означает, что квадратное уравнение имеет два комплексных корня.
т. е. метод построения графика НЕ помогает найти корни, если они являются комплексными числами. Мы можем использовать квадратичную формулу (которая объясняется в следующем разделе), чтобы найти любой тип корней.
Решение квадратных уравнений по квадратичной формуле
Как мы уже видели, предыдущие методы решения квадратных уравнений имеют некоторые ограничения, например, метод разложения полезен только тогда, когда квадратное выражение факторизуемо, метод построения графика полезен только тогда, когда квадратное уравнение имеет действительные корни и т. д. Но 9Решение квадратных уравнений 0003 по квадратной формуле преодолевает все эти ограничения и полезно для решения любого типа квадратных уравнений. Вот пошаговое объяснение решения квадратного уравнения по формуле квадратного уравнения.
- Шаг — 1: Входим в стандартную форму.
- Шаг — 2: Сравните уравнение с ax 2 + bx + c = 0 и найдите значения a, b и c.
- Шаг — 3: Подставьте значения в квадратную формулу, которая говорит x = [-b ± √(b² — 4ac)] / (2a). Тогда мы получим
- Шаг — 4: Упрощение.
Пример: Решите квадратное уравнение 2x 2 = 3x — 5 по квадратной формуле.
Решение:
Приведенное выше уравнение в стандартной форме 2x 2 — 3x + 5 = 0.
Сравнивая уравнение с ax 2 + bx + c = 0, получаем a = 2, b = -3. и c = 5.
Подставляем значения в квадратную формулу
x = [-(-3) ± √((-3)² — 4(2)(5))] / (2(2))
= [ 3 ± √(9 — 40) ] / 4
= [ 3 ± √(-31) ] / 4
= [ 3 ± i√(31) ] / 4
Таким образом, корнями квадратного уравнения 2x 2 = 3x — 5 являются [ 3 + i√(31) ] / 4 и [ 3 — i√(31) ) ] / 4. В квадратичной формуле выражение b² — 4ac называется дискриминантом (обозначается буквой D). т. е. D = b² — 4ac. Это используется для определения характера корней квадратного уравнения.
Характер корней с использованием дискриминанта
- Если D > 0, то уравнение ax 2 + bx + c = 0 имеет два действительных и различных корня.
- Если D = 0, то уравнение ax 2 + bx + c = 0 имеет только один действительный корень.
- Если D < 0, то уравнение ax 2 + bx + c = 0 имеет два различных комплексных корня.
Таким образом, используя дискриминант, мы можем найти количество решений квадратных уравнений, фактически не решая его.
Важные замечания по решению квадратных уравнений:
- Метод факторизации нельзя применять, если квадратное выражение НЕ факторизуемо.
- Графический метод не может дать комплексные корни, а также не может дать точные корни в случае, если квадратное уравнение имеет иррациональные корни.
- Завершение метода квадратов и метода квадратичных формул может быть применено для решения любого типа квадратного уравнения.
- Корни квадратного уравнения также известны как «решения» или «нули».
- Для любого квадратного уравнения ax 2 + bx + c = 0,
сумма корней = -b/a
произведение корней = с/а.
☛Связанные темы:
- Решение квадратных уравнений с помощью калькулятора квадратных формул
- Решение квадратных уравнений с помощью квадратного калькулятора
- Калькулятор корней квадратного уравнения
- Решение квадратных уравнений с помощью калькулятора факторинга
Часто задаваемые вопросы о решении квадратных уравнений
В чем смысл решения квадратных уравнений?
Решение квадратных уравнений означает нахождение их решений или корней. т. е. это процесс нахождения значений переменной, удовлетворяющих уравнению.
Какие самые популярные способы решения квадратных уравнений?
Существуют разные способы решения квадратичных уравнений. Но самыми популярными способами являются «решение квадратных уравнений факторингом» и «решение квадратных уравнений по квадратной формуле».
Какие этапы решения квадратных уравнений графически?
Чтобы решить квадратное уравнение с помощью графика, сначала приведите к стандартной форме ax 2 + bx + c = 0. Затем начертите квадратное выражение ax 2 + bx + c. Найдите, где график пересекает ось x. X-координата x-перехвата (ов) — это не что иное, как решения квадратного уравнения.
Какие 4 способа решения квадратичных уравнений?
Существует 4 способа решения квадратных уравнений.
- по факторингу
- , заполнив квадрат
- по графику
- по квадратичной формуле
Как решать квадратные уравнения по квадратным формулам?
Решения квадратного уравнения ax 2 + bx + c = 0 задаются квадратной формулой x = [-b ± √(b² — 4ac)] / (2a). Таким образом, чтобы решить квадратное уравнение с помощью квадратичной формулы, просто приведите уравнение к стандартной форме: ах 2 + bx + c = 0 и примените квадратную формулу.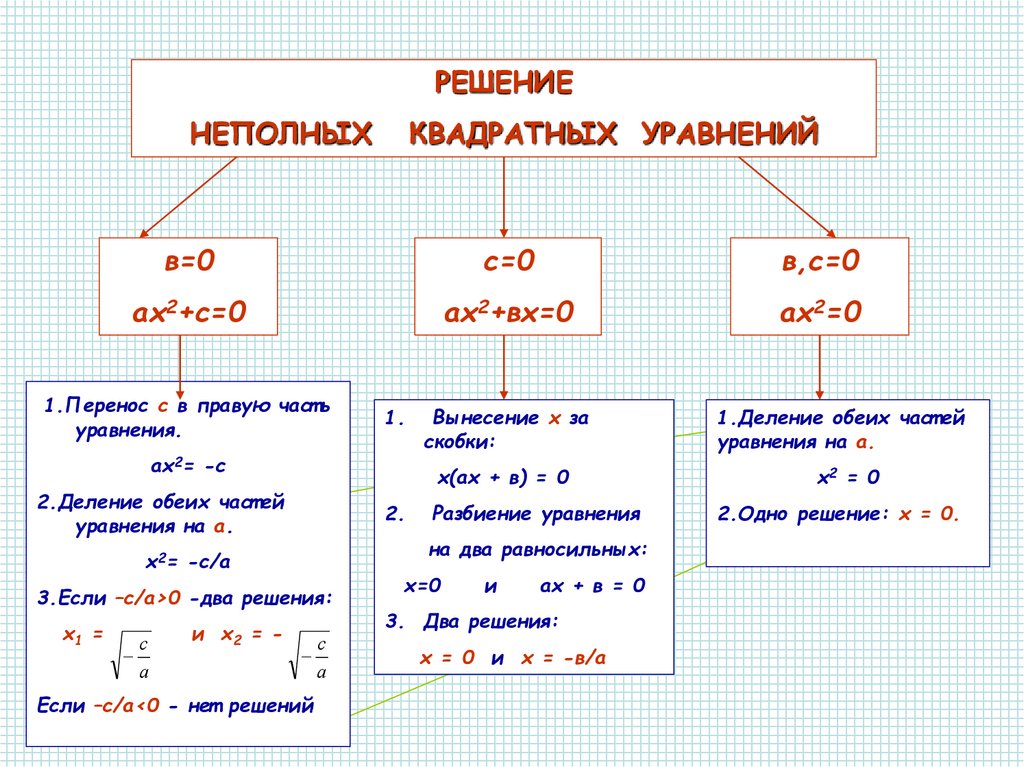
Как узнать, какой метод использовать при решении квадратных уравнений?
Мы можем решать квадратные уравнения любого типа, дополняя квадрат или квадратную формулу. Но если квадратное выражение факторизуемо, то проще всего применить метод факторинга. Мы можем решить его и графическим методом, но он дает только аппроксимированные вещественные корни (т.е. комплексные корни не могут быть найдены в этом методе).
Как проще всего решать квадратные уравнения?
Самым простым способом решения квадратных уравнений является метод факторинга. Но не всегда квадратные выражения факторизуемы. В этом случае мы можем либо использовать квадратичную формулу, либо использовать метод завершения квадрата.
Какие этапы решения квадратичных уравнений путем заполнения квадрата?
Чтобы решить квадратное уравнение ax 2 + bx + c = 0, дополнив квадрат, преобразовать ax 2 + bx + c в вершинную форму a (x — h) 2 + k, где h = -b /2a и k получается подстановкой x = h в ax 2 + бх + в.
Тогда мы можем легко решить (x — h) 2 + k = 0, изолируя x. В этом процессе нам придется извлекать квадратный корень с обеих сторон.
Как решать квадратные уравнения с помощью факторинга?
Для решения квадратных уравнений методом факторизации сначала приведите его к стандартной форме (ax 2 + bx + c = 0). Затем разложите левую часть на множители, используя методы факторизации квадратных выражений, установите каждый из множителей равными нулю, что приведет к двум линейным уравнениям, и, наконец, решите линейные уравнения.
Как факторизованная форма помогает решать квадратные уравнения?
Если квадратное выражение в стандартной форме квадратного выражения в нем факторизуемо, то мы можем просто установить каждый множитель равным нулю и решить их. Решения — это не что иное, как корни квадратного уравнения.
Как найти корни квадратных уравнений?
Корни квадратного уравнения ax 2 + bx + c = 0 можно найти с помощью квадратной формулы, которая гласит: x = [-b ± √(b² — 4ac)] / (2a).