Квадратные уравнения математика: Квадратные уравнения — урок. Алгебра, 8 класс.

alexxlab / / Разное

Содержание

Тест: Квадратные уравнения — Математика 8 класс

  • Предметы
    • »
  • Математика
    • »
  • 8 класс
    • »
  • Квадратные уравнения

Квадратные уравнения

Тест содержит 12 вопросов. Рассматриваются неполные, полные и приведенные квадратные уравнения. Применение теоремы Виета, решение задачи с помощью квадратного уравнения. Задание с параметром.

Математика 8 класс | Автор: Бурякова Вера Николаевна | ID: 1085 | Дата: 17.1.2014 +24 -6

Помещать страницу в закладки могут только зарегистрированные пользователи
Зарегистрироваться

Вопрос № 1

Запишите квадратное уравнение, у которого первый коэффициент 3, второй коэффициент 8, свободный член -7.

3х+8х2-7=0
3х2+8х-7=0
3х2+8-7х=0

Вопрос № 2

Запишите приведенное квадратное уравнение, у которого второй коэффициент 4, свободный член -3.

х2+4х-3
4х-3=0
х2+4х-3=0

Вопрос № 3

Запишите неполное квадратное уравнение, у которого первый коэффициент равен 2, второй коэффициент равен 7. Найдите его корни.

2х+7х2=0; x1= 0; x2=3,5
2х2+7х=0; x1= 0 x2=3,5
2х2+7х=0; x1=-3,5 x2=0

Вопрос № 4

Найдите значение дискриминанта D, если a= 3, b=1, c=-4

D= -47

D= 49
D= -49

Вопрос № 5

При каком условии полное квадратное уравнение имеет единственный корень?

D>0
D=0
D

Вопрос № 6

Решите уравнение х2 +2х-3=0

3; -1
-3; 1
3; 1

Вопрос № 7

Какое из чисел является корнем уравнения 2х2 -11х+5=0?

2
-1
5

Вопрос № 8

Найти значения x, при которых равно нулю значение выражения 2х2 +5х-3

-3 и 0,5
3 и -0,5
-6 и 1

Вопрос № 9

Чему равны сумма и произведение корней квадратного уравнения х2-5*х+6=0

x1+x2=-5; x1*x2=6
x1+x2=5; x1*x2=-6
x1+x2=5; x1*x2=6

Вопрос № 10

Решите задачу: Найти длины сторон прямоугольника, если его периметр равен 18 см, а площадь 20 см2.

9 см и 2 см
4 см и 5 см
10 см и 2 см

Вопрос № 11

Чему равна сумма квадратов корней уравнения?
x2(x+3)-4(x+3)=0

9
17
3

Вопрос № 12

При каком значении параметра b уравнение (b +5) х2+(2b+10)х+4=0 имеет только один корень?

b=-5
b=-5 или b=-1
b=-1

Читать онлайн «Квадратные уравнения. Часть 1», Ирина Краева – ЛитРес

Посвящаю своим ученикам школы №15 

г. Перми, в особенности одноклассникам моего сына (Алексею Макарычеву, Максиму Григорцу, Владимиру Печенкину и другим), с которыми общались незабываемые три с половиной года.

Автор

© Ирина Краева, 2019

ISBN 978-5-0050-6428-8 (т. 1)

ISBN 978-5-0050-6831-6

Создано в интеллектуальной издательской системе Ridero

ПРЕДИСЛОВИЕ

Данная книга является самой первой в серии «Школьная математика ОТ и ДО» и первой в теме «Квадратные уравнения».

Предполагается издать четыре части – квадратные уравнения: от определения до применения; от упражнений до олимпиадных задач; от древности до современности; от начальной школы до выпускных классов.

За несколько лет, которые прошли с момента возникновения общей идеи этой серии, эфемерность замысла оформилась в конкретные разработки, к реализации которых были подключены студенты математического факультета Пермского государственного педагогического, а теперь уже гуманитарно-педагогического университета.

Эти книги помогут школьникам в математическом самообразовании (первые три части), учителям – в методическом.

Студентам – как в том, так и в другом. Содержание первых трёх частей можно использовать для создания элективных курсов, курсов по выбору и разнообразных форм дополнительного математического образования, а четвёртая позволит построить оптимальную систему обучения математике в школе.

 
                                   ***
 

Казалось бы, что может быть банальней в школьном курсе математики, чем квадратные уравнения? Разве что только таблица умножения.

Нередко «оценочным признаком» низкой математической подготовки школьника служит фраза «он даже квадратные уравнения не умеет решать». Предполагается, что этот процесс должен стать инструментом, применяемым «легко и непринуждённо», а не оставаться самостоятельной задачей, требующей значительных затрат умственных ресурсов.

Однако, обидное пренебрежение этим математическим объектом, на наш взгляд, весьма ошибочно. Квадратные уравнения таят в себе удивительно занимательную теорию, полезную для взрослеющего и пытливого ума.

Собственно этими соображениями мы и хотим поделиться.

Не надо думать, что все предложенные теоретические факты необходимо запоминать (хотя некоторые стоило бы). Просто из того минимума, содержащегося в школьном курсе математики, при большом желании можно вытянуть закономерности, позволяющие существенно облегчить жизнь решателям математических задач.

Решать квадратные уравнения – что это?

Наука или искусство?

С первого – математического – взгляда, конечно наука!!!

Квадратные уравнения – это математическое понятие, процесс его решения имеет определённый алгоритм, который применяется для решения других (математических, физических, а порой и жизненных) задач.

А искусство, что оно? Только для души!

Но если решать квадратные уравнения не только для дела, но и для души, то вы с высокой вероятностью увидите красоту в этом привычном процессе.

Для изображения картин тоже необходимы техника рисунка, правила перспективы и т. д. Но каждый художник вкладывает в своё произведение собственное видение жизни.

Так и при решении квадратных уравнений можно не ограничиваться известным алгоритмом, а творчески выбирать приёмы получения корней.

В этой – первой – части саги о квадратных уравнениях мы представляем их математическую теорию, а возможность применить её у читателя будет во второй части «Квадратные уравнения от упражнений до олимпиадных задач».

Между прочим, теория – какая бы она ни была – не берётся из ниоткуда. Когда-то и квадратные уравнения были серьёзным объектом для математических исследований. Поэтому третья часть – «Квадратные уравнения от древности до современности» – ждёт своего часа.

Заранее обговорим те ограничения, которых будем придерживаться в рамках данного изложения. Прежде всего, учитывая, что квадратные уравнения начинают изучаться в восьмом классе, мы без специальных комментариев используем все математические знания «предыдущих лет». Там, где на наш взгляд, появляются спорные с точки зрения последовательности изучения факты, мы отсылаем к приложению или сноскам.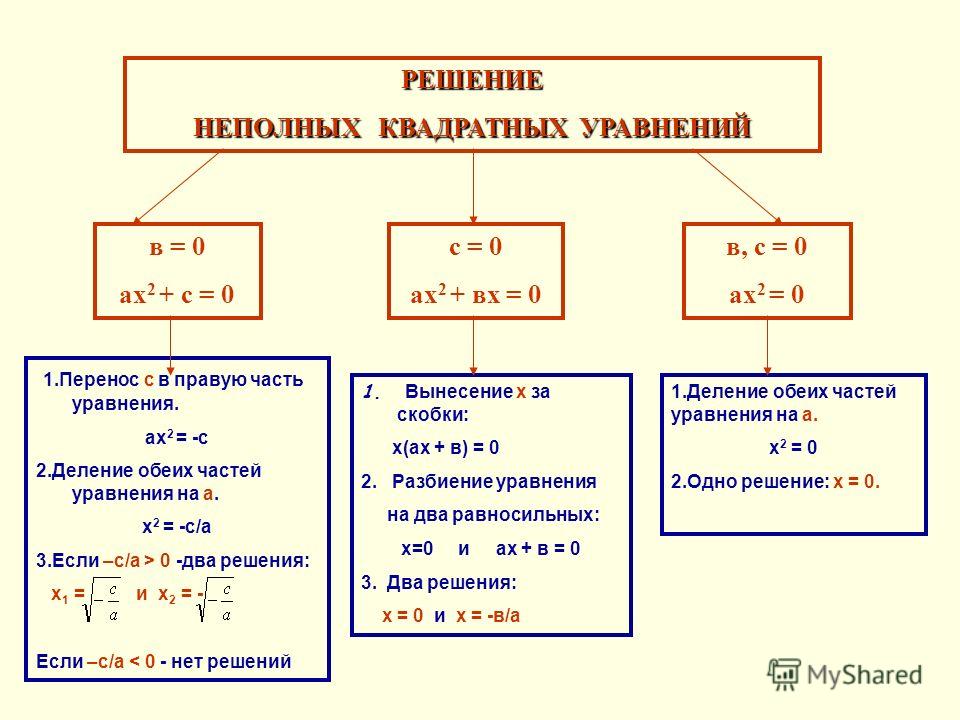

Кроме того, в основном тексте книги опущены строгие математические подробности, которые касаются таких понятий как собственно «уравнение» и его видов, дающих представление о «родословной» квадратного уравнения. Если читатель не знает (или забыл) эти факты, он может обратиться к приложению или комментариям.

Автор благодарит своих выпускниц математического факультета Пермского государственного педагогического университета Марию Волкову (2002 г.), Ольгу Крысову (2003 г.) и Инессу Баранову (2008 г.), фрагменты чьих курсовых и выпускных исследований вошли в эту книгу.

Благодарю всех, кому идея создания подобного рода книг созвучна и тех, кто, ознакомившись с книгой, не найдёт её целесообразной.

РАЗДЕЛ I.


ОПРЕДЕЛЕНИЕ, СТРУКТУРА И ЭЛЕМЕНТЫ КВАДРАТНОГО УРАВНЕНИЯ

§1. Мысли с потолка, ведущие к идее,


или Откуда что взялось?

…Забавное число – ноль. На что ни умножь – само же в результате и получается! Прямо загляденье:

 
0 × 0 = 0 × 1 = 0 × 2 = 0 × 10 = … = 0, т. е. 0 × a = 0 × 0
 

Однако, интересно, а будет ли выполняться равенство 0 × a = 02, если вместо нуля поставить произвольное число? Например, какое удвоенное число равно своему квадрату, то есть x × 2 = x2? Или утроенное x × 3 = x2?

Поставим задачу в общем виде: найти число, квадрат которого, равен произведению этого числа на конкретное данное число a. Построим модель: xx = ax или x2 = ax.

Так как мы ищем число, отличное от нуля, то, разделив обе части построенного равенства на 

x, получим, что x = a.

То есть, если удвоенное число равно своему квадрату, то это число 2, а если утроенное, то 3.

Можно этот факт запомнить – вдруг пригодится?..

 
                                        ***
 

…Инструктаж судьи на одном из этапов туристической эстафеты:

– Вам необходимо огородить участок прямоугольной формы, площадью 1 ар для стоянки. Дополнительные очки той команде, которая затратит как можно меньше страховочной верёвки. На старт, внимание, начали!

1 ар – это 100 квадратных метров. Участок может иметь размеры 20 × 5 или 25 × 4. Но наша команда знает, что наименьший периметр прямоугольника при его заданной площади будет в том случае, если он – квадрат (теперь и вы это помните!). Отлично! Значит необходимо найти сторону квадрата, если его площадь равна 100. Ну, это легко! Ещё с младших классов, благодаря большой вычислительной практике, помним, что число 10 умноженное на себя даёт сто.

Хорошо, что мы не на уроке математики, а то пришлось бы составлять уравнение x2 = 100…

 
                                   ***
 

…Не так давно с нами эксперимент проводили: надо было из множества прямоугольников разнообразной формы выбрать один, который покажется самым приятным на вид. Многочисленные повторения этого опыта показали, что чаще всего люди выбирают те прямоугольники, стороны которого относятся как «золотая пропорция». Золотое (или гармоническое) сечение – это такое деление отрезка, при котором отношение всего отрезка к большей части равно отношению большей части к меньшей 1: x = x: (1 – x).

Если воспользоваться свойством пропорции (произведение крайних членов равно произведению средних), то можно получить уравнение, чтобы найти длину большей части этого отрезка: x2 = 1 – x.

 
                                   ***
 

…В каком прямоугольном треугольнике стороны выражаются тремя последовательными натуральными числами?

Пусть n длина меньшего катета, тогда второй катет и гипотенуза выражаются как (n +1) и (n +2).

По теореме Пифагора все длины увязываем в уравнение:

 
                             n2 + (n +1) 2 = (n +2) 2…
 
 
                                   ***
 

Пифагорейцы исследовали фигурные числа, в частности, треугольные (их можно изобразить в виде треугольника).


Треугольное число с номером n можно найти как половину произведения n× (n+1). Для ответа на вопрос, является ли треугольным число 45 и если да, то каков его номер, надо решить уравнение n× (n+1) = 90…

 
                                   ***
 

Задумайте два натуральных числа от 1 до 20. Найдите их сумму и произведение. Сообщите мне. Я отгадаю задуманные вами числа. Вам интересно, как я это сделаю?..

§2. Кто есть кто,


или Определение квадратного уравнения

Квадратным называется уравнение вида ax2 + bx + c = 0, где a, b, c – некоторые заданные действительные числа, причём a ≠ 0, а x принимается за неизвестное.

 

Числа a, b, c называют так:

a – старшим или первым коэффициентом,

b – вторым,

c – свободным или третьим1.

«Нумерация» коэффициентов зависит не от их реального месторасположения, а от того, при какой степени неизвестной они находятся. Например, число 2 будет первым коэффициентом в любом из трёх уравнений:

 
5x +2x2 – 7 = 0,
3 – x +2x2 = 0,
2x2 +7x +5 = 0.
 

А вот число 5 в третьем уравнении является свободным коэффициентом, а в первом уравнении – вторым коэффициентом.

То есть первый (старший) коэффициент – это множитель при квадрате неизвестной, второй – при первой степени. Свободный (третий) коэффициент – это слагаемое без неизвестной, то есть «свободный от неизвестной».

Очевидно, что в качестве неизвестного необязательно брать букву x. Более того, привыкнув за школьные годы к этому неизменному обозначению, среднестатистический ученик начинает испытывать затруднения в восприятии (узнавании, интерпретации) квадратных уравнений, встречающихся при решении более сложных математических (физических и других) задач.

Собственно говоря, и коэффициенты квадратного уравнения не всегда могут обозначаться указанными выше буквами. Одним словом, квадратное уравнение имеет вполне определённую структуру, а как обозначаются элементы этой структуры – дело десятое. Человек со сложившимся математическим стилем мышления понимает, что квадратным уравнением будет являться любое равенство, в правой части которого стоит ноль, а в левой – сумма трёх слагаемых, одно из которых является произвольным числом, другое – произведением произвольного числа на первую степень неизвестного и третье – произведением ненулевого числа на вторую степень неизвестного.

Тогда квадратными будут уравнения:

mx2 + nx + k = 0 (относительно x, m ≠ 0),

xa2 + ya + z = 0 (относительно a, x ≠ 0).

Уравнение y2 + xy + x2 = 0 можно рассматривать как квадратное, но только либо относительно x, либо только относительно y.

Пока же договоримся, что теоретические вопросы будем излагать на привычных обозначениях.

Вернёмся к определению. Давайте выделим внешние, «бросающиеся в глаза», черты квадратного уравнения. Во-первых, наличие знака равенства. Отсутствие его с очевидностью снимает вопрос о правомерности называть объект уравнением.

(Любое ли равенство является уравнением – разговор особый и не в рамках этой книги.)

Во-вторых, левая часть нашего равенства представляет собой алгебраическую сумму трёх слагаемых.

Возникает первый вопрос: обязательно трёх?

Другими словами количество слагаемых – это определяющий признак или нет? Давайте посмотрим.

Значения второго и свободного коэффициентов квадратного уравнения в определении никак не ограничиваются (в отличие от первого). Следовательно, они могут быть равными нулю. Тогда под определение квадратного подходят уравнения вида

ax2 + bx = 0 (c = 0, ab ≠ 0),

ax2 + c = 0 (b = 0, ac ≠ 0),

ax2 = 0 (b = c = 0, a ≠ 0).

Но в левых частях этих уравнениях не три слагаемых!

Тем не менее, это – квадратные уравнения, потому что их можно записать так

ax2 + bx +0 = 0,

ax2 +0 · x + c = 0,

ax2 +0 · x +0 = 0.

Так как количество слагаемых левой части уравнений ax2 + bx = 0, ax2 + c = 0, ax2 = 0 визуально меньше, чем может быть, их называют неполными квадратными уравнениями. Тогда как квадратное уравнение ax2 + bx + c = 0, в котором все коэффициенты отличны от нуля, называют полным.

Таким образом, отсутствие в записи конкретного уравнения свободного члена или слагаемого с первой степенью неизвестного не даёт нам права сомневаться в том, что уравнение всё-таки квадратное. Однако и наличие их не является веской причиной отнести уравнение к квадратным. Об этом чуть ниже.

Следующим возникает вопрос, а почему, собственно a ≠ 0? (Конечно, искушённый читатель знает почему.) Можно ли, например, уравнение вида ax2 + (a – 1) x + a = 0 (или в общем виде f (a) x2 + g (a) x + h (a) = 0) называть квадратным?

Давайте похулиганим и поставим в качестве первого коэффициента ноль. Тогда уравнение примет вид bx + c = 0.

Но это же линейное уравнение! Оно имеет свою теорию, свои изюминки.

Пусть будут «мухи отдельно, котлеты отдельно».

Теперь понятно, что требование a ≠ 0 необходимо для сохранения в квадратном уравнении второй степени – квадрата – неизвестного. Вот этот признак будет определяющим!

В дальнейшем, говоря о квадратном уравнении, мы будем помнить, что старший коэффициент не равен нулю, не оговаривая это каждый раз. Договорились?

квадратных уравнений | Математическое моделирование

Цели обучения

  • Распознать квадратное уравнение
    • Использовать принцип нулевого произведения для решения квадратных уравнений, которые можно разложить на множители
    • Находить решения квадратных уравнений на графике
  • Квадратные корни и завершение квадрата
    • Использование свойства квадратного корня для решения квадратного уравнения
    • Заполните квадрат, чтобы решить квадратное уравнение
  • Квадратичная формула
    • Напишите квадратное уравнение в стандартной форме и определите значения a , b и c в квадратном уравнении стандартной формы.
    • Используйте квадратную формулу для поиска решений квадратного уравнения (рационального, иррационального и сложного)

Уравнение, содержащее многочлен второй степени, называется квадратным уравнением . {2}-4=0[/латекс], являются квадратными уравнениями. Они бесчисленным образом используются в инженерии, архитектуре, финансах, биологических науках и, конечно же, в математике.

Часто самый простой способ решения квадратного уравнения –  разложить на множители . Факторинг означает нахождение выражений, которые можно перемножить, чтобы получить выражение на одной стороне уравнения. Обратите внимание, что мы не будем тратить много времени на объяснение того, как учитывать факторы в этом разделе. Вы можете обратиться за помощью, если вы не уверены в факторинге.

Решение факторингом зависит от свойства нулевого произведения, которое гласит, что если [латекс]а\cdot b=0[/латекс], то [латекс]а=0[/латекс] или [латекс]b=0[ /латекс], где 9{2}+x — 6=0[/latex] имеет стандартную форму.

Мы можем использовать свойство нулевого произведения для решения квадратных уравнений, в которых мы сначала должны вынести наибольший общий множитель (НОК), а также для уравнений, которые имеют специальные формулы факторизации, такие как разность квадратов, оба из которых мы увидим позже в этом разделе.

Свойство нулевого произведения и квадратные уравнения

Свойство нулевого произведения утверждает

[латекс]\текст{Если }a\cdot b=0,\text{, то }a=0\text{ или } б=0[/латекс], 9{2}[/latex], равно 1. У нас есть один метод факторизации квадратных уравнений в этой форме.

Напоминание: дано квадратное уравнение со старшим коэффициентом 1, разложите его на множители.

  1. Найдите два числа, произведение которых равно c и сумма которых равна b .
  2. Используйте эти числа для записи двух множителей вида [латекс]\влево(х+к\вправо)\текст{ или }\влево(х-к\вправо)[/латекс], где k — одно из найденных чисел на шаге 1. Используйте числа точно так, как они есть. Другими словами, если эти два числа равны 1 и [латекс]-2[/латекс], множители будут [латекс]\влево(х+1\вправо)\влево(х — 2\вправо)[/латекс]. 9{2}+bx+c=0[/latex], умножьте [latex]a\cdot c[/latex].
  3. Найдите два числа, произведение которых равно [latex]ac[/latex] и сумма которых равна [latex]b[/latex].
  4. Перепишите уравнение, заменив член [латекс]bx[/латекс] двумя членами, используя числа, найденные на шаге 1, в качестве коэффициентов x.
  5. Умножьте первые два члена, а затем факторизируйте два последних члена. Выражения в круглых скобках должны быть точно такими же, чтобы можно было использовать группировку.
  6. Вынесите выражение в скобках на множители. 9{2}+15x+9=0[/латекс].

    Показать ответ

    Следующее видео содержит еще один пример решения квадратного уравнения с помощью факторизации с группировкой.

    Иногда нам могут дать уравнение, которое на первый взгляд не похоже на квадратное. В наших следующих примерах мы будем решать кубическое полиномиальное уравнение, где GCF каждого члена равен x, и его можно разложить на множители. {2}-2х=0[/латекс].

    Показать ответ

     

    В этом последнем видеопримере мы решаем квадратное уравнение со старшим коэффициентом -1, используя упрощенный метод факторизации и принцип нулевого произведения.

    Квадратные уравнения можно решать разными способами. Возможно, вы уже знакомы с факторингом для решения некоторых квадратных уравнений. Однако не все квадратные уравнения могут быть факторизованы. В этом разделе вы будете использовать квадратные корни, чтобы изучить другой способ решения квадратных уравнений, и этот метод будет работать с 9{2}=a[/latex], затем [latex] x=\sqrt{a}[/latex] или [latex] -\sqrt{a}[/latex].

    Приведенное выше свойство говорит о том, что вы можете извлечь квадратный корень из обеих частей уравнения, но вы должны рассмотреть два случая: положительный квадратный корень из из и отрицательный квадратный корень из из .

    Быстрый способ написать «[латекс] \sqrt{a}[/латекс]» или «[латекс] -\sqrt{а}[/латекс]»: [латекс] \pm \sqrt{a}[/ латекс]. Символ [латекс]\pm[/латекс] часто читается как «положительный или отрицательный». Если оно используется как операция (сложение или вычитание), оно читается как «плюс-минус». 9{2}=9[/latex], вы ищете всех чисел , квадрат которых равен 9. Для [latex] \sqrt{9}[/latex] вам нужен только основной (неотрицательный) квадратный корень. Отрицательное значение главного квадратного корня равно [латекс] -\sqrt{9}[/латекс]; оба будут [латекс] \pm \sqrt{9}[/латекс]. Если перед знаком радикала нет символа, требуется только неотрицательное значение!

    В приведенном выше примере вы можете легко извлечь квадратный корень из обеих сторон, потому что на каждой стороне есть только один член. В некоторых уравнениях вам может потребоваться выполнить некоторую работу, чтобы получить уравнение в этой форме. Вы обнаружите, что это включает в себя изоляцию [латекс]x^{2}[/латекс].

    В нашем первом видео мы покажем больше примеров использования свойства квадратного корня для решения квадратного уравнения.

    Иногда возводится в квадрат больше, чем просто x :

    Решение квадратного уравнения путем завершения квадрата

    Не все квадратные уравнения можно разложить на множители или решить в исходной форме, используя свойство квадратного корня. В этих случаях мы можем использовать метод решения квадратного уравнения , известный как , завершающий квадрат 9{2}–24x+16[/латекс].

    Показать ответ

    Если бы это было уравнение, мы могли бы решить его, используя либо свойство квадратного корня, либо свойство нулевого произведения. Если вы не начинаете с идеального квадратного трехчлена, вы можете завершить квадрат, чтобы превратить то, что у вас есть, в один.

    Для завершения квадрата старший коэффициент a должен быть равен 1. Если это не так, то разделить все уравнение на a . Затем мы можем использовать следующие процедуры для решения квадратного уравнения путем завершения квадрата. 9{2}-3x — 5=0[/латекс].

    Показать ответ

    В следующем видео вы увидите больше примеров того, как использовать заполнение квадрата для решения квадратного уравнения.

    Возможно, вы заметили, что, поскольку вы должны использовать оба квадратных корня, все примеры имеют два решения. Вот еще один пример, который немного отличается.

    Присмотритесь к этой проблеме, и вы можете увидеть что-то знакомое. Вместо того, чтобы достраивать квадрат, попробуйте прибавить 47 к обеим сторонам уравнения. {2}+bx+c=0[/латекс] и затем решите 9{2}+bx+c=0[/latex] называется стандартной формой квадратного уравнения. Прежде чем решать квадратное уравнение с помощью квадратной формулы, важно убедиться, что уравнение имеет именно такую ​​форму. Если вы этого не сделаете, вы можете использовать неправильные значения для a , b или c , и тогда формула даст неверные решения.

    Решение квадратного уравнения с помощью квадратной формулы

    Квадратная формула будет работать с любым квадратным уравнением , кроме 9{2}+bx+c=0[/латекс]. Чтобы использовать его, выполните следующие действия.

    • Сначала приведите уравнение в стандартной форме.
    • Определите коэффициенты a , b , и c . Будьте осторожны с включением отрицательных знаков, если вычитаются члены bx или c .
    • Аккуратно подставьте значения, отмеченные на шаге 2, в уравнение. Чтобы избежать ненужных ошибок, используйте круглые скобки вокруг каждого числа, введенного в формулу.
    • Максимально упростить.
    • Используйте [latex]\pm[/latex] перед радикалом, чтобы разделить решение на два значения: одно, в котором добавляется квадратный корень, и другое, в котором он вычитается .
    • Упростите оба значения, чтобы получить возможные решения.

    Много шагов. Давайте попробуем использовать квадратную формулу, чтобы сначала решить относительно простое уравнение; затем вы вернетесь и решите ее снова, используя другой метод факторинга.

    Вы можете проверить эти решения, подставив [латекс]1[/латекс] и [латекс]−5[/латекс] в исходное уравнение. 9{2}+4\влево(-5\вправо)=5\,\,\,\,\,\\25-20=5\,\,\,\,\,\\5=5\,\ ,\,\,\,\end{массив}[/латекс]

    Вы получаете два верных утверждения, поэтому вы знаете, что оба решения работают: [латекс]x=1[/латекс] или [латекс]-5[/латекс]. Вы успешно решили уравнение, используя квадратную формулу!

    Посмотрите это видео, чтобы увидеть пример использования квадратной формулы для решения квадратного уравнения, имеющего два действительных рациональных решения.

    Иногда бывает проще решить уравнение, используя обычные методы разложения на множители, например, найти пары чисел, которые в сумме дают одно число (в данном примере 4) и производят определенный продукт (в данном примере [латекс]−5 [/latex]) при умножении. Сила квадратичной формулы в том, что с ее помощью можно решить любые квадратные уравнения , даже те, где нахождение числовых комбинаций не получится.

    В следующем видео-примере мы показываем, что квадратная формула полезна, когда квадратное уравнение имеет два иррациональных решения, которые нельзя было получить с помощью факторизации.

    Большинство квадратных уравнений, которые вы рассматривали, имеют два решения, как и приведенное выше. Следующий пример немного отличается.

    Снова проверьте исходное уравнение. 9{2}-2\влево(4\вправо)=6\влево(4\вправо)-16\\16-8=24-16\,\,\,\,\,\,\\8=8\ ,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\end{массив}[/ латекс]

    Квадратные уравнения с комплексными решениями

    Далее мы покажем, что некоторые квадратные уравнения могут иметь комплексные решения. Поскольку мы упрощаем квадратную формулу, мы можем получить отрицательное число под квадратным корнем, которое, как мы знаем, не определено для действительных чисел.

    Мы видели два результата для решений квадратных уравнений: либо было одно, либо два решения с действительными числами. Мы также узнали, что можно извлечь квадратный корень из отрицательного числа, используя мнимые числа. Это новое знание позволяет нам исследовать еще один возможный результат, когда мы решаем квадратные уравнения. Рассмотрим это уравнение: 92+3x+6=0[/latex]

    Используя квадратичную формулу для решения этого уравнения, мы сначала идентифицируем a, b и c.

    [латекс]a = 2,b = 3,c = 6[/латекс]

    Мы можем подставить a, b и c в квадратичную формулу и упростить, чтобы получить следующий результат:

    [латекс]x=- \frac{3}{4}+\frac{\sqrt{-39}}{4}, x=-\frac{3}{4}-\frac{\sqrt{-39}}{4}[/ латекс]

    До этого момента мы бы сказали , что [латекс]\sqrt{-39}[/латекс] не определено для действительных чисел, и определили, что это уравнение не имеет решений. Но теперь, когда мы определили квадратный корень из отрицательного числа, мы также можем определить решение этого уравнения следующим образом.

    [латекс] x = — \ frac {3} {4} + i \ frac {\ sqrt {39}} {4}, x = — \ frac {3} {4} -i \ frac {\ sqrt { 39}}{4}[/latex]

    В следующем примере мы рассмотрим процесс решения квадратного уравнения с комплексными решениями. Обратите внимание, что мы упрощаем комплексные числа, поэтому, если вам нужен обзор того, как преобразовать квадратный корень из отрицательного числа в мнимое, сейчас самое подходящее время.

     

    Мы можем проверить эти решения в исходном уравнении. {2}[/латекс] на [латекс]-1[/латекс]. 92+x=-x-3[/latex]

    Показать ответ

    Попробуйте

     

    2.5: Квадратные уравнения — Математика LibreTexts

    1. Последнее обновление
    2. Сохранить как PDF
  7. Идентификатор страницы
    1487
    • ОпенСтакс
    • ОпенСтакс
    Цели обучения
    • Решение квадратных уравнений путем факторизации.
    • Решение квадратных уравнений по квадратному корню.
    • Решите квадратные уравнения, заполнив квадрат.
    • Решите квадратные уравнения, используя квадратную формулу.

    Монитор компьютера слева на рисунке \(\PageIndex{1}\) представляет собой модель с экраном \(23,6\) дюйма, а монитор справа – модель с экраном \(27\) дюйма. Пропорционально мониторы очень похожи. Если пространство ограничено и нам нужен максимально большой монитор, как нам решить, какой из них выбрать? В этом разделе мы узнаем, как решать такие проблемы, используя четыре различных метода. 92−4= 0\) являются квадратными уравнениями. Они бесчисленным образом используются в инженерии, архитектуре, финансах, биологических науках и, конечно же, в математике.

    Часто самым простым методом решения квадратного уравнения является факторизация . Факторинг означает нахождение выражений, которые можно перемножить, чтобы получить выражение на одной стороне уравнения.

    Если квадратное уравнение можно разложить на множители, оно записывается как произведение линейных членов. Решение факторингом зависит от свойства нулевого произведения, которое гласит, что если \(a⋅b=0\), то \(a = 0\) или \(b =0\), где a и b — действительные числа или алгебраические выражения. Другими словами, если произведение двух чисел или двух выражений равно нулю, то одно из чисел или одно из выражений должно быть равно нулю, потому что ноль, умноженный на что-либо, равен нулю. 92 +x−6= 0\) имеет стандартный вид.

    Мы можем использовать свойство нулевого произведения для решения квадратных уравнений, в которых мы сначала должны вынести наибольший общий множитель (НОД), а также для уравнений, которые имеют специальные формулы факторизации, такие как разность квадратов, оба которые мы увидим позже в этом разделе.

    СВОЙСТВО НУЛЕВОГО ПРОИЗВЕДЕНИЯ И КВАДРАТИЧНЫЕ УРАВНЕНИЯ

    свойство нулевого произведения утверждает

    2\), есть \(1\). У нас есть один метод факторизации квадратных уравнений в этой форме.

    Как: Фактор квадратного уравнения со старшим коэффициентом 1
    1. Найдите два числа, произведение которых равно \(c\) и сумма которых равна \(b\).
    2. Используйте эти числа, чтобы записать два множителя в форме \((x+k)\) или \((x−k)\), где k — одно из чисел, найденных на шаге 1. Используйте числа точно так, как они есть . Другими словами, если два числа равны \(1\) и \(−2\), множители равны \((x+1)(x−2)\). 92 +x−6=0\), мы ищем два числа, произведение которых равно \(−6\) и сумма которых равна \(1\). Начните с рассмотрения возможных множителей \(−6\).

      \[1⋅(−6) \нечисло \]

      \[(−6)⋅1 \нечисло \]

      \[2⋅(−3) \нечисло \]

      \[3⋅(− 2) \nonumber \]

      Последняя пара \(3⋅(−2)\) в сумме дает \(1\), так что это числа. Обратите внимание, что будет работать только одна пара чисел. Затем напишите факторы.

      \[(x−2)(x+3)=0 \nonumber \]

      Чтобы решить это уравнение, мы используем свойство нулевого произведения. Приравняйте каждый множитель к нулю и решите. 92+8х+15=0\).

      Решение

      Найдите два числа, произведение которых равно \(15\), а сумма равна \(8\). Перечислите факторы \(15\).

      \[1⋅15 \нечисло \]

      \[3⋅5 \нечисло \]

      \[(−1)⋅(−15) \нечисло \]

      \[(−3)⋅(− 5) \nonumber \]

      Числа, которые добавляются к \(8\), это \(3\) и \(5\). Затем запишите множители, приравняйте каждый множитель к нулю и решите.

      \[\begin{align*} (x+3)(x+5)&= 0\\ (x+3)&= 0\\ x&= -3\\ (x+5)&= 0\ \ x&= -5 \end{align*}\] 92−25=0\).

      Ответить

      \((х+5)(х-5)=0, х=-5, х=5\)

      Факторизация и решение квадратного уравнения более высокого порядка

      Когда старший коэффициент не равен \(1\), мы факторизуем квадратное уравнение, используя метод, называемый группировкой , который требует четырех членов.

      Группировка: этапы факторизации квадратных уравнений

      Имея уравнение в стандартной форме, давайте рассмотрим процедуры группировки

      2+bx+c=0\), умножьте \(a⋅c\).
    3. Найдите два числа, произведение которых равно ac, а сумма равна \(b\).
    4. Перепишите уравнение, заменив член \(bx\) двумя членами, используя числа, найденные на шаге \(1\), в качестве коэффициентов при \(x\).
    5. Умножьте первые два члена, а затем факторизируйте два последних члена. Выражения в круглых скобках должны быть точно такими же, чтобы можно было использовать группировку.
    6. Вынесите выражение в скобках на множители.
    7. Установите выражения равными нулю и найдите переменную. 92+15х+9=0\).

      Решение

      Сначала умножьте \(ac:4(9)=36\). Затем перечислите факторы \(36\).

      \[1⋅36 \нечисло\]

      \[2⋅18 \нечисло\]

      \[3⋅12 \нечисло\]

      \[4⋅9 \нечисло\]

      \[6⋅ 6 \nonumber\]

      Единственная пара множителей, которая в сумме дает \(15\), это \(3+12\). Перепишите уравнение, заменив член b, \(15x\), двумя членами, используя \(3\) и \(12\) в качестве коэффициентов \(x\). Умножьте первые два члена, а затем факторизируйте два последних. 92+3x+2x+2)&= 0 \qquad \text{Использовать группировку выражения в скобках}\\
      -x[3x(x+1)+2(x+1)]&= 0\\
      -x(3x+2)(x+1)&= 0\\
      \text{Теперь воспользуемся свойством нулевого произведения. Обратите внимание, что у нас есть три множителя.}\\
      -x&= 0\\
      x&= 0\\
      3x+2&= 0\\
      x&= -\dfrac{2}{3}\\
      x+1&= 0\\
      x&= -1
      \end{align*}\]

      Решения: \(0\), \(-\dfrac{2}{3}\) и \(-1\). 2+10x=0\). 92=15\).

      Ответить

      \(х=4±\sqrt{5}\)

      Завершение квадрата

      Не все квадратные уравнения можно разложить на множители или решить в исходной форме, используя свойство квадратного корня. В этих случаях мы можем использовать метод решения квадратного уравнения , известного как , дополняющего квадрат . Используя этот метод, мы добавляем или вычитаем члены к обеим сторонам уравнения, пока у нас не получится идеальный квадратный трехчлен с одной стороны от знака равенства. Затем мы применяем свойство квадратного корня. Чтобы завершить квадрат, старший коэффициент \(a\) должен быть равен \(1\). Если это не так, то разделите все уравнение на \(а\). Затем мы можем использовать следующие процедуры для решения квадратного уравнения путем завершения квадрата. 92−6x=13\).

      Ответить

      \(x=3±\sqrt{22}\)

      Использование квадратной формулы

      Четвертый метод решения квадратного уравнения заключается в использовании квадратной формулы , которая решает все квадратные уравнения. Хотя квадратная формула работает с любым квадратным уравнением в стандартной форме, легко сделать ошибку при подстановке значений в формулу. Будьте внимательны при подстановке и используйте круглые скобки при вставке отрицательного числа. 92\), где \(а\) и \(b\) относятся к катетам прямоугольного треугольника, прилежащим к углу \(90°\), а \(с\) относятся к гипотенузе. Он имеет неизмеримое применение в архитектуре, технике, естественных науках, геометрии, тригонометрии и алгебре, а также в повседневных приложениях.

      Мы используем теорему Пифагора, чтобы найти длину одной стороны треугольника, зная длины двух других. Поскольку каждое из слагаемых в теореме возводится в квадрат, когда мы находим сторону треугольника, у нас получается квадратное уравнение. Мы можем использовать методы решения квадратных уравнений, которые мы изучили в этом разделе, чтобы найти недостающую сторону. 92\]

      где \(a\) и \(b\) относятся к катетам прямоугольного треугольника, смежного с углом \(90°\), а \(c\) относятся к гипотенузе, как показано на .

      Рисунок \(\PageIndex{4}\)
      Пример \(\PageIndex{12}\): нахождение длины недостающей стороны прямоугольного треугольника

      Найдите длину недостающей стороны прямоугольного треугольника на рисунке \ (\PageIndex{5}\).

      Рисунок \(\PageIndex{5}\)

      Решение

      Поскольку у нас есть измерения стороны \(b\) и гипотенузы, недостающая сторона равна \(a\). 92&= 128\\ a&= \sqrt{128}\\ &= 8\sqrt{2} \end{align*}\]

      Упражнение \(\PageIndex{9}\)

      Используйте теорему Пифагора для решения Задача прямоугольного треугольника: Длина стороны a равна 4 единицам, длина стороны b равна 3 единицам. Найдите длину гипотенузы.

      Ответить

      \(5\) шт.

      Медиа

      Доступ к этим онлайн-ресурсам для получения дополнительных инструкций и практики с квадратными уравнениями.

      1. Решение квадратных уравнений методом факторинга 92-4ас}}{2а}\)

        Ключевые понятия

        • Многие квадратные уравнения могут быть решены с помощью разложения на множители, если уравнение имеет старший коэффициент \(1\) или если уравнение представляет собой разность квадратов. Затем свойство нулевого фактора используется для поиска решений. См. пример, пример и пример.
        • Многие квадратные уравнения со старшим коэффициентом, отличным от \(1\), могут быть решены путем факторизации с использованием метода группировки. См. пример и пример.
        • Другим методом решения квадратичных уравнений является свойство квадратного корня. Переменная возводится в квадрат. Мы выделяем квадрат члена и берем квадратный корень из обеих частей уравнения. Решение даст положительное и отрицательное решение. См. пример и пример.
        • Завершение квадрата — это метод решения квадратных уравнений, когда уравнение нельзя разложить на множители. См. Пример.
        • Очень надежным методом решения квадратных уравнений является квадратичная формула, основанная на коэффициентах и ​​постоянном члене уравнения. См. Пример.
        • Дискриминант используется для указания характера корней, которые даст квадратное уравнение: действительные или комплексные, рациональные или иррациональные, а также их количество. См. Пример.
        • Теорема Пифагора, одна из самых известных теорем в истории, используется для решения задач о прямоугольных треугольниках и имеет приложения во многих областях. Чтобы найти длину одной стороны прямоугольного треугольника, нужно решить квадратное уравнение. См. Пример.

        Эта страница под названием 2.5: Quadratic Equations распространяется под лицензией CC BY 4.0 и была создана, изменена и/или курирована OpenStax с использованием исходного контента, который был отредактирован в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.

        1. Наверх
          • Была ли эта статья полезной?
          1. Тип изделия
            Раздел или страница
            Автор
            ОпенСтакс
            Лицензия
            СС BY
            Версия лицензии
            4,0
            Программа OER или Publisher
            ОпенСтакс
            Показать страницу TOC
            №
          2. Теги
            1. заполнение квадрата
            2. дискриминант
            3. метод группировки
            4. Теорема Пифагора
            5. квадратные уравнения
            6. квадратичная формула
            7. источник@https://openstax.

              No related posts.

    Добавить комментарий

    Ваш адрес email не будет опубликован. Обязательные поля помечены *