Полный ранг | это… Что такое Полный ранг?
ТолкованиеПеревод
- Полный ранг
Пусть задана любая матрица А с m строк и n столбцов. Рангом системы строк (столбцов) матрицы А называется максимальное число линейно независимых строк(столбцов). Несколько строк (столбцов) называются линейно-независимыми, если не одна из них не выражается линейно через другие. Ранг системы строк всегда равен рангу системы столбцов и это число называется рангом матрицы. Ранг матрицы — наивысший из порядков миноров этой матрицы, отличных от нуля. Ранг матрицы равен наибольшему числу линейно независимых строк (или столбцов) матрицы.
Обычно ранг матрицы A обозначается () или . Оба обозначения пришли к нам из иностранных языков, потому и употребляться могут оба. Последний вариант свойственен для английского языка, в то время как первый — для немецкого, французского и ряда других языков.
Содержание
- 1 Определение
- 2 Связанные определения
- 3 Пример
- 4 Свойства
- 5 См. также
- 6 Ссылки
Определение
Пусть — прямоугольная матрица.
Тогда по определению рангом матрицы A является:
- нуль, если A — нулевая матрица;
- число , где Mr — минор матрицы A порядка r, а Mr + 1 — окаймляющий к нему минор порядка (r + 1), если они существуют.
Теорема (о корректности определения рангов). Пусть все миноры матрицы порядка k равны нулю (Mk = 0). Тогда , если они существуют.
Связанные определения
- Ранг матрицы M размера называют полным, если .
- Базисный минор матрицы A — любой минор матрицы A порядка r, где .
- Строки и столбцы, на пересечении которых стоит базисный минор, называются базисными строками и столбцами. (Они определены неоднозначно в силу неоднозначности базисного минора.)
Пример
Матрица
имеет ранг 2, так как есть минор второго порядка, отличный от нуля, а миноров третьего порядка нет.
Свойства
- Теорема (о базисном миноре): Пусть — базисный минор матрицы A, тогда:
- базисные строки и базисные столбцы линейно независимы;
- любая строка (столбец) матрицы A есть линейная комбинация базисных строк (столбцов).
- Следствия:
- Если ранг матрицы равен r, то любые p:p > r строк или столбцов этой матрицы будут линейно зависимы.
- Если A — квадратная матрица, и строки и столбцы этой матрицы линейно зависимы.
- Пусть , тогда максимальное количество линейно независимых строк (столбцов) этой матрицы равно r.
- Теорема (об инвариантности ранга при элементарных преобразованиях): Введём обозначение для матриц, полученных друг из друга элементарными преобразованиями. Тогда справедливо утверждение: Если , то их ранги равны
- Теорема Кронекера — Капелли: Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг её основной матрицы равен рангу её расширенной матрицы. В частности:
- Количество главных переменных системы равно рангу системы.
- Совместная система будет определена (её решение единственно), если ранг системы равен числу всех её переменных.
См. также
Ссылки
- Расчет ранга матрицы онлайн
- Здесь можно вычислить ранг матрицы (с подробным отображением хода вычисления)
Wikimedia Foundation. 2010.
Игры ⚽ Поможем написать реферат
- Полный прообраз
- Полный список объектов на Северском Донце
Полезное
Решения линейных матричных уравнений с ограничениями по рангу с использованием PowerFactorization
- Список журналов
- Рукописи авторов HHS
- PMC32
IEEE Signal Process Lett.
Авторская рукопись; доступно в PMC 2012 29 февраля.
Опубликовано в окончательной редакции как:
IEEE Signal Process Lett. 2009 г.; 16(7): 584–587.
DOI: 10.1109/LSP.2009.2018223
PMCID: PMC32
NIHMSID: NIHMS348948
PMID: 22389578
. ограничения имеют важное применение во многих контекстах обработки сигналов. Недавно теоретические гарантии восстановления матриц минимального ранга были доказаны для минимизация ядерной нормы (NNM), которую можно решить с помощью стандартных подходов выпуклой оптимизации. Хотя минимизация ядерной нормы эффективна, она может требовать больших вычислительных ресурсов. В этой работе мы исследуем использование алгоритма PowerFactorization (PF) в качестве инструмента для восстановления матрицы с ограничениями по рангу. Эмпирические результаты показывают, что PF с увеличенным рангом значительно успешнее, чем NNM, при восстановлении матриц низкого ранга, в дополнение к тому, что он быстрее.
Индексы: Сжатое зондирование, быстрые алгоритмы, матрицы низкого ранга, восстановление матрицы
В последнее время наблюдается значительный интерес к решению задачи минимизации аффинного ранга [1]–[3], определяемой как
минимизация ранга(X) при условии A(X)=b
(1)
где x ∈ ℂ M × N — неизвестная матрица, которая должна быть восстановлена, а линейный оператор 𝒜: ℂ M × N → ℂ P и Vector B ∈ P и Vector B ∈ P и Vect0045 p . Несмотря на то, что задача оптимизации этого типа в общем случае является NP-трудной [1], в литературе [4]–[6] был предложен ряд эвристических алгоритмов. Особо следует отметить эвристику ядерной нормы [4], которая заменяет (1) на
минимизировать∥X∥∗ при условии A(X)=b
(2)
где ∥X∥ ∗ — ядерная норма числа X и определяется как сумма его сингулярных значений.
Ядерная норма выпукла, и ее использование в качестве заменителя матричного ранга аналогично тому, как l 1 норма используется в качестве заменителя векторной разреженности в формирующейся области сжатого зондирования [7], [8]. Подобно результатам сжатого зондирования, теоретические условия эквивалентности (1) и (2) были получены [1]–[3] и основаны на том, что 𝒜 обладает особыми свойствами ограниченной изометрии или некогерентности .
Минимизация ядерной нормы (NNM) может быть представлена как задача полуопределенного программирования (SDP) и может быть решена с использованием готовых решателей внутренних точек, таких как SDPT3 [9] или SeDuMi [10]. Однако для задач больших размеров эти методы ограничены большими требованиями к вычислениям и памяти. В результате появились различные быстрые алгоритмы для NNM [1], [11], [12].
В этой работе мы предлагаем использовать алгоритм PowerFactorization (PF) [13] для решения рангового аналога (1).
PF пытается найти матрицу, которую можно разложить на множители как X = UV , где U ∈ ℂ m × r и V ∈ ℂ r × n , так что rank( X ) ≤ r . Этот тип низкоранговой параметризации использовался в предыдущих алгоритмах NNM [1], [11] для повышения вычислительной эффективности за счет введения невыпуклости. В отличие от методов NNM, PF оптимизирует U и V попеременно, чтобы найти локальное решение для
(3)
Мы находим, что решения PF с постепенно увеличивающимся r , часто превосходят решения (2) при восстановлении матриц низкого ранга из небольшого числа p измерений. Это говорит о том, что во многих случаях одного ограничения ранга достаточно для надежного восстановления матрицы, и что использование NNM может быть субоптимальным. Это улучшение производительности неудивительно в том смысле, что известные теоретические условия для уникального согласованного с данными решения с ограниченным рангом для (1) (см.
[1, Theor. 3.2]) значительно менее строги, чем известные условия для основанного на NNM решения. восстановление без ранговых ограничений (см. [1, Теор. 3.3]). Что удивительно, так это то, что невыпуклость, вносимая низкоранговой параметризацией, часто не мешает простой процедуре ПФ.
Начнем описание PF с введения дополнительных полезных обозначений. В частности, мы выражаем действие линейного оператора 𝒜 как
[A(X)]k=∑i=1m∑j=1naijk[X](i,j)=∑i=1m∑j=1naijk∑l=1r[U](i,l)[V] (л, к)
(4)
для соответствующих констант a ijk , а для k = 1,2,…, p . Как следствие, мы можем написать
𝒜(UV) ≡ A U vec(V) ≡ A V vec(U)
(5)
где vec(·) объединяет столбцы своего матричного аргумента в один вектор-столбец. Матрицы A U ∈ ℂ P × R N и A V ∈ ℂ P × M R AS DEFINE AS DEL AS M R .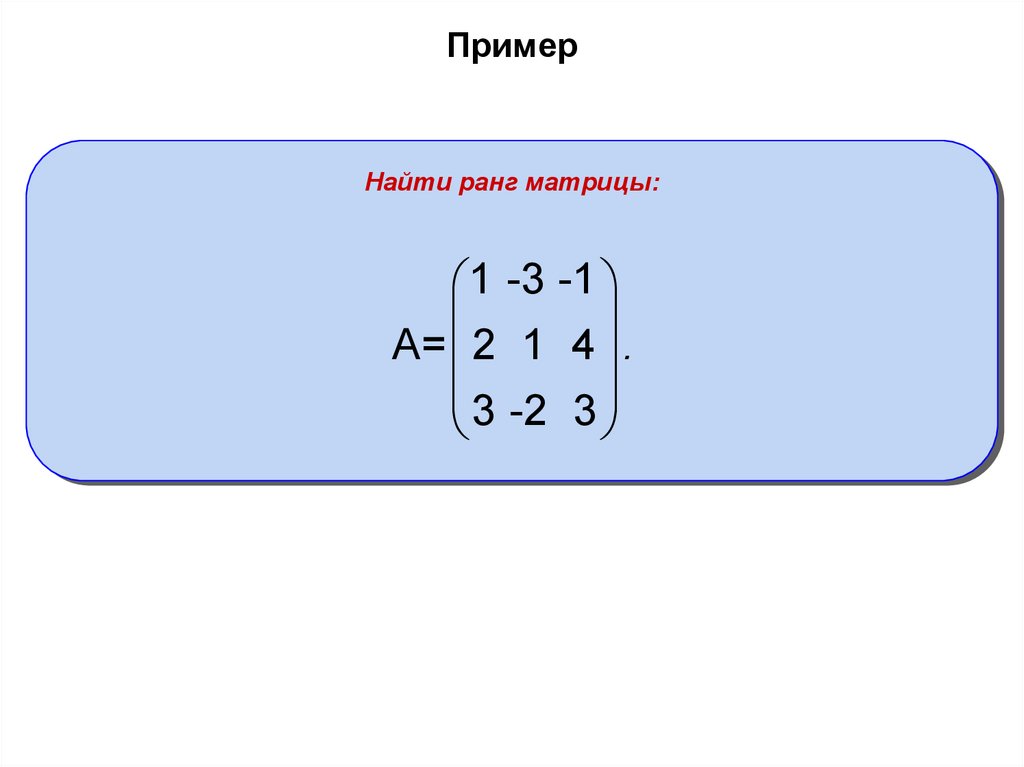
[AU](k,l+r(j−1))=∑i=1maijk[U](i,l)
(6)
а также
[AV](k,i+m(l−1))=∑j=1naijk[V](l,j)
(7)
соответственно, для k ∈ {1,…, p }, l ∈ {1,…, r }, j ∈ {1,…, n }, и i ∈ {1,…, m }.
Алгоритм PF повторяется путем попеременной оптимизации U и V с использованием процедуры линейного метода наименьших квадратов (LLS). Алгоритм работает следующим образом.
Инициализация (произвольно) (U ∈ ℂ M × R , V ∈ ℂ R × N ) = (U (0) , V ) = (U (0) N ) = (U (0) N ) = (U (0) N ) = (U (0) N ) =0045 (0) ). Установить номер итерации q = 0.
Hold V ( q ) фиксировано, найти U ( q 1) решение
40 + 5
U(q+1)=argminU∥AV(q)vec(U)−b∥22.
(8)
Теперь закрепляем U ( q +1) , находим V ( q +1) 9
V(q+1)=argminV∥AU(q+1)vec(V)−b∥22.
(9)
Приращение q . Если q превышает максимальное число итераций, если итерации стагнируют, или если относительная ошибка ∥ 2 меньше желаемого порога ε , затем завершаем итерационную процедуру. В противном случае повторите шаги 2)–4).
Для восстановления матрицы мы получили наилучшие результаты, начав PF с r = 1 и постепенно увеличивая до тех пор, пока не будет достигнуто желаемое ограничение ранга (или до точки, где относительная ошибка меньше ε в случае, когда истинный ранг неизвестен). В этой версии PF с увеличенным рангом (IRPF) мы инициализируем новые компоненты U и V , используя соответствие PF ранга 1 текущему остатку.
Основным вычислением в процедуре PF является решение задач LLS в (8) и (9). Однако задачи LLS являются классическими, и существует ряд эффективных алгоритмов для вычисления решений [14]. Отметим, что в ряде случаев матрицы A U и A V не будет иметь полный ранг столбца, что означает, что решение LLS неуникально; например, если V инициализировано тождественно нулю, то A V также тождественно равно нулю. В этих ситуациях полезно выбрать решение LLS, отличное от решения методом наименьших квадратов с минимальной нормой; в нашей реализации мы случайным образом выбираем вектор из линейного множества решений LLS.
По построению PF монотонно уменьшает функцию стоимости в (3), и, таким образом, значение функции стоимости гарантированно сходится, поскольку оно ограничено снизу 0. В общем, сходимость самих итераций не гарантируется, особенно в случай, когда существует устойчивый дефицит ранга в задачах LLS.
Наши эмпирические результаты показывают, что обычно это не проблема, когда количество измерений p достаточно велико.
Алгоритм IRPF был реализован в MATLAB и по нескольким параметрам сравнивался с реализацией NNM в SDP. Все SDP решались с помощью SDPT3 [9]. Наши эксперименты аналогичны экспериментам [1]-[3] и [12].
A. Сравнение скорости
Чтобы проверить скорость IRPF по сравнению с NNM, мы создали тестовый набор случайных 𝒜 операторов и матриц X для серии задач разного размера. a ijk , определяющие операторы 𝒜, были выбраны из i.i.d. Гауссово распределение. Матрицы X были созданы путем выборки двух матриц M L ∈ C m ×3 и M R ∈ C 3× n i. Гауссовы записи и настройка X = M L M R .
Во всех экспериментах использовалось м = n . Алгоритм IRPF был остановлен при r = 3 (т. е. истинном ранге) и повторялся до тех пор, пока его относительная ошибка не достигла ε = 10 −10 . Матрицы были успешно восстановлены во всех случаях для обоих алгоритмов, где восстановление объявлялось, если оценочная матрица X̂ удовлетворяла || X̂ – X || F /|| Х || F < 10 −3 , где || · || F – норма Фробениуса.
показывает результат этого сравнения скоростей и указывает время выполнения в секундах (на ЦП 3,16 ГГц) для каждого из двух алгоритмов, усредненное по 5 реализациям. Существует четкая разница в скорости IRPF и NNM с SDP.
TABLE I
EXECUTION TIMES FOR IRPF AND NNM
| Unknown X | Time (s) | |||
|---|---|---|---|---|
| size ( n × n ) | p (2n−r)r | p/n 2 | IRPF | NNM |
| 5 | 0. 95 | 1.6 | 123.5 | |
| 30×30 | 4 | 0.76 | 1.4 | 141.1 |
| 3 | 0.57 | 1.5 | 89.9 | |
| 5 | 0. 72 | 3.8 | 768.5 | |
| 40×40 | 4 | 0.58 | 3.5 | 555.1 |
| 3 | 0.43 | 3.6 | 413.2 | |
| 5 | 058 | 7. 1 | 2331.1 | |
| 50×50 | 4 | 0.47 | 6.8 | 1616.7 |
| 3 | 0.35 | 7.2 | 1223.6 | |
Открыть в отдельном окне
B.
Сравнение восстановления В первой серии экспериментов по восстановлению линейные операторы 𝒜 и матрицы 30 × 30 X были сгенерированы случайным образом из распределения Гаусса, как и в предыдущем эксперименте по сравнению скорости. Тестовые примеры были сгенерированы для множества различных комбинаций количества измерений p и ранга ( X ) (предположительно известного), и для каждой пары ( p , r ) было вычислено 10 реализаций. Второй набор экспериментов по восстановлению был идентичен первому набору, за исключением того, что линейные операторы 𝒜 были выбраны для непосредственного наблюдения p записей (равномерно выбранных случайным образом) из X . Это соответствует так называемой задаче завершения матриц [2], [11]-[13]. Теоретические свойства NNM для гауссовых наблюдений и матричного пополнения обсуждаются в [1] и [2] соответственно. показывает результаты эксперимента с гауссовскими наблюдениями. В то время как NNM может успешно восстановить большую часть матриц низкого ранга, IRPF может восстановить значительную дополнительную часть, которую NNM не может восстановить. Как и в NNM [1]-[3], для IRPF с гауссовскими измерениями наблюдается фазовый переход, хотя граница этого фазового перехода появляется в другом месте.
Открыть в отдельном окне
Результаты восстановления матрицы для (а) IRPF и (б) NNM с гауссовскими наблюдениями. Цвет каждой ячейки соответствует эмпирической скорости восстановления, при этом белый цвет означает идеальное восстановление, а черный — неудачу во всех 10 экспериментах. Вертикальная ось равна r (2 n – r )/ p , что является отношением числа степеней свободы для матрицы n × n rank- r к матрице количество измерений стр .
показывает результаты эксперимента по заполнению матрицы. Опять же, значительная часть матриц успешно восстанавливается с помощью IRPF, но не восстанавливается с помощью NNM. Однако в этом эксперименте мы наблюдаем небольшое количество случаев, когда NNM удается, а IRPF терпит неудачу, потому что она попадает в ловушку в стационарной точке функции стоимости. Эти несколько случаев легко идентифицировать, не зная истинного X , из-за большой остаточной ошибки данных. Для проблем среднего размера это можно эффективно преодолеть, выполнив IRPF несколько раз со случайно выбранными инициализациями.
Открыть в отдельном окне
Результаты заполнения матрицы для (a) IRPF и (b) NNM. Цвет каждой ячейки соответствует эмпирической скорости извлечения, как в .
Эти результаты были получены для относительно небольших матриц. Предварительные эксперименты показывают, что преимущество IRPF над NNM сохраняется для больших матриц, хотя асимптотическое поведение неизвестно.
C. Восстановление с использованием PF по сравнению с IRPF
Хотя IRPF более успешен при восстановлении матрицы и может сходиться быстрее, чем классический PF, сам по себе PF также может работать на удивление хорошо при достаточном количестве измерений и правильно выбранном r. Чтобы проиллюстрировать это, мы снова сгенерировали гауссовские операторы наблюдения 𝒜 для различных p значений и случайные матрицы 40 × 40 X ранга 8. Мы протестировали PF с этим набором данных, позволив r варьироваться от 1 до 20. Результаты этого эксперимента, усредненные по десяти реализациям, показаны в .
Открыть в отдельном окне
Средняя относительная ошибка реконструкции с использованием PF для различных значений r . Истинный ранг равен 8. Синим цветом отмечены непроверенные случаи (количество степеней свободы превысило p ). Режимы успеха/неудачи для NNM и IRPF обозначены желтыми и розовыми линиями соответственно.
В этой работе изучался алгоритм IRPF как альтернатива NNM в контексте восстановления матриц низкого ранга. IRPF значительно быстрее, чем алгоритмы NNM на основе SDP, и эмпирически имеет лучшие свойства восстановления, чем NNM. Хотя его теоретические свойства еще не полностью установлены, IRPF обладает многообещающим потенциалом для решения практических задач восстановления матрицы.
Авторы выражают благодарность Ю. Ма и Дж. Райту за полезные обсуждения.
Эта работа была поддержана грантами NIH-R01-CA098717, NIH-P41-EB03631 и NSF-CBET-07-30623, а также благодаря стипендиям Института Бекмана и Университета Иллинойса.
Цветные версии одного или нескольких рисунков в этом документе доступны в Интернете по адресу http://ieeexplore.ieee.org.
Заместителем редактора, координировавшим рецензирование этой рукописи и утверждавшим ее для публикации, был профессор Кеннет Э. Барнер.
[1] Рехт Б., Фазель М., Паррило П.А. Решения линейных матричных уравнений с гарантированным минимальным рангом с помощью препринта «Минимизация ядерной нормы». 2008 [Онлайн]. Доступно: http://arxiv.org/abs/0706.4138 [Google Scholar]
[2] Кандес Э., Рехт Б. Точное завершение матрицы с помощью препринта выпуклой оптимизации. 2008 [Онлайн]. Доступно: http://arxiv.org/abs/0805.4471 [Google Scholar]
[3] Рехт Б., Сюй В., Хассиби Б. Необходимые и достаточные условия успеха эвристики ядерной нормы для препринта минимизации ранга. 2008 [Онлайн]. Доступно: http://arxiv.org/abs/0809.1260 [Google Scholar]
[4] Fazel M, Hindi H, Boyd S. Proc. амер. Конф. управления Арлингтон, Вирджиния: 2001. «Эвристика минимизации ранга с применением к аппроксимации системы минимального порядка», стр. 4734–4739.. [Google Scholar]
[5] Fazel M, Hindi H, Boyd S. Proc. амер. Конф. управления Денвер, Колорадо: 2003. «Эвристика Log-det для минимизации ранга матрицы с приложениями к ганкелевым и евклидовым матрицам расстояний», стр. 2156–2162. [Google Scholar]
[6] Григориадис К., Беран Э. «Алгоритмы альтернативной проекции для задач линейного матричного неравенства с ограничениями ранга», В: Ghaoui LE, Niculescu S-I, редакторы. Достижения в методах линейного матричного неравенства в управлении. СИАМ; Филадельфия, Пенсильвания: 2000. стр. 251–267. [Академия Google]
[7] Кандес Э., Ромберг Дж., Тао Т. «Надежные принципы неопределенности: точное восстановление сигнала на основе крайне неполной информации о частоте», IEEE Trans. Поставить в известность. Теория. 2006 г., февраль; 52 (2): 489–509. [Google Scholar]
[8] Донохо Д. «Сжатое зондирование», IEEE Trans Inform. Теория. 2006 г., апрель; 52 (4): 1289–1306. [Google Scholar]
[9] Toh KC, Todd MJ, Tütüncü RH. SDPT3 — программный пакет MATLAB для полуопределенно-квадратично-линейного программирования. [Онлайн]. Доступно: http://www.math.nus.edu.sg/mattohkc/sdpt3.html [Google Scholar]
[10] Штурм Дж.Ф. «Использование SeDuMi 1.02, набора инструментов MATLAB для оптимизации по симметричным конусам», Optim. Мет. ПО 1999;11–12:625–653. [Google Scholar]
[11] Rennie JDM, Srebro N. Proc. ICML. 2005. «Быстрая факторизация матрицы максимальной маржи для совместного прогнозирования», [Google Scholar]
[12] Cai J-F, Candes E, Shen Z. A Singular Value Thresholding Algorithm for Matrix Completion preprint. 2008 [Онлайн]. Доступно: http://arxiv.org/abs/0810.3286 [Google Scholar]
[13] Видал Р., Трон Р., Хартли Р. «Многокадровая сегментация движения с отсутствующими данными с использованием PowerFactorization и GPCA», Int. Дж. Вычисл. Вис. 2008; 79: 85–105. [Google Scholar]
[14] Голуб Г., Ван Лоан К. Матричные вычисления. 3-е изд. Университет Джона Хопкинса. Нажимать; Балтимор, Мэриленд: 1996. [Google Scholar]
.Калькулятор пустого пространства — Найдите пустое пространство в матрице
Онлайн-калькулятор нулевого пространства поможет вам вычислить недействительность и пустое пространство данной матрицы. Пустота и пустое пространство (ядро) — наиболее распространенные понятия в линейной алгебре, которые в основном используются для определения линейной связи между различными атрибутами. Когда вы подставляете размер и значения для матрицы, нулевое пространство матричного калькулятора уменьшает форму эшелона строк для обеспечения пошаговых вычислений.
Что такое пустое пространство?Нулевое пространство или ядро — это подпространство, состоящее из всех векторов нулевого вектора, отображаемых в пространство. В математической записи матрицы A с n столбцами это векторы v = (a₁, a₂, …, aₙ), для которых
A · v = 0
Где 0 — нулевой вектор, (·) означает умножение матриц x = (x,x,. ..,x) имеет n координат.
Примечание:
- Нулевой вектор всегда находится в нулевом пространстве. Какая бы у нас не была матрица, если мы умножим ее на ноль, то получим нуль.
- Ядро матрицы обычно содержит неограниченное количество элементов. На самом деле, если (a₁, a₂, …, aₙ) находится в нулевом пространстве, то (ax₁, ax₂, …, axₙ) одно и то же для каждого действительного числа a.
Нулевое пространство в матрице — это просто подпространство элементов, удовлетворяющих формуле. Однако онлайн-калькулятор определителя позволяет вычислить определитель заданных входных элементов матрицы.
Что такое ничтожность? Недействительность можно определить как количество векторов в пустом пространстве данной матрицы. Размерность нулевого пространства матрицы X называется нулевым значением матрицы X. Количество линейных отношений между атрибутами определяется размером нулевого пространства. Вектор нулевого пространства Y можно использовать для идентификации этих линейных взаимосвязей.
Вы можете использовать ранговую теорему недействительности, чтобы найти недействительность.
Теорема о недействительности ранга помогает связать недействительность матрицы данных с ранжированием и количеством атрибутов в данных. Теорема ранга-недействительности определяется как
– Недействительность X + Ранг X = общее количество атрибутов X (то есть общее количество столбцов в X)
Как найти нулевое пространство матрицы?При попытке определить недействительность и ядро матрицы наиболее важным инструментом является исключение Гаусса-Жордана. Это полезный алгоритм, который может преобразовать заданную матрицу в ее сокращенную ступенчатую форму строк. Идея используется для того, чтобы «уничтожить» как можно больше матричных элементов. Это:
- Поменять местами две строки матрицы;
- Умножить строку на ненулевую константу;
Ключевым свойством здесь является то, что исходная матрица и ее сокращенная ступенчатая форма строк имеют одинаковый нуль и один и тот же ранг. Благодаря своей полезности наша основа для калькулятора нулевого пространства может показать вам, как выглядит входная матрица после удаления исключения Гаусса Жордана.
Пример 1:
Поиск нулевого пространства матрицы имеет 3 строки и 4 столбца.
⌈ х₁ х₂ х₃ х₄ ⌉
| y₁ y₂ y₃ y₄ ｜
⌊ z₁ z₂ z₃ z₄ ⌋
Матричный калькулятор нулевого пространства на первом этапе использует исключение Гаусса Жордана, чтобы взять первую ячейку первой строки, x₁ (пока она не станет равной нулю), и удалить следующие элементы через операции с атомарными строками. Мы добавляем соответствующее кратное верхней строки к двум другим, чтобы получить следующую матрицу:
⌈ x₁ x₂ x₃ x₄ ⌉
| 0 y₂ y₃ y₄ ｜
⌊ 0 z₂ z₃ z₄ ⌋
Далее нулевое пространство матричного калькулятора аналогично средней строке. Мы берем r₂ (пока он не равен нулю) и используем его для удаления записей под ним. В итоге у нас получился массив вида:
⌈ х₁ х₂ х₃ х₄ ⌉
| 0 y₂ y₃ y₄ ｜
⌊ 0 0 z₃ z₄ ⌋
Теперь разница между методом исключения Гаусса Жордана и его упрощенной формой: калькулятор с нулевым пространством делит каждую строку на первую запись в этой строке, которая не равна 0. Это дает:
⌈ 1 x₂ x₃ x₄ ⌉
| 0 1 y₃ y₄ ｜
⌊ 0 0 1 z₄ ⌋
И здесь мы часто заканчиваем алгоритм, например, когда ищем пространство столбца в массиве. На самом деле, мы уже можем считывать полезную информацию с имеющихся у нас матриц. Те, которые появляются в первом ненулевом элементе каждой строки, называются ведущими. В примере они находятся в первом, втором и третьем столбцах из четырех столбцов.
Однако, чтобы найти основу нулевого пространства, мы немного изменим матрицу. Мы снова воспользуемся базовой операцией со строками, но на этот раз пойдем снизу вверх. Во-первых, мы используем 1 в третьей строке, чтобы удалить запись над ней.
⌈ 1 x₂ 0 x₄ ⌉
| 0 1 0 y₄ ｜
⌊ 0 0 1 z₄ ⌋
Теперь проделываем то же самое с 1 в среднем ряду, чтобы уничтожить верхнюю ячейку.
⌈ 1 0 0 x₄ ⌉
| 0 1 0 y₄ ｜
⌊ 0 0 1 z₄ ⌋
В конце концов, это матрица, которая дает нам основу нулевого пространства. Чтобы его определить, нужно соблюдать несколько простых правил.
: Если в матрице нет столбцов без инициалов, то нулевое пространство тривиально. Он имеет размерность 0 и содержит только нулевой вектор.
Если матрица содержит столбцы только с нулями, то базисным вектором eₖ является элемент базиса, который является вектором с 1 в k-й координате, в противном случае он равен нулю.
Однако онлайн-калькулятор Вронскиана поможет вам определить вронскиан заданного набора функций.
Пример 2:
Найти нулевое пространство матрицы:
[3 7 2 9 7 6 5 3 8 3 2 9 3 2 8 3]
Решение:
Данная матрица:
[3 7 2 9 7 6 5 3 8 3 2 9 3 2 8 3]
Сокращенная ступенчатая форма строки матрицы:
[1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1]
Чтобы найти нулевое пространство, решите матричное уравнение:
[ 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1] [x_1x_2x_3x_4] = [0 0 0 0]
Пустая космическая матрица:
[0 0 0 0]
Недействительность матрицы: 0
Как работает калькулятор нулевого пространства?Онлайн-калькулятор пустого пространства может найти основу для нулевого пространства матрицы, выполнив следующие шаги:
Ввод:- Введите размер строк и столбцов матрицы и подставьте данные значения во все поля .
- Если вы хотите найти нулевое пространство матрицы для случайных значений, нажмите кнопку «Создать матрицу».
- Нажмите кнопку «Вычислить нулевое пространство».
- Пустое пространство матричного калькулятора находит основу для нулевого пространства матрицы с сокращенной ступенчатой формой строки матрицы.
Пустое пространство всегда содержит нулевой вектор, но могут существовать и другие векторы.
Что является основой матрицы?При поиске основания нулевого пространства матрицы мы удаляем все избыточные векторы-столбцы из нулевого пространства и сохраняем векторы-столбцы линейно независимыми. Итак, базис — это просто комбинация всех линейно независимых векторов.
Вывод: Используйте онлайн-калькулятор нулевого пространства для вычисления всех векторов, которые отображаются в ноль по заданному массиву.