Квадратный корень. Действия с квадратными корнями. Модуль. Сравнение квадратных корней
Факт 1.
\(\bullet\) Возьмем некоторое неотрицательное число \(a\) (то есть \(a\geqslant 0\)). Тогда (арифметическим) квадратным корнем из числа \(a\) называется такое неотрицательное число \(b\), при возведении которого в квадрат мы получим число \(a\): \[\sqrt a=b\quad \text{то же самое, что }\quad a=b^2\] Из определения следует, что \(a\geqslant 0, b\geqslant 0\). Эти ограничения являются важным условием существования квадратного корня и их следует запомнить!
Вспомним, что любое число при возведении в квадрат дает неотрицательный результат. То есть \(100^2=10000\geqslant 0\) и \((-100)^2=10000\geqslant 0\).
\(\bullet\) Чему равен \(\sqrt{25}\)? Мы знаем, что \(5^2=25\) и \((-5)^2=25\). Так как по определению мы должны найти неотрицательное число, то \(-5\) не подходит, следовательно, \(\sqrt{25}=5\) (так как \(25=5^2\)).
Нахождение значения \(\sqrt a\) называется извлечением квадратного корня из числа \(a\), а число \(a\) называется подкоренным выражением.
\(\bullet\) Исходя из определения, выражения \(\sqrt{-25}\), \(\sqrt{-4}\) и т.п. не имеют смысла.
Факт 2.
Для быстрых вычислений полезно будет выучить таблицу квадратов натуральных чисел от \(1\) до \(20\): \[\begin{array}{|ll|}
\hline
1^2=1 & \quad11^2=121 \\
2^2=4 & \quad12^2=144\\
3^2=9 & \quad13^2=169\\
4^2=16 & \quad14^2=196\\
5^2=25 & \quad15^2=225\\
6^2=36 & \quad16^2=256\\
7^2=49 & \quad17^2=289\\
8^2=64 & \quad18^2=324\\
9^2=81 & \quad19^2=361\\
10^2=100& \quad20^2=400\\
\hline \end{array}\]
Факт 3.
Какие действия можно выполнять с квадратными корнями?
\(\bullet\) Сумма или разность квадратных корней НЕ РАВНА квадратному корню из суммы или разности, то есть \[\sqrt a\pm\sqrt b\ne \sqrt{a\pm b}\] Таким образом, если вам нужно вычислить, например, \(\sqrt{25}+\sqrt{49}\), то первоначально вы должны найти значения \(\sqrt{25}\) и \(\sqrt{49}\), а затем их сложить. Следовательно, \[\sqrt{25}+\sqrt{49}=5+7=12\] Если значения \(\sqrt a\) или \(\sqrt b\) при сложении \(\sqrt
a+\sqrt b\) найти не удается, то такое выражение дальше не преобразуется и остается таким, как есть. Например, в сумме \(\sqrt
2+ \sqrt {49}\) мы можем найти \(\sqrt{49}\) – это \(7\), а вот \(\sqrt
2\) никак преобразовать нельзя, поэтому \(\sqrt 2+\sqrt{49}=\sqrt
2+7\). Дальше это выражение, к сожалению, упростить никак нельзя
\(\bullet\) Произведение/частное квадратных корней равно квадратному корню из произведения/частного, то есть \[\sqrt a\cdot \sqrt b=\sqrt{ab}\quad \text{и}\quad
\sqrt a:\sqrt b=\sqrt{a:b}\] (
Пример: \(\sqrt{32}\cdot \sqrt 2=\sqrt{32\cdot
2}=\sqrt{64}=8\);
\(\sqrt{768}:\sqrt3=\sqrt{768:3}=\sqrt{256}=16\);
\(\sqrt{(-25)\cdot (-64)}=\sqrt{25\cdot 64}=\sqrt{25}\cdot \sqrt{64}=
5\cdot 8=40\).
\(\bullet\) Пользуясь этими свойствами, удобно находить квадратные корни из больших чисел путем разложения их на множители.
Рассмотрим пример. Найдем \(\sqrt{44100}\). Так как \(44100:100=441\), то \(44100=100\cdot 441\). По признаку делимости число \(441\) делится на \(9\) (так как сумма его цифр равна 9 и делится на 9), следовательно, \(441:9=49\), то есть \(441=9\cdot 49\).
Таким образом, мы получили: \[\sqrt{44100}=\sqrt{9\cdot 49\cdot 100}=
\sqrt9\cdot \sqrt{49}\cdot \sqrt{100}=3\cdot 7\cdot 10=210\] Рассмотрим еще один пример: \[\sqrt{\dfrac{32\cdot 294}{27}}=
\sqrt{\dfrac{16\cdot 2\cdot 3\cdot 49\cdot 2}{9\cdot 3}}= \sqrt{
\dfrac{16\cdot4\cdot49}{9}}=\dfrac{\sqrt{16}\cdot \sqrt4 \cdot
\sqrt{49}}{\sqrt9}=\dfrac{4\cdot 2\cdot 7}3=\dfrac{56}3\]
1) \(\sqrt2+3\sqrt2=4\sqrt2\),
2) \(5\sqrt3-\sqrt3=4\sqrt3\)
3) \(\sqrt a+\sqrt a=2\sqrt a\).
Почему так? Объясним на примере 1). Как вы уже поняли, как-то преобразовать число \(\sqrt2\) мы не можем. Представим, что \(\sqrt2\) – это некоторое число \(a\). Соответственно, выражение \(\sqrt2+3\sqrt2\) есть не что иное, как \(a+3a\) (одно число \(a\) плюс еще три таких же числа \(a\)). А мы знаем, что это равно четырем таким числам \(a\), то есть \(4\sqrt2\).
Факт 4.
\(\bullet\) Часто говорят “нельзя извлечь корень”, когда не удается избавиться от знака \(\sqrt {} \ \) корня (радикала) при нахождении значения какого-то числа. Например, извлечь корень из числа \(16\) можно, потому что \(16=4^2\), поэтому \(\sqrt{16}=4\). А вот извлечь корень из числа \(3\), то есть найти \(\sqrt3\), нельзя, потому что нет такого числа, которое в квадрате даст \(3\).
Также иррациональными являются числа \(\pi\) (число “пи”, приблизительно равное \(3,14\)), \(e\) (это число называют числом Эйлера, приблизительно оно равно \(2,7\)) и т.д.
\(\bullet\) Обращаем ваше внимание на то, что любое число будет либо рациональным, либо иррациональным. А вместе все рациональные и все иррациональные числа образуют множество, называющееся множеством действительных (вещественных) чисел. Обозначается это множество буквой \(\mathbb{R}\).
Значит, все числа, которые на данный момент мы знаем, называются вещественными числами.
Факт 5.
\(\bullet\) Модуль вещественного числа \(a\) – это неотрицательное число \(|a|\), равное расстоянию от точки \(a\) до \(0\) на вещественной прямой. Например, \(|3|\) и \(|-3|\) равны 3, так как расстояния от точек \(3\) и \(-3\) до \(0\) одинаковы и равны \(3\). 
\(\bullet\) Если \(a\) – неотрицательное число, то \(|a|=a\).
Пример: \(|5|=5\); \(\qquad |\sqrt2|=\sqrt2\).
\(\bullet\) Если \(a\) – отрицательное число, то \(|a|=-a\).
Пример: \(|-5|=-(-5)=5\); \(\qquad |-\sqrt3|=-(-\sqrt3)=\sqrt3\).
Говорят, что у отрицательных чисел модуль “съедает” минус, а положительные числа, а также число \(0\), модуль оставляет без изменений.
НО такое правило годится только для чисел. Если у вас под знаком модуля находится неизвестная \(x\) (или какая-то другая неизвестная), например, \(|x|\), про которую мы не знаем, положительная она, равна нулю или отрицательная, то избавиться от модуля мы не можем. В этом случае это выражение таким и остается: \(|x|\).
\(\bullet\) Имеют место следующие формулы: \[{\large{\sqrt{a^2}=|a|}}\] \[{\large{(\sqrt{a})^2=a}},
\text{ при условии } a\geqslant 0\] Очень часто допускается такая ошибка: говорят, что \(\sqrt{a^2}\) и \((\sqrt a)^2\) – одно и то же. Это верно только в том случае, когда \(a\) – положительное число или ноль. А вот если \(a\) – отрицательное число, то это неверно. Достаточно рассмотреть такой пример. Возьмем вместо \(a\) число \(-1\). Тогда \(\sqrt{(-1)^2}=\sqrt{1}=1\), а вот выражение \((\sqrt {-1})^2\) вообще не существует (ведь нельзя под знак корня помещать отрицательные числа!).
Поэтому обращаем ваше внимание на то, что \(\sqrt{a^2}\) не равен \((\sqrt a)^2\)!
Пример: 1) \(\sqrt{\left(-\sqrt2\right)^2}=|-\sqrt2|=\sqrt2\), т.к. \(-\sqrt2<0\);
\(\phantom{00000}\) 2) \((\sqrt{2})^2=2\).
\(\bullet\) Так как \(\sqrt{a^2}=|a|\), то \[\sqrt{a^{2n}}=|a^n|\] (выражение \(2n\) обозначает четное число)
То есть при извлечении корня из числа, находящегося в какой-то степени, эта степень уменьшается в два раза.
Пример:
1) \(\sqrt{4^6}=|4^3|=4^3=64\)
2) \(\sqrt{(-25)^2}=|-25|=25\) (заметим, что если модуль не поставить, то получится, что корень из числа равен \(-25\); но мы помним, что по определению корня такого быть не может: у нас всегда при извлечении корня должно получаться положительное число или ноль)
3) \(\sqrt{x^{16}}=|x^8|=x^8\) (так как любое число в четной степени неотрицательно)
Факт 6.
Как сравнить два квадратных корня?
\(\bullet\) Для квадратных корней верно: если \(\sqrt a<\sqrt b\), то \(a<b\); если \(\sqrt a=\sqrt b\), то \(a=b\).
Пример:
1) сравним \(\sqrt{50}\) и \(6\sqrt2\). Для начала преобразуем второе выражение в \(\sqrt{36}\cdot \sqrt2=\sqrt{36\cdot 2}=\sqrt{72}\). Таким образом, так как \(50<72\), то и \(\sqrt{50}<\sqrt{72}\). Следовательно, \(\sqrt{50}<6\sqrt2\).
2) Между какими целыми числами находится \(\sqrt{50}\)?
Так как \(\sqrt{49}=7\), \(\sqrt{64}=8\), а \(49<50<64\), то \(7<\sqrt{50}<8\), то есть число \(\sqrt{50}\) находится между числами \(7\) и \(8\).
3) Сравним \(\sqrt 2-1\) и \(0,5\). Предположим, что \(\sqrt2-1>0,5\): \[\begin{aligned}
&\sqrt 2-1>0,5 \ \big| +1\quad \text{(прибавим единицу к обеим
частям)}\\[1ex]
&\sqrt2>0,5+1 \ \big| \ ^2 \quad\text{(возведем обе части в
квадрат)}\\[1ex]
&2>1,5^2\\
&2>2,25 \end{aligned}\] Видим, что мы получили неверное неравенство. Следовательно, наше предположение было неверным и \(\sqrt 2-1<0,5\).
Заметим, что прибавление некоторого числа к обеим частям неравенства не влияет на его знак. Умножение/деление обеих частей неравенства на положительное число также не влияет на его знак, а умножение/деление на отрицательное число меняет знак неравенства на противоположный!
Возводить обе части уравнения/неравенства в квадрат можно ТОЛЬКО ТОГДА, когда обе части неотрицательные. Например, в неравенстве из предыдущего примера возводить обе части в квадрат можно, в неравенстве \(-3<\sqrt2\) нельзя (убедитесь в этом сами)!
\(\bullet\) Следует запомнить, что \[\begin{aligned}
&\sqrt 2\approx 1,4\\[1ex]
&\sqrt 3\approx 1,7 \end{aligned}\] Знание приблизительного значения данных чисел поможет вам при сравнении чисел!
\(\bullet\) Для того, чтобы извлечь корень (если он извлекается) из какого-то большого числа, которого нет в таблице квадратов, нужно сначала определить, между какими “сотнями” оно находится, затем – между какими “десятками”, а потом уже определить последнюю цифру этого числа. Покажем, как это работает, на примере.
Возьмем \(\sqrt{28224}\). Мы знаем, что \(100^2=10\,000\), \(200^2=40\,000\) и т.д. Заметим, что \(28224\) находится между \(10\,000\) и \(40\,000\). Следовательно, \(\sqrt{28224}\) находится между \(100\) и \(200\).
Теперь определим, между какими “десятками” находится наше число (то есть, например, между \(120\) и \(130\)). Также из таблицы квадратов знаем, что \(11^2=121\), \(12^2=144\) и т.д., тогда \(110^2=12100\), \(120^2=14400\), \(130^2=16900\), \(140^2=19600\), \(150^2=22500\), \(160^2=25600\), \(170^2=28900\). Таким образом, мы видим, что \(28224\) находится между \(160^2\) и \(170^2\). Следовательно, число \(\sqrt{28224}\) находится между \(160\) и \(170\).
Попробуем определить последнюю цифру. Давайте вспомним, какие однозначные числа при возведении в квадрат дают на конце \(4\)? Это \(2^2\) и \(8^2\). Следовательно, \(\sqrt{28224}\) будет заканчиваться либо на 2, либо на 8. Проверим это. Найдем \(162^2\) и \(168^2\):
\(162^2=162\cdot 162=26224\)
\(168^2=168\cdot 168=28224\).
Следовательно, \(\sqrt{28224}=168\). Вуаля!
Корни и степени. Квадратный корень, кубический корень.
Степенью называется выражение вида .
Здесь — основание степени, — показатель степени.
Степень с натуральным показателем
Проще всего определяется степень с натуральным (то есть целым положительным) показателем.
По определению, .
Выражения «возвести в квадрат» и «возвести в куб» нам давно знакомы.
Возвести число в квадрат — значит умножить его само на себя.
.
Возвести число в куб — значит умножить его само на себя три раза.
.
Возвести число в натуральную степень — значит умножить его само на себя раз:
Степень с целым показателем
Показатель степени может быть не только натуральным (то есть целым положительным), но и равным нулю, а также целым отрицательным.
По определению,
.
Это верно для . Выражение 00 не определено.
Определим также, что такое степень с целым отрицательным показателем.
Конечно, все это верно для , поскольку на ноль делить нельзя.
Например,
Заметим, что при возведении в минус первую степень дробь переворачивается.
Показатель степени может быть не только целым, но и дробным, то есть рациональным числом. В статье «Числовые множества» мы говорили, что такое рациональные числа. Это числа, которые можно записать в виде дроби , где — целое, — натуральное.
Здесь нам понадобится новое понятие — корень -степени. Корни и степени — две взаимосвязанные темы. Начнем с уже знакомого вам арифметического квадратного корня.
Арифметический квадратный корень из числа — это такое неотрицательное число, квадрат которого равен .
Согласно определению,
В школьной математике мы извлекаем корень только из неотрицательных чисел. Выражение для нас сейчас имеет смысл только при .
Выражение всегда неотрицательно, т.е. . Например, .
Свойства арифметического квадратного корня:
Кубический корень
Аналогично, кубический корень из — это такое число, которое при возведении в третью степень дает число .
Например, , так как ;
, так как ;
, так как .
Обратите внимание, что корень третьей степени можно извлекать как из положительных, так и из отрицательных чисел.
Теперь мы можем дать определение корня -ной степени для любого целого .
Корень -ной степени
Корень -ной степени из числа — это такое число, при возведении которого в -ную степень получается число .
Например,
Заметим, что корень третьей, пятой, девятой — словом, любой нечетной степени, — можно извлекать как из положительных, так и из отрицательных чисел.
Квадратный корень, а также корень четвертой, десятой, в общем, любой четной степени можно извлекать только из неотрицательных чисел.
Итак, — такое число, что . Оказывается, корни можно записывать в виде степеней с рациональным показателем. Это удобно.
По определению,
в общем случае .
Сразу договоримся, что основание степени больше 0.
Например,
Выражение по определению равно .
При этом также выполняется условие, что больше 0.
Например,
Запомним правила действий со степенями:
— при перемножении степеней показатели складываются
— при делении степени на степень показатели вычитаются
— при возведении степени в степень показатели перемножаются
Ты нашел то, что искал? Поделись с друзьями!
Покажем, как применяются эти формулы в заданиях ЕГЭ по математике:
1.
Внесли все под общий корень, разложили на множители, сократили дробь и извлекли корень.
2.
3.
Здесь мы записали корни в виде степеней и использовали формулы действий со степенями.
Квадратный корень из 2 — это… Что такое Квадратный корень из 2?
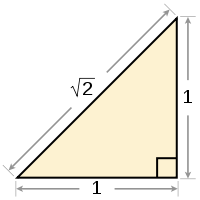 Квадратный корень из 2 равен длине гипотенузы в прямоугольном треугольнике с длиной катетов 1.
Квадратный корень из 2 равен длине гипотенузы в прямоугольном треугольнике с длиной катетов 1.Квадратный корень из числа 2 — положительное вещественное число, которое при умножении само на себя даёт число 2. Обозначение: Приведём значение корня из 2 с 65 знаками после запятой:
- 1,414 213 562 373 095 048 801 688 724 209 698 078 569 671 875 376 948 073 176 679 737 99…
Геометрически корень из 2 можно представить как длину диагонали квадрата со стороной 1 (это следует из теоремы Пифагора). Вероятно, это было первое известное в истории математики иррациональное число (то есть число, которое нельзя точно представить в виде дроби).
 Квадратный корень из 2.
Квадратный корень из 2.Хорошим и часто используемым приближением к является дробь . Несмотря на то, что числитель и знаменатель дроби лишь двузначные целые, оно отличается от реального значения меньше, чем на 1/10000.
История
 Вавилонская глиняная табличка с примечаниями.
Вавилонская глиняная табличка с примечаниями.Вавилонская глиняная табличка (ок. 1800—1600 до н. э.) даёт приближённое значение в четырёх шестидесятеричных цифрах, что составляет 8 десятичных цифр:
Другое раннее приближение этого числа в древнеиндийском математическом тексте, Шульба-сутры (ок. 800—200 до н. э.) даётся следующим образом:
Пифагорейцы обнаружили, что диагональ квадрата несоизмерима с его стороной, или на современном языке, что квадратный корень из двух является иррациональным. Мало что известно с определённостью о времени и обстоятельствах этого выдающегося открытия, но традиционно его авторство приписывается Гиппасу из Метапонта.
Алгоритмы вычисления
Существует множество алгоритмов для вычисления значения квадратного корня из двух. В результате алгоритма получается приблизительное значение в виде обыкновенной или десятичной дроби. Самый популярный алгоритм для этого, который используется во многих компьютерах и калькуляторах, это вавилонский метод вычисления квадратных корней. Он состоит в следующем:
Чем больше повторений в алгоритме (то есть, чем больше «n»), тем лучше приближение квадратного корня из двух. Каждое повторение приблизительно удваивает количество правильных цифр. Приведём несколько первых приближений:
- 3/2 = 1.5
- 17/12 = 1.416…
- 577/408 = 1.414215…
- 665857/470832 = 1.4142135623746…
В 1997 году Ясумаса Канада вычислил значение √2 до 137,438,953,444 десятичных знаков после запятой. В феврале 2007 года рекорд был побит: Шигеру Кондо вычислил 200 миллиардов десятичных знаков после запятой в течение 13 дней и 14 часов, используя процессор 3.6 GHz с 16 ГБ ОЗУ. Среди математических констант только было вычислено более точно.
Свойства квадратного корня из двух
Половина √2 приблизительно равна 0.70710 67811 86548; эта величина даёт в геометрии и тригонометрии координаты единичного вектора,образующего угол 45° с координатными осями:
Одно из интересных свойств √2 состоит в следующем:
- .Потому что
Это является результатом свойства серебряного сечения.
Другое интересное свойство √2:
Квадратный корень из двух может быть выражен в мнимых единицах i используя только квадратные корни и арифметические операции:
- и
Квадратный корень из 2 является единственным числом, отличным от 1, чья бесконечная тетрация равна его квадрату.
Квадратный корень из двух может быть также использован для приближения π:
С точки зрения высшей алгебры, является корнем многочлена и поэтому является целым алгебраическим числом. Множество чисел вида , где — рациональные числа, образует алгебраическое поле. Оно обозначается и является подполем поля вещественных чисел.
Доказательство иррациональности
Применим доказательство от противного: допустим, рационален, то есть представляется в виде несократимой дроби , где и — целые числа. Возведём предполагаемое равенство в квадрат:
- .
Отсюда следует, что чётно, значит, чётно и . Пусть , где целое. Тогда
Следовательно, чётно, значит, чётно и . Мы получили, что и чётны, что противоречит несократимости дроби . Значит, исходное предположение было неверным, и — иррациональное число.
Непрерывная дробь
Квадратный корень из двух может быть представлен в виде непрерывной дроби:
Подходящие дроби данной непрерывной дроби дают приближённые значения, быстро сходящиеся к точному квадратному корню из двух. Способ их вычисления прост: если обозначить предыдущую подходящую дробь , то последующая имеет вид . Скорость сходимости здесь меньше, чем у метода Ньютона, но вычисления гораздо проще. Выпишем несколько первых приближений:
Квадрат последней приведенной дроби равен (округлённо) 2,000000177.
Размер бумаги
Квадратный корень из двух является пропорцией формата бумаги ISO 216. Соотношение сторон таково, что при разрезании листа пополам параллельно его короткой стороне получатся два листа той же пропорции.
См. также
«Квадратный корень из 9 = +-3 или только +3?» – Яндекс.Кью
Либо 9, либо 1. Как вам больше нравится.
Всё зависит от вашего использования следующего правила:
Другими словами, если вы подразумеваете, что пропущенный знак — это алгебраическое умножение, сопровождающее скобку, то вашим ответом будет 1.
Если же вы подразумеваете, что пропущенный знак — это простое арифметическое умножение, то вашим ответом будет 9. Однако в этом случае возникает вопрос: а с какой целью вы его пропустили, если не подразумевали алгебраического умножения?
Вот статья по этому поводу:
https://denis-demakhin.livejournal.com/63537.html
Квадратный корень из 2 — Википедия
1,4142135623 7309504880 1688724209 6980785696 7187537694 8073176679 7379907324 7846210703 8850387534 3276415727 3501384623 0912297024 9248360558 5073721264 4121497099 9358314132 2266592750 5592755799 9505011527 8206057147 0109559971 6059702745 3459686201 4728517418 6408891986 0955232923 0484308714 3214508397 6260362799 5251407989 6872533965 4633180882 9640620615 2583523950 5474575028 7759961729 8355752203 3753185701 1354374603 4084988471 6038689997 0699004815 0305440277 9031645424 7823068492 9369186215 8057846311 1596668713 0130156185 6898723723 5288509264 8612494977 1542183342 0428568606 0146824720 7714358548 7415565706 9677653720 2264854470 1585880162 0758474922 6572260020 8558446652 1458398893 9443709265 9180031138 8246468157 0826301005 9485870400 3186480342 1948972782 9064104507 2636881313 7398552561 1732204024 5091227700 2269411275 7362728049 5738108967 5040183698 6836845072 5799364729 0607629969 4138047565 4823728997 1803268024 7442062926 9124859052 1810044598 4215059112 0249441341 7285314781 0580360337 1077309182 8693147101 7111168391 6581726889 4197587165 8215212822 9518488472
Первые 1000 знаков значения √2[1].
 Квадратный корень из 2 равен длине гипотенузы в прямоугольном треугольнике с длиной катетов 1.
Квадратный корень из 2 равен длине гипотенузы в прямоугольном треугольнике с длиной катетов 1.Квадратный корень из числа 2 — положительное вещественное число, которое при умножении само на себя даёт число 2. Обозначение: 2 . {\displaystyle {\sqrt {2}}.}
Геометрически корень из 2 можно представить как длину диагонали квадрата со стороной 1 (это следует из теоремы Пифагора). Вероятно, это было первое известное в истории математики иррациональное число (то есть число, которое нельзя точно представить в виде дроби).
 Квадратный корень из 2.
Квадратный корень из 2.Хорошим и часто используемым приближением к 2 {\displaystyle {\sqrt {2}}} является дробь 99 70 {\displaystyle {\tfrac {99}{70}}} . Несмотря на то, что числитель и знаменатель дроби лишь двузначные целые, оно отличается от реального значения меньше, чем на 1/10000.
История
 Вавилонская глиняная табличка с максимально точным указанием длины диагонали единичного квадрата четырёхзначным шестидесятеричным числом.
Вавилонская глиняная табличка с максимально точным указанием длины диагонали единичного квадрата четырёхзначным шестидесятеричным числом.Вавилонская глиняная табличка (ок. 1800—1600 до н. э.) даёт наиболее точное приближённое значение 2 {\displaystyle {\sqrt {2}}} при записи в четырёх шестидесятеричных цифрах, что после округления составляет 6 точных десятичных цифр:
- 1 + 24 60 + 51 60 2 + 10 60 3 = 1.41421 296 ¯ . {\displaystyle 1+{\frac {24}{60}}+{\frac {51}{60^{2}}}+{\frac {10}{60^{3}}}=1.41421{\overline {296}}.}
Другое раннее приближение этого числа в древнеиндийском математическом тексте, Шульба-сутры (ок. 800—200 до н. э.) даётся следующим образом:
- 1 + 1 3 + 1 3 ⋅ 4 − 1 3 ⋅ 4 ⋅ 34 = 577 408 ≈ 1.414215686. {\displaystyle 1+{\frac {1}{3}}+{\frac {1}{3\cdot 4}}-{\frac {1}{3\cdot 4\cdot 34}}={\frac {577}{408}}\approx 1.414215686.}
Пифагорейцы обнаружили, что диагональ квадрата несоизмерима с его стороной, или на современном языке, что квадратный корень из двух является иррациональным. Мало что известно с определённостью о времени и обстоятельствах этого выдающегося открытия, но традиционно его авторство приписывается Гиппасу из Метапонта, которого за это открытие, по разным вариантам легенды, пифагорейцы не то убили, не то изгнали, поставив ему в вину разрушение главной пифагорейской доктрины о том, что «всё есть [натуральное] число». Поэтому квадратный корень из 2 иногда называют постоянной Пифагора, так как именно пифагорейцы доказали его иррациональность, тем самым открыв существование иррациональных чисел[источник не указан 1850 дней].
Алгоритмы вычисления
Существует множество алгоритмов для вычисления значения квадратного корня из двух. В результате алгоритма получается приблизительное значение 2 {\displaystyle {\sqrt {2}}} в виде обыкновенной или десятичной дроби. Самый популярный алгоритм для этого, который используется во многих компьютерах и калькуляторах, это вавилонский метод вычисления квадратных корней. Он состоит в следующем:
- a n + 1 = a n + 2 a n 2 = a n 2 + 1 a n . {\displaystyle a_{n+1}={\frac {a_{n}+{\frac {2}{a_{n}}}}{2}}={\frac {a_{n}}{2}}+{\frac {1}{a_{n}}}.}
Чем больше повторений в алгоритме (то есть, чем больше «n»), тем лучше приближение квадратного корня из двух. Каждое повторение приблизительно удваивает количество правильных цифр. Несколько первых приближений, начиная с a 0 = 1 {\displaystyle a_{0}=1} :
- 3/2 = 1,5
- 17/12 = 1,416…
- 577/408 = 1,414215…
- 665857/470832 = 1,4142135623746…
В 1997 году Ясумаса Канада вычислил значение 2 {\displaystyle {\sqrt {2}}} до 137 438 953 444 десятичных знаков после запятой. В феврале 2007 года рекорд был побит: Сигэру Кондо вычислил 200 миллиардов десятичных знаков после запятой в течение 13 дней и 14 часов, используя процессор с частотой 3,6 ГГц и 16 ГБ ОЗУ.
Мнемоническое правило
Для запоминания значения корня из двойки с восемью знаками после запятой (1,41421356) можно воспользоваться следующим текстом (число букв в каждом слове соответствует десятичной цифре): «И плод у меня, но у них много корней».
Свойства квадратного корня из двух
Половина 2 {\displaystyle {\sqrt {2}}} приблизительно равна 0,70710 67811 86548; эта величина даёт в геометрии и тригонометрии координаты единичного вектора, образующего угол 45° с координатными осями:
- 2 2 = 1 2 = 1 2 = cos ( 45 ∘ ) = sin ( 45 ∘ ) . {\displaystyle {\frac {\sqrt {2}}{2}}={\sqrt {\frac {1}{2}}}={\frac {1}{\sqrt {2}}}=\cos(45^{\circ })=\sin(45^{\circ }).}
Одно из интересных свойств 2 {\displaystyle {\sqrt {2}}} состоит в следующем:
- 1 2 − 1 = 2 + 1 {\displaystyle \ {1 \over {{\sqrt {2}}-1}}={\sqrt {2}}+1} . Потому что ( 2 + 1 ) ( 2 − 1 ) = 2 − 1 = 1. {\displaystyle ({\sqrt {2}}+1)({\sqrt {2}}-1)=2-1=1.}
Это является результатом свойства серебряного сечения.
Другое интересное свойство 2 {\displaystyle {\sqrt {2}}} :
- 2 + 2 + 2 + ⋯ = 2. {\displaystyle {\sqrt {2+{\sqrt {2+{\sqrt {2+\cdots }}}}}}=2.}
Квадратный корень из двух может быть выражен в мнимых единицах i, используя только квадратные корни и арифметические операции:
- i + i i i {\displaystyle {\frac {{\sqrt {i}}+i{\sqrt {i}}}{i}}} и − i − i − i − i . {\displaystyle {\frac {{\sqrt {-i}}-i{\sqrt {-i}}}{-i}}.}
Квадратный корень из 2 является единственным числом, отличным от 1, чья бесконечная тетрация равна его квадрату.
- 2 2 2 ⋅ ⋅ ⋅ = 2 {\displaystyle {\sqrt {2}}^{{\sqrt {2}}^{{\sqrt {2}}^{\ \cdot ^{\cdot ^{\cdot }}}}}=2}
Квадратный корень из двух может быть также использован для приближения π {\displaystyle \pi } :
- 2 m 2 − 2 + 2 + ⋯ + 2 → π as m → ∞ {\displaystyle 2^{m}{\sqrt {2-{\sqrt {2+{\sqrt {2+\cdots +{\sqrt {2}}}}}}}}\to \pi {\text{ as }}m\to \infty }
С точки зрения высшей алгебры, 2 {\displaystyle {\sqrt {2}}} является корнем многочлена x 2 − 2 {\displaystyle x^{2}-2} и поэтому является целым алгебраическим числом[2]. Множество чисел вида a + b 2 {\displaystyle a+b{\sqrt {2}}} , где a , b {\displaystyle a,b} — рациональные числа, образует алгебраическое поле. Оно обозначается Q [ 2 ] {\displaystyle \mathbb {Q} [{\sqrt {2}}]} и является подполем поля вещественных чисел.
Доказательство иррациональности
Применим доказательство от противного: допустим, 2 {\displaystyle {\sqrt {2}}} рационален, то есть представляется в виде дроби m n {\displaystyle {\frac {m}{n}}} , где m {\displaystyle m} и n {\displaystyle n} — целые числа.
Возведём предполагаемое равенство в квадрат:
- 2 = m n ⇒ 2 = m 2 n 2 ⇒ m 2 = 2 n 2 {\displaystyle {\sqrt {2}}={\frac {m}{n}}\Rightarrow 2={\frac {m^{2}}{n^{2}}}\Rightarrow m^{2}=2n^{2}} .
Так как разложение m2 на простые множители содержит 2 в четной степени, а 2n2 — в нечетной, равенство m2=2n2 невозможно. Значит, исходное предположение было неверным, и 2 {\displaystyle {\sqrt {2}}} — иррациональное число.
Непрерывная дробь
Квадратный корень из двух может быть представлен в виде непрерывной дроби:
- 2 = 1 + 1 2 + 1 2 + 1 2 + 1 2 + ⋱ . {\displaystyle \ {\sqrt {2}}=1+{\cfrac {1}{2+{\cfrac {1}{2+{\cfrac {1}{2+{\cfrac {1}{2+\ddots }}}}}}}}.}
Подходящие дроби данной непрерывной дроби дают приближённые значения, быстро сходящиеся к точному квадратному корню из двух. Способ их вычисления прост: если обозначить предыдущую подходящую дробь m n {\displaystyle {\frac {m}{n}}} , то последующая имеет вид m + 2 n m + n {\displaystyle {\frac {m+2n}{m+n}}} . Скорость сходимости здесь меньше, чем у метода Ньютона, но вычисления гораздо проще. Выпишем несколько первых приближений:
- 3 2 ; 7 5 ; 17 12 ; 41 29 ; 99 70 ; 239 169 ; 577 408 ; 1393 985 ; 3363 2378 … {\displaystyle {\frac {3}{2}};\ {\frac {7}{5}};\ {\frac {17}{12}};\ {\frac {41}{29}};\ {\frac {99}{70}};\ {\frac {239}{169}};\ {\frac {577}{408}};\ {\frac {1393}{985}};\ {\frac {3363}{2378}}\dots }
Квадрат последней приведенной дроби равен (округлённо) 2,000000177.
Размер бумаги
Квадратный корень из двух используется в соотношении сторон листа бумаги формата ISO 216. Соотношение сторон равно 1 : 2 {\displaystyle 1:{\sqrt {2}}} . При разрезании листа пополам параллельно его короткой стороне получатся два листа той же пропорции. Это позволяет нумеровать форматы бумаги одним числом по убыванию площади листа (числу разрезов): А0, А1, А2, А3, А4,…
См. также
Примечания
Литература
- Клауди Альсина. Секта чисел. Теорема Пифагора. — М.: Де Агостини, 2014. — 152 с. — (Мир математики: в 45 томах, том 5). — ISBN 978-5-9774-0633-8.
Ссылки
Квадратный корень из 3 — это… Что такое Квадратный корень из 3?
Квадратный корень из числа 3 — положительное действительное число, которое при умножении само на себя даёт число 3.
Его приблизительным значением с 69 цифрами после запятой является:
Округленное значение 1.732 является правильным с точностью до 0,01 %. Приблизительной правильной дробью является (1,7321 42857…).
Квадратный корень из 3 является иррациональным числом. Также известен как Феодоровская постоянная, названная в честь Феодора Киренского.
Может быть выражен в виде непрерывной дроби [1; 1, 2, 1, 2, 1, 2, …].
Геометрия
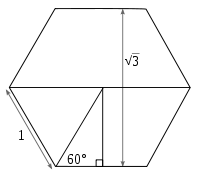 Квадратный корень из 3 равен длине между параллельными сторонами правильного шестиугольника со сторонами 1.
Квадратный корень из 3 равен длине между параллельными сторонами правильного шестиугольника со сторонами 1.Если равносторонний треугольник со сторонами длиной 1 делится на две равные половины, пересечением внутреннего угла для составления прямого угла с одной стороной, то получившийся прямоугольный треугольник имеет гипотенузу со стороной 1 и катеты длиной 1/2 и Поэтому тангенс 60° равен
Так же, это расстояние между параллельными сторонами правильного шестиугольника со сторонами 1.
является длиной диагонали куба со стороной 1.
Использование в других областях
Энергетика
При трехфазной системе токов модуль напряжения между двумя фазами (линейное напряжение) в больше модуля фазного напряжения
См. также
Ссылки
Квадратный корень из 2 — Википедия
1,4142135623 7309504880 1688724209 6980785696 7187537694 8073176679 7379907324 7846210703 8850387534 3276415727 3501384623 0912297024 9248360558 5073721264 4121497099 9358314132 2266592750 5592755799 9505011527 8206057147 0109559971 6059702745 3459686201 4728517418 6408891986 0955232923 0484308714 3214508397 6260362799 5251407989 6872533965 4633180882 9640620615 2583523950 5474575028 7759961729 8355752203 3753185701 1354374603 4084988471 6038689997 0699004815 0305440277 9031645424 7823068492 9369186215 8057846311 1596668713 0130156185 6898723723 5288509264 8612494977 1542183342 0428568606 0146824720 7714358548 7415565706 9677653720 2264854470 1585880162 0758474922 6572260020 8558446652 1458398893 9443709265 9180031138 8246468157 0826301005 9485870400 3186480342 1948972782 9064104507 2636881313 7398552561 1732204024 5091227700 2269411275 7362728049 5738108967 5040183698 6836845072 5799364729 0607629969 4138047565 4823728997 1803268024 7442062926 9124859052 1810044598 4215059112 0249441341 7285314781 0580360337 1077309182 8693147101 7111168391 6581726889 4197587165 8215212822 9518488472
Первые 1000 знаков значения √2[1].
 Квадратный корень из 2 равен длине гипотенузы в прямоугольном треугольнике с длиной катетов 1.
Квадратный корень из 2 равен длине гипотенузы в прямоугольном треугольнике с длиной катетов 1.Квадратный корень из числа 2 — положительное вещественное число, которое при умножении само на себя даёт число 2. Обозначение: 2 . {\displaystyle {\sqrt {2}}.}
Геометрически корень из 2 можно представить как длину диагонали квадрата со стороной 1 (это следует из теоремы Пифагора). Вероятно, это было первое известное в истории математики иррациональное число (то есть число, которое нельзя точно представить в виде дроби).
 Квадратный корень из 2.
Квадратный корень из 2.Хорошим и часто используемым приближением к 2 {\displaystyle {\sqrt {2}}} является дробь 99 70 {\displaystyle {\tfrac {99}{70}}} . Несмотря на то, что числитель и знаменатель дроби лишь двузначные целые, оно отличается от реального значения меньше, чем на 1/10000.
История
 Вавилонская глиняная табличка с максимально точным указанием длины диагонали единичного квадрата четырёхзначным шестидесятеричным числом.
Вавилонская глиняная табличка с максимально точным указанием длины диагонали единичного квадрата четырёхзначным шестидесятеричным числом.Вавилонская глиняная табличка (ок. 1800—1600 до н. э.) даёт наиболее точное приближённое значение 2 {\displaystyle {\sqrt {2}}} при записи в четырёх шестидесятеричных цифрах, что после округления составляет 6 точных десятичных цифр:
- 1 + 24 60 + 51 60 2 + 10 60 3 = 1.41421 296 ¯ . {\displaystyle 1+{\frac {24}{60}}+{\frac {51}{60^{2}}}+{\frac {10}{60^{3}}}=1.41421{\overline {296}}.}
Другое раннее приближение этого числа в древнеиндийском математическом тексте, Шульба-сутры (ок. 800—200 до н. э.) даётся следующим образом:
- 1 + 1 3 + 1 3 ⋅ 4 − 1 3 ⋅ 4 ⋅ 34 = 577 408 ≈ 1.414215686. {\displaystyle 1+{\frac {1}{3}}+{\frac {1}{3\cdot 4}}-{\frac {1}{3\cdot 4\cdot 34}}={\frac {577}{408}}\approx 1.414215686.}
Пифагорейцы обнаружили, что диагональ квадрата несоизмерима с его стороной, или на современном языке, что квадратный корень из двух является иррациональным. Мало что известно с определённостью о времени и обстоятельствах этого выдающегося открытия, но традиционно его авторство приписывается Гиппасу из Метапонта, которого за это открытие, по разным вариантам легенды, пифагорейцы не то убили, не то изгнали, поставив ему в вину разрушение главной пифагорейской доктрины о том, что «всё есть [натуральное] число». Поэтому квадратный корень из 2 иногда называют постоянной Пифагора, так как именно пифагорейцы доказали его иррациональность, тем самым открыв существование иррациональных чисел[источник не указан 1850 дней].
Алгоритмы вычисления
Существует множество алгоритмов для вычисления значения квадратного корня из двух. В результате алгоритма получается приблизительное значение 2 {\displaystyle {\sqrt {2}}} в виде обыкновенной или десятичной дроби. Самый популярный алгоритм для этого, который используется во многих компьютерах и калькуляторах, это вавилонский метод вычисления квадратных корней. Он состоит в следующем:
- a n + 1 = a n + 2 a n 2 = a n 2 + 1 a n . {\displaystyle a_{n+1}={\frac {a_{n}+{\frac {2}{a_{n}}}}{2}}={\frac {a_{n}}{2}}+{\frac {1}{a_{n}}}.}
Чем больше повторений в алгоритме (то есть, чем больше «n»), тем лучше приближение квадратного корня из двух. Каждое повторение приблизительно удваивает количество правильных цифр. Несколько первых приближений, начиная с a 0 = 1 {\displaystyle a_{0}=1} :
- 3/2 = 1,5
- 17/12 = 1,416…
- 577/408 = 1,414215…
- 665857/470832 = 1,4142135623746…
В 1997 году Ясумаса Канада вычислил значение 2 {\displaystyle {\sqrt {2}}} до 137 438 953 444 десятичных знаков после запятой. В феврале 2007 года рекорд был побит: Сигэру Кондо вычислил 200 миллиардов десятичных знаков после запятой в течение 13 дней и 14 часов, используя процессор с частотой 3,6 ГГц и 16 ГБ ОЗУ.
Мнемоническое правило
Для запоминания значения корня из двойки с восемью знаками после запятой (1,41421356) можно воспользоваться следующим текстом (число букв в каждом слове соответствует десятичной цифре): «И плод у меня, но у них много корней».
Свойства квадратного корня из двух
Половина 2 {\displaystyle {\sqrt {2}}} приблизительно равна 0,70710 67811 86548; эта величина даёт в геометрии и тригонометрии координаты единичного вектора, образующего угол 45° с координатными осями:
- 2 2 = 1 2 = 1 2 = cos ( 45 ∘ ) = sin ( 45 ∘ ) . {\displaystyle {\frac {\sqrt {2}}{2}}={\sqrt {\frac {1}{2}}}={\frac {1}{\sqrt {2}}}=\cos(45^{\circ })=\sin(45^{\circ }).}
Одно из интересных свойств 2 {\displaystyle {\sqrt {2}}} состоит в следующем:
- 1 2 − 1 = 2 + 1 {\displaystyle \ {1 \over {{\sqrt {2}}-1}}={\sqrt {2}}+1} . Потому что ( 2 + 1 ) ( 2 − 1 ) = 2 − 1 = 1. {\displaystyle ({\sqrt {2}}+1)({\sqrt {2}}-1)=2-1=1.}
Это является результатом свойства серебряного сечения.
Другое интересное свойство 2 {\displaystyle {\sqrt {2}}} :
- 2 + 2 + 2 + ⋯ = 2. {\displaystyle {\sqrt {2+{\sqrt {2+{\sqrt {2+\cdots }}}}}}=2.}
Квадратный корень из двух может быть выражен в мнимых единицах i, используя только квадратные корни и арифметические операции:
- i + i i i {\displaystyle {\frac {{\sqrt {i}}+i{\sqrt {i}}}{i}}} и − i − i − i − i . {\displaystyle {\frac {{\sqrt {-i}}-i{\sqrt {-i}}}{-i}}.}
Квадратный корень из 2 является единственным числом, отличным от 1, чья бесконечная тетрация равна его квадрату.
- 2 2 2 ⋅ ⋅ ⋅ = 2 {\displaystyle {\sqrt {2}}^{{\sqrt {2}}^{{\sqrt {2}}^{\ \cdot ^{\cdot ^{\cdot }}}}}=2}
Квадратный корень из двух может быть также использован для приближения π {\displaystyle \pi } :
- 2 m 2 − 2 + 2 + ⋯ + 2 → π as m → ∞ {\displaystyle 2^{m}{\sqrt {2-{\sqrt {2+{\sqrt {2+\cdots +{\sqrt {2}}}}}}}}\to \pi {\text{ as }}m\to \infty }
С точки зрения высшей алгебры, 2 {\displaystyle {\sqrt {2}}} является корнем многочлена x 2 − 2 {\displaystyle x^{2}-2} и поэтому является целым алгебраическим числом[2]. Множество чисел вида a + b 2 {\displaystyle a+b{\sqrt {2}}} , где a , b {\displaystyle a,b} — рациональные числа, образует алгебраическое поле. Оно обозначается Q [ 2 ] {\displaystyle \mathbb {Q} [{\sqrt {2}}]} и является подполем поля вещественных чисел.
Доказательство иррациональности
Применим доказательство от противного: допустим, 2 {\displaystyle {\sqrt {2}}} рационален, то есть представляется в виде дроби m n {\displaystyle {\frac {m}{n}}} , где m {\displaystyle m} и n {\displaystyle n} — целые числа.
Возведём предполагаемое равенство в квадрат:
- 2 = m n ⇒ 2 = m 2 n 2 ⇒ m 2 = 2 n 2 {\displaystyle {\sqrt {2}}={\frac {m}{n}}\Rightarrow 2={\frac {m^{2}}{n^{2}}}\Rightarrow m^{2}=2n^{2}} .
Так как разложение m2 на простые множители содержит 2 в четной степени, а 2n2 — в нечетной, равенство m2=2n2 невозможно. Значит, исходное предположение было неверным, и 2 {\displaystyle {\sqrt {2}}} — иррациональное число.
Непрерывная дробь
Квадратный корень из двух может быть представлен в виде непрерывной дроби:
- 2 = 1 + 1 2 + 1 2 + 1 2 + 1 2 + ⋱ . {\displaystyle \ {\sqrt {2}}=1+{\cfrac {1}{2+{\cfrac {1}{2+{\cfrac {1}{2+{\cfrac {1}{2+\ddots }}}}}}}}.}
Подходящие дроби данной непрерывной дроби дают приближённые значения, быстро сходящиеся к точному квадратному корню из двух. Способ их вычисления прост: если обозначить предыдущую подходящую дробь m n {\displaystyle {\frac {m}{n}}} , то последующая имеет вид m + 2 n m + n {\displaystyle {\frac {m+2n}{m+n}}} . Скорость сходимости здесь меньше, чем у метода Ньютона, но вычисления гораздо проще. Выпишем несколько первых приближений:
- 3 2 ; 7 5 ; 17 12 ; 41 29 ; 99 70 ; 239 169 ; 577 408 ; 1393 985 ; 3363 2378 … {\displaystyle {\frac {3}{2}};\ {\frac {7}{5}};\ {\frac {17}{12}};\ {\frac {41}{29}};\ {\frac {99}{70}};\ {\frac {239}{169}};\ {\frac {577}{408}};\ {\frac {1393}{985}};\ {\frac {3363}{2378}}\dots }
Квадрат последней приведенной дроби равен (округлённо) 2,000000177.
Размер бумаги
Квадратный корень из двух используется в соотношении сторон листа бумаги формата ISO 216. Соотношение сторон равно 1 : 2 {\displaystyle 1:{\sqrt {2}}} . При разрезании листа пополам параллельно его короткой стороне получатся два листа той же пропорции. Это позволяет нумеровать форматы бумаги одним числом по убыванию площади листа (числу разрезов): А0, А1, А2, А3, А4,…
См. также
Примечания
Литература
- Клауди Альсина. Секта чисел. Теорема Пифагора. — М.: Де Агостини, 2014. — 152 с. — (Мир математики: в 45 томах, том 5). — ISBN 978-5-9774-0633-8.
Ссылки
Mathway | Популярные задачи
Mathway | Популярные проблемыПопулярные задачи
Основы математики Предварительно Алгебра Алгебра тригонометрия тригонометрия и алгебра Исчисление Конечная математика Линейная алгебра ХимияMathway требует javascript и современного браузера.
Этот веб-сайт использует файлы cookie, чтобы обеспечить вам максимальное удобство работы с ним.
Убедитесь, что ваш пароль состоит не менее чем из 8 символов и содержит каждое из следующих значений:
- номер
- письмо
- специальный символ: @ $ #!% *? &
Почему квадратный корень из 2 иррационален
Квадратный корень из 2
Является ли квадратный корень из 2 дробью?
Давайте представим , что это , и посмотрим, что произойдет.
Если это дробь, то мы должны иметь возможность записать ее в виде упрощенной дроби, например:
м / п
(m и n — целые числа)
И мы надеемся, что возведя его в квадрат, мы получим 2:
(м / п) 2 = 2
, что совпадает с
м 2 / п 2 = 2
или иными словами, m 2 вдвое больше n 2 :
м 2 = 2 × n 2
Попробуйте сами
Посмотрите, сможете ли вы найти значение для m и n , которое работает!
Пример : давайте попробуем m = 17 и n = 12 :
м / п = 17/12
Когда мы возводим в квадрат, получаем
17 2 /12 2 = 289/144 = 2.0069444 …
Что близко к 2, но не совсем верно
Как видите, мы действительно хотим, чтобы m 2 было дважды n 2 (289 примерно вдвое 144). Вы можете лучше?
Четное и нечетное
Теперь давайте примем идею, что m 2 = 2 × n 2
На самом деле это означает, что м 2 должно быть четным числом.
Почему? Потому что всякий раз, когда мы умножаем на четное число (в данном случае 2), результатом будет четное число.Как это:
| Операция | Результат | Пример |
|---|---|---|
| Четное × Четное | Даже | 2 × 8 = 16 |
| Четное × Нечетное | Даже | 2 × 7 = 14 |
| Нечетное × Четное | Даже | 5 × 8 = 40 |
| Нечетное × Нечетное | Нечетный | 5 × 7 = 35 |
И если m 2 четное, то m должно быть четным (если m было нечетным, то m 2 также нечетным).Итак:
м равно
И все четные числа кратны 2, поэтому м кратно 2 , поэтому м 2 кратно 4 .
И если m 2 кратно 4, то n 2 должно быть кратно 2 (помня, что m 2 / n 2 = 2).
А так …
n тоже четное
Но подождите … если и m, и n равны , мы сможем упростить дробь m / n.
Пример: 2/12 можно упростить до 1/6
Но мы уже говорили, что это было упрощенным …
… и если он еще не упрощен, давайте упростим его сейчас и начнем снова. Но это все равно дает тот же результат: и n, и m равны . Что ж, это глупо — мы можем показать, что и n, и m равны , всегда даже , независимо от того, что мы уже упростили дробь. |
Значит, что-то ужасно не так … это должно быть наше первое предположение, что квадратный корень из 2 является дробью. Не может быть.
Итак, квадратный корень из 2 не может быть записан как дробь .
Иррациональный
Мы называем такие числа «иррациональными» не потому, что они сумасшедшие, а потому, что они не могут быть записаны как , отношение (или дробь). И мы говорим:
«Корень квадратный из 2 иррационален»
Считается первым обнаруженным иррациональным числом.Но есть еще много чего.
Reductio ad absurdum
Между прочим, метод, который мы использовали, чтобы доказать это (сначала сделав предположение, а затем проверив, хорошо ли оно работает), называется «доказательство от противного» или «reductio ad absurdum».
Reduction ad absurdum : тип логического аргумента, при котором кто-то принимает утверждение ради аргумента и получает абсурдный или нелепый результат, а затем приходит к выводу, что исходное утверждение должно быть ошибочным, поскольку привело к абсурдному результату.(из Википедии)
История
Много лет назад (около 500 г. до н.э.) греческие математики, такие как Пифагор, считали, что все числа могут быть представлены в виде дробей.
И они думали, что числовая прямая полностью состоит из дробей, потому что для любых двух дробей мы всегда можем найти дробь между ними (чтобы мы могли смотреть все ближе и ближе к числовой прямой и находить все больше и больше дробей).
Пример: от 1/4 до 1/2 равно 1/3. Между 1/3 и 1/2 — 2/5, между 1/3 и 2/5 — 3/8 и так далее.
(Примечание: простой способ найти дробь между двумя другими дробями — это сложить верхние и нижние части, так что между 3/8 и 2/5 будет (3 + 2) / (8 + 5) = 5 / 13).
Итак, поскольку этот процесс не имеет конца, таких точек бесконечно много. И это, кажется, заполняет числовую строку, не так ли?
И они были очень довольны этим … пока они не обнаружили, что квадратный корень из 2 составляет , а не дробь , и им пришлось полностью переосмыслить свои идеи!
Заключение
Квадратный корень из 2 «иррациональный» (не может быть записан в виде дроби)… потому что , если бы можно было записать как дробь, тогда мы имели бы абсурдный случай , в котором дробь имела бы четные числа как вверху, так и внизу, и поэтому ее всегда можно было бы упростить.
,Калькулятор квадратного корняГрафический калькулятор Texas Instruments TI-84 Plus
Чтобы извлечь квадратный корень из числа, нажмите [2ND] (дополнительная функциональная клавиша), а затем [ √ & nbsp ] (клавиша с символом корня, которая используется для извлечения квадратного корня из числа), затем число, из которого вы хотите найти квадратный корень, а затем клавишу [ENTER].
Пример :
Чтобы найти квадратный корень из 2, нажмите:
[2ND] [
√
] 2 [ENTER]
Это даст вам ответ: 1.414213562, если все сделано правильно.
(Примечание: этот же метод также работает с калькуляторами TI-83 и TI-81)
График :
Чтобы построить график функции квадратного корня y =
√x
Нажмите [Y =] [2ND] [
√ & nbsp
] [X, T, O, n] [GRAPH]
Используйте клавишу [Trace] и клавиши со стрелками, чтобы отслеживать и отображать значения на графике.
(Чтобы увидеть, как выглядит график на этом калькуляторе, нажмите кнопку «Показать график» под изображением калькулятора на этой странице.)
Плюсы:
Его можно использовать на многих вступительных экзаменах в колледж (проверьте критерии экзамена).
Это популярный калькулятор. (Если вам нужна помощь, вероятность найти того, кто умеет ею пользоваться, выше).
На дисплее отображается семь строк ввода / вывода. Можно просматривать и проверять длинные уравнения. (Это приятное преимущество графических калькуляторов по сравнению с научными калькуляторами, у которых может быть только однострочный дисплей.) Еще одно преимущество большого дисплея — вы можете сравнить свой текущий ответ с прошлыми ответами, которые все еще отображаются на экране.Это часто может помочь вам обнаружить ошибку ввода, которая в противном случае могла бы остаться незамеченной.
Минусы:
Он более громоздкий, чем научный калькулятор.
Он стоит примерно на 85 долларов больше, чем научный калькулятор.
Цена:
Лучшая цена для этого калькулятора на 9-2-2014 составляет около 94 долларов США.
Графический калькулятор Casio (FX-9750GII)
Чтобы извлечь квадратный корень из числа, нажмите [SHIFT], а затем [ √ ] (радикальный символ находится над клавишей x 2 ), затем число, из которого вы хотите найти квадратный корень, а затем клавишу [EXE].
Пример :
Чтобы найти квадратный корень из 2, нажмите:
[СДВИГ] [
√ & nbsp
] 2 [EXE]
Это даст вам ответ: 1.414213562, если введен правильно.
График :
Чтобы построить график функции квадратного корня y =
√x
Нажмите [MENU], выберите Graph, [EXE]
[СДВИГ] [
√ & nbsp
] [X, O, T] [EXE] [F6]
Используйте клавишу [F6] для переключения между экраном графика и экраном уравнения.
Используйте клавишу [F1] и клавиши со стрелками для отслеживания и отображения значений на графике.
(Чтобы увидеть этот график, нажмите кнопку «Показать график» под изображением калькулятора на этой странице.)
Плюсы:
Стоимость составляет половину стоимости калькулятора ТИ-84.
Он немного меньше калькулятора ТИ-84.
Его можно использовать на многих вступительных экзаменах в колледж (проверьте критерии экзамена).
На дисплее отображается семь строк ввода / вывода.
Минусы:
Он не так популярен, как калькулятор ТИ-84. (Если у вас есть вопрос о том, как пользоваться калькулятором, найти кого-то, кто поможет, может быть сложнее.)
Цена:
Лучшая цена на 9-2-2014 составляет около 42,74 доллара США.
Mathway | Популярные задачи
Mathway | Популярные проблемыПопулярные задачи
Основы математики Предварительно Алгебра Алгебра тригонометрия тригонометрия и алгебра Исчисление Конечная математика Линейная алгебра ХимияMathway требует javascript и современного браузера.
Этот веб-сайт использует файлы cookie, чтобы обеспечить вам максимальное удобство работы с ним.
Убедитесь, что ваш пароль состоит не менее чем из 8 символов и содержит каждое из следующих значений:
- номер
- письмо
- специальный символ: @ $ #!% *? &
