Формула нахождения объема цилиндра онлайн
Цилиндром является геометрическое тело, состоящее из цилиндрической боковой поверхности и двух перпендикулярных ее оси плоскостей (оснований). При вращении прямоугольника вокруг любой из его сторон получается цилиндр. В переводе с греческого цилиндр означает каток, валик. Если в основании цилиндра находится круг — это круговой цилиндр. Объем цилиндра рассчитывается 2-мя способами. В 1-м случае объем равняется произведению пл. основания цилиндра на его высоту. Формула для расчета объема цилиндра:
R — радиус вращения;
h – высота.
Расчет объема цилиндра через радиус и высоту
Во втором случае объем цилиндра рассчитывается как произведение квадрата радиуса цилиндра на его высоту и постоянное число пи по формуле:
В данной формуле:
h – высота цилиндра;
S — площадь основания.
Расчет объема цилиндра через площадь основания
infofaq.ru
Объем цилиндра: формула, калькулятор — 24СМИ
Как отличить человека технической специальности от человека с гуманитарным складом ума? Спросите каждого, что такое цилиндр. Первый скажет, что это геометрическое тело, второй вспомнит мужской головной убор 19 века. Оба будут правы, да и шляпа получила такое название благодаря особенной форме, основой которой являлась та самая фигура из геометрии. Итак, каковы особенности цилиндра и как рассчитать его объем.
Расчет объема цилиндра
Слово «цилиндр» произошло от древнегреческого kylindros, означающего «валик». Математики дают несколько определений цилиндру:
- Цилиндр — геометрическое тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими ее под прямым углом.
- Цилиндр — это тело вращения, которое получается при вращении прямоугольника вокруг его стороны.
- Цилиндр — геометрическое тело, которое сформировано вращением прямоугольника на оси, совпадающей с одной из его сторон.
 Фигура цилиндр
Фигура цилиндрВсе эти определения верны. Также стоит отметить основные части цилиндра:
- Основания — плоские фигуры, образованные пересечением цилиндрической поверхности с двумя параллельными плоскостями.
- Боковая поверхность цилиндра — поверхность между плоскостями оснований.
Если в основании цилиндра лежит круг, то его называют круговым. Существуют и другие виды цилиндров, в зависимости от формы основания — эллиптический, гиперболический, параболический и т.д.
Также все цилиндры делятся на прямые и наклонные. У каждого цилиндра есть образующие — это отрезки, соединяющие соответствующие точки оснований. Если образующие перпендикулярны основаниям, то цилиндр называется прямым, а если образующие расположены под углом — цилиндр наклонный или косой.
 Рисунок цилиндра
Рисунок цилиндраЕсть и другие общие понятия для цилиндров:
- Основания цилиндра равны и лежат в параллельных плоскостях. У цилиндра образующие параллельны и равны.
- Поверхность цилиндра состоит из оснований и боковой поверхности. Боковая поверхность составлена из образующих.
- Радиусом цилиндра называется радиус его основания.
- Высотой цилиндра называется расстояние между плоскостями оснований.
- Осью цилиндра называется прямая, проходящая через центры оснований.
- Сечение цилиндра плоскостью, проходящей через ось цилиндра, называется осевым сечением.
- Плоскость, проходящая через образующую прямого цилиндра и перпендикулярная осевому сечению, проведенному через эту образующую, называется касательной плоскостью цилиндра.
Итак, как же вычислить объем цилиндра. Посчитать объем прямого кругового цилиндра можно на калькуляторе. Он равен произведению площади основания на высоту.
V = πR2h,
где V — объем цилиндра, R — радиус основания, h — высота цилиндра, а «пи» — константа, равная 3,14.
 Объем цилиндр
Объем цилиндрТаким же образом вычисляется объем прямого кругового цилиндра через диаметр окружности основания — d.
V = πhd2/4
Если цилиндр прямой, но не круговой, то формула вычисления объема представляет произведение длины образующей – n на площадь сечения цилиндра плоскостью, перпендикулярной образующей — S.
V = n * S
 Наклонный цилиндр
Наклонный цилиндрЕсли цилиндр наклонный, то в формуле участвует и синус угла наклона (альфа) образующей к основанию. В этом случае объем вычисляется по формуле:
V = S * n * sin α
Исчисляется объем цилиндра в кубических единицах.
Если стоит задача найти объем описанного вокруг сферы цилиндра, то расчеты будут такими:
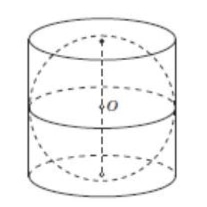 Цилиндр и сфера
Цилиндр и сфераРадиус цилиндра равен радиусу сферы — R. Высота цилиндра равна диаметру сферы. Диаметр есть удвоенный радиус — 2R. Таким образом объем прямого описанного цилиндра равен произведению площади основания πR2 («пи» умножить на радиус в квадрате) на высоту, т. е. 2R.
V = 2R * πR2
Приведя формулу к должному виду получим:
V = 2πR3
Если цилиндр вписан в прямоугольный параллелепипед, то, зная длину стороны его основания и высоту, можно найти объем.
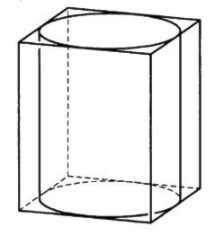 Цилиндр, вписанный в параллелепипед
Цилиндр, вписанный в параллелепипедВ этом случае радиус основания цилиндра равен половине длины стороны основания параллелепипеда — а. Высота цилиндра и параллелепипеда совпадают, обозначим h. Тогда объем вычисляется по формуле:
V = πh(a/2)2
Где применяется расчет объема цилиндра
Расчет объема цилиндра учащиеся проходят в средней школе. Во взрослой жизни эти знания применяют в своей работе инженеры и конструкторы различных машин и механизмов, потребительских товаров, а также архитекторы.
Из товаров народного потребления форму цилиндра имеют стаканы, кружки, бокалы, кастрюли, термосы и прочая посуда, а также некоторые вазы, банки и упаковки напитков либо средств бытовой химии. Объем таких цилиндрических предметов исчисляется в литрах.
 Стаканы имеют цилиндрическую форму
Стаканы имеют цилиндрическую формуРассчитывается объем цилиндра при производстве медицинских шприцов. От полученного объема зависит точное количество медикаментов, вводимое пациенту при инъекциях. Лекарства в жидкой форме, суспензии, растворы помещаются в стеклянные или пластиковые бутылочки цилиндрической формы, а на бирке указывается объем средства.
Распространены цилиндры и в технике: такой вид имеют валы и их отдельные составные части, используемые в двигателях внутреннего сгорания. К тому же, расчет объема цилиндра – задача, которую приходится решать конструкторам при проектировании современных бензиновых и дизельных силовых агрегатов, ведь от этого параметра зависят характеристики, в первую очередь, мощность. Двигатели внутреннего сгорания снабжаются поршнями, которые также имеют цилиндрическую форму.
 Расчет цилиндрического вала
Расчет цилиндрического валаАрхитекторам приходится рассчитывать объем цилиндра при проектировании зданий, снабженных колоннами. Правда, эти архитектурные элементы в классическом варианте (вместе с базой и капителем) встречаются редко, но упрощенные разновидности, состоящие из одного ствола (который и представляет собой цилиндр) используются часто.
Чрезвычайно распространенные детали, которые присутствуют в конструкциях технических устройств — роликовые подшипники. Как нетрудно догадаться по названию, главный компонент — прочные и износостойкие металлические цилиндрические ролики. Благодаря такой геометрии, эти детали обладают большой несущей способностью и способны выдерживать нагрузки. Роликовые подшипники — высокоточные детали, и поэтому при их создании правильный расчет объема цилиндра (ролика) играет немаловажную роль.
24smi.org
Формула объема цилиндра
Прежде чем говорить о формуле объема цилиндра разберемся с основополагающими моментами.
Цилиндр сам по себе является геометрической фигурой, которую ограничивают две находящиеся друг против друга области и пересекают цилиндрическую область. Данную цилиндрическую область можно получить путем направленных вперед движений образующих прямые линии так, чтобы образующая точка двигалась продольно направляющей кривой. Боковая область — та область фигуры которая ограничивается цилиндрической поверхностью. На основание приходиться другая часть, тем самым формы границы и направляющей совпадают.
Чаще всего это тело представляют в виде кругового прямого цилиндра, в котором окружность , прямая дающая направление и две основные области относительно образующей будут перпендикулярны. В данном теле будет ось симметрии.
Есть много типов цилиндров, которые различаются по форме основания, разрезу или наклону образующей. Бывают косые и наклонные, эллиптические, параболические и гиперболические.
Для того чтобы узнать объем цилиндра, необходимо знать высоту данного цилиндра или другими словами расстояние от одного основания до другого.
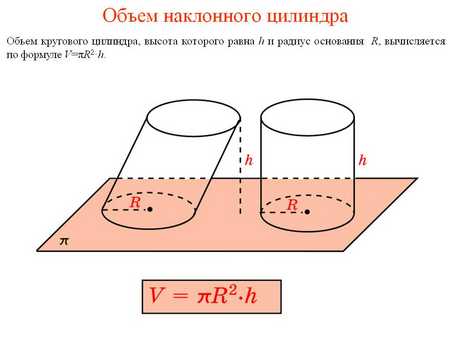
Объем цилиндра конечно же находиться при помощи формул, о которых и пойдет речь дальше. Для этого существуют две формулы: Формула объема цилиндра №1.
V = Sо*h
в которой V — это объем, Sо — площадь основания, h — это высота тела.Формула объема цилиндра №2.
V = ? * R2 * h
в которой V — это объем, R — это радиус, h- это высота.
С помощью данной формулы, объем находится при помощи радиуса, числа ? и высоты. Данная формула применима только для кругового прямого цилиндра.
При использовании данных формул можно вычислить объем любой емкости, единственная поправка — это то что значения будут в метрах. А результат в кубических метрах.
Рассчитаем для наглядности
Дан цилиндр размер которого 0,5м. высота и диаметр 0,3м
Воспользуемся в расчетах формулой №2, в результате чего получаем:
V = 3,14 * 0,15 * 0,15 * 0,5 = 0,035325 кб/м
0,035325 кб/м = 35,325 литров.
Как видите в этом нет ничего сложного. Интересных вам вычислений!
Если вы ищите Полиуретан, пенополиуретан, оборудование для ППУ (http://puinfo.ru/), перейдите по ссылке на информационный сайт, в котором Вы найдете много нужной и интересной информации.
Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:
reshit.ru
Объём части цилиндра
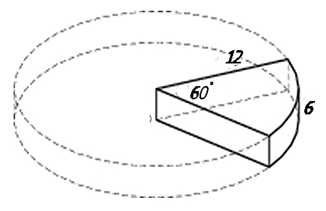
Объём части цилиндра. Здравствуйте, друзья! Для вас ещё одна статья с задачами про объём цилиндра. На момент написания этих строк данная группа задач исключена из открытого банка заданий ЕГЭ по математике, но они всегда туда могут «вернуться», и разумеется, их присутствие в составе заданий на самом экзамене вполне возможно. Это задачи на вычисление объёма части цилиндра. Задачки простенькие, решаются в 1-2 действия. Посмотрите, объём каких тел требуется найти:

*В условии задаются радиус основания, высота и угол сектора.
Если вы ещё не изучили статью, где речь шла об объёме части конуса, то посмотрите обязательно, здесь принцип решения тот же. Повторять его не буду. Напомню только формулу объёма цилиндра:

*Ещё можете посмотреть статью, в которой мы уже разобрали несколько заданий, связанных с объёмом цилиндра.
Также есть следующие формы тел, объём которых требуется найти, вот эскизы:

Процесс решения прост!
Рисунок Б. Тело состоит из цилиндра, на который как бы сверху поставили ещё полцилиндра. То есть чтобы найти объём такого тела, необходимо вычислить объёмы двух этих отдельных тел (цилиндра и полуцилиндра) и суммировать их.
Рисунок В. Тело представляет собой цилиндр, из которого как бы «вырезан» другой цилиндр. Для вычисления объёма тела достаточно найти объём «полного» цилиндра и затем из него вычесть объём пустого пространства (он тоже имеет форму цилиндра и объём вычисляется без труда). Рассмотрим задачи:
25739. Найдите объем V части цилиндра, изображённой на рисунке. В ответе укажите V/Пи.

Вычислим объём цилиндра:
Часть цилиндра построенного на секторе круга с углом в 900 составляет четвёртую часть от полного объёма:
Результат делим на Пи и записываем ответ.
Ответ: 9
25743. Найдите объем V части цилиндра, изображенной на рисунке. В ответе укажите V/Пи.

Вычислим объём цилиндра:
Часть цилиндра построенного на секторе круга с углом в 2700 (из трёхсот шестидесяти мы вычли девяносто) составляет три четвёртых от полного объёма:
Результат делим на Пи и записываем ответ.
Ответ: 15
27199. Найдите объем V части цилиндра, изображенной на рисунке. В ответе укажите V/Пи.

Вычислим объём цилиндра:
Часть цилиндра построенного на секторе круга с углом в 3000 (из трёхсот шестидесяти мы вычли шестьдесят) составляет:
от полного объёма. Таким образом
Результат делим на Пи и записываем ответ.
Ответ: 937,5
25755. Найдите объем V части цилиндра, изображенной на рисунке. В ответе укажите V/Пи.

Вычислим объём цилиндра:
Часть цилиндра построенного на секторе круга с углом в 600 составляет:
от полного объёма. Таким образом
Результат делим на Пи и записываем ответ.
Ответ: 112,5
25779. Найдите объем V части цилиндра, изображенной на рисунке. В ответе укажите V/Пи.

Вычисляем объём цилиндра с радиусом равным 4 и высотой равной 3:
Вычисляем объём половины цилиндра с радиусом 4 и высотой равной 4 – 3 = 1
Объём тела будет равен:
Результат делим на Пи и записываем ответ.
Ответ: 56
25781. Найдите объем V части цилиндра, изображенной на рисунке. В ответе укажите V/Пи.

Вычисляем объём цилиндра с радиусом равным 4 и высотой 5:
Вычисляем объём «вырезанного» цилиндра (пустой части) с радиусом 2 и высотой 5:
Объём тела будет равен:
Результат делим на Пи и записываем ответ.
Ответ: 60
27196. Найдите объем V части цилиндра, изображенной на рисунке. В ответе укажите V/Пи.

Посмотреть решение
27197. Найдите объем V части цилиндра, изображенной на рисунке. В ответе укажите V/Пи.
Посмотреть решение
27198. Найдите объем V части цилиндра, изображенной на рисунке. В ответе укажите V/Пи.
Посмотреть решение
27200. Найдите объем V части цилиндра, изображенной на рисунке. В ответе укажите V/Пи.

Посмотреть решение
27201. Найдите объем V части цилиндра, изображенной на рисунке. В ответе укажите V/Пи.

Посмотреть решение
На этом всё! Успеха вам!
С уважением, Александр.
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
matematikalegko.ru
Вычисление объема цилиндра
Цилиндр это геометрическое тело, которое сформировано вращением прямоугольника на оси, совпадающей с одним из его сторон. Слово «цилиндр» происходит от греческого слова «kylindros».
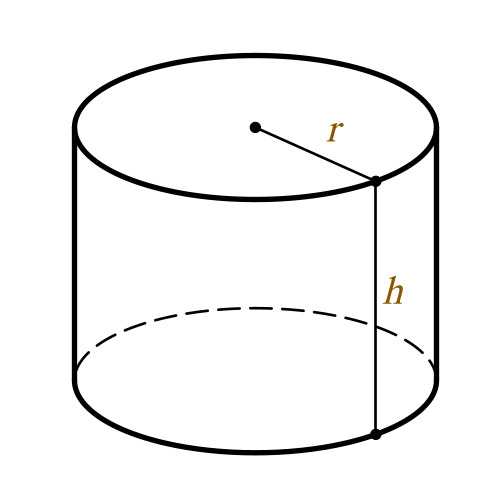
Вычисление объема цилиндра
Вычисление объема цилиндра
производится по следующей формуле:V = π r2h
V – объем цилиндра
h – высота цилиндра
r – радиус основания
π – 3.14
Как рассчитать объем цилиндра, все мы проходили в средней школе, и этими знаниями наиболее активно пользуются в своей работе конструкторы различных машин и механизмов, потребительских товаров, а также архитекторы.
Инженерам приходится производить расчет объема цилиндра в тех случаях, когда они занимаются проектированием заданий, снабженных колоннами. Правда, в последнее время эти архитектурные элементы в их, так сказать, «классическом» варианте (то есть вместе с базой и капителем) встречаются достаточно редко, но их «упрощенные» разновидности, состоящие из одного ствола (который, собственно говоря, и представляет собой цилиндр
Расчет объема цилиндра осуществляется тогда, когда ведётся разработка разнообразных емкостей соответствующей формы. В качестве наглядного примера таковых можно привести, скажем, медицинские шприцы, а также колбы термосов. Следует заметить, что в первом случае такой параметр, как объем, имеет очень важное значение, поскольку от него зависит точное количество медикаментов, вводимого пациенту при инъекциях.
В технике цилиндры распространены чрезвычайно широко: достаточно сказать, что их форму имеют практически все валы и их отдельные составные части, используемые, скажем, в двигателях внутреннего сгорания. К тому же, расчет объема цилиндра – одна из важнейших задач, которую приходится решать конструкторами при проектировании современных бензиновых и дизельных силовых агрегатов, ведь от этого параметра зависит множество их характеристик, и в первую очередь такая важнейшая, как мощность. Почти все типы ДВС снабжаются поршнями, которые также имеют цилиндрическую форму.
Чрезвычайно распространенными деталями, которые присутствуют в конструкции многих сложных технических устройств, являются роликовые подшипники. Как нетрудно догадаться по самому их названию, одними из основных их компонентов являются прочные и износостойкие металлические ролики, имеющие цилиндрическую форму. Именно благодаря такой геометрии, эти детали имеют достаточно большую несущую способность и в большинстве случаев способны выдерживать весьма значительные нагрузки, чем их шариковые аналоги. Роликовые подшипники являются высокоточными деталями, и поэтому при их разработке и проектировании правильный
simple-math.ru
Калькулятор для расчета рабочего объема цилиндров двигателя автомобиля
Рабочий объем цилиндра представляет собой объем находящийся между крайними позициями движения поршня.
Формула расчета цилиндра известна еще со школьной программы – объем равен произведению площади основания на высоту. И для того чтобы вычислить объем двигателя автомобиля либо мотоцикла также нужно воспользоваться этими множителями. Рабочий объём любого цилиндра двигателя рассчитывается так:
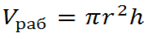
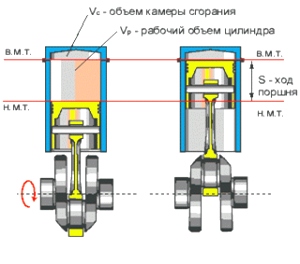
где,
h — длина хода поршня мм в цилиндре от ВМТ до НМТ (Верхняя и Нижняя мёртвая точки)
r — радиус поршня мм
п — 3,14 не именное число.
Как узнать объем двигателя
Для расчета рабочего объема двигателя вам будет нужно посчитать объем одного цилиндра и затем умножить на их количество у ДВС. И того получается:
Vдвиг = число Пи умножено на квадрат радиуса (диаметр поршня) умноженное на высоту хода и умноженное на кол-во цилиндров.
Поскольку, как правило, параметры поршня везде указываются в миллиметрах, а объем двигателя измеряется в см. куб., то для перевода единиц измерения, результат придется разделить еще на 1000.
Заметьте, что полный объем и рабочий, отличаются, так как поршень имеет выпуклости и выточки под клапана и в него также входить объем камеры сгорания. Поэтому не стоит путать эти два понятия. И чтобы рассчитать реальный (полный) объем цилиндра, нужно суммировать объем камеры и рабочий объем.
Определить объем двигателя можно обычным калькулятором, зная параметры цилиндра и поршня, но посчитать рабочий объем в см³ нашим, в режиме онлайн, будет намного проще и быстрее, тем более, если вам расчеты нужны, дабы узнать мощность двигателя, поскольку эти показатели напрямую зависят друг от друга.
Объем двигателя внутреннего сгорания очень часто также могут называть литражом, поскольку измеряется как в кубических сантиметрах (более точное значение), так и литрах (округленное), 1000 см³ равняется 1 л.
Расчет объема ДВС калькулятором
Чтобы посчитать объем интересующего вас двигателя нужно внести 3 цифры в соответствующие поля, — результат появится автоматически. Все три значения можно посмотреть в паспортных данных автомобиля или тех. характеристиках конкретной детали либо же определить, какой объем поршневой поможет штангенциркуль.
Таким образом, если к примеру у вас получилось что объем равен 1598 см³, то в литрах он будет обозначен как 1,6 л, а если вышло число 2429 см³, то 2,4 литра.
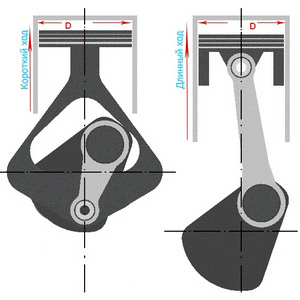
Длинноходный и короткоходный поршень
Также замете, что при одинаковом количестве цилиндров и рабочем объеме двигатели могут иметь разный диаметр цилиндров, ход поршней и мощность таких моторов так же будет разной. Движок с короткоходными поршнями очень прожорлив и имеет малый КПД, но достигает большой мощности на высоких оборотах. А длинноходные стоят там, где нужна тяга и экономичность.
Следовательно, на вопрос «как узнать объем двигателя по лошадиным силам» можно дать твердый ответ – никак. Ведь лошадиные силы хоть и имеют связь с объемом двигателя, но вычислить его по ним не получится, поскольку формула их взаимоотношения еще включает много разных показателей. Так что определить кубические сантиметры двигателя можно исключительно по параметрам поршневой.
Зачем нужно проверять объем двигателя
Чаще всего узнают объем двигателя когда хотят увеличить степень сжатия, то есть если хотят расточить цилиндры с целью тюнинга. Поскольку чем больше степень сжатия, тем больше будет давление на поршень при сгорании смеси, а следовательно, двигатель будет более мощным. Технология изменения объема в большую сторону, дабы нарастить степень сжатия, очень выгодна — ведь порция топливной смеси такая же, а полезной работы больше. Но всему есть свой предел и чрезмерное её увеличение грозит самовоспламенением, вследствие чего происходит детонация, которая не только уменьшает мощность, но и грозит разрушением мотора.
etlib.ru
Объема цилиндра: теория, расчет, формула
Дата публикации
Применение геометрических фигур активно осуществляется абсолютно во всех отраслях народного хозяйства, промышленности и так далее. Именно поэтому данный предмет так детально изучается в школьной программе. Но далеко не все из нас хорошо овладели этой интересной наукой, поэтому вашему вниманию предлагается вспомнить о том, что такое цилиндр и как рассчитать его объем? То есть прежде чем выяснить, что такое объем цилиндра, нужно понимать, что это за фигура такая. Цилиндр – это объемная фигура, состоящая из следующих элементов: двух параллельных одинаковых окружностей (площади кругов равны) и образующих цилиндра, соединяющих эти окружности. Но есть одно условие – образующие цилиндра и ось оного должны быть перпендикулярными к обеим окружностям, то есть одна окружность является в буквальном смысле слова зеркальным отображением другой.
Нами был описан самый простой пример – прямой круговой цилиндр. Но в жизни мы можем встретить не только таковые, ведь их разнообразие настолько велико, что описать их все практически невозможно. Но не будем углубляться, а рассмотрим самый обычный простой цилиндр. Итак, теперь, когда мы знаем, что такое цилиндр, можно вычислить его объем. А что такое объем? Другими словами можно провести небольшое сравнение – это своеобразная вместимость сосуда. Из этого определения понятно, что такой характеристикой не могут обладать идеальные плоские фигуры, а лишь трехмерные, коим и является цилиндр.
Теперь перейдем немного к цифрам и вычислениям. Чтобы узнать, чему равен объем цилиндра, необходимо воспользоваться хорошо всем известной формулой, по которой он вычисляется: V= πr² h
Теперь рассмотрим все величины данной формулы:
V – объем цилиндра;
π – число Пи;
r – радиус окружности;
h – высота цилиндра.
С объемом цилиндра мы разобрались, радиус окружности понятен, а что такое число Пи и высота цилиндра?
Число Пи – это постоянная, показывающая отношение длины окружности к длине ее диаметра. Принято считать, что численно оно равно 3,14. Хотя на самом деле это число после целой части имеет 10 триллионов знаков (по вычислениям за 2011 год)! Но для удобства мы будем пользоваться общепринятым размером, так как нам вовсе не нужны высокоточные расчеты. Хотя, например, в космонавтике используют максимально возможное количество символов после запятой!
Высота цилиндра – это перпендикулярное расстояние между двумя его плоскостями, в нашем случае – окружностями. Высотой является образующая цилиндра. Причем самое интересное, что данная величина абсолютно одинакова по всей длине сопряженных окружностей цилиндра.
Теперь, когда известны все переменные в уравнении, появляется вопрос о том, а почему именно так? Объясним это на примере параллелепипеда. Всем известно, что его объем равен произведению трех его измерений: длины, ширины и высоты. А площадь основания данной фигуры равна произведению длины на ширину, т.е. получается, что объем равен произведению площади основания на высоту. А теперь вернемся к нашему цилиндру, все аналогично: V=Sh, где S – площадь основания цилиндра, так как в основании у нас окружность, а площадь окружности равна: S=πr².
Теперь мы с вами знаем, как вычислить объем цилиндра, но что это может нам дать? Каково практическое применение приобретенным знаниям? В быту эти знания сводятся к минимуму, например, можно рассчитать, какой объем воды наполнит тот или иной цилиндрический объект, сколько поместится сыпучих материалов в той или иной цилиндрической таре. Хотя нам можно обойтись и без этого. А вот в промышленности без таких знаний просто не обойтись. Например, при производстве труб различного назначения можно рассчитать, какой объем жидкости или газа они будут пропускать за единицу времени и т.д.
Опубликовано в Образование и наука
Добавить комментарий
www.vigivanie.com
