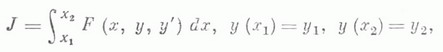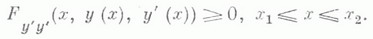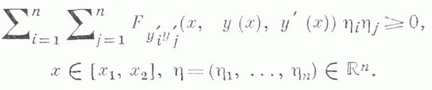Полином Лежандра — это… Что такое Полином Лежандра?
- Полином Лежандра
Многочлены Лежандра — определённая ортогональная система многочленов, на отрезке [ − 1,1] по мере Лебега. Многочлены Лежандра могут быть получены из многочленов
 ортогонализацией Грама ― Шмидта.
ортогонализацией Грама ― Шмидта.Названы по имени французского математика Адриен Мари Лежандра.
Определение
Многочлены Лежандра определяются по формуле (называемой формулой Родрига)
часто записываемой в виде
Они также могут быть вычислены по рекуррентной формуле
Присоединённые многочлены Лежандра определяются по формуле
которую также можно представить в виде
При m = 0 функция
 совпадает с Pn.
совпадает с Pn.Примеры
Первые четыре многочлена Лежандра равны:
- P0(x) = 1
- P1(x) = x


Свойства
- При каждом m > 0 система присоединённых функций Лежандра
 полна в L2( − 1,1).
полна в L2( − 1,1). - В зависимости от m и n присоединённые многочлены Лежандра могут быть как чётными, так и нечётными функциями:
Функции Лежандра
Многочлены Лежандра (вместе с присоединёнными функциями Лежандра Pn,m(x)) естественно возникают в теории потенциала. Сферические функции — это функции (в сферических координатах r,θ,φ) вида
 и
и  ,
,
где
 — присоединённые многочлены Лежандра. Сферические функции удовлетворяют уравнению Лапласа всюду в
— присоединённые многочлены Лежандра. Сферические функции удовлетворяют уравнению Лапласа всюду в  (при n < 0 — всюду, кроме нуля) и служат ортогональным базисом для функций.
(при n < 0 — всюду, кроме нуля) и служат ортогональным базисом для функций.Литература
- В.С. Владимиров, В.В. Жаринов. Уравнения математической физики. — М.: Физматлит, 2004. — ISBN 5-9221-0310-5
Wikimedia Foundation. 2010.
- Полином Лагранжа
- Полином Чебышева
Смотреть что такое «Полином Лежандра» в других словарях:
полином Лежандра — Ležandro daugianaris statusas T sritis fizika atitikmenys: angl. Legendre polynomial vok. Legendresches Polynom, n rus. многочлен Лежандра, m; полином Лежандра, m pranc. polynôme de Legendre, m … Fizikos terminų žodynas
присоединённый полином Лежандра — prijungtinis Ležandro daugianaris statusas T sritis fizika atitikmenys: angl. associated Legendre polynomial vok. Legendresches zugeordnetes Polynom, n; zugeordnetes Legendresches Polynom, n rus. присоединённый многочлен Лежандра, m;… … Fizikos terminų žodynas
Многочлены Лежандра — Многочлен Лежандра многочлен, который в наименьшей степени отклоняется от нуля в смысле среднего квадратического. Образует ортогональную систему многочленов, на отрезке по мере Лебега. Многочлены Лежандра могут быть получены из многочленов… … Википедия
многочлен Лежандра — Ležandro daugianaris statusas T sritis fizika atitikmenys: angl. Legendre polynomial vok. Legendresches Polynom, n rus. многочлен Лежандра, m; полином Лежандра, m pranc. polynôme de Legendre, m … Fizikos terminų žodynas
присоединённый многочлен Лежандра — prijungtinis Ležandro daugianaris statusas T sritis fizika atitikmenys: angl. associated Legendre polynomial vok. Legendresches zugeordnetes Polynom, n; zugeordnetes Legendresches Polynom, n rus. присоединённый многочлен Лежандра, m;… … Fizikos terminų žodynas
РАССЕЯНИЕ МИКРОЧАСТИЦ — процесс столкновения ч ц, в результате к рого меняются импульсы ч ц (у п р у г о е р а с с е я н и е) или наряду с изменением импульсов меняются также внутр. состояния ч ц (к в а з и у п р у г и е п р о ц е с с ы) либо образуются др. ч цы (н е у… … Физическая энциклопедия
СФЕРИЧЕСКИЕ ФУНКЦИИ — (сферические гармоники) спец. функции, возникающие, напр., при отыскании ограниченных решений ур ния Лапласа Du = 0 в сферич. координатах (r, q, j) методом разделения переменных. Введены в кон. 18 в. А. Лежандром и П. Лапласом. Полагая и = и(r,q … Физическая энциклопедия
Юпитер — У этого термина существуют и другие значения, см. Юпитер (значения). Юпитер … Википедия
Гипергеометрическая функция — (функция Гаусса) определяется внутри круга как сумма гипергеометрического ряда а при как её аналитическое продолжение. Она является решением линейного обыкновенного дифференциального уравнения (ОДУ) второго порядка называемого… … Википедия
Legendre polynomial — Ležandro daugianaris statusas T sritis fizika atitikmenys: angl. Legendre polynomial vok. Legendresches Polynom, n rus. многочлен Лежандра, m; полином Лежандра, m pranc. polynôme de Legendre, m … Fizikos terminų žodynas
Многочлены Лежандра — это… Что такое Многочлены Лежандра?
Многочлен Лежа́ндра — многочлен, который в наименьшей степени отклоняется от нуля в смысле среднего квадратического. Образует ортогональную систему многочленов, на отрезке по мере Лебега. Многочлены Лежандра могут быть получены из многочленов ортогонализацией Грама ― Шмидта.
Названы по имени французского математика Адриен Мари Лежандра.
Определение
Полиномы Лежандра и присоединённые функции Лежандра первого и второго рода
Рассмотрим дифференциальное уравнение вида
| (УравнПолЛеж) |
где — комплексная переменная. Решения этого уравнения при целых имеют вид многочленов, называемых многочленами Лежандра. Полином Лежандра степени можно представить через формулу Родрига в виде[1]
Часто вместо записывают косинус полярного угла:
Уравнение (УравнПолЛеж) можно получить из частного случая гипергеометрического уравнения, называемого уравнением Лежандра
| (УравнЛеж) |
где , — произвольные комплексные постоянные. Интерес представляют его решения, являющиеся однозначными и регулярными при (в частности, при действительных ) или когда действительная часть числа больше единицы. Его решения называют присоединёнными функциями Лежандра или шаровыми функциями. Подстановка вида в (УравнЛеж) даёт уравнение Гаусса, решение которого в области принимает вид
где F — гипергеометрическая функция. Подстановка в (УравнЛеж) приводит к решению вида
определённым на . Функции и называют функциями Лежандра первого и второго рода.[2]
Справедливы соотношения[3]
и
Формулы с
- Многочлены Лежандра также определяются по следующим формулам:
- , если ;
- , если .
Рекуррентная формула
Формулы с разложениями
- Многочлены Лежандра также определяются следующими разложениями:
для ± :
и для ± :
Следовательно,
Присоединённые многочлены Лежандра
- Присоединённые многочлены Лежандра определяются по формуле:
которую также можно представить в виде:
При функция совпадает с .
Матрица функции многочлена Лежандра
Эта матрица является верхнетреугольной. Её определитель равен нулю, а собственные значения равны , где .
Примеры
Первые 6 многочленов Лежандра. Первые многочлены Лежандра равны:Поскольку , то
Свойства
- Что также можно записать как:
где — символ Кронекера.
- Для , норма равна:
- Нормированная функция многочленов Лежандра связана с нормой следующим соотношением:
- — четная функция;
- — нечетная функция.
Ряды многочленов Лежандра
Разложение липшицевой функции в ряд многочленов Лежандра
Липшицевая функция является функцией со свойством:
- , где .
Эта функция разлагается в ряд многочленов Лежандра.
Пусть — пространство непрерывных отображений на отрезке , и .
Пусть
тогда удовлетворяет следующему условию:
Пусть и удовлетворяет следующим условиям:
- , где
Липшецевую функцию можно записать следующим образом:
Разложение голоморфной функции
Всякая функция f, голоморфная внутри эллипса с фокусами −1 и +1, может быть представлена в виде ряда:
Теорема сложения
Для величин, удовлетворяющих условиям , , , — действительное число, можно записать теорему сложения для полиномов Лежандра первого рода:[4]
или, в альтернативной форме через гамма-функцию:
Для полиномов Лежандра второго рода теорема сложения выглядит как[5]
при условиях , , ,
Функции Лежандра
Многочлены Лежандра (вместе с присоединёнными функциями Лежандра ) естественно возникают в теории потенциала.
Шаровые функции — это функции (в сферических координатах ) вида (с точностью до константы)
- и
где — присоединённые многочлены Лежандра;
а точнее вида , где — сферические функции.
Шаровые функции удовлетворяют уравнению Лапласа всюду в .Примечания
- ↑ Градштейн, Рыжик, 1963, с. 1039
- ↑ Бейтмен, Эрдейи, Т. 1, 1973, с. 126—127
- ↑ Бейтмен, Эрдейи, Т. 1, 1973, с. 140
- ↑ Градштейн, Рыжик, 1963, с. 1027
- ↑ Градштейн, Рыжик, 1963, с. 1028
Литература
- Бейтмен Г., Эрдейи А. Высшие трансцендентные функции = Higher Transcendental Functions / Пер. Н. Я. Виленкина. — Изд. 2-е,. — М.: Наука, 1973. — Т. 1. — 296 с. — 14 000 экз.
- Владимиров В. С., Жаринов В. В. Уравнения математической физики. — М.: Физматлит, 2004. — ISBN 5-9221-0310-5
- Градштейн И. С., Рыжик И. М. Таблицы интегралов, сумм, рядов и произведений. — Изд. 4-е, перераб. — М.: Государственное издательство физико-математической литературы, 1963. — 19 000 экз.
- Кампе де Ферье Ж., Кемпбелл Р., Петьо Г., Фогель Т. Функции математической физики. — М.: Физматлит, 1963.
- Никольский С. М. Квадратурные формулы. — М.: Наука, 1988.
Присоединённые многочлены Лежандра — это… Что такое Присоединённые многочлены Лежандра?
- Присоединённые многочлены Лежандра
Многочлены Лежандра — определённая ортогональная система многочленов, на отрезке [ − 1,1] по мере Лебега. Многочлены Лежандра могут быть получены из многочленов
 ортогонализацией Грама ― Шмидта.
ортогонализацией Грама ― Шмидта.Названы по имени французского математика Адриен Мари Лежандра.
Определение
Многочлены Лежандра определяются по формуле (называемой формулой Родрига)
часто записываемой в виде
Они также могут быть вычислены по рекуррентной формуле
Присоединённые многочлены Лежандра определяются по формуле
которую также можно представить в виде
При m = 0 функция
 совпадает с Pn.
совпадает с Pn.Примеры
Первые четыре многочлена Лежандра равны:
- P0(x) = 1
- P1(x) = x


Свойства
- При каждом m > 0 система присоединённых функций Лежандра
 полна в L2( − 1,1).
полна в L2( − 1,1). - В зависимости от m и n присоединённые многочлены Лежандра могут быть как чётными, так и нечётными функциями:
Функции Лежандра
Многочлены Лежандра (вместе с присоединёнными функциями Лежандра Pn,m(x)) естественно возникают в теории потенциала. Сферические функции — это функции (в сферических координатах r,θ,φ) вида
 и
и  ,
,
где
 — присоединённые многочлены Лежандра. Сферические функции удовлетворяют уравнению Лапласа всюду в
— присоединённые многочлены Лежандра. Сферические функции удовлетворяют уравнению Лапласа всюду в  (при n < 0 — всюду, кроме нуля) и служат ортогональным базисом для функций.
(при n < 0 — всюду, кроме нуля) и служат ортогональным базисом для функций.Литература
- В.С. Владимиров, В.В. Жаринов. Уравнения математической физики. — М.: Физматлит, 2004. — ISBN 5-9221-0310-5
Wikimedia Foundation. 2010.
- Присоединённое представление лиевой алгебры
- Присосконоги
Смотреть что такое «Присоединённые многочлены Лежандра» в других словарях:
Многочлены Лежандра — Многочлен Лежандра многочлен, который в наименьшей степени отклоняется от нуля в смысле среднего квадратического. Образует ортогональную систему многочленов, на отрезке по мере Лебега. Многочлены Лежандра могут быть получены из многочленов… … Википедия
Многочлен Лежандра — Многочлены Лежандра определённая ортогональная система многочленов, на отрезке [ − 1,1] по мере Лебега. Многочлены Лежандра могут быть получены из многочленов ортогонализацией Грама ― Шмидта. Названы по имени французского математика Адриен Мари… … Википедия
Полином Лежандра — Многочлены Лежандра определённая ортогональная система многочленов, на отрезке [ − 1,1] по мере Лебега. Многочлены Лежандра могут быть получены из многочленов ортогонализацией Грама ― Шмидта. Названы по имени французского математика Адриен Мари… … Википедия
Полиномы Лежандра — Многочлены Лежандра определённая ортогональная система многочленов, на отрезке [ − 1,1] по мере Лебега. Многочлены Лежандра могут быть получены из многочленов ортогонализацией Грама ― Шмидта. Названы по имени французского математика Адриен Мари… … Википедия
Функция Лежандра — Многочлены Лежандра определённая ортогональная система многочленов, на отрезке [ − 1,1] по мере Лебега. Многочлены Лежандра могут быть получены из многочленов ортогонализацией Грама ― Шмидта. Названы по имени французского математика Адриен Мари… … Википедия
C++ Technical Report 1 — (TR1) является общим названием для стандарта ISO / IEC TR 19768, библиотеки расширений C++ это документ с предложением дополнений в стандарт библиотеки С++. Дополнения включают регулярные выражения, умные указатели, хэш таблицы, и… … Википедия
Сферические функции — представляют собой угловую часть семейства ортогональных решений уравнения Лапласа, записанную в сферических координатах. Они широко используются для изучения физических явлений в пространственных областях, ограниченных сферическими поверхностями … Википедия
Функция Лежандра — это… Что такое Функция Лежандра?
- Функция Лежандра
Многочлены Лежандра — определённая ортогональная система многочленов, на отрезке [ − 1,1] по мере Лебега. Многочлены Лежандра могут быть получены из многочленов
 ортогонализацией Грама ― Шмидта.
ортогонализацией Грама ― Шмидта.Названы по имени французского математика Адриен Мари Лежандра.
Определение
Многочлены Лежандра определяются по формуле (называемой формулой Родрига)
часто записываемой в виде
Они также могут быть вычислены по рекуррентной формуле
Присоединённые многочлены Лежандра определяются по формуле
которую также можно представить в виде
При m = 0 функция
 совпадает с Pn.
совпадает с Pn.Примеры
Первые четыре многочлена Лежандра равны:
- P0(x) = 1
- P1(x) = x


Свойства
- При каждом m > 0 система присоединённых функций Лежандра
 полна в L2( − 1,1).
полна в L2( − 1,1). - В зависимости от m и n присоединённые многочлены Лежандра могут быть как чётными, так и нечётными функциями:
Функции Лежандра
Многочлены Лежандра (вместе с присоединёнными функциями Лежандра Pn,m(x)) естественно возникают в теории потенциала. Сферические функции — это функции (в сферических координатах r,θ,φ) вида
 и
и  ,
,
где
 — присоединённые многочлены Лежандра. Сферические функции удовлетворяют уравнению Лапласа всюду в
— присоединённые многочлены Лежандра. Сферические функции удовлетворяют уравнению Лапласа всюду в  (при n < 0 — всюду, кроме нуля) и служат ортогональным базисом для функций.
(при n < 0 — всюду, кроме нуля) и служат ортогональным базисом для функций.Литература
- В.С. Владимиров, В.В. Жаринов. Уравнения математической физики. — М.: Физматлит, 2004. — ISBN 5-9221-0310-5
Wikimedia Foundation. 2010.
- Функция Дирака
- Функция Мебиуса
Смотреть что такое «Функция Лежандра» в других словарях:
Хи-функция Лежандра — это специальная функция, названная по имени французского математика Адриен Мари Лежандра. Хи функция Лежандра определяется рядом Тейлора также являющимся рядом Дирихле: Таким образом Хи функция Лежандра тривиально выражается через полилогарифм:… … Википедия
ЛЕЖАНДРА ПРЕОБРАЗОВАНИЕ — 1) Преобразование математич. анализа, осуществляющее двойственность между объектами в дуальных пространствах (наряду с проективной двойственностью в аналитич. еометрии и полярной двойственностью в выпуклой геометрии). Пусть гладкая функция,… … Математическая энциклопедия
Лежандра символ — Символ Лежандра функция, используемая в теории чисел. Введён французским математиком А. М. Лежандром. Символ Лежандра является частным случаем символа Якоби, который в свою очередь является частным случаем символа Кронекера Якоби. Определение… … Википедия
ЛЕЖАНДРА МНОГОЧЛЕНЫ — сферические многочлены, многочлены, ортогональные на сегменте [ 1,1] с единичным весом Стандартизованные Л. м. определяются Родрига формулой и имеют представление Наиболее употребительны формулы Л. м. можно определить как коэффициенты разложения… … Математическая энциклопедия
Функция Эйлера — Не следует путать с функцией распределения простых чисел. Первая тысяча значений Функция Эйлера φ(n) мультипликативная … Википедия
Функция Гамильтона — У этого термина существуют и другие значения, см. Гамильтониан. Функция Гамильтона, или Гамильтониан функция, зависящая от обобщённых координат, импульсов и, возможно, времени, описывающая динамику механической системы в гамильтоновой… … Википедия
Функция гамильтона — Гамильтониан (функция Гамильтона) функция, зависящая от обобщённых координат, импульсов и, возможно, времени, описывающая динамику механической системы в гамильтоновой формулировке классической механики, а также оператор в квантовой механике и… … Википедия
Лежандра многочлены — сферические многочлены, специальная система многочленов последовательно возрастающих степеней. Впервые рассматривалась А. Лежандром и П. Лапласом (в 1782 85) независимо друг от друга. Для n = 0,1,2,… Л. м. Р (х) могут быть определены… … Большая советская энциклопедия
ЛЕЖАНДРА СИМВОЛ — арифметическая функция чисел р к а, определенная для простых нечетных ри целых а, не делящихся на р. Л. с. обозначается Л. с. если сравнение разрешимо; в противном же случае Иногда Л. с. доопределяют и для чисел а, делящихся на р, полагая, что в… … Математическая энциклопедия
Гипергеометрическая функция — (функция Гаусса) определяется внутри круга как сумма гипергеометрического ряда а при как её аналитическое продолжение. Она является решением линейного обыкновенного дифференциального уравнения (ОДУ) второго порядка называемого… … Википедия
Присоединенные функции Лежандра — Студопедия.Нет
Глава 1. Сферические функции
Сферические функции были введены в связи с изучением решений уравнения Лапласа, и в частности с теорией потенциала. В §1 мы рассматриваем полиномы Лежандра, которые используются затем для построения шаровых и сферических функций в §2. Сферические функции являются весьма мощным аппаратом для решения многих задач математической физики.
Полиномы Лежандра
Производящая функция и полиномы Лежандра
Полиномы Лежандра тесно связаны с фундаментальным решением уравнения Лапласа 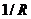 , где R – расстояние от точки М до фиксированной точки М0. Пусть r и r0 – радиусы векторы точек М и М0, а
, где R – расстояние от точки М до фиксированной точки М0. Пусть r и r0 – радиусы векторы точек М и М0, а 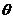 — угол между ними. Очевидно можно записать
— угол между ними. Очевидно можно записать
 (1)
(1)

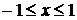
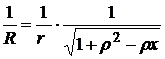

при 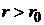

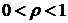

при 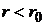

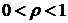
 ,
, 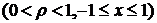
производящая функция полиномов Лежандра.
Разложим функцию  в ряд по степеням
в ряд по степеням  :
:
 (2)
(2)
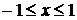 ,
, 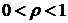
Коэффициенты 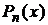 в разложение (2) являются полиномами n-й степени и называются полиномами Лежандра.
в разложение (2) являются полиномами n-й степени и называются полиномами Лежандра.
В силу теоремы Коши из формулы (2) следует, что
 (3)
(3)
от 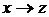 ,
, 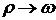 (перейдем в комплексную плоскость). Используя интегральную формулу Коши и производную
(перейдем в комплексную плоскость). Используя интегральную формулу Коши и производную
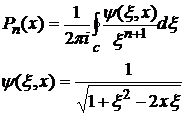 (4)
(4)
Полагая 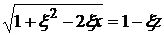 , находим
, находим 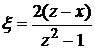 ,
, 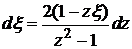 ,
,
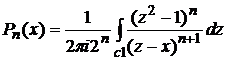 , (5)
, (5)
где С1— любой контур, окружающий точку x=z. Подинтегральная функция имеет особенность, а именно полюс (n+1) порядка.
 ,
,

 . (6)
. (6)
Из формулы (6) непосредственно видно что:
1. Получили полином степени n;
2. Полином содержит степени x той же четности, что и номер n, так что
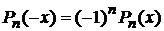 . (7)
. (7)
Просмотрим граничные условия:
x=1,
 ,
,
 ,
,
Формула (6) называется дифференциальной формулой для полиномов Лежандра или формулой Родрига. С учетом (7)
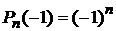 .
.

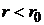 ,
,
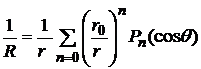
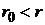 . (8)
. (8)
Рекуррентные формулы
Используя производящую функцию
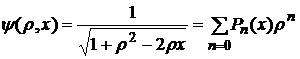 ,
,
и найдем частные производные по  и по
и по 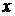
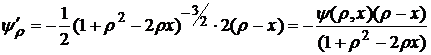 ,
,
 , (9)
, (9)
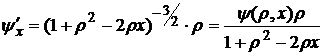 , (9а)
, (9а)
Запишем левую часть формулы (9) в виде степенного ряда относительно  , подставив в нее ряд (3) для
, подставив в нее ряд (3) для  и ряд
и ряд
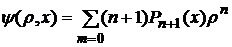 .
.
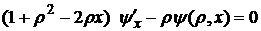 . (10)
. (10)
 ,
,
Возьмем производную по  :
:
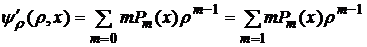
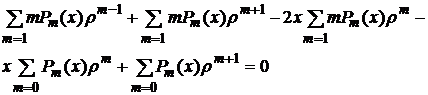
m-1=n 1-a m+1=n 2-a m=1 3-a m=0 4-ая m+1=n 5-ая
m=n+1 сумма m=n-1 сумма n=m сумма m=n сумма m=n-1 сумма
n=0,1,2 n=2,3,4, n=1,2 n=0 n=1,2
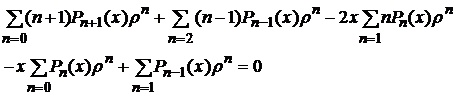
Запишем коэффициенты при  0,
0,  1,…,
1,…,  n.
n.
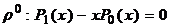
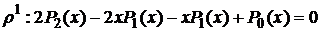
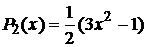
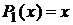
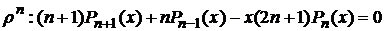 , где n ≥2. (11)
, где n ≥2. (11)
Таким образом, выражение (11) представляет собой рекуррентное соотношение.
Домножим (9) на  ,(10) на (
,(10) на (  ) и вычтем
) и вычтем

 , (12)
, (12)
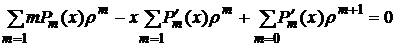 ,
,
При любом m получаем m+1=n, n=1
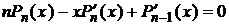 , (13)
, (13)
рекуррентная формула
 , (14)
, (14)
Продифференцируем по x соотношение (11):
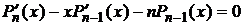 , (15)
, (15)
Уравнение Лежандра
Найдем дифференциальное уравнение, решением которого является 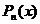 . Для этого исключим Pn-1 и Pn-1 из (14) и (15). Подставляем (14) в (15):
. Для этого исключим Pn-1 и Pn-1 из (14) и (15). Подставляем (14) в (15):
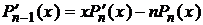 ,
,
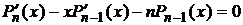 ,
,
 ,
,
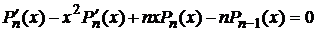 .
.
Продифференцируем:
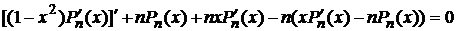 .
.
 . (16)
. (16)
Соотношение (16) представляет собой уравнения Лежандра. Тем самым доказано что полиномы Лежандра являются собственными функциями, соответствующими собственным значениям  , следующей задачи.
, следующей задачи.
Найти такие значения λ, для которых на отрезке  существуют нетривиальное решение уравнение Лежандра
существуют нетривиальное решение уравнение Лежандра
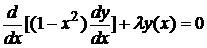 , (17)
, (17)
с областью 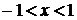 с условием
с условием 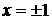
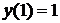 . Таким образом нетривиальное решение существует при
. Таким образом нетривиальное решение существует при 
 .
.
Ортогональность полиномов Лежандра и их норма
Докажем что полиномам Лежандра различных порядков ортогональны на отрезке 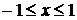 . Согласно общей теореме присоединенные функции
. Согласно общей теореме присоединенные функции 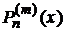 образуют ортогональную систему. Вычислим норму
образуют ортогональную систему. Вычислим норму  присоединенных функций. Попутно будет доказана их ортогональность.
присоединенных функций. Попутно будет доказана их ортогональность.
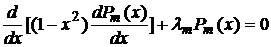 , (1)
, (1)
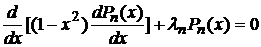 , (2)
, (2)
где  ,
, 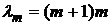 . Домножим (1) на
. Домножим (1) на 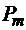 (x), а (2) на
(x), а (2) на 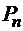 (x), а затем вычтем (1) из (2):
(x), а затем вычтем (1) из (2):
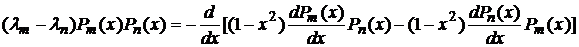 ,
,
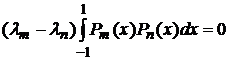 , (3)
, (3)
Доказать ортогональность если  . Если
. Если  , то полиномы Лежандра разных порядков ортогональны между собой:
, то полиномы Лежандра разных порядков ортогональны между собой:
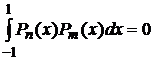
 . (4)
. (4)
Норма полиномов Лежандра
Вычислим норму полиномов Лежандра 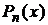
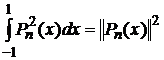
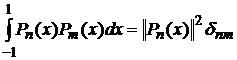 (5)
(5)
Применим рекуррентную формулу (11) (§1.1) дважды: сначала выразим из нее (предварительно заменив в (11) n+1 на n) 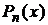 через
через  и
и 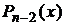 , а затем
, а затем 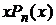 через
через  и
и 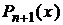 . Учитывая ортогональность полиномов
. Учитывая ортогональность полиномов 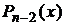 ,
,  ,
, 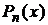 , получим:
, получим:

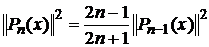 (6)
(6)
Рекуррентная формула для нормы:

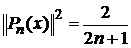
 (7)
(7)
Полиномы Лежандра образуют замкнутую систему функций. Поэтому произвольная функция может быть разложена в ряд
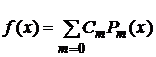 ,
,
который домножим на 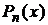 и проинтегрируем:
и проинтегрируем:

 .
.
Система ортогональных функций называют замкнутой если не существует непрерывных функции тождественно равных 0 и ортогональных ко всем функциям системы.
Система ортогональных функций 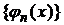 называется полной в (a,b) если любую непрерывную функцию можно аппроксимировать с любой степенью точности при помощи линейной комбинации
называется полной в (a,b) если любую непрерывную функцию можно аппроксимировать с любой степенью точности при помощи линейной комбинации  .
.
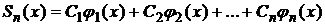


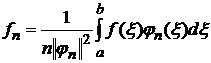
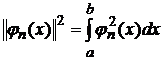
Замкнутость есть условие полноты, а полнота есть следствие замкнутости.
Упражнения
1. Получить полиномы Лежандра, используя производящую функцию, для n=0,1,2.
2. Получить полиномы Лежандра, используя формулу Родрига, для n=0,1,2,3,4,5.
3. Получить полиномы Лежандра, используя рекуррентную формулу для коэффициентов, для n=0,1,2,3,4,5,6.
Ответ:

4. Построить и исследовать (найти точки перегибов, максимумов и минимумов) полиномов Лежандра для n=0,1,2,3,4,5.
5. Получить присоединенные функции Лежандра для n, m=0,1,2,3,4. Выразить данные функции через тригонометрические функции.
6. Получить сферические функции для l=0,1,2.
7. Показать, что сферические функции ортонормированны. Ограничиться l=0,1.
8. Выполнить визуализацию сферических функций.
Ответ:
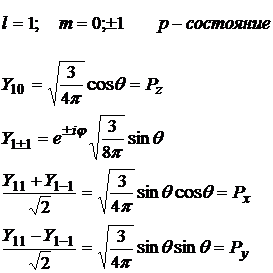

Присоединенные функции Лежандра
Присоединенные функции
Рассмотрим следующую задачу:
Найдем собственные значения и собственные функции следующего уравнения
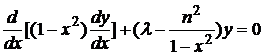 (1)
(1)
-1<x<1 при условии ограниченности
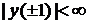 (2)
(2)
Будем искать решение в виде:
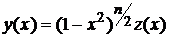 (3)
(3)
Подставим (3) в (1), найдем
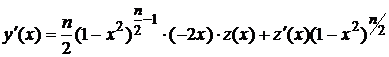 ,
,
 ,
,

 . (4)
. (4)
Это же уравнение получается для производной  решения уравнения Лежандра (17) из §1, если продифференцировать m раз.
решения уравнения Лежандра (17) из §1, если продифференцировать m раз.
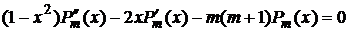 , (4а)
, (4а)
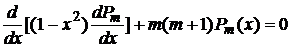 ,
,
Продифференцируем соотношение (4) n раз, тогда получим
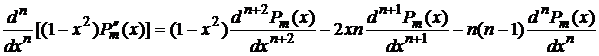 ,
,
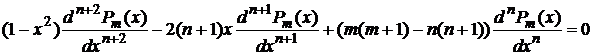 ,(5)
,(5)
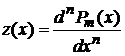 . (6)
. (6)
Нетривиальное и ограниченное решение 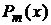 решении уравнения Лежандра существует при
решении уравнения Лежандра существует при 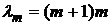 , где m>0. Решение Соотношение (6) является решением уравнения (3)
, где m>0. Решение Соотношение (6) является решением уравнения (3)
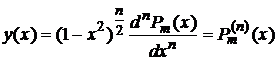 ,
,
есть собственная функция исходной задачи (1) для собственных значений 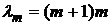 , где m-целые числа (7).
, где m-целые числа (7).  — присоединенная функция Лежандра
— присоединенная функция Лежандра
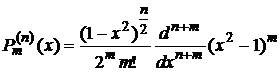 ,
,
Если n=0, то

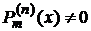 при
при 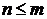 .
.
Норма присоединенной функции
Согласно общей теоремы присоединенные функции образуют ортогональную систему. Вычислим норму  и докажем ортогональность
и докажем ортогональность
 (8)
(8)
Уменьшим n на 1:
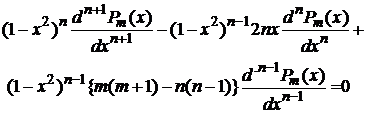 (9)
(9)
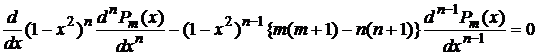 , (10)
, (10)
Введем обозначение:
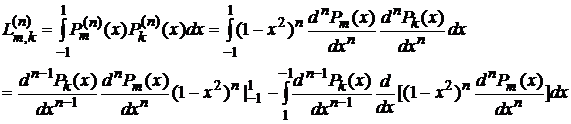
Подстановка обращается в нуль, а интеграл в силу (8) и (7) преобразуется к виду
 ,
,
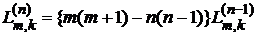 , (11)
, (11)
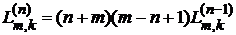 , (12)
, (12)
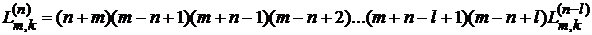

Нетрудно показать, что
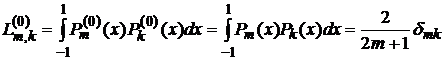 ,
,
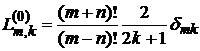 .
.
Сферические функции
Сферические функции
Сферические функции проще всего могут быть введены при решении уравнения Лапласа для шаровой области методом разделения переменных. Разделение переменных в уравнении Лапласа в сферических координатах:
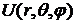 ,
,
 ,
,
где 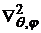 — угловая часть оператора Лапласа в сферических координатах.
— угловая часть оператора Лапласа в сферических координатах.
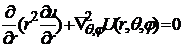 , (1)
, (1)
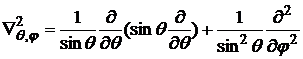 . (2)
. (2)
Решение уравнения Лапласа:
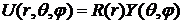 , (3)
, (3)
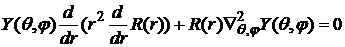 ,
,
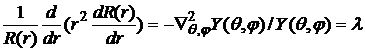 . (4)
. (4)
Для определения 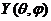 получаем уравнения
получаем уравнения
 , (5)
, (5)
где  — константа разделения.
— константа разделения.

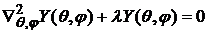 , (6)
, (6)
Для определения R(r) получаем уравнение Эйлера:
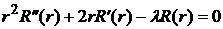 ,
,
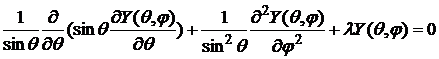 . (6а)
. (6а)
Следствия:
1. Функция 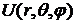 должна быть ограничена на сфере любого радиуса.
должна быть ограничена на сфере любого радиуса.
2. Функция 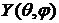 должна в точках
должна в точках 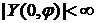 ,
, 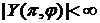 , а также
, а также 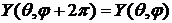 .
.
Ограниченное решение уравнения (6) обладающее непрерывными производными до второго порядка называются сферическими функциями. Решение задачи для 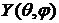 ищем также методом разделения переменных, полагая
ищем также методом разделения переменных, полагая
 . (7)
. (7)
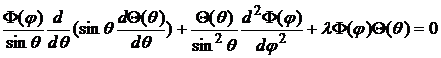 ,
,
Умножим на 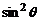 и поделим на (7)
и поделим на (7)
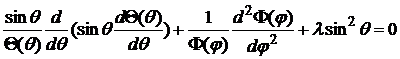 ,
,
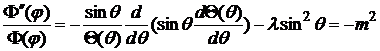 , (8)
, (8)
где m-константа разделения.
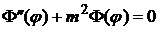 (9)
(9)
Задача для  имеет решение лишь при целом m, и линейно независимыми решениями являются функции
имеет решение лишь при целом m, и линейно независимыми решениями являются функции  и
и 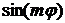 .
.
Функция 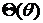 определяется из уравнения
определяется из уравнения
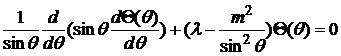 , (10)
, (10)
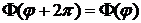 (11)
(11)
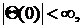
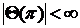 (12)
(12)
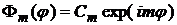 , (13)
, (13)
решение (9).
Если потребовать выполнение условия (11)
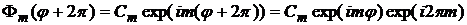 ,
,
 m- любое число m=0,1,-1,2,-2…
m- любое число m=0,1,-1,2,-2…
 ,
,
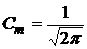
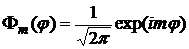 m=0,1,-1… (14)
m=0,1,-1… (14)
Выберем новую переменную  и обозначая
и обозначая 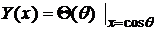 , получаем для
, получаем для 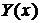 уравнение присоединенных функций (15)
уравнение присоединенных функций (15)
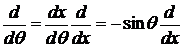

подставляем все в (10)
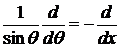
 . (15)
. (15)
Полученное уравнение является уравнением для присоединенных функций Лежандра

Потребуем чтобы функции 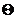 были нормированными
были нормированными

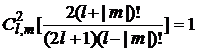
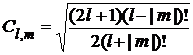 (16)
(16)
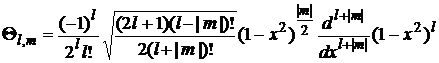 , (17)
, (17)
где 
 .
.
 (18)
(18)
Уравнение (6) имеет решение (18) при собственных значениях 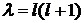 . Найдем несколько сферических функций
. Найдем несколько сферических функций
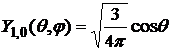
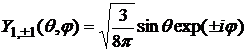
Легко проверить, что сферические функции является ортонормированными, т.е. справедливо:
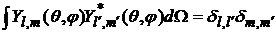


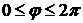
Кроме сферических функций используется понятие сферической гармоники которые определяется следующим образом:
число различных сферических функций n-го порядка  равно 2n+1. Линейная комбинация этих (2n+1) сферических функций
равно 2n+1. Линейная комбинация этих (2n+1) сферических функций
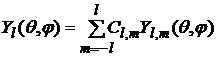 ,
,
Решение уравнения имеет вид:
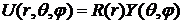
Специфика заключается в нахождении радиальной части волновой функции R(r).
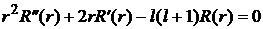 ,
,
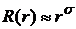
 ,
,

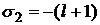 ,
,
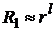
 .
.
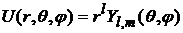 ,
,
есть внутренняя краевая задача, а
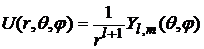
есть внешняя краевая задача.
Полиномы — это… Что такое Полиномы?
В математике, многочлены или полиномы от одной переменной — функции вида
где ci фиксированные коэффициенты, а x — переменная. Многочлены составляют один из важнейших классов элементарных функций.
Изучение полиномиальных уравнений и их решений составляло едва ли не главный объект «классической алгебры». С изучением многочленов связан целый ряд преобразований в математике: введение в рассмотрение нуля, отрицательных, а затем и комплексных чисел, а также появление теории групп как раздела математики и выделение классов специальных функций в анализе.
Техническая простота вычислений, связанных с многочленами, по сравнению с более сложными классами функций, а также тот факт, что множество многочленов плотно в пространстве непрерывных функций на компактных подмножествах евклидова пространства (смотри аппроксимационная теорема Вейерштрасса), способствовали развитию методов разложения в ряды и полиномиальной интерполяции в математическом анализе.
Многочлены также играют ключевую роль в алгебраической геометрии, объектом которой являются множества, определённые как решения систем многочленов. Особые свойства преобразования коэффициентов при умножении многочленов используются в алгебраической геометрии, алгебре, теории узлов и других разделах математики для кодирования, или выражения многочленами свойств различных объектов.
Определение
Многочлен (или полином) от n переменных — есть конечная формальная сумма вида
 ,
,
где I = (i1,i2,…,in) есть набор из целых неотрицательных чисел (называется мультииндекс), cI — число (называемое «коэффициент многочлена»), зависящее только от мультииндекса I.
В частности, многочлен от одной переменной есть конечная формальная сумма вида
Коэффициенты многочлена обычно берутся из определённого коммутативного кольца R (чаще всего поля, например, поля вещественных или комплексных чисел). В этом случае, относительно операций сложения и умножения многочлены образуют кольцо (более того ассоциативно-коммутативную алгебру над кольцом R без делителей нуля) которое обозначается
- R[x1,x2,…,xn].
Связанные определения
- Многочлен вида
 называется одночленом или мономом
называется одночленом или мономом- Одночлен, соответствующий мультииндексу
 называется свободным членом.
называется свободным членом. - В случае, когда многочлен имеет всего два ненулевых члена, его называют двучленом или биномом,
- В случае, когда многочлен имеет всего три ненулевых члена, его называют трёхчленом.
- Одночлен, соответствующий мультииндексу
- Полной степенью (ненулевого) одночлена
 называется целое число | I | = i1 + i2 + … + in.
называется целое число | I | = i1 + i2 + … + in.- Степенью многочлена называется максимальная из степеней его одночленов, тождественный нуль не имеет степени
- Множество мультииндексов I для которых коэффициенты cI ненулевые называется носителем многочлена, а его выпуклая оболочка многогранником Ньютона.
Делимость
Многочлен, который можно представить в виде произведения многочленов низших степеней с коэффициентами из данного поля, называется приводимым (над данным полем), в противном случае — неприводимым. Неприводимые многочлены играют в кольце многочленов роль, сходную с ролью простых чисел в кольце целых чисел. Например, верна теорема: если произведение pq делится на неприводимый многочлен λ, то p или q делится на λ. Каждый многочлен, степени большей нуля, разлагается в данном поле в произведение неприводимых множителей единственным образом (с точностью до множителей нулевой степени).
Например, многочлен x4 + 2, неприводимый в поле рациональных чисел, разлагается на два множителя в поле вещественных чисел и на четыре множителя в поле комплексных чисел.
Вообще, каждый многочлен от одного переменного x разлагается в поле вещественных чисел на множители первой и второй степени, в поле комплексных чисел — на множители первой степени (основная теорема алгебры).
Для двух и большего числа переменных этого уже нельзя утверждать. Над любым полем для любого n > 2 существуют многочлен от n переменных, неприводимые в любом расширении этого поля. Такие многочлены называются абсолютно неприводимыми.
Полиномиальные функции
Пусть A есть алгебра над кольцом R. Произвольный многочлен ![p(x)\in R[x_1,x_2,\dots,x_n]](/800/600/https/dic.academic.ru/pictures/wiki/files/101/e9f417dcd1b29b0e22f190644e824dc6.png) определяет полиномиальную функцию
определяет полиномиальную функцию
 .
.
Чаще всего рассматривают случай A = R.
В случае если R есть поле вещественных или комплексных чисел (а также любое другое поле с бесконечным числом элементов) то функция 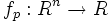 полностью определяет многочлен p. Однако в общем случае это неверно, например: многочлены
полностью определяет многочлен p. Однако в общем случае это неверно, например: многочлены 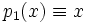 и
и 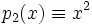 из
из ![\Z_2[x]](/800/600/https/dic.academic.ru/pictures/wiki/files/56/882d3e0463e56562452bb334bf02135f.png) определяют тождественно равные функции
определяют тождественно равные функции 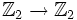 .
.
Свойства
Вариации и обобщения
- Если в определении допустить также отрицательные степени, то полученный объект называется многочленом Лорана (см. ряд Лорана).
- Квазимногочлен
- Тригонометрический многочлен
См. также
Ссылки
Wikimedia Foundation. 2010.
ЛЕЖАНДРА УСЛОВИЕ — это… Что такое ЛЕЖАНДРА УСЛОВИЕ?
- ЛЕЖАНДРА УСЛОВИЕ
— необходимое условие для решения простейшей задачи вариационного исчисления, предложенное А. Лежандром (A. Legendre, 1786): для того чтобы кривая у 0 (х). доставляла минимум функционалу

необходимо, чтобы во всех точках кривой у(х).вторая производная от подинтегральной функции по у’ была неотрицательна

Если уесть га-мерный вектор с координатами y1,. . ., у n, то Л. у. требует неотрицательности квадратичной формы

Для случая максимума функционала знак неравенства в Л. у. меняется на противоположный. Для вариационных задач на условный экстремум аналогом Л. у. является Клебша условие.
Л. у., так же как и Эйлера уравнение, является необходимым условием слабого экстремума. При нарушении Л. у. вторая вариация функционала не сохраняет свой знак и кривая у(х).не доставляет экстремум функционалу.
Если в Л. у. знак нестрогого неравенства заменен на знак строгого неравенства, то такое условие наз. усиленным условием Лежандра. Усиленное Л. у. в отличие от Л. у. не является необходимым. Усиленное Л. у. участвует в формулировке достаточных условий экстремума. Экстремаль, на к-рой выполняется усиленное Л. у., наз. неособой (неособенной) экстремалью. Такая экстремаль дважды непрерывно дифференцируема, и уравнение Эйлера для нее можно представить в виде обыкновенного дифференциального уравнения 2-го порядка, разрешенного относительно старшей производной. Если на неособой экстремали выполняется усиленное Якоби условие, то можно построить поле экстремалей, окружающее данную экстремаль, что является первым шагом при исследовании достаточных условий экстремума.
Лит.:[1] Л а в р е н т ь е в М. А., Л ю с т е р н и к Л. А., Курс вариационного исчисления, 2 изд., М., 1950; [2] Блисс Г. А., Лекции по вариационному исчислению, пер. с англ., М., 1950. И. Б. Вапнярский.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
- ЛЕЖАНДРА УРАВНЕНИЕ
- ЛЕЖАНДРА ФУНКЦИИ
Смотреть что такое «ЛЕЖАНДРА УСЛОВИЕ» в других словарях:
КЛЕБША УСЛОВИЕ — необходимое условие оптимально сти в задаче вариационного исчисления на условный экстремум; установлено Р. Клебшем [1]. Если экстремаль x(t), x: . доставляет условный минимум функционалу в Болъца задаче: то согласно правилу множителей она… … Математическая энциклопедия
Многочлены Лежандра — Многочлен Лежандра многочлен, который в наименьшей степени отклоняется от нуля в смысле среднего квадратического. Образует ортогональную систему многочленов, на отрезке по мере Лебега. Многочлены Лежандра могут быть получены из многочленов… … Википедия
Многочлен Лежандра — Многочлены Лежандра определённая ортогональная система многочленов, на отрезке [ − 1,1] по мере Лебега. Многочлены Лежандра могут быть получены из многочленов ортогонализацией Грама ― Шмидта. Названы по имени французского математика Адриен Мари… … Википедия
Полином Лежандра — Многочлены Лежандра определённая ортогональная система многочленов, на отрезке [ − 1,1] по мере Лебега. Многочлены Лежандра могут быть получены из многочленов ортогонализацией Грама ― Шмидта. Названы по имени французского математика Адриен Мари… … Википедия
Полиномы Лежандра — Многочлены Лежандра определённая ортогональная система многочленов, на отрезке [ − 1,1] по мере Лебега. Многочлены Лежандра могут быть получены из многочленов ортогонализацией Грама ― Шмидта. Названы по имени французского математика Адриен Мари… … Википедия
Присоединённые многочлены Лежандра — Многочлены Лежандра определённая ортогональная система многочленов, на отрезке [ − 1,1] по мере Лебега. Многочлены Лежандра могут быть получены из многочленов ортогонализацией Грама ― Шмидта. Названы по имени французского математика Адриен Мари… … Википедия
Функция Лежандра — Многочлены Лежандра определённая ортогональная система многочленов, на отрезке [ − 1,1] по мере Лебега. Многочлены Лежандра могут быть получены из многочленов ортогонализацией Грама ― Шмидта. Названы по имени французского математика Адриен Мари… … Википедия
ЯКОБИ УСЛОВИЕ — необходимое условие оптимальности в задачах вариационного исчисления. Я. у. является необходимым условием неотрицательности 2 й вариации минимизируемого функционала в точке его минимума (равенство нулю 1 й вариации функционала обеспечивается… … Математическая энциклопедия
СЛАБЫЙ ОТНОСИТЕЛЬНЫЙ МИНИМУМ — минимальное значение , достигаемое функционалом J(у).на кривой , такое, что для всех кривых сравнения у(х), удовлетворяющих условию e близости 1 го порядка (1) на всем промежутке [x1, х 2]. Предполагается, что кривые удовлетворяют заданным… … Математическая энциклопедия
ВЕЙЕРШТРАССА — ФУНКЦИЯ в классическом вариационном исчислении функция, выделяющая главную часть приращения функционала при варьировании экстремали при помощи локальной (игольчатой) вариации с заданным значением ее производной в фиксированной точке экстремали.… … Математическая энциклопедия
LEGENDRE_POLYNOMIAL — многочлены Лежандра
LEGENDRE_POLYNOMIAL — полиномы ЛежандраLEGENDRE_POLYNOMIAL , библиотека MATLAB, которая вычисляет полином Лежандра и связанные с ним функции.
Многочлен Лежандра P (n, x) можно определить следующим образом:
Р (0, х) = 1
P (1, х) = х
P (n, x) = (2 * n-1) / n * x * P (n-1, x) - (n-1) / n * P (n-2, x)
где n — целое неотрицательное число.N нулей P (n, x) — это абсциссы, используемые для Гаусса-Лежандра. квадратура интеграла от функции F (X) с весовой функцией 1 на интервале [-1,1].
Полиномы Лежандра ортогональны относительно внутреннего произведения, определенного как интегрирование от -1 до 1:
Интегральный (-1
Лицензирование:
Компьютерный код и файлы данных, описанные и доступные на этом
веб-страницы распространяются под
лицензия GNU LGPL.
Языки:
LEGENDRE_POLYNOMIAL доступен в
версия C и
версия C ++ и
версия FORTRAN90 и
версия MATLAB.
Связанные данные и программы:
BERNSTEIN_POLYNOMIAL,
библиотека MATLAB, которая
вычисляет полиномы Бернштейна,
полезен для равномерного приближения функций;
CHEBYSHEV_POLYNOMIAL,
библиотека MATLAB, которая
рассматривает полиномы Чебышева T (i, x), U (i, x), V (i, x) и W (i, x).Предусмотрены функции для вычисления многочленов, определения их нулей,
производят их полиномиальные коэффициенты, производят соответствующие квадратурные правила,
проецировать другие функции на эти полиномиальные базисы и интегрировать
двойные и тройные произведения многочленов.
GEGENBAUER_POLYNOMIAL,
библиотека MATLAB, которая
вычисляет полином Гегенбауэра и связанные с ним функции.
HERMITE_POLYNOMIAL,
библиотека MATLAB, которая
оценивает полином Эрмита физика, вероятностный полином Эрмита,
функция Эрмита и связанные с ней функции.
JACOBI_POLYNOMIAL,
библиотека MATLAB, которая
вычисляет полином Якоби и связанные с ним функции.
LAGUERRE_POLYNOMIAL,
библиотека MATLAB, которая
вычисляет полином Лагерра, обобщенный полином Лагерра,
и функция Лагерра.
legendre_polynomial_test
LEGENDRE_PRODUCT_POLYNOMIAL,
библиотека MATLAB, которая
определяет полиномы произведения Лежандра, создавая многомерное
полином как произведение одномерных полиномов Лежандра.
LEGENDRE_RULE,
программа MATLAB, которая
вычисляет одномерное квадратурное правило Гаусса-Лежандра.
LEGENDRE_SHIFTED_POLYNOMIAL,
библиотека MATLAB, которая
вычисляет сдвинутый полином Лежандра с областью определения [0,1].
LOBATTO_POLYNOMIAL,
библиотека MATLAB, которая
вычисляет полиномы Лобатто, аналогичные полиномам Лежандра
за исключением того, что они равны нулю на обеих конечных точках.
PCE_LEGENDRE,
программа MATLAB, которая
собирает системную матрицу двумерного стохастического уравнения в частных производных,
использование разложения полиномального хаоса в терминах полиномов Лежандра;
POLPAK,
библиотека MATLAB, которая
оценивает множество математических функций.
TEST_VALUES,
библиотека MATLAB, которая
предоставляет тестовые значения различных математических функций.
Ссылка:
-
Теодор Чихара,
Введение в ортогональные многочлены,
Gordon and Breach, 1978,
ISBN: 0677041500,
LC: QA404.5 C44.
-
Уолтер Гаучи, Ортогональные многочлены
: вычисление и приближение,
Оксфорд, 2004 г.,
ISBN: 0-19-850672-4,
LC: QA404.5 G3555.
-
Фрэнк Олвер, Даниэль Лозье, Рональд Бойсверт, Чарльз Кларк,
Справочник NIST по математическим функциям,
Cambridge University Press, 2010,
ISBN: 978-0521192255,
LC: QA331.N57.
-
Габор Сего,
ортогональных многочленов,
Американского математического общества, 1992,
ISBN: 0821810235,
LC: QA3.A5.v23.
Исходный код:
- imtqlx.m, диагонализует симметричную трехдиагональную матрицу;
- legendre_to_monomial_matrix.m, возвращает матрицу, которая преобразует полиномиальное разложение из Лежандра к мономиальному виду.
- monomial_to_legendre_matrix.m, возвращает матрицу, которая преобразует полиномиальное разложение из одночлена в форму Лежандра.
- p_exponential_product.m, экспоненциальные произведения для P (n, x).
- p_integral.m, вычисляет мономиальный интеграл, связанный с P (n, x).
- p_polynomial_coefficients.m, коэффициенты полиномов Лежандра P (n, x).
- p_polynomial_plot.m, строит один или несколько полиномов Лежандра P (n, x).
- p_polynomial_prime.м, вычисляет производную полиномов Лежандра P (n, x).
- p_polynomial_prime2.m, вычисляет вторую производную полиномов Лежандра P (n, x).
- p_polynomial_value.m, вычисляет полиномы Лежандра P (n, x).
- p_polynomial_values.m, выбранные значения полиномов Лежандра P (n, x).
- p_polynomial_zeros.м, нули функции Лежандра P (n, x).
- p_power_product.m, степенные произведения для полинома Лежандра P (n, x).
- p_quadrature_rule.m, квадратура для функции Лежандра P (n, x).
- pm_polynomial_value.m, вычисляет полиномы Лежандра Pm (n, m, x).
- pm_polynomial_values.m, возвращает значения полиномов Лежандра Pm (n, m, x).
- pmn_polynomial_value.m, вычисляет нормализованные полиномы Лежандра Pmn (n, m, x).
- pmns_polynomial_value.m, вычисляет сферические нормализованные полиномы Лежандра Pmns (n, m, x).
- pn_pair_product.m, парные произведения для нормированного полинома Лежандра Pn (n, x).
- pn_polynomial_coefficients.m, коэффициенты нормированных полиномов Лежандра Pn (n, x).
- pn_polynomial_value.m, вычисляет нормализованные полиномы Лежандра Pn (n, x).
- pn_polynomial_values.m, выбранные значения нормированных полиномов Лежандра Pn (n, x).
- r8_factorial.m, вычисляет факториальную функцию;
- r8_sign.m, возвращает знак R8.
- r8mat_print.м, печатает R8MAT;
- r8mat_print_some.m, печатает часть R8MAT;
- r8vec_linspace.m, создает вектор-столбец линейно разнесенных значений.
- r8vec_print.m, печатает R8VEC;
- r8vec2_print.m, печатает пару R8VEC;
- timestamp.m, печатает текущую дату YMDHMS как отметку времени.
Последняя редакция 13 февраля 2019 г. ,
LEGENDRE_POLYNOMIAL — многочлены Лежандра
LEGENDRE_POLYNOMIAL — полиномы ЛежандраLEGENDRE_POLYNOMIAL , код FORTRAN90, который вычисляет полином Лежандра и связанные с ним функции.
Многочлен Лежандра P (n, x) можно определить следующим образом:
Р (0, х) = 1
P (1, х) = х
P (n, x) = (2 * n-1) / n * x * P (n-1, x) - (n-1) / n * P (n-2, x)
где n — целое неотрицательное число.N нулей P (n, x) — это абсциссы, используемые для Гаусса-Лежандра. квадратура интеграла от функции F (X) с весовой функцией 1 на интервале [-1,1].
Полиномы Лежандра ортогональны относительно внутреннего произведения, определенного как интегрирование от -1 до 1:
Интегральный (-1
Лицензирование:
Компьютерный код и файлы данных, описанные и доступные на этом
веб-страницы распространяются под
лицензия GNU LGPL.
Языки:
LEGENDRE_POLYNOMIAL доступен в
версия C и
версия C ++ и
версия FORTRAN90 и
версия MATLAB и
версия Python.
Связанные данные и программы:
BERNSTEIN_POLYNOMIAL,
код FORTRAN90, который
вычисляет полиномы Бернштейна,
полезен для равномерного приближения функций;
CHEBYSHEV_POLYNOMIAL,
код FORTRAN90, который
рассматривает полиномы Чебышева T (i, x), U (i, x), V (i, x) и W (i, x).Предусмотрены функции для вычисления многочленов, определения их нулей,
производят их полиномиальные коэффициенты, производят соответствующие квадратурные правила,
проецировать другие функции на эти полиномиальные базисы и интегрировать
двойные и тройные произведения многочленов.
GEGENBAUER_POLYNOMIAL,
код FORTRAN90, который
вычисляет полином Гегенбауэра и связанные с ним функции.
HERMITE_POLYNOMIAL,
код FORTRAN90, который
оценивает полином Эрмита физика, вероятностный полином Эрмита,
функция Эрмита и связанные с ней функции.
JACOBI_POLYNOMIAL,
код FORTRAN90, который
вычисляет полином Якоби и связанные с ним функции.
LAGUERRE_POLYNOMIAL,
код FORTRAN90, который
вычисляет полином Лагерра, обобщенный полином Лагерра,
и функция Лагерра.
legendre_polynomial_test
LEGENDRE_PRODUCT_POLYNOMIAL,
код FORTRAN90, который
определяет полиномы произведения Лежандра, создавая многомерное
полином как произведение одномерных полиномов Лежандра.
LEGENDRE_RULE,
код FORTRAN90, который
вычисляет одномерное квадратурное правило Гаусса-Лежандра.
LOBATTO_POLYNOMIAL,
код FORTRAN90, который
вычисляет полиномы Лобатто, аналогичные полиномам Лежандра
за исключением того, что они равны нулю на обеих конечных точках.
POLPAK,
код FORTRAN90, который
оценивает множество математических функций.
TEST_VALUES,
код FORTRAN90, который
предоставляет тестовые значения различных математических функций.
Ссылка:
-
Теодор Чихара,
Введение в ортогональные многочлены,
Гордон и Брич, 1978,
ISBN: 0677041500,
LC: QA404.5 C44.
-
Уолтер Гаучи, Ортогональные многочлены
: вычисление и приближение,
Оксфорд, 2004 г.,
ISBN: 0-19-850672-4,
LC: QA404.5 G3555.
-
Фрэнк Олвер, Даниэль Лозье, Рональд Бойсверт, Чарльз Кларк,
Справочник NIST по математическим функциям,
Cambridge University Press, 2010,
ISBN: 978-0521192255,
LC: QA331.N57.
-
Габор Сего,
Ортогональные многочлены,
Американское математическое общество, 1992,
ISBN: 0821810235,
LC: QA3.A5.v23.
Исходный код:
Последний раз редактировалось 25 июля 2020 г. ,Серия
Legendre (numpy.polynomial.legendre) — Руководство NumPy v1.20.dev0
Этот модуль предоставляет ряд объектов (в основном функций), полезных для
имеют дело с серией Legendre, включая класс Legendre , который
инкапсулирует обычные арифметические операции. (Главная Информация
о том, как этот модуль представляет и работает с такими многочленами, находится в
docstring для его «родительского» подпакета, numpy.polynomial ).
Классы
| Класс серии Legendre. |
Арифметика
| Добавьте одну серию Legendre к другой. |
| Вычтите одну серию Лежандра из другой. |
| Умножьте ряд Лежандра на x. |
| Умножить одну серию Лежандра на другую. |
| Разделите одну серию Лежандра на другую. |
| Поднимите серию Legendre до уровня мощи. |
| Оцените ряд Лежандра в точках x. |
| Оцените двумерный ряд Лежандра в точках (x, y). |
| Оцените трехмерный ряд Лежандра в точках (x, y, z). |
| Вычислите двумерный ряд Лежандра на декартовом произведении x и y. |
| Оцените трехмерный ряд Лежандра на декартовом произведении x, y и z. |
Исчисление
| Определите серию Legendre. |
| Интегрируйте серию Legendre. |
Разные функции
| Создайте серию Лежандра с заданными корнями. |
| Вычислить корни ряда Лежандра. |
| Матрица псевдовандермонда заданной степени. |
| Матрица псевдовандермонда заданных степеней. |
| Матрица псевдовандермонда заданных степеней. |
| Квадратура Гаусса-Лежандра. |
| Весовая функция многочленов Лежандра. |
| Вернуть масштабированную сопутствующую матрицу c. |
| Наименьшее соответствие ряда Лежандра данным. |
| Удалите «маленькие» «замыкающие» коэффициенты полинома. |
Legendre (numpy.polynomial.legendre) — Руководство NumPy v1.19
Этот модуль предоставляет ряд объектов (в основном функций), полезных для
имеют дело с серией Legendre, включая класс Legendre , который
инкапсулирует обычные арифметические операции. (Главная Информация
о том, как этот модуль представляет и работает с такими многочленами, находится в
docstring для его «родительского» подпакета, numpy.polynomial ).
Классы
| Класс серии Legendre. |
Арифметика
| Добавьте одну серию Legendre к другой. |
| Вычтите одну серию Лежандра из другой. |
| Умножьте ряд Лежандра на x. |
| Умножить одну серию Лежандра на другую. |
| Разделите одну серию Лежандра на другую. |
| Поднимите серию Legendre до уровня мощи. |
| Оцените ряд Лежандра в точках x. |
| Оцените двумерный ряд Лежандра в точках (x, y). |
| Оцените трехмерный ряд Лежандра в точках (x, y, z). |
| Вычислите двумерный ряд Лежандра на декартовом произведении x и y. |
| Оцените трехмерный ряд Лежандра на декартовом произведении x, y и z. |
Исчисление
| Определите серию Legendre. |
| Интегрируйте серию Legendre. |
Разные функции
| Создайте серию Лежандра с заданными корнями. |
| Вычислить корни ряда Лежандра. |
| Матрица псевдовандермонда заданной степени. |
| Матрица псевдовандермонда заданных степеней. |
| Матрица псевдовандермонда заданных степеней. |
| Квадратура Гаусса-Лежандра. |
| Весовая функция многочленов Лежандра. |
| Вернуть масштабированную сопутствующую матрицу c. |
| Наименьшее соответствие ряда Лежандра данным. |
| Удалите «маленькие» «замыкающие» коэффициенты полинома. |
| Серия Лежандра, график которой представляет собой прямую линию. |
| Преобразует ряд Лежандра в полином. |

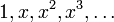 ортогонализацией Грама ― Шмидта.
ортогонализацией Грама ― Шмидта.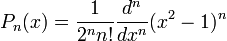
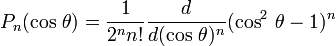
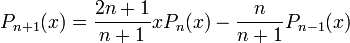
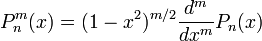
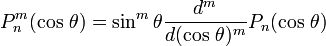
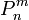 совпадает с Pn.
совпадает с Pn.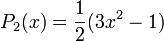
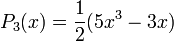
![{d \over dx} \left[ (1-x^2) {d \over dx} P_n(x) \right] - \frac{m^2}{(1-x^2)} P_n(x) + n(n+1)P_n(x) = 0.](/800/600/https/dic.academic.ru/pictures/wiki/files/57/9737be98642c29101417b8021fd720c1.png)
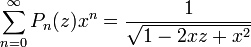
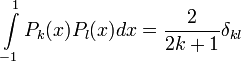
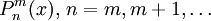 полна в L2( − 1,1).
полна в L2( − 1,1).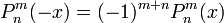
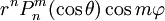 и
и 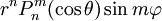 ,
,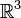 (при n < 0 — всюду, кроме нуля) и служат ортогональным базисом для функций.
(при n < 0 — всюду, кроме нуля) и служат ортогональным базисом для функций.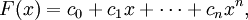
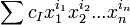 ,
,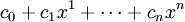
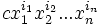 называется одночленом или мономом
называется одночленом или мономом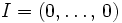 называется свободным членом.
называется свободным членом.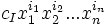 называется целое число | I | = i1 + i2 + … + in.
называется целое число | I | = i1 + i2 + … + in. .
.