Задачи на построение графов – Решение задач с помощью графа

Решение задач с помощью графа

1. GlobalLabГлобальная школьная лаборатория Присоединиться С чего начать?
   • Идеи
   • Проекты
   • Курсы
   • Сообщество
     • Участники
     • Группы
   • Новости
     • Новости
     • Блог тьютора
     • Беседа с профессионалом
     • Scholāris GlobalLabis
   • Участнику
     • О ГлобалЛаб
     • Справочник
     • Календарь
     • Конкурсы и события
     • Бонусная программа
     • Педагогу
     • Родителю
   • Магазин
     • Магазин
     • Купить подписку
     • Активировать по номеру
   • Вход на сайт
     • Мой профиль
     • Мои награды
     • Моё портфолио
     • Мои черновики
     • Мои проекты
     • Мои группы
     • Редактировать профиль
     • Мои сообщения
     • Выход
   • ru

globallab.org

Графы. Применение графов к решению задач

Разделы: Внеклассная работа

---

1. Методические рекомендации к теме “Графы”.

Понятие графа целесообразно вводить после того, как разобрано несколько задач, подобных задаче 1, решающее соображение в которых – графическое представление. Важно, чтобы ученики сразу осознали, что один и тот же граф может быть нарисован разными способами. Строгое определение графа, на мой взгляд, давать не нужно, т.к. оно слишком громоздко и это только затруднит обсуждение. На первых порах хватит и интуитивного понятия. При обсуждении понятия изоморфизма можно решить несколько упражнений на определение изоморфных и неизоморфных графов. Одно из центральных мест темы – теорема о четности числа нечетных вершин. Важно, чтобы ученики до конца разобрались в ее доказательстве и научились применять к решению задач. При разборе нескольких задач рекомендую не ссылаться на теорему, а фактически повторять ее доказательство. Чрезвычайно важно также понятие связности графа. Содержательным соображением здесь является рассмотрение компоненты связности, на это необходимо обратить особое внимание. Эйлеровы графы – тема почти игровая.

Первая и главная цель, которую нужно преследовать при изучении графов, –научить школьников видеть граф в условии задачи и грамотно переводить условие на язык теории графов. Не стоят рассказывать обе всем на нескольких занятиях подряд. Лучше разнести занятия по времени на 2–3 учебных года. (Прилагается разработка занятия “Понятие графа. Применение графов к решению задач” в 6 классе).

2. Теоретический материал к теме “Графы”.

Введение

Графы – замечательные математические объекты, с их помощью можно решать очень много различных, внешне не похожих друг на друга задач. В математике существует целый раздел – теория графов, который изучает графы, их свойства и применение. Мы же обсудим только самые основные понятия, свойства графов и некоторые способы решения задач.

Понятие графа

Рассмотрим две задачи.

Задача 1. Между девятью планетами солнечной системы установлено космическое сообщение. Рейсовые ракеты летают по следующим маршрутам: Земля – Меркурий; Плутон – Венера; Земля – Плутон; Плутон – Меркурий; Меркурий – Вене; Уран – Нептун; Нептун – Сатурн; Сатурн – Юпитер; Юпитер – Марс и Марс – Уран. Можно ли долететь на рейсовых ракетах с Земли до Марса ?

Решение: Нарисуем схему условия: планеты изобразим точками, а маршруты ракет – линиями.

Теперь сразу видно, что долететь с Земли до Марса нельзя.

Задача 2. Доска имеет форму двойного креста, который получается, если из квадрата 4×4 убрать угловые клетки.

Можно ли обойти ее ходом шахматного коня и вернуться на исходную клетку, побывав на всех клетках ровно по одному разу ?

Решение: Занумеруем последовательно клетки доски:

А теперь с помощью рисунка покажем, что такой обход таблицы, как указано в условии, возможен:

Мы рассмотрели две непохожие задачи. Однако решения этих двух задач объединяет общая идея – графическое представление решения. При этом и картинки, нарисованные для каждой задачи, оказались похожими: каждая картинка – это несколько точек, некоторые из которых соединены линиями.

Такие картинки и называются графами. Точки при этом называются вершинами, а линии – ребрами графа. Заметим, что не каждая картинка такого вида будет называться графом. Например. если вас попросят нарисовать в тетради пятиугольник, то такой рисунок графом не будет. Будем называть что рисунок такого вида, как в предыдущих задачах, графом, если есть какая-то конкретная задача для которой такой рисунок построен.

Другое замечание касается вида графа. Попробуйте проверить, что граф для одной и той же задачи можно нарисовать разными способами; и наоборот для разных задач можно нарисовать одинаковые по виду графы. Здесь важно лишь то, какие вершины соединены друг с другом, а какие – нет. Например, граф для задачи 1 можно нарисовать по-другому:

Такие одинаковые, но по-разному нарисованные графы, называются изоморфными.

Степени вершин и подсчет числа ребер графа

Запишем еще одно определение: Степенью вершины графа называется количество выходящих из нее ребер. В связи с этим, вершина, имеющая четную степень, называется четной вершиной, соответственно, вершина, имеющая нечетную степень, называется нечетной вершиной.

С понятием степени вершины связана одна из основных теорем теории графов –теорема о честности числа нечетных вершин. Докажем ее мы немного позднее, а сначала для иллюстрации рассмотрим задачу.

Задача 3. В городе Маленьком 15 телефонов. Можно ли их соединить проводами так, чтобы каждый телефон был соединен ровно с пятью другими ?

Решение: Допустим, что такое соединение телефонов возможно. Тогда представим себе граф, в котором вершины обозначают телефоны, а ребра – провода, их соединяющие. Подсчитаем, сколько всего получится проводов. К каждому телефону подключено ровно 5 проводов, т.е. степень каждой вершины нашего графа – 5. Чтобы найти число проводов, надо просуммировать степени всех вершин графа и полученный результат разделить на 2 (т.к. каждый провод имеет два конца, то при суммировании степеней каждый провод будет взят 2 раза). Но тогда количество проводов получится разным . Но это число не целое. Значит наше предположение о том, что можно соединить каждый телефон ровно с пятью другими, оказалось неверным.

Ответ. Соединить телефоны таким образом невозможно.

Теорема: Любой граф содержит четное число нечетных вершин.

Доказательство: Количество ребер графа равно половине суммы степеней его вершин. Так как количество ребер должно быть целым числом, то сумма степеней вершин должна быть четной. А это возможно только в том случае, если граф содержит четное число нечетных вершин.

Связность графа

Есть еще одно важное понятие, относящееся к графам – понятие связности.

Граф называется связным, если из любые две его вершины можно соединить путем, т.е. непрерывной последовательностью ребер. Существует целый ряд задач, решение которых основано на понятии связности графа.

Задача 4. В стране Семерка 15 городов, каждый из городов соединен дорогами не менее, чем с семью другими. Докажите, что из каждого города модно добраться в любой другой.

Доказательство: Рассмотрим два произвольных А и В города и допустим, что между ними нет пути. Каждый из них соединен дорогами не менее, чем с семью другими, причем нет такого города, который был бы соединен с обоими рассматриваемыми городами (в противном случае существовал бы путь из A в B). Нарисуем часть графа, соответствующую этим городам:

Теперь явно видно, что мы получили не менее различных 16 городов, что противоречит условию задачи. Значит утверждение доказано от противного.

Если принять во внимание предыдущее определение, то утверждение задачи можно переформулировать и по-другому: “Доказать, что граф дорог страны Семерка связен.”

Теперь вы знаете, как выглядит связный граф. Несвязный граф имеет вид нескольких “кусков”, каждый из которых – либо отдельная вершина без ребер, либо связный граф. Пример несвязного графа вы видите на рисунке:

Каждый такой отдельный кусок называется компонентой связности графа. Каждая компонента связности представляет собой связный граф и для нее выполняются все утверждения, которые мы доказали для связных графов. Рассмотрим пример задачи, в которой используется компонента связности:

Задача 5. В Тридевятом царстве только один вид транспорта – ковер-самолет. Из столицы выходит 21 ковролиния, из города Дальний – одна, а из всех остальных городов, – по 20. Докажите, что из столицы можно долететь в город Дальний.

Доказательство: Понятно, что если нарисовать граф ковролиний Царства, то он может быть несвязным. Рассмотрим компоненту связности, которая включает в себя столицу Царства. Из столицы выходит 21 ковролиния, а из любых других городов, кроме города Дальний – по 20, поэтому, чтобы выполнялся закон о четном числе нечетных вершин необходимо, чтобы и город Дальний входил в эту же самую компоненту связности. А так как компонента связности – связный граф, то из столицы существует путь по ковролиниям до города Дальний, что и требовалось доказать.

Графы Эйлера

Вы наверняка сталкивались с задачами, в которых требуется нарисовать какую-либо фигуру не отрывая карандаш от бумаги и проводя каждую линию только один раз. Оказывается, что такая задача не всегда разрешима, т.е. существуют фигуры, которые указанным способом нарисовать нельзя. Вопрос разрешимости таких задач также входит в теорию графов. Впервые его исследовал в 1736 году великий немецкий математик Леонард Эйлер, решая задачу о Кенигсбергских мостах. Поэтому графы, которые можно нарисовать указанным способом, называются Эйлеровыми графами.

Задача 6. Можно ли нарисовать изображенный на рисунке граф не отрывая карандаш от бумаги и проводя каждое ребро ровно один раз ?

Решение. Если мы будем рисовать граф так, как сказано в условии, то в каждую вершину, кроме начальной и конечной, мы войдем столько же раз, сколько выйдем из нее. То есть все вершины графа, кроме двух должны быть четными. В нашем же графе имеется три нечетные вершины, поэтому его нельзя нарисовать указанным в условии способом.

Сейчас мы доказали теорему об Эйлеровых графах:

Теорема: Эйлеров граф должен иметь не более двух нечетных вершин.

И в заключение – задача о Кенигсбергских мостах.

Задача 7. На рисунке изображена схема мостов города Кенигсберга.

Можно ли совершить прогулку так, чтобы пройти по каждому мосту ровно 1 раз?

3. Задачи к теме “Графы”

Понятие графа.

1. На квадратной доске 3×3 расставлены 4 коня так, как показано на рис.1. Можно ли сделав несколько ходов конями, переставить их в положение, показанное на рис.2?

Рис. 1

Рис. 2

Решение. Занумеруем клетки доски, как показано на рисунке:

Каждой клетке поставим в соответствие точку на плоскости и, если из одной клетки можно попасть в другую ходом шахматного коня, то соответствующие точки соединим линией. Исходная и требуемая расстановки коней показаны на рисунках:

При любой последовательности ходов конями порядок их следования, очевидно, измениться не может. Поэтому переставить коней требуемым образом невозможно.

2. В стране Цифра есть 9 городов с названиями 1, 2, 3, 4, 5, 6, 7, 8, 9. Путешественник обнаружил, что два города соединены авиалинией в том и только в том случае, если двузначное число, образованное названиями городов, делится на 3. Можно ли долететь по воздуху из города 1 в город 9 ?

Решение. Поставив в соответствие каждому городу точку и соединив точки линией, если сумма цифр делится на 3, получим граф, в котором цифры 3, 5, 9 связаны между собой, но не связаны с остальными. Значит долететь из города 1 в город 9 нельзя.

Степени вершин и подсчет числа ребер.

3. В государстве 100 городов к из каждого города выходит 4 дороги. Сколько всего дорог в государстве.

Решение. Подсчитаем общее количество выходящих городов дорог – 100 ^. 4 = 400. Однако при таком подсчете каждая дорога посчитана 2 раза – она выходит из одного города и входит в другой. Значит всего дорог в два раза меньше, т.е. 200.

4. В классе 30 человек. Может ли быть так, что 9 человек имеют по 3 друга, 11 – по 4 друга, а 10 – по 5 друзей ?

Ответ. Нет (теорема о четности числа нечетных вершин).

5. У короля 19 вассалов. Может ли оказаться так, что у каждого вассала 1, 5 или 9 соседей ?

Ответ. Нет, не может.

6. Может ли в государстве, в котором из каждого города выходит ровно 3 дороги, быть ровно 100 дорог?

Решение. Подсчитаем число городов. Число дорог равно числу городов х, умноженному на 3 (число выходящих из каждого города дорог) и разделенному на 2 (см. задачу 3). Тогда 100 = Зх/2 => Зх=200, чего не может быть при натуральном х. Значит 100 дорог в таком государстве быть не может.

7. Докажите, что число людей, живших когда-либо на Земле и сделавших нечетное число рукопожатий, четно.

Доказательство непосредственно следует из теоремы о четности числа нечетных вершин графа.

Связность.

8. В стране из каждого города выходит 100 дорог и из каждого города можно добраться до любого другого. Одну дорогу закрыли на ремонт. Докажите, что и теперь из любого города можно добраться до любого другого.

Доказательство. Рассмотрим компоненту связности, в которую входит один из городов, дорогу между которыми закрыли. По теореме о четности числа нечетных вершин в нее входит и второй город. А значит по-прежнему можно найти маршрут и добраться из одного из этих городов в другой.

Графы Эйлера.

9. Имеется группа островов, соединенных мостами так, что от каждого острова можно добраться до любого другого. Турист обошел все острова, пройдя по каждому мосту розно 1 раз. На острове Троекратном он побывал трижды. Сколько мостов ведет с Троекратного, если турист

а) не с него начал и не на нем закончил?
б) с него начал, но не на нем закончил?
в) с него начал и на нем закончил?

10. На рисунке изображен парк, разделенный на несколько частей заборами. Можно ли прогуляться по парку и его окрестностям так, чтобы перелезть через каждый забор розно 1 раз?

6.03.2007

xn--i1abbnckbmcl9fb.xn--p1ai

Графы, примеры и задачи

ГРАФЫ

Графы возникли в восемнадцатом столетии, когда известный мате­матик, Леонард Эйлер, пытался решить теперь уже классическую задачу о Кенигсбергских мостах. В то время в городе Кенигсбер­ге было два oстровa, соединенных семью мостами с берегами реки Преголь и друг с другом так, как показано на рис. 7.1. 3адача со­стоит в следующем: осуществить прогулку по городу таким образом, чтобы, пройдя ровно по одному разу по каждому мосту, вернуться в то же место, откуда начиналась прогулка. Решая эту задачу, Эйлер изобразил Кенигсберг в виде графа, отождествив его вершины с частями города, а ребра — с мостами, которыми связаны эти части. Как мы покажем в § 7.1, Эйлеру удалось доказать, что искомого маршрута обхода города не существует.

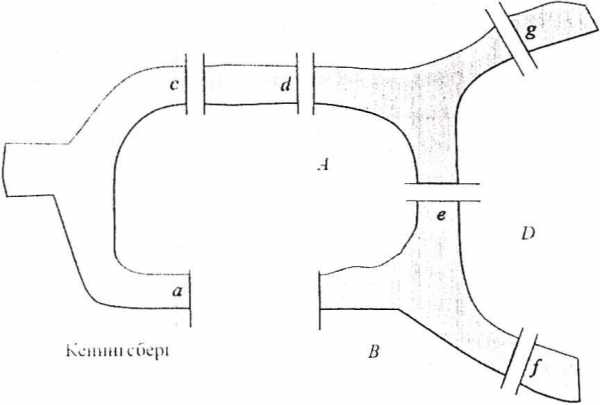
Рисунок 7.1. Схема старого Кенигсберга

В этой главе мы вводим стандартную терминологию, используемую в теории графов, и разбираем несколько конкретных задач решаемых с помощью графов. В частности, мы познакомимся с классом графов, называемых деревьями. Деревья – естественная модель, представляющая данные, организованные в иерархичную систему. Поиск по дереву для выделения отдельных предметов и сортировка данных в дереве представляет собой важные точки приложения усилий в информатике. В приложении к этой главе мы займемся сортировкой и поиском данных, организованных в деревья.

Графы и терминология

На рис. 7.1 изображены семь мостов Кенигсберга так. как они были расположены в восемнадцатом столетии. В задаче, к которой oбpa­тился Эйлер, спрашивается: можно ли найти маршрут прогулки, ко­торый проходит ровно один раз по каждому из мостов и начинается и заканчивается в одном и том же месте города?

Модель задачи — это граф, состоящий из множества вершин и множества ребер, соединяющих вершины. Вершины А, В, С и D символизируют берега реки и острова, а ребра а,в, c,d,f и g обозначают семь мостов (см. рис. 7.2). Искомый маршрут (если он существует) соответствует обходу ребер графа таким образом, что каждое из них проходится только один раз. Проход ребра, очевидно, соответствует пересечению реки по мосту.

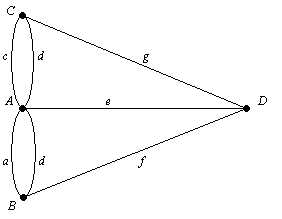
Рисунок 7.2. Модель задачи о мостах Кенигсберга

Граф, в котором найдется маршрут, найдется маршрут, на­чинающийся и заканчивающийся в одной вершине, и проходящий по всем ребрам графа ровно один раз, называется зйлеровым графом. Последовательность вер­шин (может быть и с повторениями), через которые проходит иско­мый маршрут, как и сам маршрут, называется эйлеровым циклом. Эйлер заметил, что если в графе есть эйлеров цикл, то для каждого ребра, ведущего в какую-то вершину, должно найтись другое ребро, выходящее из этой вершины¹, и получил из этого простого наблюдсния такой вывод: если в данном графе существует эйлеров цикл, то к каждой вершине должно подходить четное число ребер.

Кроме того, Эйлеру удалось доказать и противоположное утвер­ждение, так что граф, в котором любая пара вершин связана не­которой последовательностью ребер, является Эйлеровым тогда и только тогда, когда все его вершины имеют четную степень. Степенью вершины v называется число δ(v) ребер, ей инцидентных² .

Теперь совершенно очевидно, что в графе, моделирующем задачу о мостах Кенигсберга, эйлерова цикла найти нельзя. Действитель­но, степени всех его вершин нечетны: δ(B) = δ(С) = δ(D) = 3 и δ(A) = 5. С легкой руки Эйлера графы, подобные тому, который мы исследовали при решении задачи о мостах, стали использовать­ при решении многих практических задач, а их изучение выросло в значительную область математики.

Простой граф определяется как пара G = (V, Е), где V — ко­нечное множество вершин, а Е — конечное множество ребер, при­чем не может содержать петель (ребер, начинающихся и закан­чивающихся в одной вершине) и кратных ребер (кратными назы­ваются несколько ребер, соединяющих одну и ту же пару вершин). Граф, изображенный на рис. 7.2. не является простым, поскольку, например, вершины А и В соединяются двумя ребрами (как раз эти ребра и называются кратными).

Две вершины u и v в простом графе называются смежными, если они соединяются каким-то ребром е, про которое говорят, что оно инцидентно вершине u (и v). Таким образом, мы можем предста­влять себе множество Е ребер как множество пар смежных вершин, определяя тем самым нерефлексивное, симметричное отношение на множестве V. Отсутствие рефлексивности связано с тем, что в простом графе нет петель, т. е. ребер, оба конца которых находятся в одной вершине. Симметричность же отношения вытекает из того факта, что ребро е, соединяющее вершину и с v, соединяет и v с и (иначе говоря, ребра не ориентированы, т. е. не имеют направления). Единственное ребро простого графа, соединяющее пару вершин u и v, мы будем обозначать как иv (или vи).

Логическая матрица отношения на множестве вершин графа, котopoe задается его ребрами, называется ,матрицей смежности. Симметричность отношения в терминах матрицы смежности М озна­чает, что М симметрична относительно главной диагонали. А из-за нерефлексивности этого отношения на главной диагонали матрицы М стоит символ «Л».

Пример 7.1. Нарисуйте граф G(V, Е) с множеством вершин V = {а, Ь, с, d, е} и множеством ребер E = {ab, ae, bc, bd, ce, de}. Выпишите его матрицу смежности.

Решение. Граф G показан на рис. 7.3.

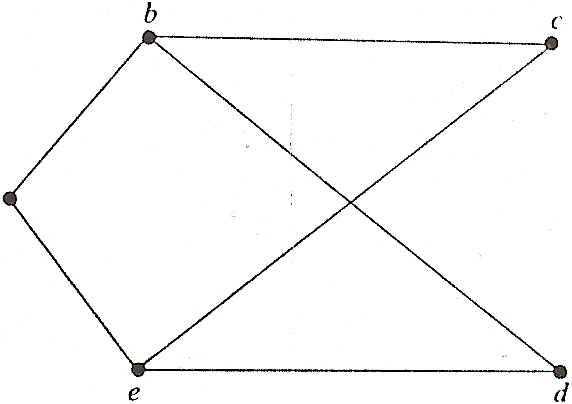
Рисунок 7.3.

Его матрица смежности имеет вид:

Для восстановления графа нам достаточно только тех элементов матрицы смежности, которые стоят над главной диагональю.

Подграфом графа G = (V, E) называется граф G’ = (V’, E’), в котором E’ C E и V’ C V.

Пример 7.2 Найдите среди графиков H, K и L, изображенных на рис. 7.4, подграфы графа G.

Решение. Обозначим вершины графов G, H и K как показано на рис. 7.5. Графы H и K – подграфы в G, как видно из наших обозначений. Граф L не является подграфом в G, поскольку у него есть вершина индекса 4, а у графа G такой нет.

Маршрутом длины k в графе G называется такая последовательность вершин v₀ , v₁ , …, v_k ,что для каждого i = 1, …, k пара v_{i – 1} v_i образует ребро графа. Мы будем обозначать такой маршрут через v₀ v₁ … v_k .Например 1 4 3 2 5 – это маршрут длины 4 в графе G из примера 7.2.

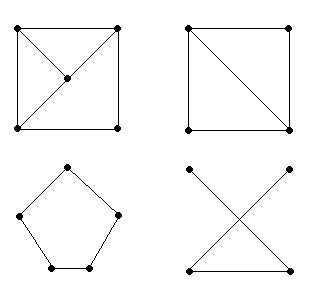G H

K L

Рисунок 7.4.

Циклом в графе принято называть последовательность вершин v₀ , v₁ , … , v_k ,каждая пара которых является концами одного ребра, причем v₀ = v₁ , а остальные вершины ( и ребра) не повторяются. Иными словами, цикл – это замкнутый маршрут, проходящий через каждую свою вершину и ребро только один раз

G H K

1 2 1 2 3

1 2

4 5 4 3 4 5

Рисунок 7.5

Пример 7.3. Найдите циклы в графе G из примера 7.2.

Решение. В этом графе есть два разных цикла длины 5:

1 3 2 5 4 1 и 1 2 5 4 3 1

Мы можем пройти эти циклы как в одном направлении так и в другом, начиная с произвольной вершины цикла. Кроме того, в графе есть три разных цикла длины 4:

1 2 5 4 1, 1 2 3 4 1 и 2 5 4 3 2,

и два цикла длины 3:

1 2 3 1 и 1 3 4 1.

Граф, в котором нет циклов, называется ацикличным. Структуры деревьев, которые возникают в вычислениях , представляют собой частный случай ацикличных графов. Позже в этой главе мы ими займемся.

Граф, называют связным, если любую пару его вершин соединяет какой – нибудь маршрут. Любой общий граф можно разбить на подграфы, каждый из которых окажется связным. Минимальное число таких связных компонент называется числом связности графа и обозначается через c(G). Вопросы связности имеют важное значение в приложениях теории графов к компьютерным сетям. Следующий алгоритм применяется для определения числа связности графа.

Алгоритм связности.

Пусть G = (V, E) – граф. Алгоритм предназначен для вычисления значения c = c(G), т.е. числа компонент связности данного графа G.

begin

V’ :=V;

c:=0;

while V’≠ ø do

begin

Выбрать y Є V’

Найти вершины, соединяющие маршрутом с у;

Удалить вершину у из V’ и

соответствующие ребра из Е;

c:=c+1;

end

end

Пример 7.4. Проследите за работой алгоритма связности на графе, изображенном на рис. 7.6.

1 5

2 6

3 7

8

4

Рисунок 7.6.

Решение. Смотри табл. 7.1.

Таблица 7.1.

	V’	c
Исходные значения	{1,2,3,4,5,6,7,8}	0
Выбор у = 1	{2,4,5,7}	1
Выбор у = 2	{7}	2
Выбор у = 7	ø	3

Итак, c(G) = 3. Соответствующие компоненты связности приведены на рис. 7.7.

5

1

6 2

3

8 4

Рисунок 7.7.

Гамильтоновы графы

Мы начали эту главу с изучения эйлеровых графов, обладающих замкнутым маршрутом, который проходит по всем ребрам графа ровно один раз. Похожая задача состоит в поиске цикла, проходящего через каждую вершину графа в точности один раз. Такой цикл, если он существует, называется гамильтоновым, а соответствующий граф – гамильтоновым графом.

Гамильтоновы графы служат моделью при составлении расписания движения поездов, для телекоммуникационных сетей и т.д. В отличие от задачи Эйлера, простого критерия гомильтоновости графа пока не известно. Поиск хорошего критерия остается одной из главных нерешенных задач теории графов.

Полный граф К₅ изображен на рис. 7.8. Его цикл a b c d e a, очевидно, является гамильтоновым. В нем есть и другие гамильтоновы циклы. Поскольку каждая вершина смежна с остальными, то начиная с вершины а, в качестве второй вершины цикла мы можем выбрать любую из четырех оставшихся. Далее у нас будет три варианта для выбора третьей вершины и два для четвертой, после чего мы вернемся в вершину а. Таким образом, у нас есть 4 · 3 · 2 = 24 цикла. Поскольку каждый цикл можно проходить как в одном направлении, так и в другом, то реально в графе К₅ есть только 12 разных гамильтоновых циклов¹.

b

a c

e d

Рисунок 7.8. Полный граф К₅

Поиск гамильтонова цикла (если он существует) в произвольном (связном) графе – задача далеко не всегда простая. Ответ на вопрос о гамильтоновости графа может оказаться довольно трудоемким.

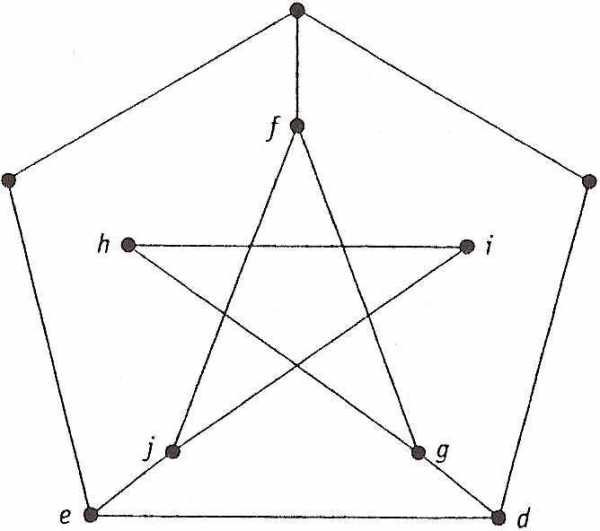
Пример 7.5. Покажите что граф, изображенный на рис. 7.9, не является гамильтоновым.

b

a c

Рисунок 7.9. Пример не гамильтонова графа

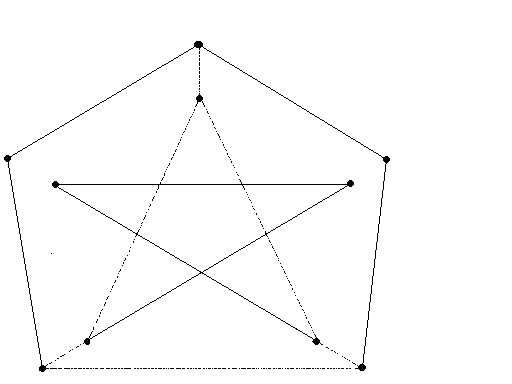
Решение. Предположим, что в связном графе найдется гамильтонов цикл. Каждая вершина v включается в гамильтонов цикл С выбором двух инцидентных с ней ребер, а значит, степень каждой вершины в гамильтоновом цикле (после удаления лишних ребер) равна 2. Степени вершин данного графа — 2 или 3. вершины степени 2 входят в цикл вместе с обоими инцидентными с ними ребрами. Следовательно, ребра ab, ae, cd, cb, hi, hg и ij в том или ином порядке входят в гамильтонов цикл С (см. рис. 7.10.).

Ребро bf не может быть часть цикла С, поскольку каждая вершина такого цикла должна иметь степень 2. Значит, ребра fi и fg обязаны входить в цикл С, чтобы включить в него вершину f. Но тогда ребра je и gd никак не могут принадлежать циклу С, поскольку в противном случае в нем появятся вершины степени три. Это вынуждает нас включить в цикл ребро ed, что приводит нас к противоречию: ребра, которые мы были вынуждены выбрать, образуют два несвязных цикла, а не один, существование которого мы предполагали. Вывод: граф, изображенный на рисунке 7.10, не является гамильтоновым.

Гамильтоновы графы применяются для моделирования многих практических задач. Основой всех таких задач служит классическая задача коммивояжера.

Коммивояжер должен совершить поездку по городам и вернуться обратно, побыв в каждом городе ровно один раз, сведя при этом затраты на передвижение к минимуму.

b

f

a c

h i

j g

e d

Рисунок 7.10. Ребра входящие в гамильтонов цикл С

Графическая модель задачи коммивояжера состоит из гамильтонова графа, вершины которого изображают города, а ребра связывающие их дороги. Кроме того, каждое ребро оснащено весом, обозначающим транспортные затраты, необходимые для путешествия по соответствующей дороге, такие, как, например, расстояние между городами или время движения по дороге². Для решения задачи нам необходимо найти гамильтонов цикл минимального общего веса.

К сожалению, эффективный алгоритм решения данной задачи пока не известен. Для сложных сетей число гамильтоновых циклов, которые необходимо просмотреть для выделения минимального, непомерно огромно. Однако существуют алгоритмы поиска субоптимального решения. Субоптимальное решение необязательно даст цикл минимального общего веса, но найденный цикл будет, как правило, значительно меньшего веса, чем большинство произвольных гамильтоновых циклов! Один из таких алгоритмов мы сейчас и изучим.

Алгоритм ближайшего соседа.

Этот алгоритм выдает субоптимальное решение задачи коммивояжера, генерируя гамильтоновы циклы в нагруженном графе с множеством вершин V. Цикл, полученный в результате работы алгоритма, будет совпадать с конечным значением переменной маршрут, а его общая длина – конечное значение переменной w.

begin

Выбрать v Є V;

маршрут := v;

w:=0;

v‘:=v;

Отметить v‘:

while остаются неотмеченными вершины do

begin

Выбрать неотмеченную вершину u,

ближайшую к v’;

маршрут:=маршрут u;

w:=w+вес ребра v’u;

v’:=u;

Отметить v’;

end

маршрут:= маршрут v;

w:=w+вес ребра v’u;

end

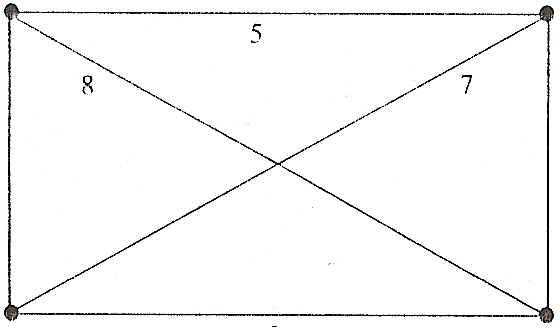
Пример 7.6. Примените алгоритм ближайшего соседа к графу, изображенному на рисунке 7.11. За исходную вершину возьмите вершину D.

A B

6 10

C D

3

Рисунок 7.11.

Решение. Смотрите табл.7.2

Таблица 7.2

	u	маршрут	w	v’
Исходные значения	—	D	0	D
	C	DC	3	C
	A	DCA	9	A
	B	DCAB	14	B
Последний проход	B	DCABD	24	B

В результате работы алгоритма был найден гамильтонов цикл DCABD общего веса 24. Делая полный перебор всех циклов в этом маленьком графе, можно обнаружить еще два других гамильтоновых цикла: ABCDA общего веса 23 и ACBDA общего веса 31. В полном графе с двадцатью вершинами существует приблизительно 6,1 · 10¹⁶ гамильтоновых циклов, перечисление которых требует чрезвычайно много машинной памяти и времени.

Деревья

Как уже упоминалось, есть класс графов, называемых деревьями, которые особенно интенсивно используются в вычислительных приложениях. Граф G= (V,E)называется деревом, если он связен и ацикличен(т.е. не содержит циклов).

Пусть G= (V,E) – граф сnвершинами иm ребрами. Можно сформулировать несколько необходимых и достаточных условий, при которыхGявляется деревом:

• Любая пара вершин в Gсоединена единственным путем.

• Gсвязен иm = n – 1.

• Gсвязен, а удаление хотя бы одного его ребра нарушает связность графа.

• Gацикличен, но если добавить хотя бы одно ребро, то вGпоявится цикл.

Эквивалентность большинства из этих условий устанавливается без особого труда. Наиболее сложно разобраться со вторым из них. В следующем примере мы докажем, что дерево с n вершинами имеет ровно n – 1 ребро.

Пример 7.7. Докажите с помощью индукции по числу вершин, что для дереваT сnвершинами иm ребрами выполнено соотношение:m = n – 1.

Решение. Поскольку дерево с единственной вершиной вообще не содержит ребер, то доказываемое утверждение справедливо приn = 1.

Рассмотрим дерево Тсnвершинами (иmребрами), гдеn > 1и предположим, что любое дерево с k < n вершинами имеет ровно k– 1 ребро.

Удалим ребро из Т. По третьему свойству деревоТпосле этой процедуры превратится в несвязный граф. Получится ровно две компоненты связности, ни одна из которых не имеет циклов (в противном случае исходный графТтоже содержал бы циклы и не мог бы быть деревом). Таким образом, полученные компоненты связности – тоже деревья.

Обозначим новые деревья Т₁иТ_2. Пустьn₁– количество вершин у дереваТ₁ , аn₂–yT_2. Посколькуn₁ + n₂ = n, то n₁ < n и n₂ < n.

По предположению индукции дерево Т₁ имеетn₁– 1 ребро, аТ₂ – n₂– 1. Следовательно, исходное деревоТнасчитывало ( с учетом одного удаленного)

(n₁ – 1) + (n₂– 1) + 1 =n– 1 ребро, что и требовалось доказать.

Несложно доказать, что в любом связном графе найдется подграф, являющийся деревом. Подграф в G , являющийся деревом и включающий в себя все вершиныG, называетсяостовным деревом. Остовное дерево в графеGстроится просто: выбираем произвольное его ребро и последовательно добавляем другие ребра, не создавая при этом циклов, до тех пор, пока нельзя будет добавить никакого ребра, не получив при этом цикла. Благодаря примеру 7.7, мы знаем, что для построения остовного дерева в графе изnвершин необходимо выбрать ровноn– 1 ребро.

Пример 7.8. Найдите два разных остовных дерева в граве, изображенном на рис. 7.12.

Рисунок 7.12. Связный граф G

Решение. В этом графе существует несколько остовных деревьев. Одно из них получается последовательным выбором ребер: a, b, d, и f. Другое – b, c, e и g. Названные деревья показаны на рисунке 7.13.

Процесс, описанный в примере 7.8, можно приспособить для решения задачи кратчайшего соединения:

Нужно построить железную сеть, связывающую некоторое число городов. Известна стоимость строительства отрезка путей между любой парой городов. Требуется найти сеть минимальной стоимости.

На языке теории графов нам нужно в нагруженном графе найти остовное дерево наименьшего общего веса. Такое дерево принято называть минимальным остовным деревом или, сокращенно МОД. В отличие от задачи коммивояжера, здесь есть эффективный алгоритм, находящий действительно минимальное остовное дерево. Он похож на алгоритм Прима.

Рисунок 7.13. Остовные деревья графа G

Алгоритм поиска минимального остовного дерева. Пусть G = (V, E) – связной взвешенный граф. Алгоритм строит МОД в графе G, последовательно выбирая ребра наименьшего возможного веса до образования остовного дерева. МОД в памяти компьютера хранится в виде множества Т ребер.

begin

e:=ребро графа G с наименьшим весом;

T:={e};

E’:=E\{e}

while E’ ≠ ø

begin

e‘:= ребро из E‘ наименьшего веса;

Т:= Т U {e‘};

E‘ := множество ребер из E‘ \{T},

чьё добавление к Т не ведет

к образованию циклов;

end

end

Пример 7.9. В таблице 7.3 дано расстояние (в милях) между пятью деревнями A, B, C, D и E. Найдите минимальное остовное дерево.

Таблица 7.3

	A	B	C	D	E
A	—	13	3	9	9
B	13	—	11	11	13
C	3	11	—	9	7
D	9	11	9	—	2
E	9	13	7	2	—

Решение. Ребра выбираются следующим образом: первое – 1 DE веса 2; второе – AC веса 3; третье – СЕ веса 7. на этой ступени строящееся дерево выглядит так, как на рис. 7.14

Рисунок 7.14. Вид дерева после трех шагов

Следующие повесу ребра – AD, AE и CD, каждое из которых имеет вес 9. Однако какое бы из них мы не добавили, получится цикл. Поэтому перечисленные ребра следует исключить из доступных для строительства. Далее идут ребра ВС и ВD веса 11. Можно присоединить любое из них, получив при этом два разных МОД: {AC, BC, CE, DE} или {AC, BD, CE, DE} веса 23 каждое.

Зачастую, нам хотелось бы иметь деревья, представляющие собой формацию с учетом естественной иерархической структуры, такие как, например, генеалогическое дерево (рис.7.15). На нем показаны некоторые члены семьи Бернулли, каждый из которых был известным швейцарским математиком.

Генеалогическое дерево можно изобразить и более сжато. Схема приведенная на рисунке 7.16, представляет собой пример так называемого дерева с корнем. Деревом с корнем называется дерево с одной выделенной вершиной. Именно эта выделенная вершина и является корнем дерева. Вершины дерева, лежащие непосредственно под корнем, называются сыновьями. С другой стороны, вершина, стоящая непосредственно перед сыном, называется ее отцом.

studfiles.net

Применение теории графов к решению задач

Разделы: Начальная школа

---

Приложение. (Слайд 1).

Графы существуют везде, и даже маленькие дети неожиданно сталкиваются с ними, когда рисуют или играют. Они встречаются на картах дорог, созвездий, при построении схем и чертежей. Графы лежат в основе многих компьютерных программ, которые делают возможными современную коммуникацию и технологические процессы.

Графы способствуют развитию мышления как логического, так и абстрактного.

При решении задач, наверное, не раз приходилось изображать объекты точками, соединять их отрезками или стрелками, при этом для решения задачи был использован специальный математический аппарат, а именно была применена теория графов.

Исторически сложилось так, что теория графов зародилась двести с лишним лет назад именно в ходе решения головоломок. Первая работа о графах появилась в 1736 году в публикациях Петербургской академии наук. Она принадлежит Леонарду Эйлеру и связана с решением задачи о кенигсбергских мостах. Вопрос заключался в том, можно ли совершить прогулку так, чтобы выйдя из дома, вернуться обратно, пройдя в точности по одному разу каждый из семи кенигсбергских мостов. (Слайд 2). Эту задачу можно представить в виде геометрической схемы, на которой точки изображают части суши, а линии, их соединяющие – мосты. (Слайд 3).

Схема такого вида называется графом. Точки – вершины графа, соединяющие их линии – ребра.

С теорией графов связаны также задачи на вычерчивание фигуры одним росчерком. Если степени всех вершин четные, то можно обойти все вершины графа без повторений, также можно обойти все вершины, если на графе только 2 нечетные вершины, если же нечетных вершин больше, то обойти все вершины графа не удастся.

В переводе на задачи “одним росчерком” это звучит так: “Если на рисунке все точки четные, то такой рисунок можно нарисовать одной линией, не отрывая карандаша от бумаги и не проводя дважды по одной линии; если на рисунке 2 нечетные точки (если есть одна нечетная точка, то обязательно есть и вторая), то такой рисунок также можно нарисовать одним росчерком, причем следует начинать с одной нечетной точки и заканчивать в другой нечетной точке; если же нечетных точек больше двух, то нарисовать такой рисунок одним росчерком не удастся.”

Так обвести одной линией рисунок (слайд 4) нельзя, т.к. он содержит сразу 8 нечетных точек.

Толчок же к развитию теория графов получила на рубеже XIX–XX столетий, когда резко выросло число работ в области топологии и комбинаторики, с которыми ее связывают самые тесные узы родства. Как отдельная математическая дисциплина теория графов была впервые представлена в 30 годы ХХ столетия.

Однако теория графов пока не нашла своего отражения в большинстве учебниках математики. Отличаясь простотой теоретических сведений, наглядностью и доступностью, теория графов может с пользой найти отражение на самом раннем этапе обучения школьников. С помощью этой теории можно решить на доступном для младших школьников уровне ряд достаточно сложных задач.

Граф представляет собой непустое множество точек и множество отрезков, оба конца которых принадлежат заданному множеству точек.

При изображении графов на рисунках или схемах отрезки могут быть прямолинейными и криволинейными; длины отрезков и расположение точек произвольны.

Как уже было сказано выше, точки, изображающие элементы множества, называются вершинами графа; отрезки – ребрами графа. Вершины графа на рисунке выделяют обычно кружками или квадратиками хотя бы потому, чтобы точки пересечения ребер не принимались за вершины графа. Обозначают вершины обычно заглавными буквами русского или латинского алфавитов и иногда числами.

Можно выделить (слайд 5)

• неориентированный граф;
• граф с цветными ребрами;
• ориентированный граф;
• граф-дерево или дерево возможностей .

Рассмотрим применение всех этих видов графов к решению задач.

Неориентированные графы. (Слайд 6). В них ребрами являются отрезки или части кривой линии.

Рассмотрим задачу: “В шахматном турнире участвовали 4 человека. Каждый спортсмен сыграл со всеми другими участниками соревнований по одному разу. Сколько всего было сыграно партий?” (Слайд 7). Изобразим участников турнира точками, а сыгранные ими партии – отрезками. (Слайд 8). Для того чтобы ответить на вопрос задачи, надо лишь подсчитать число проведенных отрезков, их 6, следовательно, было сыграно 6 партий.

Рассмотрим еще одну подобную задачу: “На лесной опушке встретились заяц, белка, лиса, волк, медведь и куница. Каждый, здороваясь, пожал каждому лапу. Сколько всего лапкопожатий было сделано? (Слайд 9). На графе 15 ребер, следовательно, было сделано 15 лапкопожатий. Для того чтобы упростить подсчет ребер графа, можно рассуждать так: из каждой из 6 точек выходит 5 отрезков, т.е. для подсчета отрезков умножаем 5 на 6, получаем 30, но при этом каждый отрезок мы посчитаем дважды (например, белка – лиса и лиса – белка). Следовательно, чтобы найти число ребер графа, надо 30 разделить на 2, получим.15. Такие рассуждения будут особенно полезны, когда граф содержит большее число вершин и подсчет числа ребер становится затруднительным.

Рассмотрим обратную задачу: “Несколько мальчиков встретились на вокзале, чтобы поехать за город в лес. При встрече все они поздоровались друг с другом за руку. Сколько мальчиков поехало за город, если всего было10 рукопожатий?” (Слайд 10).

Предположим, что встретились два мальчика, изобразим их точками, а рукопожатие линией, соединяющей эти точки. (Слайд 11). Добавляем третьего приятеля и получаем три рукопожатия. (Слайд 12). Значит, необходимо добавить еще четвертого мальчика. Если встретились четыре мальчика, то рукопожатий будет шесть. (Слайд 13). Необходимо добавить следующего, пятого мальчика. На получившемся графе видно (Слайд 14), что рукопожатий получилось 10. Следовательно, на вокзале встретилось пять мальчиков.

Рассмотрим еще один вид задач, где применимы неориентированные графы: “В первенстве класса по шашкам 5 участников: Аня, Боря, Влад, Гриша, Даша. Первенство проводится по круговой системе – каждый из участников играет с каждым из остальных один раз. К настоящему времени некоторые игры уже проведены: Аня сыграла с Борей, Владом и Дашей; Боря сыграл, как уже говорилось, с Аней и еще с Гришей; Влад – с Аней и Дашей, Гриша – с Борей, Даша – с Аней и Гришей. Сколько игр проведено к настоящему времени и сколько еще осталось?” (Слайд 15).

Участников соревнований изобразим точками, которые назовем первыми буквами имен детей. Если двое участников уже сыграли между собой, соединим изображающие их точки отрезками. Получим граф. (Слайд 16).

Число игр, проведенных к настоящему моменту, равно числу ребер, т.е. шести. Чтобы узнать число игр, которые осталось провести, соединим линиями другого цвета (или пунктиром) тех участников, которые еще не играли друг с другом. Таких ребер получилось 4, значит, осталось провести 4 игры: Борис – Влад, Борис – Даша, Влад – Гриша, Гриша – Аня. (Слайд 16).

Применить теорию графов можно и при решении следующей задачи: “В стране алфавит 8 городов: А, Б, В, Г, Д, Е, Ж, З и восемь непересекающихся дорог между городами А и Б, Е и Д, Б и Ж, З и А, В и Г, Г и Д, Ж и З, В и Е. Можно ли по этим дорогам проехать из А в Г?” (Слайд 17).

Построим по условию задачи граф, при этом все вершины графа сразу отмечать не будем. Начнем с построения ребер графа, учитывая то условие, что они не пересекаются. Построим отрезки АБ и ЕД, присоединим к отрезку АБ отрезки БЖ и ЗА. Построим отрезок ВГ, не пересекающий ни один из построенных отрезков и соединим точки Г и Д, Ж и З, В и Е (не обязательно отрезками, можно и кривыми линиями). По графу видно, что точки А и Г друг с другом не соединены, а значит, по указанным дорогам из города А в город Г проехать нельзя. (Слайд 18).

Для решении задач на упорядочивание множеств будем применять ориентированные графы. (Слайд 19). В этом случае одну вершину считают началом ребра, а другую – концом. В ориентированном графе все ребра должны быть ориентированы.

Рассмотрим задачу: “Из лагеря вышли четыре туриста: Вася, Галя, Толя и Лена. Вася идет впереди Лены, Толя впереди Гали, а Лена впереди Толи. В каком порядке идут дети?

Попробуем вначале эту задачу решить без использования графа. При этом условие, что Толя идет впереди Гали придется вначале пропустить, т.к. неясно, они идут перед Васей и Леной или позади их. И только после прочтения последнего условия и установления, что Толя идет за Леной, можно определить месторасположение Гали. (Слайд 20).

Когда же мы решаем эту задачу при помощи графов, нам лишь необходимо представить условие задачи на графе. Изобразим всех туристов точками, которые обозначим первыми буквами имен детей. В задаче рассматривается отношение “идти впереди”, поэтому стрелку будем ставить от впереди идущего к идущему вслед за ним. Вася идет впереди Лены, значит стрелку ставим от Васи к Лене. Толя впереди Гали – стрелку ставим от Толи к Гале. Также ставим стрелку от Лены к Толе, т.к. она идет впереди него. На графе видно (Слайд 21), что первый идет Вася, за ним Лена, Толя и Галя идет последней.

Рассмотрим еще одну задачу: “В детском лагере отдыха в одной комнате живут четыре девочки: Маша, Валя, Таня и Галя. Две из них ровесницы. Известно, что Таня старше Маши, которая моложе Гали. Таня моложе Вали, которая старше Гали. Кто ровесницы?” При решении задачи без использования графа будем расставлять первые буквы имен девочек от младшей к старшей. Из условия, что Маша моложе Гали непонятно, где поставить букву Г, слева или справа от буквы Т. И только после прочтения последнего условия можно сделать вывод, что Г стоит между Т и В. Получаем, что ровесниками могут быть только Таня и Валя. (Слайд 22).

Рассмотрим решение этой же задачи при помощи графа. В задаче рассматриваются два отношения “быть младше” и “быть старше”. Выберем одно из низ и построим граф отношения “быть старше”. При этом стрелку будем ставить от старшей девочки к младшей. (Слайд 23). По графу видно, что старше всех Валя, а Маша – младшая из девочек. Следовательно, ровесницы – это Галя и Таня.

Если такие простые задачи, в которых рассматривается множество, состоящее из небольшого числа элементов, еще можно решить без помощи графов, хотя такой способ решения является более сложным, то при решении задач на упорядочивание множества, состоящего из большого числа элементов, это становится практически невозможным.

Рассмотрим задачу: “На пришкольном участке растут 8 деревьев: яблоня, тополь, береза, рябина, дуб, клен, лиственница и сосна. Рябина выше лиственницы, яблоня выше клена, дуб ниже березы, но выше сосны, сосна выше рябины, береза ниже тополя, а лиственница выше яблони. Расположите деревья от самого низкого к самому высокому”. (Слайд 24). Будем решать ее при помощи графа. Для этого отметим все деревья точками, а точки обозначим первыми буквами названия деревьев. В задаче рассматриваются два отношения: “быть ниже” и “быть выше”. В нашем случае удобнее рассматривать отношение “быть ниже” и вести стрелку от более низкого дерева к более высокому. Если в задаче сказано, что рябина выше лиственницы, то стрелку ставим от лиственницы к рябине и т.д. Получаем граф, на котором видно, что самое низкое дерево – клен, затем идут яблоня, лиственница, рябина, сосна, дуб, береза и тополь. (Слайд 25).

Следующий тип графов, которые можно использовать при решении задач в начальной школе – это граф-дерево или дерево возможностей. Графы такого вида используются при решении комбинаторных задач, когда надо осуществить перебор всех возможных вариантов. (Слайд 26).

Рассмотрим задачу: “В столовой на горячее можно заказать щуку, грибы и баранину, на гарнир – картофель и рис, а из напитков – чай и кофе. Сколько различных вариантов обедов можно составить из указанных блюд? (Слайд 27).

Т.к. горячих блюд три, то поставим три точки. Каждую точку обозначим первой буквой названия блюда. От этих точек проведем по две линии вниз и поставим точки, т.к. гарниров два. Их также обозначим первыми буквами названий. От каждого гарнира также проведем по две линии, точки будут обозначать напиток. Каждый путь по этому графу соответствует одному из способов выбора. Число таких путей будет соответствовать числу точек в нижнем ряду. Сосчитаем точки третьего ряда на нашем графе. Их 12, значит, можно составить 12 различных обедов. (Слайд 28).

Рассмотрим еще одну, более сложную задачу: “Из наборного полотна взяли 2 карточки с цифрой 1 и 3 карточки с цифрой 5. Сколько различных пятизначных чисел можно составить из этих карточек?” (Слайд 29).

По графу видно, что всего таких чисел можно составить 10, причем все их можно легко перечислить. (Слайд 30).

Последний вид графов, которые мы рассмотрим – это граф с ребрами двух цветов. (Слайд 31). Эти графы соответствуют таким ситуациям, в которых одни пары элементов множества находятся между собой в данном отношении, а другие – нет.

Рассмотрим задачу: “В одном классе учатся Иван, Петр и Сергей. Их фамилии Иванов, Петров и Сергеев. Установи фамилию каждого из ребят, если известно, что Иван не Иванов, Петр не Петров и Сергей не Сергеев и что Сергей живет в одном доме Петровым”. (Слайд 32).

В этой задаче речь идет о двух множествах: множестве имен и множестве фамилий. В этом случае, конечно, можно решить задачу с использованием таблицы, но для решения задач с тремя множествами таблицы уже будут непригодны. В этом случае решение задачи можно осуществить с помощью графов. Обозначим имена мальчиков точками, точно также поступим и с множеством фамилий. Если для данной пары элементов отношение выполняется, то соединим их красной линией, а если нет – черной. (Слайд 33). На графе видно, что Иван не Иванов, Петр – не Петров, Сергей – не Сергеев и не Петров, т.к. Сергей и Петров живут в одном доме. Поскольку Сергей – не Сергеев и не Петров, то, значит, он Иванов. Проведем красную линию от Сергея к Иванову. Тогда Ивановым Петр быть не может – соединим соответствующие точки черной линией. Итак, Петр – не Иванов и не Петров, следовательно, он Сергеев. Остается, что Иван носит фамилию Петров.

Рассмотрим задачу, в которой требуется установить соответствие между тремя множествами: “Три друга – Алеша, Сергей и Денис – купили щенков разной породы: щенка ротвейлера, щенка колли и щенка овчарки. Известно, что: щенок Алеши темнее по окрасу, чем ротвейлер, Леси и Гриф; щенок Сергея старше Грифа, ротвейлера и овчарки; Джек и ротвейлер всегда гуляют вместе. У кого какой породы щенок? Назовите клички щенков.” (Слайд 34).

Изобразим условие задачи при помощи графа. (Слайды 35–37). В результате получим, что у Сергея щенок породы колли Леси, у Алеши щенок овчарки Джек, у Дениса щенок ротвейлера по кличке Гриф.

Рассмотренные выше задания составляют большую часть решаемых с помощью графов задач, доступных по уровню сложности младшим школьникам.

28.04.2011

xn--i1abbnckbmcl9fb.xn--p1ai

ЗАДАЧИ НА ПРИМЕНЕНИЕ ТЕОРИИ ГРАФОВ.

Поиск Лекций

---

 

В данном параграфе будут рассмотрены некоторые задачи, при решении которых используется теория графов. Они считаются классическими.

 

Задача 4.1. Необходимо составить фрагмент расписания для одного дня с учетом следующих обстоятельств:

1. учитель истории может дать либо первый, либо второй, либо третий уроки, но только один урок;

2. учитель литературы может дать один, либо второй, либо третий урок;

3. математик готов дать либо только первый, либо только второй урок;

4. преподаватель физкультуры согласен дать только последний урок.

Сколько и каких вариантов расписания, удовлетворяющего всем вышеперечисленным условиям одновременно, может составить завуч школы?

 

Решение.Без сомнения, эту задачу можно решить путем обыкновенного перебора всех возможных вариантов, но решение будет наиболее простым, если вычертить граф в виде дерева.

Данная задача является классическим примером удачного использования теории графов. В настоящее время существует программа «Расписание 3.0» компьютерной фирмы ЛинTex, в которой она решена с использованием современных технологий.

Рассмотрим еще одну задачу, решением которой также является граф.

 

Задача 4.2. В составе экспедиции должно быть 6 специалистов: биолог, врач, синоптик, гидролог, механик и радист. Имеется 8 кандидатов, из которых и нужно выбрать участников экспедиции; условные имена претендентов: A, B, C, D, E, F, G и H. Обязанности биолога могут исполнять E и G, врача – A и D, синоптика – F и G, гидролога – B и F,радиста – С и D, механика – C и H. Предусмотрено, что в экспедиции каждый из них будет выполнять только одну обязанность. Кого и в какой должности следует включить в состав экспедицию, если Fне может ехать без B, D–без Hи C, Cне может ехать вместе с G, A– вместе с B?

 

Решение. Процесс решения задачи во всех подробностях мы рассматривать не будем. Заметим только, что задать возможный вариант решения, то есть описать точный состав экспедиции, можно с помощью четного графа, в котором вершины разделены на две группы, а ребра могут соединять лишь вершины разных групп.

Применительно к задаче об экспедиции одна группа вершин есть группа из 8 кандидатов, а вторая – из 6 должностей.

Задача 4.3.Планета имеет форму выпуклого многогранника, причем в его вершинах расположены города, а каждое ребро является дорогой. Две дороги закрыты на ремонт. Докажите, что из любого города можно проехать в любой другой по оставшимся дорогам.

 

Решение. Пусть Aи B – данные города. Докажем сначала, что из Aв B можно было проехать до закрытия на ремонт двух дорог. Рассмотрим для этого проекцию многогранника на некоторую прямую, не перпендикулярную ни одному из его ребер (при такой проекции вершины многогранника не сливаются).

Пусть A’иB’ –проекции точек AиB,а M’и N’–крайние точки проекции многогранника (в точки M’и N’ проецируютсявершины Mи N).Если идти из вершины Aтак, что в проекции движение будет происходить по направлению от M’к N’, то, в конце концов, мы обязательно попадем в вершину N. Аналогично из вершины B можно пройти в N. Таким образом, можно проехать из A в B (через N).

Если полученный путь из AиB проходит через закрытую дорогу, то есть еще два объезда по граням, для которых это ребро является общим. Вторая закрытая дорога не может находиться сразу на двух этих объездах. Значит, из города Aв городB можно проехать, по крайней мере, одним путем.

 

Итак, в данном параграфе рассмотрены некоторые задачи, для решения которых применяется теория графов. В §5 мы приведем условия и решения задач школьного курса математики.

 

ПРИМЕНЕНИЕ ТЕОРИИ ГРАФОВ В ШКОЛЬНОМ

КУРСЕ МАТЕМАТИКИ.

В соответствии с вышесказанным, в данном параграфе будут рассмотрены задачи, которые используются в школе на уроках математики.

 

Условно их можно классифицировать, подразделив на несколько групп:

1. Задачи о мостах.

2. Логические задачи

3. Задачи о «правильном» раскрашивании карт

4. Задачи на построение уникурсальных графов

5.

Рассмотрим несколько типичных примеров решения задач каждого вида.

 

Одной из наиболее известных задач о мостах является эйлерова задача; все остальные сформулированы похожим образом и решаются по тому же принципу. Поэтому в данном параграфе мы не будем подробно останавливаться разборе этого типа задач.

 

Основой применения графов для решения логических задач служит выявление и последовательное исключение возможностей, заданных в условии. Это выявление логических возможностей часто может быть истолковано с помощью построения и рассмотрения соответствующих графов.

 

Задача 5.1.Из трех человек, стоящих рядом, один всегда говорит правду (правдолюб), другой всегда лжет (лжец), а третий, смотря по обстоятельствам, говорит либо правду, либо ложь (дипломат). У стоящего слева спросили: «Кто стоит рядом с тобой?». Он ответил: «Правдолюб». Стоящему в центре задали вопрос: «Кто ты?», и он ответил: «Я дипломат». Когда у стоящего справа спросили: «Кто стоит рядом с тобой?», он сказал: «Лжец». Кто где стоял?

Решение: Если в данной задаче ребро графа будет соответствовать месту, занимаемому тем или иным человеком, то нам могут представиться следующие возможности .

 

Рассмотрим первую возможность. Если «правдолюб» стоит слева, то рядом с ним, судя по его ответу, также стоит «правдолюб». У нас же стоит «лжец». Следовательно, эта расстановка не удовлетворяет условию задачи. Рассмотрев таким образом все остальные возможности, мы придем к выводу, что позиция «дипломат», «лжец», «правдолюб» удовлетворяет задаче. Действительно, если «правдолюб» стоит справа, то, по его ответу, рядом с ним стоит «лжец», что выполняется. Стоящий в центре заявляет, что он «дипломат», и, следовательно, лжет (что возможно из условия), а стоящий справа также лжет. Таким образом, все условия задачи выполнены.

 

Задача 5.2. В обеденный перерыв члены строительной бригады разговорились о том, кто сколько газет читает. Выяснилось, что каждый выписывает и читает две и только две газеты, каждую газету читает пять человек, и любая комбинация читается одним человеком. Сколько различных газет выписывают члены бригады? Сколько человек в бригаде?

Решение: Решение этой задачи достигается построением следующего графа, где каждая вершина обозначает соответствующую газету и соответственно 5 подписчиков, а каждое ребро будет соответствовать одному подписчику.

Иными словами, суть метода решения этой и подобных ей задач состоит в установлении связей между множеством вершин и множеством ребер графа.

 

Любая географическая карта является многоугольным графом, в котором страны будут гранями, границы – ребрами, а окружающий страны Мировой океан – бесконечной гранью.

Для лучшего зрительного восприятия необходимо, чтобы страны с общей границей были раскрашены в разные цвета. Такую карту называют «правильно» раскрашенной.

Широко известное предположение состоит в том, что каждая карта может быть раскрашена с соблюдением требуемых условий при помощи четырех красок. Этому вопросу уделяется большое внимание в популярной литературе, и здесь мы не будем останавливаться на его рассмотрении.

 

Задачи на проведение эйлеровых линий без повторений и без отрыва карандаша от бумаги являются одним из математических развлечений. При решении подобных задач необходимо помнить следующее положение. Для того, чтобы на графе имелась цепь, соединяющая АА и ВВ, содержащая все его ребра в точности по одному разу, необходимо и достаточно, чтобы АА и ВВ были единственными нечетными вершинами, т. е. вершинами с нечетной степенью.

Рекомендуемые страницы:

Поиск по сайту

poisk-ru.ru

Применение графов при решении задач

2.2. Применение графов при решении задач

Задачи на вычерчивание фигур одним росчерком

Задача 1. О Кенигсбергских мостах. Город Кенигсберг расположен на берегах реки Прегель и двух островах. Различные части города были соединены семью мостами. По воскресеньям горожане совершали прогулки по городу.

Вопрос: можно ли совершить прогулку таким образом, чтобы, выйдя из дома, вернуться обратно, пройдя в точности один раз по каждому мосту. Благодаря этой задаче была создана теория графов.

Мосты через реку Прегель расположены как на рисунке.
(приложение 2 рис.1).

Рассмотрим граф, соответствующий схеме мостов

Проблема семи мостов Кёнигсберга.
Суть: можно ли пройти по 7 мостам города Кёнигсберга, не ступив на каждый более одного раза.

Решение: было найдено русско-немецким математиком Леонардом Эйлером(1736 год).

Его рассуждения заключались в следующем:

1) Число нечётных вершин графа должно быть чётно (теорема 2).
2) Если все вершины графа чётные, то можно, не отрывая карандаша от бумаги, начертить граф, при этом можно начинать с любой вершины графа и завершить его в той же вершине.
3) Граф с более чем двумя нечётными вершинами невозможно начертить одним росчерком.
4) Граф кёнигсбергских мостов имел четыре нечётные вершины, следовательно, невозможно пройти по всем мостам, не проходя ни по одному из них дважды.

Задача 2. Между 9 планетами Солнечной системы введено космическое сообщение. Ракеты летают по следующим маршрутам: Земля–Меркурий, Плутон–Венера, Земля–Плутон, Плутон–Меркурий, Меркурий–Венера, Уран–Нептун, Нептун–Сатурн, Сатурн–Юпитер, Юпитер–Марс и Марс–Уран. Можно ли добраться с Земли до Марса?

Решение: Нарисуем схему: планетам будут соответствовать точки, а соединяющим их маршруты – не пересекающиеся между собой линии.

Ответ: с Земли до Марса добраться нельзя.

Логические задачи.

Задача 3. В соревнованиях по борьбе, проходящих по олимпийской системе, участвуют 20 борцов. За какое минимальное время можно провести соревнование, если в спортивном зале есть только три борцовских ковра, и на каждую схватку, включая разминку и отдых, отводится час? Изобразите схему соревнований с помощью корневого дерева.

Решение: одна из возможных схем приведена на рисунке.

(приложение 2 рис.2)

Ответ: На соревнование уйдет 7 часов.

Задача 4. Среди девяти монет есть одна фальшивая, которая легче других. Определите ее с помощью двух взвешиваний на рычажных весах.

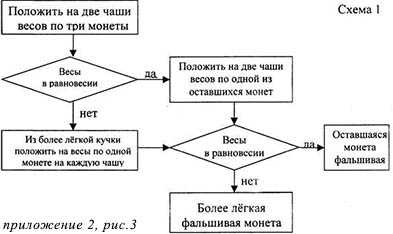Решение: Разобьем монеты на три группы по три монеты. Положим монеты двух групп на разные чашки весов.

Если чашки придут в равновесие, то фальшивая монета — в третьей группе. Если чашки не придут в равновесии, то фальшивая — в более легкой группе. Поиск фальшивой монеты среди троих: положим две монеты на разные чашки весов.

Если чашки придут в равновесие, то фальшивая — третья монета. Если чашки не придут в равновесии, то фальшивая — более легкая монета.

Решение этой задачи легко изобразить в виде графа-дерева, похожего на алгоритм. (приложение 2, рис.3)

Задачи на группу знакомств
Задача 5. Однажды Андрей, Борис, Володя, Даша и Галя договорились вечером пойти в кино. Выбор кинотеатра и сеанса они решили согласовать по телефону. Было также решено, что если с кем-то созвониться не удастся, то поход в кино отменяется. Вечером у кинотеатра собрались не все, и поэтому посещение кино сорвалось. На следующий день стали выяснять, кто кому звонил. Оказалось, что Андрей звонил Борису и Володе, Володя звонил Борису и Даше, Борис звонил Андрею и Даше, Даша звонила Андрею и Володе, а Галя звонила Андрею, Володе и Борису. Кто не сумел созвониться и поэтому не пришёл на встречу?

Решение:
Нарисуем пять точек и обозначим их буквами А, Б, В, Г, Д.

Это первые буквы имён.

Соединим те точки, которые соответствуют именам созвонившихся ребят.

(приложение 2, рис.4)

Задача 6. В первенстве класса по настольному теннису 6 участников: Андрей, Борис Виктор, Галина, Дмитрий и Елена. Первенство проводят по круговой системе – каждый из участников играет с каждым из остальных один раз. К настоящему моменту некоторые игры уже проведены: Андрей сыграл с Борисом, Галиной, Еленой; Борис – с Андреем, Галиной; Виктор – с Галиной, Дмитрием, Еленой; Галина – с Андреем, Виктором и Борисом. Сколько игр проведено к настоящему моменту и сколько еще осталось?

Решение: Получим, что сыграно 7 игр, а осталось – 8. Можно проверить: в графе 6 вершин тогда всего ребер 6*5/2=15 (7+8).

Логическая задача на переливание. В ведре 8 л воды, и имеется две кастрюли емкостью 5 и 3 л. Требуется отлить в пятилитровую кастрюлю 4 л воды и оставить в ведре 4 л, т. е. разлить воду поровну в ведро и большую кастрюлю.

Решение:

Ситуацию в каждый момент можно описать тремя числами (приложение рис.16).

В результате получаем два решения:

одно в 7 ходов, другое в 8 ходов.

(приложение 2, рис.5)

Задача 7. Имеется шахматная доска 3×3, в верхних двух углах стоят два чёрных коня, в нижних – два белых (рисунок ниже). За 16 ходов поставьте белых коней на место чёрных, а чёрных на место белых и докажите, что за меньшее число ходов это сделать невозможно.

Решение: Развернув граф возможных ходов коней в круг, получим, что в начале кони стояли так, как на рисунке ниже. А в конце кони должны поменяться местами, при этом каждый конь должен сделать 4 хода, а меньшим числом ходов обойтись не удастся, т. к. кони не могут перепрыгивать через друг друга.

Тогда, передвигая коней в графе, каждый раз перемещая всех коней, как показано на рисунках 1-4, мы получим за 16 ходов белых коней на месте чёрных, а чёрных на месте белых (рис.5). (приложение 2, рис.6)

Примеры задач, решаемых методом графов в приложении 3.

Перейти к разделу 2.3. Генеалогическое древо – один из способов применения теории графов

obuchonok.ru

Граф. Решение задач с помощью графа, 6 класс

Назарбаев Интеллектуальная школа физико- математического направления

г. Кокшетау Акмолинская область

Конспект урока по информатике

в 6 классе

«Граф.

Решение задач с помощью графа».

Подготовила учитель информатики

Нурмуханова Асель Сериковна

Кокшетау

2011

Тема урока: Граф. Решение задач с помощью графа.

Цель урока: Составить представление об организации информации в виде дерева (графа). Освоить понятие граф. Научиться решать задачи с помощью графов.

Знание

Оборудование: компьютер, таблицы, карточки. Длительность урока:40 мин

План урока

I этап – Орг.момент (3 мин)

II этап – Новая тема. Понятие графа.(8 мин)

Графы являются существенным элементом математических моделей в самых разнообразных областях науки и практики. Они помогают наглядно представить взаимоотношения между объектами или событиями в сложных системах. Многие алгоритмические задачи дискретной математики могут быть сформулированы как задачи, так или иначе связанные с графами, например задачи, в которых требуется выяснить какие-либо особенности устройства графа, или найти в графе часть, удовлетворяющую некоторым требованиям, или построить граф с заданными свойствами.

Легко найти примеры графов в самых разных областях науки и практики. Сеть дорог, трубопроводов, электрическая цепь, структурная формула химического соединения, блок-схема программы

Решение многих математических задач упрощается, если удается использовать графы. Представление данных в виде графа придает им наглядность и простоту. Многие математические доказательства также упрощаются, приобретают убедительность, если пользоваться графами. Для решения логических задач удобно использовать графы.

Графы – это рисунки, которые состоят из точек и линий, соединяющих эти точки.

Каждая пара точек в графе может быть соединена линиями. Линия указывает на связь между двумя точками.

Точки называются вершинами графа, а линиями рёбрами.

Ребро может иметь направление, которое указывается стрелочкой.

У графа обязательно есть вершины.

Граф без рёбер называется пустым.

Примеры различных графов приведены на рисунке.

Дерево (граф) – это способ организации информации об отношениях между объектами.

Слово «дерево» в теории графов означает граф, в котором нет циклов, то есть в котором нельзя из некоторой вершины пройти по нескольким различным ребрам и вернуться в ту же вершину.

Первая работа по теории графов принадлежит Леонардо Эйлеру (1736г).

Термин граф впервые ввёл 1936г Венгерский математик Денеш Кениг. Графами были названы схемы состоящие из точек и соединяющие эти точки отрезков прямых или кривых.

С помощью графов часто упрощалось решение задач, сформулированных в разных областях знаний: в автоматике , электронике, физике, химии.

С помощью графов изображаются схемы дорог, газопроводов, тепло и электро сетей.

Графы в которых не построены все возможные рёбра называется не полными графами.

III этап. Представление информации в виде дерева. (2 мин)

Особым видом графа является дерево. Данная форма модели применяется тогда, когда элементы моделируемого объекта находятся в состоянии какого-либо подчинения и соподчинения, когда есть отношение иерархичности. Модель управления предприятием (школой, театральным коллективом и т. д.) очень удобно представлять в виде дерева.

Описать граф- это значит, ответить на вопросы:

Сколько вершин?

Есть рёбра?

Есть направление?

Все ли вершины соединены рёбрами?

На каких школьных предметах вы встречались с графами, приведите примеры?

Учитель приводит несколько примеров. Вам хорошо известно понятие «родословное дерево» и вы можете изобразить в такой форме ваши родственные отношения. Каталог файлов на диске, также как и библиотечный каталог — примеры информационных моделей в форме дерева.

IV этап.Заполнение схемы. Применение графа. (3мин)

V этап. Применение знаний и закрепление изученного. (15 мин)

Рассмотрим одну из простейших задач: «Крас­ный, синий, желтый и зеленый карандаши лежат в четырех коробках по одному. Цвет карандаша от­личается от цвета коробки. Известно, что зеленый карандаш лежит в синей коробке, а красный не лежит в желтой. В какой коробке лежит каждый карандаш?»

Обозначим точками карандаши и коробки. Сплошная линия будет обозначать, что карандаш лежит в соответствующей коробке, а пунктирная, что не лежит. Тогда с учетом задачи имеем граф (1).

Далее достраиваем граф по следующему прави­лу: поскольку в каждой коробке может лежать ровно один карандаш, то из каждой точки должны выходить одна сплошная линия и три пунктирные. Получается граф (2) дающий решение задачи.

Задача1: Алия решила маме на день рождения подарить букет цветов (розы, тюльпаны или гвоздики) и поставить из или в вазу или в кувшин.

Сколькими способами это можно сделать.

Решение. Отметим точками цветы (РТГВК) (вершины графа)

А связи между ними -линиями между точками (рёбра графа)

По рисунку видно, что таких сопопбов — 6

* розы * тюльпан *гвоздики

* ваза *кувшин

Задача2. Ранним утром Миша Маша, Асем обменялись приветствиями каждый с каждым. Сколько всего было приветствий. Решите задачу с помощью графа. Нарисуй граф в рабочей тетради.

Задача3. Шесть футбольных команд должны сыграть матчи, каждая с каждой. Уже сыграли матчи.

А с В, Г,Е Г с А,Д,Е

Б с В,Д,Е Д с Б,Г,Е

В с А,Б Е с А,Б,Г,Д

Сколько матчей сыграно и сколько осталось сыграть.

Задача4. Мадии утром собрался в школу, но по пути он должен зайти в аптеку за лекарствами. Сколькими способами он может это сделать.

Задача5. В квартирах №1,2,3 жили три друга: Айдар, Тима и Саша. Известно, что в квартирах №1 и 2 жил не Айдар. Тима жил не в квартире №1. В какой квартире жил каждый из друзей.

Ответ:

Задача6. Арман, Мадии, Тимур, Сергей заняли на математической олимпиаде четыре первых места. Когда их спросили о распределений мест, они дали три ответа: Сергей – первый, Мади– второй, Сергей -второй, Арман – третий, Тимур – второй, Арман – четвертый. Известно, что в каждом ответе только одно утверждение верно. Как распределились места?

Ответ: С-1 Т-2 А -3 М-4.

Задача7. Григорий играли в шахматы. Каждый сыграл с каждым по одной партии. Сколько партий было сыграно?

Решение: Решим задачу с помощью полного графа с четырьмя вершинами А, Б, В, Г, обозначенными по первым буквам имен каждого из мальчиков. В полном графе проводятся всевозмож­ные ребра.

В данном случае отрезки-ребра обозна­чают сыгранные шахматные партии. Из рисунка видно, что граф имеет 6 ребер, значит, и партий было сыграно 6.

Задача8.Из города А в город Б ведут две дороги, из города Б в городок В -тоже две дороги и из города А в город В – тоже две дороги. Нарисуй схему и сосчитай все возможные пути из города А в город В. Ответ: 6 партий .

Задача9. Андрей, Борис, Виктор и Григорий после возвращения из спортивного лагеря подари­ли на память друг другу свои фотографии. Причем каждый мальчик подарил каждому из своих друзей
по одной фотографии. Сколько всего фотографий было подарено?

Решение. I способ. С помощью стрелок на ре­брах полного графа с вершинами А, Б, В и Г показан процесс обмена фотографиями. Очевидно, стрелок в 2 раза больше, чем ребер, т.е. 6*2 = 12. Столько же было подарено и фотографий.

II способ. Каждый из четверых мальчиков пода­рил друзьям 3 фотографии, следовательно, всего было роздано 3 • 4 = 12 фотографий.

О т в е т: 12 фотографий.

VI этап. Рефлексия. (5 мин)

«Почему понятие графа изучается в школьном курсе информатики?»

Дополнительные вопросы:

• Нужно ли на уроках информатики знакомиться с понятием графа и учиться строить их?

• Как вы считаете, с какой целью было введено понятие графа в школьный курс информатики?

• Какие качества личности позволяет развить умение строить графы?

Попробуйте сделать вывод о значении информатики и графов в частности для остальных учебных предметов. Информатика дает инструмент для познания любой научной дисциплины.

VII этап. Домашнее задание: Дополнить схему примерами применения графов. (1 мин)

VIII этап. Итог урока. Выставление оценок. (1 мин)

Список литературы:

1. Нагибин Ф.Ф. Применение графов для решения логических задач.

// Математика в школе. — 1964. — № 3.

2. Шедивы Я. Решение логических задач при помощи графов.

// Математика в школе. — 1967. — № 6.

3. Березина Л.Ю. Графы помогают решать логические задачи.

// Математика в школе. — 1972. — № 2.

4. Федосеев В.Н. Элементы теории вероятностей для VII—VIII классов средней школы.

// Математика в школе. — 2002. — № 4.

Ученик знает назначение графов
Понимание	Умеет приводить примеры использования графов в различных учебных предметах (химия, информатика, биология, геометрия и др.) и повседневной жизни.
Применение	Умеет записывать арифметические выражения в виде графов, отражать информацию в виде семантической сети, изображать классификации различных объектов в виде дерева
Анализ	Умеет из множества предметов вычленить объекты, обозначить связи между ними.
Айдар	Тима	Саша
№1	—	—	+
№2	—	+	—
№3	+	—	—

doc4web.ru

No related posts.