Оценка параметров надежности при нормальном законе распределения отказов средствами Excel
В статье проведена оценка показателей надежности безотказной работы системы. На примере показан расчет основных показателей средствами Excel.
Ключевые слова: безотказная работа, доверительный интервал, испытания, нормальный закон распределения, число отказов.
Определение показателей надёжности необходимо для формулирования требования по надежности к проектируемым устройствам или системам. Показатель надежности — это количественная характеристика одного или нескольких свойств, составляющих надежность объекта [1].
Поскольку отказы и сбои элементов являются случайными событиями, то теория вероятностей и математическая статистика являются основным аппаратом, используемым при исследовании надежности, а сами характеристики надежности должны выбираться из числа показателей, принятых в теории вероятностей [2, с.
Количественные характеристики надежности при нормальном законе распределения отказов могут быть определены из следующих выражений:
(1)
P(t)= (2)
λ( )= (3),
где нормированная и центрированная функция Лапласа.
Произведем расчет параметров надежности испытаний, проведенных в течение 100 часов на 100 деталях, 34 из которых вышли из строя.
Для построения статистического ряда время испытаний разбивают на интервалы (разряды) и подсчитывают частоту, интенсивность и вероятность отказов, используя выражения (1), (2) и (3). Определяют доверительные интервалы математического ожидания и среднеквадратичного отклонения при нормальном законе распределения отказов и заданном коэффициенте доверия [3, с. 60].
Результаты вычислений представлены в таблице Excel (Таблица 1).
Таблица 1
Результаты расчета основных показателей испытаний
Параметр | Разряды | |||||||||
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
t | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 |
n* | 5 | 3 | 5 | 2 | 2 | 3 | 3 | 3 | 5 | 3 |
Pн(t) | 0,935 | 0,917 | 0,896 | 0,870 | 0,841 | 0,805 | 0,767 | 0,725 | 0,680 | 0,633 |
fн(t) | 0,983 | 0,986 | 0,988 | 0,990 | 0,991 | 0,992 | 0,993 | 0,993 | 0,994 | 0,994 |
| 1,050 | 1,074 | 1,102 | 1,137 | 1,178 | 1,232 | 1,294 | 1,369 | 1,460 | 1,570 |
Qн(t) | 0,064 | 0,082 | 0,103 | 0,129 | 0,158 | 0,194 | 0,232 | 0,274 | 0,319 | 0,366 |
Dн | 0,014 | 0,002 | 0,026 | 0,020 | 0,011 | 0,005 | 0,002 | 0,014 | 0,009 | 0,026 |
λн | 0,085065269 | |||||||||
Листинг фрагмента программы расчета показателей при нормальном законе распределения:
‘Вычислим 43 строку таблицы(45)=============================Рн(t)
СтрокаТаблицы = 45
‘a=(t-Tср)/Сигма
СтолбецТаблицы = 4
For n = СтолбецТаблицы To (КоличествоСтолбцовТаблицы + СтолбецТаблицы — 1)
a = Abs(Sheets(«ОсновнаяТаблица»). Cells(3, n).Value — Tcp) / Сигма
Cells(3, n).Value — Tcp) / Сигма
‘b=Фо
СтрокаТаблФункцЛапласа = 2
While Sheets(«Таблица функции Лапласа»).Cells(СтрокаТаблФункцЛапласа, 1).Value <> «»
СтрокаТаблФункцЛапласа = СтрокаТаблФункцЛапласа + 1
Wend
If a <= Sheets(«Таблица функции Лапласа»).Cells(2, 1).Value Then
ф0 = Sheets(«Таблица функции Лапласа»).Cells(2, 2).Value
GoTo далее
End If
If a >= Sheets(«Таблица функции Лапласа»).Cells(СтрокаТаблФункцЛапласа — 1, 1).Value Then
ф0 = Sheets(«Таблица функции Лапласа»).Cells(СтрокаТаблФункцЛапласа — 1, 2).Value
GoTo далее
End If
СтрокаТаблФункцЛапласа = 2
While Sheets(«Таблица функции Лапласа»).Cells(СтрокаТаблФункцЛапласа, 1).Value <> «»
If Sheets(«Таблица функции Лапласа»).Cells(СтрокаТаблФункцЛапласа, 1).Value = a Then
ф0 = Sheets(«Таблица функции Лапласа»).Cells(СтрокаТаблФункцЛапласа, 2).Value
GoTo далее3
End If
If a < Sheets(«Таблица функции Лапласа»). Cells(СтрокаТаблФункцЛапласа, 1).Value And a > Sheets(«Таблица функции Лапласа»).Cells(СтрокаТаблФункцЛапласа — 1, 1).Value Then
Cells(СтрокаТаблФункцЛапласа, 1).Value And a > Sheets(«Таблица функции Лапласа»).Cells(СтрокаТаблФункцЛапласа — 1, 1).Value Then
If Sheets(«Таблица функции Лапласа»).Cells(СтрокаТаблФункцЛапласа, 1).Value — a < a — Sheets(«Таблица функции Лапласа»).Cells(СтрокаТаблФункцЛапласа — 1, 1).Value Then
ф0 = Sheets(«Таблица функции Лапласа»).Cells(СтрокаТаблФункцЛапласа, 2).Value
Else
ф0 = Sheets(«Таблица функции Лапласа»).Cells(СтрокаТаблФункцЛапласа — 1, 2).Value
End If
GoTo далее3
End If
СтрокаТаблФункцЛапласа = СтрокаТаблФункцЛапласа + 1
Wend
далее3:
Sheets(«ОсновнаяТаблица»).Cells(СтрокаТаблицы, n).Value = 0.5 + ф0
Next
‘Вычислим 44 строку таблицы(46)=============================fн(t)
СтрокаТаблицы = 46
СтолбецТаблицы = 4
Pi = Application.WorksheetFunction.Pi
For n = СтолбецТаблицы To (КоличествоСтолбцовТаблицы + СтолбецТаблицы — 1)
Sheets(«ОсновнаяТаблица»). 2)))
2)))
Next
‘Заполним 45 строку таблицы(47)=============================Лямбда н(t)
СтрокаТаблицы = 47
СтолбецТаблицы = 4
For n = СтолбецТаблицы To (КоличествоСтолбцовТаблицы + СтолбецТаблицы — 1)
Sheets(«ОсновнаяТаблица»).Cells(СтрокаТаблицы, n).Value = Sheets(«ОсновнаяТаблица»).Cells(46, n).Value / Sheets(«ОсновнаяТаблица»).Cells(45, n).Value
Next
Для определения доверительного интервала для математического ожидания по таблице квантилей распределения Стьюдента находят квантиль вероятности. Используя выражения (4) и (5) проводят расчеты
(4)
(5)
‘Заполним 30 строку таблицы(32)=============================Tср min
СтрокаТаблицы = 32
СтолбецТаблицы = 4
For n = СтолбецТаблицы To (КоличествоСтолбцовТаблицы + СтолбецТаблицы — 1)
Next
СтепеньСвободыПриНормРаспред = КоличествоСтолбцовТаблицы + 1 — 2
Sheets(«ОсновнаяТаблица»).Cells(СтрокаТаблицы, 4).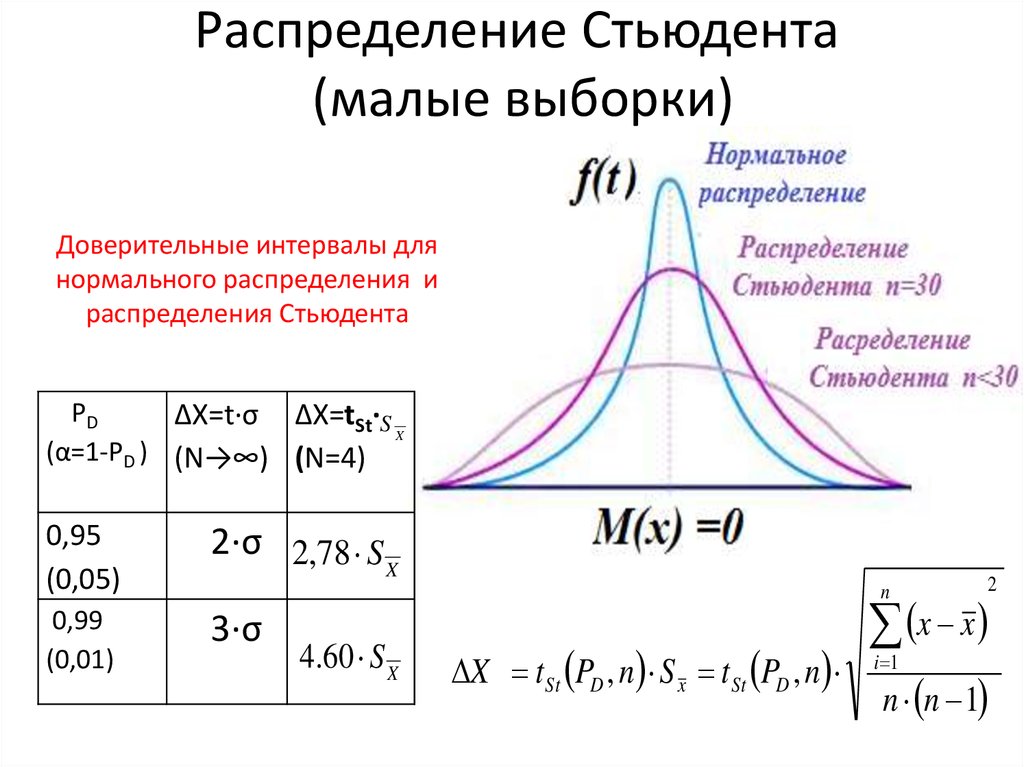 Value = Tcp — Sheets(«ОсновнаяТаблица»).Cells(31, 4).Value * Сигма / Sqr(СтепеньСвободыПриНормРаспред)
Value = Tcp — Sheets(«ОсновнаяТаблица»).Cells(31, 4).Value * Сигма / Sqr(СтепеньСвободыПриНормРаспред)
Sheets(«ОсновнаяТаблица»).Range(Cells(СтрокаТаблицы, 4), Cells(СтрокаТаблицы, n — 1)).MergeCells = True
Sheets(«ОсновнаяТаблица»).Range(Cells(СтрокаТаблицы, 4), Cells(СтрокаТаблицы, n — 1)).HorizontalAlignment = xlCenter
‘Заполним 31 строку таблицы(33)=============================Tср max
СтрокаТаблицы = 33
СтолбецТаблицы = 4
For n = СтолбецТаблицы To (КоличествоСтолбцовТаблицы + СтолбецТаблицы — 1)
Next
Sheets(«ОсновнаяТаблица»).Cells(СтрокаТаблицы, 4).Value = Tcp + Sheets(«ОсновнаяТаблица»).Cells(31, 4).Value * Сигма / Sqr(СтепеньСвободыПриНормРаспред)
Sheets(«ОсновнаяТаблица»).Range(Cells(СтрокаТаблицы, 4), Cells(СтрокаТаблицы, n — 1)).MergeCells = True
Sheets(«ОсновнаяТаблица»).Range(Cells(СтрокаТаблицы, 4), Cells(СтрокаТаблицы, n — 1)).HorizontalAlignment = xlCenter
Тср, min = | 79,29380755 ч. |
Тср, max = | 172,43129 ч. |
Для определения доверительного интервала для среднеквадратичного отклонения по таблице квантилей χ 2 – квадрат распределения определяют квантили для заданных вероятностей P 1 и P 2 .
(0,05) = | 3,32511 |
(0,95) = | 16,919 |
‘Заполним 32 строку таблицы(34)=============================X1(0,05)
СтрокаОсновнойТаблицы = 34
СтрокаТаблКвантили = 4
ВходнаяСтрочнаяВеличина = СтепеньСвободыПриНормРаспред
While Sheets(«Квантили распределения хи»).Cells(СтрокаТаблКвантили, 1).Value <> «»
СтрокаТаблКвантили = СтрокаТаблКвантили + 1
Wend
If ВходнаяСтрочнаяВеличина <= Sheets(«Квантили распределения хи»). Cells(4, 1).Value Then
Cells(4, 1).Value Then
СтрокаТабл = 4
GoTo СледующийПоиск10
End If
If ВходнаяСтрочнаяВеличина >= Sheets(«Квантили распределения хи»).Cells(СтрокаТаблКвантили — 1, 1).Value Then
СтрокаТабл = СтрокаТаблКвантили — 1
GoTo СледующийПоиск10
End If
СтрокаТаблКвантили = 4
While Sheets(«Квантили распределения хи»).Cells(СтрокаТаблКвантили, 1).Value <> «»
If Sheets(«Квантили распределения хи»).Cells(СтрокаТаблКвантили, 1).Value = ВходнаяСтрочнаяВеличина Then
СтрокаТабл = СтрокаТаблКвантили
GoTo СледующийПоиск10
End If
If ВходнаяСтрочнаяВеличина < Sheets(«Квантили распределения хи»).Cells(СтрокаТаблКвантили, 1).Value And ВходнаяСтрочнаяВеличина > Sheets(«Квантили распределения хи»).Cells(СтрокаТаблКвантили — 1, 1).Value Then
If Sheets(«Квантили распределения хи»).Cells(СтрокаТаблКвантили, 1).Value — ВходнаяСтрочнаяВеличина < ВходнаяСтрочнаяВеличина — Sheets(«Квантили распределения хи»). Cells(СтрокаТаблКвантили — 1, 1).Value Then
Cells(СтрокаТаблКвантили — 1, 1).Value Then
СтрокаТабл = СтрокаТаблКвантили
Else
СтрокаТабл = СтрокаТаблКвантили — 1
End If
GoTo СледующийПоиск10
End If
СтрокаТаблКвантили = СтрокаТаблКвантили + 1
Wend
СледующийПоиск10:
СтолбецТаблКвантили = 2
ВходнаяВертикальнаяВеличина = 0.05
While Sheets(«Квантили распределения хи»).Cells(3, СтолбецТаблКвантили).Value <> «»
СтолбецТаблКвантили = СтолбецТаблКвантили + 1
Wend
If ВходнаяВертикальнаяВеличина <= Sheets(«Квантили распределения хи»).Cells(3, 2).Value Then
СтолбецТабл = 2
GoTo СледующийПоиск11
End If
If ВходнаяВертикальнаяВеличина >= Sheets(«Квантили распределения хи»).Cells(3, СтолбецТаблКвантили — 1).Value Then
СтолбецТабл = СтолбецТаблКвантили — 1
GoTo СледующийПоиск11
End If
СледующийПоиск11:
СтолбецТаблКвантили = 11
While Sheets(«Квантили распределения хи»). Cells(3, СтолбецТаблКвантили).Value <> «»
Cells(3, СтолбецТаблКвантили).Value <> «»
If Sheets(«Квантили распределения хи»).Cells(3, СтолбецТаблКвантили).Value = ВходнаяВертикальнаяВеличина Then
СтолбецТабл = СтолбецТаблКвантили
GoTo СледующийПоиск12
End If
If ВходнаяСтрочнаяВеличина < Sheets(«Квантили распределения хи»).Cells(3, СтолбецТаблКвантили).Value And ВходнаяВертикальнаяВеличина > Sheets(«Квантили распределения хи»).Cells(3, СтолбецТаблКвантили — 1).Value Then
If Sheets(«Квантили распределения хи»).Cells(3, СтолбецТаблКвантили).Value — ВходнаяВертикальнаяВеличина < ВходнаяВертикальнаяВеличина — Sheets(«Квантили распределения хи»).Cells(3, СтолбецТаблКвантили — 1).Value Then
СтолбецТабл = СтолбецТаблКвантили
Else
СтолбецТабл = СтолбецТаблКвантили — 1
End If
GoTo СледующийПоиск12
End If
СтолбецТаблКвантили = СтолбецТаблКвантили + 1
Wend
СледующийПоиск12:
x1 = Sheets(«Квантили распределения хи»). Cells(СтрокаТабл, СтолбецТабл).Value
Cells(СтрокаТабл, СтолбецТабл).Value
Sheets(«ОсновнаяТаблица»).Cells(СтрокаОсновнойТаблицы, 4).Value = x1
Sheets(«ОсновнаяТаблица»).Range(Cells(СтрокаОсновнойТаблицы, 4), Cells(СтрокаОсновнойТаблицы, n — 1)).MergeCells = True
Sheets(«ОсновнаяТаблица»).Range(Cells(СтрокаОсновнойТаблицы, 4), Cells(СтрокаОсновнойТаблицы, n — 1)).HorizontalAlignment = xlCenter
‘Заполним 33 строку таблицы(35)=============================X2(0,95)
СтрокаОсновнойТаблицы = 35
СтрокаТаблКвантили = 4
ВходнаяСтрочнаяВеличина = СтепеньСвободыПриНормРаспред
While Sheets(«Квантили распределения хи»).Cells(СтрокаТаблКвантили, 1).Value <> «»
СтрокаТаблКвантили = СтрокаТаблКвантили + 1
Wend
If ВходнаяСтрочнаяВеличина <= Sheets(«Квантили распределения хи»).Cells(4, 1).Value Then
СтрокаТабл = 4
GoTo СледующийПоиск13
End If
If ВходнаяСтрочнаяВеличина >= Sheets(«Квантили распределения хи»). Cells(СтрокаТаблКвантили — 1, 1).Value Then
Cells(СтрокаТаблКвантили — 1, 1).Value Then
СтрокаТабл = СтрокаТаблКвантили — 1
GoTo СледующийПоиск13
End If
СтрокаТаблКвантили = 4
While Sheets(«Квантили распределения хи»).Cells(СтрокаТаблКвантили, 1).Value <> «»
If Sheets(«Квантили распределения хи»).Cells(СтрокаТаблКвантили, 1).Value = ВходнаяСтрочнаяВеличина Then
СтрокаТабл = СтрокаТаблКвантили
GoTo СледующийПоиск13
End If
If ВходнаяСтрочнаяВеличина < Sheets(«Квантили распределения хи»).Cells(СтрокаТаблКвантили, 1).Value And ВходнаяСтрочнаяВеличина > Sheets(«Квантили распределения хи»).Cells(СтрокаТаблКвантили — 1, 1).Value Then
If Sheets(«Квантили распределения хи»).Cells(СтрокаТаблКвантили, 1).Value — ВходнаяСтрочнаяВеличина < ВходнаяСтрочнаяВеличина — Sheets(«Квантили распределения хи»).Cells(СтрокаТаблКвантили — 1, 1).Value Then
СтрокаТабл = СтрокаТаблКвантили
Else
СтрокаТабл = СтрокаТаблКвантили — 1
End If
GoTo СледующийПоиск13
End If
СтрокаТаблКвантили = СтрокаТаблКвантили + 1
Wend
СледующийПоиск13:
СтолбецТаблКвантили = 2
ВходнаяВертикальнаяВеличина = 0. 95
95
While Sheets(«Квантили распределения хи»).Cells(3, СтолбецТаблКвантили).Value <> «»
СтолбецТаблКвантили = СтолбецТаблКвантили + 1
Wend
If ВходнаяВертикальнаяВеличина <= Sheets(«Квантили распределения хи»).Cells(3, 2).Value Then
СтолбецТабл = 2
GoTo СледующийПоиск14
End If
If ВходнаяВертикальнаяВеличина >= Sheets(«Квантили распределения хи»).Cells(3, СтолбецТаблКвантили — 1).Value Then
СтолбецТабл = СтолбецТаблКвантили — 1
GoTo СледующийПоиск14
End If
СледующийПоиск14:
СтолбецТаблКвантили = 2
While Sheets(«Квантили распределения хи»).Cells(3, СтолбецТаблКвантили).Value <> «»
If Sheets(«Квантили распределения хи»).Cells(3, СтолбецТаблКвантили).Value = ВходнаяВертикальнаяВеличина Then
СтолбецТабл = СтолбецТаблКвантили
GoTo СледующийПоиск15
End If
If ВходнаяСтрочнаяВеличина < Sheets(«Квантили распределения хи»).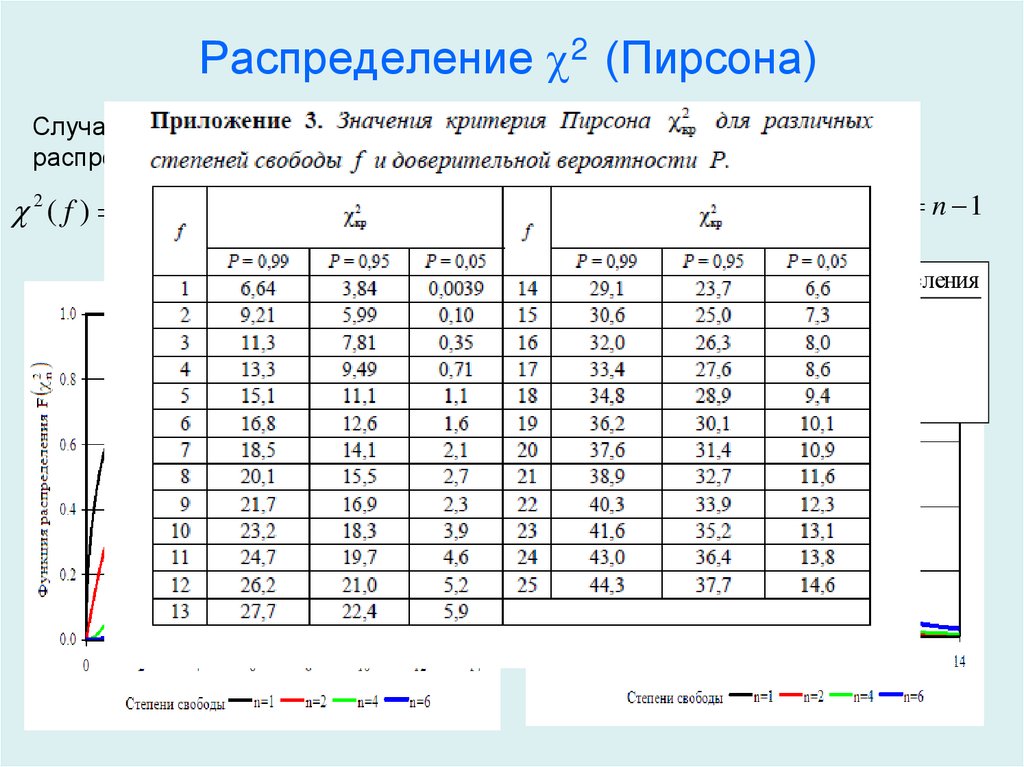 Cells(3, СтолбецТаблКвантили).Value And ВходнаяВертикальнаяВеличина > Sheets(«Квантили распределения хи»).Cells(3, СтолбецТаблКвантили — 1).Value Then
Cells(3, СтолбецТаблКвантили).Value And ВходнаяВертикальнаяВеличина > Sheets(«Квантили распределения хи»).Cells(3, СтолбецТаблКвантили — 1).Value Then
If Sheets(«Квантили распределения хи»).Cells(3, СтолбецТаблКвантили).Value — ВходнаяВертикальнаяВеличина < ВходнаяВертикальнаяВеличина — Sheets(«Квантили распределения хи»).Cells(3, СтолбецТаблКвантили — 1).Value Then
СтолбецТабл = СтолбецТаблКвантили
Else
СтолбецТабл = СтолбецТаблКвантили — 1
End If
GoTo СледующийПоиск15
End If
СтолбецТаблКвантили = СтолбецТаблКвантили + 1
Wend
СледующийПоиск15:
x1 = Sheets(«Квантили распределения хи»).Cells(СтрокаТабл, СтолбецТабл).Value
Sheets(«ОсновнаяТаблица»).Cells(СтрокаОсновнойТаблицы, 4).Value = x1
Sheets(«ОсновнаяТаблица»).Range(Cells(СтрокаОсновнойТаблицы, 4), Cells(СтрокаОсновнойТаблицы, n — 1)).MergeCells = True
Sheets(«ОсновнаяТаблица»).Range(Cells(СтрокаОсновнойТаблицы, 4), Cells(СтрокаОсновнойТаблицы, n — 1)). HorizontalAlignment = xlCenter
HorizontalAlignment = xlCenter
Получим минимальное σ min и максимальное σ max значения среднеквадратического отклонения:
(6)
(7)
‘Заполним 34 строку таблицы(36)=============================Сигма min
СтрокаТаблицы = 36
СтолбецТаблицы = 4
For n = СтолбецТаблицы To (КоличествоСтолбцовТаблицы + СтолбецТаблицы — 1)
Next
Sheets(«ОсновнаяТаблица»).Cells(СтрокаТаблицы, 4).Value = Сигма * Sqr((СтепеньСвободыПриНормРаспред — 1) / Sheets(«ОсновнаяТаблица»).Cells(35, 4).Value)
Sheets(«ОсновнаяТаблица»).Range(Cells(СтрокаТаблицы, 4), Cells(СтрокаТаблицы, n — 1)).MergeCells = True
Sheets(«ОсновнаяТаблица»).Range(Cells(СтрокаТаблицы, 4), Cells(СтрокаТаблицы, n — 1)).HorizontalAlignment = xlCenter
‘Заполним 35 строку таблицы(37)=============================Сигма max
СтрокаТаблицы = 37
СтолбецТаблицы = 4
For n = СтолбецТаблицы To (КоличествоСтолбцовТаблицы + СтолбецТаблицы — 1)
Next
СтепеньСвободыПриНормРаспред = КоличествоСтолбцовТаблицы + 1 — 2
Sheets(«ОсновнаяТаблица»). Cells(СтрокаТаблицы, 4).Value = Сигма * Sqr((СтепеньСвободыПриНормРаспред — 1) / Sheets(«ОсновнаяТаблица»).Cells(34, 4).Value)
Cells(СтрокаТаблицы, 4).Value = Сигма * Sqr((СтепеньСвободыПриНормРаспред — 1) / Sheets(«ОсновнаяТаблица»).Cells(34, 4).Value)
Sheets(«ОсновнаяТаблица»).Range(Cells(СтрокаТаблицы, 4), Cells(СтрокаТаблицы, n — 1)).MergeCells = True
Sheets(«ОсновнаяТаблица»).Range(Cells(СтрокаТаблицы, 4), Cells(СтрокаТаблицы, n — 1)).HorizontalAlignment = xlCenter
52,40646615 | |
118,2140815 |
Число разрядов, на которые следует группировать статистический ряд, не должно быть слишком большим (тогда ряд распределения становится невыразительным, и часто в нем обнаруживают незакономерные колебания), с другой стороны, оно не должен быть слишком малым (свойства распределения при этом описываются статистическим рядом слишком грубо).
Литература:
- ГОСТ 27.
 002-89 Надежность в технике (ССНТ). Основные понятия. Термины и определения.
002-89 Надежность в технике (ССНТ). Основные понятия. Термины и определения. - Федотов, А. В. Основы теории надежности и технической диагностики: конспект лекций / А. В. Федотов, Н. Г. Скабкин. – Омск : Изд-во ОмГТУ, 2010 – 64 с.
- Коваленко, В. Н. Надежность устройств железнодорожной автоматики, телемеханики : учеб. пособие / В. Н. Коваленко. – Екатеринбург : Изд-во УрГУПС, 2013. – 87 с.
Основные термины (генерируются автоматически): Таблица функции, строка таблицы, доверительный интервал, Сигма, математическое ожидание, распределение отказов, среднеквадратичное отклонение, статистический ряд, таблица, теория вероятностей.
КОРРЕЛЯЦИОННЫЙ И РЕГРЕССИОННЫЙ АНАЛИЗ В EXCEL
1. ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА ПАРНОЙ КОРРЕЛЯЦИИ В ПРОГРАММЕ EXCEL t-статистика=0,99*(КОРЕНЬ(20-2)/КОРЕНЬ(1-0,99*0,99))=29,7745296027549 Коэффициент корреляции=0,991477169252612 Распределение Стьюдента=2,10092204024104 Расчетное значение t-статистики больше квантиля распределения Стьюдента, следовательно величина коэффициента корреляции является значимой. 2. ПОСТРОЕНИЕ РЕГРЕССИОННОЙ МОДЕЛИ СВЯЗИ МЕЖДУ ДВУМЯ ВЕЛИЧИНАМИ 1-ый способ
FРАСПОБР=4,4139 Проверили адекватность построенной модели, используя расчетный уровень значимости (P): 2,18499711496499E-17 2 –й способ
Для данного примера уравнение модели имеет вид:Y=2,53+0,5X Проверка адекватности модели выполняется по расчетному уровню значимости P,
указанному в столбце Значимость F. Проверка статистической значимости коэффициентов модели выполняется по расчетным уровням значимости P, указанным в столбце P-значение. Если расчетный уровень значимости меньше заданного уровня значимости α =0,05, то соответствующий коэффициент модели статистически значим. Множественный R – коэффициент корреляции. Чем ближе его величина к 1, тем более тесная связь между изучаемыми показателями. Для данного примера R= 0,99. Это позволяет сделать вывод, что качество земли – один из основных факторов, от которого зависит урожайность зерновых культур. R-квадрат – коэффициент детерминации. Он получается возведением в квадрат коэффициента корреляции – R2=0,98. Он показывает, что урожайность зерновых культур на 98% зависит от качества почвы, а на долю других факторов приходится 0,02%. 3-ий способ (графический) |
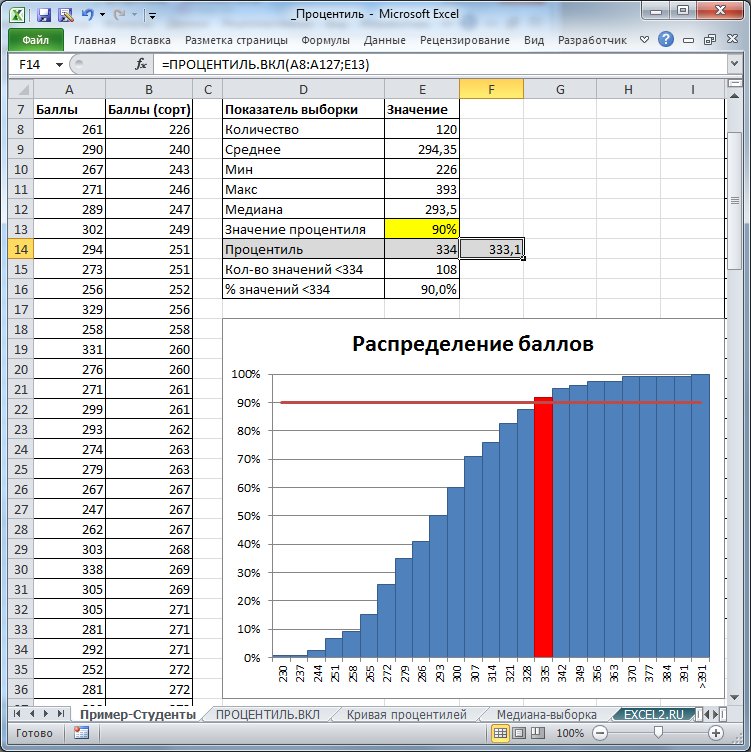
Расчет квантилей или процентилей в Excel
В этом руководстве показано, как вычислять квантили или процентили, связанные с доверительными интервалами, в Excel с помощью программного обеспечения XLSTAT.
Квантиль и процентили
XLSTAT имеет полный инструмент для вычисления квантилей или процентилей, их доверительного интервала и графического представления.
Квантили являются важными статистическими показателями, их легко понять. Квантиль 0,5 — это значение, при котором половина выборки находится ниже, а другая половина — выше. Его еще называют средним. Квантиль называется процентилем, если он основан на шкале от 0 до 100. 0,95-квантиль эквивалентен 95-процентилю и таков, что 95 % выборки ниже его значения, а 5 % выше.
Набор данных для создания квантиля
Набор данных был получен от [Lewis T. and Taylor L.R. (1967). Введение в экспериментальную экологию, Нью-Йорк: Academic Press, Inc. Это касается 237 детей, описанных по полу и росту в сантиметрах (1 см = 0,4 дюйма).
Настройка расчета определенного квантиля
После открытия XLSTAT выберите XLSTAT / Description / Quantiles , или нажмите на соответствующую кнопку панели инструментов «Описание» (см. ниже).
ниже).
После нажатия кнопки появится диалоговое окно Quantile . Выберите данные на листе Excel.
В нашем случае; переменная — это «Высота». Данные должны быть количественными .
Поскольку для переменных был выбран заголовок столбца, необходимо активировать опцию Метки переменных .
Мы выбираем метод оценки по умолчанию ( средневзвешенное значение при x(Np) ) и оба типа доверительных интервалов с доверительной вероятностью 95 % .
Подробную информацию о статистических методах можно найти в справке XLSTAT.
Во вкладке диаграммы выбираем все диаграммы и нас интересует 67-процентиль (две трети детей меньше, а одна треть выше).
Вычисления начинаются после того, как вы нажмете на ОК . Затем будут отображены результаты.
Интерпретация результатов генерации квантилей
В первой таблице показаны некоторые описательные статистические данные о переменной высоты. Во второй таблице отображаются квантили и связанные с ними доверительные интервалы для различных часто используемых значений. Например, медиана 159,9 см. 95-процентиль показывает, что 95% детей меньше 174,98 см.
Во второй таблице отображаются квантили и связанные с ними доверительные интервалы для различных часто используемых значений. Например, медиана 159,9 см. 95-процентиль показывает, что 95% детей меньше 174,98 см.
Затем отображается значение 67-процентиля. Две трети детей меньше 164,58 см.
Первый график (см. ниже) позволяет нам визуализировать эмпирическую кумулятивную функцию распределения со значением 67-го процентиля.
Вторая и третья диаграммы представляют собой коробчатую диаграмму и диаграмму рассеяния. 67-процентиль отображается синей линией.
Вы также можете использовать подвыборки, например пол можно использовать в качестве групповой переменной. Веса, связанные с наблюдениями, также могут быть включены.
Была ли эта статья полезной?
- Да
- №
Квантиль (квартиль, дециль и процентиль): расчет вручную + Microsoft
Квантиль — важная статистическая концепция, позволяющая разделить данные на равные группы.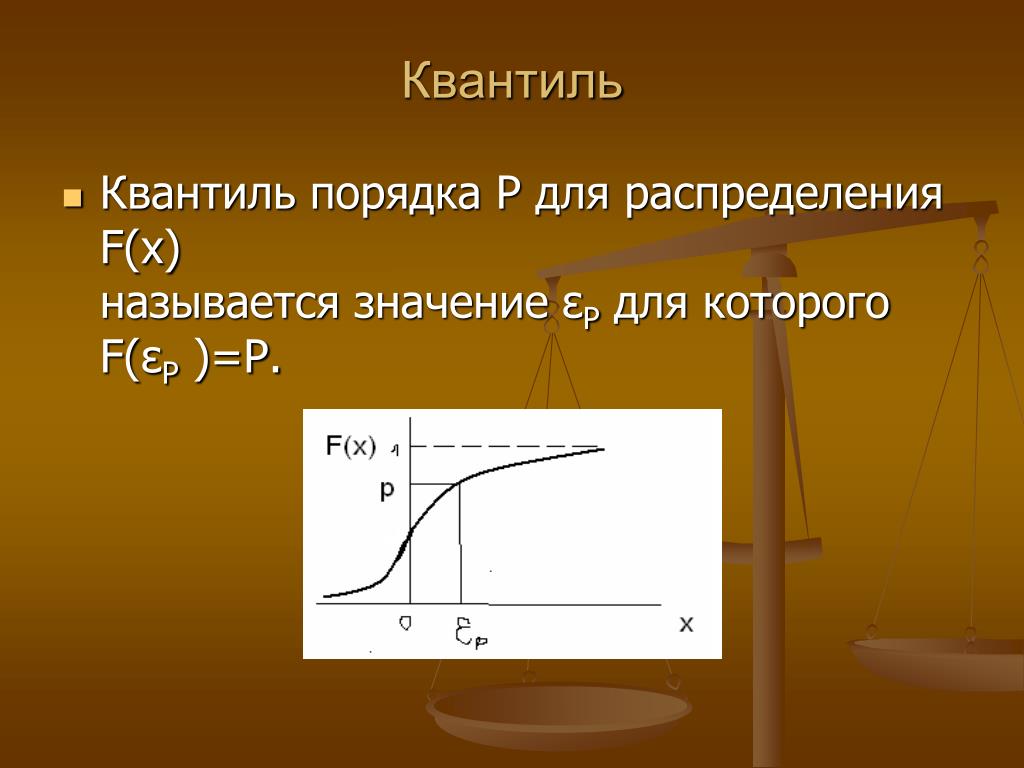 Они часто используются для выявления и анализа шаблонов данных и проведения значимых сравнений между различными наборами данных. В этом кратком руководстве мы рассмотрим основы квантилей и более подробно рассмотрим некоторые из наиболее распространенных типов: квартили, децили и процентили.
Они часто используются для выявления и анализа шаблонов данных и проведения значимых сравнений между различными наборами данных. В этом кратком руководстве мы рассмотрим основы квантилей и более подробно рассмотрим некоторые из наиболее распространенных типов: квартили, децили и процентили.
Квантиль
Квантиль — это мера, указывающая значение, ниже которого падает определенная доля наблюдений в группе наблюдений. Квантиль используется в статистике для разделения группы наблюдений на группы одинакового размера. Например, квантиль 0,25 — это значение, ниже которого падают 25% наблюдений; квантиль 0,50 — это значение, ниже которого падает 50%, и так далее. Другим родственным измерением является медиана, которая совпадает с квантилем 0,50, поскольку 50% данных находятся ниже медианы.
Какие общие квантили существуют?
Некоторые распространенные квантили включают:
1. Квартиль
Квартиль — это тип квантиля, который делит группу наблюдений на четыре группы одинакового размера. Например, в группе наблюдений первый квартиль (Q1) — это значение, ниже которого опускаются первые 25 % наблюдений, второй квартиль (Q2, также известный как медиана) — это значение, ниже которого средние 50 % наблюдений падают, а третий квартиль (Q3) — это значение, ниже которого падают последние 25% наблюдений.
Например, в группе наблюдений первый квартиль (Q1) — это значение, ниже которого опускаются первые 25 % наблюдений, второй квартиль (Q2, также известный как медиана) — это значение, ниже которого средние 50 % наблюдений падают, а третий квартиль (Q3) — это значение, ниже которого падают последние 25% наблюдений.
2. Дециль
Дециль – это мера, которая делит группу наблюдений на десять групп одинакового размера. Например, в группе наблюдений первый дециль (D1) — это значение, ниже которого попадают первые 10% наблюдений, второй дециль (D2) — это значение, ниже которого попадают первые 20% наблюдений, и скоро. 9-й дециль (D9) — это значение, ниже которого опускаются последние 10% наблюдений.
3. Процентиль
Процентиль — это мера, указывающая значение, ниже которого находится определенный процент наблюдений в группе наблюдений. Например, в группе наблюдений 20-й процентиль (P20) — это значение, ниже которого опускаются первые 20% наблюдений, 50-й процентиль (P50) — это значение, ниже которого опускаются средние 50% наблюдений, и 95-й процентиль (P95) — это значение, ниже которого падают последние 95% наблюдений.
50-й процентиль также является медианой, вторым квартилем и 5-м децилем.
Процентиль: Расчет вручную / Microsoft Excel
Процентиль — это мера, используемая в статистике для указания значения, ниже которого находится определенный процент наблюдений в группе наблюдений.
Чтобы найти местоположение определенного процентиля, такие программы, как Minitab, Python, R и Excel, используют следующие шаги:
- Расположите наблюдения в порядке возрастания.
- Используйте формулу для определения положения процентиля, чтобы вычислить положение, в котором будет располагаться значение процентиля, используя желаемое значение процентиля и общее количество наблюдений в качестве входных данных. Существует два подхода: EXC (Exclusive) и INC (Inclusive). Процентное положение в подходе EXC определяется формулой \(K(N+1)\), а положение в подходе INC определяется формулой \(K(N-1)+1\).
- Если местоположение процентиля является целым числом, значение в этой позиции в упорядоченном списке наблюдений является значением процентиля.

- Если местоположение процентиля не является целым числом, значение процентиля рассчитывается путем вычисления значения на пропорциональной основе между этими двумя числами.
Чтобы найти 65-й процентиль в группе из 8 наблюдений, вы должны сначала расположить наблюдения в порядке возрастания: 8, 9, 12, 22, 23, 33, 55, 61.
Затем вы должны использовать формулу для местоположения процентиля, чтобы вычислить положение, в котором будет расположен 65-й процентиль:
Для ПРОЦЕНТИЛЬ.ИСКЛ рассчитанный ранг равен \(K(N+1)\).
Расположение в процентиле (с использованием эксклюзивного подхода) = \(\left(\frac{65}{100}\right)(8+1)\) = 5,85
Поскольку положение в процентиле не является целым числом, 65-й процентиль будет между 5-м пунктом (номер 23) и 6-м пунктом (номер 33) на пропорциональной основе. Это будет \(23+0,85(33-23) = 31,5\).
Для PERCENTILE.INC (и PERCENTILE) рассчитанный ранг равен \(K(N-1)+1\).
Расположение в процентах (с использованием инклюзивного подхода) = \((65/100) (8-1)+1\) = 5,55
Поскольку местоположение процентиля не является целым числом, 65-й процентиль будет почти посередине между 5-м элементом (число 23) и 6-м элементом (число 33). Пропорционально получится \(23+0,55(33-23)\) = 28,5.
Пропорционально получится \(23+0,55(33-23)\) = 28,5.
Квартиль: пример расчета вручную
Квартиль — это статистическое значение, которое делит набор данных на четыре равные части или четверти. Первый квартиль, также известный как нижний квартиль или Q1, — это значение, которое отделяет самые низкие 25 % данных от остальных. Второй квартиль, также известный как медиана или Q2, представляет собой значение, которое отделяет самые низкие 50% данных от самых высоких 50% данных. Третий квартиль, также известный как верхний квартиль или Q3, — это значение, которое отделяет самые высокие 25% данных от остальных.
Например, если у нас есть следующие числа: 14, 9, 10, 11, 11 и 6, мы можем разделить данные на четыре равные группы, найдя первый, второй и третий квартили.
Чтобы найти квартили набора данных, нам сначала нужно расположить данные в порядке возрастания следующим образом: 6, 9, 10, 11, 11, 14.
Затем нам нужно найти медиану, или Q2, которая является средним значением в наборе данных. В этом случае в наборе данных шесть чисел, поэтому медиана — это среднее значение третьего и четвертого значений, равное 10,5.
В этом случае в наборе данных шесть чисел, поэтому медиана — это среднее значение третьего и четвертого значений, равное 10,5.
Чтобы найти нижний квартиль или Q1, мы берем медиану значений ниже медианы. В данном случае это будет медиана 9. Чтобы найти верхнюю квартиль или Q3, мы берем медиану значений выше медианы. В данном случае это будет медиана 11, 11 и 14, что равно 11.
Таким образом, для этого набора данных квартили: эти числа расчета квартиля не совпадают с расчетом Excel?
Квартиль Использование Excel:
Для расчета квартилей такие программы, как Microsoft Excel и Minitab, используют метод процентилей, как объяснялось ранее. Q1 рассчитывается как 25-й процентиль, Q2 — как 50-й и Q3 — как 75-й процентиль. Это приводит к тому, что значение квартиля иногда отличается от значения, рассчитанного с использованием обычного ручного метода расчета.
Возьмем тот же пример, который мы использовали ранее в ручном расчете для расчета первого квартиля (Q1).
Чтобы найти квартили набора данных, нам сначала нужно расположить данные в порядке возрастания следующим образом: 6, 9, 10, 11, 11, 14.
Вы можете использовать функцию КВАРТИЛЬ.ИСКЛ или КВАРТИЛЬ.ВКЛ. найти квартили набора чисел в Excel.
Quartile.Exc
Для QUARTILE.EXC расчетный ранг равен K*(N+1). Чтобы рассчитать положение Q1 (или 25-го процентиля), подставим в эту формулу соответствующие значения.
Местоположение 1-го квартиля (с использованием эксклюзивного подхода) = (25/100) * (6+1) = 1,75
Поскольку положение процентиля не является целым числом, 1-й квартиль будет между 1-м элементом (номер 6) и 2-м элементом (номер 9) на пропорциональной основе. Получится \(6 + (9-6)*0,75\) = 8,25.
Использование Minitab: Если вы используете Minitab для расчета Q1, это значение (8,25), которое вы получите в описательной статистике. Minitab использует метод EXC для расчета процентилей и квартилей.
Квартиль.Вкл
Для КВАРТИЛЬ.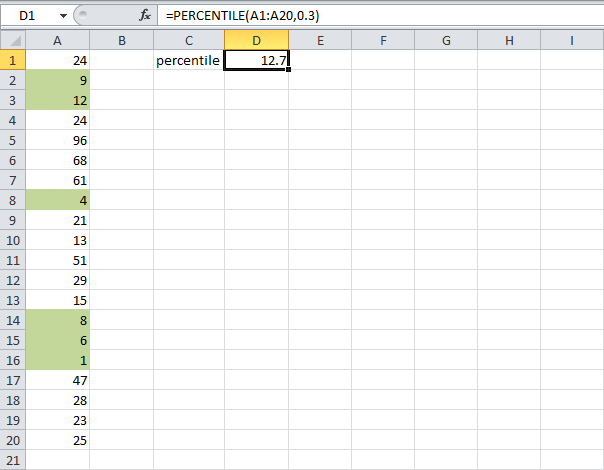

 002-89 Надежность в технике (ССНТ). Основные понятия. Термины и определения.
002-89 Надежность в технике (ССНТ). Основные понятия. Термины и определения.
 Если
расчетный уровень значимости меньше заданного уровня значимости α =0,05, то модель адекватна.
Если
расчетный уровень значимости меньше заданного уровня значимости α =0,05, то модель адекватна.