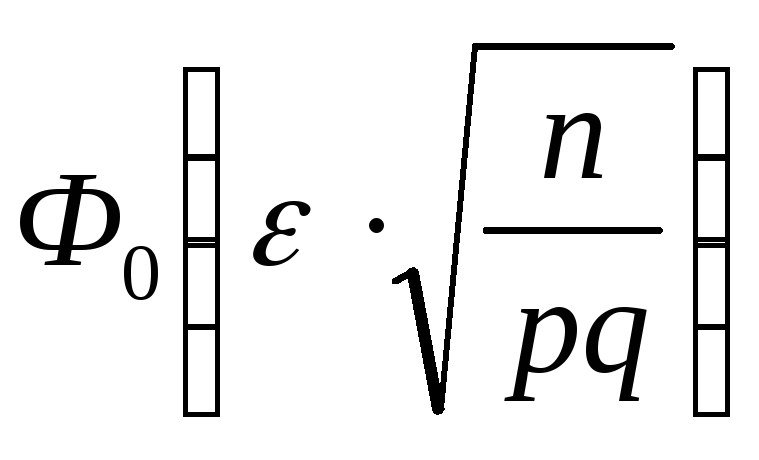Линейная алгебра
Линейная алгебра
ОглавлениеПРЕДИСЛОВИЕ К ЧЕТВЕРТОМУ ИЗДАНИЮВВЕДЕНИЕ ГЛАВА 1.  МАТРИЦЫ И ОПРЕДЕЛИТЕЛИ1. Понятие матрицы. 2. Основные операции над матрицами и их свойства. 3. Блочные матрицы. § 2. Определители 2. Выражение определителя непосредственно через его элементы. 3. Теорема Лапласа. 4. Свойства определителей. 5. Примеры вычисления определителей. 6. Определитель суммы и произведения матриц. 7. Понятие обратной матрицы. § 3. Теорема о базисном миноре матрицы 1. Понятие линейной зависимости строк. 2. Теорема о базисном мнноре. 3. Необходимое и достаточное условие равенства нулю определителя. ГЛАВА 2. ЛИНЕЙНЫЕ ПРОСТРАНСТВА § 1. Понятие линейного пространства 2. Некоторые свойства произвольных линейных пространств. § 2. Базис и размерность линейного пространства 1. Понятие линейной зависимости элементов линейного пространства. 2. Базис и координаты. 3. Размерность линейного пространства. 4. Понятие изоморфизма линейных пространств. § 3. Подпространства линейных пространств 1.  Понятие подпространства и линейной оболочки.2. Новое определение ранга матрицы. 3. Сумма и пересечение подпространств. 4. Разложение линейного пространства в прямую сумму подпространств. § 4. Преобразование координат при преобразовании базиса n-мерного линейного пространства 2. Связь между преобразованием базисов и преобразованием соответствующих координат. ГЛАВА 3. СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ § 1. Условие совместности линейной системы 2. Нетривиальная совместность однородной системы. 3. Условие совместности общей линейной системы. § 2. Отыскание решений линейной системы 2. Отыскание всех решений общей линейной системы. 4. Заключительные замечания о решении линейных систем. ГЛАВА 4. ЕВКЛИДОВЫ ПРОСТРАНСТВА § 1. Вещественное евклидово пространство и его простейшие свойства 2. Простейшие свойства произвольного евклидова пространства. § 2. Ортонормированный базис конечномерного евклидова пространства 2.  Свойства ортонормированного базиса.3. Разложение n-мерного евклидова пространства на прямую сумму подпространства и его ортогонального дополнения. 4. Изоморфизм n-мерных евклидовых пространств. § 3. Комплексное евклидово пространство 2. Неравенство Коши — Буняковского. Понятие нормы. 3. Ортонормированный базис и его свойства. § 4. Метод регуляризации для отыскания нормального решения линейной системы ГЛАВА 5. ЛИНЕЙНЫЕ ОПЕРАТОРЫ § 1. Понятие линейного оператора. Основные свойства 2. Действия над линейными операторами. Пространство линейных операторов. 3. Свойства множества L(V, V) линейных операторов. § 2. Матричная запись линейных операторов 2. Преобразование матрицы линейного оператора при переходе к новому базису. 3. Характеристический многочлен линейного оператора. § 3. Собственные значения и собственные векторы линейных операторов § 4. Линейные и полуторалинейные формы в евклидовом пространстве 2. Полуторалинейные формы в евклидовом пространстве.  Специальное представление таких форм.§ 5. Линейные самосопряженные операторы в евклидовом пространстве 2. Самосопряженные операторы. Основные свойства. 3. Норма линейного оператора. 4. Дальнейшие свойства самосопряженных операторов. 5. Спектральное разложение самосопряженных операторов. Теорема Гамильтона—Кэли. 6. Положительные операторы. Корни m-й степени из оператора. § 7. Унитарные и нормальные операторы § 8. Канонический вид линейных операторов § 9. Линейные операторы в вещественном евклидовом пространстве 2. Ортогональные операторы. ГЛАВА 6. ИТЕРАЦИОННЫЕ МЕТОДЫ РЕШЕНИЯ ЛИНЕЙНЫХ СИСТЕМ И ЗАДАЧ НА СОБСТВЕННЫЕ ЗНАЧЕНИЯ § 1. Итерационные методы решения линейных систем 2. Общий неявный метод простой итерации. 3. Модифицированный метод простой итерации. 4. Метод Зейделя. 5. Метод верхней релаксации. 6. Случай несимметричной матрицы А. 7. Итерационный метод П.  Л. Чебышева.§ 2. Решение полной проблемы собственных значений методом вращений ГЛАВА 7. БИЛИНЕЙНЫЕ И КВАДРАТИЧНЫЕ ФОРМЫ § 1. Билинейные формы 2. Представление билинейной формы в конечномерном линейном пространстве. 3. Преобразование матрицы билинейной формы при переходе к новому базису. Ранг билинейной формы. § 2. Квадратичные формы § 3. Приведение квадратичной формы к сумме квадратов 2. Метод Якоби. § 4. Закон инерции квадратичных форм. Классификация квадратичных форм 2. Классификация квадратичных форм. 3. Критерий Сильвестра знакоопределенности квадратичной формы. § 5. Полилинейные формы § 6. Билинейные и квадратичные формы в евклидовом пространстве 2. Приведение квадратичной формы к сумме квадратов в ортогональном базисе. 3. Одновременное приведение двух квадратичных форм к сумме квадратов в линейном пространстве. 4. Экстремальные свойства квадратичной формы. § 7. Гиперповерхности второго порядка 2. Параллельные переносы в евклидовом пространстве.  Преобразования ортонормированных базисов в ортонормированные.3. Преобразование общего уравнения гиперповерхности второго порядка при параллельном переносе. 5. Инварианты общего уравнения гиперповерхности второго порядка. 6. Центр гиперповерхности второго порядка. 7. Стандартное упрощение любого уравнения гиперповерхности второго порядка путем преобразования ортонормированного базиса. 8. Упрощение уравнения центральной гиперповерхности второго порядка. Классификация центральных гиперповерхностей. 9. Упрощение уравнения нецентральной гиперповерхности второго порядка. Классификация нецентральных гиперповерхностей. ГЛАВА 8. ТЕНЗОРЫ § 1. Преобразование базисов и координат 2. Взаимные базисы. Ковариантные и контравариантные координаты векторов. 3. Преобразования базиса и координат. § 2. Понятие тензора. Основные операции над тензорами 2.  n.4. Дискриминантный тензор. 5. Ориентированный объем. 6. Векторное произведение. 7. Двойное векторное произведение. § 4. Метрический тензор псевдоевклидова пространства 2. Галилеевы координаты. Преобразования Лоренца. 3. Преобразования Лоренца пространства § 5. Тензор момента инерции ГЛАВА 9. ЭЛЕМЕНТЫ ТЕОРИИ ГРУПП § 1. Понятие группы. Основные свойства групп 2. Понятие группы. Некоторые свойства групп. 3. Изоморфизм групп. Подгруппы. 4. Смежные классы. Нормальные делители. 5. Гомоморфизмы. Фактор-группы. § 2. Группы преобразований 2. Группа линейных преобразований. 3. Сходимость элементов в группе GL(n). Подгруппы группы GL(n). 4. Группа ортогональных преобразований. 5. Некоторые дискретные и конечные подгруппы ортогональной группы. 6. Группа Лоренца. 7. Унитарные группы. § 3. Представления групп 2. Матрицы линейных представлений. Эквивалентные представления. 3. Приводимые и неприводимые представления.  4. Характеры. 5. Примеры представлений групп. |
теория вероятности, примеры, таблица значений для вычисления определителей
Содержание:
-
Локальная и интегральная теоремы Муавра-Лапласа
- Локальная теорема Лапласа
- Интегральная предельная теорема Муавра-Лапласа
- Таблица значений для вычисления определителей
- Пример решения задачи
Содержание
-
Локальная и интегральная теоремы Муавра-Лапласа
- Локальная теорема Лапласа
- Интегральная предельная теорема Муавра-Лапласа
- Таблица значений для вычисления определителей
- Пример решения задачи
Локальная и интегральная теоремы Муавра-Лапласа
В том случае, когда количество манипуляций достаточно большое, применять формулу Бернулли становится нецелесообразно.
Рассматриваемые теоремы активно применяют в решении задач по данным большого количества экспериментов для нахождения приближенного значения вероятности. С помощью локальной теоремы можно вычислить определенное число явлений. Благодаря интегральной теореме Муавра-Лапласа, достаточно просто найти ответ при заданном диапазоне вероятного количества возникновения событий.
Локальная теорема Лапласа
В том случае, когда вероятность p возникновения явления A характеризуется постоянством, и \(p\ne 0\) и \(p\ne 1\), то вероятность \(P_n ( k )\) того, что событие A возникнет k раз в n экспериментах, равна приближенно (увеличивая n, получаем более точный результат испытаний и меньше погрешность) значению функции \(y=\frac { 1 } { \sqrt { n\cdot p\cdot q } } \cdot \frac { 1 } { \sqrt { 2\pi } } \cdot e^ { — { x^2 } / 2 } =\frac { 1 } { \sqrt { n\cdot p\cdot q } } \cdot \varphi ( x )\)
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления).
Если нет возможности написать самому, закажите тут.
В данном случае\( x=\frac { k-n\cdot p } { \sqrt { n\cdot p\cdot q } }\)
Из выражения можно сделать вывод:
\(label { eq2 } P_n ( k )\approx \frac { 1 } { \sqrt { n\cdot p\cdot q } } \cdot \varphi ( x )\)
где \(x=\frac { k-n\cdot p } { \sqrt { n\cdot p\cdot q } }\)
Следует отметить, что функция \(\varphi ( x )=\varphi ( { -x } )\) является четной.
Свойства представленной функции:
- функция является четной;
- если аргумент обладает значением больше, чем 4, то функция будет сколь угодно мала.
Интегральная предельная теорема Муавра-Лапласа
Вероятность P, что возникнет событие A, для каждого эксперимента по порядку обладает стабильным значением, и \(p\ne 0\) и \(p\ne 1\), тогда вероятность \(P_n ( { k_1 ,k_2 } )\) того, что явление A наступит от \(k_ { 1 }\) до \(k_ { 2 }\) раз в n опытах, равна \(P_n ( { k_1 ,k_2 } )\approx \frac { 1 } { \sqrt { 2\cdot \pi } } \int\limits_ { x_1 } ^ { x_2 } { e^ { — { z^2 } / 2 } dz } =\Phi ( { x_2 } )-\Phi ( { x_1 } )\)
В смысле данной формулировки,\( x_1 =\frac { k_1 -n\cdot p } { \sqrt { n\cdot p\cdot q } }\) , \(x_2 =\frac { k_2 -n\cdot p } { \sqrt { n\cdot p\cdot q } }\)
Следует отметить, что \(\Phi ( x )=\frac { 1 } { \sqrt { 2\cdot \pi } } \int { e^ { — { z^2 } / 2 } dz }\) можно определить с помощью специальных табличных схем.
\(\Phi ( { -x } )=-\Phi ( x )\) является нечетной функцией.
Рассматриваемая функция обладает следующими основными свойствами:
- функция является нечетной;
- если аргумент больше, чем 5, то значение функции составляет 0,5.
Таблица значений для вычисления определителей
В случае применения локальной теории Лапласа целесообразно использовать специальные таблицы:
Источник: ekonomika-st.ru Источник: ekonomika-st.ru Источник: ekonomika-st.ru Источник: ekonomika-st.ruТаблица значений интегральной функции Лапласа имеет следующий вид:
Источник: ekonomika-st.ru Источник: ekonomika-st.ru Источник: ekonomika-st.ruПрименительно к вероятностям распределения Пуассона сформирована таблица:
Источник: ekonomika-st.ru
Источник: ekonomika-st.ru
Источник: ekonomika-st.ru
Источник: ekonomika-st.
ru
Пример решения задачи
Задача № 1
Требуется определить, какова вероятность возникновения события А в течение 80 раз во время проведения 400 опытов. Следует учитывать вероятность появления данного события в каждом эксперименте составляет\( р = 0,2.\)
Решение:
В том случае, когда р = 0,2: q = 1 – p = 1 – 0,2 = 0,8
Таким образом:
\(P_ { 400 } ( { 80 } )\approx \frac { 1 } { \sqrt { n\cdot p\cdot q } } \varphi ( x )\,,\,\)
где \(x=\frac { k-n\cdot p } { \sqrt { n\cdot p\cdot q } }\)
В таком случае:
\(\begin{array} { l } x=\frac { k-n\cdot p } { \sqrt { n\cdot p\cdot q } } =\frac { 80-400\cdot 0,2 } { \sqrt { 400\cdot 0,2\cdot 0,8 } } =\frac { 80-80 } { \sqrt { 400\cdot 0,16 } } =0 \\ \varphi ( 0 )=0,3989\,,\,P_ { 400 } ( { 80 } )\approx \frac { 0,3989 } { 20\cdot 0,4 } =\frac { 0,3989 } { 8 } =0,0498 \\ \end{array}\)
Ответ: вероятность равна 0,0498
Задача № 2
По условиям задания, в процессе контроля качества выявляют 10% брака от произведенных изделий.
Для этой процедуры выбирают 625 изделий. Необходимо определить вероятность того, что в объеме отобранных изделий имеется не меньше 550 и не больше 575 качественных экземпляров.
Решение:
В том случае, когда брак составляет 10% от изделий, то качественные экземпляры должны определяться, как 90%. При таком условии:
\(n=625, \ p=0,9, \ q=0,1, \ k_1 =550,\ k_2 =575\)
Тогда:
\(n\cdot p=625\cdot 0,9=562,5\)
Исходя из полученного выражения, определим:
\(\begin{array} { l } P_ { 625 } (550,575)\approx \Phi ( { \frac { 575-562,5 } { \sqrt { 625\cdot 0,9\cdot 0,1 } } } )- \Phi ( { \frac { 550-562,5 } { \sqrt { 626\cdot 0,9\cdot 0,1 } } } )\approx \Phi (1,67)- \Phi (-1,67)=2 \Phi (1,67)=0,9052 \\ \end{array}\)
Ответ: вероятность составит 0,9052
Насколько полезной была для вас статья?
У этой статьи пока нет оценок.
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Поиск по содержимому
14.
1 Применение теоремы о расходимости: уравнение Лапласа 14.1 Применение теоремы о расходимости: уравнение Лапласа
| ||
Комбинация div grad , ( )
или
называется « лапласиан » дифференциальный оператор,
Уравнение ( )
f = 0 называется уравнением Лапласа . Статическое электричество и стационарное состояние
магнитные поля подчиняются этому уравнению, где нет зарядов или тока.
Любое решение этого уравнения в R обладает тем свойством, что его значение на
центр сферы в пределах R является средним значением на поверхности сферы .
Если g( r ) подчиняется уравнению Лапласа внутри сферической поверхности S радиуса
а, с центром в r’, имеем
Уравнение Лапласа
Таким образом, решения уравнения Лапласа очень гладкие: у них нет выпуклостей
максимумы или минимумы в R и по существу плавно «интерполировать» между
их значения на границах R. Мы докажем этот важный факт как приложение
теоремы о расходимости.
Этот результат также означает, что если мы знаем дивергенцию вектора v и его
закручиваются везде, они везде дифференцируемы, и v обращается в нуль
на бесконечности однозначно определяется v . пробник( если были
два решения v и v’ с одинаковыми расходимостью и ротором, то
применяя тождество двойного перекрестного произведения, мы обнаруживаем, что каждый компонент
их разность всюду подчиняется уравнению Лапласа. Его значение в любом месте
затем его среднее значение на огромном круге в бесконечности, которое по предположению равно 0.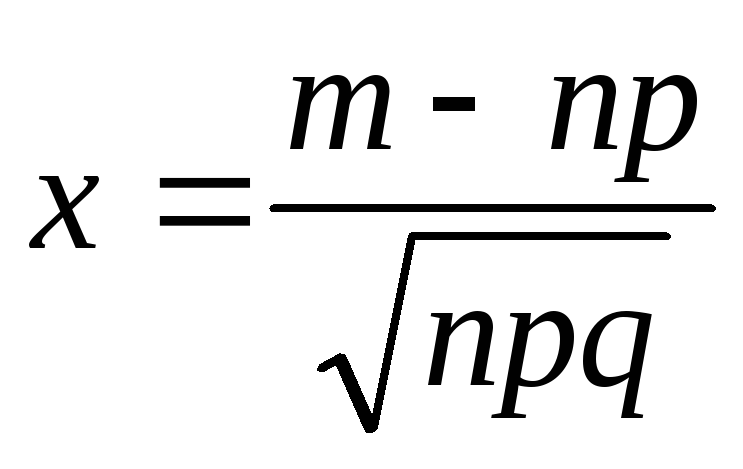
Тот же вывод справедлив, если v и v’ должны вести себя при
бесконечности таким же образом, так что v — v’ должны стремиться к 0 для больших
аргументы.)
Доказательство
Предположим, что наша функция f( r) подчиняется уравнению Лапласа в некоторой сфере S с центром в r’ :
деление град f = ( ) f = 0 внутри S
Применим теорему о расходимости к вектору f г — г ф в сфере с поверхностью S, за исключением крошечной сферы радиуса b с поверхностью S’ с одним и тем же центром. Получаем
, последний получается заменой g. Второй интеграл на
вторая линия здесь исчезает, как можно видеть, применяя теорему о расходимости
снова внутри S и заметив, что лапласиан, примененный к f, равен 0,
.
Здесь правая часть — среднее значение f на S. Аналогичный интеграл
над S’ вычисляется точно так же и является средним значением f на
С’.
Мы заключаем, что среднее значение v на любой сфере с центром в r’
та же. Очевидно, что когда сфера приближается к радиусу 0, среднее значение
становится значением f в р’ .
Метод, используемый в этом аргументе, является очень важным и общим, т.
используется при решении многих дифференциальных уравнений. На самом деле использование дивергенции
теорему в использованной выше форме часто называют «теоремой Грина».
А функция g, определенная выше, называется «функцией Грина» для
Уравнение Лапласа.
Мы можем использовать эту функцию g, чтобы найти векторное поле v , которое обращается в нуль при
бесконечность подчиняется div v = ,
curl v = 0. (мы предполагаем, что r достаточно хорошо себя ведет, интегрируемо,
исчезает в бесконечности и т. д.) Предположим, мы записываем v как grad f.
Получаем
(Это уравнение называется уравнением Пуассона и ему подчиняется потенциал
производится распределением заряда с плотностью заряда .
)
Решение, исчезающее на бесконечности, определяется выражением
.Доказательство
Тот же подход можно использовать для получения векторного потенциала A и определения вектор v , подчиняющийся
в = 0, v = и
С v = А получаем
( ( А )) = j
и с двойным крестом
( ( А )) = ( А ) — ( ) А
и «калибровочное» условие (которое мы можем принять)) A = 0, мы находим, что каждая компонента A подчиняется уравнению Пуассона с
источник — соответствующий компонент j.
Таким образом, мы можем найти формулу для каждой координаты A точно так же, как
соответствующую формулу для скалярного потенциала V.
Снова v может быть
восстановлен из A дифференцированием.
Эти результаты могут быть полезны при изучении электромагнитных полей, но они
не решить все проблемы. Часто известные заряды и токи индуцируют неизвестные
заряды и токи в проводящих поверхностях, и нужно определить
поля, в условиях, когда есть какие-то неизвестные заряды и/или токи
и вы знаете условия на поле на поверхности проводников вместо
заряды и токи в них.
Упражнения
▷ Теоремы преобразования Лапласа
Наш верный пользователь Насир продолжает серию статей о преобразовании Лапласа. Сегодня пусть он резюмирует некоторые теоремы…
Введение
Преобразование Лапласа — это способ преобразования дифференциальных уравнений в алгебраические уравнения. Интеграл Лапласа определяется как:
Поскольку мы изучали преобразование Лапласа некоторых основных элементарных функций и свойства преобразования Лапласа, есть несколько теорем, которые применимы к преобразованию Лапласа и упрощают их решение.
Мы также увидим, как можно использовать эти теоремы над интегралом Лапласа точно так же, как мы делали это со свойствами. Некоторые теоремы Лапласа также рассматриваются как свойства, поэтому вам может показаться, что вы уже изучили их в статье о свойствах, но здесь мы обсудим немного другой контекст.
Давайте взглянем на основные теоремы:
1. Теорема существования
Основная теорема анализа существования преобразования Лапласа функции. Он говорит, что для кусочно-непрерывной функции f (t) L (f (t)) существует тогда и только тогда, когда t ≥ 0 и s > t.
2. Первая теорема о сдвиге
Первая теорема о сдвиге утверждает, что если функция f(t) находится во временной области и умножается на e -at , результат s-области сдвигается на величину a.
Математически,
3. Вторая теорема о сдвиге
Вторая теорема о сдвиге очень похожа на первую, но результаты совершенно разные. Функция единичного шага преобразует экспоненциальную функцию из t-области в s-область.
Математически теорему можно сформулировать так:
4. Первая теорема о переносе
Эта теорема применима, когда функция, скажем, f (t) умножается на экспоненту в . Преобразование Лапласа их произведения задается как:
Когда мы оцениваем этот интеграл, мы получаем первую теорему о переносе. Итак, мы имеем:
Здесь мы заменили s на s-a в F(s).
Обратная форма первой теоремы о переносе
Поскольку мы это знаем,
Обратная теорема задается как:
Так как это обратная форма, то здесь мы должны заменить s-a на s.
5. Вторая теорема о переносе
Рассмотрим функцию f (t-a) и единичную ступенчатую функцию u (t-a), преобразование их произведения задается как e — как F(s). Аналогично для другой функции g (t) и той же единичной ступенчатой функции u (t-a) преобразование их произведения задается как e — as L {g (t+a)}.
Математически вторая теорема о переносе представляется как:
Обратная форма второй теоремы о переносе
Чтобы найти обратную вторую теорему о переносе, возьмите обратное уравнение:
6. Теорема о начальном значении
Эту теорему мы также обсуждали в свойствах. Теорема для начального значения:
Или
Чтобы доказать эту теорему, мы возьмем производное правило:
Затем мы используем определение преобразования Лапласа и интеграл распада в двух частях быть вытянутым. С правой стороны первый член можно вытащить, что дает такое же обоснование. Также, если бесконечность должна быть помещена для s во втором члене, тогда экспоненциальный член стремится к нулю.
f (0-) отменяется с обеих сторон и остается только теорема о начальных значениях.
7. Теорема об окончательном значении
Возможно, вы помните, что мы обсуждали эту теорему в свойствах.
В отличие от теоремы о начальном значении, в теореме о конечном значении остается только конечное значение функции
или
функция синуса и рампы не имеет окончательных значений. Чтобы показать теорему об окончательном значении, мы начнем с производной преобразования Лапласа
Принятие предела s стремится к нулю,
При s→0 экспоненциальный член исчезает из интеграла. Кроме того, мы можем вытащить f(0-) из предела, так как он не зависит от s.
Мы можем вычислить интеграл
В левом выражении нет члена, зависящего от s, поэтому мы можем снять предел. Путем упрощения получим теорему об окончательном значении
8. Теорема о суперпозиции
Если мы возьмем 1 и 2 в качестве констант, то теорема будет
008 Для произвольная константа a>0
11. Теорема о производной
Принимая f(t) как случайную функцию времени, для которой производная существует, если t>0
12.
