Площадь прямоугольника как обозначается: Какой буквой обозначается площадь в математике

Как найти площадь и ширину прямоугольника?

Статьи › Находится › Как находится площадь прямоугольника формула?

Ширину можно вычислить по длине, если известна еще площадь или периметр прямоугольника. Например, зная площадь и длину, можно найти ширину по формуле а = S/b. А зная периметр и длину, можно вычислить ширину по формуле a = (P — 2b) / 2.

1. Как найти ширину прямоугольника?
2. Как найти ширину и периметр прямоугольника?
3. Как определить площадь прямоугольника?
4. Как можно вычислить площадь прямоугольника двумя способами?
5. Как определить ширину?
6. Чему равна ширина прямоугольника?
7. Как определить ширину комнаты?
8. Как найти ширину прямоугольного треугольника?
9. Как обозначается ширина прямоугольника?
10. Как найти площадь ширину и длину?
11. Как найти площадь прямоугольника 3 класс примеры?
12. Как правильно посчитать площадь?
13. Как вычислить площадь прямоугольника 4 класс?
14. Как найти площадь прямоугольника со сторонами?
15. Как можно найти пример и площадь прямоугольника?
16. Как найти ширину если известна длина и высота?
17. Что называют длину и ширину прямоугольника?
18. Как найти стороны прямоугольника?

Как найти ширину прямоугольника?

Определение прямоугольника

Длинную сторону прямоугольника называют длиной (обозначается латинской буквой — a), а короткую — шириной (обозначается латинской буквой — b). Стороны прямоугольника одновременно является его высотами (см. Рис. 1).

Как найти ширину и периметр прямоугольника?

1. Периметр прямоугольника находится по формуле Р = 2 * (а + b), где Р — периметр, а — длина, b — ширина. Выведем из этой формулы формулу ширины: b = Р / 2 — а.

Как определить площадь прямоугольника?

2) Для вычисления площади прямоугольника нужно умножить его длину на ширину. Формула для вычисления площади прямоугольника имеет следующий вид: S = a*b.

Как можно вычислить площадь прямоугольника двумя способами?

S = b * a. Оба полученных выражения равны (по тому же переместительному свойству умножения), т. e: S = a * b = b * a.

Как определить ширину?

Шириной же, в отличии от длины, является промежуток между такими двумя точками плоскости, которые находятся друг от друга на наименьшем расстоянии, то есть наоборот по определению длины. Длина предмета находится в продольном направлении, а его ширина — размещается поперек длины.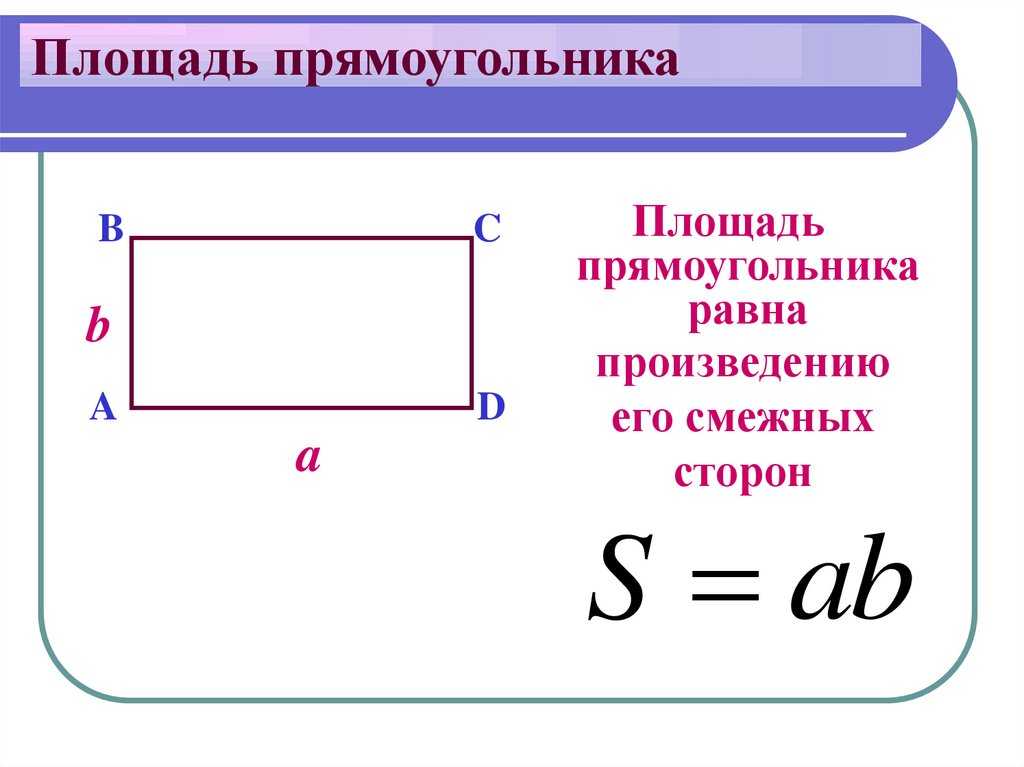

Чему равна ширина прямоугольника?

Нахождение ширины прямоугольника по формуле P = a * 2 + b * 2.

Как определить ширину комнаты?

Чтобы найти ширину данной комнаты, необходимо площадь разделить на известную длину, то есть вычисляет по формуле b = S: а: b = S: а = 21: 7 = 3 метра.

Как найти ширину прямоугольного треугольника?

Объем прямоугольного параллелепипеда равен произведению трех его величин: длины, ширины и высоты. V = a * b * c. Чтобы найти ширину, нужно объем разделить на произведение известных величин.

Как обозначается ширина прямоугольника?

Обозначается буквой l. Ширина — одно из пространственных измерений объекта при измерении в поперечном направлении. обозначается буквой B.

Как найти площадь ширину и длину?

Когда известно значение длины и ширины фигуры

Для вычисления необходимо умножить их друг на друга. S = a × b, где S — площадь; a, b — длина и ширина.

Как найти площадь прямоугольника 3 класс примеры?

Чтобы найти площадь прямоугольника, надо найти произведение длин его сторон.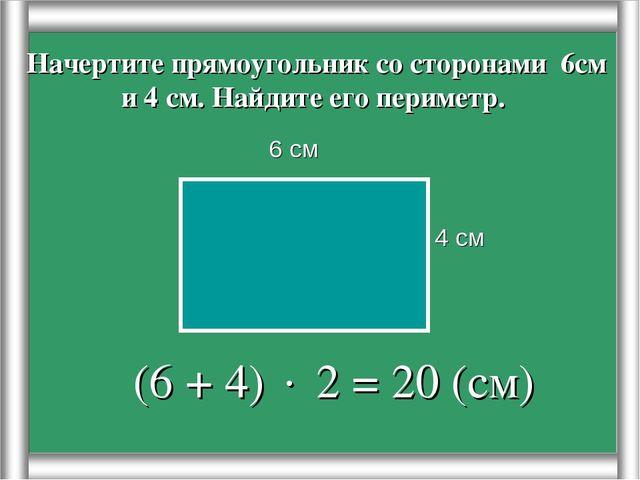 2 см ⋅ 4 см = 8 см 2. Длина и ширина прямоугольника должны быть выражены (записаны) в одинаковых единицах длины.

Как правильно посчитать площадь?

Для этого необходимо с помощью рулетки измерить длину и ширину пола, а затем умножить значения между собой. Так можно узнать площадь комнаты в квадратных метрах по полу. Если у комнаты есть выступающие части, то для подсчета площади необходимо вычесть их площадь из общего размера комнаты.

Как вычислить площадь прямоугольника 4 класс?

Известно, что площадь прямоугольника равна произведению длин его сторон: S пр = a ⋅ b.

Как найти площадь прямоугольника со сторонами?

Площадь прямоугольника равна произведению его сторон. То есть умножаем длину на ширину. Получаем следующее решение. S = a * b.

Как можно найти пример и площадь прямоугольника?

Площадь прямоугольника равна произведению его длины и ширины. S = · b, где S — площадь, — длина, b — ширина прямоугольника. Периметр прямоугольника равен удвоенной сумме его длины и ширины. P = (+ b) · 2, где P — периметр, — длина, b — ширина прямоугольника.

Как найти ширину если известна длина и высота?

Находим ширину. Делим объем на произведение высоты и длины. 2 / (0,5 * 0,2) = 2 / 0,1 = 20 дм.

Что называют длину и ширину прямоугольника?

Длиной прямоугольника называют длину более длинной пары его сторон, а шириной — длину более короткой пары сторон. Величина площади прямоугольника равна произведению ширины прямоугольника на его длину. Периметр прямоугольника равен удвоенной сумме длин его ширины и длины.

Как найти стороны прямоугольника?

А = S: b, где S — площадь прямоугольника, b — сторона прямоугольника.

Какой буквой обозначается сторона прямоугольника?

Какой буквой обозначается сторона прямоугольника?

– Раз у прямоугольника противоположные стороны равны, то в математике принято обозначать стороны прямоугольника двумя латинскими буквами – а (длина), с (ширина).

Как называются стороны прямоугольника?

Прямоугольник — это четырехугольник у которого две противоположные стороны равны и все четыре угла одинаковы. … Длинную сторону прямоугольника называют длиной прямоугольника, а короткую — шириной прямоугольника. Стороны прямоугольника одновременно является его высотами.

Как найти одну из сторон прямоугольника зная его площадь?

S ( площадь пямоугольника) = a*b т. е. одну сторону нужно умножить на другую. А чтобы найти одну из сторон ( а или b ), нужно площадь разделить на известную сторону.

Как найти вторую сторону прямоугольника?

Как найти сторону прямоугольника если известен периметр и 1 сторона

1. как решить
2. из периметра отнять два раза известную сторону,так как противолежащие стороны равны и останется сумма других двух сторон, а так как они равны то делим сумму пополам и получаем неизвестную сторону. Р — ( а + а ) / 2 = в , где Р — периметр

Как найти стороны прямоугольник?

сторона прямоугольника равняется половине разности между периметром и удвоенной другой стороной.

Как найти периметр прямоугольника по площади?

Площадь прямоугольника равна произведению его длины и ширины. S = · b, где S — площадь, — длина, b — ширина прямоугольника. Периметр прямоугольника равен удвоенной сумме его длины и ширины. P = ( + b) · 2, где P — периметр, — длина, b — ширина прямоугольника.

Как найти площадь прямоугольника если известна площадь?

Выучите формулу нахождения площади прямоугольника: S = a * b, где S — площадь, a — длина, b — ширина, то есть, площадь равна произведению сторон.

Как найти площадь прямоугольника если известна диагональ и периметр?

Площадь прямоугольника равна произведению длины стороны a на длину стороны b. Периметр прямоугольника равен удвоенной сумме сторон a и b. Диагональ прямоугольника равна квадратному корню из суммы квадратов сторон a и b.

Как найти площадь прямоугольника по диагонали?

Формула для нахождения площади прямоугольника через диагонали и угол между ними: S = d 2 2 ⋅ sin ⁡ ( α ) {S= \dfrac{d^2}{2} \cdot \sin({\alpha})} S=2d2⋅sin(α), где d — диагональ прямоугольника, α — угол между диагоналями.

Чему равен периметр квадрата со стороной 8 см?

Ответ, проверенный экспертом (10+6)*2=32(см)-периметр прямоугольника.

Как найти периметр пятиугольника 3 класс?

Перемножьте значение стороны на количество сторон, чтобы вычислить периметр. Формула для нахождения периметра правильного многоугольника: периметр = количество сторон x длину любой стороны.

Определение, площадь, формула, свойства и примеры

Объект с четырьмя сторонами и четырьмя внутренними углами в двух измерениях называется прямоугольником. Равные количества присутствуют на противоположных сторонах и углах. Форма четырехугольника с четырьмя сторонами и противоположными сторонами и углами, которые равны и параллельны друг другу, — это то, что подразумевается под этим определением. Задаются размеры прямоугольного изделия, а именно его длина и ширина. Самая длинная сторона прямоугольника служит его длиной, а самая короткая сторона служит его шириной.

В нашей повседневной жизни мы часто видим и взаимодействуем с объектами прямоугольной формы, включая столы, книги, коробки, мобильные телефоны, стены, поля для игры в крикет, телевизор или компьютерные экраны, мебель, матрасы, альмиры и двери.

Цифровой маркетингГрафический дизайнMS Excel (10 часов)Курс подготовки к собеседованиюПрограмма предпринимательстваНаписание контента Программа «Чемпион» (средний язык хинди) Группа биологии 12-й класс Программа «Чемпион» (средний английский) Группа математики 12-й класс Программа «Чемпион» (средний английский язык) Группа биологии 10-й класс Программа «Чемпион» (средний язык хинди) 10-й класс Программа «Чемпион» (средний английский язык)

Бесплатные демо-классы

Зарегистрируйтесь здесь, чтобы получить бесплатные демо-классы

Выберите категориюНавыкиПравительствоАкадемические науки

Выберите курс

Пожалуйста, заполните имя

Пожалуйста, введите только 10-значный номер мобильного телефона

Пожалуйста, выберите курс

Пожалуйста, заполните адрес электронной почты

Что-то пошло не так!

Загрузите приложение и начните обучение

Источник: Safalta. com

Для лучшего понимания принципов прямоугольника в этой статье мы изучим прямоугольник, его свойства, площадь прямоугольника, формулы, периметр прямоугольника и некоторые решаемые на его основе задачи. Если вы готовитесь к конкурсным экзаменам и ищете рекомендации экспертов, вы можете загрузить нашу Бесплатную электронную книгу «Общие знания»  Скачать сейчас.

Бесплатная электронная книга в формате PDF: Скачать здесь  
Попробуйте бесплатные пробные тесты — нажмите здесь

Содержание

• Прямоугольник
• Прямоугольник: Площадь
• Прямоугольник: форма
• Прямоугольник: Формула площади
• Площадь прямоугольника : Используется диагностика
• Формула прямоугольника
• Формула периметра прямоугольника
• Свойства прямоугольника
• Прямоугольник: Решенные примеры

Любая замкнутая двумерная фигура с четырьмя сторонами, у которых противоположные стороны и углы равны, называется прямоугольником.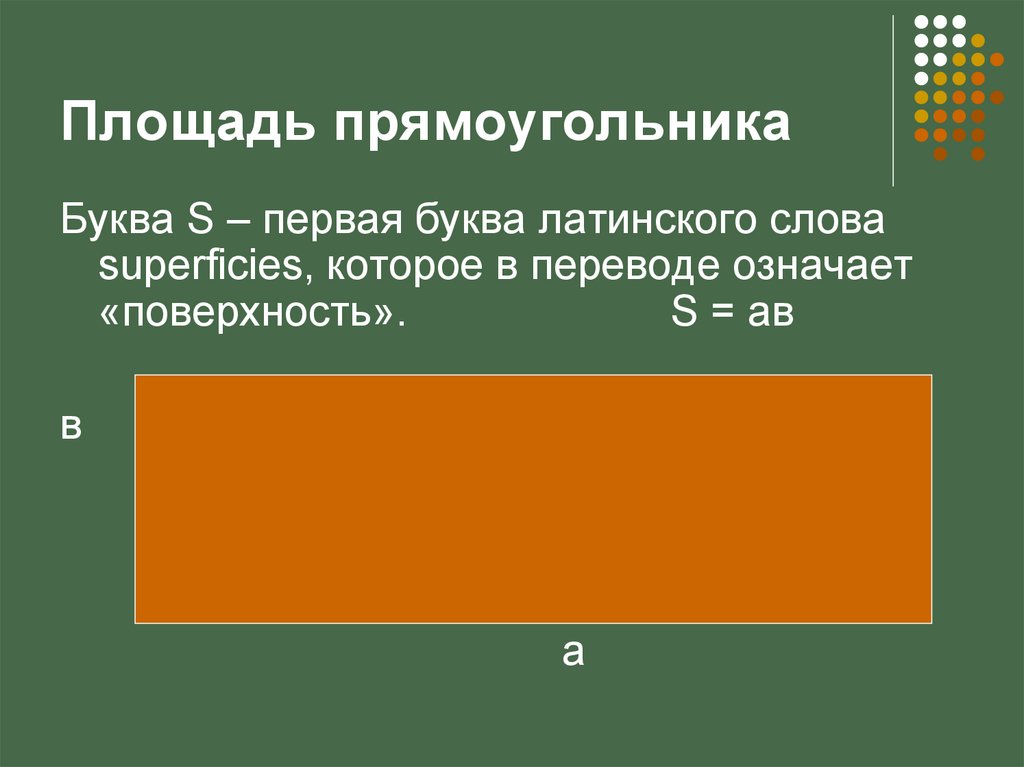 Противоборствующие стороны усматривают параллель в том, что никогда не взаимодействуют. Все четыре внутренних угла прямоугольника равны 90 градусов. На рисунке ниже вы можете видеть стороны и углы прямоугольника.

На приведенном выше рисунке показан прямоугольник ABCD, стороны которого имеют длины сторон AB = CD = l, AD = BC = b и AD || Британская Колумбия, AB || CD. Значения внутренних углов равны 90°.

Пространство, заключенное между четырьмя сторонами прямоугольника, называется его площадью. Площадь прямоугольника можно вычислить математически, подсчитав количество единичных квадратов, которые могут поместиться внутри него. В повседневной жизни мы видим много прямоугольных вещей, поэтому определение их площади также необходимо. Примерами служат многочисленные прямоугольные предметы, в том числе книги, столы, экраны ноутбуков, процессоры и т. д. Только длина и ширина прямоугольника прямоугольника определяют его площадь. Приведенную ниже формулу блеска можно использовать для получения площади прямоугольника. В квадратных единицах площадь прямоугольника выражается как кв. м, кв. см, или кв. мм.

Площадь прямоугольника = длина × ширина

A = L × B Квадратные единицы

Как мы уже обсуждали, прямоугольник-это закрытая двумерная фигура с четырьмя сторонами. В прямоугольнике четыре внутренних угла, каждый из которых равен 9.0 градусов и противоположные стороны, равные и параллельные друг другу. Мы часто приходим с прямоугольными объектами, такими как стены, ящики, столы, матрасы, экраны ноутбуков и компьютеров и многое другое.

Пространство, заключенное внутри внешнего периметра прямоугольника, называется его площадью. Произведение длины на ширину можно использовать для вычисления площади прямоугольника. Формула для определения площади прямоугольника представляет собой произведение его длины и ширины. Например, если длина прямоугольника равна l, его ширина равна b, а его площадь обозначается буквой A.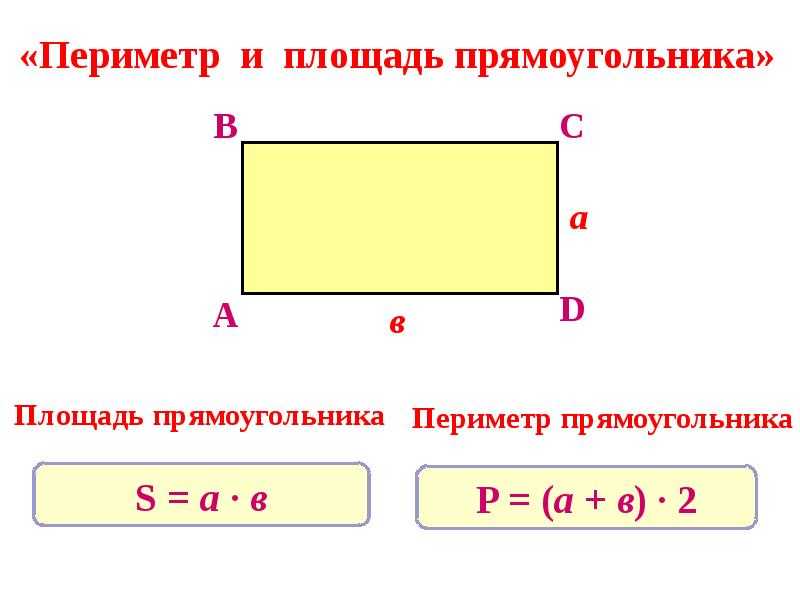

Площадь прямоугольника выражается в квадратных единицах.

Площадь прямоугольника = длина × ширина

A = L × B Квадратные единицы

Как будет показано позже, диагонали также можно использовать для вычисления площади прямоугольника.

• (Диагональ)2 = (Длина)2 + (Ширина)2 92 × ширина

Вышеприведенное обсуждение подробно описывает, как вычислить площадь прямоугольника. Формула для вычисления площади прямоугольника состоит в том, чтобы умножить длину и ширину прямоугольника на их соответствующие величины. Пусть L — длина, W — ширина, а A — площадь прямоугольника. Таким образом, формула площади прямоугольника выражается следующим образом:

A = L × W квадратных единиц

Сумма внешних границ прямоугольника называется его периметром. Она равна длине прямоугольника плюс ширина, умноженная на два. Значение параметра прямоугольника получается путем добавления периметра, который представляет собой линейное измерение внешних сторон прямоугольника. Он описывается с использованием единиц длины, таких как м, см или мм.

Рассмотрим прямоугольник ABCD, размеры которого равны l и b. Периметр прямоугольника ABCD обозначается

Периметр прямоугольника = 2 (l + b)

Многочисленные характеристики прямоугольника используются в геометрии и других контекстах, где это указано. Ниже приведен список основных атрибутов прямоугольника.

• Примером четырехугольника является прямоугольник.
• Противоположные стороны прямоугольника равны и параллельны друг другу.
• Каждая вершина прямоугольника имеет внутренний угол 90°.
• Внутренние углы прямоугольников в сумме составляют 360° (90°+90°+90°+90°).
• Диагонали прямоугольника делят друг друга пополам.
• Две диагонали прямоугольника имеют одинаковую длину.
• Теорему Пифагора можно использовать для определения длины диагоналей. Когда стороны диагонали равны a и b, ее длина равна (a2 + b2).
• Прямоугольник также называют параллелограммом, так как его стороны параллельны.
• Все параллелограммы абсолютно прямоугольники, но не все прямоугольники параллелограммы.

1. Если длина прямоугольника 8 см, а ширина 5 см. Найдите площадь прямоугольника.

Решение: Даны l = 8 см и b = 5 см

, тогда площадь прямоугольника A = l × b

A = 8 × 5

A = 40 кв. см

2. Длина и ширина прямоугольного двора равны 75 м и 32 м. Найдите стоимость его выравнивания из расчета 3 долл. за м2. Также найдите расстояние, пройденное мальчиком за 4 круга двора.

Решение: Длина двора = 75 м

Ширина двора = 32 м

Периметр двора = 2 (75 + 32) м

= 2 × 107 м

= 214 м

Расстояние, пройденное мальчиком за 4 круга = периметр двора

= 4 × 214

= 856 м

Мы знаем, что площадь двора = длина × ширина

= 75 × 32 м22

= 2400 м22

За 1 м22 стоимость выравнивания = 3$

Для 2400 м2 стоимость выравнивания = 3$ × 2400

= 7200$

3. У Шьяма есть прямоугольная фоторамка длиной 9 дюймов и шириной 5 дюймов. Помогите Шьяму найти площадь фоторамки?

Решение: Мы знаем формулу для вычисления площади прямоугольника

Площадь прямоугольника = (Длина × Ширина).

Таким образом, площадь прямоугольной рамки = 9 × 5 = 45 квадратных дюймов

Следовательно, площадь фоторамки = 45 квадратных дюймов

4. Найдите периметр и площадь прямоугольника o длиной 17 см и шириной 13 см.

Решение: Дана длина = 17 см, ширина = 13 см

Периметр прямоугольника = 2 (длина + ширина)

= 2 (17 + 13) см

= 2 × 30 см

= 60 см

Мы знаем, что площадь прямоугольника = длина × ширина

= (17 × 13) см2

= 221 см2

5. Проволока в форме прямоугольника длиной 35 см и шириной 18 см перегибается, образуя квадрат. Какова будет мера каждой стороны?

Решение: Периметр прямоугольника = 2 (35 + 18) см

= 2 × 53

= 106 см

Периметр квадрата стороны х см =, Следовательно, периметр прямоугольника = Периметр квадрата

106 см = 4x

⇒ x = 26,5

Следовательно, каждая сторона квадрата = 26,5 см

 

Каковы 7 свойств прямоугольника?

Основные свойства прямоугольников:

• Прямоугольник — это четырехугольник.
• Противоположные стороны параллельны и равны друг другу.
• Каждый внутренний угол равен 90 градусам.
• Сумма всех внутренних углов равна 360 градусов.
• Диагонали делят друг друга пополам.
• Обе диагонали имеют одинаковую длину.

Прямоугольник — это четырехсторонняя фигура с четырьмя прямыми углами (углы в 90 градусов). Существует  два типа  специальных прямоугольников, включая квадрат и прямоугольник Фибоначчи

Фалес Милетский жил около 600 г. до н.э., и ему приписывают многие из самых ранних известных геометрических доказательств.

блог

Искусство решения задач

В математике площадь относится к размеру области, которую занимает двумерная фигура. Размер области в более высоких измерениях называется объемом.

Часто можно элементарными средствами найти площадь области, ограниченной частями окружностей и отрезками. Можно найти площадь еще более сложных областей с помощью исчисления.

Прямоугольники — самые простые фигуры, площадь которых мы можем изучать. Имеет смысл, что площадь прямоугольника с длиной и шириной просто равна .

Зная площадь прямоугольника, мы можем легко найти площадь треугольника, просто заметив, что если наш треугольник имеет основание и высоту , то площадь прямоугольника с длиной и шириной ровно в два раза больше площади исходного треугольника. Таким образом, площадь треугольника равна

Теперь мы можем найти площадь любого многоугольника, разбив его на треугольники.

Содержание

• 1 Ознакомительные видео
• 2 Обозначение
• 3 Площадь правильного многоугольника
• 4 Площадь треугольника
  • 4.1 Другие формулы, эквивалентные формуле Герона
    • 4.1.1 Тоже верно, но сложнее, чем выше
• 5 Площадь четырехугольника
• 6 См. также

Ознакомительные видео

https://youtu.be/51K3uCzntWs?t=842 \\

Обозначение

Буквы и часто используются для обозначения площади. Когда рассматривается несколько регионов, часто используются нижние индексы: могут использоваться для обозначения областей определенных регионов или . Например, будет означать площадь шестиугольника.

В качестве альтернативного обозначения можно использовать квадратные скобки вокруг названия региона для обозначения его площади, например. для площади треугольника.

Площадь правильного многоугольника

Площадь любого правильного многоугольника можно найти следующим образом:

Впишите фигуру со сторонами длиной , в круг и проведите линию из двух соседних вершин в центр описанной окружности. Это создает треугольник общей площади (в качестве примера рассмотрим правильный восьмиугольник ниже).

Рисование апофемы создает два прямоугольных треугольника, каждый с углом в верхней вершине. Если у многоугольника есть длина стороны, высота треугольника может быть найдена с помощью тригонометрии, чтобы быть длиной.

Площадь каждого треугольника равна произведению основания на высоту, что также может быть выражено как и площадь всего многоугольника равна .

Площадь треугольника

Существует множество способов найти площадь треугольника. Во всех этих формулах будет использоваться для обозначения площади.

• где — основание, а — высота треугольника до этого основания.
• Формула Герона: , где и — длины сторон и — полупериметр .
• , где — радиус вписанной окружности, а s — полупериметр.
• где и — смежные стороны треугольника, а — мера угла между ними.
• , где длины сторон треугольника и радиус описанной окружности.
• , где и треугольник имеет высоты , , .

Другие формулы, эквивалентные формуле Герона

Они особенно полезны, когда для:

Тоже верно, но сложнее

Площадь четырехугольника

. Однако для некоторых четырехугольников есть специальные формулы для нахождения их площадей. Опять же, это площадь.

• Воздушный змей — где s представляет длину диагоналей воздушного змея.

• Параллелограмм — , где основание и высота до этого основания.

• Трапеция — , где s параллельные стороны и расстояние между этими основаниями.

• Ромб — частный случай воздушного змея и параллелограмма, поэтому здесь можно использовать любую формулу.

• Прямоугольник — , где длина прямоугольника, а ширина. (Это частный случай формулы параллелограмма, где высота и сторона совпадают.)

• Квадрат — , где длина стороны.

• Любой четырехугольник — , где – полупериметр, , , , – длины сторон, и – меры углов и , соответственно.

• Вписанный четырехугольник — где полупериметр и , , , и длины сторон. (Это частный случай формулы площади любого четырехугольника; .)

См.