Линейное программирование это: Основные понятия линейного программирования.

Линейное программирование | это… Что такое Линейное программирование?

Линейное программирование — математическая дисциплина, посвящённая теории и методам решения экстремальных задач на множествах -мерного векторного пространства, задаваемых системами линейных уравнений и неравенств.

Линейное программирование является частным случаем выпуклого программирования, которое в свою очередь является частным случаем математического программирования. Одновременно оно — основа нескольких методов решения задач целочисленного и нелинейного программирования. Одним из обобщений линейного программирования является дробно-линейное программирование.

Многие свойства задач линейного программирования можно интерпретировать также как свойства многогранников и таким образом геометрически формулировать и доказывать их.

Содержание 1 История 2 Задачи 3 Примеры задач 3.1 Максимальное паросочетание 3.2 Максимальный поток 3. 3 Транспортная задача 3.4 Игра с нулевой суммой 4 Алгоритмы решения 5 См. также 6 Примечания 7 Литература 8 Ссылки

История

В 1939 году Леонид Витальевич Канторович опубликовал работу «Математические методы организации и планирования производства», в которой сформулировал новый класс экстремальных задач с ограничениями и разработал эффективный метод их решения, таким образом были заложены основы линейного программирования.

Термин «программирование» нужно понимать в смысле «планирования» (один из переводов англ. programming). Он был предложен в середине 1940-х годов Джорджем Данцигом, одним из основателей линейного программирования, ещё до того, как компьютеры были использованы для решения линейных задач оптимизации.

Метод внутренних точек был впервые упомянут И. И. Дикиным в 1967 году.^[1]

Задачи

Основной (стандартной) задачей линейного программирования называется задача нахождения минимума линейной целевой функции (линейной формы) вида^[2]:

при условиях

,

.

Задача линейного программирования будет иметь канонический вид, если в основной задаче вместо первой системы неравенств имеет место система уравнений^[3]:

,

Основную задачу можно свести к канонической путём введения дополнительных переменных.

Задачи линейного программирования наиболее общего вида (задачи со смешанными ограничениями: равенствами и неравенствами, наличием переменных, свободных от ограничений) могут быть приведены к эквивалентным (имеющим то же множество решений) заменами переменных и заменой равенств на пару неравенств

[4].

Легко заметить, что задачу нахождения максимума можно заменить задачей нахождения минимума, взяв коэффициенты с обратным знаком.

Примеры задач

Максимальное паросочетание

Рассмотрим задачу о максимальном паросочетании в двудольном графе: есть несколько юношей и девушек, причём для каждых юноши и девушки известно, симпатичны ли они друг другу. Нужно поженить максимальное число пар со взаимной симпатией.

Введём переменные , которые соответствуют паре из -того юноши и -той девушки и удовлетворяют ограничениям:

с целевой функцией . Можно показать, что среди оптимальных решений этой задачи найдётся целочисленное. Переменные, равные 1, будут соответствовать парам, которые следует поженить.

Максимальный поток

Пусть имеется граф (с ориентированными рёбрами), в котором для каждого ребра указана его пропускная способность. И заданы две вершины: сток и исток. Нужно указать для каждого ребра, сколько через него будет протекать жидкости (не больше его пропускной способности) так, чтобы максимизировать суммарный поток из истока в сток (жидкость не может появляться или исчезать во всех вершинах, кроме стока и истока).

Возьмём в качестве переменных  — количество жидкости, протекающих через -тое ребро. Тогда

,

где  — пропускная способность -того ребра. Эти неравенства надо дополнить равенством количества втекающей и вытекающей жидкости для каждой вершины, кроме стока и истока. В качестве функции естественно взять разность между количеством вытекающей и втекающей жидкости в истоке.

Обобщение предыдущей задачи — максимальный поток минимальной стоимости. В этой задаче даны стоимости для каждого ребра и нужно среди максимальных потоков выбрать поток с минимальной стоимостью. Эта задача сводится к двум задачам линейного программирования: сначала нужно решить задачу о максимальном потоке, а потом добавить к этой задаче ограничение , где  — величина максимального потока, и решить задачу с новой функцией  — стоимостью потока.

Эти задачи могут быть решены быстрее, чем общими алгоритмами решения задач линейного программирования, за счёт особой структуры уравнений и неравенств.

Транспортная задача

Имеется некий однородный груз, который нужно перевести с складов на заводов. Для каждого склада известно, сколько в нём находится груза , а для каждого завода известна его потребность в грузе. Стоимость перевозки пропорциональна расстоянию от склада до завода (все расстояния от -го склада до -го завода известны). Требуется составить наиболее дешёвый план перевозки.

Решающими переменными в данном случае являются  — количества груза, перевезённого из -го склада на -й завод. Они удовлетворяют ограничениям:

Целевая функция имеет вид: , которую надо минимизировать.

Игра с нулевой суммой

Есть матрица размера . Первый игрок выбирает число от 1 до , второй — от 1 до . Затем они сверяют числа и первый игрок получает очков, а второй очков ( — число, выбранное первым игроком,  — вторым). Нужно найти оптимальную стратегию первого игрока.

Пусть в оптимальной стратегии, например, первого игрока число нужно выбирать с вероятностью . Тогда оптимальная стратегия является решением следующей задачи линейного программирования:

,

,

(),

в которой нужно максимизировать функцию . Значение в оптимальном решении будет математическим ожиданием выигрыша первого игрока в наихудшем случае.

Алгоритмы решения

Наиболее известным и широко применяемым на практике для решения общей задачи линейного программирования (ЛП) является симплекс-метод. Несмотря на то, что симплекс-метод является достаточно эффективным алгоритмом, показавшим хорошие результаты при решении прикладных задач ЛП, он является алгоритмом с экспоненциальной сложностью. Причина этого состоит в комбинаторном характере симплекс-метода, последовательно перебирающего вершины многогранника допустимых решений при поиске оптимального решения.

Первый полиномиальный алгоритм, метод эллипсоидов, был предложен в 1979 году советским математиком Л. Хачияном, разрешив таким образом проблему, долгое время остававшуюся нерешённой. Метод эллипсоидов имеет совершенно другую, некомбинаторную, природу, нежели симплекс-метод. Однако в вычислительном плане этот метод оказался неперспективным. Тем не менее, сам факт полиномиальной сложности задач привёл к созданию целого класса эффективных алгоритмов ЛП — методов внутренней точки, первым из которых был алгоритм Н. Кармаркара, предложенный в 1984 году. Алгоритмы этого типа используют непрерывную трактовку задачи ЛП, когда вместо перебора вершин многогранника решений задачи ЛП осуществляется поиск вдоль траекторий в пространстве переменных задачи, не проходящих через вершины многогранника. Метод внутренних точек, который, в отличие от симплекс-метода, обходит точки из внутренней части области допустимых значений, использует методы логарифмических барьерных функций нелинейного программирования, разработанные в 1960-х годах Фиако (Fiacco) и МакКормиком (McCormick).

См. также

• Нелинейное программирование
• Алгоритм Данцига
• Графический метод решения задачи линейного программирования
• Дробно-линейное программирование

Примечания

1. ↑ Дикин И. И. Итеративное решение задач линейного и квадратичного программирования // Докл. АН СССР. — 1967. — Т. 174. — № 4. — С. 747-748.
2. ↑ Карманов, 1986, с. 63
3. ↑ Карманов, 1986, с. 80
4. ↑ Карманов, 1986, с. 77

Литература

• Томас Х. Кормен и др. Глава 29. Линейное программирование // Алгоритмы: построение и анализ = INTRODUCTION TO ALGORITHMS. — 2-е изд. — М.: «Вильямс», 2006. — С. 1296.  — ISBN 5-8459-0857-4
• Акулич И.Л. Глава 1. Задачи линейного программирования, Глава 2. Специальные задачи линейного программирования // Математическое программирование в примерах и задачах. — М.: Высшая школа, 1986. — 319 с. — ISBN 5-06-002663-9
• Карманов В. Г. Математическое программирование. — 3-е издание. — М.: Наука, 1986. — 288 с.
• Данциг Джордж Бернард «Воспоминания о начале линейного программирования»

Ссылки

• Linear Program Solver (LiPS) — Бесплатный оптимизационный пакет, предназначенный для решения задач линейного, целочисленного и целевого программирования.
• Вершик А. М. «O Л. В. Канторовиче и линейном программировании»
• Слайды по линейному программированию
• Большакова И. В., Кураленко М. В. «Линейное программирование. Учебно-методическое пособие к контрольной работе».
• Барсов А. С. «Что такое линейное программирование», Популярные лекции по математике, Гостехиздат, 1959.
• М. Н. Вялый Линейные неравенства и комбинаторика. — МЦНМО, 2003.

2. Что такое математическое и линейное программирование?

Математическое программирование — область математики, разрабатывающая теорию и численные методы решения многомерных экстремальных задач с ограничениями, т.е. задач на экстремум функций многих переменных с ограничениями на область изменения этих переменных.

Линейное программирование – область математики, разрабатывающая теорию и численные методы решения задач нахождения экстремума (максимума или минимума) линейной функции многих переменных при наличии линейных ограничений, т.е. равенств или неравенств, связывающих эти переменные.

Линейное программирование – частный случай математического программирования.

3. Какова общая форма записи модели лп?

4. Что такое допустимое и оптимальное решения?

Набор управляющих параметров (переменных) при проведении операции называется решением. Решение называется допустимым, если оно удовлетворяет набору определенных условий. Решение называется оптимальным, если оно допустимо и по определенным признакам, предпочтительнее других или, по крайней мере, не хуже.

5. Каковы основные этапы построения математической модели лп?

Математической моделью экономической задачи называется совокупность математических соотношений, описывающих экономический процесс.

Для составления математической модели необходимо:

1. выбрать переменные задачи;

2. составить систему ограничений;

3. задать целевую функцию.

Переменные задачи – это x1,x2,…,xn.

Система ограничений – совокупность уравнений и неравенств, которым удовлетворяют переменные задачи и которые следуют из ограниченности ресурсов и других экономических условий, например, положительности переменных.

Целевая функция – это функция n переменных задачи, которая характеризует качество выполнения задачи и экстремум который требуется найти.

6. В чем заключаются особенность задач лп?

Особенность задач линейного программирования — линейность целевой функции и системы ограничений.

7. Какого вида бывают целевая функция?

Целевая функция – это количественный показатель предпочтительности или эффективности решений.

Используются следующие четыре формы целевой функции.

1) Наиболее часто используется целевая функция одного внешнего параметра

2) Вторая форма целевой функции – это сумма параметров одной размерности или сумма функций от этих параметров

3) Третья форма целевой функции – ранжированная форма – представляет собой упорядоченную совокупность целевых функций первой формы с приоритетами

4) Четвертая – наиболее общая – форма целевой функции представляет собой произвольную зависимость от всех или части (но не меньше двух) разнородных внешних параметров

8. Что такое область допустимых решений?

Область допустимых решений — это множество всех возможных точек (значений переменных) задачи оптимизации, которые удовлетворяют ограничениям задачи. Эти ограничения могут включать неравенства, равенства и требование целочисленности решения.

Область допустимых решений является начальной областью поиска кандидатов в решение задачи, и эта область во время поиска может сужаться.

9. Может ли у задачи ЛП не быть решения?

Да, может.

ЗЛП не разрешима (не имеет оптимального решения), если:

1) Система ограничений не совместна(не имеет решений)

2) Целевая функция не ограничена на множестве решений(Другими словами, при решении ЗЛП на max значение целевой функции стремится к бесконечности, а в случае ЗЛП на min – к минус бесконечности.)

10. В чем особенность задачи ОЗЛП?

Для упрощения решения общая задача линейного программирования сводится к более узкой задаче, называемой основной задачей линейного программирования (ОЗЛП). Отличие ОЗЛП от общей задачи составляют требования положительности значений всех переменных и ограничений только в виде равенств.

11. Как привести задачу ЛП к каноническому виду?

12. Может ли в области допустимых решений быть одна точка?

Да, может. Эта единственная точка и будет оптимальным решением.

13. Постановка задачи линейного программирования (на примерах).

Методы линейного программирования применяют к практическим задачам, в которых:

1) необходимо выбрать наилучшее решение (оптимальный план) из множества возможных;

2) решение можно выразить как набор значений некоторых переменных величин;

3) ограничения, накладываемые на допустимые решения специфическими условиями задачи, формулируются в виде линейных уравнений или неравенств;

4) цель выражается в форме линейной функции основных переменных.

Значения целевой функции, позволяя сопоставлять различные решения, служат критерием качества решения. Для практического решения экономической задачи математическими методами прежде всего ее следует записать с помощью математических выражений: уравнений, неравенств и т.п., т.е. составить экономикоматематическую модель. Исходя из отмеченных выше особенностей задач линейного программирования, можно наметить следующую общую схему формирования модели:

1) выбор некоторого числа переменных величин, заданием числовых значений которых однозначно определяется одно из возможных состояний исследуемого явления;

2) выражение взаимосвязей, присущих исследуемому явлению, в виде математических соотношений (уравнений, неравенств). Эти соотношения образуют систему ограничений задачи;

3) количественное выражение выбранного критерия оптимальности в форме целевой функции;

4) математическая формулировка задачи как задачи отыскания экстремума целевой функции при условии выполнения ограничений, накладываемых на переменные. В свою очередь в линейном программировании существуют классы задач, структура которых позволяет создать специальные методы их решения, выгодно отличающиеся от методов решения задач общего характера. Так, в линейном программировании появился раздел транспортных задач, блочного программирования и др.

Оптимизация | Определение, методы и факты

проблема оптимизации

Просмотреть все СМИ

Ключевые люди:

Ричард Карп

Похожие темы:

теория игры теория управления математическое программирование максимальное значение минимаксное значение

Просмотреть весь связанный контент →

Резюме

Прочтите краткий обзор этой темы

оптимизация , также известная как математическое программирование , набор математических принципов и методов, используемых для решения количественных задач во многих дисциплинах, включая физику, биологию, инженерию, экономику и бизнес. Предмет вырос из осознания того, что количественные задачи в явно разных дисциплинах имеют важные общие математические элементы. Из-за этой общности многие проблемы могут быть сформулированы и решены с использованием единого набора идей и методов, составляющих область оптимизации. 9. Математическое программирование включает изучение математической структуры задач оптимизации, изобретение методов решения этих задач, изучение математических свойств этих методов и реализацию этих методов на ЭВМ. Более быстрые компьютеры значительно расширили размер и сложность решаемых задач оптимизации. Развитие методов оптимизации шло параллельно с достижениями не только в информатике, но и в исследованиях операций, численном анализе, теории игр, математической экономике, теории управления и комбинаторике.

Проблемы оптимизации обычно состоят из трех основных элементов. Первый — это одна числовая величина или целевая функция, которую необходимо максимизировать или минимизировать. Целью может быть ожидаемая доходность портфеля акций, производственные затраты или прибыль компании, время прибытия транспортного средства в указанный пункт назначения или доля голосов политического кандидата. Второй элемент представляет собой набор переменных, то есть величин, значениями которых можно управлять для оптимизации цели. Примеры включают в себя количество запасов, которые должны быть куплены или проданы, количество различных ресурсов, которые должны быть выделены для различных производственных операций, маршрут, по которому должно следовать транспортное средство через транспортную сеть, или политика, которую должен отстаивать кандидат. Третий элемент задачи оптимизации — это набор ограничений, то есть ограничений на значения, которые могут принимать переменные. Например, производственный процесс не может требовать больше ресурсов, чем доступно, и не может использовать меньше, чем ноль ресурсов. В этих широких рамках задачи оптимизации могут иметь различные математические свойства. Задачи, в которых переменные являются непрерывными величинами (как в примере с распределением ресурсов), требуют иного подхода, чем задачи, в которых переменные являются дискретными или комбинаторными величинами (например, при выборе маршрута транспортного средства из заранее определенного набора возможностей).

Важный класс оптимизации известен как линейное программирование. Linear указывает, что никакие переменные не возводятся в более высокие степени, например квадраты. Для этого класса задачи включают в себя минимизацию (или максимизацию) линейной целевой функции, переменные которой являются действительными числами, которые должны удовлетворять системе линейных равенств и неравенств. Другой важный класс оптимизации известен как нелинейное программирование. В нелинейном программировании переменными являются действительные числа, а целью или некоторыми ограничениями являются нелинейные функции (возможно, включающие квадраты, квадратные корни, тригонометрические функции или произведения переменных). В этой статье обсуждаются как линейное, так и нелинейное программирование. Другие важные классы задач оптимизации, не рассмотренные в этой статье, включают стохастическое программирование, в котором целевая функция или ограничения зависят от случайных величин, так что оптимум находится в некотором «ожидаемом» или вероятностном смысле; оптимизация сети, которая включает в себя оптимизацию некоторых свойств потока через сеть, таких как максимизация количества материала, который может транспортироваться между двумя заданными точками в сети; и комбинаторная оптимизация, в которой решение должно быть найдено среди конечного, но очень большого набора возможных значений, таких как множество возможных способов назначить 20 производственных предприятий 20 местоположениям.

Происхождение и влияние

Хотя линейное программирование широко используется в настоящее время для решения повседневных задач принятия решений, до 1947 года оно было относительно неизвестно. До этой даты не проводилось никаких значительных работ, хотя французский математик Жозеф Фурье, казалось, знал о возможности предмета уже в 1823 г. В 1939 г. русский математик Леонид Витальевич Канторович опубликовал обширную монографию «Математические методы организации и планирования производства 9».0032 («Математические методы организации и планирования производства»), который в настоящее время считается первым трактатом, признавшим, что некоторые важные широкие классы задач планирования имеют четко определенные математические структуры. К сожалению, предложения Канторовича почти два десятилетия оставались практически неизвестными как в Советском Союзе, так и за его пределами. Тем временем линейное программирование значительно развилось в США и Западной Европе. В период после Второй мировой войны официальные лица в правительстве Соединенных Штатов пришли к выводу, что эффективная координация энергии и ресурсов всей нации в случае ядерной войны потребует использования методов научного планирования. Появление компьютера сделало такой подход возможным.

Интенсивная работа началась в 1947 году в ВВС США. Модель линейного программирования была предложена потому, что она была относительно проста с математической точки зрения, и в то же время обеспечивала достаточно общую и практическую основу для представления взаимозависимых действий, которые совместно используют ограниченные ресурсы. В модели линейного программирования разработчик модели рассматривает оптимизируемую систему как состоящую из различных действий, которые, как предполагается, требуют потока входов (например, рабочей силы и сырья) и выходов (например, готовых товаров и услуг) различных типов. типы пропорциональны уровню активности. Предполагается, что уровни активности могут быть представлены неотрицательными числами. Революционная особенность подхода заключается в выражении цели процесса принятия решений в терминах минимизации или максимизации линейной целевой функции — например, максимизации возможных боевых вылетов в случае военно-воздушных сил или максимизации прибыли в промышленности. До 1947 все практическое планирование характеризовалось серией навязанных властями правил процедуры и приоритетов. Общие цели никогда не формулировались, вероятно, из-за невозможности выполнения расчетов, необходимых для минимизации целевой функции при ограничениях. В 1947 г. был введен метод (описанный в разделе Симплекс-метод), который оказался эффективным для решения практических задач. Интерес к линейному программированию быстро рос, и к 1951 году его использование распространилось на промышленность. Сегодня почти невозможно назвать отрасль, которая не использует математическое программирование в той или иной форме, хотя области применения и степень его использования сильно различаются даже в пределах одной отрасли.

Оформите подписку Britannica Premium и получите доступ к эксклюзивному контенту. Подпишитесь сейчас

Интерес к линейному программированию распространился и на экономику. В 1937 году математик венгерского происхождения Джон фон Нейман проанализировал неуклонно расширяющуюся экономику, основанную на альтернативных методах производства и фиксированных технологических коэффициентах. Что касается истории математики, то до 1936 г. изучение систем линейных неравенств практически не вызывало интереса. решить задачу, связанную с оптимизацией, и в 1941 движение по ребрам было предложено для транспортной задачи. Заслуга в создании большей части математических основ, вероятно, должна принадлежать фон Нейману. В 1928 году он опубликовал свою знаменитую статью по теории игр, а кульминацией его работы стала публикация в 1944 году в сотрудничестве с австрийским экономистом Оскаром Моргенштерном классической книги «Теория игр и экономическое поведение ». В 1947 году фон Нейман предположил эквивалентность линейных программ и матричных игр, ввел важное понятие двойственности и сделал несколько предложений по численному решению задач линейного программирования и игр. Серьезный интерес со стороны других математиков начался в 1948 со строгим развитием дуальности и связанных с ней вопросов.

Общий симплексный метод был впервые запрограммирован в 1951 году для компьютера SEAC Бюро стандартов США. Начиная с 1952 года симплекс-метод был запрограммирован для использования на различных компьютерах IBM, а затем и на компьютерах других компаний. В результате быстро росло коммерческое применение линейных программ в промышленности и правительстве. Продолжали разрабатываться новые вычислительные методы и вариации старых методов.

В последнее время появился большой интерес к решению больших линейных задач со специальными структурами — например, корпоративные модели и модели национального планирования, которые являются многоступенчатыми, динамичными и демонстрируют иерархическую структуру. Подсчитано, что некоторые развивающиеся страны будут иметь потенциал для увеличения своего валового национального продукта (ВНП) на 10–15 процентов в год, если удастся построить, оптимизировать и внедрить подробные модели роста экономики.

Что такое линейное программирование (ЛП)?

Что означает линейное программирование (LP)?

Линейное программирование — это математический метод, который используется для определения наилучшего возможного результата или решения из заданного набора параметров или списка требований, которые представлены в виде линейных отношений.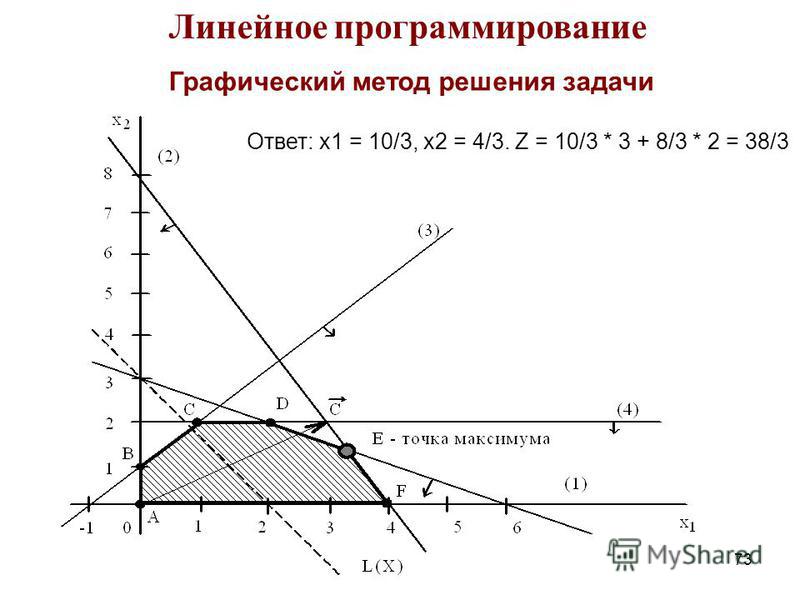 Чаще всего он используется в компьютерном моделировании или симуляции, чтобы найти наилучшее решение при распределении ограниченных ресурсов, таких как деньги, энергия, рабочая сила, машинные ресурсы, время, пространство и многие другие переменные. В большинстве случаев «наилучший результат», необходимый для линейного программирования, — это максимальная прибыль или минимальные затраты.

Из-за своей природы линейное программирование также называют линейной оптимизацией.

Реклама

Techopedia объясняет линейное программирование (LP)

Линейное программирование используется в качестве математического метода для определения и планирования наилучших результатов и было разработано во время Второй мировой войны Леонидом Канторовичем в 1937 году. Это был метод, используемый для планирования расходов и доходов таким образом, чтобы сократить расходы для военных и, возможно, вызвало обратное у противника.

Линейное программирование является частью важной области математики, называемой «методами оптимизации», поскольку оно буквально используется для поиска наиболее оптимизированного решения данной задачи. Самый простой пример использования линейной оптимизации — логистика или «метод эффективного перемещения вещей». Например, предположим, что имеется 1000 ящиков одинакового размера по 1 кубическому метру каждый; 3 грузовика, способные перевозить 100 ящиков, 70 ящиков и 40 ящиков соответственно; несколько возможных маршрутов; и 48 часов, чтобы доставить все коробки. Линейное программирование предоставляет математические уравнения для определения оптимальной загрузки грузовика и маршрута, по которому нужно следовать требованию доставки всех ящиков из точки А в точку Б с наименьшим количеством поездок туда и обратно и, конечно же, с наименьшими затратами. максимально быстрое время.

Основными компонентами линейного программирования являются следующие:

• Переменные решения — Это величины, которые необходимо определить.

  No related posts.