Линейное программирование — Orange, jazz, dark chocolate & lagrange function — LiveJournal
Линейное программирование — математическая дисциплина, посвященная теории и методам решения задач об экстремумах линейных функций на множествах n-мерного векторного пространства, задаваемых системами линейных уравнений и неравенств.
Линейное программирование является частным случаем выпуклого программирования, которое в свою очередь является частным случаем математического программирования. Одновременно оно — основа нескольких методов решения задач целочисленного и нелинейного программирования.
Математическая формулировка задачи линейного программирования
Нужно максимизировать
при условиях
при .
Иногда на xi также накладывается некоторый набор ограничений в виде равенств, но от них можно избавиться, последовательно выражая одну переменную через другие и подставляя ее во всех остальных равенствах и неравенствах (а также в функции f).
Такую задачу называют «основной» или «стандартной» в линейном программировании.
Примеры задач линейного программирования
Поток и паросочетание
Рассмотрим задачу о максимальном паросочетании: есть несколько юношей и девушек; для каждой пары известно, любят ли они друг друга. Нужно поженить максимальное число пар. Введем переменные xij — они соответствуют паре из i-того юноши и j-той девушки. Введем ограничения: , , , , . Можно показать, что среди оптимальных решений этой задачи найдется целочисленное. Переменные, равные 1, будут соответствовать парам, которые следует поженить.
Вторая важная задача — максимальный поток. Пусть имеется граф (с ориентированными ребрами), в котором для каждого ребра указана его пропускная способность. И заданы 2 вершины: сток и исток. Нужно указать для каждого ребра, сколько через него будет протекать жидкости (не больше его пропускной способности) так, чтобы максимизировать суммарный поток из стока в исток (жидкость не может появляться или исчезать во всех вершинах, кроме стока и истока).
Возьмем в качестве переменных xi — количество жидкости, протекающих через i-тое ребро. Тогда , , где ci — пропускная способность i-того ребра. Эти неравенства надо дополнить равенством количества втекающей и вытекающей жидкости для каждой вершины, кроме стока и истока. В качестве функции f естественно взять разность между количеством вытекающей и втекающей жидкости в истоке.
Обобщение предыдущей задачи — максимальный поток минимальной стоимости. В этой задаче даны стоимости для каждого ребра и нужно среди максимальных потоков выбрать поток с минимальной стоимостью. Эта задача сводится к 2 задачам линейного программирования: сначала нужно решить задачу о максимальном потоке, а потом добавить к этой задаче ограничение , где m — величина максимального потока, и решить задачу с новой функцией f(x) — стоимостью потока.
Все эти задачи могут быть решены быстрее, чем с помощью общих алгоритмов решения задач линейного программирования, за счет особой структуры уравнений и неравенств.
Транспортная задача
Имеется некий однородный груз, который нужно перевести с n складов на m заводов. Для каждого склада i известно, сколько в нем находится груза ai, а для каждого завода известна его потребность bj в грузе. Стоимость перевозки пропорциональна расстоянию от склада до завода (все расстояния cij от i-го склада до j-го завода известны). Требуется составить наиболее дешевый план перевозки. Решающими переменными в данном случае являются xij — количества груза, перевезенного из i-го склада на j-й завод.
Ограничениями будут и
.
Целевая функция имеет вид: , которую надо минимизировать.
Игра с нулевой суммой
Есть матрица A размера . Первый игрок выбирает число от 1 до n, второй — от 1 до m. Затем они сверяют числа и первый игрок получает aij очков, а второй ( − aij) очков (i — число, выбранное первым игроком, j — вторым).
Нужно найти оптимальную стратегию первого игрока. Пусть в оптимальной стратегии число i нужно выбирать с вероятностью pi. Тогда оптимальная стратегия является решением следующей задачи линейного программирования: , , , (), в которой нужно максимизировать функцию . c в оптимальном решении будет математическим ожиданием выигрыша первого игрока в наихудшем случае.
Алгоритмы решения общей задачи линейного программирования
Наиболее известным и широко применяемым на практике для решения общей задачи линейного программирования (ЛП) является симплекс-метод. Несмотря на то, что симплекс-метод является достаточно эффективным алгоритмом, показавшим хорошие результаты при решении прикладных задач ЛП, он является алгоритмом с экспоненциальной сложностью. Причина этого состоит в комбинаторном характере симплекс-метода, последовательно перебирающего вершины многогранника допустимых решений при поиске оптимального решения.
Первый полиномиальный алгоритм, метод эллипсоидов, был предложен в 1979 г.
советским математиком Л.Хачияном, разрешив таким образом проблему, долгое время остававшуюся нерешенной. Метод эллипсоидов имеет совершенно другую, некомбинаторную, природу, нежели симплекс-метод. Однако в вычислительном плане этот метод оказался неперспективным. Тем не менее сам факт полиномиальной сложности задач привел к созданию целого класса эффективных алгоритмов ЛП — методов внутренней точки, первым из которых был алгоритм Н. Кармаркара, предложенный в 1984 г. Алгоритмы этого типа используют непрерывную трактовку задачи ЛП, когда вместо перебора вершин многогранника решений задачи ЛП осуществляется поиск вдоль траекторий в пространстве переменных задачи, не проходящих через вершины многогранника. Метод внутренних точек, который, в отличие от симплекс-метода, обходит точки из внутренней части области допустимых значений, использует методы логарифмических барьерных функций нелинейного программирования , разработанные в 60-х гг. Fiacco и McCormick.
Решение интервальной задачи дробно-линейного программирования сведением к задаче линейного программирования
Библиографическое описание: Немкова, Е.
А. Решение интервальной задачи дробно-линейного программирования сведением к задаче линейного программирования / Е. А. Немкова, В. И. Левин. — Текст : непосредственный // Молодой ученый. — 2011. — № 8 (31). — Т. 1. — С. 30-34. — URL: https://moluch.ru/archive/31/3511/ (дата обращения: 13.01.2023).
В настоящее время широко разработаны вопросы
традиционной оптимизации систем с детерминированными параметрами
[1,2]. С математической точки зрения такая оптимизация есть отыскание
экстремумов функции, параметры которых детерминированные (полностью
определенные) величины. Однако на практике чаще встречаются системы с
недетерминированными (не полностью определенными) параметрами. Такая
оптимизация значит сложнее традиционной [1,2], так как для нее
дополнительно необходимы обобщение понятия экстремума функции,
выяснение условий существования экстремума недетерминированной
функции и разработка специальных методов поиска экстремумов таких
функций.
Общая задача дробно-линейного программирования в детерминированной постановке состоит в нахождении максимального значения дробно-линейной функции
(1),
при условиях (2)
где
-
некоторые постоянные числа. Также предполагается, что знаменатель
функции
в области неотрицательных решений системы линейных уравнений (2).
Решение этой задачи имеет своей целью минимизировать себестоимость
выпускаемых изделий.
Рассмотрим недетерминированный (интервальный) вариант задачи (1),(2), состоящий в определении максимального значения интервального обобщения функции (1)
(3),
при детерминированных условиях (4)
где и — интервалы вида , , в которых , — минимальные значения интервальных коэффициентов (нижние границы интервалов), а , - максимальные значения интервальных коэффициентов (верхние границы интервалов), - некоторые постоянные числа, .
Будем решать поставленную интервальную задачу
методом детерминизации, т.е. сведением к двум аналогичным
детерминированным задачам. Так как целевая функция является
нелинейной и представляет собой отношение двух линейных функций, то
нижняя граничная задача задачи (3), (4) может быть получена при
замене всех интервальных коэффициентов числителя целевой функции (1)
их нижними границами, а всех интервальных коэффициентов знаменателя
целевой функции их верхними границами.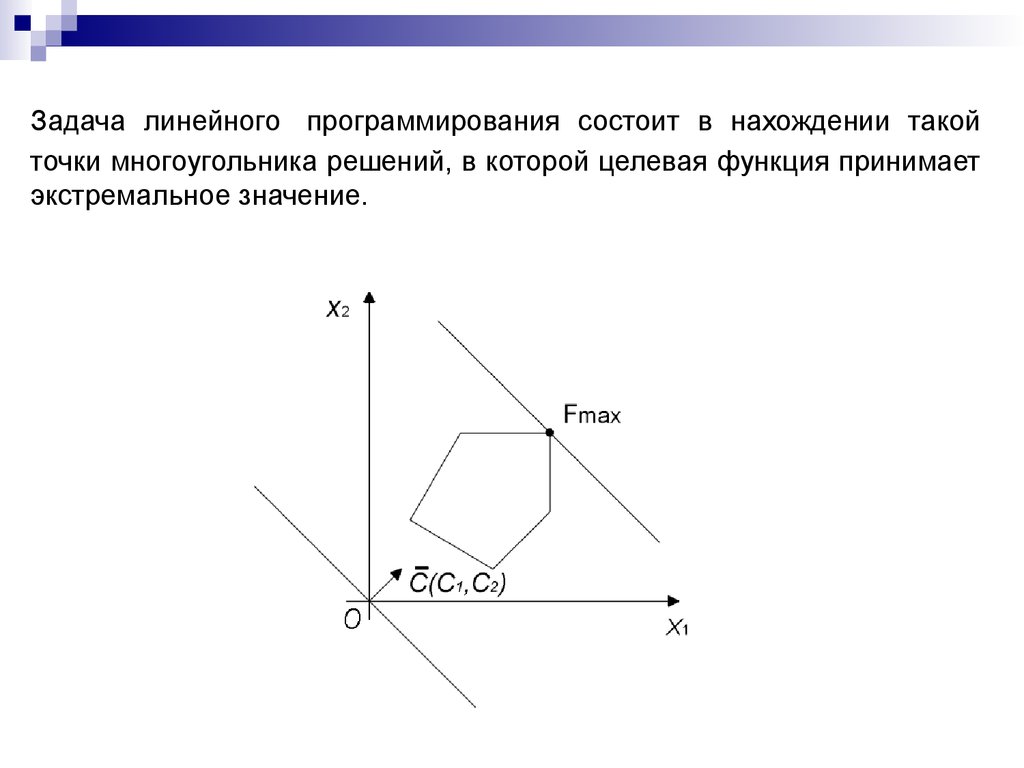
Верхняя граничная задача
задачи (3), (4) может быть получена при замене всех интервальных
коэффициентов числителя целевой функции их верхними границами, а всех
интервальных коэффициентов знаменателя целевой функции их нижними
границами. В результате необходимых действий получим два решения двух
введенных детерминированных задач. Решение нижней граничной задачи
дает максимальное значение
ее
целевой функции
,
являющееся нижней границей интервала-решения исходной задачи (3),
(4), решение верхней граничной задачи дает максимальное значение
ее
целевой функции
,
являющееся верхней границей интервала-решения исходной задачи (3),
(4). Т.о. решение исходной задачи, т.е. максимум интервальной
целевой функции
будет достигаться в некоторой точке
,
а значение этого максимума целевой функции при заданных
ограничениях будет
.
Итак, нам необходимо решить две граничные детерминированные
оптимизационные задачи – нижнюю граничную и верхнюю граничную.
Задача 1(нижняя граничная задача): Найти максимум функции
(5)
при условиях (6)
Сформулированная задача может быть сведена к задаче линейного программирования. Для этого обозначим
(7)
И введем новые переменные (8)
Используя введенные переменные, сведем задачу 1 к следующей задаче: найти максимум функции
(9)
при условиях
(10)
(11)
.
Задача (9)-(11) является задачей линейного программирования.
Следовательно, ее решение можно найти соответствующими известными
методами [1,2]. Зная оптимальный план решения этой задачи на основе
соотношении (8) получаем оптимальный план решения задачи 1.
Максимальное значение
целевой функции
задачи
1- нижней граничной задачи исходной задачи (3),(4) — является нижней
границей интервального максимального значения функции (3).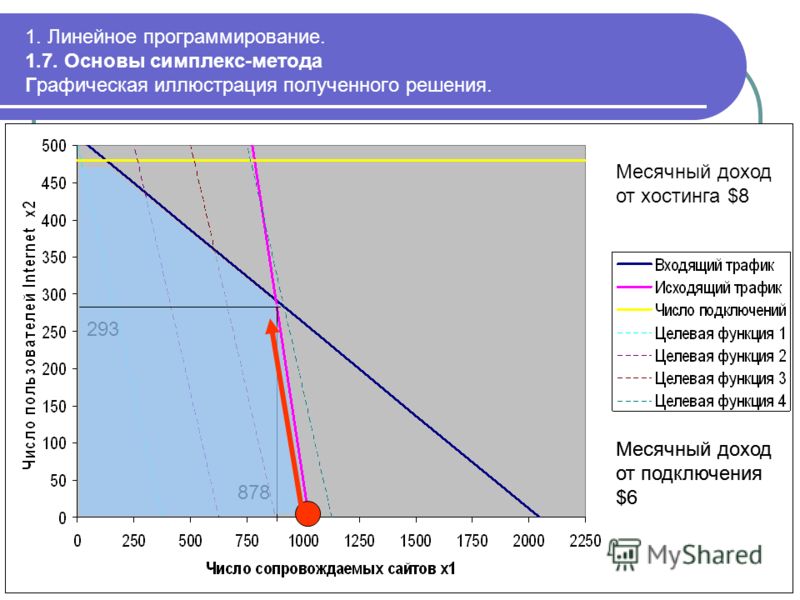
Задача 2 (верхняя граничная задача): Найти максимум функции
(12)
при условиях (13)
Сформулированная задача, как и задача 1, может быть сведена к задаче линейного программирования. Для этого обозначим
(14)
и введем новые переменные . (15)
Используя введенные переменные, сведем задачу 2 к следующей: найти максимум функции
(16)
при условиях
, (17)
, (18)
, .
Задачу (16)-(18), как и задачу (9)-(11), решаем известными методами решения задач линейного программирования.
В результате получаем максимальное значение
целевой функции
задачи 2 верхней граничной задачи исходной задачи (3), (4). Это
значение является верхней границей интервального максимального
значения
функции (3).
Так как система ограничений (4) интервальной задачи (3),(4) была детерминированной, то системы ограничений (6) и (13) задач 1 и 2 совпадают. При этом, оказалось, что точки максимума целевых функции в задачах 1 и 2 тоже совпадают. В результате решений задач 1 и 2 получаются граничные значения интервального максимума целевой функции интервальной задачи (3),(4). Т.о. интервальный максимум значений целевой функции (3) при заданных ограничениях (4) получается в виде , где — решение задачи 1, — решение задачи 2.
Пример: Найти максимальное значение функции (19)
при условиях (20)
и , , , , , .
Переменные могут принимать только лишь неотрицательные значения.
Таким образом, математическая постановка задачи состоит в определении
неотрицательного решения системы линейных неравенств (4), при котором
достигается максимум функции F.
Решим нижнюю граничную задачу. Рассмотрим значение целевой функции при нижних границах интервалов коэффициентов и верхних границах коэффициентов .
(21)
От неравенств перейдем к равенствам, введем дополнительные переменные
(22)
Введем новую переменную , перейдем к новым переменным .
Целевая функция
Запишем систему ограничений в новых переменных
(23)
Решив задачу симплекс-методом, получим следующие значения переменных , , , . Сделав возврат к исходным переменным, получим следующее решение в виде точки , , . Значение целевой функции .
Решим верхнюю граничную задачу. Рассмотрим значение целевой функции при верхних границах интервалов коэффициентов и нижних границах интервалов коэффициентов .
(24).
От неравенств перейдем к равенствам, введем дополнительные переменные
(25)
Введем новую переменную , перейдем к новым переменным
Целевая функция
Запишем систему ограничений в новых переменных
(26)
Решив задачу симплекс-методом, получим следующие значения переменных , , . Сделав возврат к исходным переменным, получим следующее решение в виде точки , , . Соответствующее максимальное значение целевой функции .
Искомый максимум интервальной целевой функции (3) при заданных ограничениях (4) находится в общей точке (70;0;0) решения двух граничных задач, а сам максимум целевой функции получаем соединением двух максимальных значений целевой функции двух граничных задач .
-
- Литература:
Акулич И.Л. Математическое программирование в примерах и задачах.
–
М.: Высшая школа, 1986. 317 с.Волошин Г.Я. Методы оптимизации в экономике. – М.: Дело и сервис, 2004. 320с.
Левин В.И. Интервальные методы оптимизации систем в условиях неопределенности. – Пенза: Изд-во ПТИ, 1999. 101с.
–
М.: Высшая школа, 1986. 317 с.Основные термины (генерируются автоматически): целевая функция, задача, максимальное значение, верхняя граничная задача, исходная задача, линейное программирование, максимум функции, нижняя граничная задача, переменная, система ограничений.
Что такое линейное программирование? Для чего его используют?
Практические задачи WordБольше примеровЧетыре переменных
Purplemath
Что такое линейное программирование?
Линейное программирование — это процесс использования различных линейных неравенств (называемых «ограничениями»), относящихся к некоторой ситуации, и поиска наилучшего значения, достижимого в этих условиях. Типичным примером может быть использование ограничений материалов и рабочей силы, а затем определение оптимальных уровней производства для получения максимальной прибыли в этих условиях.
Содержание продолжается ниже
MathHelp.com
Полезно ли линейное программирование в реальной жизни?
В реальной жизни линейное программирование является частью очень важной области математики, называемой «методами оптимизации».
Эта область исследований (или, по крайней мере, ее прикладные результаты) ежедневно используется при организации и распределении ресурсов. В этих реальных системах могут быть десятки, сотни или даже больше переменных. (Для любопытных история линейного программирования: PDF)
Однако в алгебре вы будете работать только с простым (и наглядным) линейным случаем с двумя переменными.
Как решить задачу линейного программирования?
Общий процесс решения упражнений по линейному программированию выглядит следующим образом:
- Нарисуйте график системы линейных неравенств. Область, отгороженная различными неравенствами, называется «областью осуществимости».
- Используя версии неравенств «равно», решите пары прямых, чтобы найти угловые точки (или «вершины») допустимой области.
- Подставьте координаты каждой вершины в модель для данной ситуации (то есть в уравнение оптимизации).
- Если вы максимизируете, возьмите угол, который дает вам наибольшее значение; в противном случае выберите вариант с наименьшим значением.
- Для текстовых задач интерпретируйте результат в заданном контексте (например, скажите «восемь метров в ширину и три метра в высоту», а не просто «(8, 3)»).
Почему вы тестируете только углы?
Кто-то вычислил, что при заданной системе линейных неравенств и уравнении, которое необходимо оптимизировать (то есть максимизировать или минимизировать), оптимальное решение системы всегда будет на грани.
Этому есть сложные объяснения, но есть и интуитивные (для простого случая с двумя переменными, с которым мы будем работать). В любом случае, углы там, где они есть.
- Найдите максимальное и минимальное значение z = 3 x + 4 y с учетом следующих ограничений:
Три неравенства в фигурных скобках являются ограничениями.
Область плоскости, которую они отмечают, будет областью осуществимости. Формула « z = 3 x + 4 y » является уравнением оптимизации. Мне нужно найти ( x , y ) угловые точки области выполнимости, которые возвращают наибольшее и наименьшее значения з .
Мой первый шаг — решить каждое неравенство для эквивалентных форм, которые легче изобразить графически:
Начертить систему легко; вы берете версию «равно» каждого неравенства (эти версии «равно» представляют собой линии, образующие края допустимой области), и решаете систему линейных уравнений, образованную каждой парой линий:
Чтобы найти угловые точки — которые не всегда ясны на графике — я сопоставлю линии (таким образом сформирую систему линейных уравнений) и решу:
y = −( 1 / 2 ) x + 7
y = 3 x
−( 1 / 2 ) x + 7 = 3 x
− x + 14 = 6 x
14 = 7 x
2 = x
y = 3(2) = 6
угловая точка в (2, 6)
y = −( 1 / 2 ) x + 7
y = x — 2
— ( 1 / 2 ) — ( 1 / 2 ) — ( 1 / 2 ) — 7 + .
. . . . . . . . . . . . . . . . .
— x + 14 = 2 x — 4
18 = 3 x
6 = x
Y = (6) — 2 = 4
. (6, 4)
у = 3 х
y = x − 2
3 x = x − 2
2 x = −2
x = −1
y = 3 (−1) = −3
угловая точка в точке (−1, −3)
Таким образом, угловые точки — точки, которые я буду подставлять в уравнение оптимизации — это (2, 6), (6, 4) и (−1, −3). Чтобы найти решение этого упражнения, мне нужно только подставить эти три точки в » z = 3 x + 4 y «.
(2, 6): z = 3(2) + 4(6) = 6 + 24 = 30
(6, 4): z = 3(6) + 4(4) = 18 + 16 = 34
(−1, −3): z = 3(−1) + 4(−3) = −3 −12 = −15
Тогда максимум z = 34 приходится на (6, 4) ,
, а минимум z = −15 приходится на (−1, −3).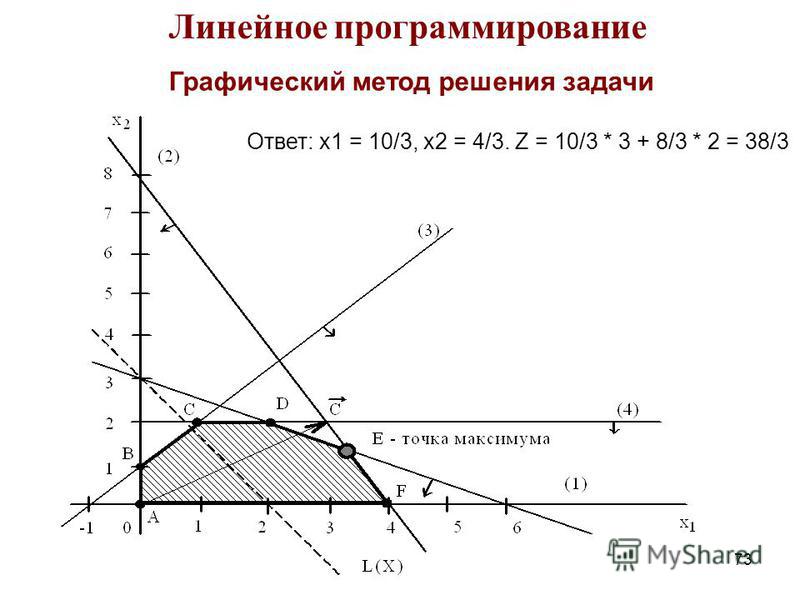
Как видите, решение упражнения по линейному программированию может быть длительным процессом, но каждый отдельный шаг довольно прост. Просто не торопитесь, маркируйте четко и работайте аккуратно, и вы получите это!
URL: https://www.purplemath.com/modules/linprog.htm
Стр. 2 Стр. 3 Стр. 4 Стр. с учетом ограничений, линейного равенства и ограничений неравенства. Примеры проблем включают смешивание в перерабатывающих отраслях, планирование производства в обрабатывающей промышленности, согласование денежных потоков в финансах и планирование в энергетике и транспорте.
Линейное программирование — это математическая задача поиска вектора x, минимизирующего функцию: 9{\mathsf{T}}x\right\}\]
С учетом ограничений:
\[\begin{eqnarray}Ax \leq b & \quad & \text{(ограничение неравенства)} \\A_{ eq}x = b_{eq} & \quad & \text{(ограничение равенства)} \\lb \leq x \leq ub & \quad & \text{(граничное ограничение)}\end{eqnarray}\]
Вы можете использовать MATLAB ® для реализации следующих часто используемых алгоритмов для решения задач линейной оптимизации:
- Внутренняя точка: использует алгоритм прямого-двойственного предиктора-корректора и особенно полезен для крупномасштабных линейных программ, которые имеют структуру или могут быть определены с помощью разреженных матриц.
- Симплекс: Использует систематическую процедуру для создания и тестирования возможных вершинных решений для линейной программы. Симплексный алгоритм и связанный с ним двойной симплексный алгоритм являются наиболее широко используемыми алгоритмами линейного программирования.
Алгоритмы для некоторых особых случаев линейных программ, где ограничения имеют сетевую структуру, обычно быстрее, чем алгоритмы внутренних точек и симплексные алгоритмы общего назначения. К особым случаям относятся:
- Максимальный сетевой поток: используются алгоритмы увеличения пути и принудительной перемаркировки.
- Кратчайший путь: используются алгоритмы Дейкстры, Беллмана-Форда и алгоритмы поиска.
- Линейное присвоение: использует алгоритм двудольного сопоставления.
Для получения дополнительной информации об алгоритмах и линейном программировании смотрите Optimization Toolbox™.
Примеры и инструкции
- Начало работы с линейным программированием в MATLAB — Пример
- Математическое моделирование с оптимизацией, часть 1: от описания задачи к математической программе (8:51) — Видео
- Математическое моделирование с оптимизацией, часть 2a: линейное программирование на основе задач (6:04) — Видео
- Классы графов и орграфов (5:44) — Видео
- Максимизируйте долгосрочные инвестиции с помощью линейного программирования — Пример
- Производственное планирование — Пример
Варианты использования
- Канадский институт биодиагностики разрабатывает инструмент визуализации — История пользователя
- Gas Natural Fenosa (теперь Naturgy Energy Group S.
