| 1 | Найти точное значение | sin(30) | |
| 2 | Найти точное значение | sin(45) | |
| 3 | Найти точное значение | sin(30 град. ) | |
| 4 | Найти точное значение | sin(60 град. ) | |
| 5 | Найти точное значение | tan(30 град. ) | |
| 6 | Найти точное значение | arcsin(-1) | |
| 7 | Найти точное значение | sin(pi/6) | |
| 8 | cos(pi/4) | ||
| 9 | Найти точное значение | sin(45 град. ) ) | |
| 10 | Найти точное значение | sin(pi/3) | |
| 11 | Найти точное значение | arctan(-1) | |
| 12 | Найти точное значение | cos(45 град. ) | |
| 13 | Найти точное значение | cos(30 град. ) | |
| 14 | Найти точное значение | tan(60) | |
| 15 | Найти точное значение | csc(45 град. ) | |
| 16 | Найти точное значение | tan(60 град. ) | |
| 17 | Найти точное значение | sec(30 град. ) ) | |
| 18 | Найти точное значение | cos(60 град. ) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | sin(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | tan(45 град. ) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 град. ) | |
| 25 | Найти точное значение | sec(45 град.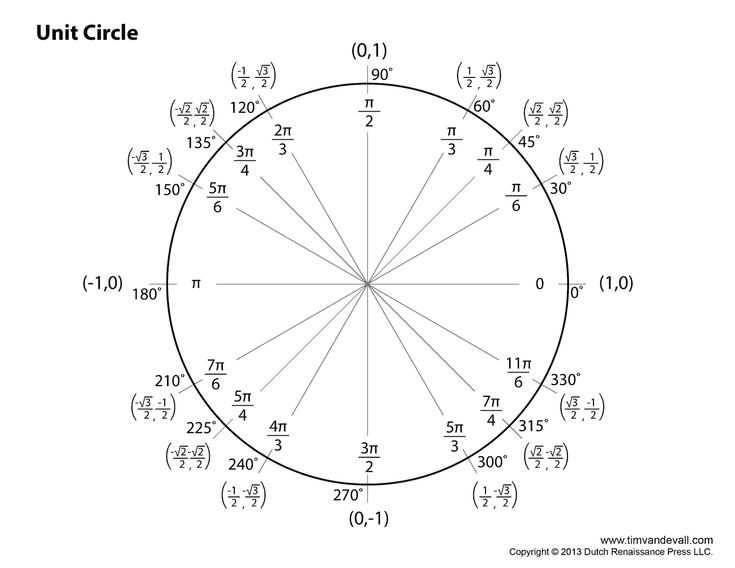 ) ) | |
| 26 | Найти точное значение | csc(30 град. ) | |
| 27 | Найти точное значение | sin(0) | |
| 28 | Найти точное значение | sin(120) | |
| 29 | Найти точное значение | cos(90) | |
| 30 | Преобразовать из радианов в градусы | pi/3 | |
| 31 | Найти точное значение | tan(30) | |
| 32 | Преобразовать из градусов в радианы | 45 | |
| 33 | Найти точное значение | cos(45) | |
| 34 | Упростить | sin(theta)^2+cos(theta)^2 | |
| 35 | Преобразовать из радианов в градусы | pi/6 | |
| 36 | Найти точное значение | cot(30 град.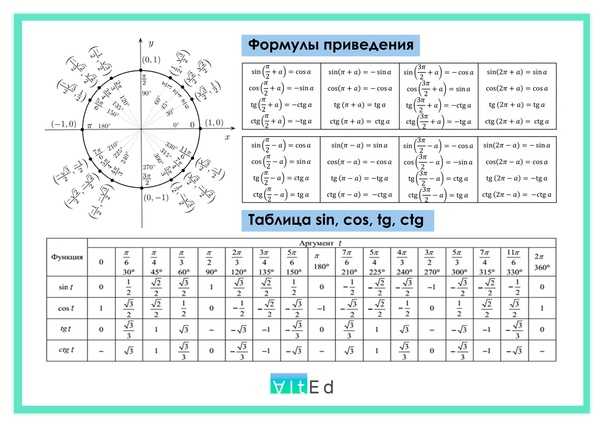 ) ) | |
| 37 | Найти точное значение | arccos(-1) | |
| 38 | Найти точное значение | arctan(0) | |
| 39 | Найти точное значение | cot(60 град. ) | |
| 40 | Преобразовать из градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2pi)/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | tan(pi/2) | |
| 45 | Найти точное значение | sin(300) | |
| 46 | Найти точное значение | cos(30) | |
| 47 | Найти точное значение | cos(60) | |
| 48 | Найти точное значение | cos(0) | |
| 49 | Найти точное значение | cos(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | sec(60 град.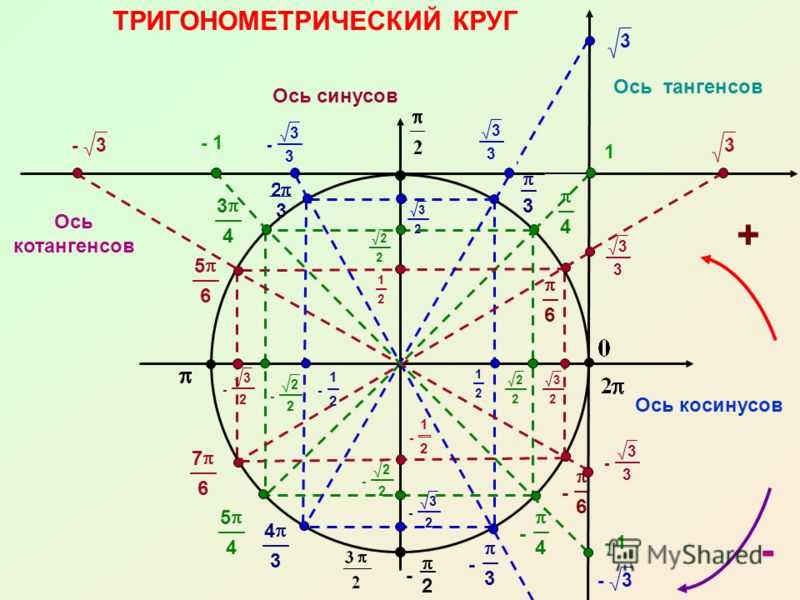 ) ) | |
| 53 | Найти точное значение | sin(300 град. ) | |
| 54 | Преобразовать из градусов в радианы | 135 | |
| 55 | Преобразовать из градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5pi)/6 | |
| 57 | Преобразовать из радианов в градусы | (5pi)/3 | |
| 58 | Преобразовать из градусов в радианы | 89 град. | |
| 59 | Преобразовать из градусов в радианы | 60 | |
| 60 | Найти точное значение | sin(135 град.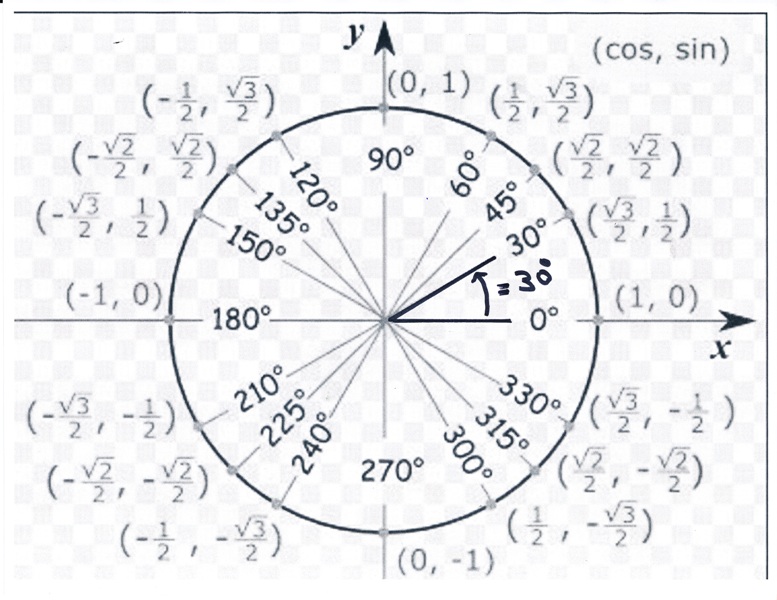 ) ) | |
| 61 | Найти точное значение | sin(150) | |
| 62 | Найти точное значение | sin(240 град. ) | |
| 63 | Найти точное значение | cot(45 град. ) | |
| 64 | Преобразовать из радианов в градусы | (5pi)/4 | |
| 65 | Найти точное значение | sin(225) | |
| 66 | Найти точное значение | sin(240) | |
| 67 | Найти точное значение | cos(150 град. ) | |
| 68 | Найти точное значение | tan(45) | |
| 69 | Вычислить | sin(30 град. ) ) | |
| 70 | Найти точное значение | sec(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | csc(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | tan((5pi)/3) | |
| 75 | Найти точное значение | tan(0) | |
| 76 | Вычислить | sin(60 град. ) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | arcsin(-1/2) | |
| Найти точное значение | sin((4pi)/3) | ||
| 82 | Найти точное значение | csc(45) | |
| 83 | Упростить | arctan( квадратный корень из 3) | |
| 84 | Найти точное значение | sin(135) | |
| 85 | Найти точное значение | sin(105) | |
| 86 | Найти точное значение | sin(150 град. ) ) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | tan((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | pi/4 | |
| 90 | Найти точное значение | sin(pi/2) | |
| 91 | Найти точное значение | sec(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | arcsin(0) | |
| 95 | Найти точное значение | sin(120 град. ) ) | |
| 96 | Найти точное значение | tan((7pi)/6) | |
| 97 | Найти точное значение | cos(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразовать из градусов в радианы | 88 град. |
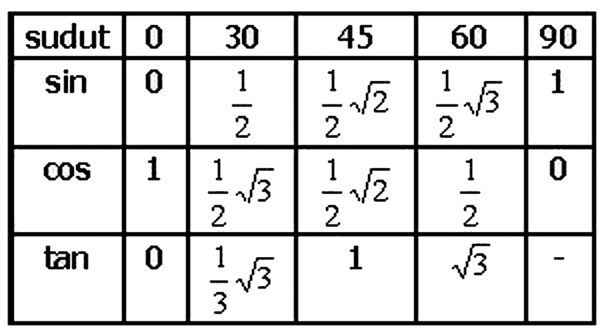
Примечание . В данной таблице значений тригонометрических функций используется знак √ для обозначения квадратного корня. Для обозначения дроби — символ «/». См. также полезные материалы: Для определения значения тригонометрической функции , найдите его на пересечении строки с указанием тригонометрической функции. Например, синус 30 градусов — ищем колонку с заголовком sin (синус) и находим пересечение этой колонки таблицы со строкой «30 градусов», на их пересечении считываем результат — одна вторая. Аналогично находим косинус 60 градусов, синус 60 градусов (еще раз, в пересечении колонки sin (синус) и строки 60 градусов находим значение sin 60 = √3/2) и т. Синус пи, косинус пи, тангенс пи и других углов в радианахПриведенная ниже таблица косинусов, синусов и тангенсов также подходит для нахождения значения тригонометрических функций, аргумент которых задан в радианах . Для этого воспользуйтесь второй колонкой значений угла. Благодаря этому можно перевести значение популярных углов из градусов в радианы. Например, найдем угол 60 градусов в первой строке и под ним прочитаем его значение в радианах. 60 градусов равно π/3 радиан. Число пи однозначно выражает зависимость длины окружности от градусной меры угла. Таким образом, пи радиан равны 180 градусам. Любое число, выраженное через пи (радиан) можно легко перевести в градусную меру, заменив число пи (π) на 180 . Примеры : 2. Косинус пи . 3. Тангенс пи Таблица значений синуса, косинуса, тангенса для углов 0 — 360 градусов (часто встречающиеся значения)
Если в таблице значений тригонометрических функций вместо значения функции указан прочерк (тангенс (tg) 90 градусов, котангенс (ctg) 180 градусов) значит при данном значении градусной меры угла функция не имеет определенного значения. Таблица значений тригонометрических функций sin, cos, tg для наиболее популярных углов0, 15, 30, 45, 60, 90 … 360 градусов (цифровые значения «как по таблицам Брадиса»)
|
| 1 | Найти точное значение | грех(30) | |
| 2 | Найти точное значение | грех(45) | |
| 3 | Найти точное значение | грех(30 градусов) | |
| 4 | Найти точное значение | грех(60 градусов) | |
| 5 | Найти точное значение | загар (30 градусов) | |
| 6 | Найти точное значение | угловой синус(-1) | |
| 7 | Найти точное значение | грех(пи/6) | |
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | грех(45 градусов) | |
| 10 | Найти точное значение | грех(пи/3) | |
| 11 | Найти точное значение | арктан(-1) | |
| 12 | Найти точное значение | cos(45 градусов) | |
| 13 | Найти точное значение | cos(30 градусов) | |
| 14 | Найти точное значение | желтовато-коричневый(60) | |
| 15 | Найти точное значение | csc(45 градусов) | |
| 16 | Найти точное значение | загар (60 градусов) | |
| 17 | Найти точное значение | сек(30 градусов) | |
| 18 | Найти точное значение | cos(60 градусов) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | грех(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | загар (45 градусов) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 градусов) | |
| 25 | Найти точное значение | сек(45 градусов) | |
| 26 | Найти точное значение | csc(30 градусов) | |
| 27 | Найти точное значение | грех(0) | |
| 28 | Найти точное значение | грех(120) | |
| 29 | Найти точное значение | соз(90) | |
| 30 | Преобразовать из радианов в градусы | пи/3 | |
| 31 | Найти точное значение | желтовато-коричневый(30) | |
| 32 | 92|||
| 35 | Преобразовать из радианов в градусы | пи/6 | |
| 36 | Найти точное значение | детская кроватка(30 градусов) | |
| 37 | Найти точное значение | арккос(-1) | |
| 38 | Найти точное значение | арктан(0) | |
| 39 | Найти точное значение | детская кроватка(60 градусов) | |
| 40 | Преобразование градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2 шт. )/3 )/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | тан(пи/2) | |
| 45 | Найти точное значение | грех(300) | |
| 46 | Найти точное значение | соз(30) | |
| 47 | Найти точное значение | соз(60) | |
| 48 | Найти точное значение | соз(0) | |
| 49 | Найти точное значение | соз(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | сек(60 градусов) | |
| 53 | Найти точное значение | грех(300 градусов) | |
| 54 | Преобразование градусов в радианы | 135 | |
| 55 | Преобразование градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5 дюймов)/6 | |
| 57 | Преобразовать из радианов в градусы | (5 дюймов)/3 | |
| 58 | Преобразование градусов в радианы | 89 градусов | |
| 59 | Преобразование градусов в радианы | 60 | |
| 60 | Найти точное значение | грех(135 градусов) | |
| 61 | Найти точное значение | грех(150) | |
| 62 | Найти точное значение | грех(240 градусов) | |
| 63 | Найти точное значение | детская кроватка(45 градусов) | |
| 64 | Преобразовать из радианов в градусы | (5 дюймов)/4 | |
| 65 | Найти точное значение | грех(225) | |
| 66 | Найти точное значение | грех(240) | |
| 67 | Найти точное значение | cos(150 градусов) | |
| 68 | Найти точное значение | желтовато-коричневый(45) | |
| 69 | Оценить | грех(30 градусов) | |
| 70 | Найти точное значение | сек(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | КСК(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | загар((5pi)/3) | |
| 75 | Найти точное значение | желтовато-коричневый(0) | |
| 76 | Оценить | грех(60 градусов) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3 пи)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | угловой синус(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | КСК(45) | |
| 83 | Упростить | арктан(квадратный корень из 3) | |
| 84 | Найти точное значение | грех(135) | |
| 85 | Найти точное значение | грех(105) | |
| 86 | Найти точное значение | грех(150 градусов) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | загар((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | пи/4 | |
| 90 | Найти точное значение | грех(пи/2) | |
| 91 | Найти точное значение | сек(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | угловой синус(0) | |
| 95 | Найти точное значение | грех(120 градусов) | |
| 96 | Найти точное значение | желтовато-коричневый ((7pi)/6) | |
| 97 | Найти точное значение | соз(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразование градусов в радианы | 88 градусов |
Sin 150 градусов — Найти значение Sin 150 градусов
LearnPracticeDownload
Значение sin 150 градусов равно 0,5 .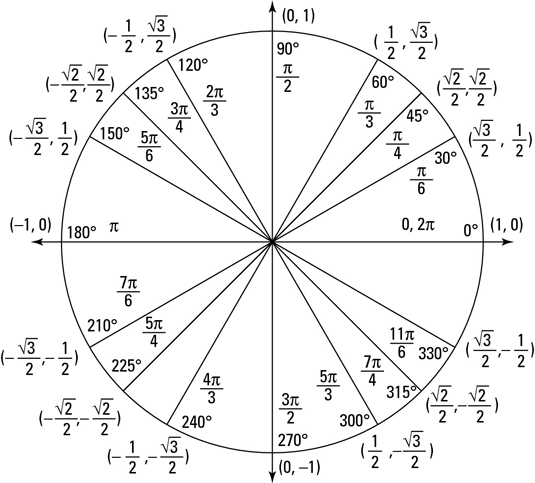 Sin 150 градусов в радианах записывается как sin (150° × π/180°), то есть sin (5π/6) или sin (2,617993…). В этой статье мы обсудим способы нахождения значения sin 150 градусов на примерах.
Sin 150 градусов в радианах записывается как sin (150° × π/180°), то есть sin (5π/6) или sin (2,617993…). В этой статье мы обсудим способы нахождения значения sin 150 градусов на примерах.
- Sin 150°: 0,5
- Sin 150° в дробях: 1/2
- Грех (-150 градусов): -0,5
- Sin 150° в радианах: грех (5π/6) или грех (2,6179938 . . .)
Сколько стоит грех 150 градусов?
Значение sin 150 градусов в десятичной системе равно 0,5. Sin 150 градусов также можно выразить с помощью эквивалента заданного угла (150 градусов) в радианах (2,61799 . . .).
Мы знаем, используя преобразование градусов в радианы, что θ в радианах = θ в градусах × (pi/180°)
⇒ 150 градусов = 150° × (π/180°) рад = 5π/6 или 2,6179. . .
∴ sin 150° = sin(2,6179) = 1/2 или 0,5
Объяснение:
Для sin 150 градусов угол 150° лежит между 90° и 180° (второй квадрант).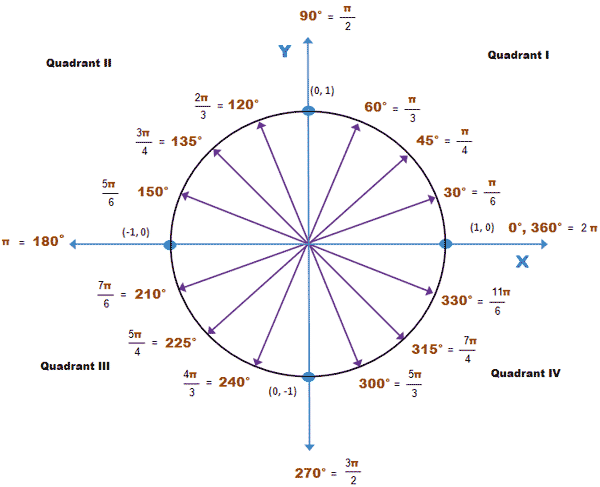 Поскольку функция синуса положительна во втором квадранте, значение sin 150° = 1/2 или 0,5
Поскольку функция синуса положительна во втором квадранте, значение sin 150° = 1/2 или 0,5
Поскольку функция синуса является периодической функцией, мы можем представить sin 150° как sin 150 градусов = sin(150° + n × 360°), n ∈ Z.
⇒ sin 150° = sin 510° = sin 870° и так далее.
Примечание: Поскольку синус является нечетной функцией, значение sin(-150°) = -sin(150°).
Методы определения значения Sin 150 градусов
Функция синуса положительна во 2-м квадранте. Значение sin 150° принимается равным 0,5. Мы можем найти значение sin 150 градусов по:
- Используя единичный круг
- Использование тригонометрических функций
Sin 150 градусов с помощью единичной окружности
Чтобы найти значение sin 150 градусов с помощью единичной окружности:
- Поверните ‘r’ против часовой стрелки, чтобы образовать угол 150° с положительной осью x.
- Грех в 150 градусов равен координате y(0,5) точки пересечения (-0,866, 0,5) единичной окружности и r.

Следовательно, значение sin 150° = y = 0,5
Sin 150° в терминах тригонометрических функций
Используя формулы тригонометрии, мы можем представить sin 150° как: ))
Примечание. Поскольку 150° лежит во 2-м квадранте, конечное значение sin 150° будет положительным.
Мы можем использовать тригонометрические тождества для представления sin 150° как
- sin(180° — 150°) = sin 30°
- -sin(180° + 150°) = -sin 330°
- cos(90° — 150°) = cos(-60°)
- -cos(90° + 150°) = -cos 240°
☛ Также проверьте:
- sin 50 градусов
- грех 30 градусов
- грех 90 градусов
- грех 8 градусов
- грех 89 градусов
- грех 32 градуса
Примеры использования Sin 150 градусов
Пример 1.
 Найдите значение 2 × (sin 75° cos 75°). [Подсказка: используйте sin 150° = 0,5]
Найдите значение 2 × (sin 75° cos 75°). [Подсказка: используйте sin 150° = 0,5] Решение:
Используя формулу sin 2a,
2 sin 75° cos 75° = sin(2 × 75°) = sin 150°
∵ sin 150° = 0,5
⇒ 2 × (sin 75° cos 75°) = 0,5Пример 2: Упростить: 2 (sin 150°/sin 510°)
Решение:
Мы знаем sin 150° = sin 510°
⇒ 2 sin 150°/sin 510° = 2(sin 150°/sin 150°)
= 2(1) = 2Пример 3. Найдите значение 5 sin(150°)/7 cos(-60°).
Решение:
Используя тригонометрические тождества, мы знаем, что sin(150°) = cos(90° — 150°) = cos(-60°).
⇒ sin(150°) = cos(-60°)
⇒ Значение 5 sin(150°)/7 cos(-60°) = 5/7
перейти к слайдуперейти к слайдуперейти к слайду
Готовы посмотреть на мир глазами математика?
Математика лежит в основе всего, что мы делаем.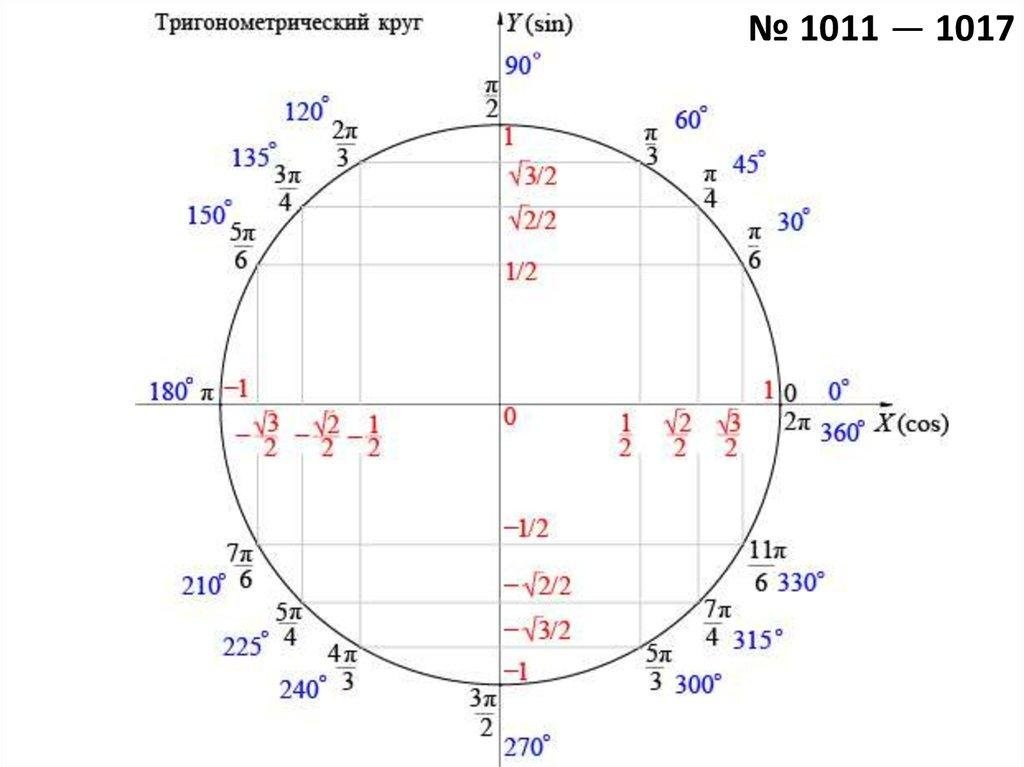 Наслаждайтесь решением реальных математических задач на живых уроках и станьте экспертом во всем.
Наслаждайтесь решением реальных математических задач на живых уроках и станьте экспертом во всем.
Забронируйте бесплатный пробный урок
Часто задаваемые вопросы о Sin 150 Degrees
Что такое Sin 150 Degrees?
Sin 150 градусов — значение тригонометрической функции синуса для угла, равного 150 градусам. Значение sin 150° равно 1/2 или 0,5.
Каково значение Sin 150° в пересчете на Cosec 150°?
Поскольку функция косеканса является обратной величиной функции синуса, мы можем записать sin 150° как 1/cosec(150°). Значение cosec 150° равно 2.
Как найти Sin 150° в терминах других тригонометрических функций?
Используя формулу тригонометрии, значение sin 150° можно выразить через другие тригонометрические функции следующим образом:
- ± √(1-cos²(150°))
- ± тангенс 150°/√(1 + тангенс²(150°))
- ± 1/√(1 + раскладушка²(150°))
- ± √(сек²(150°) — 1)/сек 150°
- 1/косек 150°
☛ Также проверьте: тригонометрическую таблицу
Как найти значение Sin 150 градусов?
Значение sin 150 градусов можно рассчитать, построив угол 150° с осью x и затем найдя координаты соответствующей точки (-0,866, 0,5) на единичной окружности.


 Особенно с числом «Пи», которое так и норовит запутать нас в хитрых заданиях, да…
Особенно с числом «Пи», которое так и норовит запутать нас в хитрых заданиях, да… 1 градус — это 1/360 часть окружности. И всё. Могли разбить на 100 частей. Или на 1000. Но разбили на 360. Кстати, почему именно на 360? Чем 360 лучше 100? 100, вроде, как-то ровнее… Попробуйте ответить на этот вопрос. Или слабо против Древнего Вавилона?
1 градус — это 1/360 часть окружности. И всё. Могли разбить на 100 частей. Или на 1000. Но разбили на 360. Кстати, почему именно на 360? Чем 360 лучше 100? 100, вроде, как-то ровнее… Попробуйте ответить на этот вопрос. Или слабо против Древнего Вавилона? Никогда.
Никогда.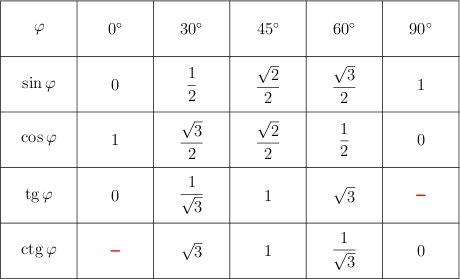 Но…
Но…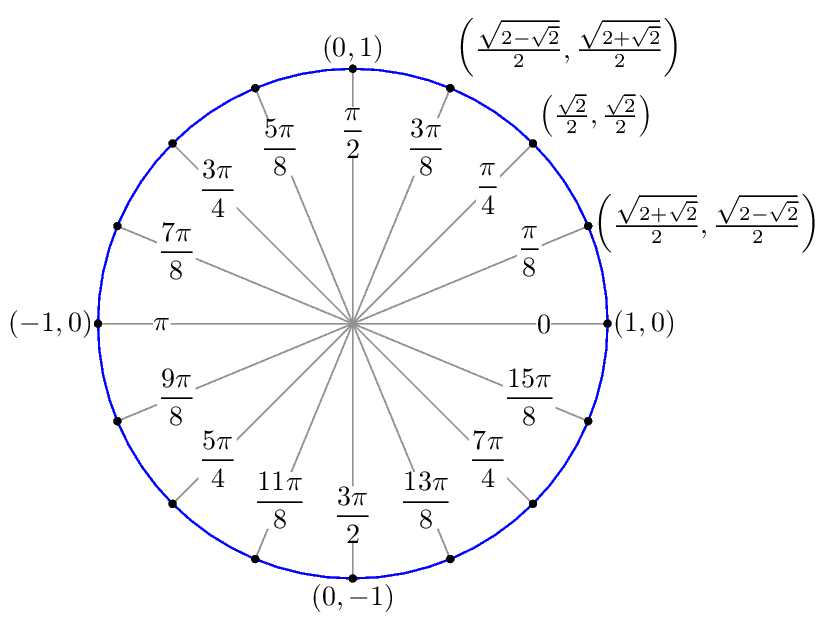 На которой я нарисовал полукруг. Развёрнутый угол размером, естественно, в 180°.
На которой я нарисовал полукруг. Развёрнутый угол размером, естественно, в 180°.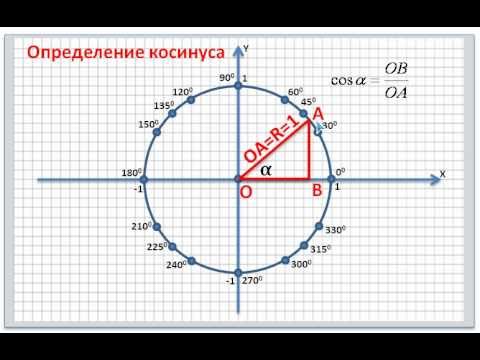 В тригонометрии очень часто приходится прикидывать, оценивать ситуацию. Вот тут это знание очень помогает.
В тригонометрии очень часто приходится прикидывать, оценивать ситуацию. Вот тут это знание очень помогает. Получаем, что один градус равен:
Получаем, что один градус равен: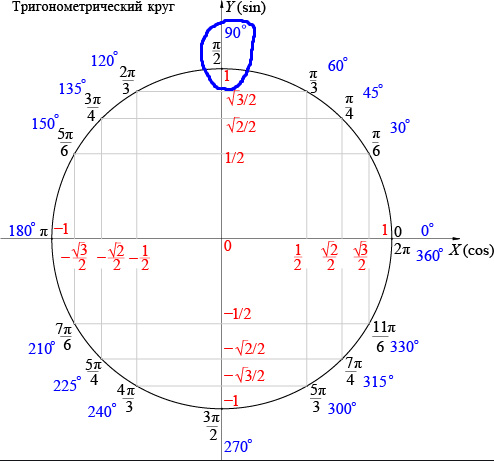 Иррациональное, но число. Такое же, как 5 или 8. Можно, к примеру, сделать примерно «Пи» шагов. Три шага и ещё маленько. Или купить «Пи» килограммов конфет. Если продавец образованный попадётся…
Иррациональное, но число. Такое же, как 5 или 8. Можно, к примеру, сделать примерно «Пи» шагов. Три шага и ещё маленько. Или купить «Пи» килограммов конфет. Если продавец образованный попадётся…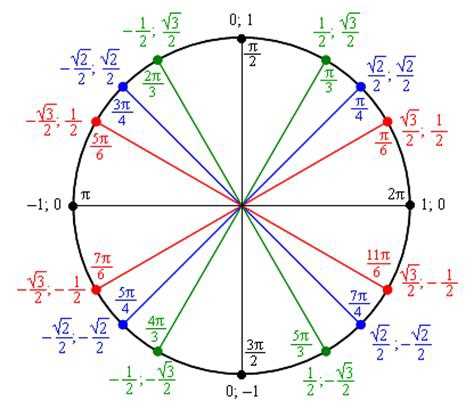 Смотрим, какие синусы у этих углов. Короче, всё, как в конце темы про тригонометрический круг расписано. На круге (даже самом кривом!) будет чётко видно, что sin60° существенно больше, чем sin1,05° .
Смотрим, какие синусы у этих углов. Короче, всё, как в конце темы про тригонометрический круг расписано. На круге (даже самом кривом!) будет чётко видно, что sin60° существенно больше, чем sin1,05° .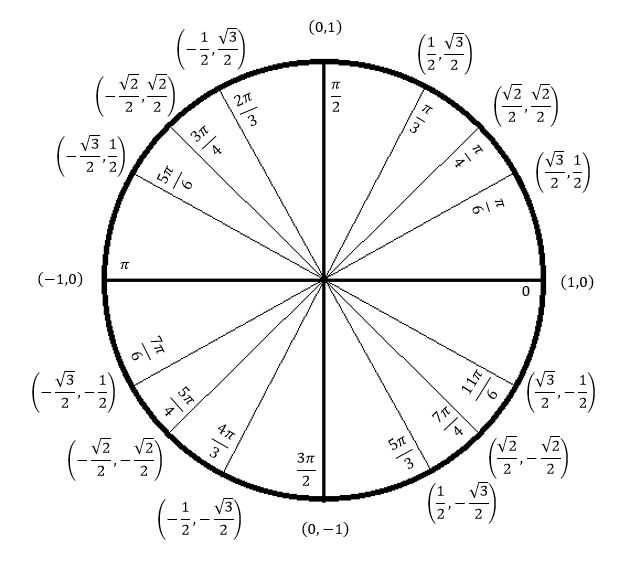 А то некоторые этот угол никак на круге найти не могут… И, соответственно, в тригонометрических функциях нуля путаются… Другое дело, что положение подвижной стороны в нуле градусов совпадает с положением в 360°, так совпадения на круге — сплошь и рядом.
А то некоторые этот угол никак на круге найти не могут… И, соответственно, в тригонометрических функциях нуля путаются… Другое дело, что положение подвижной стороны в нуле градусов совпадает с положением в 360°, так совпадения на круге — сплошь и рядом.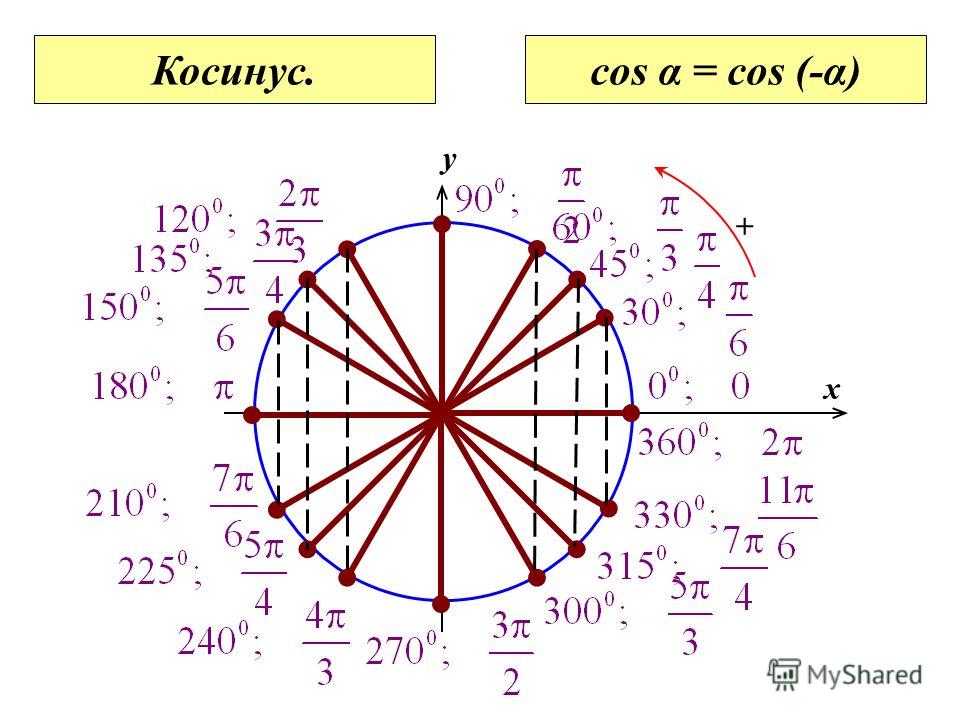 ) Но перевод углов — это первый шаг к постижению тригонометрии. Там же ещё с синусами-косинусами работать надо. Да и с тангенсами, котангенсами тоже…
) Но перевод углов — это первый шаг к постижению тригонометрии. Там же ещё с синусами-косинусами работать надо. Да и с тангенсами, котангенсами тоже…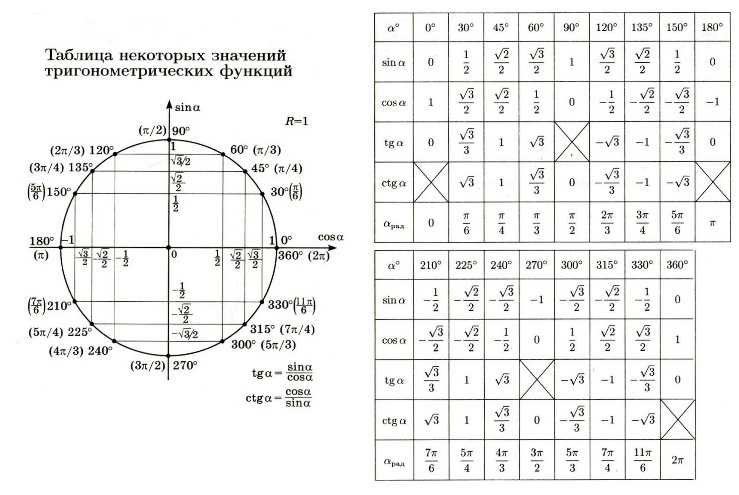 ..)
..)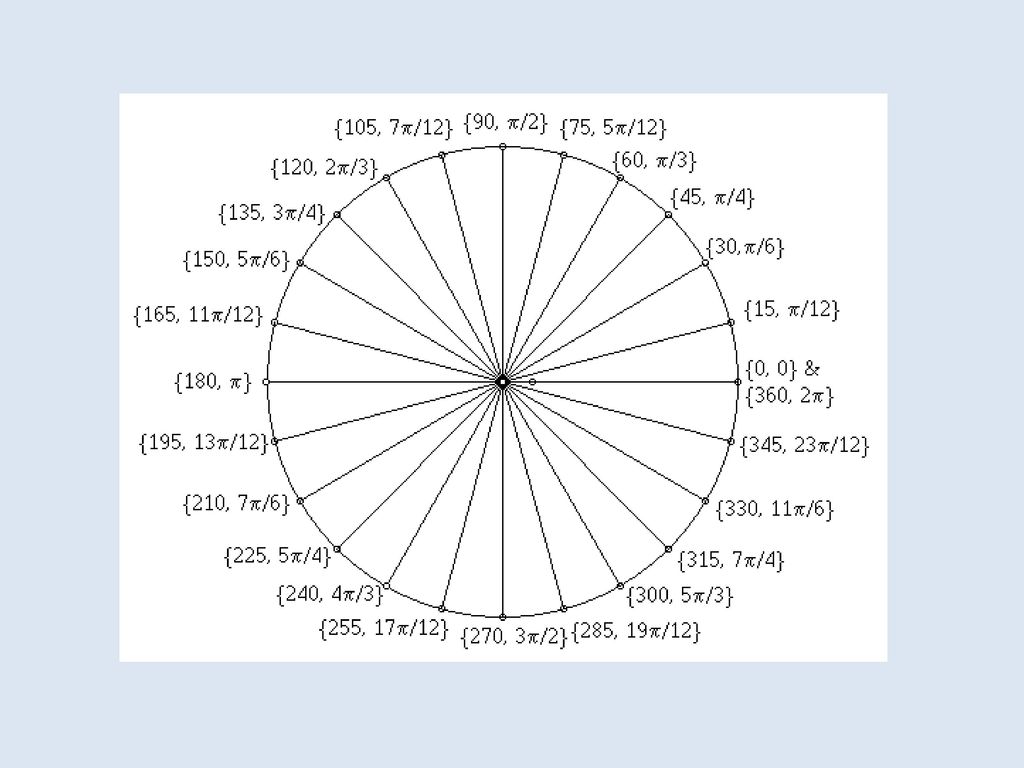 ..
.. 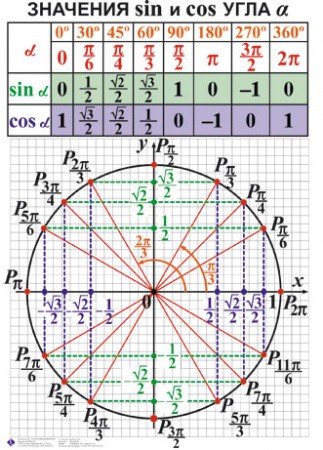 д. Точно так же находятся значения синусов, косинусов и тангенсов других «популярных» углов.
д. Точно так же находятся значения синусов, косинусов и тангенсов других «популярных» углов.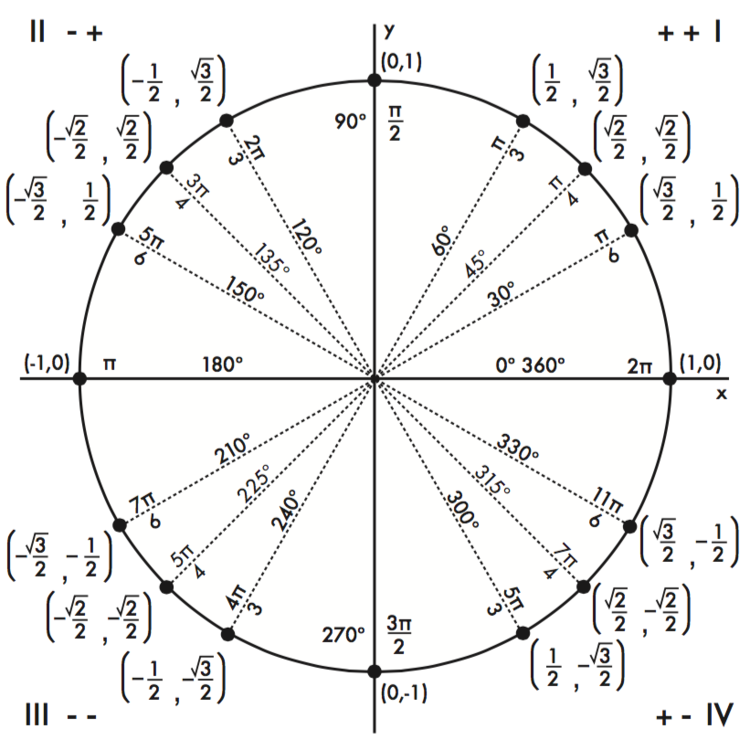
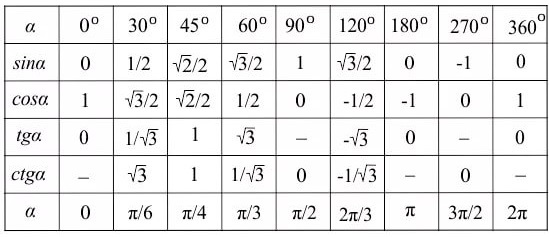 Если же прочерка нет — клетка пуста, значит мы еще не внесли нужное значение. Мы интересуемся, по каким запросам к нам приходят пользователи и дополняем таблицу новыми значениями, несмотря на то, что текущих данных о значениях косинусов, синусов и тангенсов самых часто встречающихся значений углов вполне достаточно для решения большинства задач.
Если же прочерка нет — клетка пуста, значит мы еще не внесли нужное значение. Мы интересуемся, по каким запросам к нам приходят пользователи и дополняем таблицу новыми значениями, несмотря на то, что текущих данных о значениях косинусов, синусов и тангенсов самых часто встречающихся значений углов вполне достаточно для решения большинства задач.
 Найдите значение 2 × (sin 75° cos 75°). [Подсказка: используйте sin 150° = 0,5]
Найдите значение 2 × (sin 75° cos 75°). [Подсказка: используйте sin 150° = 0,5]