Линейные задачи паскаль: Решение задач на линейные алгоритмы

Линейные алгоритмы

Линейные алгоритмы

Обмен значений численных переменных

8 сентября 202114.7к.admin

Пользователь вводит два числа. Одно присваивается одной переменной, а второе — другой. Необходимо поменять значения переменных так, чтобы значение

Линейные алгоритмы

Форматированный вывод данных

8 сентября 202103.8к.admin

В языках программирования, имеющих практическое значение, предусмотрены специальные синтаксические конструкции, позволяющие выводить данные в поля заданной

Задачи средней сложности

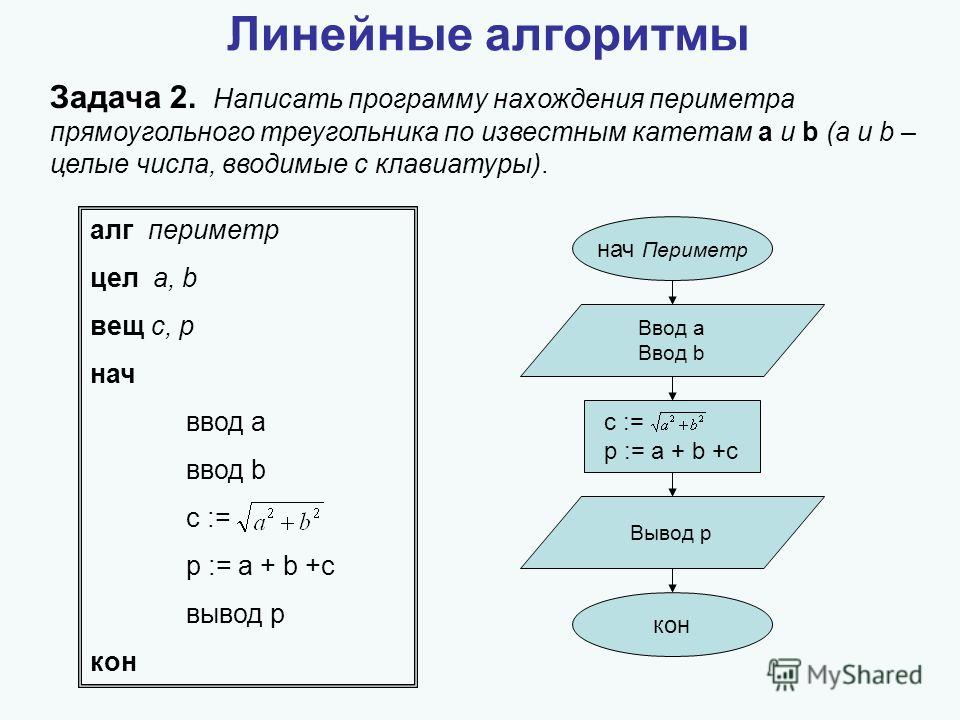
Вычисление площадей и периметров фигур

8 сентября 202125к.admin

Площади и периметры фигур можно найти по следующим формулам. Периметр треугольника: P = a + b + cПлощадь треугольника: S = √(p(p-a)(p-b)(p-c)), где p =

Линейные алгоритмы

Рассчитать выплаты по кредиту

8 сентября 202105. 8к.admin

Месячные выплаты находятся по формуле:m = (n * p * (1 + p)y) / (12 * ((1 + p)y – 1)), где p выражается в долях единицы, а не процентах.

Задачи средней сложности

Сумма и произведение цифр числа

8 сентября 202117.4к.admin

Если трехзначное число нацело разделить на 100, то получим число сотен, т.е. первую цифру этого числа. Если найти остаток от деления на 10 любого целого

Задачи средней сложности

Битовые операции над числами

8 сентября 202103.1к.admin

Обычно в языках программирования предусмотрены так называемые логические побитовые операции. Они выполняются не над самими числами, а над их двоичным представлением.

Задачи средней сложности

Вывести уравнение прямой по координатам двух точек

8 сентября 2021020. 6к.admin

Общее уравнение прямой имеет вид y = kx + b. Для какой-то конкретной прямой в уравнении коэффициенты k и b заменяются на числа

Задачи средней сложности

Случайные числа и символы

8 сентября 202112.1к.admin

В языках программирования есть функции, генерирующие случайные (псевдослучайные) числа. В одних языках функция генерирует целое число, в других —

Задачи средней сложности

Найти длину гипотенузы

8 сентября 202105.5к.admin

Катеты и гипотенуза — это стороны прямоугольного треугольника. Если известны длины катетов, то длина гипотенузы находится по теореме Пифагора: «

Задачи средней сложности

Количество символов между двумя буквами алфавита. Определение буквы по ее номеру в алфавите

8 сентября 202101. 7к.admin

Чтобы определить позицию буквы в алфавите, надо знать по используемой таблице символов коды первой буквы алфавита и той, позиция которой определяется.

Алгоритмы в Pascal OTUS

Программирование – процесс, требующий от разработчика определенного спектра навыков и знаний. Особую роль здесь играют так называемые алгоритмы. 

В данной статье поговорим о том, что собой представляют алгоритмы в разработке. За основу используем язык Pascal.

Определение

Algorithm – это последовательность команд, операций или действий, необходимых для достижения изначально поставленной задачи. Трактовок данного понятия несколько:

• вычислительные шаги, помогающие добиться желаемого результата;
• корректно определенная процедура, когда на вход подается информация, а на выходе получается набор значений;
• точное и понятное указание исполнителю сделать последовательность манипуляций, ориентированных на достижение указанной цели.

Algorithm должен быть разработан так, чтобы его выполнение обязательно приводило к изначально задуманному результату. Это весьма творческий процесс. Для одной и той же задачи могут существовать несколько разных последовательностей в пределах одного языка программирования. А для некоторых вариантов существует единственное верное решение.

Классификация

Паскаль – язык, который изучается преимущественно в школьной программе. Он позволяет ознакомиться с алгоритмами, а также разобраться с основами разработки ПО. Здесь выделяют несколько algorithm-типов:

• линейный алгоритм;
• разветвленный;
• циклический.

Каждый вариант подразумевает свои собственные особенности. Далее они будут рассмотрены более подробно. Предложенные концепции подходят не только для Паскаль, но и для других языков разработки.

Линейный

Это инструкции, в которых команды будут выполняться последовательно друг за другом. Самые простые. На них базируются не только элементарные программы, но и сложные проекты. Линейные последовательности с легкостью осваиваются новичками.

Вот пример в ЯП Паскаль, который помогает разобраться в принципах реализации рассматриваемого метода. В нем нужно найти объем куба и площадь его поверхности, если длина ребра равна a:

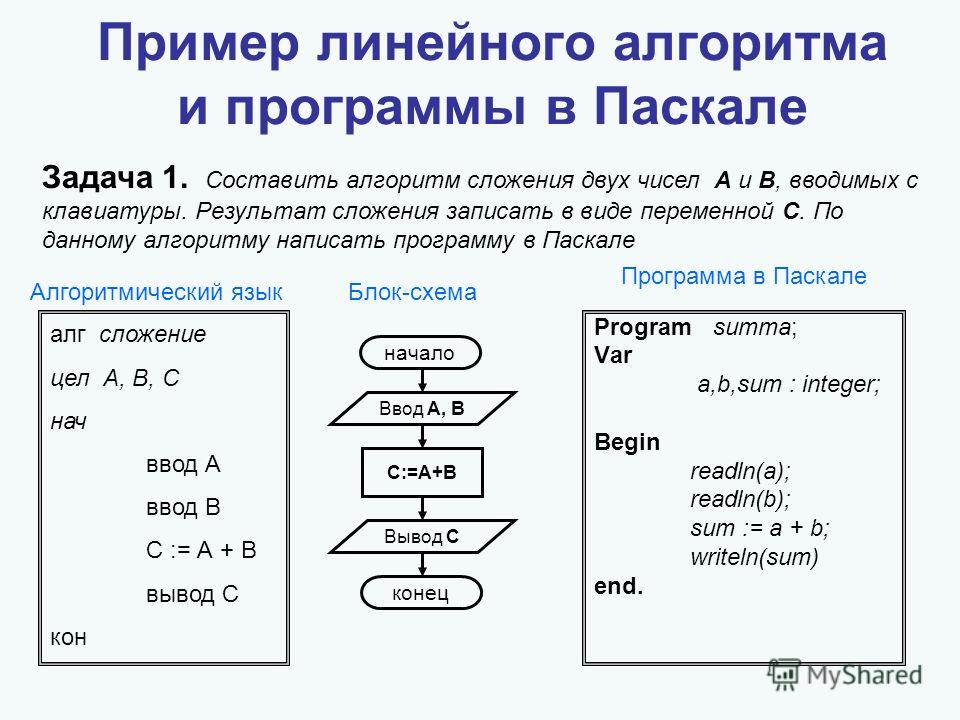
А вот – пример программы, которая вычисляет сумму двух чисел. После расчетов она выведет получившийся результат непосредственно на экран устройства:

Это – база, без которой не получится разобраться с остальными видами «последовательностей» при формировании кода приложения.

Разветвленный

В них ход решения зависит непосредственно от выполнения или невыполнения заданного условия. В приложении реализация сводится к принципу выбора действия в зависимости от ответа «да» или «нет».

Выше – пример блок-схемы, наглядно демонстрирующий соответствующий вариант. Разобраться с соответствующей последовательностью тоже не составляет особого труда.

Циклический

Алгоритм программы в Паскале или другом ЯП, в котором определенная часть вычислений производится многократно. Простыми словами – цикл. В нем имеется итоговое количество повторений.

Факториал

Отдельно стоит изучить несколько «базовых» алгоритмов, которые используются в Pascal, но не относятся к ранее перечисленным типам.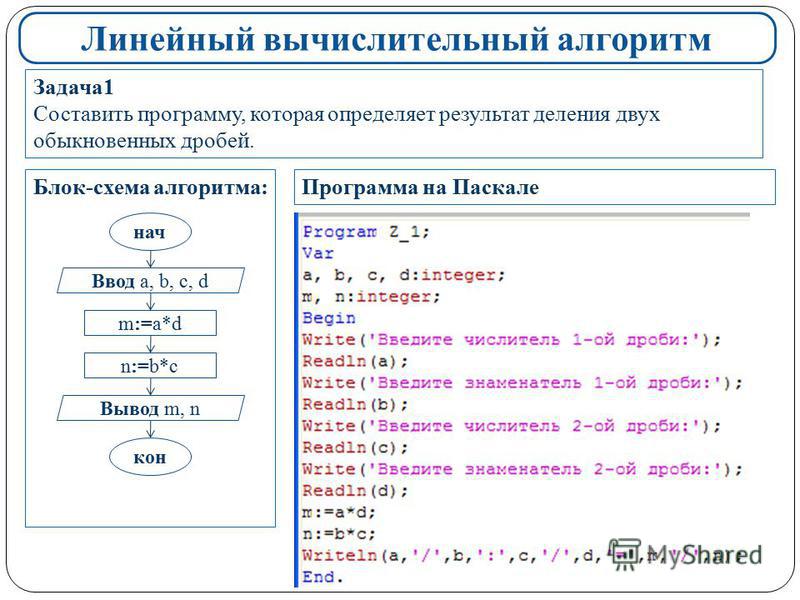 Первый вариант – факториал натурального числа. Его можно назвать линейным. Связано это с определением самого факториала – произведение натуральных чисел от 1 до самого заданного числа.

Выше – наглядный пример реализации в программном коде Pascal. Его можно использовать в качестве шаблона для решения характерных задач.

Наименьшее общее кратное и делитель

А вот еще один алгоритм, который помогает при формировании некоторых приложений. Речь идет об обнаружении наименьшего общего кратного двух чисел.

При решении математических задач может потребоваться найти наибольший общий делитель. Еще один алгоритм для программы, с которым разберется даже новичок.

Наименьшим общим делителем называется минимальное число, которое нацело делит несколько чисел.

Способы выражения

Существуют различные способы выражения алгоритмов – не только в программировании, но и в реальной жизни:

1. Вербальный. Ситуация, при которой алгоритм программы описывается языком, понятным человеку.
2. Графический. Для описания используются графики или схемы, иногда – рисунки и иные изображения. Самый распространенный вариант (своеобразный эталон) – использование блок-схем.
3. Символьный. Характеристика при помощи некоторого символьного набора.

Выше – пример того, как грамотно составлять блок-схему для той или иной задачи, не обязательно связанной с созданием программы.

Свойства

Каждый algorithm имеет определенные свойства. Запомнить их просто:

1. Определенность (или точность). Ход решения поставленной задачи должен быть точным, а также понятным. Он исключает возможность неправильного или произвольного толкования. Вычислительные процессы строятся так, чтобы их можно было повторить.
2. Массовость. Подобранная последовательность применяется к огромному количеству однотипных задач с изменением исходных условий.
3. Дискретность. Итоговая цель разделяется на элементарные шаги-операции. Это помогает достигнуть итогового решения. Одна и та же задача может быть решена сразу несколькими методами. Каждый вариант поддерживает возможность разделения на более мелкие и простые подзадачи.
4. Результативность. Решение задачи в программе должно приводить к тому или иному результату.
5. Корректность. При выполнении заданной последовательности в программе должен быть получен правильный результат.

Если отсутствует хотя бы один «параметр», используемая последовательность не является алгоритмом.

Как быстро освоить

Чтобы быстрее разобраться с разработкой программ, а также с алгоритмами не только Pascal, но и других ЯП, рекомендуется закончить специализированные компьютерные дистанционные курсы.

Вместе с ними пользователь с нуля сможет освоить любой язык разработки и изучить его особенности. Курс обучения составляет до 12 месяцев. В процессе гарантированы:

• кураторство;
• помощь в формировании портфолио;
• интересные домашние задания и практика.

В конце обучения пользователю выдадут сертификат в электронном виде, указывающий на приобретенный спектр знаний и навыков.

6.9 Треугольник Паскаля и биномиальное разложение – Промежуточная алгебра

Перейти к содержанию

Глава 6: Многочлены

Треугольник Паскаля (1653 г.) был обнаружен в работах математиков, относящихся ко II веку до нашей эры. Хотя треугольник Паскаля полезен во многих различных математических ситуациях, он будет применяться для разложения биномов. В этом приложении треугольник Паскаля будет генерировать старший коэффициент каждого члена биномиального разложения в виде: 97 \end{массив}[/латекс]

Генерация каждой строки треугольника Паскаля осуществляется путем сложения двух чисел над ней.

[латекс]\begin{array}{cl} 1&\text{Начать с 1} \\ 1+1&\text{Внешнее число всегда 1} \\ 1+2+1&\text{Две единицы в последняя строка прибавляется к 2} \\ 1+3+3+1&1+2 \text{выше добавляется к 3} \\ 1+4+6+4+1& \\ 1+5+10+10+5+1& \ \ 1+6+15+20+15+6+1& \\ 1+7+21+35+35+21+7+1 & \text{Используя это, мы можем расширить треугольник Паскаля} \\ 1+8+28 +56+70+56+28+8+1&(а+б)^8 \\ 1+9{12}.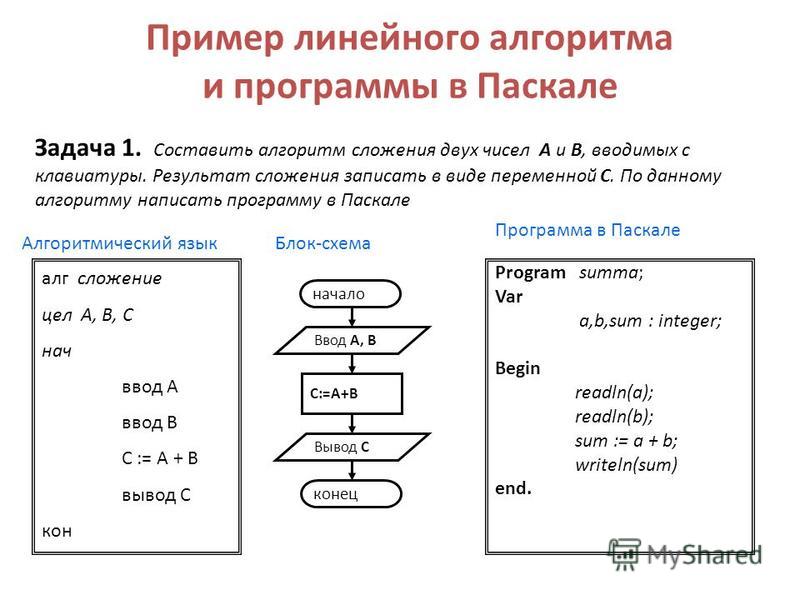

[/латекс]

Обычно считается, что четвертое расширение бинома представляет время, а первые три расширения представляют собой ширину, длину и высоту. Пока мы живем в четырехмерной вселенной (теория струн предполагает десять измерений), попытки представить четвертое измерение времени сложны. Карл Саган описывает четвертое измерение, используя аналогию, созданную Эдвином Эбботом (Abbot: Flatland: A Romance of Many Dimensions ). Видеоклип Сагана «Tesseract, 4th Dimension Made Easy» можно найти на YouTube.

License

Промежуточная алгебра Терренса Берга находится под лицензией Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, если не указано иное.

Поделиться этой книгой

Поделиться в Твиттере

Любимые задачи Паскаля Койрана

Любимые задачи Паскаля Койрана
Предупреждение: эта страница последний раз обновлялась в 20 веке.

Определимость замкнутых по Зарисскому множеств

Подмножество X n-мерного евклидова пространства замкнуто тогда и только тогда для каждой точки, не принадлежащей X,
существует открытый шар вокруг этой точки, который не пересекает X.
Следовательно, свойство «X замкнуто» может быть выражено через формула первого порядка языка (R,+,-,*, Есть ли такая формула над комплексными числами?
Точнее, хотелось бы иметь формулу первого порядка F на языке (C,+,-,*,=,I_n)
такой, что для любого определимого (т.е. конструируемого) подмножества n-мерного комплексного пространства,
X закрыто тогда и только тогда, когда F истинно, когда I_n интерпретируется как принадлежность к X.

Соответствующая публикация:

О. Шапюи и П. Койран. Определяемость геометрических свойств в алгебраически замкнутых полях.
Отчет об исследовании LIP 98-32. Для публикации в Ежеквартальном издании Mathematical Logic.

Можно задать много других вопросов определимости. Например, можно показать, что для вещественных алгебраических многообразий
неприводимость не определима.

П. Койран. Об определении неприводимости. препринт, 19н.
Пусть x(t) — вектор состояния в момент времени t. Сначала применим фиксированное линейное преобразование A к x(t).
Затем вектор состояния в момент времени t+1 получается из y(t)=A.x(t) путем усечения всех компонентов y(t)
, которые меньше -1 или больше 1, до -1 и 1 соответственно.

У меня есть показано в документе с Венсаном Блонделем, Оливье Бурне и Джон Цициклис, что устойчивость
(точнее, «глобальная асимптотическая устойчивость») насыщенных линейных систем неразрешима.
Это ответ на вопрос Эдуардо Зонтага.
Несколько связанных свойств (глобальная конвергенция, смертность и нильпотентность) также неразрешимы.
Однако наша работа поднимает ряд новых вопросов.
Например, эквивалентна ли стабильность глобальной конвергенции? Нильпотентность эквивалентна смертности?
Являются ли эти свойства неразрешимыми для систем фиксированной размерности?

Итерированные карты на интервале

Пусть F — кусочно-линейное отображение на единичном интервале и x точку на этом интервале.
Считаем последовательность итераций начиная с x: x, F(x), F(F(x)), и так далее.
Учитывая F и x, можно ли решить, достигает ли эта последовательность неподвижная точка F ?

Даже если F состоит всего из двух линейных частей, у меня нет алгоритм решения.

Чтобы эта проблема имела смысл, F и x должны иметь конечное описание.
Здесь мы предполагаем, что x рационально, и что наклоны и точки излома F также рациональны.

Известно, что эта же задача неразрешима в размерности 2. Если кусочно-линейные функции заменить полиномами, проблема открыта в любом измерении.

Две соответствующие публикации:

П. Койран и К. Мур. Аналитические карты закрытой формы в одном и двух измерениях могут имитировать Тьюринга. машины. Технический отчет DIMACS 96-25. Theoretical Computer Science , 210(1):217-223, 1999.

П. Койран, М. Коснард и М. Гарсон. Вычислимость с низкоразмерными динамическими системами. Теоретическая информатика , 132:113-128, 1994.

Вопрос о том, актуальна ли следующая публикация, остается открытым.

П. Койран. Семейство универсальных рекуррентных сетей. Theoretical Computer Science , 168(2):473-480, 1996.

Системы алгебраических уравнений

Какова сложность определения выполнимости системы алгебраические уравнения
в алгебраически замкнутом поле положительных характеристика?

Я показал, что в характеристике 0 эта проблема находится во втором уровень полиномиальной иерархии (на самом деле это АМ, класс «Артур-Мерлин») если верить в обобщенную гипотезу Римана.
В положительной характеристике довольно большой разрыв между известная верхняя граница (PSPACE) и нижняя граница (NP). Можно, например, попытаться представить эту задачу полиномом иерархии или доказать, что это PSPACE-сложно.

Говоря языком математической логики, определение того, является ли система удовлетворительным является решение «экзистенциальной формулы».
Можно также рассматривать формулы с несколькими блоками кванторов. Даже если есть только два блока, неизвестно, проблема решения в характеристике 0 находится в полиномиальной иерархии.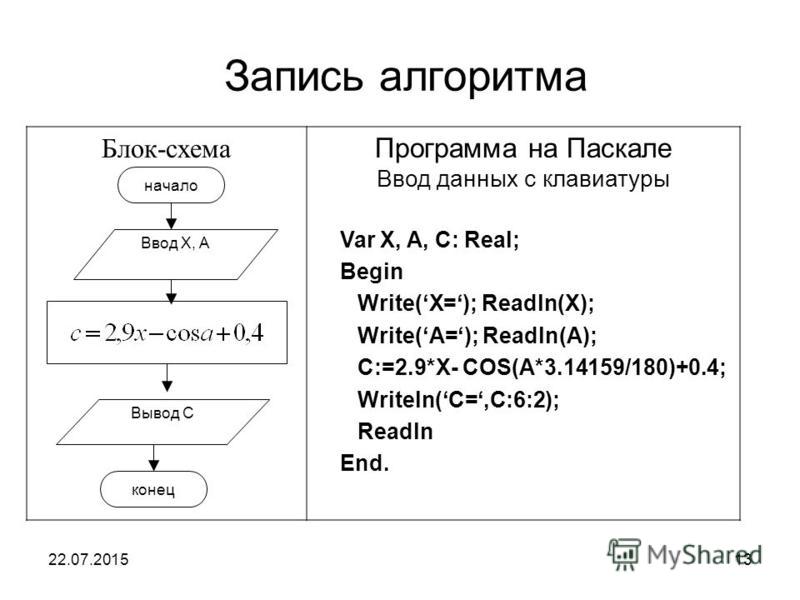

Одна соответствующая публикация:

П. Койран. Nullstellensatz Гильберта находится в полиномиальной иерархии. Journal of Complexity , 12(4):273-286, 1996. Есть более длинная бумага ( Технический отчет DIMACS 96-27) и опечатка.

Алгебраические деревья решений

Пусть PAR будет классом задач, которые можно решать параллельно полиномиальное время над вещественными числами.
Проблема пустоты для полуалгебраические множества и многие другие естественные геометрические задачи, как известно, находятся в PAR.

Может ли любая проблема в PAR быть решена с помощью алгебраических деревьев решений полиномиальная глубина?

Я предполагаю, что ответ может быть положительным. Было бы уже интересно ответить на этот вопрос для конкретных задач в PAR, например, для линейного программирования проблема осуществимости.

Как ни странно, соответствующая проблема в модели вычисления только с добавлением и порядком имеет положительный ответ.
Это было доказано (немного другим языком) Мейер ауф дер Хайде [Быстрые алгоритмы для n-мерных ограничения сложных задач. JACM, 35(3):740—747, 1988]
и Мейзер [Точечное расположение в расположении гиперплоскостей, Информация и вычисления 106 (1993), стр. 286-303].
Некоторые последствия этих результатов обсуждаются в

H. Fournier and P. Koiran. Нижние границы проще реалы?
Отчет об исследовании LIP 97-38.

Обратите внимание, что в модели только со сложением и равенством соответствующая задача теперь имеет отрицательный ответ. Действительно, он указан в

П. Койран. Вычисления над реалами с дополнением и порядком. Теоретическая информатика , 133(1):35-48, 1994. Отчет об исследовании LIP 93-25.

что задача о ранце не может быть решена деревья решений полиномиальной глубины.
Верно ли это и в отношении комплексных чисел?

Насыщение теории вычислений над вещественными числами

Кристиан Мишо ввел класс P/const в теорию вычислений. над реалами. Грубо говоря, проблема в P/const, если ее можно решается за полиномиальное время с постоянным количеством советов. Более того, совет для входных данных размера n также должен работать для всех входы размера
меньше n.

Большой вопрос заключается в том, является ли P=P/const.

Если это верно, то теорема о переносе для проблемы P = NP будет следовать: P=NP над вещественными числами тогда и только тогда, когда P=NP над любым вещественно-замкнутым полем содержащие реалы.

Легко видеть, что P=P/const над комплексными числами (это происходит из-за омега-насыщенности C). Аналогичная теорема о переносе затем следует.

Одна соответствующая публикация:

О. Шапюи и П. Койран. Насыщение и устойчивость в теории вычисления над вещественными числами. Технический отчет 1997/3, Институт Жирара Дезарга, Университет Клода Бернара Lyon I, 1997.

Размерность VC арифметических схем

Какова размерность Вапника-Червоненкиса цепей из линейных и ворота равенства?
Это практически единственный пробел, оставшийся в классификация приведена в:

П.

No related posts.