Определить Токи Электрической Схемы — tokzamer.ru
Подставив 1.
Рассчитайте схему цепи
Рекомендуем: Подключение 2 х клавишного выключателя
Основные понятия
Рассмотрим пример. В заданной схеме, см.
Токи в резисторах В данном случае удобно проверить задачу с помощью первого закона Кирхгофа, согласно которому сумма токов сходящихся, в узле равна нулю. Выполняем все поэтапно.
В табл.
Ток в сопротивлении R3, являющийся общим для обоих контуров, равен разности контурных токов I11 и I22, так как эти токи направлены в ветви с R3 встречно. Управляемые элементы работают под влиянием управляющего воздействия тиристоры, транзисторы и другие.
Пусть, например, задана величина приложенного к току напряжения U и требуется определить ток в цепи и распределение напряжений на ее участках. Последовательное соединение нелинейных элементов. Управляемые элементы работают под влиянием управляющего воздействия тиристоры, транзисторы и другие.
Последовательное соединение нелинейных элементов. Управляемые элементы работают под влиянием управляющего воздействия тиристоры, транзисторы и другие.
Примеры решения задач на законы Кирхгофа
В схеме рис. После проведенных преобразований рис.
Приступаем к основному этапу — составлению системы уравнений контурных токов. Про комплексные числа можно подробнее прочитать на нашем сайте. Определим параметры электрической цепи рис. Уравнения по второму закону составляют для независимых контуров. Но с помощью закона Кирхгофа удобно проверять простые цепи, имеющие один контур.
Переменный ток.
В цепи должен соблюдаться баланс мощностей, то есть энергия отданная источниками должна быть равна энергии полученной приемниками.
Последним этапом находим действительные токи, для этого нужно записать для них выражения. Работа активного двухполюсника под нагрузкой в номинальном режиме определяется уравнением 1.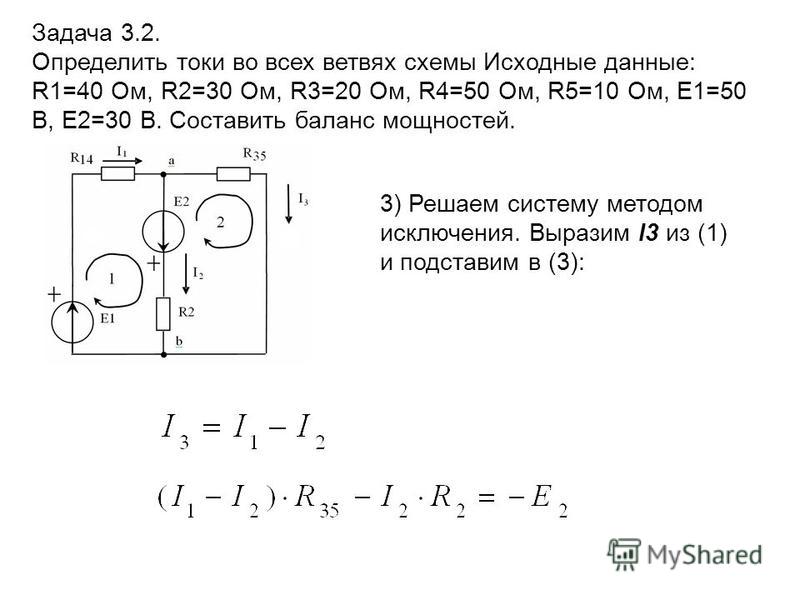
Определим параметры электрической цепи рис. Неуправляемые нелинейные элементы имеют одну вольт-амперную характеристику; управляемые — семейство характеристик.
Определить ток I1 в заданной по условию схеме с источником тока, используя метод эквивалентного генератора. Чтобы решить такую систему можно воспользоваться программой MathCad. В цепи должен соблюдаться баланс мощностей, то есть энергия отданная источниками должна быть равна энергии полученной приемниками. Свернуть цепь можно с помощью эквивалентных преобразований последовательного, параллельного и смешанного соединений.
Читайте дополнительно: Нормы прокладки кабеля под землей
АГЗ МЧС РГР №1 Расчёт линейных цепей постоянного тока
Уравнения по второму закону составляют для независимых контуров. Определим параметры электрической цепи рис. Контурный ток равен действительному току, который принадлежит только этому контуру. Свернуть цепь можно с помощью эквивалентных преобразований последовательного, параллельного и смешанного соединений.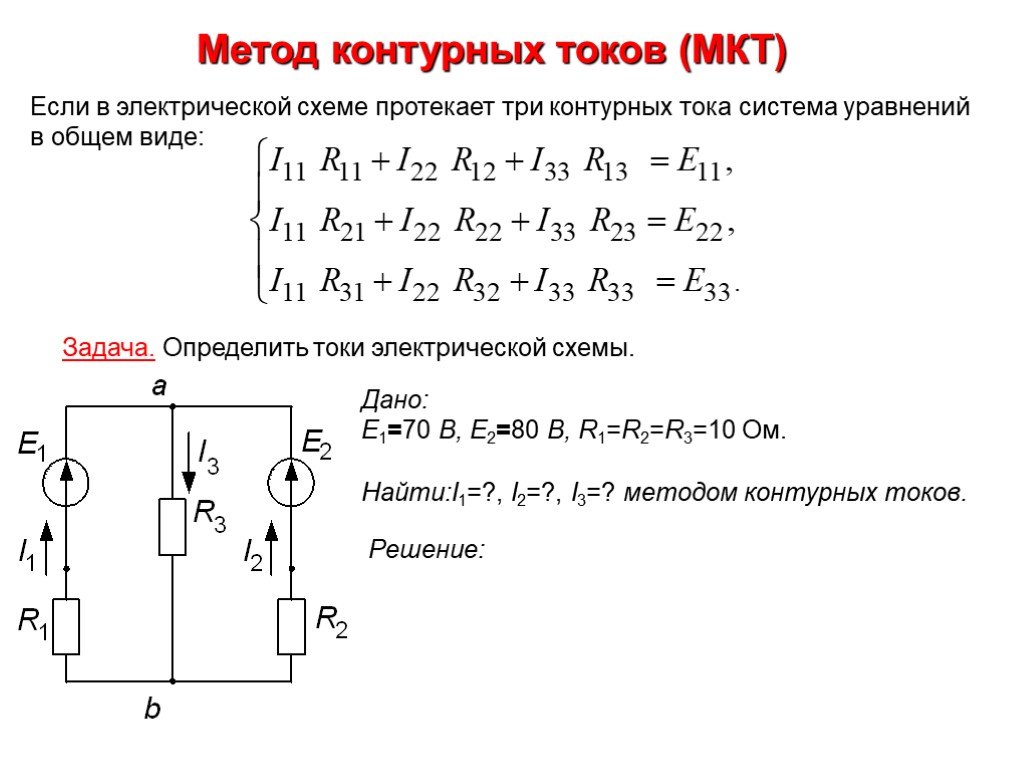
Направление обхода контура совпадает с направлением контурных токов. Режим работы электрической цепи рис. Переменный синусоидальный ток или напряжение задается уравнением: Здесь Im — амплитуда тока. Например, с помощью закона Кирхгофа, который гласит, что сумма ЭДС в контуре равна сумме напряжений в нем. Метод контурных токов заключается в том, что вместо токов в ветвях определяются, на основании второго закона Кирхгофа, так называемые контурные токи, замыкающиеся в контурах.
Определить токи во всех ветвях схемы на основании метода наложения.
Эта вольт-амперная характеристика строится по двум точкам 1 и 2 рис. Для этого необходимо найти напряжение в цепи, которое будет общим для обоих резисторов, так как соединение параллельное. Следовательно, схема источника тока рис. Вычислим коэффициент подобия.
Метод наложения токов. Пример решения
ТОЭ примеры решения метод
Наряду с методом контурных токов для анализа электрических цепей используется другой метод – метод наложения.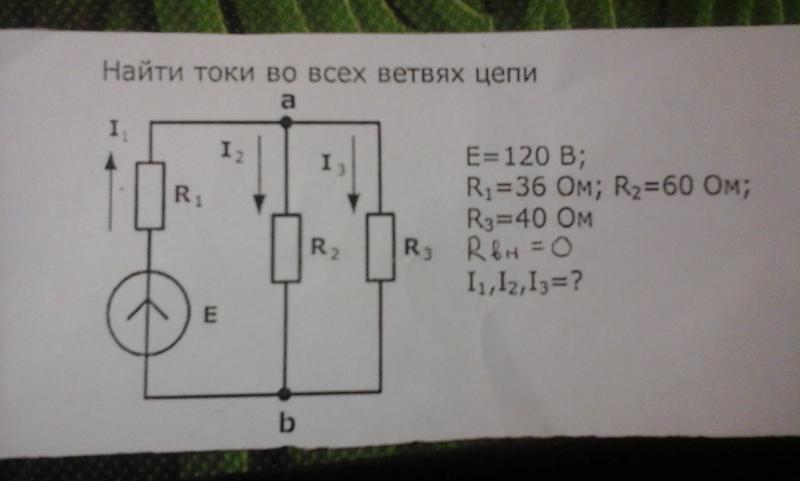 Этот метод основан на принципе наложения, который применяется только к линейным системам.
Этот метод основан на принципе наложения, который применяется только к линейным системам.
Метод наложения относительно прост, и в основном применяется для не сложных электрических цепей.
Его суть заключается в том, что токи в ветвях определяются как алгебраическая сумма их составляющих от каждого источника. То есть каждый источник тока вносит свою часть в каждый ток в цепи, а чтобы найти эти токи, нужно найти и сложить все составляющие. Таким образом, мы сводим решение одной сложной цепи к нескольким простым (с одним источником).
Порядок расчета
1 – Составление частных схем, с одним источником ЭДС, остальные источники исключаются, от них остаются только их внутренние сопротивления.
2 – Определение частичных токов в частных схемах, обычно это несложно, так как цепь получается простой.
3 – Алгебраическое суммирование всех частичных токов, для нахождения токов в исходной цепи.
Пример решения методом наложения
1. Для начала произвольно выберем направление токов, если в итоге какой либо ток получится со знаком минус, значит нужно изменить направление данного тока на противоположное.
Для начала произвольно выберем направление токов, если в итоге какой либо ток получится со знаком минус, значит нужно изменить направление данного тока на противоположное.
2. Составим частную схему с первым источником ЭДС и рассчитаем частные токи в ней, убрав второй источник. Для удобства частичные токи будем обозначать штрихами.
Свернем схему к одному контуру, с сопротивлением источника и эквивалентным сопротивлением цепи для нахождения тока источника I 1. Для тех, у кого возникают затруднения с нахождением эквивалентного сопротивления рекомендуем прочесть статью виды соединения проводников.
Найдем ток по закону Ома для полной цепи
Найдем напряжение на R2345
Тогда ток I3 равен
А ток I4
Определим напряжение на R25
Найдем токи I2 и I5
3. Составим частную схему со вторым источником ЭДС
Составим частную схему со вторым источником ЭДС
Аналогичным образом вычислим все частичные токи от второй ЭДС
4. Найдем токи в исходной цепи, для этого просуммируем частичные токи, учитывая их направление. Если направление частичного тока совпадает с направлением исходного тока, то берем со знаком плюс, в противном случае со знаком минус.
5. Проверим с правильность решения с помощью баланса мощностей.
Небольшая погрешность связана с округлениями промежуточных значений в ходе выполнения вычислений.
Читайте также — Метод узловых потенциалов
Метод ветвей тока
Поиск
В методе ветвей тока законы напряжения и тока Кирхгофа используются для определения тока в каждой ветви цепи. Зная токи ветвей, можно определить напряжения.
ШАГИ
Ниже приведены общие шаги, используемые при применении метода тока ответвления.
Шаг 1: Назначьте ток в каждой цепи, которую она разветвляет в направлении.
Шаг 2: Показать полярность напряжений резисторов в соответствии с назначенным направлением тока ветви.
Шаг 3: Примените закон Кирхгофа для напряжений вокруг каждого замкнутого контура (сумма напряжений равна нулю).
Шаг 4: Применить текущий закон Кирхгофа на минимальном количестве узлов так, чтобы были учтены все токи ветвей (сумма токов в узле равна нулю).
Шаг 5: Решите уравнения, полученные в результате шагов 3 и 4, для значений тока ответвления.
СХЕМА ДЛЯ ДЕМОНСТРАЦИИ АНАЛИЗА ТОКОВ ВЕТКИ
| Первый | Ток ответвления I 1 , I 2 и I 3 назначаются в направлении, как показано на рисунке-1. На данный момент не беспокойтесь о фактических текущих направлениях. |
| Второй | Полярности падения напряжения на R 1 , R 2 и R 3 направления тока указаны на рисунке-1. |
| Третий | Закон напряжения Кирхгофа, примененный к двум петлям, дает следующие уравнения. Уравнение 1: R 1 I 1 + R 2 I 2 —- V S1 = 0 для петли 1 Уравнение 2: R 2 I 2 + R 3 I 3 ——V S2 = 0 для контура 2 |
| Четвертый | Текущий закон Кирхгофа применяется ко всем узлам, включая все токи А, как следует из него. Уравнение 3: I 1 — I 2 + I 3 = 0 отрицательные знаки означают, что I 2 находится вне соединения. |
| Пятый | Необходимо решить три уравнения для трех неизвестных токов: I 1 , I 2 и I 3 . |
Три уравнения на предыдущих шагах называются одновременными уравнениями и могут быть решены путем подстановки.
МЕТОД ТОКА ВЕТКИ ПРИМЕР
Определение тока в каждой ветви с использованием метода тока ветки.
| Шаг 1: | Назначить ток ответвления. Имейте в виду, что вы можете принять любое направление тока в этой точке и что окончательное решение будет иметь отрицательный знак, если фактический ток противоположен назначенному току. |
| Шаг 2: | Отметьте полярность падения напряжения на резисторе, как показано на рисунке. |
| Шаг 3: | Применение Закона о напряжении Кирхгоффа вокруг левой петли дает 47i 1 + 22i 2 — 10 = 0 Вокруг правого петли. |
| Step 4: | At node A, the current equation is I 1 — I 2 + I 3 = 0 |
| Step 5: | Уравнение решается подстановкой следующим образом. Первая находка I, с точки зрения I 2 и I 3 I 1 = I 2 — I 3 Теперь заменитель I 2 — I 3 для I 1 2 — I 3 для I 1 — I 3 для I 1 2 — I 3 для I 2 — I 3 для I 2 — I в уравнении левой петли. 47 (I 2 — I 3 ) + 22i 2 = 10 47i 2 — 47i 3 + 22i 2 = 10 — 47I — 47I — 47I — 47I — 47I — 47I — 47I — 47I — 47I — 47I — 47I — 47I — 47I — 47I — 470041 3 = 10 Затем возьмите уравнение правой петли и решите I 2 через I 3 22I 2 = 5 — 68I 3 I 2 3 ) /22 Заменить это выражение на i2 69i 2 — 47i 3 = 10 Вы получите 69 (5-68i 3 /22) — 47i 3 = 100003 = 100003 = 100003 = 100003 = 100003 = 100003 = 100003 = 100003 = 100003 = 100003 = 100003 = 100003 = 100003 = 100003 = 100003 = 100003 = 100003 = 100003 = 100003 = 100003 = 100003 = 100003 = 100003 = 100003 = 100003 = 100003 = 100003 = 100003 = 100003 = 100003 = 100003 = 100003 = 100003 = 100003 = 100003 = 100003 = 100003 = 100003 = 100003 = 100003 = 100003 = 100003 = 100003. (345 — 4692I 3 )/22 — 47I 3 = 10 -260,27I 3 = -5,68 I 3 = 5,68/260,27 = 0,0218 A = 21,8 мА Теперь подставьте это значение I 3 в уравнение правого контура. 22I 2 + 68(0.0218) = 5 Solve for I 2 I 2 = (5 — 68(0.0218))/22 = 3.52/22 = 0.16 A = 160 mA Подставив значения I 2 и I 3 в текущее уравнение в узле A, вы получите I 1 — 0,16 + 0,0218 = 0 I 1 = 0,16 — 0,0218 = 0,138 А = 138 мА |
Категория
Базовая электроника
1 Метод тока ветви
1
Применение метода ветвей тока для расчета токов и напряжений в электрических цепях. Рассмотрены электрические цепи постоянного тока и электрические цепи переменного тока. Метод ветвей тока основан на законе тока Кирхгофа ( KCL ) и законе напряжения Кирхгофа ( КВЛ ).
Текущий закон Кирхгофа (KCL) говорит нам, что алгебраическая сумма токов, втекающих в узел и вытекающих из него, равна нулю. Текущий закон Кирхгофа произошел от принципа сохранения электрического заряда . Когда мы применяем закон тока Кирхгофа, мы используем соглашение, что токи, которые текут в направлении к узлу, имеют знак «+», а токи, которые текут в направлении от узла, имеют знак «-».
903:50
Закон напряжения Кирхгофа (KVL) говорит нам, что алгебраическая сумма напряжений в указанной сетке равна нулю. Закон напряжения Кирхгофа произошел из принципа сохранения энергии . Применение закона Кирхгофа о волатильности выглядит следующим образом. В указанной сетке отмечаем направление циркуляции напряжений. Когда напряжения в сетке имеют одинаковое направление, мы присваиваем им знак «+», в противном случае мы присваиваем им знак «-».
Процедура текущего метода ответвления следующая. В этом методе мы должны написать уравнения для закона тока Кирхгофа и закона напряжения Кирхгофа. Количество уравнений для каждого закона задается и задается следующими формулами:
Количество уравнений для текущего закона Кирхгофа равно количеству узлов минус один. Символически запишем это:
KCL → (n-1)
где:
n – количество узлов
Количество уравнений для закона напряжения Кирхгофа равно количеству ветвей в цепи минус количество уравнений для тока Кирхгофа. Помните, что текущий источник не является ветвью. Символически пишем это:
КВЛ → m-(n-1)
где
m – количество ответвлений
n – количество узлов
Пример метода тока ответвления 1
Применение метода ветвей тока для электрической цепи, построенной из четырех источников напряжения и пяти резисторов.
Метод тока ответвления – пример 1
Метод тока ответвления, пример 2
Применение метода ветвей тока для электрической цепи, построенной из двух источников тока, трех источников напряжения и четырех резисторов.
Метод тока ответвления – пример 2
Метод тока ответвления, пример 3
Применение метода ветвей тока для электрической цепи, построенной из двух источников тока, трех источников напряжения и пяти резисторов.
Метод ответвления током – пример 3
Метод ответвления тока пример 4
Электрическая схема представляет собой модель однофазного трехфазного двигателя переменного тока. Модель фазы асинхронного двигателя часто используется для теоретического расчета токов. В этом упражнении Метод ответвленных токов будет использоваться для нахождения выражений для токов в модели двигателя переменного тока.
Метод ответвления тока – пример 4
Метод ответвления тока пример 5
Метод ответвленных токов будет применяться для расчета ответвленных токов в электрической цепи переменного тока. Электрическая схема построена с источником переменного напряжения E , источником переменного тока I . Электрическая цепь имеет в своей топологии и пассивные элементы. Цепь содержит три импеданса, которые получены из следующих элементов: индуктивности L1, конденсатора C1 и резистора R1. Токи ветвей рассчитываются в примере с применением комплексных чисел.
Электрическая цепь имеет в своей топологии и пассивные элементы. Цепь содержит три импеданса, которые получены из следующих элементов: индуктивности L1, конденсатора C1 и резистора R1. Токи ветвей рассчитываются в примере с применением комплексных чисел.
Метод тока ответвления – пример 5
Метод тока ответвления, пример 6
Токи ветвей будут рассчитаны в электрической цепи переменного тока. Электрическая цепь содержит в своей топологии один источник переменного напряжения В s и один источник переменного тока I s . Поскольку это цепь переменного тока, все расчеты производятся с использованием комплексных чисел. Цепь состоит из пяти импедансов, которые связаны с пассивными элементами, такими как индуктивности L1 и L2, резисторы R1 и R2 и один конденсатор C1.
Метод тока ответвления – пример 6
Метод тока ответвления, пример 7
Токи ветвей будут рассчитаны для электрической цепи постоянного тока.



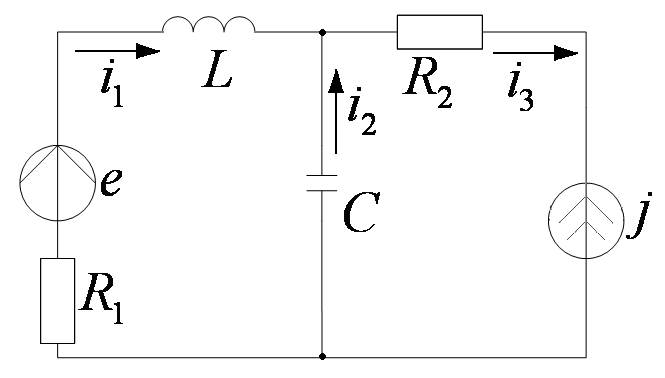 3 — 5 = 0
3 — 5 = 0