Линией уровня функций f x y называется: 14 Функции многих переменных

14 Функции многих переменных

Функции многих переменных

§1. Понятие функции многих переменных.

Пусть имеется n переменных величин . Каждый набор обозначает точку n—мерного множества (п-мерный вектор).

Пусть даны множества и .

Опр. Если каждой точке ставится в соответствие единственное число , то говорят, что задана числовая функция n переменных:

.

называют областью определения, — множеством значений данной функции.

В случае n=2 вместо обычно пишут x, y, z. Тогда функция двух переменных имеет вид:

z=f(x,y).

Например, — функция двух переменных;

— функция трех переменных;

— линейная функция n переменных.

Опр. Графиком функции n переменных называется n—мерная гиперповерхность в пространстве , каждая точка которой задается координатами

.

Например, графиком функции двух переменных z=f(x,y) является поверхность в трехмерном пространстве, каждая точка которой задается координатами (x,y,z), где , и .

Поскольку график функции трех и более переменных изобразить не представляется возможным, в основном мы будем (для наглядности) рассматривать функции двух переменных.

Построение графиков функций двух переменных является довольно сложной задачей. Существенную помощь в ее решении может оказать построение так называемых линий уровня.

Опр. Линией уровня функции двух переменных z=f(x,y) называется множество точек плоскости ХОУ, являющихся проекцией сечения графика функции плоскостью, параллельной ХОУ. В каждой точке линии уровня функция имеет одно и то же значение. Линии уровня описываются уравнением f(x,y)=с, где с – некоторое число. Линий уровня бесконечно много, и через каждую точку области определения можно провести одну из них.

Опр. Поверхностью уровня функции n переменных y=f () называется гиперповерхность в пространстве , в каждой точке которой значение функции постоянно и равно некоторому значению с. Уравнение поверхности уровня: f ()=с.

Пример. Построить график функции двух переменных

.

.

При с=1: ; .

При с=4: ; .

При с=9: ; .

Линии уровня – концентрические окружности, радиус которых уменьшается с ростом z.

§2. Предел и непрерывность функции многих переменных.

Для функций многих переменных определяются те же понятия, что и для функции одной переменной. Например, можно дать определения предела и непрерывности функции.

Опр. Число А называется пределом функции двух переменных z=f(x,y) при , и обозначается , если для любого положительного числа найдется положительное число , такое, что если точка удалена от точки на расстояние меньше , то величины

f(x,y) и А отличаются меньше чем на .

Опр. Если функция z=f(x,y) определена в точке и имеет в этой точке предел, равный значению функции , то она называется непрерывной в данной точке.

Пример.

.

.

§3. Частные производные функции многих переменных.

Рассмотрим функцию двух переменных .

Зафиксируем значение одного из ее аргументов, например , положив . Тогда функция есть функция одной переменной . Пусть она имеет производную в точке :

.

Данная производная называется частной производной (или частной производной первого порядка) функции по в точке и обозначается: ; ; ; .

Разность называется частным приращением по и обозначается :

.

Учитывая приведенные обозначения, можно записать

.

Аналогично определяется

.

Частной производной функции нескольких переменных по одной из этих переменных называется предел отношения частного приращения функции к приращению соответствующей независимой переменной, когда это приращение стремится к нулю.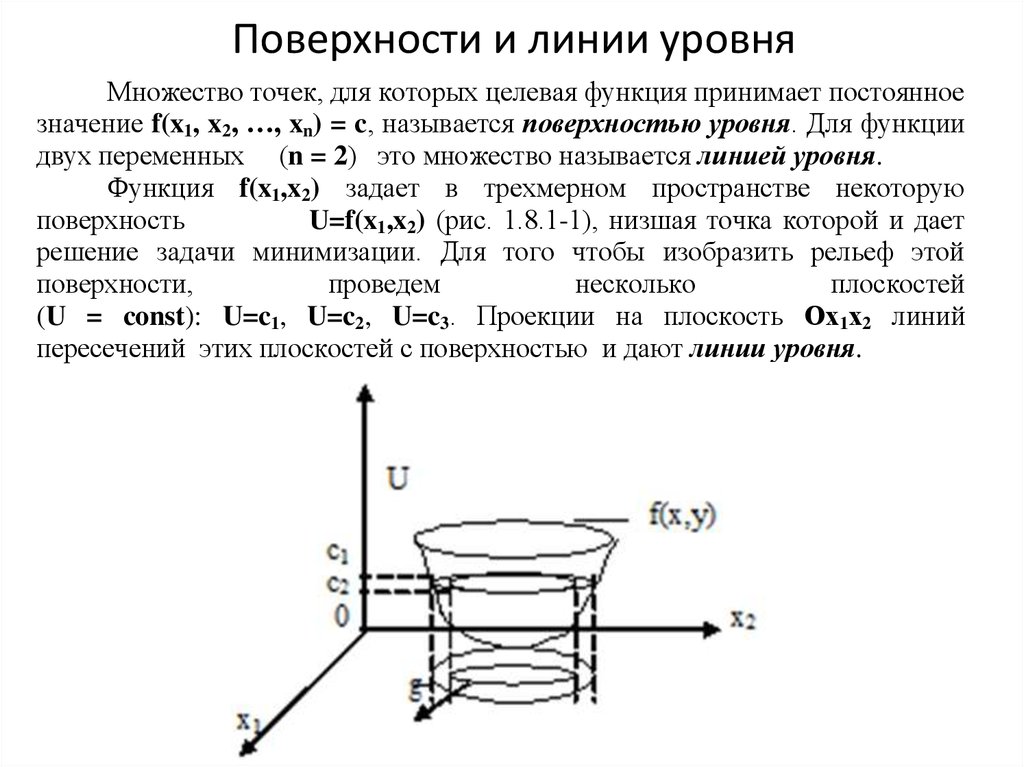

При нахождении частной производной по какому-либо аргументу другие аргументы считаются постоянными. Все правила и формулы дифференцирования функций одной переменной справедливы для частных производных функции многих переменных.

Заметим, что частные производные функции являются функциями тех же переменных. Эти функции, в свою очередь, могут иметь частные производные, которые называются вторыми частными производными (или частными производными второго порядка) исходной функции.

Например, функция имеет четыре частных производных второго порядка, которые обозначаются следующим образом:

; ;

; .

и — смешанные частные производные.

Пример. Найти частные производные второго порядка для функции

.

Решение. , .

, .

, .

Задание.

1. Найти частные производные второго порядка для функций

, ;

2. Для функции доказать, что .

Полный дифференциал функции многих переменных.

При одновременном изменении величин х и у функция изменится на величину , называемую полным приращением функции z в точке . Так же, как и в случае функции одной переменной, возникает задача о приближенной замене приращения на линейную функцию от и . Роль линейного приближения выполняет полный дифференциал функции:

Полный дифференциал второго порядка:

=

= .

=.

В общем виде полный дифференциал п-го порядка имеет вид:

Производная по направлению. Градиент.

Пусть функция z=f(x

,y) определена в некоторой окрестности точки M(x,y) и — некоторое направление, задаваемое единичным вектором . Координаты единичного вектора выражаются через косинусы углов, образуемых вектором и осями координат и называемых направляющими косинусами:

,

.

При перемещении точки M(x,y) в данном направлении l в точку функция z получит приращение

,

называемое приращением функции в данном направлении l.

Если ММ₁=∆l, то

.

Т

огда

.

О

пр. Производной функции z=f(x,y)по направлению называется предел отношения приращения функции в этом направлении к величине перемещения ∆l при стремлении последней к нулю:

.

Производная по направлению характеризует скорость изменения функции в данном направлении. Очевидно, что частные производные и представляют собой производные по направлениям, параллельным осям Ox и Oy. Нетрудно показать, что

.

Пример. Вычислить производную функции в точке (1;1) по направлению .

Опр. Градиентом функции z

=f(x,y) называется вектор с координатами, равными частным производным:

.

Рассмотрим скалярное произведение векторов и :

Легко видеть, что , т.е. производная по направлению равна скалярному произведению градиента и единичного вектора направления .

Поскольку , то скалярное произведение максимально, когда векторы одинаково направлены. Таким образом, градиент функции в точке задает направление наискорейшего возрастания функции в этой точке, а модуль градиента равен максимальной скорости роста функции.

Зная градиент функции, можно локально строить линии уровня функции.

Теорема. Пусть задана дифференцируемая функция z=f(x,y) и в точке градиент функции не равен нулю: . Тогда градиент перпендикулярен линии уровня, проходящей через данную точку.

Таким образом, если, начиная с некоторой точки, строить в близких точках градиент функции и малую часть перпендикулярной ему линии уровня, то можно (с некоторой погрешностью) построить линии уровня.

Локальный экстремум функции двух переменных

Пусть функция определена и непрерывна в некоторой окрестности точки .

Опр. Точка называется точкой локального максимума функции , если существует такая окрестность точки , в которой для любой точки выполняется неравенство:

.

Аналогично вводится понятие локального минимума.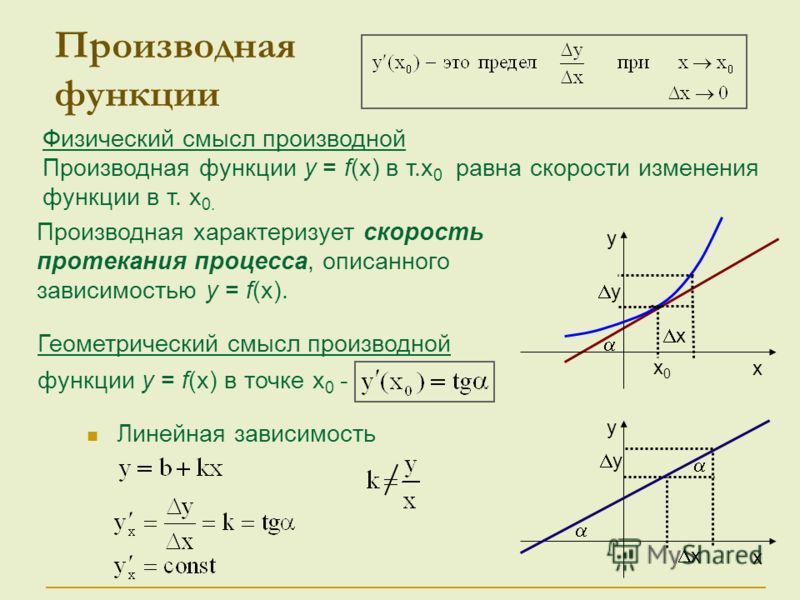

Теорема (необходимое условие локального экстремума).

Для того, чтобы дифференцируемая функция имела локальный экстремум в точке , необходимо, чтобы все ее частные производные первого порядка в этой точке были равны нулю:

Итак, точками возможного наличия экстремума являются те точки, в которых функция дифференцируема, а ее градиент равен 0: . Как и в случае функции одной переменной, такие точки называются стационарными.

Пример. .

1)Определение функции двух переменных

Если каждой паре ( x;y) значений двух независимых друг от друга переменных величин х и у из некоторого множества D соответствует единственное значение величины, то говорят, что z есть функция двух независимых переменных x и y, определенная на множестве D.

Обозначается: z=f(x;y) или z=z(x;y).

Например, S=ab, S=S(a;b)- функции двух переменных; V=abc, V=V(a,b.c) – функция трех переменных;

2)Область определения ф-ии двух переменных

Область определения функции z=f(x,y) называется совокупность пар чисел (x,y), которым соответствуют действительные значения функции. D={(x,y)}

Множество Z={f(x,y)} – множество значений функции.

3)График функции двух переменных. Линии уровня. Поверхности уровня.

Графиком функции z= f(x,y) называется поверхность, представляющая собой геометрическое место точек функции, когда точка (x,y) принимает все значения из области определения.

Линией уровня функции z= f(x,y) называется геометрическое место точек (x,y) плоскости, в которой функция принимает одно и то же значение С. Линию уровня можно построить, спроектировав на плоскость XOY множество точек пространства. Уравнение линии уровня имеет вид f(x,y)=С.

Поверхностью уровня u=с функции u= f(x,y,z) называется поверхность f(x,y,z)=с, в точках которой функция u= f(x,y,z) сохраняет значение, равное с.

4)Предел и непрерывность ф-ии нескольких переменных.

Введем понятие D-окрестности точки М0 (Х0 , у0) на плоскости ОХу как круга радиуса D с центром в данной точке. Аналогично можно определить D-окрестность в трехмерном пространстве как шар радиуса D с центром в точке М0 (Х0 , у0 , Z0). Для N-мерного пространства будем называть D-окрестностью точки М0 множество точек М С координатами , удовлетворяющими условию

Координаты точки М0. Иногда это множество называют «шаром» в N-мерном пространстве.

Число А называется Пределом функции нескольких переменных

В точке М0, если

Такое, что | F(M) – A| < ε для любой точки М из δ-окрестности М0.

Обозначения:

Необходимо учитывать, что при этом точка М может приближаться к М0, условно говоря, по любой траектории внутри D-окрестности точки М0. Поэтому следует отличать предел функции нескольких переменных в общем смысле от так называемых Повторных пределов, получаемых последовательными предельными переходами по каждому аргу

Функция Называется Непрерывной в точке М0 Если

Если ввести обозначения

То это условие можно переписать в форме

Внутренняя точка М0 Области определения функции Z = F (M) называется Точкой разрыва функции, если в этой точке не выполняется условие

Замечание. Множество точек разрыва может образовывать на плоскости или в пространстве Линии Или Поверхности разрыва.

5)Определение частных производных

Частные производные функции y=f(M)в том случае, если они существуют не в одной точке, а на некотором множестве A’, являются функциями, определенными на этом множестве. Поэтому удобно ввести следующие обозначения:

F’x1=g1(M), f’x2=g2(M)….

Полученные функции g1, g2….gn, определенные в A’, могут быть непрерывными и иметь частные производные в различных точках A’.Назовем частные производные от функций g1,g2…gn. частными производными высшего порядка от функции f(M) и примем для каждого j (j=1,2,3…n)

(fx1)’xj=f’’x1xj , (f’x2)’xj=f’’x2xj,…, (f’xn)’xj=f’’xnxj или (f’xi)’xj=f’’xixj, где I и j= 1,2,3…n.

Эти производные разбиваются на две группы: вторые частные производные от f по переменным xi

f’’x²i= (f’xi)’xj, i=1,2,…n, j=1,2,…n.

и смешанные частные производные от f по переменным xi и xj (i≠j)

f’’xixj=(f’xi)’xj, i=1,2…n, j=1,2…n.

Число вторых частных производных функции f(M)равно n, а число смешанных частных производных – разности n²-n=n(n-1). При этом величина n² определяет общее число всех старших производных и совпадает с числом элементов квадратной матрицы порядка n. Элементы такой матрицы имеют индексы I и j, которые находятся во взаимно однозначном соответствии с координатными индексами xi, xj, определяющими порядок частной производной.

2\to\R$ отображает пару значений $(x,y)$ в единственное действительное число. Трехмерная система координат у нас есть уже используется, это удобный способ визуализации таких функций: выше на каждую точку $(x,y)$ плоскости $x$-$y$ наносим точку $(x,y,z)$, где, конечно, $z=f(x,y)$.

Пример 16.1.1. Рассмотрим $f(x,y)=3x+4y-5$. Написание этого как $z=3x+4y-5$ и затем $3x+4y-z=5$ узнаем уравнение самолет. В форме $f(x,y)=3x+4y-5$ акцент сместился: теперь мы думайте о $x$ и $y$ как о независимых переменных и $z$ как о переменной зависит от них, но геометрия неизменна. $\квадрат$ 92

Пример 16.1.3. Рассмотрим $f=\sqrt x+\sqrt y$. Эта функция определяется только тогда, когда оба $x$ и $y$ неотрицательны. Когда $y=0$, мы получаем $f(x,y)=\sqrt x$, знакомая функция квадратного корня в плоскости $x$-$z$, а при $x=0$ мы получаем такую ​​же кривую в плоскости $y$-$z$. Вообще говоря, мы видим что, начиная с $f(0,0)=0$, эта функция становится больше во всех направлениях примерно так же, как функция квадратного корня получает больше.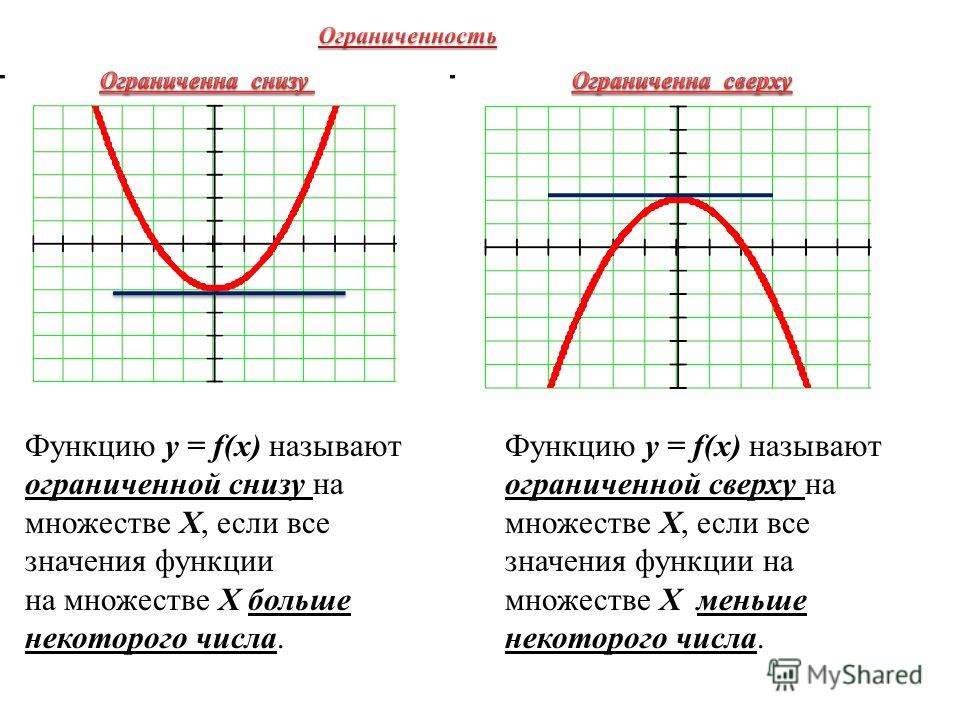 Например, если мы ограничим внимание строкой $x=y$, мы получаем $f(x,y)=2\sqrt x$ и вдоль строки $y=2x$ имеем $f(x,y)=\sqrt x+\sqrt{2x}=(1+\sqrt2)\sqrt x$. $\квадрат$

Рисунок 16.1.1. $f(x,y)=\sqrt x+\sqrt y$

Компьютерная программа, рисующая такие поверхности, может быть очень полезной, так как она часто трудно получить хорошее представление о том, как они выглядят. Все еще, полезно уметь визуализировать относительно простые поверхности без таких пособий. Как и в предыдущем примере, часто бывает хорошей идеей исследовать функцию на ограниченных подмножествах плоскости, особенно линии. Также может быть полезно определить те точки $(x,y)$, которые имеют общее $z$-значение. 92$

Как и в этом примере, точки $(x,y)$ такие, что $f(x,y)=k$ обычно образуют кривую, называемую кривой уровня функция. График некоторых кривых уровня может дать хорошее представление о форма поверхности; это очень похоже на топографическая карта принадлежащий поверхность. На рисунке 16.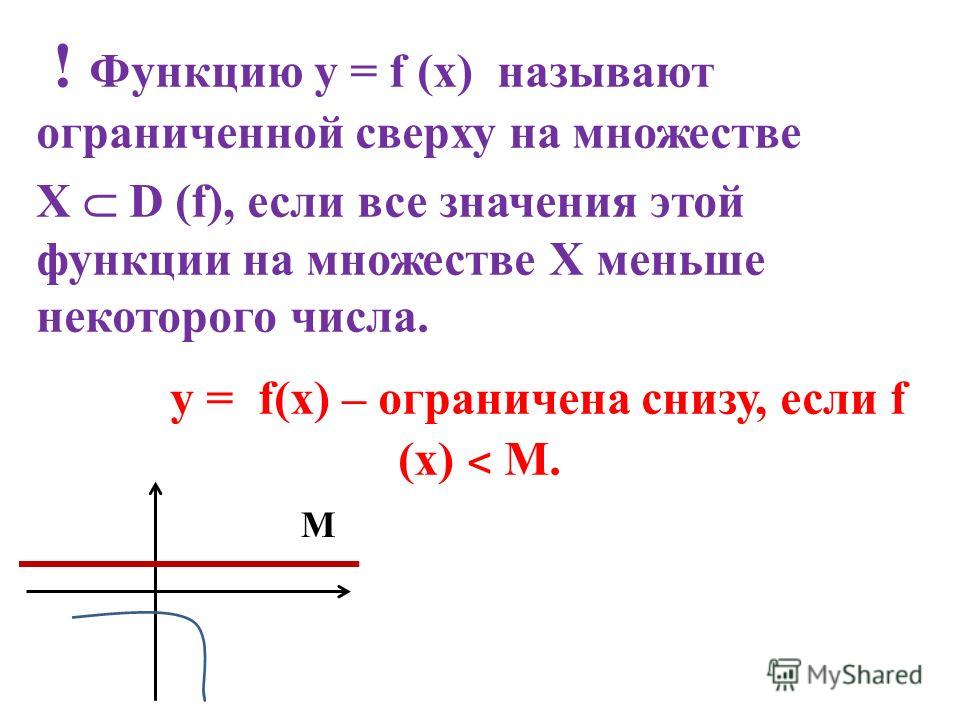 1.2 как поверхность, так и показаны связанные с ним кривые уровня. Обратите внимание, что, как и в случае с на топографической карте высоты, соответствующие кривым уровня, равны равномерно распределены, так что там, где кривые расположены ближе друг к другу, поверхность круче. 9n\to\R$ ведут себя как функции двух переменные; мы будем при случае обсуждать функции трех переменных. Основная трудность с такими функциями заключается в том, чтобы визуализировать их, как они не «вписываются» в три измерения, с которыми мы знакомы. три переменных существуют различные способы интерпретации функций, которые сделать их более понятными. Например, $f(x,y,z)$ может представляют собой температуру в точке $(x,y,z)$, или давление, или сила магнитного поля. По-прежнему полезно рассмотреть те точки, в которых $f(x,y,z)=k$, где $k$ — некоторая постоянная величина. Если $f(x,y,z)$ — температура, множество точек $(x,y,z)$ таких, что $f(x,y,z)=k$ — совокупность точек пространства с температурой $k$; вообще это называется 92}$

(отвечать)

Пример 16. 1.7 Ниже приведены два набора кривых уровня. Один для конуса, один это для параболоида. Какой какой? Объяснять.

Поверхности, часть 6

Поверхности, часть 6

Поверхности и контурные графики

Часть 6: Контурные линии

Контурная линия (также известная как как кривая уровня ) для данной поверхности есть кривая пересечения поверхность с горизонтальной плоскостью, z  =  с . Представитель совокупность контурных линий, спроецированных на плоскость xy , представляет собой контур карта или контурный участок поверхности .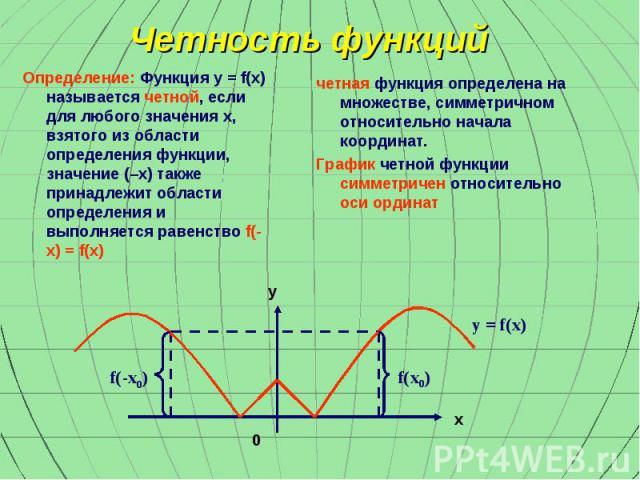

В частности, если поверхность график функции две переменные, скажем, z = f ( x , y ), то контуры определяются неявно уравнениями вида f ( x , y ) =  в , г = с . Проекции на плоскость xy , которые составляют контурную карту, определяемую как f ( x , y ) =  c , z  = 0, опять же для репрезентативного набора констант c . На следующем рисунке мы показываем обычный график графика функции на слева и соответствующая контурная карта справа. На этой карте цвета используются для отображения разных высот, более светлые цвета на более высоких высотах.

 

1. Убедитесь, что вы понимаете, как контурная карта представляет функцию на рисунке выше. Как вы можете сказать из контурной карты где есть «вершина» на поверхности? Долина»? «седловая точка»? [Седловая точка — это ровная точка, с которой вы может идти вниз в каком-то направлении и вверх в каком-то другом направлении. ] Дайте приблизительное xy -координаты для каждого из этих трех объектов.
2. Запишите уравнения уровня кривые для f ( x , y ) = x ²  + y ² для четырех значений c . Нарисуйте эту поверхность и эти кривые уровня на вашем рабочий лист. Если в вашей системе компьютерной алгебры есть параметр контура, используйте его для начертите контурные линии как на поверхности, так и в проекции на xy -плоскость.

Широко используются контурные графики в географии для обозначения высоты земли над точкой на карте. Такой карты называются топографическими картами . Следующий рисунок является примером.

3. Определите вершину горы в топографическая карта, показанная на рисунке выше. Как можно использовать контуры, чтобы уверен в этом? Как отличить относительно крутые места на горный склон из не очень крутых мест?
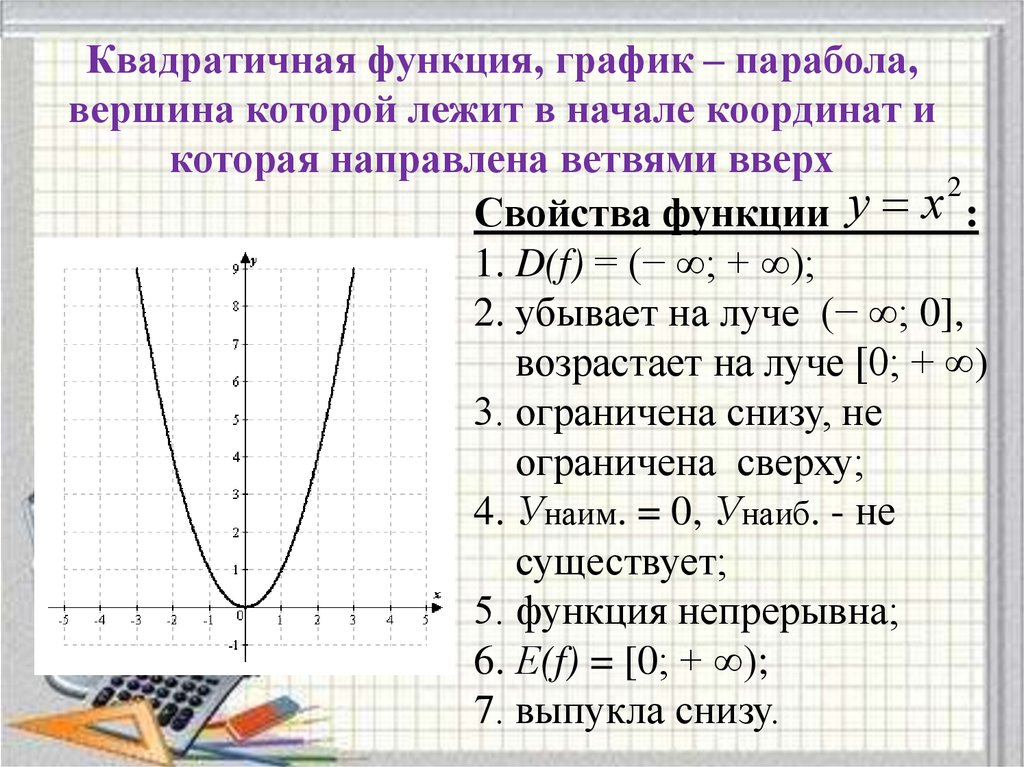
4. На рисунке ниже показан контур график математической функции.

   No related posts.