Какие из векторов изображенных на рисунке 146: Какие из векторов, изображенных на рис. 146: а) коллинеарны; б) сонаправлены; в) противоположно направлены;

alexxlab / / Разное

Укажите Самостоятельная работа 32. Вариант 2. № 1 Геометрия 8 класс Зив Б.Г. – Рамблер/класс

Укажите Самостоятельная работа 32. Вариант 2. № 1 Геометрия 8 класс Зив Б.Г. – Рамблер/класс

Интересные вопросы

Школа

Подскажите, как бороться с грубым отношением одноклассников к моему ребенку?

Новости

Поделитесь, сколько вы потратили на подготовку ребенка к учебному году?

Школа

Объясните, это правда, что родители теперь будут информироваться о снижении успеваемости в школе?

Школа

Когда в 2018 году намечено проведение основного периода ЕГЭ?

Новости

Будет ли как-то улучшаться система проверки и организации итоговых сочинений?

Вузы

Подскажите, почему закрыли прием в Московский институт телевидения и радиовещания «Останкино»?

ABCD — параллелограмм. Укажи-
те пары векторов, изображенных на

рисунке 12, которые:
а)   коллинеарны;
б)   сонаправлены;
в)   противоположно направлены;
г)   имеют равные длины.
Можно ли на прямой АВ от точ-
ки В отложить вектор, равный век-
тору 
 

ответы


Да, можно.

ваш ответ

Можно ввести 4000 cимволов

отправить

дежурный

Нажимая кнопку «отправить», вы принимаете условия  пользовательского соглашения

похожие темы

Экскурсии

Мякишев Г.Я.

Психология

Химия

похожие вопросы 5

Докажите, что треугольники подобны. Вопросы и задачи 64, Геометрия, 10-11 класс, Атанасян Л.С.

Привет. Запуталась при решении, нужна помощь знатоков!!!
 
Три прямые, проходящие через одну точку и не лежащие в одной (Подробнее…)

ГДЗГеометрия11 класс10 классАтанасян Л.

С.

Приготовление раствора сахара и расчёт его массовой доли в растворе. Химия. 8 класс. Габриелян. ГДЗ. Хим. практикум № 1. Практ. работа № 5.

Попробуйте провести следующий опыт. Приготовление раствора
сахара и расчёт его массовой доли в растворе.
Отмерьте мерным (Подробнее…)

ГДЗШкола8 классХимияГабриелян О.С.

Самостоятельная работа 19. Вариант 2. № 2 ГДЗ Геометрия 9 класс Зив Б.Г. Помогите доказать, используя параллельный перенос

Используя параллельный перенос, докажите, что углы при основании равнобедренной трапеции равны между собой.
 

ГДЗЭкзаменыГеометрия9 классЗив Б. Г.

11. Выпишите слово, в котором на месте пропуска пишется буква Е. Русский язык ЕГЭ-2017 Цыбулько И. П. ГДЗ. Вариант 12.

11.
Выпишите слово, в котором на месте пропуска пишется буква Е.

произнос., шь (Подробнее…)

ГДЗЕГЭРусский языкЦыбулько И.П.

ЕГЭ-2017 Цыбулько И. П. Русский язык ГДЗ. Вариант 12. 18. Расставьте все знаки препинания: укажите цифру(-ы), на месте которой(-ых)…

18.
Расставьте все знаки препинания: укажите цифру(-ы), на месте которой(-ых)
в предложении должна(-ы) стоять запятая(-ые). (Подробнее…)

ГДЗЕГЭРусский языкЦыбулько И.П.

Решебник по физике за 9 класс А.В.Перышкин, Е.М.ГутникЗадачи, предлагаемые для повторения и при 3 часах физики в неделю

Решебники и ГДЗ

    Начните вводить часть условия (например, могут ли, чему равен или найти):

    • 1. Для каждого из векторов, изображенных на рисунке 191, определите: а) координаты начала и конца; б) проекции на ось у; в) модули проекций на ось у, г) модули векторов.
    • 2. На рисунке 192 векторы а и с перпендикулярны оси X, а векторы b и d параллельны ей. Выразите проекции ах, bх, сх и dx через модули этих векторов или соответствующие числа.
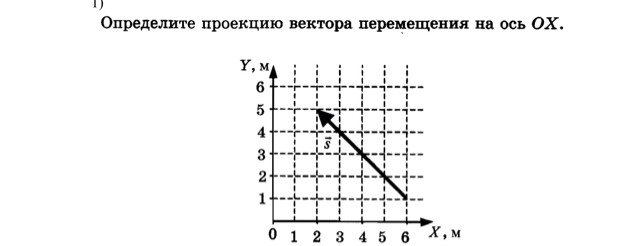
    • 3. На рисунке 193 изображена траектория движения шарика, переместившегося из точки А в точку В. Определите: а) координаты начального и конечного положений шарика; б) проекции sx и sy перемещения шарика; в) модули |sх| и |sy| проекций перемещения; г) модул
    • 4. Катер переместился относительно пристани из точки А(-8; —2) в точку В(4; 3). Сделайте чертеж, совместив начало координат с пристанью и указав на нем точки А и В. Определите перемещение катера АВ. Мог ли путь, проделанный катером, быть больше совершенно
    • 5. Известно, что для определения координаты прямолинейно движущегося тела используется уравнение х = х0 + sx. Докажите, что координата тела при его прямолинейном равномерном движении для любого момента времени определяется с помощью уравнения х = х0 + vxt
    • 6. Запишите уравнение для определения координаты тела, движущегося прямолинейно со скоростью 5 м/с вдоль оси X, если в момент начала наблюдения его координата была равна 3 м.
    • 7. Два поезда — пассажирский и товарный — движутся по параллельным путям. Относительно здания вокзала движение пассажирского поезда описывается уравнением xп= 260 — 10t, а товарного — уравнением хт = -100 + 8t. Приняв вокзал и поезда за материальные точки
    • 8. Туристы сплавляются на плоту по реке. На рисунке 194 показано. как меняется со временем координата плота относительно места стоянки туристов (точки О). Начало наблюдения совпадает с моментом спуска плота на воду и началом движения. Где плот был спущен
    • 9. Мальчик съезжает с горы на санках, двигаясь из состояния покоя прямолинейно и равноускоренно. За первые 2 с после начала движения его скорость возрастает до 3 м/с. Через какой промежуток времени от начала движения скорость мальчика станет равной 4,5 м/
    • 10. Преобразуйте формулу к виду:
    • 11. Исходя из того, что выведите формулу
    • 12. На рисунке 27 показаны положения шарика через каждую 0,1с его равноускоренного падения из состояния покоя. Координаты всех шести положений отмечены черточками по правому краю линейки. Пользуясь рисунком, определите среднюю скорость шарика за первые 0,
    • 13. Два лифта — обычный и скоростной — одновременно приходят в движение и в течение одного и того же промежутка времени движутся равноускоренно. Во сколько раз путь, который пройдет за это время скоростной лифт, больше пути, пройденного обычным лифтом, ес
    • 14. На рисунке 195 представлен график зависимости проекции скорости лифта при разгоне от времени. Перечертите этот график в тетрадь и в тех же координатных осях постройте аналогичный график для скоростного лифта, ускорение которого в 3 раза больше, чем об
    • 15. Автомобиль движется прямолинейно вдоль оси X. Уравнение зависимости проекции вектора скорости автомобиля от времени в СИ выглядит так: vx = 10 + 0,5t. Определите модуль и направление начальной скорости и ускорения автомобиля. Как меняется модуль векто
    • 16. От удара клюшкой шайба приобрела начальную скорость 5 м/с и стала скользить по льду с ускорением 1 м/с2. Запишите уравнение зависимости проекции вектора скорости шайбы от времени и постройте соответствующий этому уравнению график.
    • 17. Известно, что для определения координаты прямолинейно движущегося тела используется уравнение Докажите, что координата тела при его прямолинейном равноускоренном движении для любого момента времени определяется с помощью уравнения
    • 18. Лыжник скатывается с горы, двигаясь прямолинейно с постоянным ускорением 0,1 м/с2. Напишите уравнения, выражающие зависимость от времени координаты и проекции вектора скорости движения лыжника, если его начальные координата и скорость равны нулю.
    • 19. Велосипедист движется по шоссе прямолинейно со скоростью, модуль которой равен 40 км/ч относительно земли. Параллельно ему движется автомобиль. Что можно сказать о модуле вектора скорости и направлении движения автомобиля относительно земли, если отно
    • 20. Скорость катера относительно воды в реке в 5 раз больше скорости течения воды относительно берега. Рассматривая движение катера относительно берега, определите, во сколько раз быстрее катер движется по течению, чем против него.
    • 21. Мальчик держит в руках шарик массой 3,87 г и объемом 3 ⋅ 10-3 м3. Что произойдет с этим шариком, если его выпустить из рук?
    • 22. Стальной шар равномерно катится по горизонтальной поверхности и сталкивается с неподвижным алюминиевым шаром, в результате чего алюминиевый шар получает некоторое ускорение. Может ли при этом модуль ускорения стального шара быть равен нулю? быть больш
    • 23. Пусть МЗ и RЗ— соответственно масса и радиус земного шара, g0 — ускорение свободного падения на поверхности Земли, a g — на высоте h. Исходя из формул выведите формулу:
    • 24. На рисунке 196 изображены равные по массе шарики 1 и 2, привязанные к нитям длиной к и 2к соответственно и движущиеся по окружностям с одинаковой по модулю скоростью v. Сравните центростремительные ускорения, с которыми движутся шарики, и силу натяжен
    • 25. Исходя из формулы для определения центростремительного ускорения при движении по окружности и формулы выведенной вами при решении задачи 23, получите следующую формулу для расчета первой космической скорости на высоте h над поверхностью Земли:
    • 26. Среднее значение радиуса Земли равно 6400 км, а ускорение свободного падения у земной поверхности равно 9,8 м/с2. Пользуясь только этими данными, вычислите первую космическую скорость на высоте 3600 км над поверхностью Земли.
    • 27. Постройте график зависимости проекции вектора скорости от времени для тела, свободно падающего в течение 4 с (v0 = 0, считать g= 10 м/с2).
    • 28. Тело массой 0,3 кг свободно падает из состояния покоя в течение 3 с. На сколько увеличивается его импульс за первую секунду падения? за вторую секунду падения?
    • 29. С помощью графика, построенного вами при решении задачи 27, покажите, что импульс свободно падающего тела за равные промежутки времени меняется на одну и ту же величину.
    • 30. Алюминиевый и медный шарики одинакового объема свободно падают из состояния покоя с одной и той же высоты в течение 2,5 с. Импульс какого из шариков будет больше и во сколько раз к концу первой секунды падения? к концу второй секунды падения? Ответы о
    • 31. Два одинаковых бильярдных шара, двигаясь вдоль одной прямой, сталкиваются друг с другом. Перед столкновением проекция вектора скорости первого шара на ось X была равна 0,2 м/с, а второго — 0,1 м/с. Определите проекцию вектора скорости второго шара пос
    • 32. Решите предыдущую задачу для случая, при котором v1x = 0,2 м/с, v2x= -0,1 м/с, v’1x = -0,1 м/с (где v1x и v2x — проекции векторов скорости соответственно 1-го и 2-го шаров до их столкновения, a v’1x — проекция вектора скорости 1-го шара после столкнов
    • 33. Используя данные и результат решения задачи 32, покажите, что при столкновении шаров выполняется закон сохранения полной механической энергии.
    • 34. На рисунке 197 показано, как меняется с течением времени проекция вектора скорости одной из точек сидения качелей. С какой частотой происходит это изменение? Какова частота изменения скорости любой другой точки качелей, совершающей колебания?
    • 35. Струна арфы совершает гармонические колебания с частотой 40 Гц. Постройте график зависимости координаты от времени для средней точки струны, амплитуда колебаний которой равна 3 мм. (Для построения графика рекомендуем разметить ось t так, как показано
    • 36. Как добиться звучания одного из двух одинаковых камертонов на резонаторных ящиках, не дотрагиваясь до него? Как при этом следует расположить отверстия резонаторных ящиков по отношению друг к другу? Ответы поясните. Какое физическое явление лежит в осн
    • 37. Качели периодически подталкивают рукой, т. е. действуют на них вынуждающей силой. На рисунке 199 изображен график зависимости амплитуды установившихся колебаний качелей от частоты данной вынуждающей силы. Пользуясь этим графиком, определите: а) При ка
    • 38. На рисунке 200 изображен проводник АВ длиной 10 см и массой 2 г, помещенный в однородное магнитное поле с индукцией 4 • 10 2 Тл перпендикулярно линиям магнитной индукции. По проводнику протекает электрический ток (подводимый по тонким проводам, на кот
    • 39. В камеру Вильсона, помещенную в однородное магнитное поле, влетает электрон и движется по дуге окружности (см. белую штриховую линию на рисунке 201). Под действием какой силы меняется направление скорости электрона? В какой точке он влетел в камеру?
    • 40. Известно, что сила F, с которой однородное магнитное поле с индукцией В действует на частицу с зарядом е, движущуюся со скоростью о перпендикулярно линиям магнитной индукции, определяется по формуле: F = Bev. По дуге окружности какого радиуса будет дв
    • 41. В результате какого радиоактивного распада углерод 146C превращается в азот 147N?
    • 42. При бомбардировке ядер алюминия 2713Al нейтронами из образовавшегося ядра выбрасывается α-частица. Напишите уравнение этой реакции.
    • 43. Пользуясь законом сохранения массового и зарядового чисел, заполните пропуск в записи следующей ядерной реакции: В 105B+ … → 73Li + 42He.
    • 44. Какой химический элемент образуется в результате α-распада изотопа урана 23892U? Запишите эту реакцию.
    • 45. В результате какого числа β-распадов ядро атома тория 23490Th превращается в ядро атома урана 23892U?

    Поиск по сайту

    miR-146a подавляет экспрессию SUMO1 и вызывает сердечную дисфункцию при дезадаптивной гипертрофии

    1. Отмечает AR. Белки, вращающие кальций, и сердечная недостаточность: механизмы и терапия. Джей Клин Инвест. 2012;123(1):46–52. [Бесплатная статья PMC] [PubMed] [Google Scholar]

    2. Luo M, Anderson ME. Механизмы измененной обработки Ca(2)(+) при сердечной недостаточности. Цирк Рез. 2013;113(6):690–708. [Бесплатная статья PMC] [PubMed] [Google Scholar]

    3. Mozaffarian D, Benjamin EJ, Go AS, Arnett DK, Blaha MJ, Cushman M, Das SR, de Ferranti S, Despres JP, Fullerton HJ, Howard VJ, Хаффман М.Д., Исаси Ч.Р., Хименес М.С., Джадд С.Е., Киссела Б.М., Лихтман Д.Х., Лизабет Л.Д., Лю С., Макки Р.Х., Магид Д.Дж., Макгуайр Д.К., Молер Э.Р., 3-й, Мой К.С., Мантнер П., Муссолино М.Э., Насир К., Ноймар Р.В., Никол Г., Паланиаппан Л., Пандей Д.К., Ривз М.Дж., Родригес С.Дж., Розамонд В., Сорли П.Д., Стейн Дж., Тауфиги А., Туран Т.Н., Вирани С.С., Ву Д., Йе Р.В., Тернер М.Б. Обновление статистики сердечных заболеваний и инсультов за 2016 год: отчет Американской кардиологической ассоциации. Тираж. 2016;133(4):e38–360. [PubMed] [Академия Google]

    4. Миямото М.И., Дель Монте Ф., Шмидт У., ДиСальво Т.С., Канг З.Б., Мацуи Т., Герреро Дж.Л., Гватмей Дж.К., Розенцвейг А., Хаджар Р.Дж. Аденовирусный перенос гена SERCA2a улучшает функцию левого желудочка у крыс с перевязкой аорты при переходе к сердечной недостаточности. Proc Natl Acad Sci U S A. 2000;97(2):793–798. [Бесплатная статья PMC] [PubMed] [Google Scholar]

    5. del Monte F, Hajjar RJ, Harding SE. Неопровержимые доказательства положительного эффекта переноса генов SERCA при сердечной недостаточности. Цирк Рез. 2001;88(11):E66–67. [PubMed] [Академия Google]

    6. Sakata S, Lebeche D, Sakata Y, Sakata N, Chemaly ER, Liang L, Nakajima-Takenaka C, Tsuji T, Konishi N, del Monte F, Hajjar RJ, Takaki M. Транскоронарный перенос генов SERCA2a увеличивает коронарные кровоток и уменьшает размер кардиомиоцитов в модели крыс с диабетом 2 типа. Am J Physiol Heart Circ Physiol. 2007; 292(2):h2204–1207. [PubMed] [Google Scholar]

    7. Кавасэ Ю., штаб-квартира Ли, Прунье ​​Ф., Лебеш Д., Ши Ю., Джин Х., Хадри Л., Йонеяма Р., Хосино К., Такева Ю., Саката С., Пелузо Р., Зебо К., Гватми Дж.К., Тардиф Дж.С., Тангуай Дж.Ф., Хаджар Р.Дж. Реверсия сердечной дисфункции после длительной экспрессии SERCA2a путем переноса генов в доклинической модели сердечной недостаточности. J Am Coll Кардиол. 2008; 51(11):1112–1119.. [PubMed] [Google Scholar]

    8. Jaski BE, Jessup ML, Mancini DM, Cappola TP, Pauly DF, Greenberg B, Borow K, Dittrich H, Zsebo KM, Hajjar RJ. Повышение уровня кальция путем чрескожного введения генной терапии при сердечных заболеваниях (испытание CUPID), первое клиническое испытание фазы 1/2 на людях. Ошибка карты J. 2009;15(3):171–181. [Бесплатная статья PMC] [PubMed] [Google Scholar]

    9. Джессуп М., Гринберг Б., Манчини Д., Каппола Т., Поли Д.Ф., Яски Б., Ярошинский А., Зебо К.М., Диттрих Х., Хаджар Р.Дж. Активация кальция путем чрескожного введения генной терапии при сердечных заболеваниях (CUPID): испытание фазы 2 интракоронарной генной терапии Са2+-АТФазы саркоплазматического ретикулума у ​​пациентов с прогрессирующей сердечной недостаточностью. Тираж. 2011;124(3):304–313. [Бесплатная статья PMC] [PubMed] [Google Scholar]

    10. Хо К., Ли А., Чон Д., О Дж. Г., Чаанин А. Х., Кизана Э., Пак В. Дж., Хаджар Р. Дж. SUMO1-зависимая модуляция SERCA2a при сердечной недостаточности. Природа. 2011; 477(7366):601–605. [Бесплатная статья PMC] [PubMed] [Google Scholar]

    11. Tilemann L, Lee A, Ishikawa K, Aguero J, Rapti K, Santos-Gallego C, Kohlbrenner E, Fish KM, Kho C, Hajjar RJ. Перенос гена SUMO-1 улучшает сердечную функцию в модели сердечной недостаточности у крупных животных. Sci Transl Med. 2013;5(211):211ra159. [PubMed] [Академия Google]

    12. Lee A, Jeong D, Mitsuyama S, Oh JG, Liang L, Ikeda Y, Sadoshima J, Hajjar RJ, Kho C. Роль SUMO-1 в окислительном стрессе и гипертрофии сердца. Антиоксидный окислительно-восстановительный сигнал. 2014;21(14):1986–2001. [Бесплатная статья PMC] [PubMed] [Google Scholar]

    13. Bartel DP. МикроРНК: распознавание мишеней и регуляторные функции. Клетка. 2009;136(2):215–233. [PMC бесплатная статья] [PubMed] [Google Scholar]

    14. Melman YF, Shah R, Das S. МикроРНК при сердечной недостаточности: становится ли картина менее туманной? Круговая сердечная недостаточность. 2014;7(1):203–214. [PubMed] [Академия Google]

    15. ван Ройдж Э., Маршалл В.С., Олсон Э.Н. На пути к терапии сердечно-сосудистых заболеваний на основе микроРНК: смысл в антисмысле. Цирк Рез. 2008;103(9):919–928. [Бесплатная статья PMC] [PubMed] [Google Scholar]

    16. Wahlquist C, Jeong D, Rojas-Munoz A, Kho C, Lee A, Mitsuyama S, van Mil A, Park WJ, Sluijter JP, Doevendans PA, Hajjar Р.Дж., Меркола М. Ингибирование миР-25 улучшает сократительную способность сердца при сердечной недостаточности. Природа. 2014;508(7497):531–535. [Бесплатная статья PMC] [PubMed] [Google Scholar]

    17. Таганов К.Д., Болдин М.П., ​​Чанг К.Дж., Балтимор Д. NF-каппаВ-зависимая индукция микроРНК миР-146, ингибитора, нацеленного на сигнальные белки врожденных иммунных ответов. Proc Natl Acad Sci U S A. 2006;103(33):12481–12486. [Бесплатная статья PMC] [PubMed] [Google Scholar]

    18. Guo M, Mao X, Ji Q, Lang M, Li S, Peng Y, Zhou W, Xiong B, Zeng Q. miR-146a в PBMCs модулирует Th2 функции у больных с острым коронарным синдромом. Иммунол Селл Биол. 2010;88(5):555–564. [PubMed] [Академия Google]

    19. Pauley KM, Stewart CM, Gauna AE, Dupre LC, Kuklani R, Chan AL, Pauley BA, Reeves WH, Chan EK, Cha S. Измененная экспрессия miR-146a при синдроме Шегрена и ее функциональная роль во врожденном иммунитете. Евр Дж Иммунол. 2011;41(7):2029–2039. [Бесплатная статья PMC] [PubMed] [Google Scholar]

    20. Xu WD, Lu MM, Pan HF, Ye DQ. Ассоциация микроРНК-146а с аутоиммунными заболеваниями. Воспаление. 2012;35(4):1525–1529. [PubMed] [Google Scholar]

    21. Wang X, Ha T, Liu L, Zou J, Zhang X, Kalbfleisch J, Gao X, Williams D, Li C. Повышенная экспрессия микроРНК-146a снижает ишемию/реперфузию миокарда. . Кардиовасц Рез. 2013;97(3):432–442. [Бесплатная статья PMC] [PubMed] [Google Scholar]

    22. Gao M, Wang X, Zhang X, Ha T, Ma H, Liu L, Kalbfleisch JH, Gao X, Kao RL, Williams DL, Li C. Затухание сердечной дисфункции при полимикробном сепсисе с помощью микроРНК-146a опосредуется посредством нацеливания на экспрессию IRAK1 и TRAF6. Дж Иммунол. 2015;195(2):672–682. [Бесплатная статья PMC] [PubMed] [Google Scholar]

    23. Feng B, Chen S, Gordon AD, Chakrabarti S. miR-146a опосредует воспалительные изменения и фиброз в сердце при диабете. Дж Мол Селл Кардиол. 2017;105:70–76. [PubMed] [Академия Google]

    24. Horie T, Ono K, Nishi H, Nagao K, Kinoshita M, Watanabe S, Kuwabara Y, Nakashima Y, Takanabe-Mori R, Nishi E, Hasegawa K, Kita T, Kimura T. Острая кардиотоксичность доксорубицина связана с миР-146a-индуцированным ингибированием пути нейрегулин-ErbB. Кардиовасц Рез. 2010;87(4):656–664. [Бесплатная статья PMC] [PubMed] [Google Scholar]

    25. Halkein J, Tabruyn SP, Ricke-Hoch M, Haghikia A, Nguyen NQ, Scherr M, Castermans K, Malvaux L, Lambert V, Thiry M, Sliwa K , Noel A, Martial JA, Hilfiker-Kleiner D, Struman I. МикроРНК-146a является терапевтической мишенью и биомаркером перипартальной кардиомиопатии. Джей Клин Инвест. 2013;123(5):2143–2154. [Бесплатная статья PMC] [PubMed] [Google Scholar]

    26. Хеггермонт В.А., Папагеоргиу А.П., Куэгебеур А., Деккс С., Карай П., Верхесен В., Илен Г., Шорс С., ван Леувен Р., Алексеев С., Эльзенаар И., Винкиер С., Покрейс П., Уолравенс А.С., Гийсберс Р., Van Den Haute C, Nickel A, Schroen B, van Bilsen M, Janssens S, Maack C, Pinto Y, Carmeliet P, Heymans S. Ингибирование микроРНК-146a и сверхэкспрессия ее целевой дигидролипоилсукцинилтрансферазы защищают от гипертрофии сердца, вызванной перегрузкой давлением и Дисфункция. Тираж. 2017;136(8):747–761. [PubMed] [Академия Google]

    27. Александр М., Ху Р., Рунч М.С., Кагеле Д.А., Мосбругер Т.Л., Толмачова Т., Сибра М.С., Раунд Дж.Л., Уорд Д.М., О’Коннелл Р.М. МикроРНК, доставляемые экзосомами, модулируют воспалительную реакцию на эндотоксин. Нац коммун. 2015;6:7321. [Бесплатная статья PMC] [PubMed] [Google Scholar]

    28.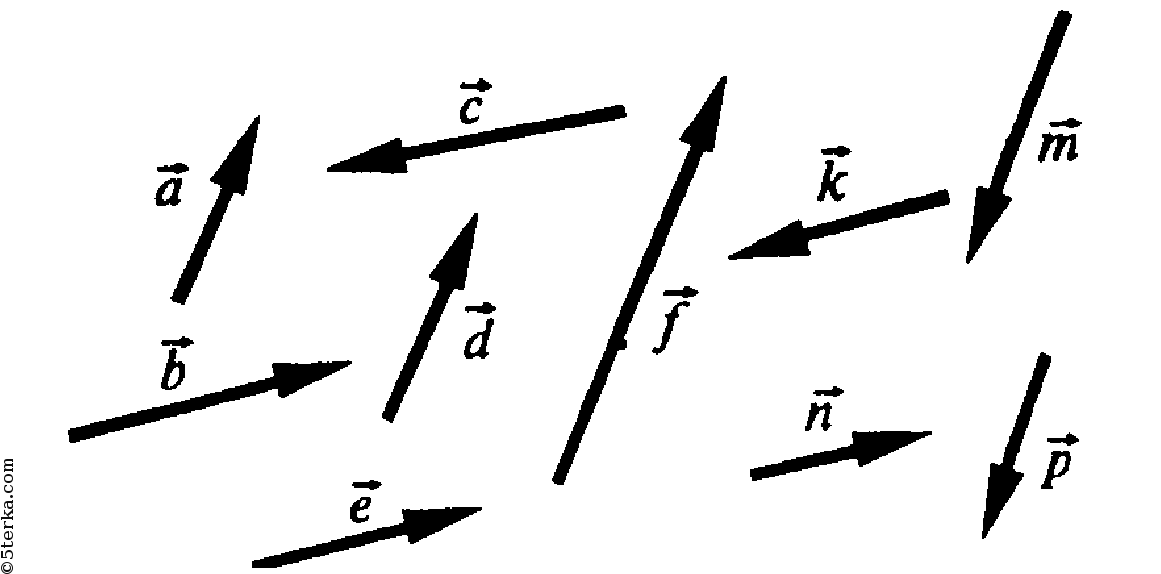 Paterson MR, Kriegel AJ. МиР-146a/b: семейство с общими семенами и разными корнями. Физиол Геномика. 2017;49(4):243–252. [Бесплатная статья PMC] [PubMed] [Google Scholar]

    29. Муллокандов Г., Баккарини А., Рузо А., Джаяпракаш А.Д., Тунг Н., Исраэлоу Б., Эванс М.Дж., Сачиданандам Р., Браун Б.Д. Высокопроизводительная оценка активности и функции микроРНК с использованием сенсоров микроРНК и библиотек-приманок. Нат Методы. 2012;9(8): 840–846. [Бесплатная статья PMC] [PubMed] [Google Scholar]

    30. Travers JG, Kamal FA, Robbins J, Yutzey KE, Blaxall BC. Сердечный фиброз: пробуждение фибробластов. Цирк Рез. 2016;118(6):1021–1040. [Бесплатная статья PMC] [PubMed] [Google Scholar]

    31. Gyongyosi M, Winkler J, Ramos I, Do QT, Firat H, McDonald K, Gonzalez A, Thum T, Diez J, Jaisser F, Pizard A, Zannad F. Миокардиальный фиброз: биомедицинское исследование от лабораторного до прикроватного. Сердечная недостаточность Eur J. 2017;19(2):177–191. [Бесплатная статья PMC] [PubMed] [Google Scholar]

    32. Добачевски М., Чен В., Франгогианнис Н.Г. Передача сигналов трансформирующего фактора роста (TGF)-бета при ремоделировании сердца. Дж Мол Селл Кардиол. 2011;51(4):600–606. [Бесплатная статья PMC] [PubMed] [Google Scholar]

    33. Стемпьен-Отеро А., Ким Д.Х., Дэвис Дж. Молекулярные сети, лежащие в основе судьбы миофибробластов и фиброза. Дж Мол Селл Кардиол. 2016;97:153–161. [Бесплатная статья PMC] [PubMed] [Google Scholar]

    34. Гейсс-Фридлендер Р., Мельхиор Ф. Концепции сумоилирования: десятилетие спустя. Nat Rev Mol Cell Biol. 2007;8(12):947–956. [PubMed] [Google Scholar]

    35. Wang J, Chen L, Wen S, Zhu H, Yu W, Moskowitz IP, Shaw GM, Finnell RH, Schwartz RJ. Нарушенный путь сумоилирования приводит к врожденному пороку сердца. Врожденные дефекты Res A Clin Mol Teratol. 2011;91(6):468–476. [Бесплатная статья PMC] [PubMed] [Google Scholar]

    36. Kang X, Qi Y, Zuo Y, Wang Q, Zou Y, Schwartz RJ, Cheng J, Yeh ET. SUMO-специфическая протеаза 2 необходима для подавления опосредованного белком группы поликомб сайленсинга генов во время эмбрионального развития. Мол Ячейка. 2010;38(2):191–201. [Бесплатная статья PMC] [PubMed] [Google Scholar]

    37. Kim EY, Chen L, Ma Y, Yu W, Chang J, Moskowitz IP, Wang J. Усиленное десумоилирование в мышиных сердцах с помощью сверхэкспрессии SENP2 приводит к врожденным порокам сердца. и сердечная дисфункция. Дж Мол Селл Кардиол. 2012;52(3):638–649. [Бесплатная статья PMC] [PubMed] [Google Scholar]

    38. Kho C, Lee A, Jeong D, Oh JG, Gorski PA, Fish K, Sanchez R, DeVita RJ, Christensen G, Dahl R, Hajjar RJ. Низкомолекулярная активация SERCA2a SUMOylation для лечения сердечной недостаточности. Нац коммун. 2015;6:7229. [Бесплатная статья PMC] [PubMed] [Google Scholar]

    39. Huang W, Tian SS, Hang PZ, Sun C, Guo J, Du ZM. Комбинация микроРНК-21 и микроРНК-146a ослабляет сердечную дисфункцию и апоптоз во время острого инфаркта миокарда у мышей. Молекулярные нуклеиновые кислоты. 2015;5:e296. [Бесплатная статья PMC] [PubMed] [Google Scholar]

    40. Паломер X, Капдевила-Бускетс Э., Боттери Г. , Дэвидсон М.М., Родригес С., Мартинес-Гонсалес Дж., Видаль Ф., Барросо Э., Чан Т.О., Фельдман А.М., Vazquez-Carrera M. miR-146a нацелена на экспрессию Fos в клетках сердца человека. Dis Model Mech. 2015;8(9): 1081–1091. [Бесплатная статья PMC] [PubMed] [Google Scholar]

    41. Odiete O, Hill MF, Sawyer DB. Нейрегулин при сердечно-сосудистых заболеваниях. Цирк Рез. 2012;111(10):1376–1385. [Бесплатная статья PMC] [PubMed] [Google Scholar]

    42. Дик С.А., Эпельман С. Хроническая сердечная недостаточность и воспаление: что мы действительно знаем? Цирк Рез. 2016;119(1):159–176. [PubMed] [Google Scholar]

    43. Косака Н., Йошиока Ю., Хагивара К., Томинага Н., Кацуда Т., Очия Т. Мусор или сокровище: внеклеточные микроРНК и межклеточная связь. Фронт Жене. 2013; 4:173. [Бесплатная статья PMC] [PubMed] [Google Scholar]

    44. Raposo G, Stoorvogel W. Внеклеточные везикулы: экзосомы, микровезикулы и друзья. Джей Селл Биол. 2013;200(4):373–383. [Бесплатная статья PMC] [PubMed] [Google Scholar]

    45. Bang C, Batkai S, Dangwal S, Gupta SK, Foinquinos A, Holzmann A, Just A, Remke J, Zimmer K, Zeug A, Ponimaskin E, Schmiedl A, Yin X, Mayr M, Halder R, Fischer A, Engelhardt S, Wei Y, Schober A, Fiedler J, Thum T. Кардиальные фибробластные экзосомы, обогащенные пассажирскими цепями микроРНК, опосредуют гипертрофию кардиомиоцитов. Джей Клин Инвест. 2014;124(5):2136–2146. [Бесплатная статья PMC] [PubMed] [Google Scholar]

    46. Ван С, Хуан В, Лю Г, Цай В, Миллард РВ, Ван И, Чанг Дж, Пэн Т, Фан Г.К. Кардиомиоциты опосредуют антиангиогенез у крыс с диабетом 2 типа посредством экзосомального переноса миР-320 в эндотелиальные клетки. Дж Мол Селл Кардиол. 2014;74:139–150. [Бесплатная статья PMC] [PubMed] [Google Scholar]

    баз данных зон Бриллюэна

    баз данных зон Бриллюэна
    Кристаллографический сервер Бильбао Помощь

    Каждая k -векторную таблицу возглавляет соответствующий символ Германа-Могена пространственной группы, его номер IT A и символ арифметического кристаллического класса, к которому принадлежит пространственная группа [1]. Если имеется более одной таблицы для арифметического класса кристалла, то эти таблицы относятся к разным геометрическим условиям для параметров решетки, которые указаны после символа арифметического класса кристалла. Например, условия «√3a < √2c или √3a > √2c» различают две топологически разные зоны Бриллюэна для ромбоэдрических пространственных групп. Пространственные группы арифметического кристаллического класса также указаны в блоке заголовка. За ними следует символ группа обратного пространства тип ( например ‘( R3 ) * No. 146′ для арифметического кристаллического класса 3R в таблице k-векторов R3 вместе с условиями для констант решетки обратной решетки, если таковая имеется Из таблицы k -векторов есть ссылка на соответствующий рисунок зоны Бриллюэна.

    Каждая таблица состоит из двух основных частей. Первые два столбца под заголовком « k -векторное описание» относятся к описанию k -векторов, найденных в таблицах 3. 9 и 3.11 CDML [2]. Он состоит из меток k-векторов (столбец 1) и описания их параметров (столбец 2). (Обратите внимание, что CDML заменяет греческие обозначения точек и линий симметрии внутри зоны Бриллюэна символом, состоящим из двух латинских букв, например, GM вместо Γ, LD вместо Λ и т. д.) Диапазоны параметров не указаны. в КДМЛ. Помимо меток точек, линий и плоскостей CDML, которые сохранены в списках базы данных зон Бриллюэна, точкам и линиям, не перечисленным в CDML, было дано много новых имен. В таких случаях строки, эквивалентные, например, строке H или конечные точки линии H , а также точки, эквивалентные точке H , также могут обозначаться буквой H , но различаться индексами. Чтобы легко распознавать точки и линии, индексы точек всегда четные: H 0 , H 2 , H 4 ; строки всегда нечетные: H 1 , H 3 . Новые k -векторы эквивалентны векторам CDML и необходимы для включения однорукавное описание из k -векторных типов. Знак ‘~’ относится к эквивалентным k -векторам, см. e. г. строки S ∼ S 1 = [HL 0 ] в таблица и цифра пространственной группы P321 (№ 150), или строка P ∼ P 1 = [P 0 T] и точку T ∼ T 2 в таблицах и рисунках пространственной группы R3 (№ 146).

    Разное к -векторы с одной и той же меткой CDML всегда принадлежат одному и тому же k -типу вектора, i. е. они соответствуют одной и той же позиции Вайкоффа. k -векторы с разными метками CDML могут принадлежать как одному, так и разным типам k -векторов. Когда k -векторов с разными метками CDML принадлежат к одному и тому же k -типу, за описаниями соответствующих параметров следуют буквы «ex». Точки симметрии, линии симметрии или плоскости CDML, относящиеся к одной и той же позиции Вайкоффа, группируются в блок. В k -векторные таблицы, соседние блоки Wyckoff-position отличаются небольшой разницей в цвете фона. Например, k-векторы R3 распределяются по двум типам k -векторов:

    1. блок положения Вайкоффа 3 a , образованный специальными волновыми векторами k -векторной линии вдоль k -векторной линии вдоль оси третьего порядка,
    2. общий k -векторы соответствующие блоку общего положения 9 б Р3.
    Описание параметра одноплечевой области типа k -вектора показано в последней строке соответствующего блока позиции Вайкоффа.

    Описание параметра региона может быть описано вершинами этого региона в скобках [. . . ]. Один символ в скобках, е. г. [ P ], означает точку P . Две точки в скобках, е. г. [ A B ] означает строку от A 9от 0108 до В . Три точки в скобках, эл. г. [ ABC ] означает треугольную область плоскости с вершинами A , B и C . Четыре и более точек могут означать область плоскости или трехмерного тела, в зависимости от положения точек. Значение можно узнать, изучив соответствующий рисунок. Запятые между точками, е. г. [ A , B , C ] указать набор { A , B , C } из трех точек A , B и C .

    Коэффициенты волнового вектора CDML (столбец 2 таблиц k -векторов) всегда относятся к примитивному базису, независимо от того, относится ли обычное описание пространственной группы в IT A к центрированному или примитивному базису. По этой причине для пространственных групп с центрированными решетками коэффициенты волнового вектора относительно обычного базиса взаимности я. е. , двойственное относительно обычного центрированного базиса в прямом пространстве IT A, также перечислены в столбце под заголовком «Традиционный базис» k -векторных таблиц. Соотношения между «обычными» и «примитивными» коэффициентами волновых векторов сведены в следующую таблицу:


    Например, k -векторная точка линии LD R3 с примитивными коэффициентами (1/4, 1/4, 1/4) описывается как (0, 0, 3/4) с относительно базиса, двойственного к обычной шестиугольной установке Р3 . Для пространственных групп с примитивными решетками коэффициенты волновых векторов, относящиеся к примитивному базису, совпадают с коэффициентами, относящимися к базису, двойственному к обычному из IT A.

    Данные для схемы кристаллографической классификации волновых векторов перечислены под заголовком «Описание ITA» таблиц k -векторов. Столбцы «Позиции Вайкоффа» показывают данные «кратности», «буквы Вайкоффа» и «сайтовой симметрии» позиций Вайкоффа симморфной пространственной группы G 0 из IT A, который изоморфен группе обратного пространства (G) * . Кратность позиции Вайкоффа, деленная на число узлов решетки в условной элементарной ячейке IT A, равна числу плеч звезды k -вектора блока позиции Вайкоффа. Алфавитная последовательность позиций Вайкоффа определяет последовательность меток CDML. Таблицы начинаются с буквы Вайкоффа a для положения Вайкоффа с наивысшей симметрией сайта и продолжаются в алфавитном порядке до Общее положение (GP) достигнуто. «Ориентированные» символы точечных групп используются для обозначения групп узловой симметрии, которые совпадают с малыми когруппами волновых векторов (для «ориентированных» символов точечных групп см. IT A, раздел 2.2.12). ). Описание параметров положения Вайкоффа G 0 показано в последнем столбце таблиц волновых векторов. Алгебраические операторы используются для описания диапазонов параметров. Согласно ИТ Описание, строка DT из P321 соответствует положению Вайкоффа 2 g с группой узловой симметрии 3… Его описание параметра 0, 0, z : 0 < z < 1/2 указывает, что независимый отрезок прямой 0, 0, z ограничен специальными k -векторными точками Γ (z = 0) и A (z = 1/2), где z изменяется от 0 до 1/2. В некоторых случаях алгебраические выражения заменяются обозначением области параметра во избежание громоздкости записи. Описание параметров 9Флагштоки 0107 и крылья показаны под k -векторными таблицами.

    Из-за зависимости формы зоны Бриллюэна от соотношения параметров решетки могут быть вершины зоны Бриллюэна с переменной координатой. Если такая точка отображается и обозначается в таблицах и рисунках прописной буквой, то метка ее переменного коэффициента, используемая в описаниях диапазонов параметров, является той же буквой, но строчной. Таким образом, переменный коэффициент точки G 0 is g 0 , LD 0 is ld 0 и т. д. ( ср. таблица пространственной группы R3 ).

    Как уже указывалось, диапазоны параметров выбираются таким образом, чтобы каждая орбита положения Вайкоффа IT A, i. е. также каждая k -векторная орбита указана ровно один раз. В результате обычно получаются довольно сложные описания областей независимых параметров, входящих в Общее положение 9.Блок 0108. Например, утверждение, найденное в таблице пространственной группы P321 (№ 150):

    ГП у, в, ш 6 л 1 x, y, z: -x < y < x/2, 2x-1
    U x, -x, z : 0 < x < 1/3, 0 < z < 1/2 U
    U x, x/2, z : 0 < x < 2/3, 0 < z <1/2 U
    U x, 2x-1, z : 1/3 < x < 2/3, 0 < z < 1/2

    означает, что описание асимметричного узла разбито на тело и три плоскости. Граничная плоскость z = 1/2 тела включена, все остальные границы исключены. Вместе регионы содержат ровно одного представителя для каждой k-векторной орбиты Общего положения (ВП) группы обратного пространства.

    В нижней части веб-страницы с k -векторная таблица, можно найти вспомогательный инструмент, который позволяет получить полную характеристику любого волнового вектора обратного пространства (не ограничиваясь первой зоной Бриллюэна): заданные k -векторные коэффициенты относятся либо к примитиву (CDML) или на условном базисе программа сопоставляет k -вектору соответствующий тип симметрии волнового вектора, указывает его метку CDML, вычисляет малую когруппу и рукава k -векторных звезд. Рассмотрим, например, k -вектор с коэффициентами (0.4, 1.3, 0) пространственной группы P321 (№150) . Это вектор вне зоны Бриллюэна, и его коэффициенты не соответствуют ни одному из описаний параметров представителей k -векторов, перечисленных в таблице пространственной группы P321 (№ 150).

    No related posts.

    Добавить комментарий

    Ваш адрес email не будет опубликован. Обязательные поля помечены *