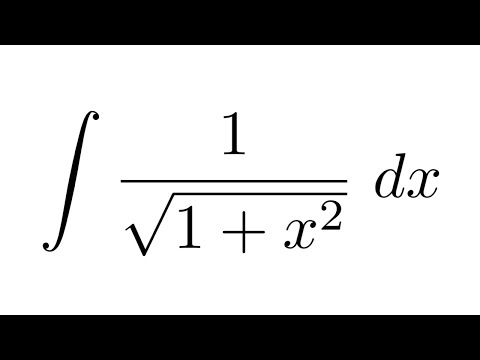Ручной кран Valtec VT.007.LN.04 1/2″НВ боковой угловой
В связи с ежедневными изменениями курса валют ЦБ и большой нагрузкой временно принимаем заказы от 30 000 р. У Вас есть перечень необходимых материалов? — присылайте на
почту [email protected] (расчет актуальных цен выполняем бесплатно).
Клапан ручной регулировки Valtec VT.007.LN 1/2″ВР х 1/2″НР с боковым угловым подключением
- Описание
- Документация
- Отзывы
- Доставка
Характеристики
| Товар | кран подключения |
| Страна | Италия |
| Высота, мм | 67 |
| Ширина, мм | |
| Бренд | Valtec |
| Серия |
vt. 007.ln
|
| Материал | Никелированная латунь |
| Длина, мм | 68 |
| Назначение | Для радиаторов отопления |
| Гарантия | 7 лет |
| Подводка | подающая |
Бренд (рус. )
|
Валтек |
| Тип подключения | |
| Рабочее давление, бар | 10 |
| Вид | ручной |
| Пропускная способность (kv), м³/ч | 2,15 |
| Наличие | Есть |
| Исполнение | компактное |
| Подключение к трубопроводу | g 1/2″ вр |
| Подключение к радиатору | G 1/2″ нр |
Упаковка, шт.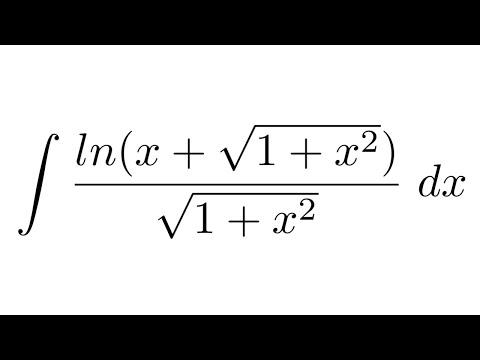
|
8 |
| макс. рабочая температура, °c | 110 |
Технический паспорт
Каталог продукции 2020
Сертификат соответствия
Экспертное заключение
Информационное письмо
+ Добавить комментарий
//»ProductVideo»
Бренд:
Валтек
Серия:
vt.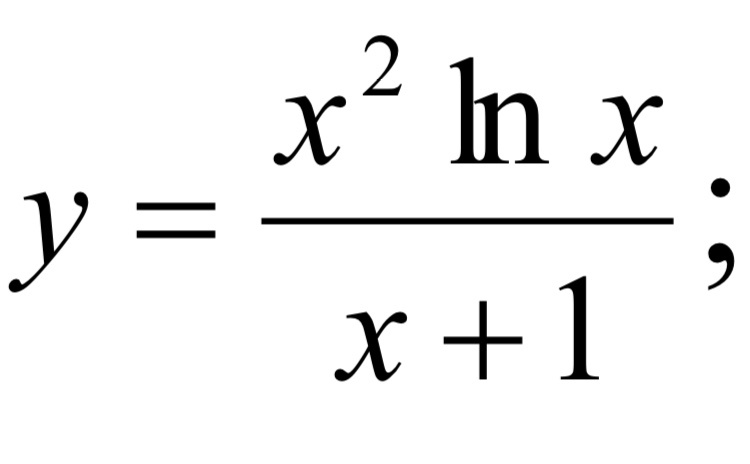
007.ln
Модель:
Страна:
Италия
Артикул:
VT.007.LN.04
реальный анализ — Как сравнить значения $\sqrt 2$ и $\ln(3).$
спросил
Изменено 1 год, 2 месяца назад
Просмотрено 772 раза
$\begingroup$
Как сравнить значения $\sqrt 2$ и $\ln(3)?$ Я знаю только $\ln(x) $\endgroup$ 2 $\begingroup$ «Аргумент» 1 Вычислить: $\sqrt{2}\приблизительно 1. Следовательно, $\frac{1}{2\sqrt{t}} \geq \frac{1}{t+1} > 0$ для всех $t>0$. Поскольку интегрирование положительных функций сохраняет неравенство, мы имеем $F(x) \geq G(x)$ для всех $x>0$. В частности, $F(2) \geq G(2)$, поэтому $\sqrt{2}\geq \ln(3)$. $\endgroup$
92=49/25<2$ И готово. $\endgroup$ 4 $\begingroup$ Весь фокус в том, чтобы посмотреть на $f(x) = \sqrt{x} — \ln(1+x)$. Обратите внимание, что для $x = 1$, $$1 — \ln(2) > 0$$ Это верно, поскольку $\ln(x)$ является возрастающей функцией и $1 < 2 < e$ влечет $$0 = \ln(1) < \ln(2) < \ln(e) = 1$$ Теперь посмотрим на производную $$f'(x) = \frac{1}{2\sqrt{x}} — \frac{1}{x+1}$$ Мы хотим показать, что $f'(x) \ge 0$ для $x > 1$, что означает, что $f(x)$ возрастает и, следовательно, должно быть положительным для $x > 1$ (поскольку оно уже положительно при $x=1$, как указано выше). Рассмотрим следующие эквивалентные неравенства (при $x > 1$): $$\begin{eqnarray}
\frac{1}{2\sqrt{x}} — \frac{1}{x+1} &\ge& 0\\
\frac{1}{2\sqrt{x}} &\ge& \frac{1}{x+1}\\
х + 1 &\ge& 2\sqrt{х}
\end{eqnarray}$$ Для последнего неравенства, $1+1 = 2 = 2\sqrt{1}$ и для $x > 1$, снова взятие производных показывает, что левая часть растет со скоростью $1$, а правая часть растет со скоростью скорость $\frac{2}{2\sqrt{x}} = \frac{1}{\sqrt{x}} < 1$, когда $x > 1$. Таким образом, последнее эквивалентное неравенство верно для $x > 1$, откуда следует, что $f'(x) \ge 0$ при $x > 1$, откуда следует, что $f(x)$ положительна при $x > 1$. В частности, $f(2) = \sqrt{2} — \ln(3) > 0$. Поэтому $\sqrt{2} > \ln(3)$. 9n$ и заменив $0$ на $n = \frac{1}{2}$. Тогда $\sqrt{2} — \ln 3$ равно: $$\left(1 + \frac{1}{2} — \frac{1}{8} + \frac{1}{16 } \cdots \справа) — \слева(\ln2
+ \frac{1}{2} — \frac{1}{8} + \frac{1}{24} \right)$$
$$=\frac{49}{48} — \ln 2$$ и приближает $\ln 2$ как $1 — \frac{1}{2} + \frac{1}{3} — \frac{ 1}{4} = \frac{7}{12}$, имеем: $$\frac{49}{48} — \frac{7}{12} = \frac{7}{16} $ $ Ошибка Лагранжа для $\sqrt{1+x}$: 93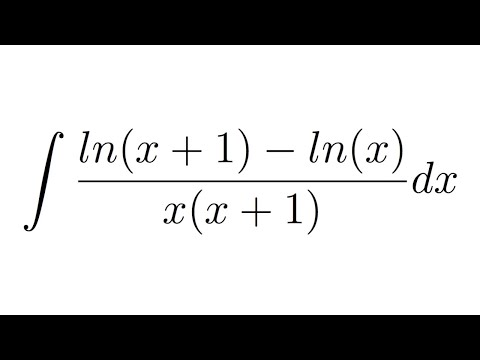
2 \\
&= 2 + \sqrt{2} \\
&> 2 + 1 \\
&= 3
\end{выравнивание*} 9х \frac{1}{t+1}\ dt $$
Теперь заметьте, что
$$ 2\sqrt{t} \leq t+1 $$
с равенством, достигаемым при $t=1$, так как $2\sqrt{t}$ вогнута вниз, а функция $t\mapsto t+1$ есть уравнение касательной к $2\sqrt{t}$ в точке $t =1$.
6 Решить для ? cos(x)=1/2 7 Найдите x sin(x)=-1/2 8 Преобразование градусов в радианы 225 9 Решить для ? cos(x)=(квадратный корень из 2)/2 10 Найдите x cos(x)=(квадратный корень из 3)/2 11 Найдите x sin(x)=(квадратный корень из 3)/2 92=9 14 Преобразование градусов в радианы 120 градусов 15 Преобразование градусов в радианы 180 16 Найдите точное значение желтовато-коричневый(195) 92-4 38 Найдите точное значение грех(255) 39 Оценить основание бревна 27 из 36 40 Преобразовать из радианов в градусы 2 шт. 