Log a b log a c: Формулы логарифмов, свойства — Таловская средняя школа

Содержание

Определение логарифма — презентация онлайн

Похожие презентации:

Элементы комбинаторики ( 9-11 классы)

Применение производной в науке и в жизни

Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»

Знакомство детей с математическими знаками и монетами

Тренажёр по математике «Собираем урожай». Счет в пределах 10

Методы обработки экспериментальных данных

Лекция 6. Корреляционный и регрессионный анализ

Решение задач обязательной части ОГЭ по геометрии

Дифференциальные уравнения

Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи

1. 1. Определение логарифма

Рассмотрим показательное уравнение
а х b, где а 0 и а 1, x R.
При b 0 это уравнение не имеет решений;
при b 0 показательное уравнение имеет
единственный
корень.
Этот
корень
называют логарифмом b по основанию а и
обозначают log a b .

2. Определение.

Логарифмом положительного числа b
по основанию а, где а 0 , a 1,
называется показатель степени, в
которую надо возвести основание а,
чтобы получить число b, т.

е.
а b; x log a b , a
х
log a b
b
Формулу a loga b b
(где b 0, а 0, а 1 ) называют
основным логарифмическим тождеством.

4. Примеры. Заполнить пропуски:

1.
log 2 8 …, т.к. 2 8, а 2, b 8
2.
1
log 3 …,
9
log 7 7 …,
3.
…
1
1
т.к. 3 , а 3, b
9
9
т.к. 7… 7, а 7, b 7
…
4.
log 4 1 …, т.к. 4 1, а 4, b 1;
5.
log … 16 4, т.к. … 16;
6.
1
1
5
log …
5, т.к. …
;
32
32
…
4

5. Примеры. Заполнить пропуски:

Примеры.
7.
8.
9.
10.
…;
log4 5
4
1
2
log 1 3
log … 4
5
2
…;
4
log1 3 …
13
Заполнить пропуски:
3
.
4

6. Примеры.

11. Вычислить log 64 128 ?
log 64 128 х,
по определению : 64 х 128
26 х 27
6х 7
7
x
6
7
Ответ : log 64 128 .
6

7. Примеры.

2 log3 5
12.

3
log3 5 2
3
5
13. Решить уравнение
log 3 1 х 2
3 1 х
2
х 8
2
1 25;

8. 2. Свойства логарифмов

При работе с логарифмами
применяются следующие их свойства,
вытекающие из свойств показательной
функции:
При любом а 0 а 1 и любых
положительных чисел х и у выполнены
равенства:

9. Свойства логарифмов:

1.
log a 1 0, т.к. а 1
2.
log a а 1, т.к. а а
0
1
3.
логарифм произведения равен сумме логарифмов:
4.
логарифм частного равен разности логарифмов:
log a ху log a х log a у
х
log a log a х log a у
у
5.
логарифм степени равен произведению
показателя степени на логарифм основания этой степени:
log a х р р log a х, где р R
Основные свойства логарифмов
широко применяются в ходе
преобразований выражений,
содержащих логарифмы. При этом
используются формулы перехода от
одного основания логарифма к
другому основанию:
log c b
, где b 0, a 0, a 1, c 1, c 0.

1. log a b
log c a
1
2. log a b
log b a
3. log1 a b log a b
1
4. log a p b log a b,
p
.
a 0, a 1, b 0, p 0.

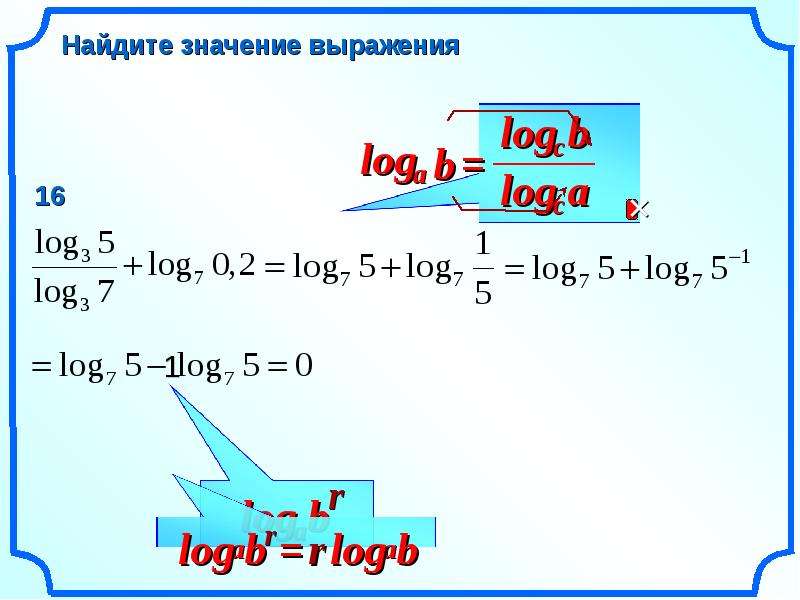
12. Примеры:

14. log 12 2 log 12 72
15
15. log 2 15 log 2
16
5
log
16.
13 169
17. log 8 12 log 8 15 log 8 20
18.
log 3 8
log 3 16

13. Примеры:

14. log12 2 log12 72 log12 2 72 log12 144 2
15
15
log 2
log 2 16 4
15. log 2 15 log 2
16
15 16
16. log13
17.log
5
1
5
2
5
2
2
169 log13 169 log13 13 log13 13
5
5
8 x 16
4
12 20
3x
4
log 8 16 2 2
8 12 log 8 15 log 8 20 log 8
3
15
x 4 3
3
log
8
log
2
3 log 3 2 3
18.
3
3
4
log 3 16 log 3 2
4 log 3 2 4

14. 3. Логарифмирование и потенцирование

Действие нахождения логарифма числа
называют логарифмированием.
Нахождение положительного числа по его
логарифму называют потенцированием.

15. Примеры.

19. Прологарифмировать выражения:
а) х 2а b; б) х
3
ab
3
;
в)
х
а
b
3
c
Ответ. а) log х log 2 3 log а log b;
1
б) log х log a log b 3 log c ;
2
1
1
в) log х log a log b.
2
6
20. Пропотенцировать выражения:
1
1
а) log х log a log b;
3
2
1
3
2
б) log х log a log b log с.
4
4
3
Ответ.
а) х
3
а
; б) х
b
4
3
ab
c
3
2
.

17. 4. Десятичные и натуральные логарифмы.

Десятичным логарифмом числа
называют логарифм этого числа по
основанию 10 и пишут:
log 10 b lg b
Натуральным логарифмом числа
называют логарифм этого числа по
основанию е, где e 2,7182818… 2,7
– иррациональное число, и пишут:
log e b ln b

18. Вычислите самостоятельно:

à) log 2 16 …;
á) log 2 64 …;
â) log 2 2 …;
ã) log 2 1 …;
1
ä) log 2 …;
2
log3 18
æ) 3
.

..;
1
å) log 2 ….;
8
5 log3 2
ç) 3
….

19. Упростить выражения, пользуясь основным логарифмическим тождеством:

1
à)
2
6 log 1 2
á) 0,3
â) 7
ã) 8
2
2 log0 , 3 6
1
log7 9
2
log2 5
ä) 9 log3 12
å) 16
log4 7
æ) 0,125
log0 , 5 7

20. Упростить выражения, пользуясь основным логарифмическим тождеством:

1
à)
2
6 log1 2
2
1
2
log1 2
2
6
26 64;

21. Упростить выражения, пользуясь основным логарифмическим тождеством:

1
à)
2
6 log 1 2
á) 0,3
2
1
2
2 log0 , 3 6
log 1 2
2
6
26 64;
log0 , 3 6 2
0,3
6 2 36;

22. Упростить выражения, пользуясь основным логарифмическим тождеством:

1
à)
2
6 log 1 2
á) 0,3
â) 7
2
1
2
2 log0 , 3 6
1
log7 9
2
log 1 2
26 64;
log0 , 3 6 2
0,3
7
2
6
1
log7 9 2
1
2
6 2 36;
9 3;

23.

Найти число х по определению логарифма: log 6 x 3 log 2 5 x 3
6 x
2 5 x
x 216
x 3
3
3
log 1 0,5 x 1
6
1
1
0,5 x
6
6 0,5 x
x 5,5

English Русский Правила

2.1.6 Логарифмические уравнения

Видеоурок 1: Логарифмические уравнения

Видеоурок 2: Логарифмические уравнения с заменой переменных

Лекция: Логарифмические уравнения

Если Вам попалось выражение, функция или уравнение, содержащее логарифмы, то для их упрощения или решения необходимо четко знать и использовать определение и свойства логарифмов.

Следует помнить, что логарифм любого положительного числа b по основанию положительного числа а, не равного единице, называется некоторый показатель степени с, в который возводят число а, для получения b.

log_ab = c <=> a^c = b.

Также следует помнить основное тождество:

Свойства логарифмов

1. Если имеется логарифм произведения двух чисел больших нуля, то данный логарифм можно записать в виде суммы:

Данное свойство вытекает из основного свойства степени — при умножении степеней их показатели складываются.

2. Логарифм частного двух чисел равен разности двух логарифмов:

Данное свойство было получено из свойства деления степеней — при делении степеней, показатели вычитаются.

3. Если некоторое число в степени находится под знаком логарифма, то показатель степени можно вынести вперед, тем самым, умножив логарифм на показатель:

Данное свойство вытекает из одного из основных свойств степенной функции — при возведении степени в степень показатели степеней перемножаются.

4. Если число и основание логарифма совпадает, то значение такого логарифма равно единице:

5. Логарифм по любому основанию равен нулю, если число равно единице:

6. При любом логарифме можно перейти от одного основания к другому. Для этого необходимо просто воспользоваться формулами:

Основная ошибка, которую допускают большинство — использование некоторого логарифма суммы. Запомните, не существует данной формулы: log_a(b±c) ≠ log_ab ± log_ac.

Свойства логарифмической функции

Для любой логарифмической функции с положительным основанием, не равным единице, справедливы следующие свойства:

Областью определения данной функции являются все положительные числа.
Значением логарифмической функции является множество действительных чисел.
Для основания степени, большего единицы, функция возрастает на всем промежутке рассмотрения.
Если основание находится в пределах от нуля до единицы, то функция убывает на всем рассматриваемом промежутке.
Данная функция не является парной или непарной.
Если переменная равна единице, то функция превращается в ноль, то есть точка, в которой график функции пересекает ось ОХ — это (1;0).

Так как логарифмические функции являются обратными к показательны, то и решения логарифмических уравнений сводится по аналогии к решению показательных уравнений.

Существует три основных вида простейших логарифмических уравнений. Ниже представлены способы их решения:

1.6.3 Построение алгоритмов и практические вычисления

3.3 Классификация органических веществ. Номенклатура органических веществ (тривиальная и международная)

2.2 Характерные химические свойства и получение простых веществ — металлов: щелочных, щелочноземельных, алюминия; переходных элементов (меди, цинка, хрома, железа)

1.2.4 Общая характеристика неметаллов IVA – VIIA групп в связи с их положением в Периодической системе химических элементов Д.

И.Менделеева и особенностями строения их атомов

6.5 Правописание корней

Вконтакте
Сайт

2/(ab))] равно a. 0 б. 1 в. 2 д. abc

Курс
- NCERT
  - Класс 12
  - Класс 11
  - Класс 10
  - Класс 9
  - Класс 8
  - Класс 7
  - Класс 6
- IIT JEE

Экзамен
- JEE MAINS
- JEE ADVANCED
- X BOARDS
- XII BOARDS
- NEET
  - Neet Предыдущий год (по годам)
  - Физика Предыдущий год
  - Химия Предыдущий год
  - Биология Предыдущий год
  - Нет Все образцы работ
  - Образцы работ Биология
  - Образцы работ Физика
  - Образцы работ Химия

Скачать PDF-файлы
- Класс 12
- Класс 11
- Класс 10
- Класс 9
- Класс 8
- Класс 7
- Класс 6

Экзаменационный уголок

Онлайн-класс

Викторина

Задать вопрос в Whatsapp

Поиск Сомнение

900 03 Английский словарь

Toppers Talk

Блог

О нас

Карьера

Скачать

Получить приложение

Вопрос

Обновлено: 26/04/2023

RS AGGARWAL-LOGARITHMS -Все вопросы 9(c-a)=

6626474

02:53

Докажите loga2bc+logb2ca+logc2ab=0. Докажите, что 01:12

Если logxb-c=logyc-a =logza−b, затем докажите, что
xb2+bc+c2.yc2+ca+a2.za2+ab+b2=1

213713384

10:57

Докажите, что
log(a2bc)+log(b2ca) +log(c2ab)=0

234802104

01:13

log(a2bc)+log(b2ca)+log(c2ab)=0என நிறுவுக.

473094968

01:30

(log(a3bc)+log(b3ac)+log(c3ab)) равно:

510425875

02:08 901 31

logbca2+logacb2+logabc2 का मान क्या होगा ?

643168193