Log формулы: Формулы логарифмов, свойства

Свойства и формулы логарифмов

1. Что такое логарифмы?
2. Свойства логарифма
3. Формулы логарифма
4. Уравнения с логарифмами

 

Логарифмы – важная тема математического анализа, которая изучается как в старшей школе, так и в курсе высшей математики. Знания по части логарифмов являются в какой-то мере фундаментальными для изучающих математику. Дальше в тексте вы найдете всю полезную информацию об изучении логарифмов на школьном этапе.

 

Что такое логарифмы?

Понятием «логарифм» математики пользуются с XVII века. Его изобрел и внедрил в науку шотландский ученый Дж. Напье, который находил примеры логарифмов в числовых закономерностях природы и искусства.

Логарифм являет собой математическую операцию, которая определяет, сколько раз некое число, называемое основанием, нужно умножить само на себя, чтобы получить другое число. Логарифмы связывают арифметическую и геометрическую прогрессии.

Они помогают упрощать громадные вычисления и особо часто используются в навигации, геодезии, инженерии, астрономии. 

Как записываются логарифмы? Возьмем показательное уравнение. Большой лист бумаги сложили в 32 слоя. В данном случае логарифм – это количество действий по складыванию бумаги, после которых имеем результат в 32 слоя. То есть основание 2, умножаемое на себя определенное количество раз, дает число 32. Сколько умножений необходимо? В математической записи это выглядит так:  или  Поскольку 2*2*2*2*2=32:  Лист бумаги нужно сложить пополам 5 раз, чтобы получить 32 слоя.

Выходит  

До появления механических и электронных калькуляторов логарифмы считались быстрым методом вычислений. Ведь они отображают интенсивность звуков, твердость минералов и плотность кислот, расстояние между небесными телами, частотность землетрясений и прочее. 

Читайте также: Интерактивная онлайн доска — ресурс, который поможет при организации онлайн урока

 

Свойства логарифма

Свойства логарифмов связаны с упрощением логарифмических выражений. Они очень похожи на свойства экспонент и свойства показателей степени. Рассмотрим подробнее 7 основных особенностей логарифмов:

1. Если число, логарифм которого нужно определить, равно основанию логарифма, то в итоге логарифм равен 1: 
2. Логарифм единицы независимо от основания равен нулю: 
3. Если число, логарифм которого нужно найти, равно основанию логарифма и имеет степень х, то значение логарифма будет равно числу степени: 
4. Логарифм произведения являет собой сумму логарифмов каждого из умножителей. Здесь, как и с показателями степени, чтобы умножить два числа с одинаковым основанием, нужно складывать экспоненты. При этом количество умножителей не имеет значения.
5. Свойство логарифма частного также очень похоже на свойство показателей степени. Чтобы найти логарифм частного, нужно найти разницу между логарифмами делимого и делителя. Это выглядит так:  
6. Особенности логарифма степени немного отличаются от показателя степени. В случае с логарифмом степень становится умножителем.
7. Если основание логарифма определенного числа имеет степень, то она становится знаменателем дроби, в которой числителем выступает единица. В итоге эту дробь нужно умножить на значение логарифма числа при условии, что степень не равна нулю. Это выглядит так:  

Формулы логарифма

Математические особенности логарифмов описываются с помощью формул:

Ниже представлено, как эти формулы можно применить для преобразования логарифмических выражений и нахождения их значения. Для быстрых вычислений подойдет калькулятор логарифмов онлайн.

В профессиональном отношении логарифмы нужны для проведения банковских и различных финансовых вычислений, прогнозирования природных и демографических явлений, определения производственных затрат, проведения лабораторных измерений, физических, химических и астрономических исследований. Хорошо, если бы в школе ребенок получил крепкий математический фундамент.

Однако всегда можно обратиться к опытному репетитору, который адаптирует учебный материал под вашу цель обучения. Такого педагога можно легко найти на сайте BUKI. Вы можете сразу выбрать проверенного и квалифицированного преподавателя.

Читайте также: Лучшие университеты Центральной Азии

Уравнения с логарифмами

Главный способ решения уравнений – применение определения логарифма. 

 

Пример 1

 

Пример 2

 

 

Пример 3

 

Читайте также: Математика онлайн – как организовать занятия по точным наукам через Skype

 

Что такое десятичный логарифм? Логарифм

Степень отдельно взятого числа называется математическим термином, придуманным несколько столетий назад. В геометрии и алгебре встречается два варианта — десятичные и натуральные логарифмы. Они рассчитываются разными формулами, при этом уравнения, отличающиеся написанием, всегда равны друг другу. Это тождество характеризует свойства, которые относятся к полезному потенциалу функции.

Особенности и важные признаки

На данный момент различают десять известных математических качеств. Самыми распространенными и востребованными из них являются:

• Подкоренной log, разделенный на величину корня, всегда такой же, как и десятичный логарифм √.
• Произведение log всегда равно сумме производителя.
• Lg = величине степени, перемноженной на число, которое в нее возводится.
• Если от log делимого отнять делитель, получится lg частного.

Кроме того, есть уравнение, основанное на главном тождестве (считается ключевым), переход к обновленному основанию и несколько второстепенных формул.

Вычисление десятичного логарифма — довольно специфическая задача, поэтому к интегрированию свойств в решение необходимо подходить осторожно и регулярно проверять свои действия и последовательность. Нельзя забывать и о таблицах, с которыми нужно постоянно сверяться, и руководствоваться только найденными там данными.

Разновидности математического термина

Главные отличия математического числа «спрятаны» в основании (a). Если оно имеет показатель 10, то это десятичный log. В обратном случае «a» преобразуется в «у» и обладает трансцендентными и иррациональными признаками. Также стоит отметить, что натуральная величина рассчитывается специальным уравнением, где доказательством становится теория, изучаемая за пределами школьной программы старших классов.

Логарифмы десятичного типа получили широкое применение при вычислении сложных формул. Составлены целые таблицы, облегчающие расчеты и наглядно показывающие процесс решения задачи. При этом перед непосредственным переходом к делу нужно возвести log в К тому же в каждом магазине школьных принадлежностей можно найти специальную линейку с нанесенной шкалой, помогающей решить уравнение любой сложности.

Десятичный логарифм числа называется Бригговым, или цифрой Эйлера, в честь исследователя, который первым опубликовал величину и обнаружил противопоставление двух определений.

Два вида формулы

Все типы и разновидности задач на вычисление ответа, имеющие в условии термин log, обладают отдельным названием и строгим математическим устройством. Показательное уравнение является практически точной копией логарифмических расчетов, если смотреть со стороны правильности решения. Просто первый вариант включает в себя специализированное число, помогающее быстрее разобраться в условии, а второй заменяет log на обыкновенную степень. При этом вычисления с применением последней формулы должны включать в себя переменное значение.

Разница и терминология

Оба главных показателя обладают собственными особенностями, отличающими числа друг от друга:

• Десятичный логарифм. Важная деталь числа — обязательное наличие основания. Стандартный вариант величины равен 10. Маркируется последовательностью — log x или lg x.
• Натуральный. Если его основанием является знак «e», представляющий собой константу, идентичную строго рассчитанному уравнению, где n стремительно движется к бесконечности, то приблизительный размер числа в цифровом эквиваленте составляет 2.
  72. Официальная маркировка, принятая как в школьных, так и в более сложных профессиональных формулах, — ln x.
• Разные. Кроме основных логарифмов встречаются шестнадцатиричные и двоичные виды (основание 16 и 2 соответственно). Есть еще сложнейший вариант с базовым показателем 64, подпадающий под систематизированное управление адаптивного типа, с геометрической точностью производящее расчет итогового результата.

Терминология включает в себя следующие величины, входящие в алгебраическую задачу:

• значение;
• аргумент;
• основание.

Вычисление log числа

Есть три способа быстро и в устной форме сделать все необходимые расчеты по нахождению интересующего результата с обязательным правильным итогом решения. Изначально приближаем десятичный логарифм к своему порядку (научная запись числа в степени). Каждую положительную величину можно задать уравнением, где она будет равен мантиссе (цифра от 1 до 9), перемноженной на десятку в n-й степени.

Такой вариант подсчета создан на основе двух математических фактов:

• произведение и сумма log всегда имеют одинаковый показатель;
• логарифм, взятый из числа от одного до десяти, не может превышать величину в 1 пункт.

1. Если ошибка в вычислении все-таки происходит, то она никогда не бывает меньше одного в сторону вычитания.
2. Точность повышается, если учесть, что lg с основанием три имеет итоговый результат — пять десятых от единицы. Поэтому любое математическое значение больше 3 автоматически добавляет к ответу один пункт.
3. Практически идеальная точность достигается, если под рукой есть специализированная таблица, которую можно легко применять в своих оценочных действиях. С ее помощью можно выяснить, чему равен десятичный логарифм до десятых процентов от оригинального числа.

История вещественного log

Шестнадцатый век остро испытывал потребности в более сложных исчислениях, чем было известно науке того времени. Особенно это касалось деления и умножения многозначных цифр с большой последовательностью, в том числе дробей.

В конце второй половины эпохи сразу несколько умов пришли к выводу о сложении чисел с помощью таблицы, которая сопоставляла две и геометрическую. При этом все базовые расчеты должны были упираться в последнюю величину. Таким же образом ученые интегрировали и вычитание.

Первое упоминание об lg состоялось в 1614 году. Это сделал любитель-математик по фамилии Непер. Стоит отметить, что, несмотря на огромную популяризацию полученных результатов, в формуле была сделана ошибка из-за незнаний некоторых определений, появившихся позже. Она начиналась с шестого знака показателя. Наиболее близки к пониманию логарифма были братья Бернулли, а дебютное узаконивание произошло в восемнадцатом столетии Эйлером. Он же и распространил функцию в область образования.

История комплексного log

Дебютные попытки интегрировать lg в широкие массы делали на заре 18-го века Бернулли и Лейбниц. Но целостных теоретических выкладок они так и не сумели составить. По этому поводу велась целая дискуссия, но точного определения числу не присваивали.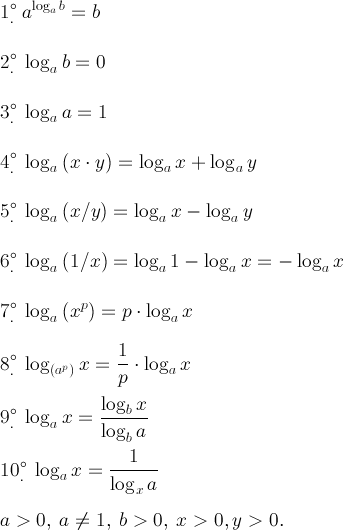 Позже диалог возобновился, но уже между Эйлером и Даламбером.

Последний был в принципе согласен со множеством фактов, предлагаемых основателем величины, но считал, что положительный и отрицательный показатели должны быть равны. В середине столетия формула была продемонстрирована в качестве окончательного варианта. Кроме того, Эйлером была опубликована производная десятичного логарифма и составлены первые графики.

Таблицы

Свойства числа указывают на то, что многозначные цифры можно не перемножать, а найти их log и сложить посредством специализированных таблиц.

Особенно ценным этот показатель стал для астрономов, которые вынуждены работать с большим набором последовательностей. В советское время десятичный логарифм искали в сборнике Брадиса, выпущенного в 1921 году. Позже, в 1971 году, появилось издание Веги.

Итак, перед нами степени двойки. Если взять число из нижней строчки, то можно легко найти степень, в которую придется возвести двойку, чтобы получилось это число. Например, чтобы получить 16, надо два возвести в четвертую степень. А чтобы получить 64, надо два возвести в шестую степень. Это видно из таблицы.

А теперь — собственно, определение логарифма:

Логарифм по основанию a от аргумента x — это степень, в которую надо возвести число a , чтобы получить число x .

Обозначение: log a x = b , где a — основание, x — аргумент, b — собственно, чему равен логарифм.

Например, 2 3 = 8 ⇒ log 2 8 = 3 (логарифм по основанию 2 от числа 8 равен трем, поскольку 2 3 = 8). С тем же успехом log 2 64 = 6, поскольку 2 6 = 64.

Операцию нахождения логарифма числа по заданному основанию называют логарифмированием. Итак, дополним нашу таблицу новой строкой:

2 1	2 2	2 3	2 4	2 5	2 6
2	4	8	16	32	64
log 2 2 = 1	log 2 4 = 2	log 2 8 = 3	log 2 16 = 4	log 2 32 = 5	log 2 64 = 6

К сожалению, далеко не все логарифмы считаются так легко. Например, попробуйте найти log 2 5. Числа 5 нет в таблице, но логика подсказывает, что логарифм будет лежать где-то на отрезке . Потому что 2 2

Такие числа называются иррациональными: цифры после запятой можно писать до бесконечности, и они никогда не повторяются. Если логарифм получается иррациональным, его лучше так и оставить: log 2 5, log 3 8, log 5 100.

Важно понимать, что логарифм — это выражение с двумя переменными (основание и аргумент). Многие на первых порах путают, где находится основание, а где — аргумент. Чтобы избежать досадных недоразумений, просто взгляните на картинку:

Перед нами — не что иное как определение логарифма. Вспомните: логарифм — это степень , в которую надо возвести основание, чтобы получить аргумент. Именно основание возводится в степень — на картинке оно выделено красным. Получается, что основание всегда находится внизу! Это замечательное правило я рассказываю своим ученикам на первом же занятии — и никакой путаницы не возникает.

С определением разобрались — осталось научиться считать логарифмы, т.е. избавляться от знака «log». Для начала отметим, что из определения следует два важных факта:

1. Аргумент и основание всегда должны быть больше нуля. Это следует из определения степени рациональным показателем, к которому сводится определение логарифма.
2. Основание должно быть отличным от единицы, поскольку единица в любой степени все равно остается единицей. Из-за этого вопрос «в какую степень надо возвести единицу, чтобы получить двойку» лишен смысла. Нет такой степени!

Такие ограничения называются областью допустимых значений (ОДЗ). Получается, что ОДЗ логарифма выглядит так: log a x = b ⇒ x > 0, a > 0, a ≠ 1.

Заметьте, что никаких ограничений на число b (значение логарифма) не накладывается. Например, логарифм вполне может быть отрицательным: log 2 0,5 = −1, т.к. 0,5 = 2 −1 .

Впрочем, сейчас мы рассматриваем лишь числовые выражения, где знать ОДЗ логарифма не требуется. Все ограничения уже учтены составителями задач. Но когда пойдут логарифмические уравнения и неравенства, требования ОДЗ станут обязательными. Ведь в основании и аргументе могут стоять весьма неслабые конструкции, которые совсем необязательно соответствуют приведенным выше ограничениям.

Теперь рассмотрим общую схему вычисления логарифмов. Она состоит из трех шагов:

1. Представить основание a и аргумент x в виде степени с минимально возможным основанием, большим единицы. Попутно лучше избавиться от десятичных дробей;
2. Решить относительно переменной b уравнение: x = a b ;
3. Полученное число b будет ответом.

Вот и все! Если логарифм окажется иррациональным, это будет видно уже на первом шаге. Требование, чтобы основание было больше единицы, весьма актуально: это снижает вероятность ошибки и значительно упрощает выкладки. Аналогично с десятичными дробями: если сразу перевести их в обычные, ошибок будет в разы меньше.

Посмотрим, как работает эта схема на конкретных примерах:

Задача. Вычислите логарифм: log 5 25

1. Представим основание и аргумент как степень пятерки: 5 = 5 1 ; 25 = 5 2 ;
2. Составим и решим уравнение:
   log 5 25 = b ⇒ (5 1) b = 5 2 ⇒ 5 b = 5 2 ⇒ b = 2;
3. Получили ответ: 2.

Задача. Вычислите логарифм:

Задача. Вычислите логарифм: log 4 64

1. Представим основание и аргумент как степень двойки: 4 = 2 2 ; 64 = 2 6 ;
2. Составим и решим уравнение:
   log 4 64 = b ⇒ (2 2) b = 2 6 ⇒ 2 2b = 2 6 ⇒ 2b = 6 ⇒ b = 3;
3. Получили ответ: 3.

Задача. Вычислите логарифм: log 16 1

1. Представим основание и аргумент как степень двойки: 16 = 2 4 ; 1 = 2 0 ;
2. Составим и решим уравнение:
   log 16 1 = b ⇒ (2 4) b = 2 0 ⇒ 2 4b = 2 0 ⇒ 4b = 0 ⇒ b = 0;
3. Получили ответ: 0.

Задача. Вычислите логарифм: log 7 14

1. Представим основание и аргумент как степень семерки: 7 = 7 1 ; 14 в виде степени семерки не представляется, поскольку 7 1
2. Из предыдущего пункта следует, что логарифм не считается;
3. Ответ — без изменений: log 7 14.

Небольшое замечание к последнему примеру. Как убедиться, что число не является точной степенью другого числа? Очень просто — достаточно разложить его на простые множители. И если такие множители нельзя собрать в степени с одинаковыми показателями, то и исходное число не является точной степенью.

Задача. Выясните, являются ли точными степенями числа: 8; 48; 81; 35; 14.

8 = 2 · 2 · 2 = 2 3 — точная степень, т.к. множитель всего один;
48 = 6 · 8 = 3 · 2 · 2 · 2 · 2 = 3 · 2 4 — не является точной степенью, поскольку есть два множителя: 3 и 2;
81 = 9 · 9 = 3 · 3 · 3 · 3 = 3 4 — точная степень;
35 = 7 · 5 — снова не является точной степенью;
14 = 7 · 2 — опять не точная степень;

Заметим также, что сами простые числа всегда являются точными степенями самих себя.

Десятичный логарифм

Некоторые логарифмы встречаются настолько часто, что имеют специальное название и обозначение.

Десятичный логарифм от аргумента x — это логарифм по основанию 10, т. е. степень, в которую надо возвести число 10, чтобы получить число x . Обозначение: lg x .

Например, lg 10 = 1; lg 100 = 2; lg 1000 = 3 — и т.д.

Отныне, когда в учебнике встречается фраза типа «Найдите lg 0,01», знайте: это не опечатка. Это десятичный логарифм. Впрочем, если вам непривычно такое обозначение, его всегда можно переписать:
lg x = log 10 x

Все, что верно для обычных логарифмов, верно и для десятичных.

Натуральный логарифм

Существует еще один логарифм, который имеет собственное обозначение. В некотором смысле, он даже более важен, чем десятичный. Речь идет о натуральном логарифме.

Натуральный логарифм от аргумента x — это логарифм по основанию e , т.е. степень, в которую надо возвести число e , чтобы получить число x . Обозначение: ln x .

Многие спросят: что еще за число e ? Это иррациональное число, его точное значение найти и записать невозможно. Приведу лишь первые его цифры:
e = 2,718281828459. ..

Не будем углубляться, что это за число и зачем нужно. Просто помните, что e — основание натурального логарифма:
ln x = log e x

Таким образом, ln e = 1; ln e 2 = 2; ln e 16 = 16 — и т.д. С другой стороны, ln 2 — иррациональное число. Вообще, натуральный логарифм любого рационального числа иррационален. Кроме, разумеется, единицы: ln 1 = 0.

Для натуральных логарифмов справедливы все правила, которые верны для обычных логарифмов.

Приведены основные свойства логарифма, график логарифма, область определения, множество значений, основные формулы, возрастание и убывание. Рассмотрено нахождение производной логарифма. А также интеграл, разложение в степенной ряд и представление посредством комплексных чисел.

Содержание

Область определения, множество значений, возрастание, убывание

Логарифм является монотонной функцией, поэтому экстремумов не имеет. Основные свойства логарифма представлены в таблице.

Область определения	0	0
Область значений	— ∞	— ∞
Монотонность	монотонно возрастает	монотонно убывает
Нули, y = 0	x = 1	x = 1
Точки пересечения с осью ординат, x = 0	нет	нет
	+ ∞	— ∞
	— ∞	+ ∞

Частные значения

Логарифм по основанию 10 называется десятичным логарифмом и обозначается так:

Логарифм по основанию e называется натуральным логарифмом :

Основные формулы логарифмов

Свойства логарифма, вытекающие из определения обратной функции:

Основное свойство логарифмов и его следствия

Формула замены основания

Логарифмирование — это математическая операция взятия логарифма. При логарифмировании, произведения сомножителей преобразуются в суммы членов.
Потенцирование — это математическая операция обратная логарифмированию. При потенцировании заданное основание возводится в степень выражения, над которым выполняется потенцирование. При этом суммы членов преобразуются в произведения сомножителей.

Доказательство основных формул логарифмов

Формулы, связанные с логарифмами вытекают из формул для показательных функций и из определения обратной функции.

Рассмотрим свойство показательной функции
.
Тогда
.
Применим свойство показательной функции
:
.

Докажем формулу замены основания.
;
.
Полагая c = b , имеем:

Обратная функция

Обратной для логарифма по основанию a является показательная функция с показателем степени a .

Если , то

Если , то

Производная логарифма

Производная логарифма от модуля x :
.
Производная n-го порядка:
.
Вывод формул > > >

Для нахождения производной логарифма, его нужно привести к основанию e .
;
.

Интеграл

Интеграл от логарифма вычисляется интегрированием по частям : .
Итак,

Выражения через комплексные числа

Рассмотрим функцию комплексного числа z :
.
Выразим комплексное число z через модуль r и аргумент φ :
.
Тогда, используя свойства логарифма, имеем:
.
Или

Однако, аргумент φ определен не однозначно. Если положить
, где n — целое,
то будет одним и тем же числом при различных n .

Поэтому логарифм, как функция от комплексного переменного, является не однозначной функцией.

Разложение в степенной ряд

При имеет место разложение:

Использованная литература:
И.Н. Бронштейн, К.А. Семендяев, Справочник по математике для инженеров и учащихся втузов, «Лань», 2009.

См. также:

Формула логарифма с примерами решения

Формула логарифма

Логарифм действительно представляет собой экспоненту или степень, которую необходимо применить к основанию, чтобы получить определенное число. Логарифмы представлены математически, так как m действительно является логарифмом n по основанию b, если b ^m = n, что альтернативно может быть записано как m = log _b n. Например, 10 ³  = 1000, тогда 3 = log ₁₀ 1000

Мы также знаем, что 10 ³ = 1000, следовательно, 3 = log ₁₀ 1000. Обычные логарифмы или логарифмы Бриггса иногда называют обычным логарифмом и логарифмом Бриггса и просто представляют как log n.

Правила логарифмирования

Существует семь принципов логарифмирования, которые важны для расширения, сокращения и решения логарифмических уравнений. Ниже приведены семь правил логарифмов:

1. Правило произведения

Log _b (P×Q) = log _b p + log _b Q

Логарифм произведения равен сумме логарифмов компонентов.

2. Правило частного .

Формула основного логарифма

Некоторые из различных формул основного логарифма приведены ниже:

Примеры

Пример 1: a) 5 ³ = 125 B) 3 ^-3 = 1 / 27.

Решение:

Использование определения логарифма,

B ^x = a ⇒ LOGB _B A = X

Использование. Это,

A) 5 ³ = 125 ⇒ log ₅ 125 = 3

B) 3 ^-3 = 1/27 ⇒ log ₃ 1/27 = -3

. а) лог ₅ 125 = 3; б) log ₃  1/27 = -3.

Пример 2: 5 log x + log y – 8 log z.

Решение:

Найти: Сжатую форму данного выражения в виде единичного логарифма, используя формулы логарифмирования.

5 log x + log y – 8 log z

= (5 log x – 8 log z) + log y (термины перегруппированы)

= (log x ⁵ – log z ⁸ ) + log y (∵ a log x = log x ^a )

= log (x ⁵ /z ⁸ ) + log y (∵ log x – log y = log (x/y)

= log ( х ⁵ г/з ⁸ ) (∵ log x + log y = log (xy)

Ответ: 5 log x + log y – 8 log z = log (x ⁵ y/z ⁸ ).

Пример 3 : Найдите целочисленное значение log3 (1/9), используя логарифмические формулы

Решение:

Log ₃ (1/9) = log ₃ 1 – log ₃  9 (∵07 log 90 b (x / y) = log _b x – log _b y)

= 0 – log ₃  32 (∵ log _b  1 = 0)

= – 2 log ₃  3 (∵ log _b ax = x log _b  a)

= -2 (1) (∵ log _b  b = 1)

200004 Ответ: log ₃  (1/9) = -2.

Сводка логарифмов: свойства, формулы, законы

Что такое $\,\log_b x\,$?	Логарифмы являются показателями! Число  ‘$\,\log_b x\,$’  – это степень (9{-1} = \фракция 13\,$
Допустимые базы для журналов	В выражении  ‘$\,\log_b x\,$’ число $\,b\,$ называется основанием 90 194 логарифма 90 195 . Число $\,b\,$ должно быть положительным и не равно $\,1\,$:   $\,b > 0\,$ и $\,b\ne 1\,$	допустимых оснований для логарифмов: $b > 0\,$ $\,b\ne 1$
Два специальных логарифма	Функция  ‘$\,\log_{10}\,$’ (логарифмическая база $\,10\,$) называется десятичным логарифмом . Часто используется сокращение просто  ‘$\,\log\,$’  (без указания основания). Функция  ‘$\,\log_{\text{e}}\,$’ (логарифмическая база $\,\text{e}\,$) называется натуральным логарифмом . Часто обозначается аббревиатурой  ‘$\,\ln$’  (без указания основания). Внимание! В некоторых дисциплинах для обозначения натурального логарифма используется  ‘$\,\log\,$’ . Всегда проверяйте запись.	$\log x$ общий логарифм $\,x$ $\ln x$ натуральный логарифм $\,x$
Допустимые входные данные для журналов	В выражении  ‘$\,\log_b x\,$’ число $\,x\,$ (входное) должно быть положительным: $\,x > 0\,$	допустимые входы для логарифмов: $х > 0$
Просмотр функции журналов	Число «$\log_b x\,$» является выходом функции «$\,\log_b\,$», когда входом является «$\,x\,$». Область определения функции $\,\log_b\,$ — это множество всех положительных действительных чисел: $\,\text{dom}(\log_b) = (0,\infty)$ Областью значений функции $\,\log_b\,$ является множество всех действительных чисел: $\,\text{ран}(\log_b) = \Bbb R$	просмотр функций логарифмов
Законы логарифмов	Позволять $\,b\gt 0\,$ $\,b\ne 1\,$ $\,x\gt 0\,$ и $\,y\gt 0\,.$ $\log_b\,xy = \log_b x + \log_b y$ Лог продукта – это сумма логов. $\displaystyle \log_b\frac{x}{y} = \log_b x — \log_b y$ Логарифм частного равен разности логов. Для этого последнего свойства $\,y\,$ может быть любым вещественным числом: 9y = y\,\log_b x$ Вы можете уменьшить степень .	См. Свойства Логарифмы для типичного доказательства этих законов.
Смена базы Формула для логарифмов	Пусть $\,a\,$ и $\,b\,$ — положительные числа, не равные $\,1\,$ , и пусть $\,x\gt 0\,. $ Затем, $$ \cssId{s54}{\log_b\,x =\frac{\log_a\,x}{\log_a\,b}} $$ Прописью: Вы можете перейти с любого основания $\,b\,$ на любое основание $\,a\,$; «корректировка» заключается в том, что вы должны разделить на журнал на новую базу ($\,a\,$) из старой базы ($\,b\,$).	См. Изменение основной формулы для логарифмов для получения этой формулы. Уравнение $$\,\cssId{s60}{\log_b x = \left(\frac 1{\log_a b}\right)(\log_a x)}\,$$ показывает, что любая логарифмическая кривая просто вертикальное масштабирование любой другой логарифмической кривой!
Логарифмические функции являются взаимно однозначными	Поскольку логарифмы — это функций, : $x = y \ \\Rightarrow\ \ \log_b x = \log_b y$ Когда входы одинаковы, выходы одинаковы. Так как логарифмы взаимно-однозначны: $\log_b x = \log_b y\ \\Rightarrow\ \ x = y$ Когда выходные данные одинаковы, входные данные одинаковы. Таким образом, для всех $\,b > 0\,$ $\,b\ne 1\,$ $\,x > 0\,$ и $\,y > 0\,$: $$\cssId{s70}{x = y\ \ \iff\ \ \log_b x = \log_b y}$$
Обратные свойства	Логарифмические функции один к одному, следовательно, есть инверсии. Обратной логарифмической функцией с основанием $\,b\,$ является показательная функция с основанием $\,b\,.$ Для $\,b > 0\,$ $\,b\ne 1\,$ и всех действительных чисел $\,x\,$: $$\cssId{s76}{\log_b b^x = x}$$ Для $\,b > 0\,$ $\,b \ne 1\,$ и $\,x > 0\,$: $$\cssId{s78}{b^{\log_b х} = х}$$ 90 = 1\,$) Эквивалентно, точка $\,(1,0)\,$ лежит на графике $\,y = \log_b x\,. No related posts. Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт