4.2. Определение логарифма и его свойства
Определение. Логарифмом от числа b по данному основанию a
называется показатель степени c , в который надо возвести основание | a , | |||||
чтобы получить заданное (логарифмируемое) число | b. |
|
| |||
Логарифм обозначается | так: loga b = c, где | а −основание логарифма, | ||||
b −заданное (логарифмируемое) число (a > 0, | b > 0, | a ≠1). |
|
| ||
Из определения логарифма можно записать показательное уравнение |
| |||||
|
| ac = b. |
|
|
|
|
и y = loga x (a > 0, a ≠1) | является | |||||
обратной по отношению к другой. |
|
|
|
| ||
Логарифмы чисел по основанию 10 принято обозначать, lg x и называют | ||||||
десятичными | логарифмами. | А логарифмы чисел по основанию | e , | где | ||
e = 2,7182K , | принято обозначать ln x −их | называют натуральными | ||||
логарифмами. | Таким образом, log10 x = lg x, | loge x = ln x. |
|
| ||
Пример. Записать с помощью знака логарифма:
|
|
|
| а) 52 | = 25; | б) 8−3 = | 1 | . | |
Решение. |
|
| 512 | ||||||
|
|
|
|
|
|
| |||
а) Т.к. | основание | степени | есть 5, показатель степени | ||||||
(логарифм) равен 2, а степень равна 25, то log5 25 = 2 . | |||||||||
б) Основание степени есть 8, показатель степени (логарифм) равен −3, а | |||||||||
степень равна |
| 1 | , то log |
| 1 | = −3. |
|
|
|
512 | 8 512 |
|
|
| |||||
|
|
|
|
|
| ||||
Пример.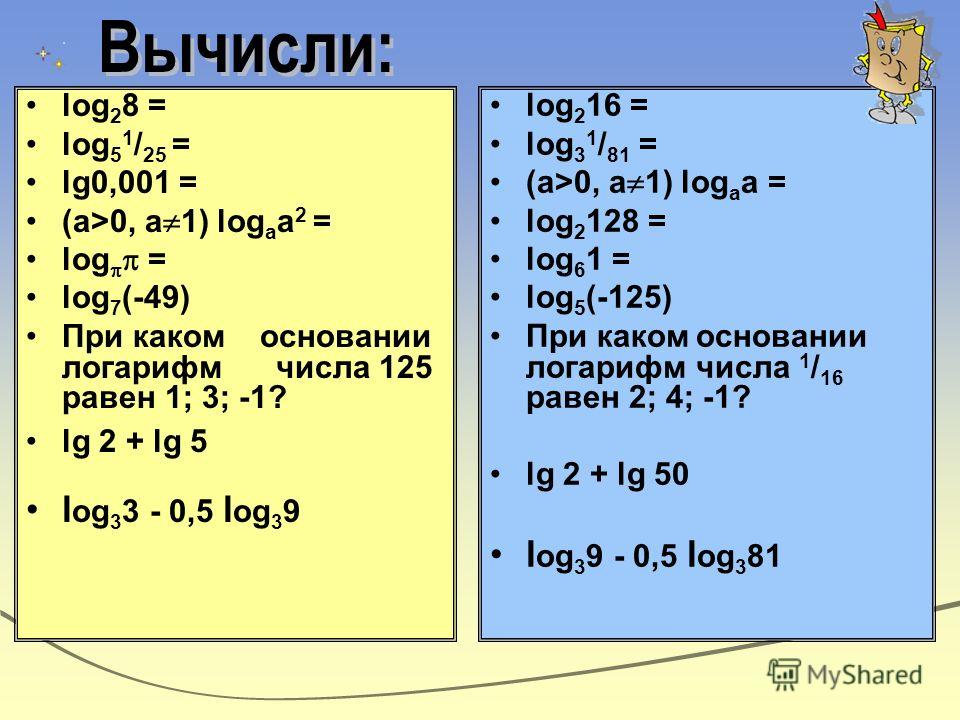
Найти логарифмы данных чисел по известным основаниям: a) log2 16; б) log6 36; в) log8 1.
Решение. а) здесь нужно найти такой показатель степени x , что 2x =16.
Решая это уравнение, получаем | 2x = 24, откуда x = 4 . Итак, log2 16 = 4. | |
б) из уравнения 6x = 36 | находим, 6x = 62, | то есть x = 2 . Значит, |
log6 36 = 2. |
|
|
в) в данном случае имеем уравнение 8x =1. | Это возможно только при | |
условии, что x = 0, откуда log8 1 = 0. |
| |
Пример. Определить x по заданным условиям:
62
a) log4 x = −3; б) logx | 1 | = | 3 . |
| 8 |
| 2 |
Решение.
а) по определению логарифма, запишем x = 4−3, откуда x = 641 .
б) согласно определению логарифма получаем уравнение x32 = 81.
Так как 18 = 2−3 и x32 = x3 ,то оно примет вид x3 = 2−3. Возведем обе части последнего равенства в квадрат:
|
|
| 2 |
| ( |
| −3 | ) | 2 |
| 3 | −6 |
|
| −2 |
| 1 |
|
| 3 |
|
|
|
|
|
|
| ||||||||||
| x |
|
| = | 2 |
|
|
| x = 2 |
| x = 2 |
| x = | 4 | . | |||
|
|
|
|
|
|
|
|
|
| |||||||||
| Свойства логарифмов | (x > 0, | a > 0, | a ≠1) |
|
| ||||||||||||
1º. Логарифм единицы равен нулю: loga 1 = 0.
2º. Логарифм основания равен единице: loga a =1, (loga an = n).
3º. Основное логарифмическое тождество: aloga x = x. 4º. Формула для логарифма произведения:
loga (x1 x2 ) = loga x1 +loga x2, x1 > 0, x2 > 0.
5º. Формула для логарифма частного:
|
| log |
|
| x1 | = log | a | x −log | x |
| , | x > 0, | ||||
|
|
|
|
|
| |||||||||||
|
|
|
|
| a x |
|
| 1 | a 2 |
| 1 | |||||
|
|
|
|
|
| 2 |
|
|
|
|
|
|
|
|
| |
6º. Формула для логарифма степени: |
|
|
| |||||||||||||
|
|
| 1 |
|
| loga x p = p loga x, | p R . | |||||||||
7º. log | a | m x = | loga x, | m R, |
|
|
|
| ||||||||
m |
|
|
|
| ||||||||||||
|
|
|
|
|
| p |
|
|
|
|
|
|
| |||
|
| log | a | m x p = | loga x, | log | a | m xm = loga | ||||||||
|
|
| ||||||||||||||
|
|
|
|
|
|
| m |
|
|
|
|
| ||||
8º.
Формула перехода к новому основанию:loga x = | logb x | , | b > 0, b ≠1. | |
logb a | ||||
|
|
|
>0.
m, p R.
63
9º. loga x = log1x a .
4.3.Тождественные преобразования показательных
илогарифмических выражений
Преобразование показательных и логарифмических выражений основаны на применении основных свойств соответствующих функций, показателя степени и свойств логарифмов.
Пример. Вычислить: 4−2log4 3 .
Решение. Используя свойства степеней и основные логарифмические тождества, получим
4−2log4 3 = (4log4 3)−2 = 3−2 = 19.
3
Пример. Вычислить: (35)log2 5 .
Решение. Используя свойства логарифмов (3º, 9º), получим
|
|
|
|
|
|
| 1 |
| 3 |
|
| 1 |
|
|
|
|
| ||
|
|
|
| 3 |
|
|
| log2 | 5 |
|
| log |
| 2 |
| ||||
|
|
|
|
| log |
| 5 |
|
| ||||||||||
( | 3 | 5)log2 | 5 |
|
| 53 |
|
| =5 |
|
| = 2. | |||||||
| = |
|
|
|
| 2 |
| =5 | 5 |
| |||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
Пример. Вычислить: log3(log2 (lg100)).
Решение. По свойствам логарифмов (6º, 1º) lg100 можно записать так
lg100 = lg102 = 2lg10 = 2.
Тогда получим
log3(log2 2) = log31 = 0.
Пример. Вычислить log49 16 , если log14 28 = a. Решение. Используя свойство 7º логарифмов, получим
log49 16 = log72 42 = log7 4 = log7 22 = 2log7 2.
Пусть log7 2 = x, тогда log49 16 = 2x .
Далее имеем
64
log |
| 28 = log7 28 = log7 | (4 | 7) = log7 4 | +log7 7 | = 2x +1. |
| |||
14 | log7 14 log7 | (2 | 7) | log7 2 | +log7 7 | x +1 |
| |||
|
|
| ||||||||
По условию log14 28 = a, тогда получим уравнение |
|
|
| |||||||
2x +1 | = a, 2x +1 = ax + a, (2 − a)x = a −1, x = | a −1 | , | |||||||
x +1 | 2 − a | |||||||||
|
|
|
|
|
|
|
| |||
тогда |
|
|
|
| 2(a −1) |
|
|
|
| |
|
| log49 16 = 2x = | . |
|
|
| ||||
|
| 2 −a |
|
|
| |||||
|
|
|
|
|
|
|
|
| ||
Часто приходится логарифмировать обе части данного выражения или, напротив, потенцировать. Логарифмирование – это преобразование, при котором логарифм выражения с переменными приводится к сумме или разности логарифмов переменных. Потенцирование – это действие, обратное логарифмированию.
Пример. Дано x = 3 |
|
| : | 2b |
| , a > 0, | b > 0, c > 0. | Найти lg x. | |||||||||||||||
| ac | ||||||||||||||||||||||
|
|
| |||||||||||||||||||||
|
|
|
|
|
|
|
|
| a2c |
|
|
|
|
|
|
|
|
|
| ||||
Решение. Логарифмируя обе части равенства, получим |
|
| |||||||||||||||||||||
|
|
|
|
|
| 2b |
|
|
|
|
| a2c |
|
|
|
| a2c |
| |||||
lg x = lg | 3 ac : |
| 3 ac | = lg 3 ac |
|
| |||||||||||||||||
|
|
|
|
|
| = lg |
| +lg |
| = | |||||||||||||
|
| 2 |
|
| |||||||||||||||||||
|
|
|
|
| a |
|
|
|
|
|
|
|
|
|
|
| 2b |
| |||||
|
|
|
|
|
|
| c |
|
|
|
|
| 2b |
|
|
|
|
| |||||
=lg(ac) 13 +lg(a2c) −lg(2b) = 13 lg ac +lg a2 +lg c −(lg2 +lgb) =
=13 lg a + 13 lg c +2lg a +lg c −lg2 −lgb = 73 lg a + 43 lg c −lg2 −lgb.
Пример. Найти x | по данному его логарифму: lg x = | 3 lg a − | 4 lgb, a > 0, |
|
| 2 | 3 |
b >0.
Решение. Воспользовавшись свойствами логарифмов и потенцируя обе части равенства, получим
|
|
|
|
|
|
|
| 32 |
|
|
|
|
|
|
|
|
|
|
|
|
| |
| 3 |
|
| 4 |
|
| a |
|
| a3 |
|
| a |
|
| a |
|
| ||||
lg x = lg a | 2 | −lgb | 3 | = lg | = lg |
|
| = lg | a | x = | a | . | ||||||||||
