|
Навигация: Главная Случайная страница Обратная связь ТОП Интересно знать Избранные Топ: Марксистская теория происхождения государства: По мнению Маркса и Энгельса, в основе развития общества, происходящих в нем изменений лежит… Оценка эффективности инструментов коммуникационной политики: Внешние коммуникации — обмен информацией между организацией и её внешней средой… Генеалогическое древо Султанов Османской империи: Османские правители, вначале, будучи еще бейлербеями Анатолии, женились на дочерях византийских императоров… Интересное: Как мы говорим и как мы слушаем: общение можно сравнить с огромным зонтиком, под которым скрыто все… Берегоукрепление оползневых склонов: На прибрежных склонах основной причиной развития оползневых процессов является подмыв водами рек естественных склонов. Отражение на счетах бухгалтерского учета процесса приобретения: Процесс заготовления представляет систему экономических событий, включающих приобретение организацией у поставщиков сырья… Дисциплины: Автоматизация Антропология Археология Архитектура Аудит Биология Бухгалтерия Военная наука Генетика География Геология Демография Журналистика Зоология Иностранные языки Информатика Искусство История Кинематография Компьютеризация Кораблестроение Кулинария Культура Лексикология Лингвистика Литература Логика Маркетинг Математика Машиностроение Медицина Менеджмент Металлургия Метрология Механика Музыкология Науковедение Образование Охрана Труда Педагогика Политология Правоотношение Предпринимательство Приборостроение Программирование Производство Промышленность Психология Радиосвязь Религия Риторика Социология Спорт Стандартизация Статистика Строительство Теология Технологии Торговля Транспорт Фармакология Физика Физиология Философия Финансы Химия Хозяйство Черчение Экология Экономика Электроника Энергетика Юриспруденция |
⇐ ПредыдущаяСтр 2 из 3Следующая ⇒ В ML существует большое количество элементарных математических функций для выполнения действий с числами: тригонометрические, степенные, логарифмические, экспоненциальные и функции округления. Существуют встроенные тригонометрические и гиперболические функции: sin(x), cos(x), tan(x), cot(x), asin(x), acos(x), atan(x), acot(x), sinh(x) и т.д. Аргументы этих функций (в следующих версиях, начиная с версии 7.0) могут задаваться в радианах и градусах. У функций в градусной мере после названия добавляется буква Некоторые часто используемые математические функции: · exp(x)–экспонента числа x; · log(x)– натуральный логарифм; · log10(x)– десятичный логарифм; · sqrt(x)– квадратный корень; · abs(x)– абсолютное значение x; · mod(x, y)– остаток от целочисленного деления с учетом знака; · rem(x, y)– остаток от целочисленного деления без учета знака; · real(z)– вещественная часть комплексного числа; · imag(z)– мнимая часть комплексного числа; · round(x)– округление до ближайшего целого. Более полный список основных математических функций MatLab:
С использованием вышеупомянутых функций, записать и сосчитать значение арифметического выражения: Вычислить: res= Составление арифметического выражения лучше всего начинать с расстановки основных скобок выражения. res = 1.0207e+006 Для эффективной работы с большими наборами данных или при необходимости многократных вычислений рассмотренных средств недостаточно. В ML существует возможность записать последовательность команд в файл, сохранить его, дать ему имя и выполнить, набрав в командной строке имя файла. Это можно сделать во встроенном редакторе системы. Такие файлы называются файлами-сценариями или скрипт-файлами. При сохранении они автоматически получают расширение системы – . Файлы-программы (их называют скриптами или сценариями) являются самым простым типом m-файлов. Script-файл состоит из последовательности команд, не содержит заголовка, а также входных и выходных параметров. Все объекты, используемые внутри script-файла, считаются глобальными. Если в рабочем пространстве есть данные, то внутри script-файла их можно использовать, а по окончании его выполнения использовать данные, созданные с его помощью. Перед запуском программы на выполнение необходимо установить каталог, содержащий скрипт-файл, в качестве текущего. Запуск файла на выполнение можно осуществить двумя способами: из окна редактора и из командного окна. Для выполнения файла-программы достаточно в командной строке указать имя этого скрипта. Для запуска программы на выполнение из окна редактора надо выбрать пункт меню Debug, Run или нажать функциональную клавишу F5, или выбрать соответствующую пиктограмму на панели инструментов. Выполнить программу, уже сохраненную на диске, можно из командного окна ML, просто набрав имя файла без расширения.
Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰). Папиллярные узоры пальцев рук — маркер спортивных способностей: дерматоглифические признаки формируются на 3-5 месяце беременности, не изменяются в течение жизни… Опора деревянной одностоечной и способы укрепление угловых опор: Опоры ВЛ — конструкции, предназначенные для поддерживания проводов на необходимой высоте над землей, водой… Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства… |
Каждая функция обладает именем и списком аргументов, которые задаются в круглых скобках и, если их несколько, перечисляются через запятую.
2-sin(x-pi/3))/(log(abs(y))+exp (sqrt (x+1))/(2*x))*1E6
Такие файлы используются для автоматизации выполнения большого набора инструкций. Их текст набирают в окне встроенного редактора ML.
..Бета-функция и ее варианты MatLab
RADIOMASTER
Лучшие смартфоны на Android в 2022 году
Серия iPhone от Apple редко чем удивляет. Когда вы получаете новый iPhone, общее впечатление, скорее всего, будет очень похожим на ваше предыдущее устройство. Однако всё совсем не так в лагере владельцев устройств на Android. Существуют телефоны Android всех форм и размеров, не говоря уже о разных ценовых категориях. Другими словами, Android-телефон может подойти многим. Однако поиск лучших телефонов на Android может быть сложной задачей.
1360 0
Документация Схемотехника CAD / CAM Статьи
MathCAD 12 MatLab OrCAD P CAD AutoCAD MathCAD 8 — 11- Главная /
- База знаний /
- CAD / CAM /
- MatLab
Урок 9. Специальные математические функции
Функции Эйри
Функции Бесселя
Бета-функция и ее варианты
Эллиптические функции и интегралы
Функции ошибки
Интегральная показательная функция
Гамма-функция и ее варианты
Ортогональные полиномы Лежандра
Что нового мы узнали?
Бета-функция определяется как
где Г (z) — гамма-функция. Неполная бета-функция определяется по формуле
beta(Z.
W)
— возвращает бета-функцию для соответствующих элементов комплексных массивов
Z и W. Массивы должны быть одинакового размера (или одна из величин может
быть скаляром).
beta i nc ( X , Z , W ) — возвращает неполную бета-функцию. Элементы X должны быть в закрытом интервале [0, 1].
beta 1 п ( Z , W ) — возвращает натуральный логарифм бета-функции log ( beta ( Z , W ) ) , без вычисления beta(Z.W). Так как сама бета-функция может принимать очень большие или очень малые значения, функция betaln(Z.W) иногда более полезна, так как позволяет избежать переполнения.
Пример:
» format rat;beta((l:10) 4 ,4)
ans=
1/4
1/20
1/60
1/140
1/280
1/504
1/840
1/1320
1/1980
1/2860
Нравится
Твитнуть
Теги MatLab САПР
Сюжеты MatLab
Знакомство с матричной лабораторией MATLAB MatLab
8169 0
Визуализация и графические средства MatLab
9677 0
Техническая документация по системе MatLab
6187 0
Комментарии (0)
Вы должны авторизоваться, чтобы оставлять комментарии.
Вход
О проекте Использование материалов Контакты
Новости Статьи База знаний
Радиомастер
© 2005–2022 radiomaster.ru
При использовании материалов данного сайта прямая и явная ссылка на сайт radiomaster.ru обязательна. 0.2234 s
журнал Matlab | Изучите различные примеры журнала Matlab
Метод журнала Matlab можно использовать для вычисления натурального логарифма или десятичного логарифма любого числа. Его также можно использовать для вычисления натурального логарифма или десятичного логарифма массива чисел или матрицы чисел. Пожалуйста, имейте в виду, что натуральный логарифм имеет основание «е», где «е» представляет число Эйлера и имеет значение 2,71828, а десятичный логарифм имеет основание 10.
Синтаксис:
- A = log (Число) используется для вычисления натурального логарифма (по основанию «е») числа в Matlab. В случае массива мы получим натуральный логарифм каждого элемента массива.
- A = log10 (Число) используется для вычисления десятичного логарифма (по основанию 10) числа в Matlab.
В случае массива мы получим десятичный логарифм каждого элемента массива.
В случае массива мы получим десятичный логарифм каждого элемента массива.Примеры журнала Matlab
Ниже показано, как вычислить натуральный логарифм в Matlab с использованием метода журнала:
Пример #1
В этом примере мы будем использовать метод log для вычисления натурального логарифма числа.
Шаг, который необходимо выполнить для этого примера:
- Передайте число, натуральный логарифм которого требуется в качестве аргумента для метода журнала.
Код:
журнал(4)
[Передача 4 в качестве аргумента метода журнала, так как нам нужен его натуральный логарифм] [Математически логарифм 4 по основанию «е» равен 1,3863]
Вот как будет выглядеть наш ввод и вывод в командном окне Matlab:
Ввод:
Вывод:
к основанию «е» как 1,3863, что совпадает с нашими ожиданиями.
Пример #2
В этом примере мы будем использовать метод log для вычисления натурального логарифма элементов массива.
Для этого примера необходимо выполнить следующие шаги:
- Инициализировать массив.
- Передать массив в качестве аргумента в метод журнала.
Код:
А = [3 6 4 8 6 1] [Инициализация массива, натуральный логарифм которого нужно вычислить]
журнал(А)
[Передача массива в качестве аргумента в метод журнала]
Вот как будет выглядеть наш ввод и вывод в командном окне Matlab:
Ввод:
Вывод:
Как мы видим в выводе, мы получили логарифм всех элементов массива по основанию «е», как и ожидали.
Пример #3
В этом примере мы будем использовать логарифмический метод для вычисления натурального логарифма элементов матрицы.
Для этого примера необходимо выполнить следующие шаги:
- Инициализировать матрицу.
- Передать матрицу в качестве аргумента в метод журнала.
Код:
А = [3 6 4; 8 6 1; 2 1 6] [Инициализация матрицы, натуральный логарифм которой нужно вычислить]
журнал(А)
[Передача матрицы в качестве аргумента в метод журнала]
Вот как будет выглядеть наш ввод и вывод в командном окне Matlab:
Ввод:
Вывод:
Как мы видим в логе вывода, мы получили все элементы в матрице по основанию «е», как мы и предполагали.
В приведенных выше 3 примерах мы вычислили натуральный логарифм чисел, используя логарифмический метод.
Далее мы вычислим десятичный логарифм чисел, используя метод log10.
Пример #4
В этом примере мы будем использовать метод log10 для вычисления десятичного логарифма числа.
Шаг, который необходимо выполнить для этого примера:
- Передайте число, натуральный логарифм которого требуется в качестве аргумента для метода журнала.
Код:
log10(5)
[Передача 5 в качестве аргумента для метода log10, так как нам нужен его десятичный логарифм] [Математически логарифм 5 по основанию «10» равен 0,6990]
Вот как будет выглядеть наш ввод и вывод в командном окне Matlab:
Ввод:
Вывод:
к основанию «10» как 0,6990, что соответствует нашим ожиданиям.
Пример #5
В этом примере мы будем использовать метод log10 для вычисления десятичного логарифма элементов массива.
В этом примере необходимо выполнить следующие шаги:
- Инициализировать массив.
- Передайте массив в качестве аргумента методу log10.
Код:
А = [4 7 1 3 6 2] [Инициализация массива, десятичный логарифм которого необходимо вычислить]
журнал 10(А)
[Передача массива в качестве аргумента методу log10]
Вот как будет выглядеть наш ввод и вывод в командном окне Matlab:
Ввод:
Вывод:
Как видно из лога, мы получили все элементы в массиве по основанию «10», как мы и предполагали.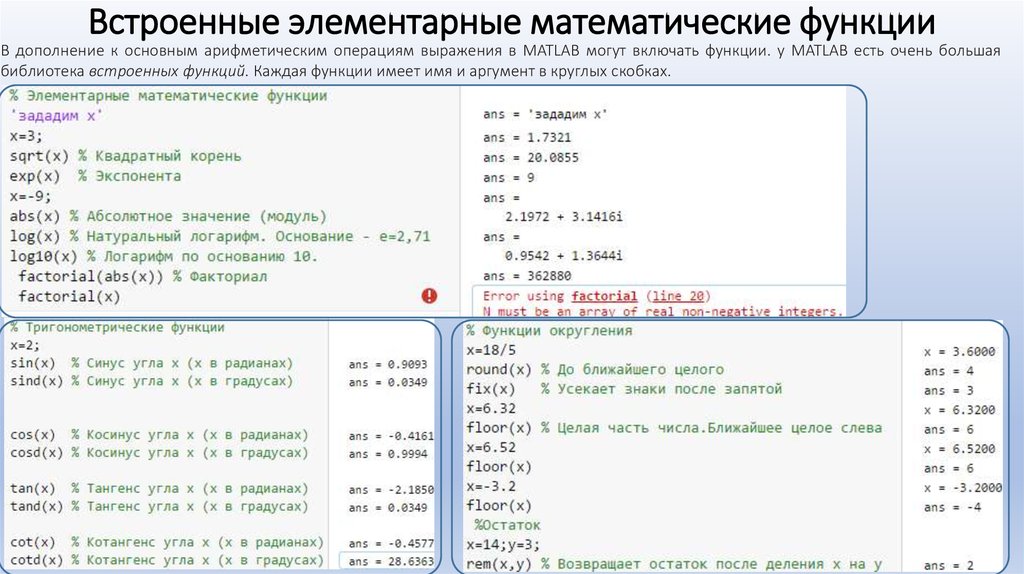
Пример #6
В этом примере мы будем использовать метод log10 для вычисления десятичного логарифма элементов матрицы.
Для этого примера необходимо выполнить следующие шаги:
- Инициализировать матрицу.
- Передать матрицу в качестве аргумента в метод log10.
Код:
А = [2 5 4; 1 6 3; 6 3 7] [Инициализация матрицы, десятичный логарифм которой необходимо вычислить]
журнал 10(А)
[Передача матрицы в качестве аргумента в метод log10]
Вот как будет выглядеть наш ввод и вывод в командном окне Matlab:
Ввод:
Вывод:
Как видно из вывода, мы получили логарифм всех элементов матрицы по основанию «10», как и ожидали.
Заключение
Логарифмический метод можно использовать в Matlab для вычисления логарифма числа, массива или матрицы. Можно вычислять как натуральный, так и десятичный логарифм.
Его также можно использовать для вычисления логарифма массивов и матриц.
Рекомендуемые статьи
Это руководство по журналу Matlab. Здесь мы обсуждаем введение в журнал Matlab вместе с примерами для лучшего понимания. Вы также можете ознакомиться со следующими статьями, чтобы узнать больше –
- Матлаб Формы
- Название графика Matlab
- Формат Matlab
- Свертка Matlab
Логарифмическая база 2 или e или 10?
Когда ваши данные охватывают большой диапазон, графики имеют тенденцию становиться уродливыми. Значения либо скучиваются внизу, либо разбросаны вверху — проблема, называемая плохое разрешение . Скорость изменений трудно отобразить, поскольку график обычно имеет очень длинный хвост, или очень жесткую заднюю часть, или и то, и другое.
Здесь пригодится логарифмическая шкала. Например, графики, использующие логарифмическую базу 10, могут упростить значения 1, 10, 100, 1000, 10000 до значений 1, 2, 3, 4, 5, помогая распознать стабильный рост и решить проблему разрешения.
Рисунок 1 : График с нормальной шкалой (слева) и логарифмической шкалой с основанием 10 (справа) . Значения данных проходят через множество степеней 10, из-за чего левый график страдает от плохого разрешения, когда данные переполнены внизу. Разрешение улучшается при использовании логарифмической шкалы с основанием 10, как показано на правом графике.
Итак, вы решили построить график в логарифмическом масштабе. Что теперь? По какому основанию логарифм брать: 2, или e , или 10?
Ответ лежит в диапазоне значений ваших данных.
Масштабирование по логарифмической базе 10, несмотря на его частое применение, лучше всего работает для наборов данных, которые проходят через многие степени 10 или большие процентные изменения. С такими данными вы не хотите, чтобы ваш график страдал от плохого разрешения, когда точки данных скапливаются в нижней части и расходятся вверх (см. рис.
1).
Логарифмическая база 10 может стать бременем для меньшего диапазона данных, потому что у вас будут проблемы с дробными степенями 10 на осях. Может быть легко оценить 0,5 степени 10, но дальнейшие дробные степени 10 требуют напряженных усилий, что затрудняет анализ данных и понимание графика.
Рисунок 2: Дробные степени числа 10, встречающиеся в наборах данных небольшого диапазона. Это затрудняет понимание графика аналитиками и зрителями.
Тогда вам следует принять логарифмическую шкалу с основанием 2, так как легче иметь дело со степенями двойки. В настоящее время компьютер позволяет безболезненно вычислять значения. Некоторые дробные степени двойки настолько близки к простым числам, что их легко вычислить.
Рисунок 3: Оценка дробных степеней 2
База журнала e отлично подходит для иллюстрации процентных изменений от -25% до 25%. Почему? Давайте посмотрим на математику. (Не паникуйте, это очень просто.
)
Предположим, u и v — это два значения данных. Изменение v относительно u, а именно r, рассчитывается следующим образом:
Что означает:
Пусть теперь d будет разностью и и u в натуральной логарифмической шкале,
Если d мало (-0,25< d < 0,25),
Итак,
Прописью: если есть небольшая разница между двумя натуральными логарифмическими значениями (d), вы можете легко оценить разницу между двумя исходными точками данных (r), поскольку r приблизительно равно d. Таким образом, процентное изменение (100% r) будет близко к 100% d, что позволит вам построить график в естественном логарифмическом масштабе без потери информации. Но эта оценка не является универсальной. Чем больше d (выше 0,25), тем менее точным он становится.
Вот еще одно предостережение: чтобы вернуться к исходному масштабу, требуется много работы.