2-6x=8\left(1-x\right)\)\(x=2,\:x=-4\)
Ответ: \(x=2,\:x=-4\).
Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!
Запишитесь на бесплатное тестирование знаний!
Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
Наши преподаватели
Михаил Николаевич Макеев
Репетитор по математике
Стаж (лет)
Образование:
Московский энергетический институт
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Павел Андреевич Демин
Репетитор по математике
Стаж (лет)
Образование:
Южно-Уральский Государственный Гуманитарно Педагогичесий Университет
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Жанна Игоревна Стефанович
Репетитор по математике
Стаж (лет)
Образование:
Гродненский государственный университет им.
Янки Купалы
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
- Математика
- Физика
- Химия
- Русский язык
- Английский язык
- Обществознание
- История России
- Биология
- География
- Информатика
Похожие статьи
- Округление десятичных дробей
- Периметр треугольника
- Стадии подготовки к экзамену по математике
- Призма
- Как разделить число на дробь
- Перевод км/час в м/с?
- Что делать, если ребенок выбрал «не ту» профессию?
- Как животные помогали людям во время ВОВ
Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
логарифмов
логарифмов
Логарифм
является показателем.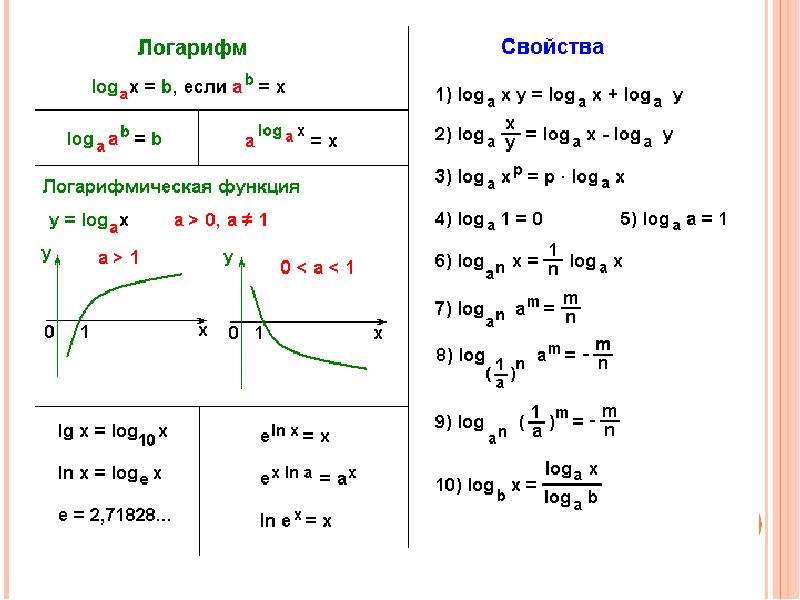
Логарифм – показатель степени, указывающий, в какой степени
основание должно быть поднято, чтобы произвести данное число.
г = б х экспоненциальная форма
x = log b y логарифмический форма
x — логарифм y по основанию b
log b y — степень, в которую нужно возвести b, чтобы получить y
Мы выражаем x через y
Примеры
x = log b y
х = журнал 2 8 Это означает логарифм 8 по основанию 2. Это показатель степени, до которого нужно возвести 2, чтобы получить 8. Мы знаем, что 2(2)(2) = 8. .Следовательно, x = 3,
х = log 6 36 Это означает логарифм 36 по основанию 6. Это показатель, в который нужно возвести 6, чтобы получить 36. Мы знаем, что 6(6) = 36. Следовательно, x = 2, .
х = log 10 10 000 Это означает логарифм 10 000 по основанию 10. Это это показатель степени, в которую нужно возвести 10, чтобы получить 10 000. Мы знаем что 10(10)(10)(10) = 10 000. Следовательно, х = 4, .
журнал б б = 1 Логарифм любого числа по тому же основанию равен 1.
х = логарифм 11 11 Это означает логарифм 11 по основанию 11. .
журнал б 1 = 0 Логарифм 1 всегда равен 0.
Любое число может служить основанием b.
Общий (бриггсовские) логарифмы Основание равно 10.Логарифмы по основанию 10 широко используются. Таким образом, обычно опускают индекс. Если основание не отображается, подразумевается, что основание равно 10.
.журнал 10 у = log у
Натуральный (Наперовы) логарифмы Основание равно e.
Помнить e — иррациональное число, где e = 2,71828… Символ «ln» относится к натуральным логарифмам.
log e x = ln x ln x — показатель степени, в которую нужно возвести e, чтобы получить x.
Почему мы хотим использовать логарифмы? Для упрощения расчетов во многих случаях.
Правила логарифмирования
Правило продукта
Правило частных
Силовое правило Это правило полезно, поскольку позволяет решать уравнения где переменная является показателем степени.
Экспоненциальные и логарифмические функции являются обратными функциямиРассмотрим следующие таблицы и соответствующие графики:
х
f(x) = e x
х
f(x)= ln x
1
1
1
2,7
2,7
1
2
7,39
7,39
2
3
20
20
3
4 [Индекс]
Что такое логарифмы и как они работают?
Упрощение с помощью The RelationshipHistory & The Natural Log
Purplemath
Что такое логарифмы?
Логарифмы противоположны экспонентам, так же как вычитание противоположно сложению, а деление противоположно умножению.
С технической точки зрения, логарифмы обратны экспонентам.
Содержание продолжается ниже
MathHelp.com
Логарифмы
В некотором смысле логарифмы сами являются показателями степени. У логарифмов есть основания, как и у экспонент; например, log 5 (25) обозначает степень, которую нужно приложить к основанию 5, чтобы получить аргумент 25. Таким образом, log 5 (25) = 2, потому что 5 2 = 25.
Но, честно говоря, я еще не встречал ученика, который понял бы это объяснение с первого раза. Мне потребовалась большая часть недели, чтобы наконец понять журналы вообще . Поэтому в течение многих лет я искал лучший способ объяснить их.
С практической точки зрения, я считаю полезным думать о журналах с точки зрения Отношения, а именно:
— Отношения —
y = b x
…… ……..эквивалентно……………
.
log b ( y ) = x
В первой строке под заголовком выше находится экспоненциальное утверждение:
Y = B x
На последней строке выше — эквивалентный логарифмический оператор:
Log B ( Y ) = x
-base-b y равно х «. Значение индексированного основания b является «основанием логарифма», точно так же, как b является основанием экспоненциального выражения b x .
И, как основание b экспоненты всегда положительно и не равно 1, так и основание b логарифма всегда положительно и не равно 1.
Все, что находится внутри логарифма, называется аргументом журнала.
Обратите внимание, что основание как в экспоненциальном уравнении, так и в логарифмическом уравнении равно b, но x и y меняются местами при переключении между двумя уравнениями.
— Отношения, Анимированные —
Отношения говорят, что независимо от того, что было аргументом журнала, становится «равным» на другой стороне уравнения, и что угодно , если бы было «равно», становится показателем экспоненты, и наоборот.
Если вы можете держать это в голове, то у вас не должно возникнуть особых проблем с логарифмами.
(Я сам придумал термин «Отношения». Вы не найдете его в своем тексте, и ваши учителя и репетиторы не поймут, о чем вы говорите, если вы упомянете их при них. «Отношения» совершенно нестандартная терминология. Почему я все равно использую ее? Потому что она работает.)
Между прочим: если вы заметили, что я поменял местами переменные между двумя ячейками, отображающими Отношения, у вас зоркий глаз. Я сделал это намеренно, чтобы подчеркнуть, что суть «Отношения» не в самих переменных, а в том, как они движутся.
- Преобразовать 6 3 = 216 в эквивалентное логарифмическое выражение.
Отношение говорит мне, что для преобразования этого экспоненциального утверждения в логарифмическую форму я должен оставить основание (то есть 6) там, где оно есть, но опустить его, чтобы сделать его основанием журнала; и у меня должны быть стороны 3 и 216, где 3 является значением журнала 6 (216). Это дает мне:
log 6 (216) = 3
- Преобразование log 4 (1024) = 5 в эквивалентное экспоненциальное выражение.
Отношение говорит мне, что для преобразования этого логарифмического выражения в экспоненциальную форму мне нужно сохранить основание (то есть 4) в левой части; и я должен иметь 1024 и 5 переключений сторон, при этом 5 будет питанием на 4. Это дает мне:
4 5 = 1024
URL: https://www.purplemath.com/modules/logs.htm
Вы можете использовать приведенный ниже виджет Mathway, чтобы попрактиковаться в преобразовании логарифмических операторов в эквивалентные им экспоненциальные операторы.
Следовательно, x = 3,
Это показатель степени
до которого нужно возвести 11, чтобы получить 11. Мы знаем, что 1 (1) = 11.
Следовательно, х = 1,
Логи отменяют экспоненты.
..(то есть означает то же самое, что и)…
Это соответствие выделено в Отношениях:
