Максимальное правдоподобие: Практическое руководство по методу максимального правдоподобия / Хабр

Содержание

Практическое руководство по методу максимального правдоподобия / Хабр

Вам наверняка доводилось когда-либо в своей жизни принимать решение о покупке, основываясь на отзывах о товарах. Как социальным существам нам свойственно покупать вещи, которые рекомендуют другие покупатели.

Недавно, в поисках новых наушников, я просмотрел все товары, которые имеют оценку 5 звезд. Меня поразило, насколько сложно принять решение о покупке, основываясь только на отзывах покупателей. Мне пришло в голову взглянуть на отзывы товаров с точки зрения статистики.

В этой статье я объясняю метод оценки максимального правдоподобия на примере сравнения двух товаров, используя гипотетические оценки, полученные на основе мнений людей о товарах.

Продукт A — смоделированные данные (не реальные)Продукт B — смоделированные данные (не реальные)

Если быть конкретным, то я смотрю на то, сколько раз товар получил оценку, отражающую степень удовлетворения людей этим товаром (от 1 до 5 звезд).

Оценка максимального правдоподобия

— это метод, который определяет значения параметров модели. Значения параметров подбираются таким образом, чтобы они максимизировали вероятность того, что процесс написания отзыва о товаре, описанный моделью, дал оценку, которая будет более близка к реальной.

Давайте построим модель и оценим параметры таким образом, чтобы они максимизировали вероятность получения значений, наблюдаемых в реальных отзывах. Чтобы освежить в памяти вероятностные обозначения, упомянутые в этой статье, почитайте мою предыдущую статью по теме.

Мы хотим оценить θi — вероятность того, что люди оценят товар числом звезд равным i. Поскольку каждый новый рейтинг (оценка) имеет значение от 1 до 5, эта вероятность соответствует категориальному распределению Cat(θ).

Для каждого конкретного товара мы наблюдаем вектор рейтингов R= [r1,r2,r3,r4,r5].

Каждая оценка r_i — это общее количество i-звездных отзывов, полученных этим товаром.

Получение каждого i-звездного отзыва происходит с вероятностью θi. Поскольку каждый отзыв r независим от других, мы можем моделировать вероятность с помощью категориального распределения:

Вероятность наблюдения вектора событий R из N независимых отзывов задается полиномиальным распределением параметризованным θ:

Вычислить его логарифмическое правдоподобие можно следующим образом:

Что позволяет нам определить оценку максимального правдоподобия (Maximum Likelihood Estimator) θ для каждого из двух товаров. Для этого мы ищем θ, которая максимизирует правдоподобие L.

Обычно это делается путем дифференцирования функции правдоподобия по

θ с использованием так называемых множителей Лагранжа.

Полагая, что все производные равны 0, мы получаем наиболее естественную оценку:

Следовательно, оценки максимального правдоподобия приведены ниже:

# количества звезд по отзывам
R_A = [10,6,10,27,109]
R_B = [57,33,29,45,246]
# оценки максимального правдоподобия
theta_A = R_A / np.sum(R_A)
theta_B = R_B / np.sum(R_B)
print("MLE for Product A: ", np.round(theta_A,3))
print("MLE for Product B: ", np.round(theta_B,3))

На основе этой оценки максимального правдоподобия θ для обеих моделей мы можем вычислить максимальное правдоподобие (Maximum Likelihood).

import math
import numpy as np
def f(n):
  return math.factorial(n)
  
def mle(R, theta):
  return (f(np.sum(R)) / (np.prod([f(r) for r in R]))) * \
         np.prod([theta[i]**R[i] for i in range(len(R))])
# максимальное правдоподобие
ml_A = mle(R_A,theta_A)
ml_B = mle(R_B,theta_B)
print("ML for Product A {:.7f}".format(ml_A))
print("ML for Product B {:.7f}".format(ml_B))
ml_products.
  py

Дает ли максимальное правдоподобие уверенность в том, что один из товаров предпочтительнее в глазах покупателей? Ответ не однозначен.

Здесь в игру вступает информационный критерий Акаике (Akaike Information Criterion), который дает нам некоторую доказательную базу. Оценка по информационному критерию Акаике награждает модели, которые достигают высокого показателя критерия адекватности (с низким максимальным правдоподобием), и штрафует модели, если они становятся чрезмерно сложными (большое количество параметров k).

Предпочтительной является модель с минимальным значением информационного критерия Акаике и максимальным правдоподобием, как показано ниже.

# информационный критерий Акаике
aic_A = 2*5 - 2*math.log(ml_A)
aic_B = 2*5 - 2*math.log(ml_B)
print("AIC for Product A: {:.2f}".format(aic_A))
print("AIC for Product B: {:.2f}".format(aic_B))

Таким образом, у нас есть некоторые свидетельства того, что люди, ответившие на опрос, предпочитают продукт B продукту A.

Мы только что рассмотрели, как использовать метод оценки максимального правдоподобия в простом контексте обзоров товаров.

Одним из недостатков метода оценки максимального правдоподобия является невозможность включить наши предпосылочные убеждения о тех параметрах, которые мы оцениваем. Например, у большинства отзывов в основном либо 5 звезд, либо 1 звезда, и очень мало средних значений.

Как я говорил в предыдущей статье, мы можем рассматривать байесовский анализ данных как расширение оценки максимального правдоподобия, что может лучше подойти в практических ситуациях. Больше информации об оценке максимального правдоподобия можно найти в этой замечательной

статье.

Материал подготовлен в рамках курса «Математика для Data Science». Если вам интересно узнать подробнее о формате обучения и программе, познакомиться с преподавателем курса — приглашаем на день открытых дверей онлайн. Регистрация здесь.

Справочник по прикладной статистике.

Том 1

Ллойд Э., Ледерман У. (ред.). Справочник по прикладной статистике. Том 1. М.: Финансы и статистика, 1989. — 510 с.

В справочнике освещены основные математико-статистические методы. Том 1 включает введение в статистику, вопросы, связанные с выборочным распределением, точечным и интервальным оцениванием, общую теорию статистических критериев, дисперсионный анализ, планирование эксперимента. Для широкой аудитории специалистов, разрабатывающих и использующих статистические методы.

ПРЕДИСЛОВИЕ К РУССКОМУ ИЗДАНИЮ
Глава I. ВВЕДЕНИЕ В СТАТИСТИКУ
1.1. СМЫСЛ ПОНЯТИЯ «СТАТИСТИКА»
1.2. ВЫБОРОЧНОЕ РАСПРЕДЕЛЕНИЕ, СТАТИСТИКА, ОЦЕНКА
1.3. ТЕМА ЭТОЙ КНИГИ
1.4. СОГЛАШЕНИЯ И ОБОЗНАЧЕНИЯ
Глава 2. ВЫБОРОЧНЫЕ РАСПРЕДЕЛЕНИЯ
2.1. МОМЕНТЫ И ДРУГИЕ СТАТИСТИКИ
2.

1.2. МОМЕНТЫ
2.2. ВЫБОРОЧНЫЕ РАСПРЕДЕЛЕНИЯ: ОПРЕДЕЛЕНИЯ И ПРИМЕРЫ
2.3. ВЫБОРОЧНЫЕ МОМЕНТЫ СТАТИСТИК
2.3.1. ПЕРВЫЕ ВЫБОРОЧНЫЕ МОМЕНТЫ СРЕДНЕГО ЗНАЧЕНИЯ ВЫБОРКИ
2.3.2. ПЕРВЫЕ ВЫБОРОЧНЫЕ МОМЕНТЫ ДИСПЕРСИИ ВЫБОРКИ
2.3.3. ВЫБОРОЧНАЯ КОВАРИАЦИЯ МЕЖДУ СРЕДНИМ ЗНАЧЕНИЕМ ВЫБОРКИ x И ДИСПЕРСИЕЙ ВЫБОРКИ v
2.3.4. ВЫБОРОЧНЫЕ МОМЕНТЫ ДЛЯ МОМЕНТОВ ВЫБОРКИ БОЛЕЕ ВЫСОКИХ ПОРЯДКОВ
2.3.5. ВЫБОРОЧНЫЕ МОМЕНТЫ СТАНДАРТНОГО ОТКЛОНЕНИЙ ВЫБОРКИ
2.3.6. ВЫБОРОЧНЫЕ МОМЕНТЫ КОЭФФИЦИЕНТА АСИММЕТРИИ ВЫБОРКИ

2.4. РАСПРЕДЕЛЕНИЯ СУММ НЕЗАВИСИМЫХ ОДИНАКОВО РАСПРЕДЕЛЕННЫХ ПЕРЕМЕННЫХ
2.5. ВЫБОРОЧНЫЕ РАСПРЕДЕЛЕНИЯ ФУНКЦИЙ НОРМАЛЬНЫХ ПЕРЕМЕННЫХ
2.5.2. РЕЗУЛЬТАТ ЛИНЕЙНОГО ПРЕОБРАЗОВАНИЯ. СТАНДАРТИЗАЦИЯ
2.5.3. ЛИНЕЙНЫЕ ФУНКЦИИ НОРМАЛЬНЫХ ПЕРЕМЕННЫХ
2.5.4. КВАДРАТИЧЕСКИЕ ФУНКЦИИ НОРМАЛЬНЫХ ПЕРЕМЕННЫХ
2.5.5. РАСПРЕДЕЛЕНИЕ СТЬЮДЕНТА (t-распределение)
2.5.6. РАСПРЕДЕЛЕНИЕ ОТНОШЕНИЯ ДИСПЕРСИЙ (F-распределение)
2.5.7. КОЭФФИЦИЕНТ КОРРЕЛЯЦИИ ВЫБОРКИ
2.5.8. НЕЗАВИСИМОСТЬ КВАДРАТИЧНЫХ ФОРМ.

ТЕОРЕМА ФИШЕРА—КОКРЕНА. ТЕОРЕМА КРЕЙГА
2.5.9. РАЗМАХ И СТЬЮДЕНТИЗИРОВАННЫЙ РАЗМАХ
2.6. АССИМПТОТИЧЕСКОЕ ВЫБОРОЧНОЕ РАСПРЕДЕЛЕНИЕ х И НЕЛИНЕЙНЫХ ФУНКЦИЙ ОТ х
2.7. ПРИБЛИЖЕНИЕ ВЫБОРОЧНЫХ МАТЕМАТИЧЕСКОГО ОЖИДАНИЯ И ДИСПЕРСИИ НЕЛИНЕЙНЫХ СТАТИСТИК. ПРЕОБРАЗОВАНИЯ, СТАБИЛИЗИРУЮЩИЕ ДИСПЕРСИЮ. НОРМАЛИЗУЮЩИЕ ПРЕОБРАЗОВАНИЯ
2.7.1. АППРОКСИМАЦИЯ
2.7.2. ПРЕОБРАЗОВАНИЯ, СТАБИЛИЗИРУЮЩИЕ ДИСПЕРСИЮ
2.7.3. НОРМАЛИЗУЮЩИЕ ПРЕОБРАЗОВАНИЯ
2.7.4. ПРЕОБРАЗОВАНИЯ, ВЫПРЯМЛЯЮЩИЕ ЗАВИСИМОСТЬ
2.7.5. ПРЕОБРАЗОВАНИЕ ВЫБОРОЧНОГО КОЭФФИЦИЕНТА КОРРЕЛЯЦИИ ПРИ r=0 В СТЬЮДЕНТОВУ ВЕЛИЧИНУ
2.7.6. ПРЕОБРАЗОВАНИЕ РАВНОМЕРНО РАСПРЕДЕЛЕННОЙ ПЕРЕМЕННОЙ В «хи-квадрат»-ПЕРЕМЕННУЮ
2.8. НЕЦЕНТРАЛЬНЫЕ ВЫБОРОЧНЫЕ РАСПРЕДЕЛЕНИЯ
2.8.1. НЕЦЕНТРАЛЬНОЕ РАСПРЕДЕЛЕНИЕ ХИ-КВАДРАТ
2.8.2. НЕЦЕНТРАЛЬНОЕ F-РАСПРЕДЕЛЕНИЕ
2.8.3. НЕЦЕНТРАЛЬНОЕ РАСПРЕДЕЛЕНИЕ СТЬЮДЕНТА
2.9. ПОЛИНОМИАЛЬНОЕ (МУЛЬТИНОМИАЛЬНОЕ) РАСПРЕДЕЛЕНИЕ В ТЕОРИИ ВЫБОРОЧНЫХ РАСПРЕДЕЛЕНИЙ
2.9.1. БИНОМИАЛЬНОЕ, ТРИНОМИАЛЬНОЕ И МУЛЬТИНОМИАЛЬНОЕ (ПОРЯДКА m) РАСПРЕДЕЛЕНИЯ
2.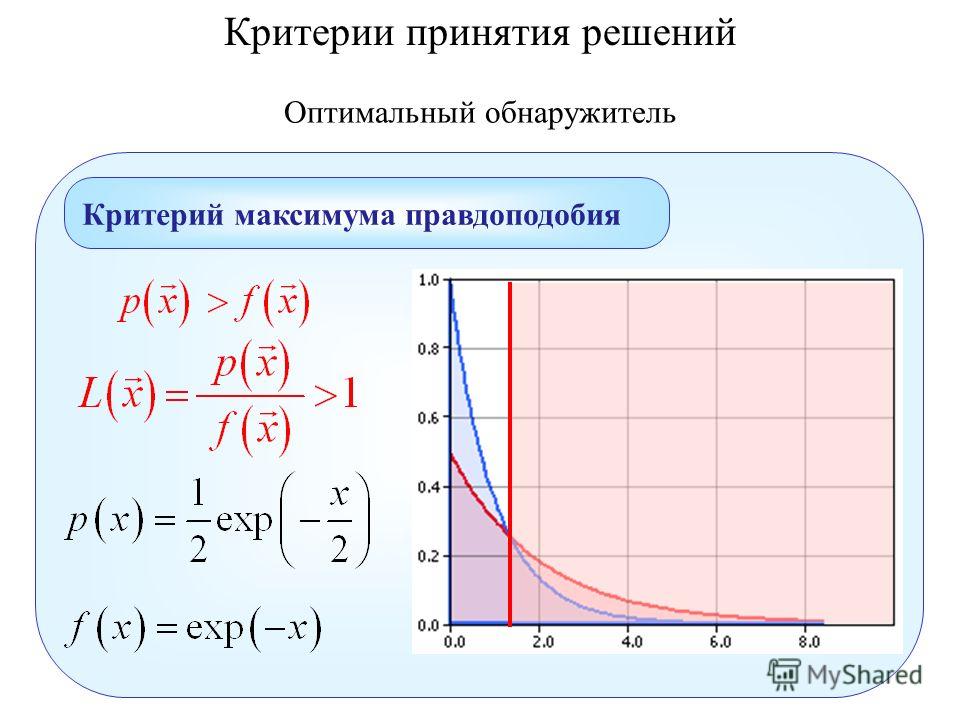

9.2. СВОЙСТВА ПОЛИНОМИАЛЬНОГО РАСПРЕДЕЛЕНИЯ
2.9.3. ПОЛИНОМИАЛЬНОЕ РАСПРЕДЕЛЕНИЕ КАК УСЛОВНОЕ ОТ СОВМЕСТНОГО РАСПРЕДЕЛЕНИЯ НЕЗАВИСИМЫХ ПУАССОНОВСКИХ ПЕРЕМЕННЫХ
2.9.4. ТАБЛИЦЫ ЧАСТОТ
2.10. ЛИТЕРАТУРА ДЛЯ ДАЛЬНЕЙШЕГО ЧТЕНИЯ
Глава 3. ОЦЕНИВАНИЕ. ВВОДНОЕ ОБОЗРЕНИЕ

3.1. ЗАДАЧА ОЦЕНИВАНИЯ
3.2. ИНТУИТИВНЫЕ ПРЕДСТАВЛЕНИЯ И ГРАФИЧЕСКИЙ МЕТОД
3.2.2. ЧАСТОТНЫЕ ТАБЛИЦЫ, ГИСТОГРАММЫ И ЭМПИРИЧЕСКАЯ ф.р.
3.3. НЕКОТОРЫЕ ОБЩИЕ КОНЦЕПЦИИ И КРИТЕРИИ ОЦЕНОК
3.3.1. ВВЕДЕНИЕ. РАЗМЕРНОСТЬ, ЗАМЕНЯЕМОСТЬ, СОСТОЯТЕЛЬНОСТЬ, КОНЦЕНТРАЦИЯ
3.3.2. НЕСМЕЩЕННЫЕ ОЦЕНКИ И НЕСМЕЩЕННЫЕ ОЦЕНКИ С МИНИМАЛЬНОЙ ДИСПЕРСИЕЙ
3.3.3. ЭФФЕКТИВНОСТЬ. ГРАНИЦА КРАМЕРА—РАО
3.4. ДОСТАТОЧНОСТЬ
3.4.2. КРИТЕРИЙ ФАКТОРИЗАЦИИ И ЭКСПОНЕНЦИАЛЬНОЕ СЕМЕЙСТВО
3.4.3. ДОСТАТОЧНОСТЬ И НЕСМЕЩЕННАЯ МИНИМАЛЬНО ДИСПЕРСНАЯ ОЦЕНКА
3.4.4. ДОСТАТОЧНОСТЬ В СЛУЧАЕ МНОГИХ ПАРАМЕТРОВ
3.5. ПРАКТИЧЕСКИЕ МЕТОДЫ ПОСТРОЕНИЯ ОЦЕНОК. ВВЕДЕНИЕ
3.5.2. НЕСМЕЩЕННЫЕ ОЦЕНКИ С МИНИМАЛЬНОЙ ДИСПЕРСИЕЙ. МЕТОД НАИМЕНЬШИХ КВАДРАТОВ
3.

5.3. МЕТОД МОМЕНТОВ
3.5.4. МЕТОД МАКСИМАЛЬНОГО ПРАВДОПОДОБИЯ
3.5.5. НОРМАЛЬНЫЕ ЛИНЕЙНЫЕ МОДЕЛИ, В КОТОРЫХ ОЦЕНКИ МАКСИМАЛЬНОГО ПРАВДОПОДОБИЯ И НАИМЕНЬШИХ КВАДРАТОВ СОВПАДАЮТ
Глава 4. ИНТЕРВАЛЬНОЕ ОЦЕНИВАНИЕ
4.1.2. СТАНДАРТНОЕ ОТКЛОНЕНИЕ
4.1.3. ИНТЕРВАЛЫ ВЕРОЯТНОСТИ
4.2. ДОВЕРИТЕЛЬНЫЕ ИНТЕРВАЛЫ И ДОВЕРИТЕЛЬНЫЕ ПРЕДЕЛЫ
4.3. ПОСТРОЕНИЕ ДОВЕРИТЕЛЬНОГО ИНТЕРВАЛА С ПОМОЩЬЮ ОПОРНОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ
4.4. ИСТОЛКОВАНИЕ ДОВЕРИТЕЛЬНОГО ИНТЕРВАЛА КАК МЕРЫ ТОЧНОСТИ ОЦЕНКИ НЕИЗВЕСТНОГО ПАРАМЕТРА
4.5. ДОВЕРИТЕЛЬНЫЕ ИНТЕРВАЛЫ ПРИ НЕСКОЛЬКИХ ПАРАМЕТРАХ
4.5.2. ДОВЕРИТЕЛЬНЫЕ ИНТЕРВАЛЫ ДЛЯ ФУНКЦИЙ ДВУХ ПАРАМЕТРОВ, ВКЛЮЧАЮЩИХ ОТНОШЕНИЕ ПАРАМЕТРОВ И ИХ РАЗНОСТЬ (ТЕОРЕМА ФЕЛЛЕРА)
4.6. ПОСТРОЕНИЕ ДОВЕРИТЕЛЬНЫХ ИНТЕРВАЛОВ БЕЗ ИСПОЛЬЗОВАНИЯ ОПОРНОЙ ПЕРЕМЕННОЙ
4.7. ПРИБЛИЖЕННЫЕ ВЫЧИСЛЕНИЯ ДОВЕРИТЕЛЬНЫХ ИНТЕРВАЛОВ ДЛЯ ПАРАМЕТРОВ ДИСКРЕТНЫХ РАСПРЕДЕЛЕНИЙ
4.8. ДОВЕРИТЕЛЬНЫЕ ИНТЕРВАЛЫ ДЛЯ КВАНТИЛЕЙ, НЕ ЗАВИСЯЩИЕ ОТ ИСХОДНОГО РАСПРЕДЕЛЕНИЯ (РАСПРЕДЕЛЕННЫЕ СВОБОДНО)
4.

9. ДОВЕРИТЕЛЬНЫЕ ОБЛАСТИ ДЛЯ МНОГОМЕРНОГО ПАРАМЕТРА
4.9.2. ЭЛЛИПТИЧЕСКИЕ ДОВЕРИТЕЛЬНЫЕ ОБЛАСТИ ДЛЯ ВЕКТОРА МАТЕМАТИЧЕСКОГО ОЖИДАНИЯ ДВУМЕРНОГО НОРМАЛЬНОГО РАСПРЕДЕЛЕНИЯ. ПРИБЛИЖЕННЫЕ ДОВЕРИТЕЛЬНЫЕ ОБЛАСТИ ДЛЯ ОЦЕНОК НАИБОЛЬШЕГО ПРАВДОПОДОБИЯ
4.10. ПОСТРОЕНИЕ ДОВЕРИТЕЛЬНЫХ ИНТЕРВАЛОВ НА ОСНОВЕ БОЛЬШИХ ВЫБОРОК С ИСПОЛЬЗОВАНИЕМ ФУНКЦИИ ПРАВДОПОДОБИЯ
4.10.2. ПОСТРОЕНИЕ ПРИБЛИЖЕННЫХ ДОВЕРИТЕЛЬНЫХ ИНТЕРВАЛОВ С ПОМОЩЬЮ ПРОИЗВОДНОЙ ЛОГАРИФМИЧЕСКОЙ ФУНКЦИИ ПРАВДОПОДОБИЯ
4.10.3. ПОСТРОЕНИЕ ДОВЕРИТЕЛЬНЫХ ИНТЕРВАЛОВ С ПОМОЩЬЮ (ПРИБЛИЖЕННО) НОРМАЛИЗУЮЩЕГО ПРЕОБРАЗОВАНИЯ
4.11. ДОВЕРИТЕЛЬНАЯ ПОЛОСА ДЛЯ НЕИЗВЕСТНОЙ НЕПРЕРЫВНОЙ ФУНКЦИИ РАСПРЕДЕЛЕНИЯ
4.11.2. РАССТОЯНИЕ КОЛМОГОРОВА—СМИРНОВА МЕЖДУ ИСТИННОЙ (ТЕОРЕТИЧЕСКОЙ) И ЭМПИРИЧЕСКОЙ ФУНКЦИЯМИ РАСПРЕДЕЛЕНИЯ
4.11.3. ВЫБОРОЧНОЕ РАСПРЕДЕЛЕНИЕ СТАТИСТИКИ КОЛМОГОРОВА—СМИРНОВА. ДОВЕРИТЕЛЬНЫЕ ПРЕДЕЛЫ ДЛЯ ФУНКЦИИ РАСПРЕДЕЛЕНИЯ
4.12. ТОЛЕРАНТНЫЕ ИНТЕРВАЛЫ
4.13. ИНТЕРВАЛЫ ПРАВДОПОДОБИЯ
4.13.2. ПРАВДОПОДОБНЫЕ ЗНАЧЕНИЯ И ИНТЕРВАЛЫ ПРАВДОПОДОБИЯ
4.

13.3. СИТУАЦИЯ С ДВУМЯ ПАРАМЕТРАМИ
4.14. БАЙЕСОВСКИЕ ИНТЕРВАЛЫ
Глава 5. СТАТИСТИЧЕСКИЕ КРИТЕРИИ
5.2.1. ДВУХСТОРОННИЙ БИНОМИАЛЬНЫЙ КРИТЕРИЙ. СОСТАВНЫЕ ЧАСТИ, ПРОЦЕДУРА И ИНТЕРПРЕТАЦИЯ
5.2.2. ТРАДИЦИОННАЯ ИНТЕРПРЕТАЦИЯ УРОВНЕЙ ЗНАЧИМОСТИ; ИСПОЛЬЗУЕМЫЕ НА ПРАКТИКЕ УРОВНИ ЗНАЧИМОСТИ; КРИТИЧЕСКАЯ ОБЛАСТЬ
5.2.3. ОДНОСТОРОННИЙ БИНОМИАЛЬНЫЙ КРИТЕРИЙ
5.2.4. КРИТЕРИИ О РАСПРЕДЕЛЕНИИ ПУАССОНА
5.2.5. КРИТЕРИИ ДЛЯ НЕПРЕРЫВНЫХ РАСПРЕДЕЛЕНИЙ
5.2.6. ВЫБОР СТАТИСТИКИ КРИТЕРИЯ
5.3. КРИТЕРИИ ДЛЯ ПРОВЕРКИ ГИПОТЕЗ
5.3.2. ФУНКЦИЯ ЧУВСТВИТЕЛЬНОСТИ ОДНОСТОРОННЕГО КРИТЕРИЯ ДЛЯ ВЫБОРКИ ИЗ НОРМАЛЬНОГО РАСПРЕДЕЛЕНИЯ, КОГДА ЗНАЧЕНИЕ «сигма» НЕИЗВЕСТНО
5.3.3. ФУНКЦИЯ ЧУВСТВИТЕЛЬНОСТИ ДВУХСТОРОННЕГО КРИТЕРИЯ
5.4. КРИТЕРИИ ДЛЯ СЛОЖНЫХ НУЛЕВЫХ ГИПОТЕЗ
5.4.2. КРИТЕРИИ НЕЗАВИСИМОСТИ ДЛЯ ТАБЛИЦ СОПРЯЖЕННОСТИ 2×2. ТОЧНЫЙ КРИТЕРИЙ ФИШЕРА
5.5. КРИТЕРИИ, СОДЕРЖАЩИЕ БОЛЕЕ ОДНОГО ПАРАМЕТРА. ОБОБЩЕННЫЕ КРИТЕРИИ ОТНОШЕНИЯ ПРАВДОПОДОБИЯ
5.6. АППРОКСИМАЦИЯ УРОВНЯ ЗНАЧИМОСТИ КРИТЕРИЯ ОТНОШЕНИЯ ПРАВДОПОДОБИЯ ДЛЯ БОЛЬШИХ ВЫБОРОК
5.

7. КРИТЕРИИ РАНДОМИЗАЦИИ
5.8. СТАНДАРТНЫЕ КРИТЕРИИ ДЛЯ МОДЕЛИ С НОРМАЛЬНЫМ РАСПРЕДЕЛЕНИЕМ
5.8.2. ЗНАЧИМОСТЬ СРЕДНЕГО, КОГДА ДИСПЕРСИЯ НЕИЗВЕСТНА. t-КРИТЕРИЙ СТЬЮДЕНТА
5.8.3. КРИТЕРИЙ ФИШЕРА-БЕРЕНСА ДЛЯ ПРОВЕРКИ ЗНАЧИМОСТИ РАЗЛИЧИЯ ДВУХ СРЕДНИХ
5.8.4. t-КРИТЕРИЙ ДЛЯ ПРОВЕРКИ ЗНАЧИМОСТИ РАЗЛИЧИЯ ДВУХ СРЕДНИХ (КОГДА ДИСПЕРСИИ РАВНЫ)
5.8.5. t-КРИТЕРИЙ ДЛЯ ПРОВЕРКИ ЗНАЧИМОСТИ КОЭФФИЦИЕНТА РЕГРЕССИИ В ПРОСТОЙ ЛИНЕЙНОЙ МОДЕЛИ
5.8.6. КРИТЕРИЙ РАВЕНСТВА ДВУХ ДИСПЕРСИЙ
5.8.7 ПРОВЕРКА РАВЕНСТВА НЕКОТОРЫХ СРЕДНИХ. ВВЕДЕНИЕ В ДИСПЕРСИОННЫЙ АНАЛИЗ
5.9. ПРОВЕРКА НОРМАЛЬНОСТИ
5.10. ПРОВЕРКА РАВЕНСТВА к ДИСПЕРСИЙ (КРИТЕРИЙ БАРТЛЕТТА)
5.11. СОЧЕТАНИЕ РЕЗУЛЬТАТОВ НЕСКОЛЬКИХ КРИТЕРИЕВ
5.12. ТЕОРИЯ НЕЙМАНА—ПИРСОНА
5.12.2. ТЕОРИЯ НЕЙМАНА-ПИРСОНА ПРОВЕРКИ ГИПОТЕЗ
Глава 6. МЕТОД МАКСИМАЛЬНОГО ПРАВДОПОДОБИЯ
6.2. МЕТОД МАКСИМАЛЬНОГО ПРАВДОПОДОБИЯ
6.2.2. ОЦЕНКА МАКСИМАЛЬНОГО ПРАВДОПОДОБИЯ
6.2.3. ОЦЕНКА МАКСИМАЛЬНОГО ПРАВДОПОДОБИЯ: ИНТУИТИВНАЯ АРГУМЕНТАЦИЯ
6.

2.4. ОЦЕНКА МАКСИМАЛЬНОГО ПРАВДОПОДОБИЯ: ТИПЫ МАКСИМУМОВ
6.2.5. ТЕОРЕТИЧЕСКОЕ ОБОСНОВАНИЕ МЕТОДА МАКСИМАЛЬНОГО ПРАВДОПОДОБИЯ. СВОЙСТВА ФУНКЦИИ ПРАВДОПОДОБИЯ
6.2.6. ОЦЕНИВАНИЕ ФУНКЦИИ ПАРАМЕТРА «тетта». СВОЙСТВО ИНВАРИАНТНОСТИ
6.3. ПРИМЕРЫ ПРИМЕНЕНИЯ МЕТОДА МАКСИМАЛЬНОГО ПРАВДОПОДОБИЯ В ОДНОПАРАМЕТРИЧЕСКОЙ СИТУАЦИИ
6.4. ПРИМЕРЫ О.М.П. В МНОГОПАРАМЕТРИЧЕСКИХ СЛУЧАЯХ
6.5. ОЦЕНКА МАКСИМАЛЬНОГО ПРАВДОПОДОБИЯ КОЭФФИЦИЕНТОВ ЛИНЕЙНОЙ РЕГРЕССИИ
6.5.2. ОЦЕНКИ МАКСИМАЛЬНОГО ПРАВДОПОДОБИЯ ДЛЯ ЛИНЕЙНОЙ РЕГРЕССИИ С ВЕСАМИ
6.5.3. ЛИНЕЙНАЯ РЕГРЕССИЯ С ОДИНАКОВЫМИ ВЕСАМИ
6.6. ОЦЕНИВАНИЕ ЗАВИСИМОСТИ ТОКСИЧНОСТИ ИНСЕКТИЦИДА ОТ УРОВНЯ ДОЗИРОВКИ
6.6.2. ВЕРОЯТНОСТНАЯ МОДЕЛЬ
6.6.3. ИССЛЕДОВАНИЕ ПОВЕРХНОСТИ ФУНКЦИИ ПРАВДОПОДОБИЯ
6.6.4. ОЦЕНКА МАКСИМАЛЬНОГО ПРАВДОПОДОБИЯ
6.6.5. ТОЧНОСТЬ ОЦЕНОК
6.6.6. ДОЗА, НЕОБХОДИМАЯ ДЛЯ ЗАДАННОГО ЗНАЧЕНИЯ ОТКЛИКА
6.7. ОЦЕНКИ МАКСИМАЛЬНОГО ПРАВДОПОДОБИЯ ПО ГРУППИРОВАННЫМ, ЦЕНЗУРИРОВАННЫМ И УСЕЧЕННЫМ ДАННЫМ
6.7.2. НЕПРЕРЫВНЫЕ ДАННЫЕ И ГРУППИРОВКА.

ПОПРАВКА ШЕППАРДА
ГЛАВА 7. СТАТИСТИКА ХИ-КВАДРАТ. КРИТЕРИИ СОГЛАСИЯ, НЕЗАВИСИМОСТИ И ОДНОРОДНОСТИ
7.1.2. АДЕКВАТНОСТЬ ЛИНЕЙНОЙ РЕГРЕССИОННОЙ МОДЕЛИ
7.2. РАССТОЯНИЕ К. ПИРСОНА: КРИТЕРИЙ «хи-квадрат»
7.3. ОБЪЕДИНЕНИЕ ЯЧЕЕК С НИЗКИМИ ЧАСТОТАМИ. КРИТЕРИЙ У. КОКРЕНА
7.4. КРИТЕРИЙ «хи-квадрат» ДЛЯ НЕПРЕРЫВНЫХ РАСПРЕДЕЛЕНИЙ
7.5. ТАБЛИЦЫ ЧАСТОТ ПЕРЕКРЕСТНОЙ КЛАССИФИКАЦИИ (ТАБЛИЦЫ СОПРЯЖЕННОСТИ). КРИТЕРИИ НЕЗАВИСИМОСТИ
7.5.2. ТАБЛИЦЫ k x m
7.6. ИНДЕКС РАССЕЯНИЯ
7.6.1. ИНДЕКС РАССЕЯНИЯ ДЛЯ ВЫБОРКИ ИЗ БИНОМИАЛЬНОГО РАСПРЕДЕЛЕНИЯ
7.6.2. ИНДЕКС РАССЕЯНИЯ ДЛЯ ПУАССОНОВСКИХ ВЫБОРОК
Глава 8. ОЦЕНИВАНИЕ МЕТОДОМ НАИМЕНЬШИХ КВАДРАТОВ И ДИСПЕРСИОННЫЙ АНАЛИЗ
8.1. ОЦЕНИВАНИЕ МЕТОДОМ НАИМЕНЬШИХ КВАДРАТОВ ДЛЯ МОДЕЛЕЙ ОБЩЕГО ВИДА
8.2. ОЦЕНИВАНИЕ МЕТОДОМ НАИМЕНЬШИХ КВАДРАТОВ ДЛЯ ЛИНЕЙНЫХ МОДЕЛЕЙ ПОЛНОГО РАНГА. НОРМАЛЬНЫЕ УРАВНЕНИЯ. ТЕОРЕМА ГАУССА—МАРКОВА
8.2.1. ПРИМЕРЫ ОЦЕНИВАНИЯ МЕТОДОМ НАИМЕНЬШИХ КВАДРАТОВ
8.2.2. МАТРИЧНОЕ ПРЕДСТАВЛЕНИЕ ЛИНЕЙНЫХ МОДЕЛЕЙ
8.

2.3. СВОЙСТВА ОЦЕНОК МЕТОДА НАИМЕНЬШИХ КВАДРАТОВ
8.2.4. ОСТАТКИ
8.2.5. ОРТОГОНАЛЬНЫЕ ПЛАНЫ И ОРТОГОНАЛЬНЫЕ ПОЛИНОМЫ
8.2.6. МОДИФИКАЦИИ ДЛЯ НЕРАВНОТОЧНЫХ НАБЛЮДЕНИЙ; ВЗВЕШЕННЫЙ МЕТОД НАИМЕНЬШИХ КВАДРАТОВ
8.2.7. МОДИФИКАЦИИ ДЛЯ НЕ НЕЗАВИСИМЫХ НАБЛЮДЕНИЙ
8.3. ДИСПЕРСИОННЫЙ АНАЛИЗ И ПРОВЕРКА ГИПОТЕЗ ДЛЯ ПЛАНОВ ПОЛНОГО РАНГА
8.3.2. ДОВЕРИТЕЛЬНЫЕ ОБЛАСТИ
8.2 3. ПРОВЕРКА ГИПОТЕЗ
8.3.4. ОСНОВНЫЕ ТОЖДЕСТВА
8.3.5. ПРОВЕРКИ ГИПОТЕЗ В ОРТОГОНАЛЬНЫХ ПЛАНАХ
8.3.6. ПРОВЕРКА ГИПОТЕЗ ДЛЯ НЕ ОРТОГОНАЛЬНЫХ ПЛАНОВ
8.3.7 ГРУППОВАЯ ОРТОГОНАЛЬНОСТЬ
8.3.8. ОБЩИЕ ЛИНЕЙНЫЕ ГИПОТЕЗЫ
Глава 9. ПЛАНИРОВАНИЕ СРАВНИТЕЛЬНЫХ ЭКСПЕРИМЕНТОВ
9.3. БОЛЕЕ СЛОЖНЫЙ ПРИМЕР: ЭКСПЕРИМЕНТ ДАРВИНА
9.4. ПОЛНОСТЬЮ РАНДОМИЗИРОВАННЫЕ БЛОЧНЫЕ ПЛАНЫ
9.5. ОБРАБОТКИ НА ОДНОМ И НА НЕСКОЛЬКИХ УРОВНЯХ
9.6. ПОТРЕБНОСТЬ В РАЗРАБОТКАХ ПО УМЕНЬШЕНИЮ РАЗМЕРОВ БЛОКОВ
9.7. СБАЛАНСИРОВАННЫЕ НЕПОЛНЫЕ БЛОКИ ДЛЯ СРАВНЕНИЯ ОДНОУРОВНЕВЫХ ОБРАБОТОК
9.8. ПОЛНЫЙ ФАКТОРНЫЙ ПЛАН
9.8.

j
9.9. НЕПОЛНЫЕ БЛОКИ: СМЕШИВАНИЕ
9.10. ЧАСТИЧНОЕ СМЕШИВАНИЕ
9.11. ФАКТОРЫ НА ТРЕХ И БОЛЕЕ УРОВНЯХ
9.11.2. ГРЕКО-ЛАТИНСКИЙ КВАДРАТ
Глава 10. МЕТОД НАИМЕНЬШИХ КВАДРАТОВ И АНАЛИЗ СТАТИСТИЧЕСКИХ ЭКСПЕРИМЕНТОВ: ВЫРОЖДЕННЫЕ МОДЕЛИ, МНОЖЕСТВЕННЫЕ КРИТЕРИИ
10.1.2. ОЦЕНИВАНИЕ. ФУНКЦИИ, ДОПУСКАЮЩИЕ ОЦЕНКУ
10.1.3. ПРОВЕРКА ГИПОТЕЗ
10.1.4. ДВУСТОРОННЯЯ (ДВУХФАКТОРНАЯ) ИЕРАРХИЧЕСКАЯ КЛАССИФИКАЦИЯ
10.1.5. ДВУСТОРОННЯЯ (ДВУХФАКТОРНАЯ) ПЕРЕКРЕСТНАЯ КЛАССИФИКАЦИЯ
10.1.6. КЛАССИФИКАЦИИ БОЛЕЕ ВЫСОКОГО ПОРЯДКА
10.1.7. КОВАРИАЦИОННЫЙ АНАЛИЗ
10.2. МНОЖЕСТВЕННЫЕ КРИТЕРИИ И СРАВНЕНИЯ
10.2.2. КОМБИНАЦИИ ПРОВЕРОК И ОБЩИЙ РАЗМЕР КРИТЕРИЯ
10.2.3. МНОЖЕСТВЕННЫЕ СРАВНЕНИЯ
10.3. ПРЕДПОЛОЖЕНИЯ ОТНОСИТЕЛЬНО ОШИБОК
10.3.2. АНАЛИЗ ОСТАТКОВ

Объяснение концепций вероятности: Оценка максимального правдоподобия | Джонни Брукс-Бартлетт

В этом посте я объясню, что такое метод максимального правдоподобия для оценки параметров, и приведу простой пример, чтобы продемонстрировать этот метод. Некоторое содержание требует знания основных концепций вероятности, таких как определение совместной вероятности и независимости событий. Я написал сообщение в блоге с этими предварительными условиями, поэтому не стесняйтесь читать его, если считаете, что вам нужно освежить знания.

Часто в машинном обучении мы используем модель для описания процесса, результатом которого являются наблюдаемые данные. Например, мы можем использовать модель случайного леса, чтобы классифицировать, могут ли клиенты отменить подписку на услугу (известную как моделирование оттока), или мы можем использовать линейную модель, чтобы предсказать доход, который будет получен для компании в зависимости от того, насколько они может потратить на рекламу (это пример линейной регрессии). Каждая модель содержит собственный набор параметров, которые в конечном итоге определяют, как выглядит модель.

Для линейной модели мы можем записать это как y = mx + c . В этом примере x могут представлять расходы на рекламу, а y — полученный доход. м и c параметры для этой модели. Различные значения этих параметров дадут разные линии (см. рисунок ниже).

Три линейные модели с разными значениями параметров.

Итак, параметры определяют план модели. Только когда для параметров выбираются конкретные значения, мы получаем конкретизацию модели, описывающей данное явление.

Оценка максимального правдоподобия — это метод, определяющий значения параметров модели. Значения параметров находятся таким образом, чтобы максимизировать вероятность того, что процесс, описанный моделью, привел к получению фактически наблюдаемых данных.

Приведенное выше определение может показаться немного загадочным, поэтому давайте рассмотрим пример, который поможет понять это.

Предположим, мы наблюдали 10 точек данных из какого-то процесса. Например, каждая точка данных может представлять время в секундах, которое требуется учащемуся для ответа на конкретный экзаменационный вопрос. Эти 10 точек данных показаны на рисунке ниже 9. 0003 10 (гипотетических) точек данных, которые мы наблюдали

Сначала мы должны решить, какая модель, по нашему мнению, лучше всего описывает процесс генерации данных. Эта часть очень важна. По крайней мере, у нас должно быть хорошее представление о том, какую модель использовать. Обычно это происходит из-за наличия некоторого опыта в предметной области, но мы не будем обсуждать это здесь.

Для этих данных мы предполагаем, что процесс генерации данных может быть адекватно описан гауссовым (нормальным) распределением. Визуальный осмотр рисунка выше показывает, что распределение Гаусса правдоподобно, потому что большинство из 10 точек сгруппированы в середине с несколькими точками, разбросанными слева и справа. (Принимать такое решение на лету только с 10 точками данных не рекомендуется, но, учитывая, что я сгенерировал эти точки данных, мы пойдем с ним).

Напомним, что распределение Гаусса имеет 2 параметра. Среднее значение μ и стандартное отклонение σ. Различные значения этих параметров приводят к различным кривым (как и в случае с прямыми линиями выше). Мы хотим знать, какая кривая, скорее всего, ответственна за создание точек данных, которые мы наблюдали? (см. рисунок ниже). Оценка максимального правдоподобия — это метод, который находит значения μ и σ, которые приводят к кривой, которая лучше всего соответствует данным.

10 точек данных и возможные распределения Гаусса, из которых были взяты данные. f1 нормально распределена со средним значением 10 и дисперсией 2,25 (дисперсия равна квадрату стандартного отклонения), это также обозначается f1 ∼ N (10, 2,25). f2 ∼ N (10, 9), f3 ∼ N (10, 0,25) и f4 ∼ N (8, 2,25). Цель максимального правдоподобия состоит в том, чтобы найти значения параметров, которые дают распределение, которое максимизирует вероятность наблюдения данных.

Истинное распределение, на основе которого были сгенерированы данные, было f1 ~ N(10, 2,25), что обозначено синей кривой на рисунке выше.

Теперь, когда у нас есть интуитивное понимание того, что такое оценка максимального правдоподобия, мы можем перейти к изучению того, как вычислять значения параметров. Значения, которые мы находим, называются оценками максимального правдоподобия (MLE).

Снова продемонстрируем это на примере. Предположим, что на этот раз у нас есть три точки данных, и мы предполагаем, что они были получены в результате процесса, адекватно описываемого распределением Гаусса. Это точки 9, 9,5 и 11. Как рассчитать оценки максимального правдоподобия значений параметров гауссовского распределения μ и σ?

Мы хотим рассчитать общую вероятность наблюдения всех данных, то есть совместное распределение вероятностей всех наблюдаемых точек данных. Для этого нам потребуется рассчитать некоторые условные вероятности, что может быть очень сложно. Итак, именно здесь мы сделаем наше первое предположение. Предполагается, что каждая точка данных генерируется независимо от других . Это предположение значительно упрощает математику. Если события (то есть процесс, который генерирует данные) независимы, то общая вероятность наблюдения всех данных является продуктом наблюдения за каждой точкой данных в отдельности (то есть продуктом предельных вероятностей).

Плотность вероятности наблюдения одной точки данных x, , полученной из распределения Гаусса, определяется как:

Точка с запятой, используемая в обозначении P(x; μ, σ) , предназначена для того, чтобы подчеркнуть, что символы, стоящие после нее, являются параметрами распределения вероятностей. Поэтому ее не следует путать с условной вероятностью (которая обычно изображается вертикальной линией, например, P(A|B)).

В нашем примере общая (совместная) плотность вероятности наблюдения трех точек данных определяется как:

Нам просто нужно вычислить значения μ и σ , что дает максимальное значение приведенного выше выражения.

Если вы изучали исчисление на уроках математики, то, вероятно, знаете, что существует метод, который может помочь нам найти максимумы (и минимумы) функций. Это называется дифференциация . Все, что нам нужно сделать, это найти производную функции, установить производную функцию равной нулю, а затем изменить уравнение, чтобы сделать интересующий параметр предметом уравнения. И вуаля, у нас будут значения MLE для наших параметров. Сейчас я пройдусь по этим шагам, но предполагаю, что читатель знает, как выполнять дифференцирование общих функций. Если вы хотите более подробное объяснение, просто дайте мне знать в комментариях.

Логарифм правдоподобия

Вышеприведенное выражение для полной вероятности на самом деле очень трудно дифференцировать, поэтому его почти всегда упрощают, беря натуральный логарифм выражения. Это абсолютно нормально, потому что натуральный логарифм является монотонно возрастающей функцией. Это означает, что если значение по оси X увеличивается, значение по оси Y также увеличивается (см. рисунок ниже). Это важно, потому что гарантирует, что максимальное значение логарифма вероятности произойдет в той же точке, что и исходная функция вероятности. Поэтому мы можем работать с более простым логарифмическим правдоподобием вместо исходного правдоподобия.

Монотонное поведение исходной функции, y = x слева и функции (натурального) логарифма y = ln(x).

Обе эти функции являются монотонными, потому что при движении слева направо по оси x значение y всегда увеличивается. Пример немонотонной функции, потому что при движении слева направо на графике значение f(x) увеличивается вверх, затем опускается, а затем снова поднимается.

Логарифмирование исходного выражения дает нам:

Это выражение можно еще раз упростить, используя законы логарифмирования, чтобы получить:

Это выражение можно дифференцировать, чтобы найти максимум. В этом примере мы найдем MLE среднего, μ. Для этого мы берем частную производную функции по µ, что дает

. Наконец, установив левую часть уравнения в ноль, а затем переставив µ, мы получим:

. Здесь мы имеем оценку максимального правдоподобия для µ . То же самое можно сделать и с σ, но я оставлю это в качестве упражнения для внимательного читателя.

Всегда ли можно точно решить оценку максимального правдоподобия?

Нет — это короткий ответ. Более вероятно, что в реальном сценарии производная функции логарифмического правдоподобия по-прежнему не поддается анализу (т. е. слишком сложно/невозможно дифференцировать функцию вручную). Поэтому итерационные методы, такие как алгоритмы максимизации ожидания, используются для поиска численных решений для оценок параметров. Хотя общая идея осталась прежней.

Так почему же максимальная вероятность, а не максимальная вероятность?

Ну, это всего лишь педантизм статистиков (но на то есть веские причины). Большинство людей склонны использовать вероятность и правдоподобие как синонимы, но статистики и теоретики вероятности проводят различие между ними. Причину путаницы лучше всего выявить, посмотрев на уравнение.

Эти выражения равны! Итак, что это значит? Давайте сначала определим P(данные; μ, σ) ? Означает «плотность вероятности наблюдения данных с параметрами модели μ и σ» . Стоит отметить, что мы можем обобщить это на любое количество параметров и любое распределение.

С другой стороны, L(μ, σ; данные) означает «вероятность того, что параметры μ и σ принимают определенные значения при условии, что мы наблюдали набор данных».

Приведенное выше уравнение говорит о том, что плотность вероятности данных с учетом параметров равна вероятности параметров с учетом данных. Но, несмотря на то, что эти две вещи равны, вероятность и плотность вероятности принципиально задают разные вопросы — один спрашивает о данных, а другой — о значениях параметров. Вот почему метод называется максимальной вероятностью, а не максимальной вероятностью.

Когда минимизация методом наименьших квадратов совпадает с оценкой максимального правдоподобия?

Минимизация методом наименьших квадратов — еще один распространенный метод оценки значений параметров модели в машинном обучении. Оказывается, когда модель предполагается гауссовой, как в приведенных выше примерах, оценки MLE эквивалентны методу наименьших квадратов. Для более глубокого математического вывода ознакомьтесь с этими слайдами.

Интуитивно мы можем интерпретировать связь между двумя методами, понимая их цели. Для оценки параметра методом наименьших квадратов мы хотим найти линию, которая минимизирует общий квадрат расстояния между точками данных и линией регрессии (см. рисунок ниже). При оценке максимального правдоподобия мы хотим максимизировать общую вероятность данных. Когда предполагается гауссово распределение, максимальная вероятность определяется, когда точки данных приближаются к среднему значению. Поскольку распределение Гаусса симметрично, это эквивалентно минимизации расстояния между точками данных и средним значением.

Линия регрессии, показывающая точки данных со случайным гауссовским шумом

Если есть что-то неясное или я допустил некоторые ошибки в приведенном выше, не стесняйтесь оставлять комментарии. В следующем посте я планирую рассказать о байесовском выводе и о том, как его можно использовать для оценки параметров.

Спасибо, что прочитали.

1.2 — Оценка максимального правдоподобия

Постановка задачи Раздел

Предположим, у нас есть случайная выборка \(X_1, X_2, \cdots, X_n\), предполагаемое распределение вероятности которой зависит от некоторого неизвестного параметра \(\theta\). 2\), то наша цель будет состоять в том, чтобы найти хорошую оценку \(\mu\), скажем, используя данные \(x_1, x_2, \cdots, x_n\), которые мы получили из нашей конкретной случайной выборки.

Представляется разумным, что хорошей оценкой неизвестного параметра \(\theta\) будет значение \(\theta\), которое максимизирует вероятность, э-э-э… то есть вероятность .. , получения данных, которые мы наблюдали. (Итак, вы видите, откуда произошло название «максимальное правдоподобие»?) Итак, то есть, в двух словах, идея, лежащая в основе метода оценки максимального правдоподобия. Но как бы мы реализовали этот метод на практике? Предположим, у нас есть случайная выборка \(X_1, X_2, \cdots, X_n\), для которой функция плотности вероятности (или массы) каждого \(X_i\) равна \(f(x_i;\theta)\). Тогда совместная функция вероятностной массы (или плотности) \(X_1, X_2, \cdots, X_n\), которую мы (не столь произвольно) назовем \(L(\theta)\), равна: 9n f(x_i;\theta)\)

Первое равенство, конечно, просто определение совместной функции массы вероятностей. Второе равенство исходит из того факта, что у нас есть случайная выборка, из которой по определению следует, что \(X_i\) независимы. И последнее равенство просто использует сокращенную математическую запись произведения индексированных терминов. Теперь, в свете основной идеи оценки максимального правдоподобия, один из разумных способов продолжить работу состоит в том, чтобы рассматривать « функцию правдоподобия » \(L(\theta)\) как функцию \(\theta\) и найти значение \(\theta\), которое максимизирует его.

Это все еще звучит как абстрактная тарабарщина? Давайте посмотрим на пример, чтобы увидеть, можем ли мы сделать его немного более конкретным.

Предположим, у нас есть случайная выборка \(X_1, X_2, \cdots, X_n\), где:

\(X_i=0\), если случайно выбранный студент не владеет спортивным автомобилем, и
\(X_i=1\), если случайно выбранный студент владеет спортивным автомобилем.

Предполагая, что \(X_i\) являются независимыми случайными величинами Бернулли с неизвестным параметром \(p\), найдите оценку максимального правдоподобия \(p\), доли студентов, владеющих спортивными автомобилями.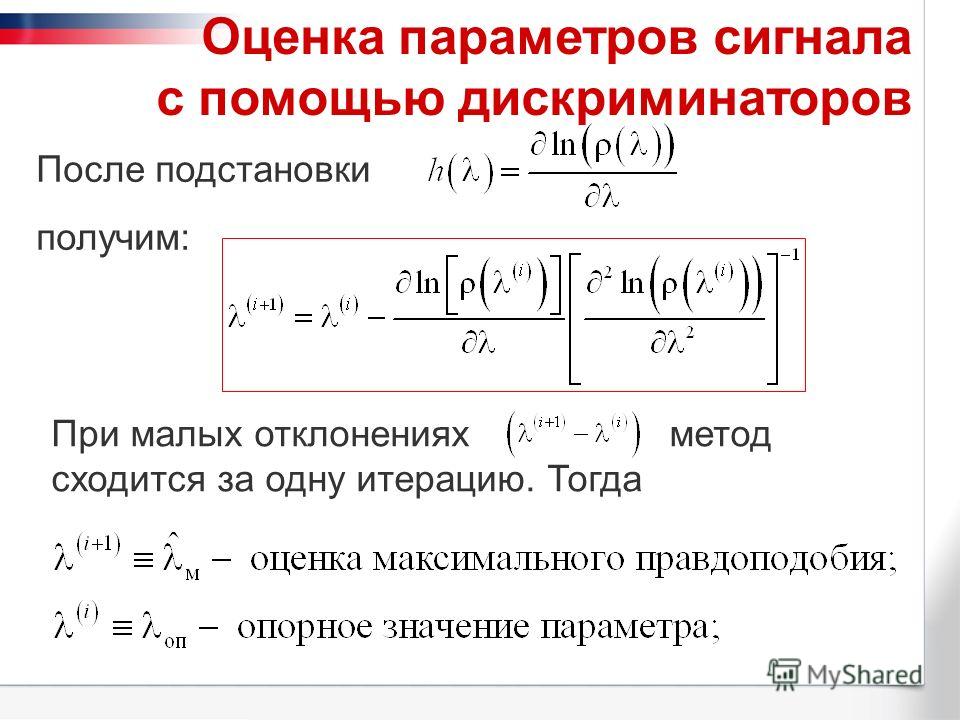 9{n-\sum x_i}\)

Теперь, чтобы реализовать метод максимального правдоподобия, нам нужно найти \(p\), которое максимизирует правдоподобие \(L(p)\). Теперь нам нужно надеть шляпы исчисления, поскольку для максимизации функции нам потребуется дифференцировать функцию правдоподобия по \(p\). При этом мы будем использовать «трюк», который часто немного упрощает дифференциацию. Обратите внимание, что натуральный логарифм является возрастающей функцией \(x\):

f(x2)f(x1)x1x1y = ln (x)

То есть, если \(x_1 )

В этом случае натуральный логарифм функции правдоподобия:

\(\text{log}L(p)=(\sum x_i)\text{log}(p)+(n-\sum x_i) \text{log}(1-p)\)

Теперь, взяв производную логарифмического правдоподобия и приравняв ее к 0, мы получим:

\(\displaystyle{\frac{\partial \log L( р) {\ парциальное р} = \ гидроразрыва {\ сумма х_ {я}} {р} — \ гидроразрыва {\ влево (п- \ сумма х_ {я} \ справа)} {1-р} \ stackrel {SET }{\equiv} 0}\)

Теперь, умножая на \(p(1-p)\), получаем:

\((\sum x_i)(1-p)-(n-\sum х_i)р=0\) 9n X_i}{n}\)

О, и мы должны технически проверить, что мы действительно получили максимум. Мы можем сделать это, убедившись, что вторая производная логарифмического правдоподобия по \(p\) отрицательна. Это так, но вы, возможно, захотите поработать, чтобы убедить себя!

Теперь, когда этот пример позади, давайте взглянем на формальные определения терминов:

Функция правдоподобия
Оценщики максимального правдоподобия
Оценки максимального правдоподобия.

Определение. Пусть \(X_1, X_2, \cdots, X_n\) будет случайной выборкой из распределения, которое зависит от одного или нескольких неизвестных параметров \(\theta_1, \theta_2, \cdots, \theta_m\) _{с плотностью вероятности (или масса) функция \(f(x_i; \theta_1, \theta_2, \cdots, \theta_m)\). Предположим, что \((\theta_1, \theta_2, \cdots, \theta_m)\) ограничено заданным пространством параметров \(\Omega\). Тогда:}

Если рассматривать как функцию от \(\theta_1, \theta_2, \cdots, \theta_m\), совместную функцию плотности вероятности (или массы) от \(X_1, X_2, \cdots, X_n\): 9n f(x_i;\theta_1,\theta_2,\ldots,\theta_m)\)
(\((\theta_1, \theta_2, \cdots, \theta_m)\) в \(\Omega\)) называется функцией правдоподобия .
Если:
\([u_1(x_1,x_2,\ldots,x_n),u_2(x_1,x_2,\ldots,x_n),\ldots,u_m(x_1,x_2,\ldots,x_n)]\)
— это \(m\)-кортеж, который максимизирует функцию правдоподобия, тогда:
\(\шляпа{\theta}_i=u_i(X_1,X_2,\ldots,X_n)\)
— это оценщик максимального правдоподобия из \(\theta_i\), для \(i=1, 2, \cdots, m\).
Соответствующие наблюдаемые значения статистики в (2), а именно:
\([u_1(x_1,x_2,\ldots,x_n),u_2(x_1,x_2,\ldots,x_n),\ldots,u_m(x_1,x_2,\ldots,x_n)]\)
называются оценками максимального правдоподобия \(\theta_i\), для \(i=1, 2, \cdots, m\).

Предположим, что веса случайно выбранных американских студенток нормально распределены с неизвестным средним \(\mu\) и стандартным отклонением \(\sigma\). Случайная выборка из 10 американских студенток колледжа дала следующие веса (в фунтах): 9n x_i=\dfrac{1}{10}(115+\cdots+180)=142,2\)

фунта. Обратите внимание, что единственная разница между формулами для оценки максимального правдоподобия и оценки максимального правдоподобия заключается в том, что:

оценка определяется с помощью заглавных букв (чтобы обозначить, что ее значение является случайным), и
оценка определяется строчными буквами (для обозначения того, что ее значение фиксировано и основано на полученной выборке)

Итак, теперь у нас есть формальные определения. В первом примере на этой странице использовалась совместная функция массы вероятности, которая зависит только от одного параметра, а именно \(p\), доли успехов. Теперь давайте рассмотрим пример, в котором используется совместная функция плотности вероятности, зависящая от двух параметров. 92}{2\theta_2}\)

Теперь, взяв частную производную логарифмической вероятности по отношению к \(\theta_1\) и приравняв к 0, мы видим, что некоторые вещи компенсируют друг друга, оставляя нас с:

\(\ displaystyle {\ frac {\ partial \ log L \ left (\ theta_ {1}, \ theta_ {2} \ right)} {\ partial \ theta_ {1}} = \ frac {- \ цвет {красный} \ отмена {\ цвет {черный} 2} \ цвет {черный} \ сумма \ влево (x_ {i} — \ theta_ {1} \ справа) \ цвет {красный} \ отмена {\ цвет {черный} (-1)}}{\color{red}\cancel{\color{black}2} \color{black} \theta_{2}} \stackrel{\text {SET}}{\equiv} 0}\)

Теперь, умножая на \(\theta_2\) и распределяя сумму, мы получаем:

\(\sum x_i-n\theta_1=0\)

Теперь, находя \(\theta_1\), и надевая шляпу, мы показали, что оценка максимального правдоподобия \(\theta_1\) _равна:

\(\hat{\theta}_1=\hat{\mu}=\dfrac{\sum x_i} {n}=\bar{x}\)

Теперь для \(\theta_2\).