Считаем и сравниваем — Ответы, ГДЗ, Тетрадь-тренажер 5-6 класс 1 часть (Лобжанидзе)
1. На карте имеются две смежные отметки горизонталей: 40 метров и 50 метров. Число заключённых между ними промежутков — три. Какова высота сечения горизонталей на карте?
3,3 местра.
2. На карте точка С находится посередине между точками А и В. По горизонталям, проходящим через них, можно определить, что высота точки В в 2 раза меньше высоты точки С и наполовину больше высоты точки А. Определите, будет ли видна точка С из точки А.
Будет.
3. Во время велосипедного похода его участники двигаются со средней скоростью 12 километров в час. Расстояние между стартом и финишем их маршрута по карте — б сантиметров, а масштаб карты равен 1:1 000000. Определите время, необходимое для велосипедного похода туристов.
6000000 см = 60 км;
60/12=5 часов.
4.
Определите, во сколько раз уменьшено расстояние на планах, построенных в масштабе:
1:50 — в 50 раз.
1:100- в 100 раз.
1:150 — в 150 раз.
1:5000 — в 5000 раз.
Какой из этих масштабов самый мелкий?
1:5000.
5. Запишите численный масштаб именованным.
1:1500 — в 1 см 15 м
1:10000 — в 1 см 100 м
1:250000 — в 1 см 2,5 км
1:35000000 — в 1 см 350 км
6. Рассчитайте, во сколько раз расстояния на местности больше, чем на плане, если местность изображена в масштабе:
в 1 сантиметре — 50 метров — в 5000 раз
в 1 сантиметре — 900 метров — в 90000 раз
в 1 сантиметре — 10 километров — в 1000000 раз
в 1 сантиметре — 250 километров — в 25000000 раз
7. Определите, какой из масштабов, представленных в каждой паре, крупнее (поставьте знак > или <):
1:10000 < 1:1000
1:250000 > в 1 см 25 км
1:500000 < в 1 см500 м
8.
Определите масштаб карт; если расстояние 150 километров на карте А равно отрезку 5 сантиметров, а на карте Б — 15 сантиметров.
А 1:3000000
Б 1:1000000
Масштаб какой из карт крупнее?
Б
9. Вычислите реальную площадь поля, если на карте его длина составляет 7 сантиметров, ширина — 5 сантиметров, а масштаб карты 1:10 000.
70000*50000=3500000000 см2 = 0,35 км2
10. Определите расстояние на карте двумя способами.
Измерьте линейкой и рассчитайте с помощью масштаба расстояние между городами:
Ереван — Баку 456 км
Осло — Стокгольм 416 км
Определите эти расстояния при помощи градусной сетки и таблицы длин дуг параллелей в километрах:
Ереван — Баку 427
Осло — Стокгольм 446,4
Сравните полученные результаты и объясните их.
Так как шаг сетки 1 градус, невозможно установить координаты города с точностью до секунды. Поэтому измерение масштаба более точное.
Масштаб. 6-й класс
Цели урока:
- Ввести понятие масштаба, научить находить расстояния на карте и на местности, пользуясь масштабом, учить решать задачи, связанные с понятием масштаба
- Развивать мышление, творческую активность, внимание, интерес к математике.
- Создать условия для развития самостоятельности.
Оборудование: компьютер, мультимедиа, презентация (приложение 1), учебник Н.Я. Виленкина, В.И. Жохова, А.С. Чеснокова, С.И. Шварцбурда «Математика 6», тетрадь, линейка, карандаши.
Тип урока — урок изучения и первичного закрепления новых знаний
Ход урока
1.
Организационный момент. (слайд 2).
Думать — коллективно!
Решать — оперативно!
Отвечать — доказательно!
Бороться — старательно!
И открытия нас ждут обязательно!
2. Сообщение темы урока (слайд 3)
Речь идет о трудной теме. Хотя уже хорошо отработаны понятия: «отношение», «пропорция», говорилось и об отношении расстояний. Теперь надо только по-новому назвать одно специфическое отношение — расстояния на карте между двумя пунктами к расстоянию между теми же пунктами на местности.
3. Устный счет: (слайд 4)
1. Выразите в километрах:
а) 32000000 см,
б) 600000 см,
в) 32000 см,
г) 5000000 см.
2. Выразите в метрах:
а) 32000000 см,
б) 600000 см,
в) 32000 см,
г) 5000000 см.
4. Изучение нового материала.
1) Подготовительная работа. (слайд 5)
— Составьте отношения:
а) 1 см к 5000 м,
б) 1 см к 210 м,
в) 1 см к 54 см,
г) 1 см к 30000 км.
— Что нужно сначала сделать?
Решение:
а) 1 : 500000,
б) 1 : 21000,
в) 1 : 54,
г) 1 : 3000000000.
— Участки земной поверхности, детали
машин, план дома и многое другое изображают на
бумаге в уменьшенном виде.
— Если на карте, чертеже, плане
встретите такие отношения, то это масштаб карты,
чертежа, плана.
2) Работа над новой темой. (слайд 7)
Определение: Отношение длины отрезка на карте к длине соответствующего отрезка на местности называют масштабом карты. (Аналогично можно сказать о чертеже, плане).
Масштаб — жезл размерный или мерило, мерник, размерник, мера линейная, принятая для чертежа или иной работы. (Из толкового словаря В.И.Даля.)
— Объясните, что обозначают данные масштабы. (слайд 8)
Ответ: Если масштаб карты 1 : 500000, то на этой карте длина каждого отрезка уменьшена в 500000 раз. На такой карте расстояние, равное 5 км, будет изображаться отрезком в 1 см.
Масштаб карты 1 : 500000 = Говорят, что карта сделана в
масштабе одна пятитысячная.
3) Работа с учебником. (слайд 9)
— Самостоятельно разберите задачу 1 на стр. 134.
Составьте задачу по карте
масштаб карты 1 : 100000 (в 1 см — 1 км)
Задача. Длина отрезка на карте 2 см. Найдите длину соответствующего отрезка на местности, если масштаб карты 1 : 100000. (слайд 10)
Решение:
Пусть х (м) — расстояние на местности.
расстояние |
масштаб |
|
На карте |
2см |
1см |
На местности |
Х см |
100000 см |
2:х = 1:100000
х = 200000
200000см = 2000 м = 2 км
Ответ: 2 км на местности.
5. Физкультминутка.
6. Закрепление изученного материала.
Рассмотрим две задачи из учебника Н.Я. Виленкина, В.И. Жохова, А.С. Чеснокова, С.И. Шварцбурда «Математика 6». (слайд 11-12)
Задача. Отрезку на карте, длина которого 3,6 см, соответствует расстояние на местности 72 км. Каково расстояние между городами, на этой карте расстояние между ними 12,6 см?
Решение. Составим таблицу. Запись: 72 км = 7 200 000 см — обязательна. Учащиеся должны каждый раз видеть, что вычисляется отношение величин, измеренных одной и той же единицей.
Таблица
На карте |
3,6см |
12,6см |
На местности |
72 км = 7 200 000 см |
Х см |
Затем, проговаривая определение
масштаба, заполняем две последние клетки в
таблице.
— Ребята! А карта у нас одна и та же? Значит, масштаб в обоих случаях один и тот же? Тогда мы можем приравнять два отношения:
3,6: 7 200 000 = 12,6: х.
Вот теперь учащиеся вступают на достаточно известную им дорогу. Они уже отработали способ решения уравнений такого вида. Записывают равенство произведения крайних членов пропорции произведению ее средних членов и находят значение х:
7 200 000 * 12,6 = 3,6 * х,
Х = (7200000 * 12,6):3,6
Здесь, как правило, учащиеся торопятся умножать. Но этого делать не следует. Надо попытаться сначала сократить дробь, воспользовавшись равными отношениями 12,6:3,6 = 126:36 = 7:2. Тогда
7200000 * 7
х = ———————
2
или х = 3600000 * 7 = 25200000(см) = 252(км).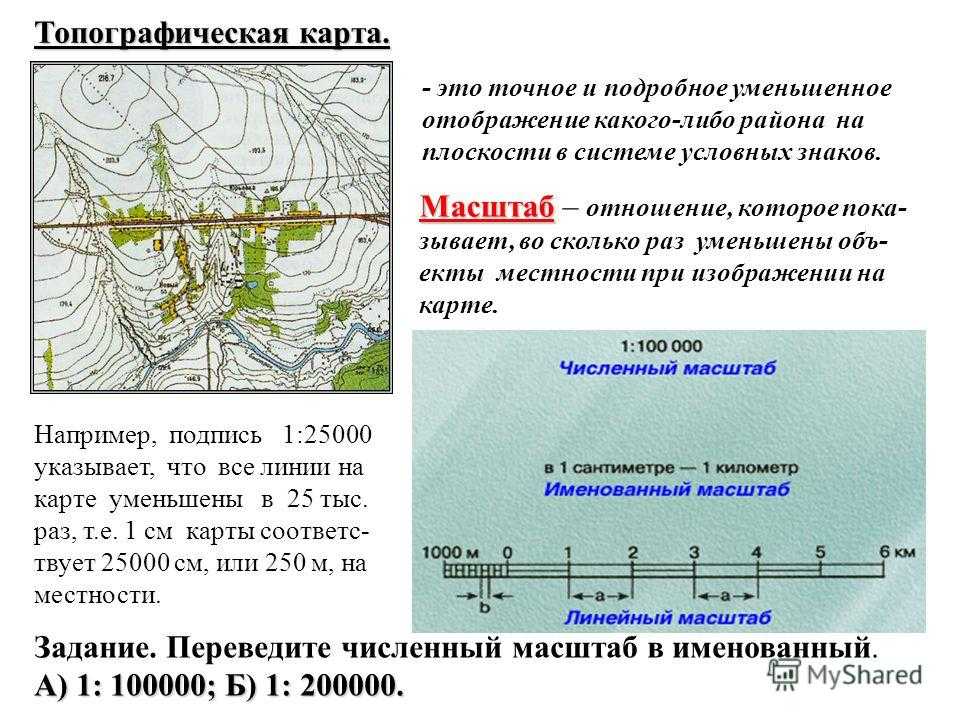
Такой подход демонстрирует учащимся возможность отказаться от калькулятора, не загружая себя скучной вычислительной работой.
Задача . Отрезок на местности длиной 3 км изображен на карте отрезком 6 см. Какова на карте длина отрезка, изображающего отрезок 10 км? Какой отрезок на местности изображает отрезок на карте длиной 1,8 см?
Решение.
Составляем таблицу, аналогичную таблице в предыдущей задаче, подробно разбирая, в какую строчку какое данное записать. При этом вводим две переменные. Это, во-первых, делает наглядной запись условия, а во-вторых, служит подготовкой к решению задач с двумя неизвестными.
Итак, на первом этапе решения появляется таблица. Строка «Масштаб» пока еще не заполнена — она заполняется по ходу решения.
Таблица
| На карте | 6 см | Х см | 1,8 см |
| На местности | 3 км=300000 см | 10 км =1 000000 см | У см |
| Масштаб |
«Что же можно узнать из второй колонки
таблицы?» — «Масштаб, он равен: 6 см: 300 000 см = 2: 100
000».
— «А как можно найти масштаб иным способом, из третьей колонки таблицы?»
Ведя такую беседу (и каждый раз проговаривая определение масштаба, что очень важно), получаем вместе с классом уравнение 2: 1 00 000 = х: 1 000 000, отсюда х = 20 (см).
Снова вспоминая понятие масштаба, получаем уравнение
2: 100 000 = 1,8: у,
у = 90 000 (см) = 0,9 (км).
Конечно, в более сильных классах можно не проговаривать определение масштаба каждый раз. Но таблица, облегчающая запись решения задач, думаю, поможет всем учащимся.
7. Самостоятельная работа. (слайд 13)
Найдите расстояние между поселком Найдорф и станицей Нововеличковской если масштаб карты 1: 100000
8. Итог урока. (слайд 14)
— Что называют масштабом карты?
— Где в практической деятельности человек пользуется этим понятием?
— Чему равен масштаб чертежа, если на нем детали увеличены в 5 раз? Уменьшены в 50 раз?
9.
Домашнее задание. (слайд 15)
Стр. 137 № 842, 844
Творческое задание: нарисуйте план своего дома в масштабе 1:100 (в 1 см — 1 метр).
Приложение №1 - Презентация к уроку по теме «Масштаб»
Масштаб карты 1:4000000$. Каково фактическое расстояние между двумя городами, если на карте расстояние между ними 5 см?
Последняя обновленная дата: 16 февраля 2023
•
Общее представление: 256,8K
•
Просмотр сегодня: 3,44K
Ответ
Проверено
256,8K+ виды
HINT: 2020202121,8K+ View
. фактическое расстояние между городами как x. Тогда мы можем взять отношение расстояния на карте к фактическому расстоянию и приравнять его к масштабу карты. Затем мы можем найти x и преобразовать в километры, чтобы получить требуемый ответ.
Полное пошаговое решение:
Нам дано, что масштаб карты $1:4000000$ .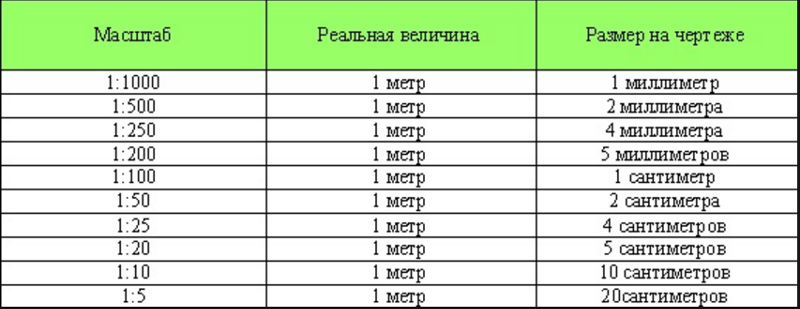
Это означает, что 1 единица на графике эквивалентна 4 000 000 единиц в действительности.
Нам нужно найти фактическое расстояние между двумя городами, расстояние между которыми составляет 5 см на карте.
Пусть x будет фактическим расстоянием между двумя городами. Таким образом, мы можем записать это как отношение расстояния на карте к фактическому расстоянию
$ \Rightarrow 5:x$
Это отношение будет пропорционально заданному масштабу карты. Таким образом, мы можем записать их как
$ \Rightarrow \dfrac{1}{{4000000}} = \dfrac{5}{x}$
При перекрестном умножении получаем
$ \Rightarrow x = 5 \times 4,000,000$
При упрощении получаем
$ \Rightarrow x = 20 000 000$
Поскольку расстояние на карте равно 5 см, единицей измерения x будет сантиметр.
$ \Rightarrow x = 20,000,000cm$
Мы знаем, что $1cm = \dfrac{1}{{100}}m$ . Итак, x станет равным
$ \Rightarrow x = \dfrac{{20,000,000}}{{100}}m$
Мы также знаем, что $1m = \dfrac{1}{{1000}}km$ .
Итак, х станет
$ \Rightarrow x = \dfrac{{20,000,000}}{{100 \times 1000}}km$
После сокращения нулей мы получаем,
$ \Rightarrow x = 200km$
городов составляет 200 км.
Примечание:
Альтернативное решение этой задачи:
Нам известно, что масштаб карты $1:4000000$ . Это означает, что 1 единица на графике эквивалентна 4 000 000 единиц в действительности.
Таким образом, 5 см на карте будут равны 5 умноженным на 4000000 см. 9{ — 5}}km$
При сокращении мощностей получаем,
$ \Rightarrow d = 20 \times 10km$
При упрощении получаем,
$ \Rightarrow d = 200km$
Следовательно, фактическое расстояние между двумя городами составляет 200 км.
Недавно обновленные страницы
Если abc — это pthq-й и r-й термины GP, то left fraccb class 11 maths JEE_Main
Если pthqth и rth термины GP — abc соответственно, математика класса 11 Ifc JEE_Main
любые четыре последовательные коэффициенты любого класса 11 математики JEE_Main
Если A1A2 являются двумя АП между двумя числами a и b, математика класса 11 JEE_Main
Если pthqthrth и sth члены AP находятся в GP, то p математика класса 11 JEE_Main
Один корень уравнения cos x x + frac12 0 лежит in class 11 maths JEE_Main
Если abc являются pthq и rth членами GP, то left fraccb class 11 maths JEE_Main
Если pthqth и rth члены GP равны abc соответственно, математика class 11 JEE_Main
Если abcda есть любые четыре последовательных коэффициента любой математики 11 класса JEE_Main
Если A1A2 являются двумя АП между двумя числами a и b, математика класса 11 JEE_Main
Если pthqthrth и sth члены AP находятся в GP, то p математика класса 11 JEE_Main
Один корень уравнения cos x x + frac12 0 лежит в 11 классе математики JEE_Main
Актуальные сомнения
I_2444_plate_1.
tif%PDF-1.6 % 1 0 объект >]/Страницы 3 0 R/Тип/Каталог>> эндообъект 2 0 объект >поток 2011-12-07T16:01:15-06:002011-12-02T14:27:39-06:002011-12-07T16:01:15-06:00Adobe Acrobat 10.0application/pdf
