Задачи и упражнения. . Математический аппарат инженера
1. Любая матрица является прямоугольной таблицей. Справедливо ли обратное утверждение, т.е. можно ли считать всякую прямоугольную таблицу матрицей? Если нет,то какие дополнительные требования выдвигаются с позиций матричной алгебры?
2. Какие из приведенных ниже совокупностей объектов представляют собой матрицы:
3. Укажите, какие из приведенных ниже матриц являются равными между собой (при x=2)%
4. При каком значении x матрицы А и В равны:
5. Найти сумму А + В и разность А — В матриц:
6. Найти произведения АВ и ВА и сравнить полученные результаты для матриц:
— 42 —
7. Проверить дистрибутивность умножения слева А(В + С) = АВ + АС и справа (А + В)С = АС + ВС относительно сложения для следующих матриц:
8.
Найти все матрицы, перестановочные с матрицей
9. Каким условиям в общем случае должны удовлетворять элементы квадратных матиц А и В второго порядка, чтобы они были перестановочными (АВ = ВА)? Как выглядят эти условия для случая, когда А симметричная матрица?
10. При каких условиях справедливы матричные соотношения:
(A + B)2 = A2 + 2AB +B2; (A-B)(A+B) = A2 — B2?
11. Каким условиям должны удовлетворять элементы ненулевых квадратных матриц А и В, чтобы АВ = 0?
12. К каким типам относятся матрицы:
13. Построить транспонированную At, комплексно-сопряженную A̅ и сопряженную А* для матрицы
14. Показать, что матрица
является эрмитовой. Что можно сказать о диагональных элементах любой эрмитовой матрицы?
15. Какого типа должна быть квадратная матрица А, чтобы она была перестановочной с диагональной матрицей D того же порядка, т.
16. К какому типу относятся треугольные матрицы, если они кроме того: а) симметричные, б) кососимметричные?
17. Показать, что (A̅B̅) = A̅ B̅ и (AB)* = B* A*.
18. Проверить соотношение (AB)* = B*A* для матриц задачи 6в.
19. Показать, что произведение AAt существует для любой матрицы А и является симметричной матрицей.
— 43 —
20. Для заданных матриц найти обратные и проверить соотношение AA-1 = 1:
21. Найти матрицы, обратные заданным, и проверить соотношение (AB)-1 = B-1A-1:
22. Дана система уравнений:
Записать эту систему в матричной форме Ax = q, вычислить обратную матрицу А
23. Зависимости между токами и напряжениями четырехполюсника (рис. 6, а) можно представить одной из систем уравнений:
Рис.
6. Соединение четырехполюсника: а — четырехполюсник; б — последовательное соединение; в — параллельное соединение.
а) Записать эти уравнения в матричной форме и установить зависимости между элементами матриц:
б) Показать, что матрица А последовательного соединения четырехполюсников (рис 6. б) равна произведению их матриц A’ и A», т.е. A = A’ A» (в порядке следования).
в) Показать, что матрица Y параллельного соединения четырехполюсников (рис. 6, в) равна сумме их матриц Y’ и Y», т.е. Y = Y’ + Y».
— 44 —
24. Выполнить умножение матриц, воспользовавшись разбиением их на блоки:Проверить результат непосредственным умножением матриц.
3. Задания и упражнения:
3.1. Напишите и отладьте программу умножения матрицы на вектор.
3.
2. Элементы матрицы
и векторадолжны определяться по формулам
,
, ,
где — номер варианта,- размерность матрицы.
3.3. Заполните таблицу:
Размер | Последовательный алгоритм | Параллельный алгоритм | |||
4 процесса | |||||
Время | Ускорение | Время | Ускорение | ||
10 | |||||
100 | |||||
1000 | |||||
2000 | |||||
5000 | |||||
10000 | |||||
В графу «Последовательный алгоритм»
внесите время выполнения последовательного
алгоритма, замеренное при проведении
тестирования последовательного
приложения.
Для того, чтобы вычислить
ускорение, разделите время выполнения
последовательного алгоритма на время
выполнения параллельного алгоритма.
Результат поместите в соответствующую
графу таблицы.
Лабораторная работа 6.
Тема: Разработка параллельного умножения матриц, блочные схемы распределения данных (алгоритмы Фокса и Кеннона). Оценка эффективности параллельного алгоритма.
Операция умножения матриц является одной из основных задач матричных вычислений. В данном разделе рассматриваются несколько разных параллельных алгоритмов для выполнения этой операции. Один из них основан на ленточной схеме разделения данных. Другие два метода основаны на блочной схеме разделения — это широко известные алгоритмы Фокса (Fox) и Кэннона (Cannon).
1. Постановка задачи.
Умножение матрицы A размера n×m и матрицы B размера m×l приводит к получению матрицы С размера n×l, каждый элемент которой определяется в соответствии с выражением
,
,.
Этот алгоритм предполагает выполнение m×n×l операций умножения и столько же операций сложения элементов исходных матриц. При умножении квадратных матриц размера n количество выполненных операций имеет порядок .
Последовательный алгоритм умножения матриц представляется тремя вложенными циклами:
double MatrixA[Size][Size];
double MatrixB[Size][Size];
double MatrixC[Size][Size];
int i,j,k;
…
for (i=0; i<Size; i++){
for (j=0; j<Size; j++){
MatrixC[i][j] = 0;
for (k=0; k<Size; k++){
MatrixC[i][j] = MatrixC[i][j] + MatrixA[i][k]*MatrixB[k][j];
}
}
}
Рисунок
6.1 – Последовательный алгоритм умножения
матриц.
2. Умножение матриц при ленточной схеме разделения данных.
Рассмотрим параллельный алгоритм умножения матриц, в которых матрицы A и B разбиваются на непрерывные последовательности строк или столбцов (полосы).
Из определения операции матричного умножения следует, что вычисление всех элементов матрицы С может быть выполнено независимо друг от друга. Как результат, возможный подход для организации параллельных вычислений состоит в использовании в качестве базовой подзадачи процедуры определения одного элемента результирующей матрицы
Рассмотрев
предложенный подход, можно отметить,
что достигнутый уровень параллелизма
является в некоторой степени избыточным.
Обычно при проведении практических
расчетов количество сформированных
подзадач превышает число имеющихся
процессоров и, как результат, неизбежным
является этап укрупнения базовых задач.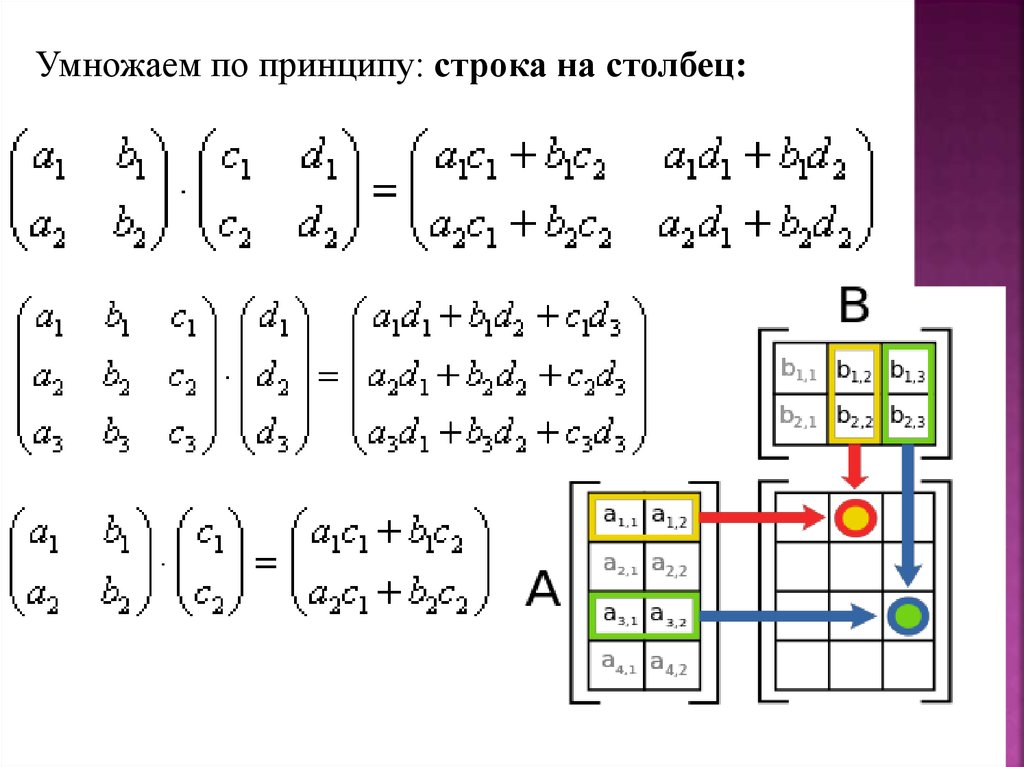
В этом плане может оказаться полезным
агрегация вычислений уже на шаге
выделения базовых подзадач. Возможное
решение может состоять в объединении
в рамках одной подзадачи всех вычислений,
связанных не с одним, а с несколькими
элементами результирующей матрицы С.
Для дальнейшего рассмотрения в рамках
данного подраздела определим базовую
задачу как процедуру вычисления всех
элементов одной из строк матрицы С.
Такой подход приводит к снижению общего
количества подзадач до величины n.
Для выполнения всех необходимых вычислений базовой подзадаче должны быть доступны одна из строк матрицы A и все столбцы матрицы B. В свою очередь для вычисления одной строки матрицы С необходимо, чтобы в каждой подзадаче содержалась строка матрицы А и был обеспечен доступ ко всем столбцам матрицы B.
Алгоритм
представляет собой итерационную
процедуру, количество итераций которой
совпадает с числом подзадач. На каждой
итерации алгоритма каждая подзадача
содержит по одной строке матрицы А и одному столбцу матрицы В.
Возможная
простая схема организации необходимой
последовательности передач столбцов
матрицы В между подзадачами состоит в представлении
топологии информационных связей подзадач
в виде кольцевой структуры. В этом
случае, на каждой итерации подзадача i,
0 ≤ i < n,
будет передавать свой столбец матрицы В подзадаче с номером i+1 (в соответствии с кольцевой структурой
подзадача n-1 передает свои данные подзадаче с номером 0)
– см.
рис. 6.2.
После выполнения всех итераций алгоритма
необходимое условие будет обеспечено
– в каждой подзадаче поочередно окажутся
все столбцы матрицы В.
Рисунок 6.2 – Общая схема передачи данных для первого параллельного алгоритма матричного умножения при ленточной схеме разделения данных
Как умножить матрицу? (+ БЕСПЛАТНЫЙ рабочий лист!)
Вот пошаговое руководство по умножению матриц. Упражнения могут помочь вам измерить свои знания об умножении матриц.
См. также
- Как складывать и вычитать матрицы
Пошаговое руководство по умножению матриц
- Шаг 1: Убедитесь, что можно перемножить две матрицы (количество столбцов в первой должно быть столько же, сколько рядов во втором.)
- Шаг 2: Элементы каждой строки первой матрицы необходимо умножить на элементы каждого столбца второй матрицы.
- Шаг 3: Добавьте продукты.
Умножение матриц – Пример 1:
\(\begin{bmatrix}-5 & -5 \\-1 & 2 \end{bmatrix}\)\(\begin{bmatrix}-2 & -3 \\ 3 & 5 \end{bmatrix}\)
Решение:
Умножьте строки первой матрицы на столбцы второй матрицы.
\(\begin{bmatrix}(-5)(-2)+(-5)(3) & (-5)(-3)+(-5)(5) \\(-1)(-2) +(2)(3) & (-1)(-3)+(2)(5) \end{bmatrix}= \begin{bmatrix}(10)+(-15) & (15)+(-25 ) \\(2)+(6) & (3)+(10) \end{bmatrix}=\begin{bmatrix}-5 & -10 \\8 & 13 \end{bmatrix}\)
Умножение матриц – Пример 2:
\(\begin{bmatrix}-4 & -6&-6 \\0 & 6&3 \end{bmatrix}\begin{bmatrix}0 \\-3 \\0 \end{ bmatrix}\)
Решение :
Умножить строки первой матрицы на столбцы второй матрицы. \(\begin{bmatrix}(-4)(0)+(-6)(-3)+(-6)(0) \\(0)(0)+(6)(-3)+(3 )(0) \end{bmatrix}=\begin{bmatrix}0+18+0 \\0-18+0 \end{bmatrix}=\begin{bmatrix}18 \\-18 \end{bmatrix}\)
Умножение матриц – Пример 3:
\(\begin{bmatrix}1 & 3 \\2 & 4 \end{bmatrix}\)\(\begin{bmatrix}2 &4 \\-2 & 1 \end{bmatrix}\)
Решение :
\(\begin{bmatrix}(1) (2)+(3)(-2) & (1) (4)+(3) (1) \\(2) (2)+ ( 4)(-2) & (2) (4)+(4) (1) \end{bmatrix}=\begin{bmatrix}(2)+(-6) & (4)+(3) \\( 4)+ (-8) & (8)+(4) \end{bmatrix}=\begin{bmatrix}-4 & 7 \\-4 & 12 \end{bmatrix}\)
Умножение матриц – Пример 4 :
\(\begin{bmatrix}2 & -1&-1 \\3 & 1&5 \end{bmatrix}\begin{bmatrix}-2 \\-1 \\4 \end{bmatrix}\)
Решение :
Умножьте строки первой матрицы на столбцы второй матрицы.
\(\begin{bmatrix}(2)(-2)+(-1)(-1)+(-1) (4)\\(3)(-2)+(1)(-1)+( 5) (4) \end{bmatrix}=\begin{bmatrix}(-4)+(1)+(-4)\\(-6)+(-1)+(20) \end{bmatrix}= \begin{bmatrix}-7 \\13 \end{bmatrix}\)
Упражнения на умножение матрицы
Решить.
- \(\color{синий}{\begin{bmatrix}0 и 2 \\-2 и -5 \end{bmatrix}\begin{bmatrix}6 и -6 \\3 & 0 \end{bmatrix} }\)
- \(\color{синий}{\begin{bmatrix}3 & -1 \\-3 & 6\\-6&-6 \end{bmatrix}\begin{bmatrix}-1 & 6 \\5 & 4 \end{bmatrix}}\)
- \(\color{blue}{\begin{bmatrix}0 & 5 \\-3 & 1\\-5&1 \end{bmatrix}\begin{bmatrix}-4 & 4 \\-2 & -4\end{bmatrix}}\)
- \(\color{blue}{\begin{bmatrix}5 & 3&5 \\1 & 5&0 \end{bmatrix}\begin{bmatrix}-4 & 2 \\-3 & 4\\3&-5 \end{bmatrix}}\)
- \(\color{blue}{\begin{bmatrix}4 & 5 \\-4 & 6\\-5&- 6 \end{bmatrix}\begin{bmatrix}4 & 6 \\6& 2\\-4&1 \end{bmatrix}}\)
- \(\color{blue}{\begin{bmatrix}-2 & -6 \\-4 & 3\\5&0 \\4&-6\end{bmatrix}\begin{bmatrix}2 & -2&2 \\ -2 &0&-3 \end{bmatrix}}\)
- \(\color{blue}{\begin{bmatrix}6 & 0 \\-27 & 12 \end{bmatrix}}\)
- \ (\color{blue}{\begin{bmatrix}-8 и 14 \\33 & 6\\ -24&-60\end{bmatrix}}\)
- \(\color{blue}{\begin{bmatrix} -10 и -20 \\10 и -16\\ 18&-24\end{bmatrix}}\)
- \(\color{blue}{\begin{bmatrix}-14 & -3 \\-19& 22 \end{bmatrix}}\)
- \(\color{blue}{Undefined}\)
- \(\color{blue}{\begin{bmatrix}8 & 4&14\\-14 & 8&-17 \\10&-10&10 \\20&-8&26\end{bmatrix}}\)
Реза
Реза — опытный преподаватель математики и эксперт по подготовке к экзаменам, который обучает студентов с 2008 года.
Он помог многим учащиеся повышают свои баллы по стандартным тестам и поступают в колледжи своей мечты. Он работает со студентами индивидуально и в группах, ведет как живые, так и онлайн-курсы по математике, а также математическую часть стандартизированных тестов. Он предлагает индивидуальный индивидуальный план обучения и индивидуальное внимание, которое меняет отношение учащихся к математике.
Связанная с этой статьей
Как умножить матрицу Умножение матриц
Другие математические статьи
- О нас
- Свяжитесь с нами
- Оптовые заказы
- Политика возврата
Математика без усилий: мы помогаем учащимся полюбить математику — © 2023
Матрицы — ACT Math
Все математические ресурсы ACT
14 диагностических тестов 767 практических тестов Вопрос дня Карточки Learn by Concept
← Предыдущая 1 2 3 4 Следующая →
ACT Math Help » Алгебра » Матрицы
Оценка:
Возможные ответы:
Правильный ответ:
Объяснение:
В этой задаче используется скалярное умножение на матрицу.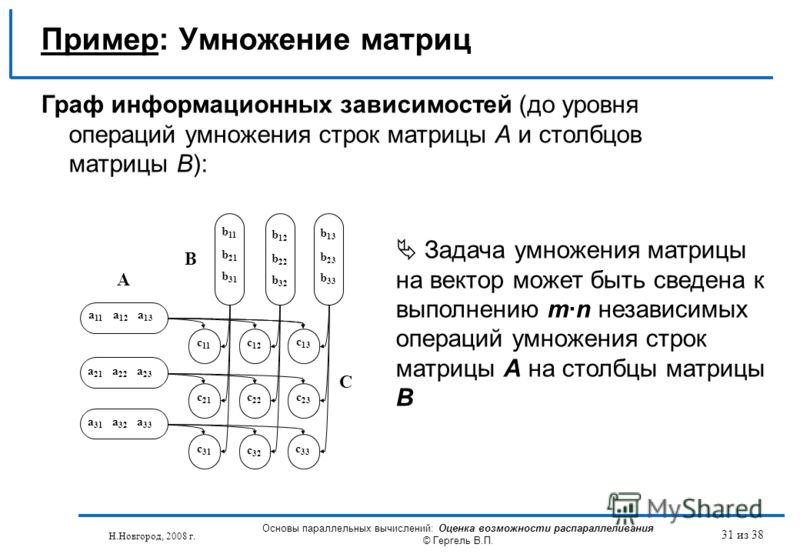
Просто распределите отрицательную тройку и умножьте это значение на каждое число в матрице 2 на 3. Строки и столбцы не изменятся.
Сообщить об ошибке
Что такое ?
Возможные ответы:
Правильный ответ:
Объяснение:
Вы можете начать с обработки этого уравнения так, как оно было:
То есть вы можете разделить обе части на :
Теперь, для скалярного умножения матриц, вам просто нужно умножить скаляр на каждый компонент:
Тогда упростите:
Поэтому
Сообщить об ошибке
Если , то что?
Возможные ответы:
Правильный ответ:
Объяснение:
Начните с распределения дроби по матрице в левой части уравнения.
Это упростит содержание, учитывая, что они являются факторами :
Теперь это означает, что ваше уравнение выглядит так:
This simply means:
and
or
Therefore,
Report an Error
Simplify:
Possible Answers:
Correct answer:
Объяснение:
Скалярное умножение и сложение матриц очень просты. Как и в случае с обычными скалярными значениями, вы сначала выполняете умножение:
Сложение матриц очень просто. Вам просто нужно добавить их непосредственно вместе, напрямую соотнеся пробелы.
Сообщить об ошибке
Упростите следующее
Возможные ответы:
Правильный ответ: 3 Пояснение: При умножении любой матрицы на скалярную величину (в нашем случае на 3) мы просто умножаем каждый член матрицы на скаляр. Следовательно, каждое число просто умножается на 3, что дает нам ответ. Сообщить об ошибке Определите матрицу , и пусть будет единичной матрицей 3×3. Если , то оцените . Возможные ответы: Правильный ответ: Объяснение: Единичная матрица 3×3 равна И скалярное умножение матрицы, и сложение матриц выполняются поэлементно, поэтому – это первый элемент в третьей строке , который равен 3; сходным образом, . Следовательно, Сообщить об ошибке Определить матрицу , пусть это будет единичная матрица 3×3. Если , то оцените . Возможные ответы: Правильный ответ: Объяснение: Единичная матрица 3×3 равна И скалярное умножение матрицы, и сложение матриц выполняются поэлементно, поэтому – это первый элемент в третьей строке , который равен 3; сходным образом, . Сообщить об ошибке Определить матрицу . Если , оцените . Возможные ответы: Правильного ответа нет среди других ответов. Правильный ответ: Объяснение: Если , то . Скалярное умножение матрицы выполняется поэлементно, поэтому – это первый элемент во второй строке , которая равна 5, поэтому Сообщить об ошибке Определить матрицу . Если , оцените . Возможные ответы: Правильного ответа нет среди других ответов. Правильный ответ: Объяснение: Скалярное умножение матрицы выполняется поэлементно, поэтому – это третий элемент во второй строке , который равен 1, поэтому Сообщить об ошибке Определить матрицу , пусть это будет единичная матрица 3×3.
Следовательно,