Математика дроби примеры 6 класс: Деление обыкновенных дробей — урок. Математика, 6 класс.

Основные правила математики с примерами. 6 класс. Часть 2.

Основные правила математики с примерами. 6 класс. Часть 2.

Содержание

Начало: Основные правила математики с примерами. 6 класс. Часть 1.

• Умножение. Свойства умножения
  
• Умножение обыкновенных дробей
• Умножение рациональных чисел
• Деление обыкновенных дробей
• Деление рациональных чисел
• Нахождение дроби от числа
• Нахождение числа по его дроби
• Степень числа

• Числовые и буквенные выражения
• Приведение подобных слагаемых
• Раскрытие скобок
• Свойства уравнений
• Отношения
• Пропорции
• Основное свойство пропорции
• Процентное отношение двух чисел
• Прямая и обратная пропорциональная зависимость

Умножение. Свойства умножения

Произведением числа на натуральное число не равное 1, называют сумму, состоящую из слагаемых, каждое из которых равно а:

a · b = a +a +a+. ..+a⏟b

4· 5 =4 + 4 + 4 + 4 + 4⏟5

Если один из двух множителей равен 1, то произведение равно второму множителю:

m · 1 = 1 · m = m

5 · 1 = 5;1 · 5 = 5.

Если один из множителей равен нулю, то произведение равно нулю:

5 · 0 = 0;0 · 5 = 0.

Если произведение равно нулю, то хотя бы один из множителей равен нулю.

!Важное правило. Помогает решать уравнения

(x — a)(x — b) = 0;Или  x — a = 0 ,или x—b = 0;2 корня x=a и x = b.(x — 5)(x +  2) = 0;Или  x — 5 = 0 ,или x+ 2 = 0;2 корня x=5 и x = —2.

Умножение обыкновенных дробей

Чтобы умножить дробь на натуральное число, надо ее числитель умножить на это число, а знаменатель оставить без изменения:

ab·n=a·nb

27 · 3=  2 · 37 = 67

Произведением двух дробей является дробь, числитель которой равен произведению числителей, а знаменатель — произведению знаменателей:

ab · cd = a · cb · d

27 · 45 = 2 · 47 · 5 = 835

Чтобы умножить смешанные числа, надо сначала записать их в виде неправильных дробей, а затем воспользоваться правилом умножения дробей.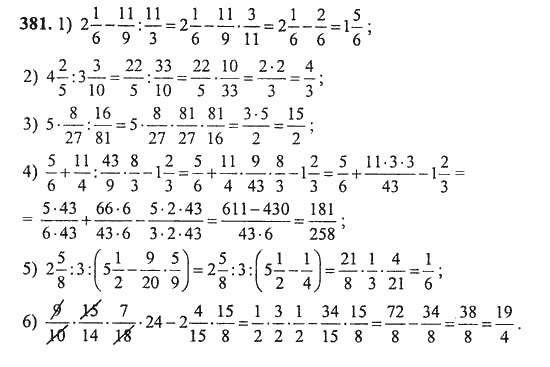

113 · 235 = 43 · 135 = 5215 = 3715

Умножение рациональных чисел

Чтобы умножить два числа с разными знаками, надо умножить их модули и перед полученным произведением поставить знак «-».

—5⏞—5=5 · 15 ⏞15=15= —(5 · 15) = —75.

Чтобы умножить два отрицательных числа, надо умножить их модули.

—8⏞—8=8 · (—5) ⏞—5=5= 8 · 5 = 40.

Для любого рационального числа :

a · (—1) = —a

12 · (—1) = —12;

Если произведение  •  — положительное, то числа и имеют одинаковые знаки;

a = 3  и  b = 2;a · b = 3 · 2 = 6 >0.а =—3 и b = —2;a · b = —3 · (—2) = 6 >0

Если произведение • — отрицательное, то числа и имеют раз­ные знаки.

a = 3  и  b = —2;a · b = 3 · (—2) =—6 < 0.а =—3 и b = 2;a · b = —3 · 2 = 6 < 0

Деление обыкновенных дробей

Чтобы разделить одну дробь на другую, надо делимое умножить на число, обратное делителю:

ab : cd = ab · dc

23 : 57 = 23 · 75 = 1415

Деление рациональных чисел

Чтобы найти частное двух чисел с разными знаками, надо мо­дуль делимого разделить на модуль делителя и перед полученным числом поставить знак «-».

—15⏞—15=15 · 5 ⏞5=5= —(15 : 5) = —3

Чтобы найти частное двух отрицательных чисел, надо модуль делимого разделить на модуль делителя.

—18⏞—18=18 : (—3) ⏞—3=3= 18 : 3 = 6

Нахождение дроби от числа

Чтобы найти дробь от числа, можно число умножить на эту дробь.

Найти 0,7 от числа 20:0,7 · 20 = 14.Найти 37 от числа 70:37 · 70 = 30

Чтобы найти проценты от числа, можно представить проценты в виде дроби и умножить число на эту дробь.

Найти 15% от числа 200:15% = 15100;15100 · 200 = 30

[ads2]

Нахождение числа по его дроби

Чтобы найти число по значению его дроби, можно это значение разделить на эту дробь.

Найти число, если известно, что

 его дробь 57 составляет число 15:15 : 57 = 15 · 75 = 153 · 751  = 21

Чтобы найти число по его процентам, можно представить про­центы в виде дроби и разделить значение процентов на эту дробь.

Найти число, если известно, что

 24% этого числа равны 48.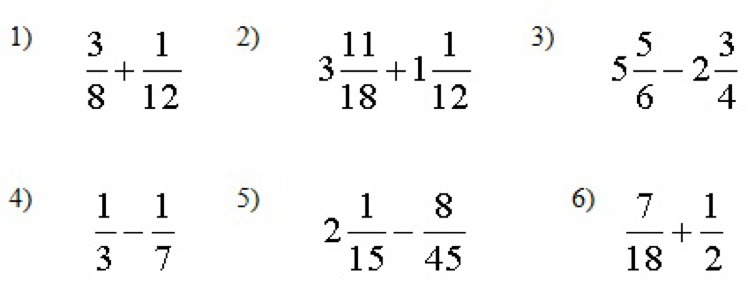 24% = 24100;48 : 24100 = 48 · 10024 = 482 · 100241 = 200

Степень числа

Степенью числа с натуральным показателем , большим , на­зывают произведение множителей, каждый из которых равен :

an=a · a · a ·…·a⏟n

Число  при этом называют основанием степени.

54 = 5 · 5 · 5 · 5;5 — основание; 4 — показатель степени

Степенью числа с показателем называют само число

a1=a

71 = 7

Вторую степень числа называют также квадратом числа. Напри­мер, запись читают: « в квадрате».
Третью степень называют кубом числа, а запись читают: « в кубе».

Если в числовое выражение входит степень, то сначала выпол­няют возведение в степень, а затем производят другие действия.

Найти значение выражения

5 · 23 +155 ·2 231 +315 = 5 · 8 + 15 = 40 + 15 =55

Числовые и буквенные выражения

Запись, составленную из чисел, знаков арифметических действий и скобок, называют числовым выражением.

2 + 3 · 5 — 7;15 : 5

Запись, составленную из чисел, букв, знаков арифметических действий и скобок, называют буквенным выражением.

2x — 3y + 6;6x

Приведение подобных слагаемых

Чтобы привести подобные слагаемые, надо сложить их коэффици­енты и полученный результат умножить на общую буквенную часть.

2x + 3x — 11x = (2 + 3 — 11)x =—6x

Раскрытие скобок

Если перед скобками стоит знак «-», то при раскрытии скобок надо опустить этот знак, а все знаки, стоящие перед слагаемыми в скобках, изменить на противоположные.

16 — (3x + 6 —15y —21) = 16 —3x — 6 + 15y + 21

Если перед скобками стоит знак « + », то при раскрытии скобок надо опустить этот знак, а все знаки, стоящие перед слагаемыми в скобках, оставить без изменений.

22 + (3x — 10 —25y) = 22 + 3x — 10 —25y

Свойства уравнений

• Если к обеим частям данного уравнения прибавить (или из обеих частей вычесть) одно и то же число, то получим уравнение, имеющее те же корни, что и данное.

2x  + 5 = 17 | —52x + 5 —5 = 17 —52x = 12x = 12 : 2x = 6

• Если данное уравнение не имеет корней, то, прибавив к обе­им его частям одно и то же число, получим уравнение, тоже не имеющее корней.

0·x = 20 —не имеет корней.0·x = 20 | +50 ·x +5 = 20 +50·x∥0 +5 =255 = 25 — неверно, корней нет.

• Если какое-либо слагаемое перенести из одной части уравнения в другую, изменив при этом его знак на противоположный, то по­лучим уравнение, имеющее те же корни, что и данное.

—2x — 5 = 9x←—9x→+5 +50—2x —9x = 50 +5—11x = 55x = 55 : (—11)x =—5. 

• Если обе части уравнения умножить (разделить) на одно и то же отличное от нуля число, то получим уравнение, имеющее те же корни, что и данное.

x2 + 34 = 6 | ×44 ·  (x2 + 34) = 4 · 64 · x2 + 4 · 34 = 242x + 3 = 242x = 24 — 32x = 21x = 21  : 2x =10,5

[ads3]

Отношения

• Частное двух чисел и , не равных нулю, еще называют от­ношением чисел и , или отношением числа к числу .

a : b = ab частное или отношение чисел а и b.a = 5 и b =7:57 частное (отношение) чисел 5 и7

• Отношение положительных чисел и показывает, во сколько раз число больше числа , или какую часть число составляет число .

a = 10 и b = 2Отношение ab = 102 = 5

показывает, что число 10 в 5 раз больше числа 2 или число 2 в 5 раз меньше числа 10.

• Отношение не изменится, если его члены умножить или раз­делить на одно и то же число, не равное нулю.

2436 — отношение.24 : 1236 : 12  = 23

Пропорции

Равенство двух отношений называют пропорцией. В буквенном виде пропорцию можно записать так:

a : b =c : d или ab = cd

Числа и называют крайними членами пропорции, а чис­ла и — средними членами пропорции.

Пропорци x : 5 = 8 : 17 или другая записьx5 = 817;x и 17 — крайние члены пропорции;5 и 8 — средние члены пропорции.

Основное свойство пропорции

Произведение крайних членов пропорции равно произведению ее средних членов:

ab = cd ⇒ ad = bc

Если , , и числа, не равные нулю, и • = • , то отношения

ab  и cd

  могут образовывать пропорцию

ab = cd

Пропорция  23 = 69 Перемножим крест накрест   по основному свойству пропорции  23 = 69Получим  2 · 9 = 3 ·  6.  Также можно составить еще 3  верные пропорции:26  = 39;96  = 32;93 = 62

Процентное отношение двух чисел

Процентное отношение двух чисел — это их отношение, выраженное в процентах. Оно показывает, сколько процентов одно число составляет от другого.
Чтобы найти процентное отношение двух чисел, надо их отношение умножить на 100 и к результату дописать знак процента.

Числа 5 и 20.Найдем отношение 5 к 20 и умножим на 100 %:51204  · 100% = 1 · 1002541% = 25%.Значит, число 5 — это 25 % от числа 20.

Прямая и обратная пропорциональная зависимость

Две величины называют прямо пропорциональными, если при увеличении (уменьшении) одной из них в несколько раз другая увеличивается (уменьшается) во столько же раз.

Формула пути S = V · t.S —путь, V —скорость, t —время.Величины S и V, а также S и t —прямо пропорциональны.Пусть V = 5 км/ч, t = 2ч.Тогда S = 5 * 2 = 10(км).Если мы увеличим, например, скорость в 5 раз V = 5 · 5 =25(км/ч)Тогда S = 25 · 2 = 50(км). Путь был 10 км, стал 50км, увеличился в 5 раз.

Если величины и обратно пропорциональны, то их соответ­ствующие значения удовлетворяют равенству

y = kx

,  где  -число, постоянное для данных величин.

V  = S tV— скорость и t  —время обратно пропорцилональны.Чем выше скорость, тем меньше времени требуется на путь. Пусть объект проехал S = 100 км за t =2ч.Тогда V = 1002 =( 50 км/ч).Если же время потребуется 5 ч, то скорость объекта V = 1005 = (20 км/ч)

 

Начало: Основные правила математики с примерами. 6 класс. Часть 1.

Правила и определения опираются  на  УМК  А.Г.Мерзляк, В.Б.Полонский, М.С. Якир.  Примеры составлены мной (Косыхина Н.В.)

 

6 класс — сравнение дробей, сокращение дробей, основное свойство дробей

Дата публикации: 12 апреля 2017.

Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания.

Все материалы проверены антивирусной программой.

---

Скачать:Дроби. Действия с дробями. Основные свойства дробей (PDF)

Обучающие пособия и тренажеры в интернет-магазине «Интеграл» для 6 класса
Электронная рабочая тетрадь по математике для 6 класса, онлайн версия
Электронное учебное пособие для 6 класса «Математика за 10 минут»

---

Основное свойство дробей. Сокращение дроби. Приведение дроби к общему знаменателю. Сравнение дробей

1. Сократите заданные дроби. Если дробь десятичная, то представьте её в виде обыкновенной дроби: ¹⁴⁄₁₈;  ¹²⁄₂₆;  0,55;  0,82.

2. Задан ряд чисел: ¹⁵⁄₂₀;  ³⁰⁄₄₄;  0,70;  ⁵⁄₂₅. Определите среди них число равное, ³⁄₄.

3. Ответьте на вопросы.
а) Какую часть от 1 килограмма составляют 250 грамм?
б) Какую часть от 1 минуты составляют 45 секунд?

в) Какую часть от 1 метра составляют 15 см?

4. Приведение дробей к знаменателю.
а) Приведите дробь ³⁄₈ к знаменателю 64.
б) Приведите дроби ⁵⁄₈ и ⁹⁄₁₂ к общему знаменателю.
в) Приведите дроби ⁷⁄₁₈ и ¹⁷⁄₂₇ к общему знаменателю.

5. Умножьте дроби: ¹⁄₃;  ⁵⁄₇;  0,3;  0,45;  ¹²⁄₁₄;  ²³⁄₂₇;  1,5 на число 4.

6. Решите задачу.
На уроке физкультуры ученики 2 класса прыгали с места. Вася прыгнул на расстояние, равное ⁷⁄₁₀ метра, а Коля – на ⁴⁄₅ метра. Чей прыжок длиннее и на сколько сантиметров?

7. Решите задачу.
Рабочие ремонтировали крышу школы. За первый день они покрыли ⁹⁄₂₀ крыши, на второй день –

2⁄₅ крыши. В какой день они выполнили большую часть работ?

8. Решите задачу.
Школьники 6 класса решали задачи. За первый час они решили ²⁄₆ примера, а за второй час – ³⁄₈ примера. В течении которого часа школьники решили больше примеров?

7. Сравните дроби: ⁴⁄₅ и ⁷⁄₁₀;     ⁹⁄₁₂ и ¹²⁄₁₆;     ¹²⁄₁₄ и ¹⁷⁄₁₉;     ²⁹⁄₄₀ и ²⁵⁄₃₅.

Сложение и вычитание дробей с разными знаменателями. Сложение и вычитание смешанных чисел

1. Решите примеры.
a) ⁸⁄₁₂ + ¹²⁄₁₈= ;     б) ⁵⁄₉ — ²⁄₁₀= ;     в) ¹⁄₃ + (⁴⁄₉ — 0,2)= .

2. Решите задачу.
Длина первого бревна равна 4

3⁄₇ метра, длина второго бревна – на ⁷⁄₁₂ метра длиннее. Какова длина второго бревна? Чему равна длина обоих бревен?

3. Решите задачу.
Для ремонта детского садика привезли столитровую бочку краски. В течении первой недели использовали ⁷⁄₂₀ части краски. За вторую неделю – на ¹⁄₂₅ больше, чем за первую неделю. Сколько литров краски осталось в бочке? Сколько литров краски было использовано за вторую неделю?

4. Решите уравнения.
а) ⁴⁄₉ + x = 5 ⁷⁄₁₂;
б) z — ³⁄₇ = ¹⁄₉.

5. Решите примеры со смешанными числами.
а) 3 — 1 ⁷⁄₁₂ + ²⁄₆= ;
б) 1 ²⁄₅ + 2 ³⁄₈

— 0,6 = .

6. Решите уравнения со смешанными числами.
а) 2 ³⁄₈ + x = 5 ¹⁄₁₆;
б) y — ³⁄₁₀ = ²⁄₁₅.

7. Решите задачу.
Маша потратила ¹⁄₁₀ часа на разогрев обеда, ³⁄₁₅ часа – на обед, 0,5 часа она подметала пол. Сколько времени потребовалось Маше на эти действия?

6-й класс Wisconsin Forward Math Worksheets: БЕСПЛАТНО и для печати

Учащиеся 6-го класса могут использовать наши 6-классные Wisconsin Forward Math Worksheets, представленные в этом посте, чтобы лучше практиковать математические концепции теста Wisconsin Forward.

Wisconsin Forward Exam — это тест для оценки успеваемости учащихся 3–8 классов. Математический раздел очень важен почти во всех тестах. Практика математических тем и понятий с помощью 6-го класса Wisconsin Forward Math Worksheet может улучшить процесс практики учащихся и вызвать у них интерес к изучению уроков математики. Решая упражнения в нашем 6-м классе Wisconsin Forward Math Worksheet, учащиеся, помимо изучения тем и лучшего отработки математических понятий, также хорошо познакомятся с различными решениями для решения вопроса. Так что не упустите эту возможность и загрузите наш БЕСПЛАТНЫЙ и полный рабочий лист Wisconsin Forward Math Worksheet для 6-го класса прямо сейчас!

ВАЖНО: УСЛОВИЯ АВТОРСКОГО ПРАВА: Эти листы предназначены для личного использования. Рабочие листы нельзя загружать в Интернет в любой форме, включая классные/личные веб-сайты или сетевые диски. Вы можете скачать рабочие листы и распечатать столько, сколько вам нужно. У вас есть разрешение на распространение печатных копий среди ваших учеников, учителей, наставников и друзей.

У вас НЕТ разрешения на отправку этих листов кому бы то ни было (по электронной почте, текстовым сообщениям или другим способом). Они ДОЛЖНЫ загрузить рабочие листы самостоятельно. Вы можете отправить адрес этой страницы своим ученикам, репетиторам, друзьям и т.д.

Связанные темы

• 4 -й класс в штате Висконсин Форвард Форвард. Абсолютно лучшая книга для сдачи 6-го класса Wisconsin Forward Math Test

  6-й класс Wisconsin Forward Mathematics Concepts

  Целые числа

  • Округление
  • Добавление и вычитание целого числа
  • Умножение и разделение целого числа
  • Об округление и оценки

  Фракции и десятичные дни

  • Упрощающие фракции
  • Добавляя и подразделение
    • . Вычитание смешанных чисел
    • Умножение и деление смешанных чисел
    • Сложение и вычитание десятичных чисел
    • Multiplying and Dividing Decimals
    • Comparing Decimals
    • Rounding Decimals
    • Factoring Numbers
    • Greatest Common Factor
    • Least Common Multiple

    Real Numbers and Integers

    • Adding and Subtracting Integers
    • Multiplying and Dividing Integers
    • Order операций
    • Порядок целых чисел и чисел
    • Целые числа и абсолютные значения

    Пропорции, отношения и проценты

    • Simplifying Ratios
    • Proportional Ratios
    • Similarity and Ratios
    • Ratio and Rates Word Problems
    • Percentage Calculations
    • Percent Problems
    • Discount, Tax, and Tip
    • Percent of Change
    • Simple Interest

    Algebraic Выражения

    • Упрощение выражений переменных
    • Упрощение полиномиальных выражений
    • Преобразование фраз в алгебраическое выражение
    • Распределительное свойство
    • Оценка одного переменного выражения
    • Оценка экспрессии двух переменных
    • , таких как термины

    Уравнения и неравенство

    • Одноэтапные уравнения
    • . Одношаговые неравенства
    • Многошаговые неравенства

    Экспоненты и радикалы

    • Свойство умножения экспонент
    • Нулевые и отрицательные экспоненты
    • Свойство экспонентов
    • Powers продуктов и коэффициентов
    • Отрицательные экспоненты и отрицательные основания
    • Научная нотация
    • квадратные корни

    Геометрия и твердые фиг.

  • Треугольники
  • Многоугольники
  • Трапеции
  • Круги
  • Кубы
  • Прямоугольная призма
  • Цилиндр
  • Pyramids and Cone

  Статистика и вероятность

  • Среднее значение и медиана
  • Режим и диапазон
  • Гистограммы
  • STEM -и LEAF
  • . Ace the Wisconsin Forward Math Test

    Математические упражнения Wisconsin Forward для 6-го класса

    Дроби и десятичные дроби

    Вещественные и целые числа

    Пропорции и коэффициенты

    процент

    Алгебраические выражения

    Уравнения и неравенства

    ЭКСПОРИТАНИЕ И РАДИКАЛЫ

    СТАТИСТИКА

    GEOMETRY

    . контрольная работа?
    Лучшие книги для сдачи 6-го класса Wisconsin Forward Math Test

    Рабочие листы по математике для 6-го класса, которые можно распечатать на основе Сингапурской математической программы.

    Выберите одну из следующих тем по математике для 6 класса с рабочими листами, основанными на учебной программе Сингапура по математике.

    Дополнение
    

    Вычитание
    

    Умножение
    

    Подразделение
    

    Дроби
    

    Десятичные числа
    

    Порядок работы
    

    Коэффициенты и множители
    

    Экспоненты
    

    Квадратные корни
    

    Проценты
    

    Соотношения и пропорции
    

    Формы и геометрия
    

    Площадь и периметр
    

    Алгебра
    

    Целые/отрицательные числа
    

    Пиктограммы
    

    Гистограммы
    

    Линейные графики
    

    Круговые диаграммы
    

    Точки построения
    

    Диаграммы Венна
    

    Сложение/вычитание в отличие от дробей
    

    Десятичные дроби и дроби — сложение дробей и десятичных дробей
    Десятичные дроби и дроби — сложение дробей и десятичных дробей
    сложение 3 дробей — сложение и ответ в простейших условиях
    сложение 3 дробей — сложение и ответ в простейших условиях
    сложение 3 дробей — сложение и ответ в простейших условиях
    вычитание 3 дробей — сложение и ответ в самых простых выражениях
    Вычитание 3 дробей — Сложение и ответ в самых простых условиях
    Вычитание 3 дробей — Сложение и ответ в самых простых условиях
    Сложение смешанных чисел — Приведение к эквиваленту и прибавление
    Прибавление смешанных чисел — Приведение к эквиваленту и прибавление
    

    Сложение смешанных чисел — Приведение к эквиваленту и сложение
    Вычитание смешанных чисел — Приведение к эквиваленту и вычитание
    Вычитание смешанных чисел — Приведение к эквиваленту и вычитание
    Вычитание смешанных чисел — Приведение к эквиваленту и вычитание 20/20 — Сложение и вычитание целых чисел от -20 до 20
    Числа от -20/20 — Сложение и вычитание целых чисел от -20 до 20
    Числа от -50/50 — Сложение и вычитание целых чисел от -50 до 50
    Числа от -50/50 — Сложение и вычитание целых чисел от -50 до 50
    Числа от -100/100 — Сложение/вычитание целых чисел от -100 до 100
    Числа от -100/100 — Сложение/вычитание целых чисел от -100 до 100
    От -1 000/1 000 — Целые числа от -1 000 до 1 000
    От -1 000/1 000 — Целые числа от -1 000 до 1 000 Целочисленные облигации в пределах -20/20
    Облигации -50/50 — Добавить целочисленные облигации в пределах -50/50
    Облигации -100/100 — Добавить целочисленные облигации в пределах -100/100
    Отсутствующие сложения — числа от -20 до 20
    Отсутствующие целые числа — числа от -20 до 20
    Отсутствующие целые числа — Отсутствующие целые числа от -20/20
    Отсутствующие целые числа — Отсутствующие целые числа в пределах 20/-20 От 50 до 50
    Отсутствующие целые числа — числа от -50 до 50
    Отсутствующие связи — Отсутствующие целые числа в пределах 50/-50
    Отсутствующие сложения — Числа от -100 до 100
    Отсутствующие целые числа — числа от -100 до 100
    Отсутствующие связи — Отсутствующие целые числа в пределах 100/-100
    
    
    

    Дополнение
    

    Вычитание
    

    Умножение
    

    Подразделение
    

    Дроби
    

    Десятичные числа
    

    Порядок работы
    

    Коэффициенты и множители
    

    Экспоненты
    

    Квадратные корни
    

    Проценты
    

    Соотношения и пропорции
    

    Формы и геометрия
    

    Площадь и периметр
    

    Алгебра
    

    Целые/отрицательные числа
    

    Пиктограммы
    

    Гистограммы
    

    Линейные графики
    

    Круговые диаграммы
    

    Точки построения
    

    Диаграммы Венна
    

    
    

    Наши рабочие листы по математике для шестого класса и учебные материалы по математике бесплатны и могут быть распечатаны в формате PDF.

    No related posts.