Матрица — прямоугольная числовая таблица, имеющая m строк и n столбцов, поэтому схематически матрицу можно изображать в виде прямоугольника.
Нулевой матрицей (нуль-матрицей) называют матрицу, все элементы которой равны нулю и обозначают 0.
Единичной матрицей называется квадратная матрица вида
Две матрицы A и B равны, если они одинакового размера и их соответствующие элементы равны.
Вырожденной матрицей называется матрица, определитель которой равен нулю (Δ = 0).
Определим основные операции над матрицами.
Сложение матриц
Определение. Суммой двух матриц A=||aik|| и B=||bik|| одинакового размера называется матрица C=||cik|| тех же размеров, элементы которой находятся по формулеcik=ai k+bik. Обозначается
Обозначается C=A+B.
Пример 6. .
Операция сложения матриц распространяется на случай любого числа слагаемых. Очевидно, чтоA+0=A.
Еще раз подчеркнем, что складывать можно только матрицы одинакового размера; для матриц разных размеров операция сложения не определена.
Вычитание матриц
Определение. Разностью B-A матриц B и A одинакового размера называется такая матрица C, чтоA+C=B.
Умножение матриц
Определение. Произведением матрицы A=||aik|| на число α называется матрица C=||cik||, получающаяся из A умножением всех ее элементов на α, cik=α·aik.Определение. Пусть даны две матрицы A=||ai k|| (i=1,2,…,m; k=1,2,…,n) и B=||bik|| (k=1,2,. ..,n; j=1,2,…,p), причем число столбцов A равно числу строк B. Произведением A на B называется матрица C=||cik||, элементы которой находятся по формуле .
..,n; j=1,2,…,p), причем число столбцов A равно числу строк B. Произведением A на B называется матрица C=||cik||, элементы которой находятся по формуле .
Обозначается C=A·B.
Схематически операцию умножения матриц можно изобразить так:
а правило вычисления элемента в произведении:
Подчеркнем еще раз, что произведение A·B имеет смысл тогда и только тогда, когда число столбцов первого сомножителя равно числу строк второго, при этом в произведении получается матрица, число строк которой равно числу строк первого сомножителя, а число столбцов равно числу столбцов второго. Проверить результат умножения можно через специальный онлайн-калькулятор.
Пример 7. Даны матрицы и . Найти матрицы C = A·B и D = B·A.
Заметим, что в общем случае
A·B≠B·A, т. е. произведение матриц антикоммутативно.
е. произведение матриц антикоммутативно.
Найдем
B·A (умножение возможно).
Пример 8. Дана матрица . Найти 3A2 – 2A.
Решение.
Отметим следующий любопытный факт.
Как известно, произведение двух отличных от нуля чисел не равно нулю. Для матриц подобное обстоятельство может и не иметь места, то есть произведение ненулевых матриц может оказаться равным нуль-матрице.
Пример 9. Если и , то
.
Умножение матрицы на число
При умножении числа b матрицы A=(aij) получается матрица, элементы которой равны b·aij (каждый элемент матрицы умножается на число b).Подробнее о том, почему нельзя делить матрицы.
Скачать.
Пример 9. Найти значение многочлена f(x) от матрицы A, если f(x)=2x2–3x+5.
2*A^2-3*A+5*B
где A — матрица из задания, B = E — единичная матрица.
Матричный метод решения систем линейных уравнений
Этот способ применяется в заданиях, где число уравнений совпадает с количеством неизвестных переменных. Определитель основной матрицы при этом не должен быть нулевым.
В основу калькулятора от Zaochnik заложена система формул, которая позволяет ввести имеющиеся данные и моментально получить точный ответ. Решение систем линейных уравнений матричным методом включает преобразование уравнения, нахождение определителя и обратной матрицы.
Рассмотрим несколько примеров решений СЛАУ с помощью онлайн-калькулятора
Онлайн-калькулятор позволяет находить решение СЛАУ, когда свободные члены, переменные и коэффициенты при них являются вещественными числами. Другими словами, калькулятор работает с целыми числами и дробями, а вот решение систем с комплексными коэффициентами ему не по зубам. Максимальное количество неизвестных в системе– 6.
Пример 1.
Возьмем простую систему уравнений с двумя неизвестными:
x1+2×2=113×1-x2=12
<>Для того, чтобы решить ее матричным методом с помощью онлайн-калькулятора:
- Укажем количество неизвестных в системе:
- Впишите коэффициенты при переменных в соответствующие поля:
- Нажмите «Рассчитать»
Калькулятор сам произведет все вычисления, а вы сможете не только получить ответ, но и ознакомиться подробным решением:
Пример 2.
Рассмотрим более сложную систему с большим количеством неизвестных:
2×1+10×2-3×3=38-3×1-24×2+5×3=-86×1+x2-5×3=27
По аналогии с первым примером, укажем количество неизвестных, введем в поля соответствующие коэффициенты, и нажмем «Рассчитать»:
Калькулятор выдаст ответ с ходом решения и промежуточными выкладками:
Заметьте, если вы вдруг введете неверные коэффициенты или запишите такую систему, которая не имеет решения, калькулятор выдаст соответствующее сообщение:
Теоретические статьи из справочника, которые помогут вам лучше разобраться в теме:
- Решение квадратных уравнений: формула корней, примеры
- Уравнение и его корни: определения, примеры
- Теорема Виета, формулы Виета
- Нахождение неизвестного слагаемого, множителя: правила, примеры, решения
- Квадратные неравенства, примеры, решения
- Решение квадратных неравенств методом интервалов
Ответ:
Решение
Ответ:
- list» :key=»`error-${eIdx}`» v-html=»e»/>
Похожие калькуляторы:
- Решение квадратных уравнений
- Решение систем линейных уравнений методом Крамера
- Решение систем линейных уравнений методом Гаусса
- Решение систем линейных уравнений методом подстановки
- Решение биквадратных уравнений
Матричный метод решения систем линейных уравнений онлайн
Калькулятором пользуются студенты для подтверждения правильности собственных вычислений, учащиеся профильных школ перед участием в олимпиадах, преподаватели при подготовке заданий ученикам.
Причины воспользоваться нашим онлайн-калькулятором:
- Точность расчетов. Чтобы получить ответ, необходимо произвести много последовательных действий. Если ошибка допущена в первом из них во время ручных расчетов, то результат тоже будет неверным. При автоматических вычислениях такой вариант исключен.
- Доступный алгоритм вычислений. Вы можете развернуть расчеты нажатием кнопки «Показать подробное решение». После этого вы увидите последовательные преобразования. На основе этой информации можно осуществлять самостоятельную подготовку к занятиям, осваивать сложный материал.
- Бесплатный инструмент. За использование калькулятора на сайте вам не придется вносить оплату. Вы можете тренироваться в расчетах без ограничений.
Если решение СЛАУ матричным методом онлайн или других задач не привело к желаемому результату, обратитесь за помощь к консультанту на сайте. Он сможет подобрать для вас специалиста или оформить заказ, включающий задачи любого уровня сложности.
Понравился калькулятор? Поделись с друзьями!
Решение матричных уравнений: теория и примеры
- Решение матричных уравнений: как это делается
- Решение матричных уравнений: примеры
Матричные уравнения имеют прямую аналогию с простыми алгебраическими уравнениями, в которых присутствует операция умножения. Например,
ax=b,
где x — неизвестное.
А, поскольку мы уже умеем находить произведение матриц, то можем приступать к рассмотрению аналогичных уравнений с матрицами, в которых буквы — это матрицы.
Итак, матричным уравнением называется уравнение вида
A ⋅ X = B
или
X ⋅ A = B,
где A и B —
известные матрицы, X — неизвестная матрица, которую требуется найти.
Как решить матричное уравнение в первом случае? Для того, чтобы решить матричное уравнение вида A ⋅ X = B, обе его части следует умножить на обратную к A матрицу слева:
.
По определению обратной матрицы, произведение обратной матрицы на данную исходную матрицу равно единичной матрице: , поэтому
.
Так как E — единичная матрица, то E ⋅ X = X. В результате получим, что неизвестная матрица X равна произведению матрицы, обратной к матрице A, слева, на матрицу B:
.
Как решить матричное уравнение во втором случае? Если дано уравнение
X ⋅ A = B,
то есть такое, в котором в произведении неизвестной матрицы X и известной матрицы A матрица A находится справа, то нужно действовать аналогично, но меняя направление умножения на матрицу, обратную матрице A, и умножать матрицу B на неё справа:
,
,
.
Как видим, очень важно, с какой стороны умножать на обратную матрицу, так как
. Обратная к A матрица умножается на матрицу
Как решить матричное уравнение в третьем случае? Встречаются случаи, когда в левой части уравнения неизвестная матрица X находится в середине произведения трёх матриц. Тогда известную матрицу из правой части уравнения следует умножить слева на матрицу, обратную той, которая в упомянутом выше произведении трёх матриц была слева, и справа на матрицу, обратную той матрице, которая располагалась справа. Таким образом, решением матричного уравнения
A ⋅ X ⋅ B = C,
является
.
Пример 1. Решить матричное уравнение
Решить матричное уравнение
.
Решение. Данное уравнение имеет вид A ⋅ X = B, то есть в произведении матрицы A и неизвестной матрицы X матрица A находится слева. Поэтому решение следует искать в виде , то есть неизвестная матрица равна произведению матрицы B на матрицу, обратную матрице A слева. Найдём матрицу, обратную матрице A.
Сначала найдём определитель матрицы A:
.
Найдём алгебраические дополнения матрицы A:
.
Составим матрицу алгебраических дополнений:
.
Транспонируя матрицу алгебраических дополнений, находим матрицу, союзную с матрицей A:
.
Теперь у нас есть всё, чтобы найти матрицу, обратную матрице A:
.
Наконец, находим неизвестную матрицу:
Решить матричное уравнение самостоятельно, а затем посмотреть решение
Пример 2. Решить матричное уравнение
.
Посмотреть правильное решение и ответ.
Пример 3. Решить матричное уравнение
.
Решение. Данное уравнение имеет вид X ⋅ A = B, то есть в произведении матрицы A и неизвестной матрицы X матрица A находится справа. Поэтому решение следует искать в виде , то есть неизвестная матрица равна произведению матрицы B на матрицу, обратную матрице A справа. Найдём матрицу, обратную матрице A.
Сначала найдём определитель матрицы A:
.
Найдём алгебраические дополнения матрицы A:
.
Составим матрицу алгебраических дополнений:
.
Транспонируя матрицу алгебраических дополнений, находим матрицу, союзную с матрицей A:
.
Находим матрицу, обратную матрице A:
.
Находим неизвестную матрицу:
Нет времени вникать в решение? Можно заказать работу!
К началу страницы
Пройти тест по теме Матрицы
До сих пор мы решали уравнения с матрицами второго порядка, а теперь настала очередь матриц третьего порядка.
Пример 4. Решить матричное уравнение
.
Решение. Это уравнение первого вида: A ⋅ X = B, то
есть в произведении матрицы A и неизвестной матрицы X матрица A находится слева.
Поэтому решение следует искать в виде ,
то есть неизвестная матрица равна произведению матрицы B на матрицу,
обратную матрице A слева. Найдём матрицу, обратную матрице A.
Найдём матрицу, обратную матрице A.
Сначала найдём определитель матрицы A:
.
Найдём алгебраические дополнения матрицы A:
Составим матрицу алгебраических дополнений:
Транспонируя матрицу алгебраических дополнений, находим матрицу, союзную с матрицей A:
.
Находим матрицу, обратную матрице A, и делаем это легко, так как определитель матрицы A равен единице:
.
Находим неизвестную матрицу:
Пример 5. Решить матричное уравнение
.
Решение. Данное уравнение имеет вид X ⋅ A = B, то
есть в произведении матрицы A и неизвестной матрицы X матрица A находится справа. Поэтому решение следует искать в виде ,
то есть неизвестная матрица равна произведению матрицы B на матрицу,
обратную матрице A справа. Найдём матрицу, обратную матрице A.
Поэтому решение следует искать в виде ,
то есть неизвестная матрица равна произведению матрицы B на матрицу,
обратную матрице A справа. Найдём матрицу, обратную матрице A.
Сначала найдём определитель матрицы A:
.
Найдём алгебраические дополнения матрицы A:
Составим матрицу алгебраических дополнений:
.
Транспонируя матрицу алгебраических дополнений, находим матрицу, союзную с матрицей A:
.
Находим матрицу, обратную матрице A:
.
Находим неизвестную матрицу:
Пример 6. Решить матричное уравнение
.
Решение. Данное уравнение имеет вид A ⋅ X ⋅ B = C, то
есть неизвестная матрица X находится в середине
произведения трёх матриц. Поэтому решение следует искать в виде
. Найдём матрицу, обратную матрице A.
Поэтому решение следует искать в виде
. Найдём матрицу, обратную матрице A.
Сначала найдём определитель матрицы A:
.
Найдём алгебраические дополнения матрицы A:
.
Составим матрицу алгебраических дополнений:
.
Транспонируя матрицу алгебраических дополнений, находим матрицу, союзную с матрицей A:
.
Находим матрицу, обратную матрице A:
.
Найдём матрицу, обратную матрице B.
Сначала найдём определитель матрицы B:
.
Найдём алгебраические дополнения матрицы B:
Составим матрицу алгебраических дополнений матрицы B:
.
Транспонируя матрицу алгебраических дополнений, находим матрицу, союзную с матрицей B:
.
Находим матрицу, обратную матрице B:
.
Находим неизвестную матрицу:
| Назад | Листать | Вперёд>>> |
Нет времени вникать в решение? Можно заказать работу!
К началу страницы
Пройти тест по теме Матрицы
Поделиться с друзьями
Начало темы «Матрицы»
Понятие матрицы
Продолжение темы «Матрицы»
Обратная матрица
Произведение двух матриц
Умножение матрицы на число
Сложение матриц
Другие темы линейной алгебры
Определители
Системы линейных уравнений
Решение матричных уравнений axb c
Содержание
- 1 Решение матричных уравнений: как это делается
- 2 Решение матричных уравнений: примеры
- 2.0.1 Предупреждение
- 3 Инструкция матричного онлайн калькулятора
- 4 Вычисление суммы, разности, произведения матриц онлайн
- 5 Вычисление обратной матрицы онлайн
- 6 Вычисление определителя матрицы онлайн
- 7 Вычисление ранга матрицы онлайн
- 8 Вычисление псевдообратной матрицы онлайн
- 9 Удаление линейно зависимых строк или столбцов матрицы онлайн
- 10 Скелетное разложение матрицы онлайн
- 11 Решение матричного уравнения или системы линейных уравнений AX=B онлайн
- 12 Исключение Гаусса или приведение матрицы к треугольному (ступенчатому) виду онлайн
- 13 LU-разложение или LUP-разложение матрицы онлайн
- 14 Построение ядра (нуль-пространства) матрицы онлайн
- 15 Ортогонализация Грамма-Шмидта и Ортонормализация Грамма-Шмидта онлайн
Решение матричных уравнений: как это делается
Матричные уравнения имеют прямую аналогию с простыми алгебраическими уравнениями, в которых присутствует операция умножения. Например,
Например,
где x — неизвестное.
А, поскольку мы уже умеем находить произведение матриц, то можем приступать к рассмотрению аналогичных уравнений с матрицами, в которых буквы — это матрицы.
Итак, матричным уравнением называется уравнение вида
где A и B — известные матрицы, X — неизвестная матрица, которую требуется найти.
Как решить матричное уравнение в первом случае? Для того, чтобы решить матричное уравнение вида A ⋅ X = B , обе его части следует умножить на обратную к A матрицу слева:
.
По определению обратной матрицы, произведение обратной матрицы на данную исходную матрицу равно единичной матрице: , поэтому
.
Так как E — единичная матрица, то E ⋅ X = X . В результате получим, что неизвестная матрица X равна произведению матрицы, обратной к матрице A , слева, на матрицу B :
.
Как решить матричное уравнение во втором случае? Если дано уравнение
то есть такое, в котором в произведении неизвестной матрицы X и известной матрицы A матрица A находится справа, то нужно действовать аналогично, но меняя направление умножения на матрицу, обратную матрице A , и умножать матрицу B на неё справа:
,
,
.
Как видим, очень важно, с какой стороны умножать на обратную матрицу, так как . Обратная к A матрица умножается на матрицу B с той стороны, с которой матрица A умножается на неизвестную матрицу X . То есть с той стороны, где в произведении с неизвестной матрицей находится матрица A .
Как решить матричное уравнение в третьем случае? Встречаются случаи, когда в левой части уравнения неизвестная матрица X находится в середине произведения трёх матриц. Тогда известную матрицу из правой части уравнения следует умножить слева на матрицу, обратную той, которая в упомянутом выше произведении трёх матриц была слева, и справа на матрицу, обратную той матрице, которая располагалась справа. Таким образом, решением матричного уравнения
Таким образом, решением матричного уравнения
.
Решение матричных уравнений: примеры
Пример 1. Решить матричное уравнение
.
Решение. Данное уравнение имеет вид A ⋅ X = B , то есть в произведении матрицы A и неизвестной матрицы X матрица A находится слева. Поэтому решение следует искать в виде , то есть неизвестная матрица равна произведению матрицы B на матрицу, обратную матрице A слева. Найдём матрицу, обратную матрице A .
Сначала найдём определитель матрицы A :
.
Найдём алгебраические дополнения матрицы A :
.
Составим матрицу алгебраических дополнений:
.
Транспонируя матрицу алгебраических дополнений, находим матрицу, союзную с матрицей A :
.
Теперь у нас есть всё, чтобы найти матрицу, обратную матрице A :
.
Наконец, находим неизвестную матрицу:
Пример 2. Решить матричное уравнение
Решить матричное уравнение
.
Пример 3. Решить матричное уравнение
.
Решение. Данное уравнение имеет вид X ⋅ A = B , то есть в произведении матрицы A и неизвестной матрицы X матрица A находится справа. Поэтому решение следует искать в виде , то есть неизвестная матрица равна произведению матрицы B на матрицу, обратную матрице A справа. Найдём матрицу, обратную матрице A .
Сначала найдём определитель матрицы A :
.
Найдём алгебраические дополнения матрицы A :
.
Составим матрицу алгебраических дополнений:
.
Транспонируя матрицу алгебраических дополнений, находим матрицу, союзную с матрицей A :
.
Находим матрицу, обратную матрице A :
.
Находим неизвестную матрицу:
До сих пор мы решали уравнения с матрицами второго порядка, а теперь настала очередь матриц третьего порядка.
Пример 4. Решить матричное уравнение
.
Решение. Это уравнение первого вида: A ⋅ X = B , то есть в произведении матрицы A и неизвестной матрицы X матрица A находится слева. Поэтому решение следует искать в виде , то есть неизвестная матрица равна произведению матрицы B на матрицу, обратную матрице A слева. Найдём матрицу, обратную матрице A .
Сначала найдём определитель матрицы A :
.
Найдём алгебраические дополнения матрицы A :
Составим матрицу алгебраических дополнений:
Транспонируя матрицу алгебраических дополнений, находим матрицу, союзную с матрицей A :
.
Находим матрицу, обратную матрице A , и делаем это легко, так как определитель матрицы A равен единице:
.
Находим неизвестную матрицу:
Пример 5. Решить матричное уравнение
.
Решение. Данное уравнение имеет вид X ⋅ A = B , то есть в произведении матрицы A и неизвестной матрицы X матрица A находится справа. Поэтому решение следует искать в виде , то есть неизвестная матрица равна произведению матрицы B на матрицу, обратную матрице A справа. Найдём матрицу, обратную матрице A .
Сначала найдём определитель матрицы A :
.
Найдём алгебраические дополнения матрицы A :
Составим матрицу алгебраических дополнений:
.
Транспонируя матрицу алгебраических дополнений, находим матрицу, союзную с матрицей A :
.
Находим матрицу, обратную матрице A :
.
Находим неизвестную матрицу:
Пример 6. Решить матричное уравнение
.
Решение. Данное уравнение имеет вид A ⋅ X ⋅ B = C , то есть неизвестная матрица X находится в середине произведения трёх матриц. Поэтому решение следует искать в виде . Найдём матрицу, обратную матрице A .
Поэтому решение следует искать в виде . Найдём матрицу, обратную матрице A .
Сначала найдём определитель матрицы A :
.
Найдём алгебраические дополнения матрицы A :
.
Составим матрицу алгебраических дополнений:
.
Транспонируя матрицу алгебраических дополнений, находим матрицу, союзную с матрицей A :
.
Находим матрицу, обратную матрице A :
.
Найдём матрицу, обратную матрице B .
Сначала найдём определитель матрицы B :
.
Найдём алгебраические дополнения матрицы B :
Составим матрицу алгебраических дополнений матрицы B :
.
Транспонируя матрицу алгебраических дополнений, находим матрицу, союзную с матрицей B :
.
Находим матрицу, обратную матрице B :
.
Предупреждение
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т. д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Инструкция матричного онлайн калькулятора
С помощью матричного онлайн калькулятора вы можете сложить, вычитать, умножить, транспонировать матрицы, вычислить обратную матрицу, псевдообратную матрицу, ранг матрицы, определитель матрицы, m-норму и l-норму матрицы, возвести матрицу в степень , умножить матрицу на число , сделать скелетное разложение матрицы, удалить из матрицы линейно зависимые строки или линейно зависимые столбцы, проводить исключение Гаусса, решить матричное уравнение AX=B, сделать LU разложение матрицы, вычислить ядро (нуль пространство) матрицы, сделать ортогонализацию Грамма-Шмидта и ортонормализацию Грамма-Шмидта.
Матричный онлайн калькулятор работает не только с десятичными числами, но и с дробями. Для ввода дроби нужно в исходные матрицы и вводить числа в виде a или a/b, где a и b целые или десятичные числа (b положительное число). Например 12/67, -67.78/7.54, 327.6, -565.
Для ввода дроби нужно в исходные матрицы и вводить числа в виде a или a/b, где a и b целые или десятичные числа (b положительное число). Например 12/67, -67.78/7.54, 327.6, -565.
Кнопка в верхем левом углу матрицы открывает меню (Рис.1) для преобразования исходной матрицы (создание единичной матрицы , нулевой матрицы , очищать содержимое ячеек ) и т.д.
При вычислениях пустая ячейка воспринимается как нуль.
Для операций с одной матрицей (т.е. транспонирование, обратное, псевдообратное, скелетное разложение и т.д.) сначала выбирается конкретная матрица с помощью радиокнопки .
Кнопки Fn1, Fn2 и Fn3 переключают разные группы функциий.
Нажимая на вычисленных матрицах открывается меню (Рис.2), что позволяет записать данную матрицу в исходные матрицы и , а также преобразовать на месте элементы матрицы в обыкновенную дробь, смешанную дробь или в десятичное число.
Вычисление суммы, разности, произведения матриц онлайн
Матричным онлайн калькулятором можно вычислить сумму, разность или произведение матриц. Для вычисления суммы или разности матриц, необходимо, чтобы они были одинаковой размерности, а для вычисления произведения матриц, количество столбцов первой матрицы должен быть равным количеству строк второй матрицы.
Для вычисления суммы или разности матриц, необходимо, чтобы они были одинаковой размерности, а для вычисления произведения матриц, количество столбцов первой матрицы должен быть равным количеству строк второй матрицы.
Для вычисления суммы, разности или произведения матриц:
- Введите размерности матриц и .
- Введите элементы матриц.
- Нажмите на кнопку «A+B «,»A-B» или «A×B».
Вычисление обратной матрицы онлайн
Матричным онлайн калькулятором можно вычислить обратную матрицу. Для того, чтобы существовала обратная матрица, исходная матрица должна быть невырожденной квадратной матрицей.
Для вычисления обратной матрицы:
- Выберите матрицу или с помощью радиокнопки .
- Введите размерность матрицы .
- Введите элементы матрицы.
- Нажмите на кнопку «обратное «.
Для подробного вычисления обратной матрицы по шагам, пользуйтесь этим калькулятором для вычисления обратной матрицы. Теорию вычисления обратной матрицы смотрите здесь.
Вычисление определителя матрицы онлайн
Матричным онлайн калькулятором можно вычислить определитель матрицы. Для того, чтобы существовал определитель матрицы, исходная матрица должна быть невырожденной квадратной матрицей.
Для вычисления определителя матрицы:
- Выберите матрицу или с помощью радиокнопки .
- Введите размерность матрицы .
- Введите элементы матрицы.
- Нажмите на кнопку «определитель «.
Для подробного вычисления определителя матрицы по шагам, пользуйтесь этим калькулятором для вычисления определителя матрицы. Теорию вычисления определителя матрицы смотрите здесь.
Вычисление ранга матрицы онлайн
Матричным онлайн калькулятором можно вычислить ранг матрицы.
Для вычисления ранга матрицы:
- Выберите матрицу или с помощью радиокнопки .
- Введите размерность матрицы .
- Введите элементы матрицы.
- Нажмите на кнопку «ранг «.
Для подробного вычисления ранга матрицы по шагам, пользуйтесь этим калькулятором для вычисления ранга матрицы. Теорию вычисления ранга матрицы смотрите здесь.
Теорию вычисления ранга матрицы смотрите здесь.
Вычисление псевдообратной матрицы онлайн
Матричным онлайн калькулятором можно вычислить псевдообратную матрицу. Псевдообратная к данной матрице всегда существует.
Для вычисления псевдообратной матрицы:
- Выберите матрицу или с помощью радиокнопки .
- Введите размерность матрицы.
- Введите элементы матрицы.
- Нажмите на кнопку «псевдообратное «.
Удаление линейно зависимых строк или столбцов матрицы онлайн
Матричным онлайн калькулятор позволяет удалить из матрицы линейно зависимые строки или столбцы, т.е. создать матрицу полного ранга.
Для удаления линейно зависимых строк или столбцов матрицы:
- Выберите матрицу или с помощью радиокнопки .
- Введите размерность матрицы.
- Введите элементы матрицы.
- Нажмите на кнопку «полный ранг строк » или «полный ранг столбцов».
Скелетное разложение матрицы онлайн
Для проведения скелетного разложения матрицы онлайн
- Выберите матрицу или с помощью радиокнопки .

- Введите размерность матрицы.
- Введите элементы матрицы.
- Нажмите на кнопку «скелетное разложение «.
Решение матричного уравнения или системы линейных уравнений AX=B онлайн
Матричным онлайн калькулятором можно решить матричное уравнение AX=B по отношению матрицы X. В частном случае, если матрица B является вектор-столбцом, то X , будет решением системы линейных уравнений AX=B.
Для решения матричного уравнения:
- Введите размерности матриц и .
- Введите элементы матриц.
- Нажмите на кнопку «решение AX=B».
Учтите, что матрицы и должны иметь равное количество строк .
Исключение Гаусса или приведение матрицы к треугольному (ступенчатому) виду онлайн
Матричный онлайн калькулятор проводит исключение Гаусса как для квадратных матриц, так и прямоугольных матриц любого ранга. Сначала проводится обычный метод Гаусса. Если на каком то этапе ведущий элемент равен нулю, то выбирается другой вариант исключения Гаусса с выбором наибольшего ведущего элемента в столбце.
Для исключения Гаусса или приведения матрицы к треугольному виду
- Выберите матрицу или с помощью радиокнопки .
- Задайте размерность матрицы.
- Введите элементы матрицы.
- Нажмите на кнопку «Треугольный вид».
LU-разложение или LUP-разложение матрицы онлайн
Данный матричный калькулятор позволяет проводить LU-разложение матрицы (A=LU) или LUP-разложение матрицы (PA=LU), где L нижняя треугольная матрица, U-верхняя треугольная (трапециевидная) матрица, P- матрица перестановок. Сначала программа проводит LU разложение, т.е. такое разложение , при котором P=E, где E-единичная матрица (т.е. PA=EA=A). Если это невозможно, то проводится LUP-разложение. Матрица A может быть как квадратной, так и прямоугольной матрицей любого ранга.
- Выберите матрицу или с помощью радиокнопки .
- Задайте размерность матрицы.
- Введите элементы матрицы.
- Нажмите на кнопку «LU-разложение».
Построение ядра (нуль-пространства) матрицы онлайн
С помощью матричного калькулятора можно построить нуль-пространство (ядро) матрицы.
Для построения нуль-пространства (ядра) матрицы:
- Выберите матрицу или с помощью радиокнопки .
- Задайте размерность матрицы.
- Введите элементы матрицы.
- Нажмите на кнопку «ядро (·)».
Ортогонализация Грамма-Шмидта и Ортонормализация Грамма-Шмидта онлайн
С помощью матричного калькулятора можно сделать ортогонализацию и ортонормализацию Грамма-Шмидта матрицы онлайн.
Для ортогонализации или ортонормализации матрицы:
- Выберите матрицу или с помощью радиокнопки .
- Задайте размерность матрицы.
- Введите элементы матрицы.
- Нажмите на кнопку «Ортогонализация Г.-Ш. (·)» или «Ортонормализация Г.-Ш. (·)».
Рассмотрим матричное уравнение вида
где [math]A[/math] и [math]B[/math] — данные матрицы, имеющие одинаковое количество строк, причем матрица [math]A[/math] квадратная. Требуется найти матрицу [math]X[/math] , удовлетворяющую уравнению (4.5).
Теорема 4.2 о существовании и единственности решения матричного уравнения (4. <-1>B[/math] . Будем искать элементы матрицы [math]X=egina&b\c&dend[/math] . Подставляя в уравнение, получаем
<-1>B[/math] . Будем искать элементы матрицы [math]X=egina&b\c&dend[/math] . Подставляя в уравнение, получаем
Находим произведение, а затем приравниваем соответствующие элементы матриц в левой и правой частях уравнения:
Здесь, учитывая пропорциональность уравнений, в системе оставлены только два уравнения из четырех. Выразим неизвестные [math]a[/math] и [math]b:[/math]
Следовательно, решение матричного уравнения имеет вид
Умный калькулятор онлайн решающий уравнения. Решение матричных уравнений
для решения математики. Быстро найти решение математического уравнения в режиме онлайн . Сайт www.сайт позволяет решить уравнение почти любого заданного алгебраического , тригонометрического или трансцендентного уравнения онлайн . При изучении практически любого раздела математики на разных этапах приходится решать уравнения онлайн . Чтобы получить ответ сразу, а главное точный ответ, необходим ресурс, позволяющий это сделать. Благодаря сайту www.сайт решение уравнений онлайн займет несколько минут. Основное преимущество www.сайт при решении математических уравнений онлайн — это скорость и точность выдаваемого ответа. Сайт способен решать любые алгебраические уравнения онлайн , тригонометрические уравнения онлайн , трансцендентные уравнения онлайн , а также уравнения с неизвестными параметрами в режиме онлайн . Уравнения служат мощным математическим аппаратом решения практических задач. C помощью математических уравнений можно выразить факты и соотношения, которые могут показаться на первый взгляд запутанными и сложными. Неизвестные величины уравнений можно найти, сформулировав задачу на математическом языке в виде уравнений и решить полученную задачу в режиме онлайн на сайте www.сайт. Любое алгебраическое уравнение , тригонометрическое уравнение или уравнения содержащие трансцендентные функции Вы легко решите онлайн и получите точный ответ.
Благодаря сайту www.сайт решение уравнений онлайн займет несколько минут. Основное преимущество www.сайт при решении математических уравнений онлайн — это скорость и точность выдаваемого ответа. Сайт способен решать любые алгебраические уравнения онлайн , тригонометрические уравнения онлайн , трансцендентные уравнения онлайн , а также уравнения с неизвестными параметрами в режиме онлайн . Уравнения служат мощным математическим аппаратом решения практических задач. C помощью математических уравнений можно выразить факты и соотношения, которые могут показаться на первый взгляд запутанными и сложными. Неизвестные величины уравнений можно найти, сформулировав задачу на математическом языке в виде уравнений и решить полученную задачу в режиме онлайн на сайте www.сайт. Любое алгебраическое уравнение , тригонометрическое уравнение или уравнения содержащие трансцендентные функции Вы легко решите онлайн и получите точный ответ. Изучая естественные науки, неизбежно сталкиваешься с необходимостью решения уравнений . При этом ответ должен быть точным и получить его необходимо сразу в режиме онлайн . Поэтому для решения математических уравнений онлайн мы рекомендуем сайт www.сайт, который станет вашим незаменимым калькулятором для решения алгебраических уравнений онлайн , тригонометрических уравнений онлайн , а также трансцендентных уравнений онлайн или уравнений с неизвестными параметрами. Для практических задач по нахождению корней различных математических уравнений ресурса www.. Решая уравнения онлайн самостоятельно, полезно проверить полученный ответ, используя онлайн решение уравнений на сайте www.сайт. Необходимо правильно записать уравнение и моментально получите онлайн решение , после чего останется только сравнить ответ с Вашим решением уравнения. Проверка ответа займет не более минуты, достаточно решить уравнение онлайн и сравнить ответы.
Изучая естественные науки, неизбежно сталкиваешься с необходимостью решения уравнений . При этом ответ должен быть точным и получить его необходимо сразу в режиме онлайн . Поэтому для решения математических уравнений онлайн мы рекомендуем сайт www.сайт, который станет вашим незаменимым калькулятором для решения алгебраических уравнений онлайн , тригонометрических уравнений онлайн , а также трансцендентных уравнений онлайн или уравнений с неизвестными параметрами. Для практических задач по нахождению корней различных математических уравнений ресурса www.. Решая уравнения онлайн самостоятельно, полезно проверить полученный ответ, используя онлайн решение уравнений на сайте www.сайт. Необходимо правильно записать уравнение и моментально получите онлайн решение , после чего останется только сравнить ответ с Вашим решением уравнения. Проверка ответа займет не более минуты, достаточно решить уравнение онлайн и сравнить ответы. Это поможет Вам избежать ошибок в решении и вовремя скорректировать ответ при решении уравнений онлайн будь то алгебраическое , тригонометрическое , трансцендентное или уравнение с неизвестными параметрами.
Это поможет Вам избежать ошибок в решении и вовремя скорректировать ответ при решении уравнений онлайн будь то алгебраическое , тригонометрическое , трансцендентное или уравнение с неизвестными параметрами.
Назначение сервиса . Матричный калькулятор предназначен для решения систем линейных уравненийматричным способом (см. пример решения подобных задач).
Инструкция . Для онлайн решения необходимо выбрать вид уравнения и задать размерность соответствующих матриц.
где А, В, С — задаваемые матрицы, Х — искомая матрица. Матричные уравнения вида (1), (2) и (3) решаются через обратную матрицу A -1 . Если задано выражение A·X — B = C , то необходимо, сначала сложить матрицы C + B , и находить решение для выражения A·X = D , где D = C + B (). Если задано выражение A*X = B 2 , то предварительно матрицу B надо возвести в квадрат .
Рекомендуется также ознакомиться с основными действиями над матрицами .
Пример №1
. Задание . Найти решение матричного уравнения
Решение . Обозначим:
Тогда матричное уравнение запишется в виде: A·X·B = C.
Определитель матрицы А равен detA=-1
Так как A невырожденная матрица, то существует обратная матрица A -1 . Умножим слева обе части уравнения на A -1:Умножаем обе части этого равенства слева на A -1 и справа на B -1: A -1 ·A·X·B·B -1 = A -1 ·C·B -1 . Так как A·A -1 = B·B -1 = E и E·X = X·E = X, то X = A -1 ·C·B -1
Обратная матрица A -1:
Найдем обратную матрицу B -1 .
Транспонированная матрица B T:
Обратная матрица B -1:
Матрицу X ищем по формуле: X = A -1 ·C·B -1
Ответ:
Пример №2
. Задание. Решить матричное уравнение
Решение . Обозначим:
Тогда матричное уравнение запишется в виде: A·X = B.
Определитель матрицы А равен detA=0
Так как A вырожденная матрица (определитель равен 0), следовательно уравнение решения не имеет.
Пример №3
. Задание. Найти решение матричного уравнения
Найти решение матричного уравнения
Решение . Обозначим:
Тогда матричное уравнение запишется в виде: X·A = B.
Определитель матрицы А равен detA=-60
Так как A невырожденная матрица, то существует обратная матрица A -1 . Умножим справа обе части уравнения на A -1: X·A·A -1 = B·A -1 , откуда находим, что X = B·A -1
Найдем обратную матрицу A -1 .
Транспонированная матрица A T:
Обратная матрица A -1:
Матрицу X ищем по формуле: X = B·A -1
Ответ: >
Применение уравнений широко распространено в нашей жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Уравнения человек использовал еще в древности и с тех пор их применение только возрастает. Степенные или показательные уравнения называют уравнения, в которых переменные находятся в степенях, а основанием является число. Например:
Решение показательного уравнения сводится к 2 довольно простым действиям:
1. Нужно проверить одинаковые ли основания у уравнения справа и слева. {nm}:\]
{nm}:\]
Прибавляем к исходному уравнению:
Вынесем за скобки \
Выразим \
Поскольку степени одинаковые, отбрасываем их:
Ответ: \
Где можно решить показательное уравнение онлайн решателем?
Решить уравнение вы можете на нашем сайте https://сайт. Бесплатный онлайн решатель позволит решить уравнение онлайн любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как решить уравнение на нашем сайте. А если у вас остались вопросы, то вы можете задать их в нашей групе Вконтакте http://vk.com/pocketteacher. Вступайте в нашу группу, мы всегда рады помочь вам.
Предлагаемый вашему вниманию бесплатный калькулятор располагает богатым арсеналом возможностей для математических вычислений. Он позволяет использовать онлайн калькулятор в различных сферах деятельности: образовательной , профессиональной и коммерческой . Конечно, применение калькулятора онлайн особенно популярно у студентов и школьников , он значительно облегчает им выполнение самых разных расчётов.
Вместе с тем калькулятор может стать полезным инструментом в некоторых направлениях бизнеса и для людей разных профессий. Безусловно, необходимость применения калькулятора в бизнесе или трудовой деятельности определяется прежде всего видом самой деятельности. Если бизнес и профессия связаны с постоянными расчётами и вычислениями, то стоит опробовать электронный калькулятор и оценить степень его полезности для конкретного дела.
Данный онлайн калькулятор может
- Корректно выполнять стандартные математические функции, записанные одной строкой типа — 12*3-(7/2) и может обрабатывать числа больше, чемсчитаем огромные числа в онлайн калькулятореМы даже не знаем, как такое число назвать правильно (тут 34 знака и это совсем не предел ).
- Кроме тангенса , косинуса , синуса и других стандартных функций — калькулятор поддерживает операции по расчёту арктангенса , арккотангенса и прочих.
- Доступны в арсенале логарифмы , факториалы и другие интересные функции
- Данный онлайн калькулятор умеет строить графики !!!
Для построения графиков, сервис использует специальную кнопку (график серый нарисован) или буквенное представление этой функции (Plot). Чтобы построить график в онлайн калькуляторе, достаточно записать функцию: plot(tan(x)),x=-360..360 .
Чтобы построить график в онлайн калькуляторе, достаточно записать функцию: plot(tan(x)),x=-360..360 .
Мы взяли самый простой график для тангенса, и после запятой указали диапазон переменной X от -360 до 360.
Построить можно абсолютно любую функцию, с любым количеством переменных, например такую: plot(cos(x)/3z, x=-180..360,z=4) или ещё более сложную, какую сможете придумать. Обращаем внимание на поведение переменной X — указан промежуток от и до с помощью двух точек.
Единственный минус (хотя трудно назвать это минусом) этого онлайн калькулятора это то, что он не умеет строить сферы и другие объёмные фигуры — только плоскость.
Как работать с Математическим калькулятором
1. Дисплей (экран калькулятора) отображает введенное выражение и результат его расчёта обычными символами, как мы пишем на бумаге. Это поле предназначено просто для просмотра текущей операции. Запись отображается на дисплее по мере набора математического выражения в строке ввода.
2. Поле ввода выражения предназначено для записи выражения, которое нужно вычислить. Здесь следует отметить, что математические символы, используемые в компьютерных программах, не всегда совпадают с теми, которые обычно мы применяем на бумаге. В обзоре каждой функции калькулятора вы найдёте правильное обозначение конкретной операции и примеры расчётов в калькуляторе. На этой странице ниже приводится перечень всех возможных операций в калькуляторе, также с указанием их правильного написания.
3. Панель инструментов — это кнопки калькулятора, которые заменяют ручной ввод математических символов, обозначающих соответствующую операцию. Некоторые кнопки калькулятора (дополнительные функции, конвертер величин, решение матриц и уравнений, графики) дополняют панель задач новыми полями, где вводятся данные для конкретного расчёта. Поле «History» содержит примеры написания математических выражений, а также ваши шесть последних записей.
Обратите внимание, при нажатии кнопок вызова дополнительных функций, конвертера величин, решения матриц и уравнений, построения графиков вся панель калькулятора смещается вверх, закрывая часть дисплея. Заполните необходимые поля и нажмите клавишу «I» (на рисунке выделена красным цветом), чтобы увидеть дисплей в полный размер.
Заполните необходимые поля и нажмите клавишу «I» (на рисунке выделена красным цветом), чтобы увидеть дисплей в полный размер.
4. Цифровая клавиатура содержит цифры и знаки арифметических действий. Кнопка «С» удаляет всю запись в поле ввода выражения. Чтобы удалять символы по одному, нужно использовать стрелочку справа от строки ввода.
Старайтесь всегда закрывать скобки в конце выражения. Для большинства операций это некритично, калькулятор online рассчитает всё верно. Однако, в некоторых случаях возможны ошибки. Например, при возведении в дробную степень незакрытые скобки приведут к тому, что знаменатель дроби в показателе степени уйдет в знаменатель основания. На дисплее закрывающая скобка обозначена бледно-серым цветом, её нужно закрыть, когда запись закончена.
| Клавиша | Символ | Операция |
|---|---|---|
| pi | pi | Постоянная pi |
| е | е | Число Эйлера |
| % | % | Процент |
| () | () | Открыть/Закрыть скобки |
| , | , | Запятая |
| sin | sin(?) | Синус угла |
| cos | cos(?) | Косинус |
| tan | tan(y) | Тангенс |
| sinh | sinh() | Гиперболический синус |
| cosh | cosh() | Гиперболический косинус |
| tanh | tanh() | Гиперболический тангенс |
| sin -1 | asin() | Обратный синус |
| cos -1 | acos() | Обратный косинус |
| tan -1 | atan() | Обратный тангенс |
| sinh -1 | asinh() | Обратный гиперболический синус |
| cosh -1 | acosh() | Обратный гиперболический косинус |
| tanh -1 | atanh() | Обратный гиперболический тангенс |
| x 2 | ^2 | Возведение в квадрат |
| х 3 | ^3 | Возведение в куб |
| x y | ^ | Возведение в степень |
| 10 x | 10^() | Возведение в степень по основанию 10 |
| e x | exp() | Возведение в степень числа Эйлера |
| vx | sqrt(x) | Квадратный корень |
| 3 vx | sqrt3(x) | Корень 3-ей степени |
| y vx | sqrt(x,y) | Извлечение корня |
| log 2 x | log2(x) | Двоичный логарифм |
| log | log(x) | Десятичный логарифм |
| ln | ln(x) | Натуральный логарифм |
| log y x | log(x,y) | Логарифм |
| I / II | Сворачивание/Вызов дополнительных функций | |
| Unit | Конвертер величин | |
| Matrix | Матрицы | |
| Solve | Уравнения и системы уравнений | |
| Построение графиков | ||
| Дополнительные функции (вызов клавишей II) | ||
| mod | mod | Деление с остатком |
| ! | ! | Факториал |
| i / j | i / j | Мнимая единица |
| Re | Re() | Выделение целой действительной части |
| Im | Im() | Исключение действительной части |
| |x| | abs() | Модуль числа |
| Arg | arg() | Аргумент функции |
| nCr | ncr() | Биноминальный коэффициент |
| gcd | gcd() | НОД |
| lcm | lcm() | НОК |
| sum | sum() | Суммарное значение всех решений |
| fac | factorize() | Разложение на простые множители |
| diff | diff() | Дифференцирование |
| Deg | Градусы | |
| Rad | Радианы | |
На этапе подготовки к заключительному тестированию учащимся старших классов необходимо подтянуть знания по теме «Показательные уравнения». Опыт прошлых лет свидетельствует о том, что подобные задания вызывают у школьников определенные затруднения. Поэтому старшеклассникам, независимо от уровня их подготовки, необходимо тщательно усвоить теорию, запомнить формулы и понять принцип решения таких уравнений. Научившись справляться с данным видом задач, выпускники смогут рассчитывать на высокие баллы при сдаче ЕГЭ по математике.
Опыт прошлых лет свидетельствует о том, что подобные задания вызывают у школьников определенные затруднения. Поэтому старшеклассникам, независимо от уровня их подготовки, необходимо тщательно усвоить теорию, запомнить формулы и понять принцип решения таких уравнений. Научившись справляться с данным видом задач, выпускники смогут рассчитывать на высокие баллы при сдаче ЕГЭ по математике.
Готовьтесь к экзаменационному тестированию вместе со «Школково»!
При повторении пройденных материалов многие учащиеся сталкиваются с проблемой поиска нужных для решения уравнений формул. Школьный учебник не всегда находится под рукой, а отбор необходимой информации по теме в Интернете занимает долгое время.
Образовательный портал «Школково» предлагает ученикам воспользоваться нашей базой знаний. Мы реализуем совершенно новый метод подготовки к итоговому тестированию. Занимаясь на нашем сайте, вы сможете выявить пробелы в знаниях и уделить внимание именно тем заданиям, которые вызывают наибольшие затруднения.
Преподаватели «Школково» собрали, систематизировали и изложили весь необходимый для успешной сдачи ЕГЭ материал в максимально простой и доступной форме.
Основные определения и формулы представлены в разделе «Теоретическая справка».
Для лучшего усвоения материала рекомендуем попрактиковаться в выполнении заданий. Внимательно просмотрите представленные на данной странице примеры показательных уравнений с решением, чтобы понять алгоритм вычисления. После этого приступайте к выполнению задач в разделе «Каталоги». Вы можете начать с самых легких заданий или сразу перейти к решению сложных показательных уравнений с несколькими неизвестными или . База упражнений на нашем сайте постоянно дополняется и обновляется.
Те примеры с показателями, которые вызвали у вас затруднения, можно добавить в «Избранное». Так вы можете быстро найти их и обсудить решение с преподавателем.
Чтобы успешно сдать ЕГЭ, занимайтесь на портале «Школково» каждый день!
Матричное уравнение ax b имеет решение: Решение матричных уравнений: теория и примеры — ЭкоДом: Дом своими руками
Содержание
Решение матричных уравнений: теория и примеры
Матричные уравнения имеют прямую аналогию с простыми алгебраическими уравнениями, в
которых присутствует операция умножения. Например,
Например,
ax=b,
где x — неизвестное.
А, поскольку мы уже умеем находить произведение матриц,
то можем приступать к рассмотрению аналогичных уравнений с матрицами, в которых буквы — это матрицы.
Итак, матричным уравнением называется уравнение вида
A ⋅ X = B
или
X ⋅ A = B,
где A и B —
известные матрицы, X — неизвестная матрица, которую требуется найти.
Как решить матричное уравнение в первом случае? Для того,
чтобы решить матричное уравнение вида A ⋅ X = B,
обе его части следует умножить на обратную к A матрицу
слева:
.
По определению обратной матрицы, произведение обратной матрицы на данную исходную
матрицу равно единичной матрице: ,
поэтому
.
Так как E — единичная матрица, то
E ⋅ X = X. В результате
получим, что неизвестная матрица X равна произведению матрицы,
обратной к матрице A, слева, на матрицу B:
.
Как решить матричное уравнение во втором случае? Если дано уравнение
X ⋅ A = B,
то есть такое, в котором в произведении неизвестной матрицы X
и известной матрицы A матрица A
находится справа, то нужно действовать аналогично, но меняя направление умножения на матрицу,
обратную матрице A, и умножать матрицу B
на неё справа:
,
,
.
Как видим, очень важно, с какой стороны умножать на обратную матрицу, так как
. Обратная к
Обратная к
A матрица умножается на матрицу B
с той стороны, с которой матрица A умножается на неизвестную
матрицу X. То есть с той стороны, где в произведении с неизвестной
матрицей находится матрица A.
Как решить матричное уравнение в третьем случае? Встречаются случаи, когда в левой
части уравнения неизвестная матрица X находится в середине
произведения трёх матриц. Тогда известную матрицу из правой части уравнения следует умножить слева
на матрицу, обратную той, которая в упомянутом выше произведении трёх матриц была слева, и справа на
матрицу, обратную той матрице, которая располагалась справа. Таким образом, решением матричного уравнения
A ⋅ X ⋅ B = C,
является
.
Пример 1. Решить матричное уравнение
Решить матричное уравнение
.
Решение. Данное уравнение имеет вид A ⋅ X = B, то
есть в произведении матрицы A и неизвестной матрицы
X матрица A находится слева.
Поэтому решение следует искать в виде ,
то есть неизвестная матрица равна произведению матрицы B на матрицу,
обратную матрице A слева. Найдём матрицу, обратную матрице
A.
Сначала найдём определитель матрицы A:
.
Найдём алгебраические дополнения матрицы A:
.
Составим матрицу алгебраических дополнений:
.
Транспонируя матрицу алгебраических дополнений, находим матрицу, союзную с матрицей
A:
.
Теперь у нас есть всё, чтобы найти матрицу, обратную матрице A:
.
Наконец, находим неизвестную матрицу:
Решить матричное уравнение самостоятельно, а затем посмотреть решение
Пример 3. Решить матричное уравнение
.
Решение. Данное уравнение имеет вид X ⋅ A = B, то
есть в произведении матрицы A и неизвестной матрицы
X матрица A находится справа.
Поэтому решение следует искать в виде ,
то есть неизвестная матрица равна произведению матрицы B на матрицу,
обратную матрице A справа. Найдём матрицу, обратную матрице
A.
Сначала найдём определитель матрицы A:
.
Найдём алгебраические дополнения матрицы A:
.
Составим матрицу алгебраических дополнений:
.
Транспонируя матрицу алгебраических дополнений, находим матрицу, союзную с матрицей
A:
.
Находим матрицу, обратную матрице A:
.
Находим неизвестную матрицу:
До сих пор мы решали уравнения с матрицами второго порядка, а теперь настала очередь
матриц третьего порядка.
Пример 4. Решить матричное уравнение
.
Решение. Это уравнение первого вида: A ⋅ X = B, то
есть в произведении матрицы A и неизвестной матрицы
X матрица A находится слева.
Поэтому решение следует искать в виде ,
то есть неизвестная матрица равна произведению матрицы B на матрицу,
обратную матрице A слева. Найдём матрицу, обратную матрице
A.
Сначала найдём определитель матрицы A:
.
Найдём алгебраические дополнения матрицы A:
Составим матрицу алгебраических дополнений:
Транспонируя матрицу алгебраических дополнений, находим матрицу, союзную с матрицей
A:
.
Находим матрицу, обратную матрице A, и делаем
это легко, так как определитель матрицы A равен единице:
.
Находим неизвестную матрицу:
Пример 5. Решить матричное уравнение
.
Решение. Данное уравнение имеет вид X ⋅ A = B, то
есть в произведении матрицы A и неизвестной матрицы
X матрица A находится справа.
Поэтому решение следует искать в виде ,
то есть неизвестная матрица равна произведению матрицы B на матрицу,
обратную матрице A справа. Найдём матрицу, обратную матрице
Найдём матрицу, обратную матрице
A.
Сначала найдём определитель матрицы A:
.
Найдём алгебраические дополнения матрицы A:
Составим матрицу алгебраических дополнений:
.
Транспонируя матрицу алгебраических дополнений, находим матрицу, союзную с матрицей
A:
.
Находим матрицу, обратную матрице A:
.
Находим неизвестную матрицу:
Пример 6. Решить матричное уравнение
.
Решение. Данное уравнение имеет вид A ⋅ X ⋅ B = C, то
есть неизвестная матрица X находится в середине
произведения трёх матриц. Поэтому решение следует искать в виде
. Найдём матрицу, обратную матрице
A.
Сначала найдём определитель матрицы A:
.
Найдём алгебраические дополнения матрицы A:
.
Составим матрицу алгебраических дополнений:
.
Транспонируя матрицу алгебраических дополнений, находим матрицу, союзную с матрицей
A:
.
Находим матрицу, обратную матрице A:
.
Найдём матрицу, обратную матрице
B.
Сначала найдём определитель матрицы B:
.
Найдём алгебраические дополнения матрицы B:
Составим матрицу алгебраических дополнений матрицы B:
. {-1}= \begin{pmatrix} -5 & 3\\ 2 & -1 \end{pmatrix}\rightarrow X= \begin{pmatrix} 3 & 5\\ 2 & 1 \end{pmatrix} \cdot \begin{pmatrix} -5 & 3\\ 2 & -1 \end{pmatrix}= \begin{pmatrix} -5 & 4\\ -8 & 5 \end{pmatrix}$
ax b
Вы искали ax b? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное
Подробное
решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и ax b матричное уравнение, не
исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению
в вуз.
И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение.
Например, «ax b».
Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как ax b,ax b матричное уравнение,ax b решить матричное уравнение,деление матриц онлайн,для невырожденной квадратной матрицы а решение системы ax b имеет вид,как решить матричное уравнение онлайн,как решить уравнение матрицы,калькулятор для матриц,калькулятор для матриц онлайн,калькулятор для матрицы,калькулятор для матрицы онлайн калькулятор,калькулятор матриц,калькулятор матриц онлайн,калькулятор матриц онлайн с подробным решением,калькулятор матриц онлайн с решением,калькулятор матриц с подробным решением,калькулятор матриц с подробным решением онлайн,калькулятор матриц уравнений,калькулятор матрица,калькулятор матрицы,калькулятор матрицы онлайн,калькулятор матрицы онлайн с подробным решением,калькулятор матрицы онлайн с решением,калькулятор матрицы с решением,калькулятор матриць,калькулятор матриць онлайн,калькулятор матричний,калькулятор матричных уравнений,калькулятор матричных уравнений онлайн,калькулятор онлайн вычисление матриц,калькулятор онлайн для матриц,калькулятор онлайн матрицы,калькулятор онлайн матрицы с подробным решением,калькулятор онлайн матрицы уравнения,калькулятор онлайн по матрицам,калькулятор по матрицам онлайн,калькулятор решение матричных уравнений,калькулятор уравнение матрицы онлайн,калькулятор уравнений матриц,калькуляторы матриц,матриц калькулятор с решением,матриц онлайн калькулятор с подробным решением,матрица калькулятор,матрица калькулятор онлайн,матрица калькулятор онлайн с решением,матрица онлайн калькулятор с подробным решением,матрица онлайн калькулятор с решением,матрица решение онлайн калькулятор,матрица решение уравнений,матрица х,матрицы калькулятор,матрицы калькулятор онлайн,матрицы калькулятор онлайн с подробным решением,матрицы калькулятор онлайн уравнение,матрицы калькулятор с решением,матрицы онлайн калькулятор,матрицы онлайн калькулятор с подробным решением,матрицы онлайн калькулятор уравнения,матрицы решение онлайн калькулятор,матрицы решение уравнений онлайн,матрицы решить уравнение,матрицы уравнение онлайн,матрицы уравнения онлайн калькулятор,матричний калькулятор,матричное уравнение ax b,матричное уравнение калькулятор,матричный калькулятор,матричный калькулятор онлайн,матричный калькулятор онлайн с подробным решением онлайн,матричный калькулятор с подробным решением онлайн,матричный калькулятор с решением,матричный онлайн калькулятор с подробным решением,найти из уравнения матрицу х,найти матрицу х из уравнения,найти неизвестную матрицу x из уравнения,онлайн калькулятор для матриц,онлайн калькулятор матриц с подробным решением,онлайн калькулятор матриц с решением,онлайн калькулятор матрица с подробным решением,онлайн калькулятор матрицы,онлайн калькулятор матрицы с подробным решением,онлайн калькулятор матрицы с решением,онлайн калькулятор матрицы уравнения,онлайн калькулятор по матрицам,онлайн калькулятор решение матриц,онлайн калькулятор решение матричного уравнения,онлайн калькулятор решение матричных уравнений,онлайн калькулятор решения матриц,онлайн калькулятор решить матрицу,онлайн калькулятор с подробным решением матриц,онлайн калькулятор уравнение матрицы,онлайн калькулятор уравнения матрицы,онлайн матрица калькулятор,онлайн матрица посчитать,онлайн подробное решение матриц,онлайн подсчет матриц,подробное решение матриц онлайн,решение матриц калькулятор,решение матриц онлайн калькулятор с подробным решением,решение матриц уравнений онлайн,решение матричного уравнения,решение матричных уравнений онлайн калькулятор,решение матричных уравнений онлайн калькулятор с подробным решением,решение уравнений матриц онлайн,решение уравнений матрицы онлайн,решение уравнений с матрицами,решение уравнений с матрицами онлайн,решите матричное уравнение,решите матричное уравнение онлайн,решить матрицу калькулятор онлайн,решить матрицу онлайн калькулятор,решить матричное уравнение,решить матричное уравнение ax b,решить матричное уравнение xa b,решить матричные уравнения,решить онлайн уравнение матрицы,решить систему линейных уравнений ax b,решить уравнение матрица,решить уравнение матрица равна нулю,решить уравнение матрицы,уравнение матрицы онлайн калькулятор,уравнения матрицы онлайн,уравнения матрицы онлайн калькулятор. На этой странице вы найдёте калькулятор,
На этой странице вы найдёте калькулятор,
который поможет решить любой вопрос, в том числе и ax b. Просто введите задачу в окошко и нажмите
«решить» здесь (например, ax b решить матричное уравнение).
Где можно решить любую задачу по математике, а так же ax b Онлайн?
Решить задачу ax b вы можете на нашем сайте https://pocketteacher.ru. Бесплатный
онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо
сделать — это просто
ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести
вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице
калькулятора.
Axb c матрицы уравнения – Тарифы на сотовую связь
106 пользователя считают данную страницу полезной.
Информация актуальна! Страница была обновлена 16. 12.2019
Решение матричных уравнений: как это делается
Матричные уравнения имеют прямую аналогию с простыми алгебраическими уравнениями, в которых присутствует операция умножения. Например,
Например,
где x – неизвестное.
А, поскольку мы уже умеем находить произведение матриц, то можем приступать к рассмотрению аналогичных уравнений с матрицами, в которых буквы – это матрицы.
Итак, матричным уравнением называется уравнение вида
где A и B – известные матрицы, X – неизвестная матрица, которую требуется найти.
Как решить матричное уравнение в первом случае? Для того, чтобы решить матричное уравнение вида A ⋅ X = B , обе его части следует умножить на обратную к A матрицу слева:
.
По определению обратной матрицы, произведение обратной матрицы на данную исходную матрицу равно единичной матрице: , поэтому
.
Так как E – единичная матрица, то E ⋅ X = X . В результате получим, что неизвестная матрица X равна произведению матрицы, обратной к матрице A , слева, на матрицу B :
.
Как решить матричное уравнение во втором случае? Если дано уравнение
то есть такое, в котором в произведении неизвестной матрицы X и известной матрицы A матрица A находится справа, то нужно действовать аналогично, но меняя направление умножения на матрицу, обратную матрице A , и умножать матрицу B на неё справа:
,
,
.
Как видим, очень важно, с какой стороны умножать на обратную матрицу, так как . Обратная к A матрица умножается на матрицу B с той стороны, с которой матрица A умножается на неизвестную матрицу X . То есть с той стороны, где в произведении с неизвестной матрицей находится матрица A .
Как решить матричное уравнение в третьем случае? Встречаются случаи, когда в левой части уравнения неизвестная матрица X находится в середине произведения трёх матриц. Тогда известную матрицу из правой части уравнения следует умножить слева на матрицу, обратную той, которая в упомянутом выше произведении трёх матриц была слева, и справа на матрицу, обратную той матрице, которая располагалась справа. Таким образом, решением матричного уравнения
Таким образом, решением матричного уравнения
.
Решение матричных уравнений: примеры
Пример 1. Решить матричное уравнение
.
Решение. Данное уравнение имеет вид A ⋅ X = B , то есть в произведении матрицы A и неизвестной матрицы X матрица A находится слева. Поэтому решение следует искать в виде , то есть неизвестная матрица равна произведению матрицы B на матрицу, обратную матрице A слева. Найдём матрицу, обратную матрице A .
Сначала найдём определитель матрицы A :
.
Найдём алгебраические дополнения матрицы A :
.
Составим матрицу алгебраических дополнений:
.
Транспонируя матрицу алгебраических дополнений, находим матрицу, союзную с матрицей A :
.
Теперь у нас есть всё, чтобы найти матрицу, обратную матрице A :
.
Наконец, находим неизвестную матрицу:
Пример 2. Решить матричное уравнение
Решить матричное уравнение
.
Пример 3. Решить матричное уравнение
.
Решение. Данное уравнение имеет вид X ⋅ A = B , то есть в произведении матрицы A и неизвестной матрицы X матрица A находится справа. Поэтому решение следует искать в виде , то есть неизвестная матрица равна произведению матрицы B на матрицу, обратную матрице A справа. Найдём матрицу, обратную матрице A .
Сначала найдём определитель матрицы A :
.
Найдём алгебраические дополнения матрицы A :
.
Составим матрицу алгебраических дополнений:
.
Транспонируя матрицу алгебраических дополнений, находим матрицу, союзную с матрицей A :
.
Находим матрицу, обратную матрице A :
.
Находим неизвестную матрицу:
До сих пор мы решали уравнения с матрицами второго порядка, а теперь настала очередь матриц третьего порядка.
Пример 4. Решить матричное уравнение
.
Решение. Это уравнение первого вида: A ⋅ X = B , то есть в произведении матрицы A и неизвестной матрицы X матрица A находится слева. Поэтому решение следует искать в виде , то есть неизвестная матрица равна произведению матрицы B на матрицу, обратную матрице A слева. Найдём матрицу, обратную матрице A .
Сначала найдём определитель матрицы A :
.
Найдём алгебраические дополнения матрицы A :
Составим матрицу алгебраических дополнений:
Транспонируя матрицу алгебраических дополнений, находим матрицу, союзную с матрицей A :
.
Находим матрицу, обратную матрице A , и делаем это легко, так как определитель матрицы A равен единице:
.
Находим неизвестную матрицу:
Пример 5. Решить матричное уравнение
.
Решение. Данное уравнение имеет вид X ⋅ A = B , то есть в произведении матрицы A и неизвестной матрицы X матрица A находится справа. Поэтому решение следует искать в виде , то есть неизвестная матрица равна произведению матрицы B на матрицу, обратную матрице A справа. Найдём матрицу, обратную матрице A .
Поэтому решение следует искать в виде , то есть неизвестная матрица равна произведению матрицы B на матрицу, обратную матрице A справа. Найдём матрицу, обратную матрице A .
Сначала найдём определитель матрицы A :
.
Найдём алгебраические дополнения матрицы A :
Составим матрицу алгебраических дополнений:
.
Транспонируя матрицу алгебраических дополнений, находим матрицу, союзную с матрицей A :
.
Находим матрицу, обратную матрице A :
.
Находим неизвестную матрицу:
Пример 6. Решить матричное уравнение
.
Решение. Данное уравнение имеет вид A ⋅ X ⋅ B = C , то есть неизвестная матрица X находится в середине произведения трёх матриц. Поэтому решение следует искать в виде . Найдём матрицу, обратную матрице A .
Сначала найдём определитель матрицы A :
.
Найдём алгебраические дополнения матрицы A :
.
Составим матрицу алгебраических дополнений:
.
Транспонируя матрицу алгебраических дополнений, находим матрицу, союзную с матрицей A :
.
Находим матрицу, обратную матрице A :
.
Найдём матрицу, обратную матрице B .
Сначала найдём определитель матрицы B :
.
Найдём алгебраические дополнения матрицы B :
Составим матрицу алгебраических дополнений матрицы B :
.
Транспонируя матрицу алгебраических дополнений, находим матрицу, союзную с матрицей B :
. <-1>= egin-5 & 3\ 2 & -1 end
ightarrow X= egin3 & 5\ 2 & 1 endcdot egin-5 & 3\ 2 & -1 end= egin-5 & 4\ -8 & 5 end$
Матричный калькулятор онлайн
Инструкция матричного онлайн калькулятора
С помощью матричного онлайн калькулятора вы можете сложить, вычитать, умножить, транспонировать матрицы, вычислить обратную матрицу, псевдообратную матрицу, ранг матрицы, определитель матрицы, m-норму и l-норму матрицы, возвести матрицу в степень, умножить матрицу на число, сделать скелетное разложение матрицы, удалить из матрицы линейно зависимые строки или линейно зависимые столбцы, проводить исключение Гаусса, решить матричное уравнение AX=B, сделать LU разложение матрицы, вычислить ядро (нуль пространство) матрицы, сделать ортогонализацию Грамма-Шмидта и ортонормализацию Грамма-Шмидта.
Матричный онлайн калькулятор работает не только с десятичными числами, но и с дробями. Для ввода дроби нужно в исходные матрицы и вводить числа в виде a или a/b, где a и b целые или десятичные числа (b положительное число). Например 12/67, -67.78/7.54, 327.6, -565.
Кнопка в верхем левом углу матрицы открывает меню (Рис.1) для преобразования исходной матрицы (создание единичной матрицы , нулевой матрицы , очищать содержимое ячеек ) и т.д.
Рис.1
При вычислениях пустая ячейка воспринимается как нуль.
Для операций с одной матрицей (т.е. транспонирование, обратное, псевдообратное, скелетное разложение и т.д.) сначала выбирается конкретная матрица с помощью радиокнопки .
Кнопки Fn1, Fn2 и Fn3 переключают разные группы функциий.
Нажимая на вычисленных матрицах открывается меню (Рис.2), что позволяет записать данную матрицу в исходные матрицы и , а также преобразовать на месте элементы матрицы в обыкновенную дробь, смешанную дробь или в десятичное число.
Рис.2
Вычисление суммы, разности, произведения матриц онлайн
Матричным онлайн калькулятором можно вычислить сумму, разность или произведение матриц. Для вычисления суммы или разности матриц, необходимо, чтобы они были одинаковой размерности, а для вычисления произведения матриц, количество столбцов первой матрицы должен быть равным количеству строк второй матрицы.
Для вычисления суммы, разности или произведения матриц:
- Введите размерности матриц и .
- Введите элементы матриц.
- Нажмите на кнопку «A+B «,»A-B» или «A×B».
Вычисление обратной матрицы онлайн
Матричным онлайн калькулятором можно вычислить обратную матрицу. Для того, чтобы существовала обратная матрица, исходная матрица должна быть невырожденной квадратной матрицей.
Для вычисления обратной матрицы:
- Выберите матрицу или с помощью радиокнопки .
- Введите размерность матрицы .
- Введите элементы матрицы.
- Нажмите на кнопку «обратное «.

Для подробного вычисления обратной матрицы по шагам, пользуйтесь этим калькулятором для вычисления обратной матрицы. Теорию вычисления обратной матрицы смотрите здесь.
Вычисление определителя матрицы онлайн
Матричным онлайн калькулятором можно вычислить определитель матрицы. Для того, чтобы существовал определитель матрицы, исходная матрица должна быть невырожденной квадратной матрицей.
Для вычисления определителя матрицы:
- Выберите матрицу или с помощью радиокнопки .
- Введите размерность матрицы .
- Введите элементы матрицы.
- Нажмите на кнопку «определитель «.
Для подробного вычисления определителя матрицы по шагам, пользуйтесь этим калькулятором для вычисления определителя матрицы. Теорию вычисления определителя матрицы смотрите здесь.
Вычисление ранга матрицы онлайн
Матричным онлайн калькулятором можно вычислить ранг матрицы.
Для вычисления ранга матрицы:
- Выберите матрицу или с помощью радиокнопки .

- Введите размерность матрицы .
- Введите элементы матрицы.
- Нажмите на кнопку «ранг «.
Для подробного вычисления ранга матрицы по шагам, пользуйтесь этим калькулятором для вычисления ранга матрицы. Теорию вычисления ранга матрицы смотрите здесь.
Вычисление псевдообратной матрицы онлайн
Матричным онлайн калькулятором можно вычислить псевдообратную матрицу. Псевдообратная к данной матрице всегда существует.
Для вычисления псевдообратной матрицы:
- Выберите матрицу или с помощью радиокнопки .
- Введите размерность матрицы.
- Введите элементы матрицы.
- Нажмите на кнопку «псевдообратное «.
Удаление линейно зависимых строк или столбцов матрицы онлайн
Матричным онлайн калькулятор позволяет удалить из матрицы линейно зависимые строки или столбцы, т.е. создать матрицу полного ранга.
Для удаления линейно зависимых строк или столбцов матрицы:
- Выберите матрицу или с помощью радиокнопки .

- Введите размерность матрицы.
- Введите элементы матрицы.
- Нажмите на кнопку «полный ранг строк » или «полный ранг столбцов».
Скелетное разложение матрицы онлайн
Для проведения скелетного разложения матрицы онлайн
- Выберите матрицу или с помощью радиокнопки .
- Введите размерность матрицы.
- Введите элементы матрицы.
- Нажмите на кнопку «скелетное разложение «.
Решение матричного уравнения или системы линейных уравнений AX=B онлайн
Матричным онлайн калькулятором можно решить матричное уравнение AX=B по отношению матрицы X. В частном случае, если матрица B является вектор-столбцом, то X , будет решением системы линейных уравнений AX=B.
Для решения матричного уравнения:
- Введите размерности матриц и .
- Введите элементы матриц.
- Нажмите на кнопку «решение AX=B».
Учтите, что матрицы и должны иметь равное количество строк .
Исключение Гаусса или приведение матрицы к треугольному (ступенчатому) виду онлайн
Матричный онлайн калькулятор проводит исключение Гаусса как для квадратных матриц, так и прямоугольных матриц любого ранга. Сначала проводится обычный метод Гаусса. Если на каком то этапе ведущий элемент равен нулю, то выбирается другой вариант исключения Гаусса с выбором наибольшего ведущего элемента в столбце.
Сначала проводится обычный метод Гаусса. Если на каком то этапе ведущий элемент равен нулю, то выбирается другой вариант исключения Гаусса с выбором наибольшего ведущего элемента в столбце.
Для исключения Гаусса или приведения матрицы к треугольному виду
- Выберите матрицу или с помощью радиокнопки .
- Задайте размерность матрицы.
- Введите элементы матрицы.
- Нажмите на кнопку «Треугольный вид».
LU-разложение или LUP-разложение матрицы онлайн
Данный матричный калькулятор позволяет проводить LU-разложение матрицы (A=LU) или LUP-разложение матрицы (PA=LU), где L нижняя треугольная матрица, U-верхняя треугольная (трапециевидная) матрица, P- матрица перестановок. Сначала программа проводит LU разложение, т.е. такое разложение , при котором P=E, где E-единичная матрица (т.е. PA=EA=A). Если это невозможно, то проводится LUP-разложение. Матрица A может быть как квадратной, так и прямоугольной матрицей любого ранга.
Для LU(LUP)-разложения:
- Выберите матрицу или с помощью радиокнопки .

- Задайте размерность матрицы.
- Введите элементы матрицы.
- Нажмите на кнопку «LU-разложение».
Построение ядра (нуль-пространства) матрицы онлайн
С помощью матричного калькулятора можно построить нуль-пространство (ядро) матрицы.
Для построения нуль-пространства (ядра) матрицы:
- Выберите матрицу или с помощью радиокнопки .
- Задайте размерность матрицы.
- Введите элементы матрицы.
- Нажмите на кнопку «ядро (·)».
Ортогонализация Грамма-Шмидта и Ортонормализация Грамма-Шмидта онлайн
С помощью матричного калькулятора можно сделать ортогонализацию и ортонормализацию Грамма-Шмидта матрицы онлайн.d, А b, как известно, находится внутри подпространства.
Я думал использовать инструменты, поставляемые с numpy, однако они работают только с квадратными матрицами. У меня был подход заполнения матрицы некоторыми линейно независимыми векторами, чтобы «square» ее, а затем решить, но я не мог понять, как выбрать эти векторы так, чтобы они были линейно независимы от базисных векторов, плюс я думаю, что это не единственный подход, и мне не хватает чего-то, что может сделать это проще.
действительно ли существует более простой подход, чем тот, о котором я упоминал? если нет, то как же мне выбрать те векторы, которые завершили бы A в квадратную матрицу?
python
numpy
matrix
Поделиться
Источник
Ron Tubman
23 сентября 2017 в 07:49
2 ответа
- Ax=B решите с помощью boost 1_58 для разреженной матрицы
Я пытаюсь изучать boost.2.
Уравнение может быть недо-, хорошо — или завышено (т. е. число линейно независимых строк а может быть меньше, равно или больше числа его линейно независимых столбцов). Если a квадрат и имеет полный ранг, то x (но для ошибки округления) является решением уравнения “exact”.
(жирная аннотация мной)
Это также упоминается в документах оригинала
np.linalg.solve:a должен быть квадратным и иметь полный ранг, то есть все строки (или, что эквивалентно, столбцы) должны быть линейно независимыми; если ни то, ни другое не верно, используйте lstsq для наименьших квадратов best “solution” из system/equation.

Поделиться
sascha23 сентября 2017 в 11:24
1Если у вас меньше уравнений, чем неизвестных (предполагая, что вы собирались ввести n < d), вы не ожидаете уникального решения.T, что дает вам одно решение.
- Ваше окончательное решение будет тем, которое вы нашли, плюс линейные комбинации базисных векторов нулевого пространства A.
- Чтобы найти базисные векторы нулевого пространства A, извлеките столбцы j из Матрицы V, соответствующие сингулярным значениям s_j из Матрицы S, которые равны нулю (или ниже некоторого порога «small»).
Вы можете довольно легко реализовать этот последний бит в Python, используя для циклов & операторы if-тяжелая работа — это сама декомпозиция. Превосходные численные рецепты Press et al охватывают линейную алгебру в главе 2 (свободно доступная версия численных рецептов в C здесь и здесь ). у них есть отличная презентация SVD, которая объясняет как теорию SVD, так и то, как это переводится в алгоритмы (в основном фокусируясь на том, как использовать результат SVD). Они предоставляют объект SVD, который имеет больше функциональности, чем numpy.linalg.svd , но, как уже упоминалось, основная функциональность — это фактическая декомпозиция, и делать такие вещи, как получение базисных векторов nullspace, — это просто одеваться для циклов и операторов if, работающих на U, S и V.
Они предоставляют объект SVD, который имеет больше функциональности, чем numpy.linalg.svd , но, как уже упоминалось, основная функциональность — это фактическая декомпозиция, и делать такие вещи, как получение базисных векторов nullspace, — это просто одеваться для циклов и операторов if, работающих на U, S и V.
Поделиться
charlesreid1
23 сентября 2017 в 08:16
Похожие вопросы:
Решение Ax=B с использованием LAPACK, где x >= 0
В настоящее время я работаю над приложением iOS, которое обрабатывает химические добавки в воду. Чтобы найти наименьшие возможные дополнения, я решаю Ax=B, где A-матрица 6×6, А B-один столбец….
Решение (плотной) линейной системы Ax=b с использованием boost
У меня есть плотная система уравнений типа Ax=b для решения в моей программе C++, и я надеялся реализовать решение с помощью UBLAS в boost. В некоторых других вопросах я обнаружил, что люди…
Решение плотных линейных систем AX = B с CUDA
Могу ли я использовать новую библиотеку cuSOLVER (CUDA 7) для решения линейных систем вида AX = B где A , X и B -плотные матрицы NxN ?
Ax=B решите с помощью boost 1_58 для разреженной матрицы
Я пытаюсь изучать boost. Я хочу просто посмотреть пример, как решить линейное уравнение Ax=B для разреженной матрицы. Я видел пример использования umfpack, но в версии boost 1_58 нет umfpack, и я…
Я хочу просто посмотреть пример, как решить линейное уравнение Ax=B для разреженной матрицы. Я видел пример использования umfpack, но в версии boost 1_58 нет umfpack, и я…
Диагонали в неквадратичной матрице-python
В предыдущем вопросе я нашел способ получить все диагонали из квадратной матрицы. Это мой код: diags=[[s[y-x][x] for x in range(n) if 0<=y-x<n] for y in range(2*n-1)] Например, у меня есть…
Пикалман с неквадратичной матрицей наблюдения
В документации Pykalman говорится, что он принимает только квадратные матрицы для Аргументов observation_matrices и transition_matrices . Есть ли способ обойти это? Я должен оценить систему…
Numpy — найти произведение Ax=b пользовательской матрицы A nxn и B nx1
Хочу найти x , из Ax=b .First всего я объявил две матрицы , A которых является nxn и B nx1 . Их формулы можно увидеть ниже. для: а для б : Матрицы могут принимать любые n . В моем коде я даю ему…
Python: решение матричного уравнения Ax = b, где A содержит переменные
Я надеюсь решить матричное уравнение вида Ax = b, где A = [[a,0,0], [0,a,0], [0,0,a], [1,1,0], [0,0,1]] x = [b,c,d] b = [0. 4,0.4,0.2,0.1,0.05] Если бы я знал значение a , я бы сделал это с помощью…
4,0.4,0.2,0.1,0.05] Если бы я знал значение a , я бы сделал это с помощью…
MemoryError на dask.linalg.solve(A, b) для решения Ax = b
Я хочу решить уравнение Ax=b с большой, симметричной, плотной матрицей A (>100 ГБ). Я пробую Dask, потому что он должен быть хорошим высоким уровнем API для python для работы с большими данными. Это…
Как решить уравнение AX = B с Python (NumPy, SciPy и т. д.), где A, X, B-матрицы и все элементы X должны быть неотрицательными
Мне нужно решить уравнение AX = B, используя Python, где A, X, B-матрицы, и все значения X должны быть неотрицательными. Лучшее решение, которое я нашел, это X = np.linalg.lstsq(A, B, rcond=None) но…
Матричные уравнения и их решение
Определение и формулы матричных уравнений
ОПРЕДЕЛЕНИЕ
Матричным уравнением называется уравнение, состоящее из нескольких матриц-коэффициентов и неизвестной матрицы
Простейшим матричным уравнением есть уравнение вида или ,
где — матрицы.
Алгоритм решения матричных уравнений
1. Матричное уравнение приводится к одному из простейших уравнений:
или
где — известные матрицы, — искомая (неизвестная) матрица.
ЗАМЕЧАНИЕ
Существует также уравнение вида , но оно является комбинацией методов решения двух первых указанных простейших уравнений.
Чтобы привести произвольное матричное уравнение к одному из видов (1), надо все известные матрицы по свойствам уравнений перенести вправо, а неизвестную матрицу в левой части и свести подобные.
2. Разрешаем полученное простейшее уравнение относительно неизвестной матрицы .
2.1 Если в результате преобразований получили простейшее уравнение , то необходимо левую и правую часть этого равенства слева умножить на обратную матрицу к матрице :
ЗАМЕЧАНИЕ
Поскольку умножение матриц некоммутативно, то нужно строго соблюдать умножение слева или справа, иначе это влияет на результат.
2.2 Для простейшего уравнения после умножения справа на обратную матрицу получаем:
ЗАМЕЧАНИЕ
Обратная матрица находится либо методом союзной матрицы, либо методом присоединенной матрицы.
3. Далее вычисляется одно из произведений или , что и определяет искомую матрицу.
4. Делаем проверку, для этого подставляем найденную матрицу в исходное уравнение.
Примеры решения задач
|
Понравился сайт? Расскажи друзьям! |
| ||
ответов на викторину 1-4
ответов на викторину 1-4
ответов на вопросы викторины 1-4
Вопрос 1. Вектор b — это линейная комбинация столбцов матрицы.
A есть и только тогда, когда уравнение Ax = b имеет хотя бы одно решение.
Ответ: Верно. Это два способа сказать одно и то же.
Вопрос 2. Уравнение Ax = b непротиворечиво, если расширенная матрица
[A b] имеет позицию поворота в каждой строке.м
находится в промежутке столбцов, что является другим способом сказать, что любой b является
линейная комбинация столбцов. Тогда уравнение непротиворечиво (см. Вопрос
Вопрос
1).
Вопрос 4 . Если уравнение Ax = b несовместимо, то b не входит в
набор, охваченный столбцами A.
Ответ: Верно.
Вопрос 5. Множество решений линейной системы, расширенная матрица которой
is [a b c d] то же самое, что и множество решений Ax = d, где A = [a b c].4. Что из следующего верно?
Ответ: Пусть x = x1 + x2. Тогда Ax = A (x1 + x2) = Ax1 + Ax2 = y1 + y2 на
дистрибутивность умножения матриц (см. задачу 35). Таким образом, x является
решение Ax = y, без дополнительной информации. Однако x не обязательно
общее решение, поскольку Ax = y может иметь бесконечное число решений.
Назад к математике 308A, неделя 2, стр.
% PDF-1.4
%
1 0 объект
> / MediaBox [0 0 362.835 272,126] / Аннотации [121 0 R 123 0 R 125 0 R 127 0 R 129 0 R 131 0 R 133 0 R 135 0 R 137 0 R 139 0 R 141 0 R 143 0 R 145 0 R 147 0 R 149 0 R 151 0 R 153 0 R 155 0 R 157 0 R 159 0 R] / Повернуть 0 >>
эндобдж
2 0 obj
> / Родительский 6 0 R / Содержание [161 0 R 162 0 R] / Тип / Страница / Ресурсы 163 0 R / Trans> / MediaBox [0 0 362. 835 272.126] / Аннотации [204 0 R 206 0 R 208 0 R 210 0 R 212 0 R 214 0 R 216 0 R 218 0 R 220 0 R 222 0 R 224 0 R 226 0 R 228 0 R 230 0 R 232 0 R 234 0 R 236 0 R 238 0 R 240 0 R 242 0 R] / Повернуть 0 >>
835 272.126] / Аннотации [204 0 R 206 0 R 208 0 R 210 0 R 212 0 R 214 0 R 216 0 R 218 0 R 220 0 R 222 0 R 224 0 R 226 0 R 228 0 R 230 0 R 232 0 R 234 0 R 236 0 R 238 0 R 240 0 R 242 0 R] / Повернуть 0 >>
эндобдж
3 0 obj
> / MediaBox [0 0 362.835 272.126] / Аннотации [266 0 R 268 0 R 270 0 R 272 0 R 274 0 R 276 0 R 278 0 R 280 0 R 282 0 R 284 0 R 286 0 R 288 0 R 290 0 R 292 0 R 294 0 R 296 0 R 298 0 R 300 0 R 302 0 R 304 0 R] / Повернуть 0 >>
эндобдж
4 0 obj
> / MediaBox [0 0 362,835 272,126] / Аннотации [347 0 349 р. 351 0 р. 353 0 р. 355 0 р. 357 0 р. 359 0 р. 361 0 р. 363 0 р. 365 0 р. 367 0 р. 369 0 р. 371 0 R 373 0 R 375 0 R 377 0 R 379 0 R 381 0 R 383 0 R 385 0 R] / Повернуть 0 >>
эндобдж
5 0 obj
> / MediaBox [0 0 362,835 272,126] / Аннотации [428 0 430 р. 432 0 р. 434 0 р. 436 0 р. 438 0 р. 440 0 р. 442 0 р. 444 0 р. 446 0 р. 448 0 р. 450 0 р. 452 0 R 454 0 R 456 0 R 458 0 R 460 0 R 462 0 R 464 0 R 466 0 R 468 0 R] / Повернуть 0 >>
эндобдж
11 0 объект
>
эндобдж
16 0 объект
>
эндобдж
20 0 объект
>
эндобдж
22 0 объект
>
эндобдж
23 0 объект
>
эндобдж
25 0 объект
>
эндобдж
26 0 объект
>
эндобдж
27 0 объект
>
эндобдж
28 0 объект
>
эндобдж
30 0 объект
>
эндобдж
31 0 объект
>
эндобдж
33 0 объект
>
эндобдж
34 0 объект
>
эндобдж
36 0 объект
>
эндобдж
470 0 объект
> / Родительский 471 0 R / Содержание [662 0 R] / Тип / Страница / Ресурсы 663 0 R / MediaBox [0 0 524. 16 651.96] / Аннотации [701 0 R 704 0 R] / Повернуть 0 >>
16 651.96] / Аннотации [701 0 R 704 0 R] / Повернуть 0 >>
эндобдж
471 0 объект
>
эндобдж
472 0 объект
>
эндобдж
473 0 объект
>
эндобдж
474 0 объект
>
эндобдж
475 0 объект
>
эндобдж
476 0 объект
>
эндобдж
477 0 объект
>
эндобдж
478 0 объект
>
эндобдж
479 0 объект
>
эндобдж
480 0 объект
>
эндобдж
481 0 объект
>
эндобдж
482 0 объект
>
эндобдж
483 0 объект
>
эндобдж
484 0 объект
>
эндобдж
485 0 объект
>
эндобдж
486 0 объект
>
эндобдж
487 0 объект
>
эндобдж
488 0 объект
>
эндобдж
489 0 объект
>
эндобдж
490 0 объект
>
эндобдж
491 0 объект
>
эндобдж
492 0 объект
>
эндобдж
493 0 объект
>
эндобдж
494 0 объект
>
эндобдж
495 0 объект
>
эндобдж
496 0 объект
>
эндобдж
497 0 объект
>
эндобдж
498 0 объект
>
эндобдж
499 0 объект
>
эндобдж
500 0 объект
>
эндобдж
501 0 объект
>
эндобдж
502 0 объект
>
эндобдж
503 0 объект
>
эндобдж
504 0 объект
>
эндобдж
505 0 объект
>
эндобдж
506 0 объект
>
эндобдж
507 0 объект
>
эндобдж
508 0 объект
>
эндобдж
509 0 объект
>
эндобдж
510 0 объект
>
эндобдж
511 0 объект
>
эндобдж
512 0 объект
>
эндобдж
513 0 объект
>
эндобдж
514 0 объект
>
эндобдж
515 0 объект
>
эндобдж
516 0 объект
>
эндобдж
517 0 объект
>
эндобдж
518 0 объект
>
эндобдж
519 0 объект
>
эндобдж
520 0 объект
>
эндобдж
521 0 объект
>
эндобдж
522 0 объект
>
эндобдж
523 0 объект
>
эндобдж
524 0 объект
>
эндобдж
525 0 объект
>
эндобдж
526 0 объект
>
эндобдж
527 0 объект
>
эндобдж
528 0 объект
>
эндобдж
529 0 объект
>
эндобдж
530 0 объект
>
эндобдж
531 0 объект
>
эндобдж
532 0 объект
>
эндобдж
533 0 объект
>
эндобдж
534 0 объект
>
эндобдж
535 0 объект
>
эндобдж
536 0 объект
>
эндобдж
537 0 объект
>
эндобдж
538 0 объект
>
эндобдж
539 0 объект
>
эндобдж
540 0 объект
>
эндобдж
541 0 объект
>
эндобдж
542 0 объект
>
эндобдж
543 0 объект
>
эндобдж
544 0 объект
>
эндобдж
545 0 объект
>
эндобдж
546 0 объект
>
эндобдж
547 0 объект
>
эндобдж
548 0 объект
>
эндобдж
549 0 объект
>
эндобдж
550 0 объект
>
эндобдж
551 0 объект
>
эндобдж
552 0 объект
>
эндобдж
553 0 объект
>
эндобдж
554 0 объект
>
эндобдж
555 0 объект
>
эндобдж
556 0 объект
>
эндобдж
557 0 объект
>
эндобдж
558 0 объект
>
эндобдж
559 0 объект
>
эндобдж
560 0 объект
>
эндобдж
561 0 объект
>
эндобдж
562 0 объект
>
эндобдж
563 0 объект
>
эндобдж
564 0 объект
>
эндобдж
565 0 объект
>
эндобдж
566 0 объект
>
эндобдж
567 0 объект
>
эндобдж
568 0 объект
>
эндобдж
569 0 объект
>
эндобдж
570 0 объект
>
эндобдж
571 0 объект
>
эндобдж
572 0 объект
>
эндобдж
573 0 объект
>
эндобдж
574 0 объект
>
эндобдж
575 0 объект
>
эндобдж
576 0 объект
>
эндобдж
577 0 объект
>
эндобдж
578 0 объект
>
эндобдж
579 0 объект
>
эндобдж
580 0 объект
>
эндобдж
581 0 объект
>
эндобдж
582 0 объект
>
эндобдж
583 0 объект
>
эндобдж
584 0 объект
>
эндобдж
585 0 объект
>
эндобдж
586 0 объект
>
эндобдж
587 0 объект
>
эндобдж
588 0 объект
>
эндобдж
589 0 объект
>
эндобдж
590 0 объект
>
эндобдж
591 0 объект
>
эндобдж
592 0 объект
>
эндобдж
593 0 объект
>
эндобдж
594 0 объект
>
эндобдж
595 0 объект
>
эндобдж
596 0 объект
>
эндобдж
597 0 объект
>
эндобдж
598 0 объект
>
эндобдж
599 0 объект
>
эндобдж
600 0 объект
>
эндобдж
601 0 объект
>
эндобдж
602 0 объект
>
эндобдж
603 0 объект
>
эндобдж
604 0 объект
>
эндобдж
605 0 объект
>
эндобдж
606 0 объект
>
эндобдж
607 0 объект
>
эндобдж
608 0 объект
>
эндобдж
609 0 объект
>
эндобдж
610 0 объект
>
эндобдж
611 0 объект
>
эндобдж
612 0 объект
>
эндобдж
613 0 объект
>
эндобдж
614 0 объект
>
эндобдж
615 0 объект
>
эндобдж
616 0 объект
>
эндобдж
617 0 объект
>
эндобдж
618 0 объект
>
эндобдж
619 0 объект
>
эндобдж
620 0 объект
>
эндобдж
621 0 объект
>
эндобдж
622 0 объект
>
эндобдж
623 0 объект
>
эндобдж
624 0 объект
>
эндобдж
625 0 объект
>
эндобдж
626 0 объект
>
эндобдж
627 0 объект
>
эндобдж
628 0 объект
>
эндобдж
629 0 объект
>
эндобдж
630 0 объект
>
эндобдж
631 0 объект
>
эндобдж
632 0 объект
>
эндобдж
633 0 объект
>
эндобдж
634 0 объект
>
эндобдж
635 0 объект
>
эндобдж
636 0 объект
>
эндобдж
637 0 объект
>
эндобдж
638 0 объект
>
эндобдж
639 0 объект
>
эндобдж
640 0 объект
>
эндобдж
641 0 объект
>
эндобдж
642 0 объект
>
эндобдж
643 0 объект
>
эндобдж
644 0 объект
>
эндобдж
645 0 объект
>
эндобдж
646 0 объект
>
эндобдж
647 0 объект
>
эндобдж
648 0 объект
>
эндобдж
649 0 объект
>
эндобдж
650 0 объект
>
эндобдж
651 0 объект
>
эндобдж
652 0 объект
>
эндобдж
653 0 объект
>
эндобдж
654 0 объект
>
эндобдж
655 0 объект
>
эндобдж
656 0 объект
>
эндобдж
657 0 объект
>
эндобдж
658 0 объект
>
эндобдж
659 0 объект
>
эндобдж
660 0 объект
>
эндобдж
661 0 объект
>
эндобдж
662 0 объект
> поток
конечный поток
эндобдж
663 0 объект
> / XObject> / ProcSet [/ PDF / ImageB] >>
эндобдж
664 0 объект
>
эндобдж
665 0 объект
>
эндобдж
17 0 объект
>
эндобдж
19 0 объект
>
эндобдж
666 0 объект
>
эндобдж
667 0 объект
>
эндобдж
668 0 объект
> поток
123
конечный поток
эндобдж
669 0 объект
> поток
123
конечный поток
эндобдж
670 0 объект
> поток
123
конечный поток
эндобдж
671 0 объект
> поток
123
конечный поток
эндобдж
672 0 объект
> поток
123
конечный поток
эндобдж
673 0 объект
> поток
123
конечный поток
эндобдж
674 0 объект
> поток
123
конечный поток
эндобдж
675 0 объект
> поток
123
конечный поток
эндобдж
676 0 объект
> поток
123
конечный поток
эндобдж
677 0 объект
> поток
123
конечный поток
эндобдж
678 0 объект
> поток
123
конечный поток
эндобдж
679 0 объект
> поток
123
конечный поток
эндобдж
680 0 объект
> поток
123
конечный поток
эндобдж
681 0 объект
> поток
123
конечный поток
эндобдж
682 0 объект
> поток
123
конечный поток
эндобдж
683 0 объект
> / Тип / XObject / Subtype / Image / ColorSpace / DeviceGray / Ширина 1456 / BitsPerComponent 1 / Длина 3 / Высота 1811 >> поток
123
конечный поток
эндобдж
684 0 объект
> поток
123
конечный поток
эндобдж
685 0 объект
> поток
123
конечный поток
эндобдж
686 0 объект
> поток
123
конечный поток
эндобдж
687 0 объект
> поток
123
конечный поток
эндобдж
688 0 объект
> поток
123
конечный поток
эндобдж
689 0 объект
> поток
123
конечный поток
эндобдж
690 0 объект
> поток
123
конечный поток
эндобдж
691 0 объект
> поток
123
конечный поток
эндобдж
692 0 объект
> поток
123
конечный поток
эндобдж
693 0 объект
> поток
123
конечный поток
эндобдж
694 0 объект
> поток
123
конечный поток
эндобдж
695 0 объект
> поток
123
конечный поток
эндобдж
696 0 объект
> поток
123
конечный поток
эндобдж
697 0 объект
> поток
123
конечный поток
эндобдж
698 0 объект
> поток
123
конечный поток
эндобдж
699 0 объект
> поток
123
конечный поток
эндобдж
700 0 объект
> поток
123
конечный поток
эндобдж
701 0 объект
> / Подтип / Ссылка / Прямоугольник [51. 2173 254,689 83,9092 282,988] / M (D: 20120116134744 + 08’00 ‘) / AP> / H / N / P 470 0 R >>
2173 254,689 83,9092 282,988] / M (D: 20120116134744 + 08’00 ‘) / AP> / H / N / P 470 0 R >>
эндобдж
702 0 объект
>
эндобдж
703 0 объект
> поток
x
линейная алгебра — Как приблизить решение матричного уравнения?
Я хочу кое-что исправить в ответах Антона и las3rjock. Надеюсь, я просто исправляю плохие обозначения.
Способ найти x ‘(используя обозначения в вопросе), как правильно указано в каждом из приведенных выше ответов, состоит в том, чтобы получить связанную проблему A T Ax’ = A T b и решить ее с помощью исключения Гаусса (также называется методом исключения Гаусса-Джордана, здесь разница техническая и не важна).Это гарантированно найдет решение.
Тот факт, что это правильное решение проблемы, зависит от свойств «ближайшей точки» точки к подпространству. Нам нужна ближайшая к b точка на подпространстве Im A. Назовем это b ‘. Свойства «ближайшей точки» подразумевают, что разница , b — b ‘ортогональна всему в Im A. Просто нарисовать картинку, чтобы убедиться, что если c находится в Im A, а b — c равно не ортогонален всему в Im A, тогда можно немного «подтолкнуть» ca, либо в сторону, либо в сторону начала координат, к c ‘, так что b — c’ короче, чем b — c.
Просто нарисовать картинку, чтобы убедиться, что если c находится в Im A, а b — c равно не ортогонален всему в Im A, тогда можно немного «подтолкнуть» ca, либо в сторону, либо в сторону начала координат, к c ‘, так что b — c’ короче, чем b — c.
Итак, b — b ‘ортогонален всему в Im A. Поскольку быть ортогональным чему-либо является линейным условием, достаточно проверить, что b — b’ ортогонален остовному множеству для Im A, для которого мы можем взять столбцы A. Поскольку мы используем стандартный внутренний продукт, это означает, что для каждого столбца, скажем, a из A, a T (b — b ‘) = 0. Соединяя их вместе, мы получаем соотношение A T (b — b ‘) = 0. Поскольку b’ находится в образе A, существует некоторый x ‘такой, что b’ = A x ‘, откуда мы видим, что x’ удовлетворяет A T b — A T A x ‘= 0, и при перестановке получите желаемую формулу.Это также гарантирует существование решения этого уравнения.
Используя тот факт, что ближайшая точка — это уникальная точка b ‘в Im A, такая, что b — b’ ортогональна всему в Im A, мы можем запустить этот аргумент в обратном порядке, чтобы увидеть, что если x ‘является решением A T A x ‘= A T b, тогда Ax’ — ближайшая точка к b в Im A.
В тех случаях, когда приведенные выше ответы ошибаются, следует говорить о матрице (A T A) -1 A T .Проблема заключается в том, что A T A может не быть обратимым (примите A как матрицу нулей 2 на 3). Существует матрица, которая , когда A T A обратима, равна (A T A) -1 A T , и это называется псевдообратной. По сути, A T пропускает ядро A T A, что означает, что состав всегда четко определен, но он может быть не разложимым, как следует из обозначений.
Это обозначение может быть стандартным, чего я не знаю, но если это так, то это плохое обозначение, потому что оно предполагает свойство, которое может не соблюдаться.По крайней мере, на нем всегда должен находиться всадник, чтобы дать понять, что обозначения носят лишь намекающий характер и не должны восприниматься буквально.
Матричное уравнение Ax = b | StudyPug
Матричное уравнение Ax = b
Что такое матричное уравнение
Из курсов алгебры мы знаем, что определение уравнения — это просто «равенство». Таким образом, уравнение — это математическое выражение, которое содержит знак равенства внутри, определяя как минимум два выражения как равные с использованием одной или нескольких переменных вместе с числовыми значениями (в зависимости от необходимости).Переменные, включенные в такие выражения, также можно назвать неизвестными, и мы решаем их, находя числовые значения, которые делают всю связь уравнения истинной.
Таким образом, уравнение — это математическое выражение, которое содержит знак равенства внутри, определяя как минимум два выражения как равные с использованием одной или нескольких переменных вместе с числовыми значениями (в зависимости от необходимости).Переменные, включенные в такие выражения, также можно назвать неизвестными, и мы решаем их, находя числовые значения, которые делают всю связь уравнения истинной.
Итак, в чем будет разница между регулярным уравнением и матричным уравнением? На самом деле это просто связано с типом обозначений, которые вы используете при написании уравнения. Типичное уравнение записывается в виде алгебраического выражения, а именно: просто коэффициенты и переменные, определяющие математическую связь. Но мы уже видели другой тип уравнения на прошлых уроках: векторное уравнение, и, если вы помните из нашего последнего урока этого курса, векторное уравнение — это уравнение, в котором вы можете выделить все коэффициенты в системе уравнений, которые связаны между собой. для каждой переменной (ниже будет пример этого, или вы можете просто вернуться к уроку о линейных комбинациях и векторных уравнениях в Rn, если вам нужен обзор).
для каждой переменной (ниже будет пример этого, или вы можете просто вернуться к уроку о линейных комбинациях и векторных уравнениях в Rn, если вам нужен обзор).
Итак, матричное уравнение — это уравнение, в котором используются обозначения матриц для выражения отношения между его коэффициентами и его переменными. Как вы увидите на этом уроке, матричное уравнение может одновременно представлять более одного простого алгебраического уравнения, и для этого мы обычно используем их для представления систем уравнений.
Как делать матричные уравнения
Поскольку матричное уравнение обычно представляет собой умножение матриц (как вы увидите ниже, некоторые из них являются векторами, некоторые из них являются матрицами коэффициентов), первое, что нам нужно узнать, это как работать и каковы свойства умножения матриц. .
Хотя мы подробно рассмотрим матричное умножение и его свойства в последующих уроках, суть операции видна на следующей диаграмме:
Уравнение 1: умножение матриц
Обратите внимание, как при умножении матриц первый фактор (матрица слева) должен содержать такое же количество столбцов, что и количество строк, найденных во втором множителе (матрица справа при умножении), чтобы быть выполнимым. В зависимости от проблемного случая, который вы пытаетесь решить, умножение матриц упрощает работу с системами уравнений и векторов, поскольку у вас есть упорядоченный способ управления коэффициентом за коэффициентом и переменной за переменной на этом пути.Давайте поработаем над следующими тремя простыми примерами умножения матриц, прежде чем продолжить наш урок:
В зависимости от проблемного случая, который вы пытаетесь решить, умножение матриц упрощает работу с системами уравнений и векторов, поскольку у вас есть упорядоченный способ управления коэффициентом за коэффициентом и переменной за переменной на этом пути.Давайте поработаем над следующими тремя простыми примерами умножения матриц, прежде чем продолжить наш урок:
Пример 1
Вычислите следующее матричное умножение:
Уравнение 2: умножение матриц
Уравнение 3: Выполнение матричного умножения
Пример 2
Вычислите следующее матричное умножение:
Уравнение 4: умножение матриц
Уравнение 5: Выполнение матричного умножения
Пример 3
Вычислите следующее матричное умножение:
Уравнение 6: умножение матриц
Это конкретное умножение не может быть выполнено, поскольку в первой матрице нет того же количества столбцов, что и строк во второй.Обязательно отметим, что это свойство умножения матриц делает его некоммутативным. Другими словами, вы не можете поменять порядок, в котором вы умножаете матрицы, и ожидать получения того же результата, в некоторых случаях вы даже не сможете получить результат, если поменяете их порядок. Возьмите случаи в примерах 1 и 2, если вы поменяете порядок, в котором умножаются матрицы, вы закончите умножениями, в которых первая матрица содержит только один столбец, а вторые матрицы будут иметь несколько строк, поэтому вы не сможете для выполнения этих умножений, в то время как у вас не было проблем с выполнением умножений, как они есть сейчас.
Возьмите случаи в примерах 1 и 2, если вы поменяете порядок, в котором умножаются матрицы, вы закончите умножениями, в которых первая матрица содержит только один столбец, а вторые матрицы будут иметь несколько строк, поэтому вы не сможете для выполнения этих умножений, в то время как у вас не было проблем с выполнением умножений, как они есть сейчас.
Тогда для матричного уравнения мы обычно находим случай, когда матрица коэффициентов (матрица только с числовыми значениями, называемая коэффициентами, потому что они могут представлять коэффициенты из системы линейных уравнений) умножается на вектор-столбец (обычно только содержащий определенные переменные, но он также может содержать коэффициенты). Давайте возьмем в качестве примера задачу, которую мы видели в нашем последнем уроке, мы начнем с системы линейных уравнений ниже:
Уравнение 7: Система линейных уравнений
, для которого мы можем получить его векторное уравнение и расширенную матрицу:
Уравнение 8: векторное уравнение для расширенной матрицы
Где расширенная матрица — это представление такого векторного уравнения, где вертикальная линия представляет знак равенства. Значения в каждом столбце расширенной матрицы слева от вертикальной линии представляют коэффициенты для каждой переменной в системе линейных уравнений, так что (помните, что имя, которое вы даете переменным, не имеет значения):
Значения в каждом столбце расширенной матрицы слева от вертикальной линии представляют коэффициенты для каждой переменной в системе линейных уравнений, так что (помните, что имя, которое вы даете переменным, не имеет значения):
Уравнение 9: Расширенная матрица из уравнения 8
Итак, матричное уравнение, которое эквивалентно такой расширенной матрице, выглядит следующим образом:
Уравнение 10: Матричное уравнение
Такое матричное уравнение имеет вид Ax = b! Давайте перейдем к следующему разделу, чтобы объяснить это более подробно.{n} Rn, то произведение A и x представляет собой линейную комбинацию столбцов в A с использованием соответствующих записей в x в качестве весов. Другими словами:
Уравнение 11: Определение матричного уравнения Ax = b
Где b = a1x1 + … + xnana_1x_1 + … + x_n a_n a1 x1 + … + xn an. Обратите внимание, что x соответствует вектору-столбцу, а A — матрице коэффициентов. Используя уравнение 10 в качестве примера для определения частей матрицы уравнения:
Уравнение 12: части матричного уравнения
И, как вы, возможно, уже догадались, важность матричного уравнения Ax = b состоит в том, чтобы предоставить способ решения для x (или, лучше сказать, для переменных в векторе-столбце x), что можно легко сделать, используя три типы матричных операций со строками и метод решения линейной системы с матрицами методом исключения Гаусса.
Здесь вы, возможно, уже заметили, что приведенные выше примеры 1, 2 и 3 являются частями матричного уравнения Ax = b, они фактически являются примерами его левой части: только умножение Ax. Теперь мы знаем, как выполнять такие простые матричные умножения и когда они не могут быть выполнены, поэтому пришло время поработать над упражнениями, в которых мы можем увидеть матричное уравнение, уже связанное с системами линейных уравнений, например, в уравнениях с 7 по 10.
Прежде чем мы перейдем к следующему разделу, где мы начнем практиковать методологию решения матричного уравнения, описанного выше, нам необходимо знать несколько его свойств.{n} Rn, и c — скаляр, тогда:
- A (u + v) = Au + AvA \ слева (u + v \ right) = Au + Av A (u + v) = Au + Av
- A (cu) = c (Au) A \ left (cu \ right) = c \ left (Au \ right) A (cu) = c (Au)
Используйте такие свойства при работе с матричными уравнениями, сокращении и решении расширенной матрицы для нахождения x или любых других требуемых процессов, которые будут показаны в методах ниже.
Как решить систему уравнений с помощью матрицы
Давайте проработаем несколько различных упражнений, в которых мы поймем, как матричные уравнения полезны при работе с системами линейных уравнений.Принцип, на котором основано использование матрицы для решения системы уравнений, заключается в том, что каждое матричное уравнение Ax = b соответствует векторному уравнению, которое случайно совпадает по своим решениям, поэтому мы можем связать их как систему различных алгебраических выражений с разными переменными.
Пример 4
Мы начинаем с преобразования системы уравнений ниже в векторное уравнение, а затем в матричное уравнение.
Уравнение 12: Система линейных уравнений
Векторное уравнение можно легко записать, разделив все различные переменные (вместе с их коэффициентами) в уравнениях и превратив их в распределение векторов-столбцов.Это векторное уравнение затем может быть преобразовано в расширенную матрицу, которая, наконец, заставит нас написать матричное уравнение само по себе. Подсказка: выполните шаги, описанные в уравнениях с 7 по 10, поскольку это точно такой же процесс, как и здесь. Как видите, здесь мы пропустили шаги, но вы можете увидеть их, следуя предложенным уравнениям или просматривая видеоролики, которые являются частью нашего урока. Результаты:
Подсказка: выполните шаги, описанные в уравнениях с 7 по 10, поскольку это точно такой же процесс, как и здесь. Как видите, здесь мы пропустили шаги, но вы можете увидеть их, следуя предложенным уравнениям или просматривая видеоролики, которые являются частью нашего урока. Результаты:
Уравнение 13: векторное уравнение и матричное уравнение в форме Ax = b из системы линейных уравнений выше
Пример 5
В предыдущем примере мы говорили о том, как мы можем также написать расширенную матрицу либо из системы алгебраических линейных уравнений, либо даже имея компоненты из матричного уравнения Ax = b.Для этого примера у нас будут такие два компонента (матрица A и b), как показано ниже:
Уравнение 14: Компоненты A и b из матричного уравнения Ax = b
Напишите расширенную матрицу для линейной системы, затем решите систему и запишите решение в виде вектора. Начнем с написания матричного уравнения Ax = b для формирования расширенной матрицы:
Уравнение 15: Матричное уравнение в виде Ax = b
Обратите внимание, что для того, чтобы узнать, сколько записей будет у x, мы использовали правило, описанное в уравнении 1 для умножения матриц. Другими словами, если A имеет два столбца, мы знаем, что x ДОЛЖЕН иметь две строки. Кроме того, если размеры mxn для A равны 2×2, а размеры b равны 2×1, что является комбинацией размеров A и x, тогда x ДОЛЖЕН иметь размеры 2×1. Итак, расширенная матрица выглядит следующим образом:
Другими словами, если A имеет два столбца, мы знаем, что x ДОЛЖЕН иметь две строки. Кроме того, если размеры mxn для A равны 2×2, а размеры b равны 2×1, что является комбинацией размеров A и x, тогда x ДОЛЖЕН иметь размеры 2×1. Итак, расширенная матрица выглядит следующим образом:
Уравнение 16: Создание расширенной матрицы
Теперь, чтобы решить матричное уравнение Ax = b с помощью этой расширенной матрицы, нам нужно решить его с помощью редукции строк и эшелонированных форм. Итак, процесс идет как:
Уравнение 17: Решение системы за счет уменьшения количества строк
И окончательный ответ в векторной форме:
Уравнение 18: Конечный вектор
Решите матричное уравнение ax b относительно x
Процесс, который мы видели до сих пор в примере 5, начиная с A и b, является общим процессом, которому мы следуем для решения матричного уравнения относительно x.Давайте рассмотрим еще один пример:
Пример 6
Запишите расширенную матрицу для линейной системы, предоставленной A и b, затем решите систему и запишите решение в виде вектора.
Имея:
Уравнение 19: Компоненты A и b из матричного уравнения Ax = b
Запишем матричное уравнение, а затем его расширенную матричную форму:
Уравнение 20: матричное уравнение в форме Ax = b и соответствующая расширенная матрица
Решаем расширенную матрицу сверху через сокращение строки:
Уравнение 21: Решение системы за счет сокращения строк
И последний вектор x:
Уравнение 22: Конечный вектор
Пример 7
Для этого примера мы решим матричное уравнение с учетом значений A и b ниже:
Уравнение 23: A и b для решения матричного уравнения
Обратите внимание, как здесь мы находимся в необходимости решить уравнение, не зная записей значений для b, и поэтому, как мы с этим работаем? Начнем с написания матричного уравнения:
Уравнение 24: Матричное уравнение
Чтобы получить значения b, при которых это уравнение имеет решение, нам нужно преобразовать уравнение в расширенную матричную форму, а затем получить его сокращенную эшелонную форму:
Уравнение 25: Исключение Гаусса-Жордана до приведенной формы эшелона
На этом остановимся, потому что мы нашли условие решения этого уравнения: только при 3b1 + b23b_1 + b_2 3b1 + b2 = 0 матричное уравнение имеет решение, если 3b1 + b23b_1 + b_2 3b1 + b2 Если бы оно было отличным от нуля, то это привело бы к уравнению 0 = любая ненулевая константа, что несовместимо! Итак, на данный момент у нас осталось только одно уравнение (которое является первой строкой расширенной матрицы) для решения нескольких неизвестных! Таким образом, мы пока не можем вычислить конкретное окончательное решение этого уравнения, НО решения существуют! Фактически существует бесконечно много решений для этого уравнения, пока выполняется условие.
Итак, вот как мы завершаем наш урок на сегодня. Мы предлагаем вам просмотреть все видео, включенные в урок, поскольку последняя часть включает доказательство свойств матричного уравнения Ax = b.
На данный момент мы рекомендуем вам посетить следующее резюме урока, содержащее раздел о матричном уравнении Ax = b, а также этот конкретный урок об обратной квадратной матрице имеет интересный раздел внизу, где вы можете увидеть, как Ax = b может использоваться для решения систем линейных уравнений и вычисления x путем обращения A.
Для данной матрицы A определите, имеет ли Ax = b уникальное решение для каждого …
Задача 5 (a) Пусть A — матрица размера n × m, и предположим, что существует матрица B размером am × n такая, что BA = 1- (i) Пусть b є Rn таково, что система уравнений Ax b имеет хотя бы один решение. Докажи это…
Задача 5 (a) Пусть A — матрица размера n × m, и предположим, что существует матрица B размером am × n такая, что BA = 1- (i) Пусть b є Rn таково, что система уравнений Ax b имеет хотя бы один решение. Докажите, что это решение должно быть уникальным. (ii) Должно ли быть так, что система уравнений Ax = b имеет решение для любого b? Докажите или приведите контрпример. (б) Пусть …
Докажите, что это решение должно быть уникальным. (ii) Должно ли быть так, что система уравнений Ax = b имеет решение для любого b? Докажите или приведите контрпример. (б) Пусть …
б. — 2-1 1 и b Пусть A = Покажите, что уравнение Ax = b …
б. — 2 -1 1 и b Пусть A = Показать, что уравнение Ax = b не имеет решения для всех возможных b, и -3 0 3 4-2 2 b3 описывают множество всех b, для которых Ax b имеет решение Как можно показать, что уравнение Ax = b не имеет решения для всех возможных b? Выберите правильный ответ ниже.O A. Найдите вектор b, для которого …
13. Определите, верно ли следующее утверждение: пусть A — матрица 5×3. Если Ax 0 имеет сингл …
13. Определите, верно ли следующее утверждение: пусть A — матрица 5×3. Если Ax 0 имеет единственное решение, то для каждого b система Ax- b имеет единственное решение 14. Определите, верно ли следующее утверждение: пусть A будет матрицей n × n, а x — вектором nxl. Система AT-0 имеет нетривиальное решение тогда и только тогда, когда система Ax 0 имеет нетривиальное решение
13. Определите, верно ли следующее утверждение: пусть …
Определите, верно ли следующее утверждение: пусть …
1-2 и b E Пусть A Покажет, что уравнение Axb не имеет решения для некоторых вариантов b, и опишет множество …
1 -2 и b E Пусть A Покажет, что уравнение Axb не имеет решения для некоторых вариантов b, и опишет множество всех b, для которых Ax b имеет решение посредством -3. Как можно показать, что уравнение Ax b не имеет решения для некоторых вариантов b? О.А. Строку уменьшите расширенную матрицу, чтобы продемонстрировать, что A b имеет опорную позицию в каждой строке A b O…
как проверить матрицу A = m * n с поворотными позициями в каждой строке,
тогда уравнение Ax = b будет …
как проверить матрицу A = m * n с поворотными позициями в каждой строке,
тогда уравнение Ax = b будет иметь решение для каждого элемента b из
Rm.
5. (8 баллов) Предположим, что B — это матрица 4 x 5, и связанное с ней линейное преобразование T (E) Bd находится на. (a) (3) Найдите dim Nul (B) (b) (2) Имеет ли Ba 5 единственное решение для каждого B (c) (3) Задайте геометрию…
5. (8 баллов) Предположим, что B — это матрица 4 x 5, и связанное с ней линейное преобразование T (E) Bd находится на. (a) (3) Найдите dim Nul (B) (b) (2) Имеет ли Ba 5 единственное решение для каждого B (c) (3) Дайте геометрическую интерпретацию множеству решений Bt- 0
(8 баллов) Предположим, что B — это матрица 4 x 5, и связанное с ней линейное преобразование T (E) Bd находится на. (a) (3) Найдите dim Nul (B) (b) (2) Имеет ли Ba 5 единственное решение для каждого B (c) (3) Дайте геометрическую интерпретацию множеству решений Bt- 0
5. (8 баллов) Предположим, что B — это матрица 4 x 5, и связанное с ней линейное преобразование T (E) Bd находится на. (a) (3) Найдите тусклый Nul (B) (b) (2) Действительно ли Ba 5 …
6) Предположим, что матричное уравнение Ax = b имеет два решения и ༼ ཡང བ найти an…
6) Предположим, что матричное уравнение Ax = b имеет два решения, и ༼ ཡང བ найти бесконечное число решений с вектором-столбцом, параметризованным t. (Подсказка: попробуйте найти решение однородного уравнения Ax = 0.)
Определите, обратима ли приведенная ниже матрица. Используйте как можно меньше вычислений. Обосновать ответ….
Определите, обратима ли приведенная ниже матрица. Используйте как можно меньше вычислений. Обосновать ответ. — 3 30 20 6 -40 9 Выберите правильный ответ ниже.O A. Матрица обратимая. Данная матрица имеет 2 опорных позиции. O B. Матрица необратима. Если данная матрица — A, столбцы A не образуют линейно независимого множества. OC. Матрица не обратима. Если задана матрица A, уравнение Ax …
Обосновать ответ. — 3 30 20 6 -40 9 Выберите правильный ответ ниже.O A. Матрица обратимая. Данная матрица имеет 2 опорных позиции. O B. Матрица необратима. Если данная матрица — A, столбцы A не образуют линейно независимого множества. OC. Матрица не обратима. Если задана матрица A, уравнение Ax …
1. Если ах-матрица A имеет собственные значения ….., каковы собственные значения a) 4 *, …
1. Если ах-матрица A имеет собственные значения ….., каковы собственные значения a) 4 *, где & — натуральное число.AE? A ‘b)’, если существует обратная матрица. в) A ‘(транспонировать). г) а, где а — действительное число. д) Есть ли какая-либо связь между собственными значениями матрицы A и собственными значениями матрицы A? Подсказка: используйте, чтобы обосновать свой ответ. 2. Вычислить спектральную норму 0 0 б) в) в) 1-1 0 …
Набор решений линейной алгебры
Предположим, что A — это матрица 3 x3 и вектор в R3, такой что уравнение Ax = b НЕ имеет решения. Существует ли вектор y в R3 такой, что уравнение Ax = y имеет единственное решение? Объяснять.
Существует ли вектор y в R3 такой, что уравнение Ax = y имеет единственное решение? Объяснять.
Линейная алгебра 5: Решение Ax = b в необратимых неквадратных матрицах | by adam dhalla
Это продолжение моей серии статей по линейной алгебре, которую следует рассматривать как дополнительный ресурс наряду с классом 18.06 Гилберта Стрэнга по OCW. Это может быть близко к Лекция 8 в его серии.
Здесь мы продолжаем обсуждение решения линейных систем с исключением. В моей серии статей с методом исключения Гаусса мы исследовали, как квадратные обратимые матрицы могут быть решены методом исключения и обмена строками, но мы никогда не углублялись в решение прямоугольных необратимых систем.
На последнем уроке мы изучили, как неквадратные системы могут быть решены с помощью исключения Гаусса. В частности, мы решили системы в формате Ax = 0 и обнаружили векторы нулевого пространства x , которые дали x = 0.
Самая большая разница между Ax = b и Ax = 0 теперь в том, что наша правая часть отлична от нуля, мы должны провести операции по с обеих сторон. Это приводит нас к нашей первой теме, а именно к условию разрешимости .
Условия разрешимости
Все эти примеры будут иметь дело с прямоугольными необратимыми матрицами.Если у вас есть квадратная и обратимая матрица (что часто бывает), используйте более простой метод исключения Гаусса .
Условия разрешимости — это то, как мы распознаем, является ли некий b в Ax = b решением, которое на самом деле является возможным. Это станет совершенно ясно на примере. Помните, что теперь, когда выполняется исключение с матрицами, которые, как мы ожидаем, будут зависимыми, мы не остановимся на на разворотах в нулевом месте. Мы просто перейдем к следующему столбцу.
Наша цель — выяснить, как должен выглядеть ответ b, чтобы проблема была решаемой.
Хорошо, первый пример.
Первая и третья строки кратны друг другу и после исключения будут сокращаться до строки нулей. После использования первой строки для удаления первой и второй строк мы получаем:
Но теперь, когда у нас есть ненулевые числа с правой стороны, мы должны выполнить те же шаги исключения с правой стороны.
Что мы сделали? Чтобы исключить вторую строку, мы умножили первую строку на отрицательную и вычли из нижней строки (или, как вы могли подумать, мы добавили первую строку).Затем мы умножили первую строку на 2 и вычли из последней строки. Итак, теперь, с нашими переменными b, , как это выглядит?
Из-за равенства мы должны выполнить те же операции со строками со строками b. Таким образом, после этого мы можем получить представление о том, как выглядят наши b и .
Условия разрешимости возникают, когда левая часть равна 0. Если бы мы записали это в виде системы уравнений, мы получили бы:
Первые два уравнения не дают нам много информации или ограничений на b, , поскольку они зависят от того, какие значения мы в конечном итоге присваиваем нашим переменным x, y, z и t.
Последнее уравнение, с другой стороны, дает нам определенное ограничение на b. Чтобы Ax = b было истинным, b3 — 2b1 must = 0. Переставляя это, мы получаем ограничение на b , которое:
Теперь мы ограничены в различных b3, которые мы можем поместить в нашу матрицу. Вот несколько примеров векторов b , которые удовлетворяют этому ограничению:
Во всех этих случаях b3 в 2 раза больше b1.
Это может дать нам быстрое представление, возможно ли Ax = b или нет, или, при составлении уравнения, может дать нам представление о возможных ответах, которые мы можем получить.
Это дает нам два разных способа, понять этот конкретный Ax = b.
- Используя наши знания о пространстве столбцов, мы знаем, что b должен быть частью пространства столбцов A. Другими словами, b ∈ C (A)
- Наше новое понимание — b должно удовлетворить все ограничения по нему.
Теперь, когда мы это знаем, давайте решим проблему.
Решение для полного решения Ax = b
Я беру этот пример прямо со страницы 91 учебника Гилберта Стрэнга «Линейная алгебра и ее приложения», 4-е издание.
Давайте возьмем эту систему:
Чтобы решить эту проблему, нам сначала нужно найти ответ b , который удовлетворяет любым ограничениям, которые могут быть у нас. Чтобы найти эти ограничения (и одновременно перейти от A к U), используйте гауссовское исключение, чтобы удалить левую и правую части.
Мы умножили первую строку на 2 и вычли из второй строки. Затем мы умножили первую строку на -1 и вычли из третьей строки (добавлено). Мы отразили те же изменения в правой части.
Теперь мы должны удалить последнюю строку с нашей второй строкой.
Этот b5 должен быть b3, но мне лень его менять.
Здесь мы дважды вычитаем вторую строку из третьей строки. Нам нужно не забыть делать это с правой стороны. Здесь все становится немного запутанным, так как мы опираемся на прошлые шаги исключения, но мы все еще можем это сделать.
И снова наше условие разрешимости находится в третьей строке. Если упростить это, мы получим наше условие разрешимости.
Теперь, когда у нас есть условие разрешимости, мы можем выбрать ответ b , который с ним работает.Почему бы нам не выбрать (1, 5, 5)? Вы можете сами убедиться, что это работает.
Напоминаем, что как только мы находим наш b , чтобы заменить его в исходном уравнении Ax = b, с A в левой части, а не U.
Теперь мы проходим тот же процесс исключения, только на этот раз с конкретными числами, и, как и было предсказано, он удовлетворяет ограничениям, которые мы на него накладываем.
Примечание о полном решении
Теперь, глядя на это, можно увидеть множество решений.Но важно отметить, что наш окончательный ответ должен также включать все ответы с нулевым пространством.
Позвольте мне объяснить. Поскольку эта матрица A не является независимой, в пустом пространстве обязательно будет хотя бы один вектор x. Этот x решает для Ax = 0.
Этот x решает для Ax = 0.
Таким образом, если мы найдем конкретное решение для этого, некоторый x, который решает Ax = b, мы также должны добавить всех наших векторов пустого пространства для полного ответа. Поскольку все векторы нулевого пространства делают Ax = 0, наш полный ответ должен включать A (x_null + x_particular) = b, поскольку добавление нулевого пространства ничего не делает с b, поскольку Ax_null = 0.
Если в этом нет смысла, давайте продолжим.
Давайте сначала найдем частное решение этого уравнения. Это x , которое непосредственно решает для Ax = b.
Нахождение частного решения
Мы стремимся найти конкретное решение, некоторое значение x, y, z и t, которое является решением для нашего ответа (1, 3, 0). Поскольку у нас есть только и два полных уравнения , мы можем найти только две из этих переменных. Для двух других нам нужно будет установить константы.
Опять же, как и в случае с нулевым пространством, переменные, которые мы установим как константы, будут свободными переменными.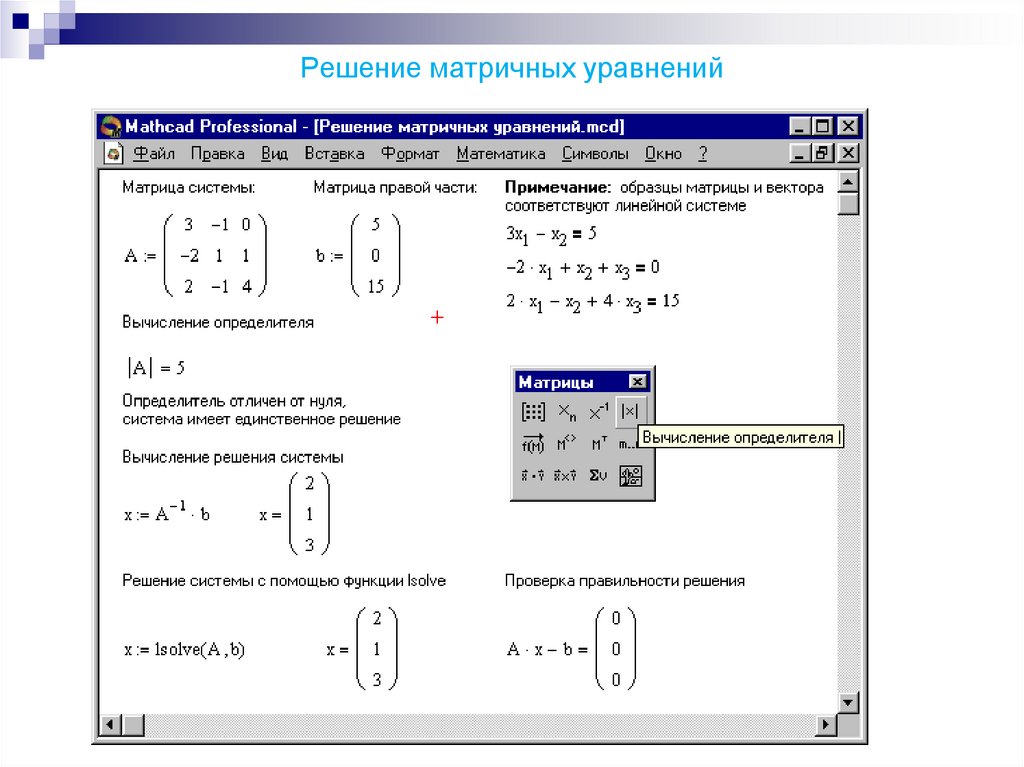 Это переменные, связанные со свободными столбцами, которые не содержат сводных столбцов.
Это переменные, связанные со свободными столбцами, которые не содержат сводных столбцов.
Выделены свободные столбцы и переменные.
У нас снова двойная бесконечность ответов, поскольку у нас есть две переменные, которые мы можем установить как любые константы . Таким образом, у нас есть бесконечное количество конкретных ответов, которые решают вопрос (1, 3, 0). Итак, если мы можем выбрать любую константу для y или t, мы можем выбрать самую простую, равную 0, для обоих.
После этого наша линейная комбинация и система уравнений будут выглядеть так:
Решение системы линейных уравнений с использованием обратной матрицы
Решение системы линейных уравнений с использованием обратной матрицы требует определения двух новых матриц: [latex] X [/ latex] — это матрица, представляющая переменные системы, а [latex] B [/ latex] — это матрица матрица, представляющая константы. Используя умножение матриц на , мы можем определить систему уравнений с таким же количеством уравнений в качестве переменных, как
[латекс] AX = B [/ латекс]
Чтобы решить систему линейных уравнений с использованием обратной матрицы , пусть [latex] A [/ latex] будет матрицей коэффициентов , пусть [latex] X [/ latex] будет переменной матрицей, и пусть [latex] B [/ latex] — постоянная матрица. Таким образом, мы хотим решить систему [латекс] AX = B [/ latex]. Например, посмотрите на следующую систему уравнений.
Таким образом, мы хотим решить систему [латекс] AX = B [/ latex]. Например, посмотрите на следующую систему уравнений.
[латекс] \ begin {array} {c} {a} _ {1} x + {b} _ {1} y = {c} _ {1} \\ {a} _ {2} x + {b} _ {2} y = {c} _ {2} \ end {array} [/ latex]
Из этой системы матрица коэффициентов равна
[латекс] A = \ left [\ begin {array} {cc} {a} _ {1} & {b} _ {1} \\ {a} _ {2} & {b} _ {2} \ конец {array} \ right] [/ latex]
Матрица переменных —
[латекс] X = \ left [\ begin {array} {c} x \\ y \ end {array} \ right] [/ latex]
А постоянная матрица
[латекс] B = \ left [\ begin {array} {c} {c} _ {1} \\ {c} _ {2} \ end {array} \ right] [/ latex]
Тогда [latex] AX = B [/ latex] выглядит как
[латекс] \ left [\ begin {array} {cc} {a} _ {1} & {b} _ {1} \\ {a} _ {2} & {b} _ {2} \ end { массив} \ right] \ text {} \ left [\ begin {array} {c} x \\ y \ end {array} \ right] = \ left [\ begin {array} {c} {c} _ {1 } \\ {c} _ {2} \ end {array} \ right] [/ latex]
Вспомните обсуждение ранее в этом разделе относительно умножения действительного числа на обратное, [латекс] \ left ({2} ^ {- 1} \ right) 2 = \ left (\ frac {1} {2} \ right) 2 = 1 [/ латекс]. {-1} \ right) b \ end {array} [/ latex]
{-1} \ right) b \ end {array} [/ latex]
Единственное различие между решением линейного уравнения и системой уравнений , записанной в матричной форме, состоит в том, что поиск обратной матрицы более сложен, а умножение матриц — более длительный процесс. Однако цель та же — изолировать переменную.
Мы рассмотрим эту идею подробно, но полезно начать с системы [латекс] 2 \ times 2 [/ latex], а затем перейти к системе [латекс] 3 \ times 3 [/ latex].{-1} \ right) B \ end {array} [/ latex]
Вопросы и ответы
Если матрица коэффициентов не имеет обратной, означает ли это, что у системы нет решения?
Нет, если матрица коэффициентов необратима, система может быть несовместимой и не иметь решения, или быть зависимой и иметь бесконечно много решений.
Пример 7: Решение системы 2 × 2 с использованием обратной матрицы
Решите данную систему уравнений, используя обратную матрицу.
[латекс] \ begin {массив} {r} \ hfill 3x + 8y = 5 \\ \ hfill 4x + 11y = 7 \ end {array} [/ latex]
Решение
Запишите систему в виде матрицы коэффициентов, матрицы переменных и постоянной матрицы. {- 1} [/ latex].{-1} \ right) B \ hfill \\ \ left [\ begin {array} {rr} \ hfill 11 & \ hfill -8 \\ \ hfill -4 & \ hfill 3 \ end {array} \ right] \ text { } \ left [\ begin {array} {cc} 3 & 8 \\ 4 & 11 \ end {array} \ right] \ text {} \ left [\ begin {array} {c} x \\ y \ end {array} \ right] = \ left [\ begin {array} {rr} \ hfill 11 & \ hfill -8 \\ \ hfill -4 & \ hfill 3 \ end {array} \ right] \ text {} \ left [\ begin {array } {c} 5 \\ 7 \ end {array} \ right] \ hfill \\ \ left [\ begin {array} {cc} 1 & 0 \\ 0 & 1 \ end {array} \ right] \ text {} \ left [\ begin {array} {c} x \\ y \ end {array} \ right] = \ left [\ begin {array} {r} \ hfill 11 \ left (5 \ right) + \ left (-8 \ right) 7 \\ \ hfill -4 \ left (5 \ right) +3 \ left (7 \ right) \ end {array} \ right] \ hfill \\ \ left [\ begin {array} {c} x \\ y \ end {array} \ right] = \ left [\ begin {array} {r} \ hfill -1 \\ \ hfill 1 \ end {array} \ right] \ hfill \ end {array} [/ latex ]
{- 1} [/ latex].{-1} \ right) B \ hfill \\ \ left [\ begin {array} {rr} \ hfill 11 & \ hfill -8 \\ \ hfill -4 & \ hfill 3 \ end {array} \ right] \ text { } \ left [\ begin {array} {cc} 3 & 8 \\ 4 & 11 \ end {array} \ right] \ text {} \ left [\ begin {array} {c} x \\ y \ end {array} \ right] = \ left [\ begin {array} {rr} \ hfill 11 & \ hfill -8 \\ \ hfill -4 & \ hfill 3 \ end {array} \ right] \ text {} \ left [\ begin {array } {c} 5 \\ 7 \ end {array} \ right] \ hfill \\ \ left [\ begin {array} {cc} 1 & 0 \\ 0 & 1 \ end {array} \ right] \ text {} \ left [\ begin {array} {c} x \\ y \ end {array} \ right] = \ left [\ begin {array} {r} \ hfill 11 \ left (5 \ right) + \ left (-8 \ right) 7 \\ \ hfill -4 \ left (5 \ right) +3 \ left (7 \ right) \ end {array} \ right] \ hfill \\ \ left [\ begin {array} {c} x \\ y \ end {array} \ right] = \ left [\ begin {array} {r} \ hfill -1 \\ \ hfill 1 \ end {array} \ right] \ hfill \ end {array} [/ latex ]
Решение [латекс] \ left (-1,1 \ right) [/ latex]. {-1} [/ latex] находился слева от [latex] A [/ latex] с левой стороны и слева от [latex] B [/ latex] с правой стороны. Поскольку умножение матриц не коммутативно, порядок имеет значение.
{-1} [/ latex] находился слева от [latex] A [/ latex] с левой стороны и слева от [latex] B [/ latex] с правой стороны. Поскольку умножение матриц не коммутативно, порядок имеет значение.
Пример 8: Решение системы 3 × 3 с использованием обратной матрицы
Решите следующую систему, используя обратную матрицу.
[латекс] \ begin {array} {r} \ hfill 5x + 15y + 56z = 35 \\ \ hfill -4x — 11y — 41z = -26 \\ \ hfill -x — 3y — 11z = -7 \ end { array} [/ latex]
Решение
Напишите уравнение [латекс] AX = B [/ латекс].
[латекс] \ left [\ begin {array} {ccc} 5 & 15 & 56 \\ -4 & -11 & -41 \\ -1 & -3 & -11 \ end {array} \ right] \ text {} \ left [\ begin {array} {c} x \\ y \\ z \ end {array} \ right] = \ left [\ begin {array} {r} \ hfill 35 \\ \ hfill -26 \\ \ hfill -7 \ конец {массив} \ справа] [/ латекс]
Во-первых, мы найдем инверсию [latex] A [/ latex] путем добавления идентификатора.
[латекс] \ left [\ begin {array} {rrr} \ hfill 5 & \ hfill 15 & \ hfill 56 \\ \ hfill -4 & \ hfill -11 & \ hfill -41 \\ \ hfill -1 & \ hfill -3 & \ hfill -11 \ end {array} | \ begin {array} {ccc} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \ end {array} \ right] [/ latex]
Умножьте строку 1 на [latex] \ frac {1} {5} [/ latex].
[латекс] \ left [\ begin {array} {ccc} 1 & 3 & \ frac {56} {5} \\ -4 & -11 & -41 \\ -1 & -3 & -11 \ end {array} | \ begin { массив} {ccc} \ frac {1} {5} & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \ end {array} \ right] [/ latex]
Умножить строку 1 на 4 и прибавить к строке 2.
[латекс] \ left [\ begin {array} {ccc} 1 & 3 & \ frac {56} {5} \\ 0 & 1 & \ frac {19} {5} \\ -1 & -3 & -11 \ end {array} | \ begin {array} {ccc} \ frac {1} {5} & 0 & 0 \\ \ frac {4} {5} & 1 & 0 \\ 0 & 0 & 1 \ end {array} \ right] [/ latex]
Добавьте строку 1 к строке 3.
[латекс] \ left [\ begin {array} {ccc} 1 & 3 & \ frac {56} {5} \\ 0 & 1 & \ frac {19} {5} \\ 0 & 0 & \ frac {1} {5} \ конец {массив} | \ begin {array} {ccc} \ frac {1} {5} & 0 & 0 \\ \ frac {4} {5} & 1 & 0 \\ \ frac {1} {5} & 0 & 1 \ end {array} \ right] [/ latex]
Умножить строку 2 на −3 и прибавить к строке 1.
[латекс] \ left [\ begin {array} {ccc} 1 & 0 & — \ frac {1} {5} \\ 0 & 1 & \ frac {19} {5} \\ 0 & 0 & \ frac {1} {5} \ end {array} | \ begin {array} {ccc} — \ frac {11} {5} & -3 & 0 \\ \ frac {4} {5} & 1 & 0 \\ \ frac {1} {5} & 0 & 1 \ end {array} \ right] [/ latex]
Умножить строку 3 на 5.
[латекс] \ left [\ begin {array} {ccc} 1 & 0 & — \ frac {1} {5} \\ 0 & 1 & \ frac {19} {5} \\ 0 & 0 & 1 \ end {array} | \ begin {array} {ccc} — \ frac {11} {5} & -3 & 0 \\ \ frac {4} {5} & 1 & 0 \\ 1 & 0 & 5 \ end {array} \ right] [/ latex]
Умножьте строку 3 на [latex] \ frac {1} {5} [/ latex] и прибавьте к строке 1.
[латекс] \ left [\ begin {array} {ccc} 1 & 0 & 0 \\ 0 & 1 & \ frac {19} {5} \\ 0 & 0 & 1 \ end {array} | \ begin {array} {ccc} — 2 & -3 & 1 \\ \ frac {4} {5} & 1 & 0 \\ 1 & 0 & 5 \ end {array} \ right] [/ latex]
Умножьте строку 3 на [latex] — \ frac {19} {5} [/ latex] и добавьте к строке 2. {- 1} B = \ left [\ begin {array} {r} \ hfill -70 + 78-7 \\ \ hfill -105 — 26 + 133 \\ \ hfill 35 + 0 — 35 \ end {array} \ right] = \ left [\ begin {array} {c} 1 \\ 2 \\ 0 \ end {array} \ right] [/ latex]
{- 1} B = \ left [\ begin {array} {r} \ hfill -70 + 78-7 \\ \ hfill -105 — 26 + 133 \\ \ hfill 35 + 0 — 35 \ end {array} \ right] = \ left [\ begin {array} {c} 1 \\ 2 \\ 0 \ end {array} \ right] [/ latex]
Решение [латекс] \ left (1,2,0 \ right) [/ latex].
Попробовать 4
Решите систему, используя обратную матрицу коэффициентов.
[латекс] \ begin {array} {l} \ text {} 2x — 17y + 11z = 0 \ hfill \\ \ text {} -x + 11y — 7z = 8 \ hfill \\ \ text {} 3y — 2z = -2 \ hfill \ end {array} [/ latex]
Как: решить систему уравнений с обращенными матрицами с помощью калькулятора.
- Сохраните матрицу коэффициентов и постоянную матрицу как матричные переменные [latex] \ left [A \ right] [/ latex] и [latex] \ left [B \ right] [/ latex].
- Введите умножение в калькулятор, вызывая при необходимости каждую матричную переменную.
- Если матрица коэффициентов обратима, калькулятор представит матрицу решения; если матрица коэффициентов необратима, калькулятор выдаст сообщение об ошибке.

Пример 9: Использование калькулятора для решения системы уравнений с инверсной матрицей
Решите систему уравнений с обратными матрицами с помощью калькулятора
[латекс] \ begin {array} {l} 2x + 3y + z = 32 \ hfill \\ 3x + 3y + z = -27 \ hfill \\ 2x + 4y + z = -2 \ hfill \ end {array} [/ латекс]
Решение
На странице матриц калькулятора введите матрицу коэффициентов как матричную переменную [latex] \ left [A \ right] [/ latex] и введите постоянную матрицу как матричную переменную [latex] \ left [B \ right] [/ латекс].
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Главы курса Основы калькулятора Mathematics Review
Основные понятия Расширенные концепции Тесты разделов Предварительное испытание Пост-тест Онлайн-калькуляторы Калькулятор окислительно-восстановительного потенциала Кинетика Аррениуса Калькулятор Калькулятор термодинамики Калькулятор ядерного распада Линейная регрессия методом наименьших квадратов Решатель уравнений методом Ньютона Калькулятор сжимаемости Калькулятор перевода единиц Калькулятор номенклатуры Ссылки на дополнительную информацию Калькуляторы Texas Instruments Калькуляторы Casio Калькуляторы Sharp Калькуляторы Hewlett Packard Связаться с веб-мастером | ПРИМЕЧАНИЕ: это приложение требует, чтобы у вас был калькулятор, способный вычислять МАТРИЦЫ.  Большинство, если не все графические калькуляторы имеют эту возможность. В этом показании в качестве примера используется графический калькулятор Texas Instrument TI-82. Большинство, если не все графические калькуляторы имеют эту возможность. В этом показании в качестве примера используется графический калькулятор Texas Instrument TI-82.В начале изучения химии у вас будет достаточно возможностей сбалансировать уравнения! Это фундаментальный навык в химии, как вы могли заметить из краткого чтения по стехиометрии! Уравнение баланса означает написание химических уравнений таким образом, чтобы количество вещества, с которым вы начинаете реакцию, равнялось количеству вещества, которое вы в конечном итоге получили в качестве продукта. Другими словами, если я начну печь хлеб из 10 фунтов муки, у меня должно получиться 10 фунтов хлеба, если только часть хлеба не упадет на пол или не сгорит в дым! Простой пример имеет большое значение. Мы можем образовать воду, смешав газообразный водород (H 2 ) и кислород (O 2 ) в присутствии электричества. Реакция выглядит так: Если вы выполните некоторые расчеты молекулярной массы грамма, вы найдете это: 2 грамма водорода + 32 грамма кислорода = 18 граммов воды Это говорит о том, что вы начинаете с 34 граммов материала и заканчиваете 18 граммами материала. Они не потеряны, мы просто не сбалансировали уравнение! Возможно, вы также заметили, что слева два кислорода и только один справа! Нам нужно получить вещи в правильных пропорциях, чтобы эта реакция была сбалансированной. Сбалансированная реакция выглядит так: Это говорит о том, что нам нужно, чтобы две молекулы водорода соединились с одной молекулой кислорода, чтобы образовались две новые молекулы воды. Если посчитать: (2 x 2 грамма водорода) + 32 грамма кислорода = (2 x 18 граммов воды) теперь у нас 36 граммов материала слева и 36 граммов справа. У нас также теперь есть 4 водорода слева, четыре водорода справа, два кислорода слева и два кислорода справа. Можно сказать, что это уравнение сбалансировано по массе. При изучении химии вам также придется заниматься балансировкой заряда, но мы позволим вашим профессорам помочь вам в этом! Уравнения баланса — это искусство, но если у вас есть калькулятор, способный справиться с так называемым «матрица», у вас есть надежный способ балансировки уравнений! Матрица — это группа чисел, расположенных в строках и столбцах, например: Это называется матрицей «2 на 2» или «2 x 2», потому что она состоит из двух строк (идущих поперек) и двух столбцов (идущих вниз).
К счастью, графические калькуляторы делают это особенно легко! Чтобы помочь вам немного понять, что вы делаете, давайте объясним, как найти определитель. определитель — это единственное число, полученное путем перекрестного умножения членов матрицы. У вас должна быть квадратная матрица (n X n), чтобы иметь возможность найти определитель. Уравнение для нахождения определителя: Пример под уравнением показывает пример расчета для матрицы 2 x 2. Обратите внимание, что вы перекрестно умножаете противоположные термины, а затем вычитаете другой набор противоположных наборов умноженных терминов. Довольно легко. Вот как это делается на графическом калькуляторе TI-82. Эти инструкции СПЕЦИАЛЬНЫ для TI-82:
Теперь мы готовы поговорить об уравнениях балансировки. Выберем простую реакцию: У нас есть два разных элемента, Cr и O, поэтому нам понадобятся два разных уравнения. Мы пытаемся вычислить значения a, b и c, коэффициенты реакции. Два уравнения выглядят так: Кр: 1а + 0б = 2с «1a» означает, что за коэффициентом «a» находится один Cr, за коэффициентом «b» — ноль Cr, а за коэффициентом c — 2 Cr. Чтобы получить значения a, b и c, выполните следующие действия:
Вот как выполнить первый шаг:
Чтобы сделать вторую часть, вычислив c:
Теперь сбалансированное уравнение: Попробуйте
|
Калькулятор числа состояний
Создано Rijk de Wet
Отзыв от Wojciech Sas, кандидата наук и Стивена Вудинга
Последнее обновление: 14 декабря 2021 г.
Содержание матрицы:- ?
- Число обусловленности матрицы в линейной алгебре
- Как найти число обусловленности матрицы?
- Как пользоваться калькулятором номера состояния?
- Как найти число обусловленности матрицы? – Пример
- Часто задаваемые вопросы
Добро пожаловать в калькулятор номера состояния . Нужно определить, является ли ваша задача линейной алгебры хорошо обусловленной или нестабильной ? Не приведут ли неправильные измерения или плохое округление к краху вашего матричного уравнения? Здесь мы покажем вам , что такое номер условия матрицы и , как найти номер состояния любой матрицы, чтобы вы могли защитить себя от любых ошибок, которые могут закрасться.
Если вам нужно повторить более простые темы по математике, взгляните на наш калькулятор пропорций!
Что такое номер состояния матрицы?
Прежде чем мы сможем понять какой-либо результат, выдаваемый нашим калькулятором числа условий, давайте сначала определим матричное число условий и то, что оно представляет. Обычно мы обозначаем число обусловленности матрицы AAA как cond(A)\text{cond}(A)cond(A) или κ(A)\kappa(A)κ(A). Мы можем определить его математически следующим образом:
9+\Vertcond(A)=∥A∥⋅∥A+∥. Это альтернативное определение по-прежнему будет давать огромных, почти бесконечных чисел состояния для необратимых матриц, тем самым по-прежнему соблюдая наше исходное определение.Число условий можно интерпретировать несколькими способами. Во-первых, cond(A)\text{cond}(A)cond(A) измеряет 90 818 отношение максимального растяжения к максимальному сжатию 90 819 в единичном векторе, когда на него умножается AAA. Следовательно, эквивалентное определение номера условия: 9{-1}cond(A)=∥x
∥=1max∥x
∥∥Ax
∥⋅(∥x
∥=1min∥x
∥0∥0) 2 x
∥0∥08 −1
В чистой математике матрица либо обратима, либо нет. Но, будучи вторым способом интерпретации числа обусловленности, cond(A)\text{cond}(A)cond(A) является мерой того, насколько обратим AAA. Поскольку cond(A)\text{cond}(A)cond(A) увеличивается , AAA становится ближе к тому, чтобы быть необратимым .
Но, будучи вторым способом интерпретации числа обусловленности, cond(A)\text{cond}(A)cond(A) является мерой того, насколько обратим AAA. Поскольку cond(A)\text{cond}(A)cond(A) увеличивается , AAA становится ближе к тому, чтобы быть необратимым .
Третье и наиболее важное использование номеров состояний — в линейная алгебра . Давайте посмотрим, почему ниже!
Число обусловленности матрицы в линейной алгебре
Когда у нас есть система линейных уравнений A⋅x⃗=b⃗A\cdot\vec{x} = \vec{b}A⋅x=b, число обусловленности приобретает особый вид значение. cond(A)\text{cond}(A)cond(A) теперь становится скоростью, с которой решение x⃗\vec{x}x изменится на по отношению к изменению b⃗\vec{b}b. По этой причине мы можем называть cond(A)\text{cond}(A)cond(A) коэффициентом увеличения ошибки задачи, равным 9.0819 . Изменения в b⃗\vec{b}b обычно происходят из-за ошибок, допущенных при формулировании задачи , таких как выполнение ошибочных измерений или ошибок округления .
Итак, предположим, что закралась какая-то ошибка , и значения, содержащиеся в b⃗\vec{b}b, немного неверны . Насколько далеко от истины наше вновь найденное решение x⃗\vec{x}x, зависит от cond(A)\text{cond}(A)cond(A):
Если номер условия матрицы AAA равен большой , x⃗\vec{x}x уязвим для ошибок . Таким образом, ошибка в x⃗\vec{x}x, возникающая из-за ошибки в b⃗\vec{b}b, будет большой .
Обратно, если cond(A)\text{cond}(A)cond(A) является маленьким , x⃗\vec{x}x будет хорошо защищенным от разумных ошибок в b⃗\vec{b}b , поэтому его ошибка будет маленькой .
Мы можем математически переформулировать это соотношение. С δb⃗\delta\vec{b}δb, представляющим ошибку в b⃗\vec{b}b, и δx⃗\delta\vec{x}δx, результирующим изменением x⃗\vec{x}x, мы можем связать относительные ошибки ∥ δb⃗∥ / ∥b⃗∥\Vert \delta\vec{b}\Vert \ /\ \Vert \vec{b}\Vert ∥δb∥ / ∥b∥ и ∥δx⃗∥ / ∥x⃗∥\Vert \delta\vec {x}\Vert \ /\ \Vert \vec{x}\Vert ∥δx∥ / ∥x∥ с:
∥δx⃗∥∥x⃗∥≤cond(A)⋅∥δb⃗∥∥b⃗∥\frac{ \Верт\дельта\век{х}\Верт }{ \Верт \vec{x}\Верт } \ле \text{условие}(A) \cdot \ гидроразрыв { \Верт\дельта\vec{b}\Верт }{ \Верт \vec{b}\Верт }∥x
∥∥δx
∥≤cond(A)⋅∥b
∥∥δb
∥
как относительная ошибка b⃗\vec{b}b , масштабированная по номеру условия .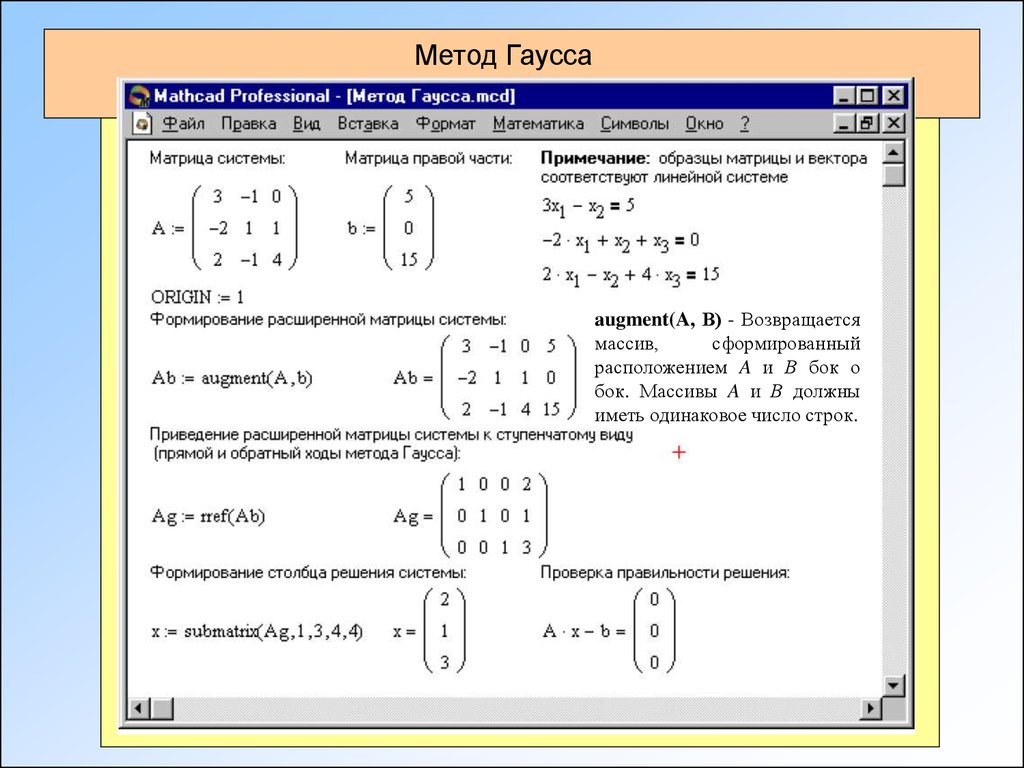
Как найти число обусловленности матрицы? 9{-1}\Верт ∥A−1∥. Крайне важно использовать одну и ту же норму, выбранную выше, во всех наших расчетах.
Умножьте нормы , чтобы найти cond(A)\text{cond}(A)cond(A).
Как пользоваться калькулятором номера состояния?
Здорово знать, как рассчитать число условий матрицы, но иногда вам просто нужен ответ немедленно, чтобы сэкономить время. Вот тут-то и пригодится наш калькулятор числа условий матрицы . Вот как это использовать:
Выберите размерность вашей матрицы . Мы поддерживаем матрицы 2×22\times22×2 и 3×33×33×3.
Введите вашу матрицу построчно. Не стесняйтесь обращаться к символическому представлению вверху.
Выберите норму матрицы или оставьте выбранную по умолчанию норму матрицы 2.
Найти cond(A)\text{cond}(A)cond(A) внизу нашего матричного калькулятора номера состояния.

Как найти число обусловленности матрицы? – Пример
Чтобы закрепить полученные знания, давайте рассмотрим пример . Предположим, у нас есть линейная система A⋅x⃗=b⃗A\cdot \vec{x} = \vec{b}A⋅x=b с:
A=[3.70.97.81.9]A = \begin{bmatrix} 3,7 и 0,9 \\ 7,8 и 1,9\\ \end{bmatrix}A=[3.77.80.91.9]
и
b⃗=[7.415.6]\vec{b} = \begin{bmatrix} 7.4\ 15,6\\ \end{bmatrix}b 9{-1}\cdot\vec{b} \\ &= \begin{bmatrix} 2 \\ 0 \end{bmatrix} \end{split}x
=A−1⋅b
=[20]
Теперь давайте посмотрим, что произойдет, если мы добавим небольшую ошибку , равную 0,010,010,01, к первому элементу b⃗\ vec{b}b, чтобы сформировать b⃗2\vec{b}_2b2.
b⃗2=[7.4115.6]\vec{b}_2 = \begin{bmatrix} 7.41\ 15,6\\ \end{bmatrix}b
2=[7.4115.6]
Вычисление x⃗2\vec{x}_2x2 в A⋅x⃗2=b⃗2A\cdot\vec{x}_2 = \vec{b}_2A⋅ x2=b2, получаем:
x⃗2=A−1⋅b⃗2=[3,9{-1}\cdot\vec{b}_2 \\
&= \begin{bmatrix} 3. 9 \\ -7.8 \end{bmatrix} \\
\end{split}x
9 \\ -7.8 \end{bmatrix} \\
\end{split}x
2=A−1⋅b
2=[3.9−7.8]
Существует огромная разница между x⃗\vec{x}x и x⃗2\vec{ х}_2x2! Как вы уже могли догадаться, это потому, что AAA имеет большой номер состояния . На самом деле cond(A)=7895,0\text{cond}(A) = 7895,0cond(A)=7895,0. Вы можете проверить этот результат в нашем калькуляторе норм матрицы!
Интересно отметить, что отношение между нашими относительными ошибками и нашим числом условий соблюдается:
∥δx⃗∥ / ∥x⃗∥=4,014∥δb⃗∥ / ∥b⃗∥=0,00058cond(A)×∥δb⃗∥ / ∥b⃗∥=4,573\begin{split} \Vert \delta\vec{x}\Vert \ /\ \Vert \vec{x}\Vert &= 4.014 \\ \Vert \delta\vec{b}\Vert \ /\ \Vert \vec{b}\Vert &= 0.00058 \\ \text{cond}(A) \times \Vert \delta\vec{b}\Vert \ /\ \Vert \vec{b}\Vert &= 4,573 \ end {split} ∥Δx
∥/∥x
∥∥ΔB
∥/∥B
∥cond (a) × ∥ΔB
∥/∥B
∥ 4.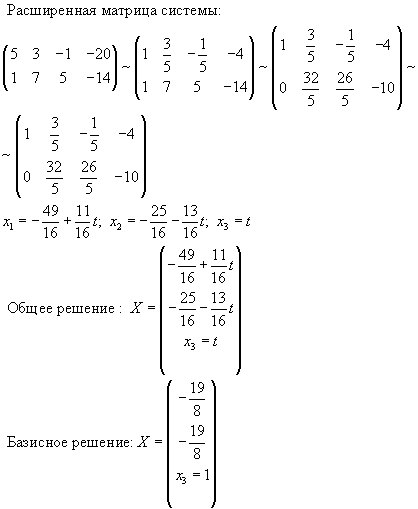 014 = 0,5014 = 0,5014 = 0,5014 = 0,5014 = 0,5014 = 0,5014 = 0,5014 = 4,5014 = 4,5014 = 4,5014 = 4.5857 ∥/∥B
014 = 0,5014 = 0,5014 = 0,5014 = 0,5014 = 0,5014 = 0,5014 = 0,5014 = 4,5014 = 4,5014 = 4,5014 = 4.5857 ∥/∥B
∥ 4,0202
∥/∥B
∥ΔB
∥/4.
4,573≤4,0144,573 \le 4,0144,573≤4,014 и, следовательно, относительная ошибка нашего решения не превышает относительная ошибка задачи , увеличенная числом условий ААА.
Часто задаваемые вопросы
Что такое номер условия матрицы идентичности?
Число обусловленности единичной матрицы любого размера равно 1 . Поскольку единичная матрица оставляет нетронутым любой вектор, на который она умножается, она не увеличивает ошибку в b . Следовательно, интуитивно понятно, что единичная матрица имеет число обусловленности 1.
1 является наименьшим возможным номером состояния матрицы , поэтому единичную матрицу можно рассматривать как оптимально хорошо обусловленную.
Что такое число обусловленности диагональной матрицы?
Число обусловленности диагональной матрицы D равно отношению между наибольшим и наименьшим элементами на ее диагонали , т. е. cond(D) = max(D ii ) / min(D ii ) . Важно отметить, что это верно только при использовании матрицы 2-норма для вычисления конд(D) . Во многом это связано с тем, что диагональные элементы D являются его собственными значениями.
Может ли число обусловленности матрицы равняться нулю?
№ Если cond(A) = 0 , то ‖δ x ‖/‖ x ‖ ≤ cond(A)·‖δ b ‖ 10/‖ 0 Следовательно, номер условия 0 будет означать, что матрица удаляет любую ошибку, что невозможно.
На самом деле, наименьший возможный номер состояния 1 , где ошибка не увеличивается и не уменьшается.
Влияет ли масштабирование матрицы на ее число обусловленности?
Нет. Любое масштабирование матрицы будет аннулировано обратным масштабированием матрицы. Это потому, что
Любое масштабирование матрицы будет аннулировано обратным масштабированием матрицы. Это потому, что (𝛾A) −1 = 𝛾 −1 A −1 . SO,
Cond (𝛾A)
= 𝛾A‖ · · (𝛾A) −1 ‖
= 𝛾𝛾A‖ · (𝛾) −1 87 = 𝛾𝛾a‖ · (𝛾) −1 87 = 𝛾𝛾a‖ · (𝛾) −1906 = 𝛾𝛾a‖ · (𝛾) .
= (𝛾·𝛾 −1 )·(‖A‖·‖A −1 ‖)
= cond(A)
Число условия измеряет отношение максимального растяжения к минимальному растяжению. If both the maximum and minimum increase by 𝛾 , the ratio wouldn't change, meaning cond(𝛾A) = cond(A)
Rijk de Wet
| A | = |
|
Matrix size
First row
Second row
Results
Matrix norm
Check out 31 similar linear algebra calculators 🔢
Adjoint matrixCharacteristic polynomialCholesky decomposition … еще 28
▷Step by Step Приложения для TI-Nspire CX и CX CAS Скачать бесплатно.
 Пройдите курсы по математике, естественным наукам и бизнесу
Пройдите курсы по математике, естественным наукам и бизнесуДля подготовки к экзаменам по математике и естественным наукам, домашнее задание. Проверьте свою работу.
--- Шаг за шагом к успеху. Приложения запускаются за считанные минуты. Сначала протестируйте наши бесплатные пробные версии.---
| 95% купили больше ПРИЛОЖЕНИЙ. | 97% сообщили об улучшении результатов. | Рейтинг: 4,89 из 5 звезд. | Доступно 46 ПРИЛОЖЕНИЙ. |
КОВИД СПЕЦИАЛЬНЫЙ
Купите 3 приложения Made Easy по цене 2 приложений.
Выберите 3 приложения. EasyBusiness Stats Made EasyCalculus with Physics Apps Calculo de Manera Facil Chemistry Made EasyChemie Leicht GemachtQuimica de Manera FacilCollege Algebra Made Easy CX CASCollege Algebra Made Easy CXComplex Analysis Made EasyConics Made EasyConico de Manera FacilDifferential Equations Made EasyEcuaciones Diferencial de Manera FacilDifferential Gleichungen Leicht Gemacht DiscreteMDisateM de Manera FacilEconomics Made EasyEinheiten Umwandler mit SchrittenElectrical Engineering Made EasyElectronik Leicht GemachtEngineering Economics Made EasyEngineering Mathematics Made EasyIngenieu r Mathematik Leicht GemachtFinance Made EasyКонечная математика Made EasyGeometry Made EasyGeometrie Leicht GmachtGeometria de Manera FacilLand Survey Made EasyLinear Algebra Made EasyLinear Algebra de Manera FacilLineare Algebra Leicht GmachtMathematical Economics Made EasyMathematical Economics Made EasyMathematical Economics Made EasyMathematical Economics Made EasyCXMatrix Made EasyЧисленный анализ Made EasyТеория чисел Made EasyPhysik LeachPhysich Research Made EasyPhysik Research Made EasyPhysik GemachtFisica de Manera FacilPortfolio & Stocks Made EasyPreCalculus Made EasyPreCalculus Made Easy CXPreCalculus Made Easy CXPreCalculo de Manera FacilReal Estate Made EasySAT Made EasySAT Subject Test MathSignals and Systems Made EasyStatistics and Probability Made EasyStatistik Leicht GemachtEstadisticas de Manera FacilStatic and Dynamics Made EasyStatik und Dynamik Leicht GemachtStep by Step Equation Solver Ecuaciones de Manera FacilПошаговый конвертер единиц измеренияThermodynamics Made EasyThermodynamik Leicht GemachtTrigonometry Made EasyTrigonometria de Manera FacilTri gonometrie Leicht GemachtVector Calculus Made EasyVektor Analysis Leicht GemachtWirtschaftsmathematik Leicht Gemacht
Calculus Made EasyACT Made EasyAccounting Made EasyAerodynamics Made EasyAnalysis Leicht GemachtAnalysis mit PhysikAlgebra Made Easy CX CASAlgebra Made Easy CXAlgebra Leicht Gemacht CX CASAlgebra de Manera FacilAlgebra de Manera Facil CXApplications and Optimizations Made EasyBiology Made EasyBiostatistics AppBusiness Calculus Made EasyBusiness Stats with Physics de Manera Facil Chemistry Made EasyChemie Leicht GemachtQuimica de Manera FacilCollege Algebra Made Easy CX CASCollege Algebra Made Easy CXComplex Analysis Made EasyConics Made EasyConico de Manera FacilDifferential Equations Made EasyEcuaciones Diferencial de Manera FacilDifferential Gleichungen Leicht GemachtDiscrete Math Made EasyMatematicas Discretas de Manera FacilEconomics Made EasyEinheiten Umwandler mit SchrittenElectrical Engineering Made EasyElectronik Leicht GemachtEngineering Economics Made EasyEngineering Mathematics Made EasyIngenieur Mathematik Leicht GemachtFinance Mad e EasyFinite Math Made EasyGeometry Made EasyGeometrie Leicht GemachtGeometria de Manera FacilLand Surveying Made EasyLinear Algebra Made EasyLinear Algebra de Manera FacilLineare Algebra Leicht GemachtMathematical Economics Made EasyMathematical Economics Made EasyMathematical Economics Made EasyCXMatrix Made EasyNumerical Analysis Made EasyNumber Theory Made EasyProperties Research Made EasyPhysik Made EasyPhysik Leicht Gemacht & Stocks Made EasyPreCalculus Made EasyPreCalculus Made Easy CXPreCalculus Made Easy CXPreCalculo de Manera FacilReal Estate Made EasySAT Made EasySAT Subject Test MathСигналы и системы Made EasyСтатистика и вероятность Made EasyStatistik Leicht GemachtEstadisticas de Manera FacilStatik und Dynamics Made EasyStatik und Dynamik Leicht GemachtStep by Step Equal SolverSolucionador de EcuacionesStep de Manera Facil by Step Unit ConverterThermodynamic Made EasyThermodynamik Leicht GemachtТригонометрия Made EasyTrigonometria de Manera FacilTrigonometrie Leicht GemachtВекторный расчет us Made EasyVektor Analysis Leicht GemachtWirtschaftsmathematik Leicht Gemacht
Calculus Made EasyACT Made EasyAccounting Made EasyAerodynamics Made EasyAnalysis Leicht GemachtAnalysis mit PhysikAlgebra Made Easy CX CASAlgebra Made Easy CXAlgebra Leicht Gemacht CX CASAlgebra de Manera FacilAlgebra de Manera Facil CXApplications and Optimizations Made EasyBiology Made EasyBiostatistics AppBusiness Calculus Made EasyBusiness Stats with Physics de Manera Facil Chemistry Made EasyChemie Leicht GemachtQuimica de Manera FacilCollege Algebra Made Easy CX CASCollege Algebra Made Easy CXComplex Analysis Made EasyConics Made EasyConico de Manera FacilDifferential Equations Made EasyEcuaciones Diferencial de Manera FacilDifferential Gleichungen Leicht GemachtDiscrete Math Made EasyMatematicas Discretas de Manera FacilEconomics Made EasyEinheiten Umwandler mit SchrittenElectrical Engineering Made EasyElectronik Leicht GemachtEngineering Economics Made EasyEngineering Mathematics Made EasyIngenieur Mathematik Leicht GemachtFinance Mad e EasyFinite Math Made EasyGeometry Made EasyGeometrie Leicht GemachtGeometria de Manera FacilLand Surveying Made EasyLinear Algebra Made EasyLinear Algebra de Manera FacilLineare Algebra Leicht GemachtMathematical Economics Made EasyMathematical Economics Made EasyMathematical Economics Made EasyCXMatrix Made EasyNumerical Analysis Made EasyNumber Theory Made EasyProperties Research Made EasyPhysik Made EasyPhysik Leicht Gemacht & Stocks Made EasyPreCalculus Made EasyPreCalculus Made Easy CXPreCalculus Made Easy CXPreCalculo de Manera FacilReal Estate Made EasySAT Made EasySAT Subject Test MathСигналы и системы Made EasyСтатистика и вероятность Made EasyStatistik Leicht GemachtEstadisticas de Manera FacilStatik und Dynamics Made EasyStatik und Dynamik Leicht GemachtStep by Step Equal SolverSolucionador de EcuacionesStep de Manera Facil by Step Unit ConverterThermodynamic Made EasyThermodynamik Leicht GemachtТригонометрия Made EasyTrigonometria de Manera FacilTrigonometrie Leicht GemachtВекторный расчет us Made EasyVektor Analysis Leicht GemachtWirtschaftsmathematik Leicht Gemacht
Введите последние 8 цифр вашего 27-значного идентификатора продукта TI-Nspire.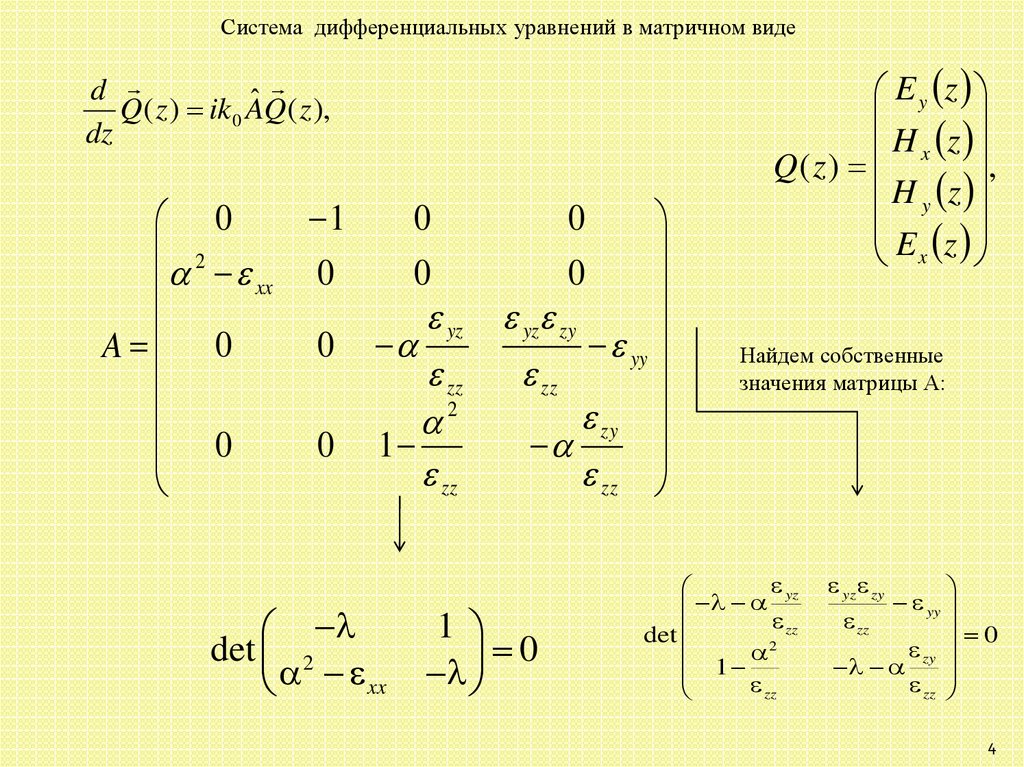
Находится в разделе 5:Настройки → 4:Статус → О программе
ID может выглядеть так: 1008000007206E210B0 BD92F455 .
ПОМОГИТЕ НАЙТИ ID.
Если бы это был ваш ID, вы бы набрали только BD92F455.
или на международном уровне:
В конце оплаты PayPal вам будет отправлено электронное письмо, содержащее ваш ключ и программное обеспечение.
Ищете калькулятор TI?
Получите самые низкие цены на калькуляторы TI
(со сравнением цен)
СРАВНИТЕ лучшие цены на Amazon, Ebay, Target, Walmart, Office Max, Best Buy.
Сравните лучшие цены на Amazon, Walmart, Ebay, Target, Best Buy и т. д.
Изучите историю цен калькуляторов за последние несколько месяцев.
Настройте оповещение по электронной почте при снижении цен, чтобы получать уведомления.
Сравните различные модели, чтобы найти калькулятор, который лучше всего соответствует вашим потребностям.
Найдите новые, обновленные, отремонтированные, подержанные калькуляторы.
Смотрите обучающие видео и читайте руководства по калькуляторам.
Читайте последние новости о калькуляторах в Интернете.
БЕСПЛАТНАЯ загрузка:
Решение квадратных уравнений (шаг за шагом)
Загрузите пошаговый решатель квадратных уравнений
. Этот решатель является частью приложения Algebra Made Easy.
- Загрузите бесплатные пробные версии здесь.
- Срок действия пробных и платных приложений неограничен.
- Будущие обновления бесплатны - навсегда!
Онлайн-репетиторство по математике
Получите онлайн-репетиторство.
Репетиторы с отличными оценками по математике будут рады помочь вам.
Получите индивидуальную помощь по математике.
Мы используем Zoom для обучения онлайн, мы шаг за шагом объясняем, как решать математические задачи.
Репетиторы в настоящее время преподают алгебру, алгебру 2, предварительное исчисление, AP исчисление AB и BC, AP статистику, тригонометрию, дискретную математику.
Репетиторы работали более 10 лет в качестве читателей AP Calculus (те люди, которые оценивают экзамены AP Calculus).
Репетиторы также обучают навыкам сдачи тестов, которые так же важны, как и само содержание.
Наши преподаватели имеют более 20 лет опыта преподавания.
1. урок стоит 50 долларов, после него 100 долларов в час.
оптом: 540 долларов за 6 часов, 1000 долларов за 12 часов.
Забронируйте сеанс репетиторства по электронной почте: [email protected]
Для вопросов, заказов и т. д.: ОБЩАЙТЕСЬ С НАМИ.
| Первый урок (50 долларов США) | Один урок (100 долларов США) | Несколько уроков |
|---|---|---|
Как решить систему уравнений на TI-84 Plus
Матрицы — идеальный инструмент для решения систем уравнений (чем больше, тем лучше). К счастью, вы можете работать с матрицами на вашем TI-84 Plus. Все, что вам нужно сделать, это решить, какой метод вы хотите использовать.
К счастью, вы можете работать с матрицами на вашем TI-84 Plus. Все, что вам нужно сделать, это решить, какой метод вы хотите использовать.
A
–1 *B метод решения системы уравненийЧто обозначают буквы A и B? Буквы A и B заглавные, потому что они относятся к матрицам. В частности, A является матрицей коэффициентов, а B является постоянной матрицей. Кроме того, X является переменной матрицей. Независимо от того, какой метод вы используете, важно уметь преобразовывать систему уравнений в матричную форму.
Вот краткое объяснение происхождения этого метода. Любую систему уравнений можно записать в виде матричного уравнения, A * X = B. Предварительно умножив каждую часть уравнения на A –1 и упростив, вы получите уравнение X = A –1 * B.
С помощью калькулятора найдите A –1 * B – это проще простого. Просто выполните следующие действия:
Введите матрицу коэффициентов, A.
Нажмите [ALPHA][ZOOM], чтобы создать матрицу с нуля, или нажмите [2nd][9].
 1390 x –1 ] для доступа к сохраненной матрице. Смотрите первый экран.
1390 x –1 ] для доступа к сохраненной матрице. Смотрите первый экран.Нажмите [ x –1 ], чтобы найти обратную матрицу A.
См. второй экран.
Введите постоянную матрицу, B.
Нажмите [ENTER], чтобы оценить матрицу переменных, X.
Переменная матрица указывает решения: x = 5, y = 0 и z = 1. См. третий экран.
Если определитель матрицы A равен нулю, вы получите сообщение об ошибке ОШИБКА: ЕДИНСТВЕННАЯ МАТРИЦА. Это означает, что система уравнений либо не имеет решений, либо имеет бесконечное число решений.
Метод увеличивающих матриц для решения системы уравнений
Добавление двух матриц позволяет добавить одну матрицу к другой матрице. Обе матрицы должны быть определены и иметь одинаковое количество строк. Используйте систему уравнений, чтобы увеличить матрицу коэффициентов и матрицу констант.
Чтобы увеличить две матрицы, выполните следующие действия:
Чтобы выбрать команду Augment из меню MATRX MATH, нажмите
Введите первую матрицу и нажмите [] (см. первый экран).
Чтобы создать матрицу с нуля, нажмите [ALPHA][ZOOM]. Чтобы получить доступ к сохраненной матрице, нажмите [2] [ x –1 ].
Введите вторую матрицу и нажмите [ENTER].
На втором экране отображается расширенная матрица.
Сохраните расширенную матрицу, нажав
Расширенная матрица хранится как [C]. Смотрите третий экран.
Системы линейных уравнений можно решить, если сначала представить расширенную матрицу системы в сокращенной ступенчато-строковой форме. Математическое определение редуцированной формы строки-эшелона здесь не важно. Это просто эквивалентная форма исходной системы уравнений, которая при обратном преобразовании в систему уравнений дает вам решения (если они есть) исходной системы уравнений.
Чтобы найти сокращенную форму строки-эшелона матрицы, выполните следующие действия:
Чтобы перейти к функции rref( в меню MATRX MATH, нажмите
и используйте клавишу со стрелкой вверх. Смотрите первый экран.
Нажмите [ENTER], чтобы вставить функцию на главный экран.
Нажмите [2nd] [ x –1 ] и нажмите [3], чтобы выбрать расширенную матрицу, которую вы только что сохранили.
Нажмите [ENTER], чтобы найти решение.
См. второй экран.
Чтобы найти решения (если они есть) исходной системы уравнений, преобразуйте редуцированную матрицу строк-ступеней в систему уравнений:
Как видите, решениями системы являются x = 5, y = 0 и z = 1. К сожалению, не все системы уравнений имеют уникальные решения, подобные этой системе. Вот примеры двух других случаев, которые вы можете увидеть при решении систем уравнений:
См. сокращенные матричные решения по строкам и эшелонам для предыдущих систем на первых двух экранах.
сокращенные матричные решения по строкам и эшелонам для предыдущих систем на первых двух экранах.
Чтобы найти решения (если они есть), преобразуйте редуцированные матрицы строк-ступеней в систему уравнений:
Поскольку одно из уравнений в первой системе упрощается до 0 = 1, эта система не имеет решения. Во второй системе одно из уравнений упрощается до 0 = 0. Это означает, что система имеет бесконечное число решений, лежащих на прямой x + 6 y = 10.
Об этой статье
Эта статья из книги:
- TI-84 Plus CE Graphing Calculator For Dummies, 3rd Edition,
Об авторе книги:
0 McCal 90al работает учителем математики в епископальной школе Святой Марии в Мемфисе, штат Теннесси. Он стал соучредителем группы суперпользователей TI-Nspire и получил Президентскую премию за выдающиеся достижения в области преподавания естественных наук и математики.
К.К. Эдвардс — преподаватель, который провел множество семинаров по использованию калькуляторов TI.
Эту статью можно найти в категории:
- Графические калькуляторы,
Я построил онлайн-калькулятор для конечных полей и линейной алгебры
Демонстрация моего нового калькулятора, умножающего матрицы в \(\mathbb{F}_4\)TL;DR: Вот он: matrixer.davidaugustat.com
Все знакомы с так называемыми действительными числами, означающие числа, которые мы используем в нашей повседневной жизни, такие как 3, -4, 0,5 или \(\pi\). Будучи студентом информатики, я посещаю математический класс в университете, где мы используем не только действительные числа, но и другие алгебраические поля, так называемые конечные поля.
В отличие от действительных чисел, конечные поля имеют только конечный набор чисел. При выполнении математических операций \(+, -, \cdot\) или \(/\) над элементами из этого ограниченного набора чисел "вырваться" из него невозможно, т. е. тот же набор.
е. тот же набор.
Маленький пример
Поле \(\mathbb{F}_5\) состоит из 5 элементов: \(0, 1, 2, 3\) и \(4\).
В этом поле, например. \(3+4 = 2\) и \(2\cdot 3 = 1\) являются допустимыми выражениями. Очевидно, что в реальных числах это не имело бы никакого смысла, но в \(\mathbb{F}_5\) имеет смысл.
Но как я вычислил эти числа?
На самом деле это не так сложно для одиночных вычислений. Все, что вам нужно сделать, это вычислить, как с действительными числами, но затем разделить результат на \(5\) и взять остаток .
Например, \(3+4\) равно \(7\) в \(\mathbb{R}\). \(7/5 = 1\), Остаток: \(2\). Поэтому \(3+4 = 2\) в \(\mathbb{F}_5\).
То же самое для умножения: \(2\cdot 3\) равно \(6\) в \(\mathbb{R}\). \(6/5 = 1\), Остаток: \(1\). Поэтому \(2\cdot 3 = 1\) в \(\mathbb{F}_5\).
Если мы проделаем это для всех элементов \(\mathbb{F}_5\), мы получим следующие таблицы для сложения и умножения:
\[\begin{массив}{c|ccccc} + & 0 & 1 & 2 & 3 & 4 \\ \hline 0 и 0 и 1 и 2 и 3 и 4 \\ 1 и 1 и 2 и 3 и 4 и 0 \\ 2 и 2 и 3 и 4 и 0 и 1 \\ 3 и 3 и 4 и 0 и 1 и 2 \\ 4 и 4 и 0 и 1 и 2 и 3 \конец{массив}\] \[\begin{массив}{c|ccccc} \cdot & 0 & 1 & 2 & 3 & 4 \\ \hline 0 и 0 и 0 и 0 и 0 и 0 \\ 1 и 0 и 1 и 2 и 3 и 4 \\ 2 и 0 и 2 и 4 и 1 и 3 \\ 3 и 0 и 3 и 1 и 4 и 2 \\ 4 и 0 и 4 и 3 и 2 и 1 \конец{массив}\]
В целом
Для любого другого конечного поля, количество элементов которого является простым числом (\(\mathbb{F}_2, \mathbb{F}_3, \mathbb{F}_5, \mathbb{F}_7, \dots\)) работает точно так же. Единственная разница в том, что вы делите не на \(5\), а на соответствующее количество элементов в поле.
Единственная разница в том, что вы делите не на \(5\), а на соответствующее количество элементов в поле.
в \(\mathbb{F}_3\) есть три элемента \(0, 1\) и \(2\).
\(1+2 = 3\) в \(\mathbb{R}\). \(3/3 = 1\), Остаток: \(0\). Поэтому \(1+2 = 0\) в \(\mathbb{F}_3\).
Как я уже сказал, эти правила применимы только к конечным полям, число элементов которых является простым числом. Это означает, что вы не можете вычислять так в \(\mathbb{F}_4\), так как \(\mathbb{F}_4\) имеет 4 элемента и \(4\) не является простым числом.
Но почему я не могу этого сделать?
Ответ таков: \(\mathbb{F}_4\) больше не было бы полем, если бы вы вычисляли таким образом. В алгебраическом поле каждый элемент (кроме \(0\)) должен иметь мультипликативный обратный элемент по определению. Мультипликативный обратный элемент \(y\) элемента \(x\) определяется как \(x \cdot y = 1\).
Другими словами: для каждого элемента в поле должен существовать элемент, так что элемент, умноженный на другой элемент, равен \(1\).
Если мы посмотрим на \(\mathbb{F}_4\), то быстро обнаружим, что оно не соответствует этому критерию, если вычисляется как поле простых чисел. Возьмем элемент \(2\) в качестве контрпримера:
\[\начать{выравнивать*} 2\cточка 0 = 0 \\ 2\cdot 1 = 2 \\ 2\cточка 2 = 0 \\ 2\cdot 3 = 2 \конец{выравнивание*}\]
Как видите, элемента нет, так что \(2\cdot y = 1\). Следовательно, \(\mathbb{F}_4\) не является полем, если мы определяем его таким образом.
Однако, если количество элементов в поле является простым числом, существует мультипликативный обратный элемент для для каждого элемента. Доказательство этого было бы слишком сложным для этой статьи, поэтому я не буду его включать.
Вот где вступают в игру расширенные поля
Тем не менее, можно определить поле с 4 элементами. Такое поле называется расширенным полем , и с ним намного сложнее производить расчеты, поскольку его элементы и правила несколько необычны.
Фактическое поле \(\mathbb{F}_4\) содержит элементы \(0, 1, \alpha\) и \(\alpha + 1\). Да, верно, \(\alpha + 1\) — это не математическое выражение, а элемент \(\mathbb{F}_4\).
Подробно объяснять как считать с этими элементами не буду, но вот таблицы:
\[\begin{массив}{c|ccccc} + & 0 & 1 & \alpha & \alpha+1\\ \hline 0 и 0 и 1 и \альфа и \альфа+1 \\ 1 и 1 и 0 и \альфа+1 и \альфа\\ \альфа & \альфа & \альфа+1 & 0 & 1 \\ \альфа+1 & \альфа+1 & \альфа & 1 & 0 \конец{массив}\] \[\begin{массив}{c|ccccc} \cdot & 0 & 1 & \alpha & \alpha+1\\ \hline 0 и 0 и 0 и 0 и 0 \\ 1 и 0 и 1 и \альфа и \альфа+1 \\ \альфа и 0 и \альфа и \альфа+1 и 1 \\ \alpha+1 & 0 & \alpha+1 & 1 & \alpha \конец{массив}\] 92\). Расчет с ними вызывает головную боль и занимает много времени.
В университете мы довольно часто используем эти конечные поля, а также занимаемся линейной алгеброй, используя конечные поля. Желаю вам удачи в перемножении этих матриц без ошибок:
\[\begin{pmatrix} 1 & \альфа & \альфа+1 \\ 0 и \альфа+1 и 1 \\ \альфа & 0 & \альфа+1 \end{pматрица} \cdot \begin{pmatrix} 1 и 1 \\ \альфа+1 и \альфа\\ 0 и \альфа+1 \end{pmatrix}\]
Matrixer
Как вы, вероятно, уже заметили, вычисления с конечными полями не так-то просто выполнить вручную. Однако, поскольку мне очень нравится программировать, я решил просто написать калькулятор, который может делать эти вычисления за меня.
Однако, поскольку мне очень нравится программировать, я решил просто написать калькулятор, который может делать эти вычисления за меня.
Все еще помните матрицы сверху? Мой калькулятор под названием «Matrixer» может сделать это менее чем за 20 миллисекунд:
Не веришь мне? Вот ссылка на этот точный расчет.
Matrixer может не только перемножать матрицы, но и делать следующие вещи:
- Базовые вычисления с числами (сложение, вычитание, умножение, деление и возведение в степень)
- Вычислить мультипликативный обратный элемент (\(x\cdot y = 1\))
- Вычислить аддитивный обратный элемент (\(x+y = 0\))
- Матрицы сложения и вычитания
- Транспонировать матрицы (поменять местами строки и столбцы)
- Умножение матрицы на вектор 905:00
- Сложение, умножение и вычитание векторов
- Решить систему однородных уравнений
- Преобразовать матрицу в сокращенную ступенчатую форму строки
Все эти вычисления можно выполнять с вещественными числами, а также с конечными полями \(\mathbb{F}_2, \mathbb{F}_3, \mathbb{F}_4, \mathbb{F}_5, \ mathbb{F}_7, \mathbb{F}_8, \mathbb{F}_9, \mathbb{F}_{11}, \mathbb{F}_{13}, \mathbb{F}_{17}\ ) и \(\mathbb{F}_{19}\).
Интерфейс 93)+(2/3)
является допустимым вводом. Матрицы: Заключены в фигурные скобки, строки разделены точкой с запятой, а столбцы разделены запятой.
Например, {1, 2, 3; 4, 5, 6} представляет следующую матрицу:
\[\begin{pматрица} 1 и 2 и 3 \\ 4 и 5 и 6 \конец{pmatrix}\]
Векторы: Заключены в квадратные скобки, строки разделены запятой.
Например, [1, 2, 3] представляет следующий вектор:
\[\begin{pматрица} 1\\ 2\\ 3 \конец{pmatrix}\] 92\)
Это означает, что приведенный выше расчет при вводе выглядит так:
{1, a, a+1; 0, а+1, 1; а, 0, а+1} * {1, 1; а+1, а; 0, a+1}
Более подробные инструкции по вводу выражений можно найти на самом сайте.
О коде
Весь калькулятор написан на языке JavaScript, работающем в интерфейсе браузера пользователя. Это означает, что веб-сайт хорошо масштабируется, поскольку на сервере не выполняется код, а пользователю отправляются только статические файлы.
Это означает, что веб-сайт хорошо масштабируется, поскольку на сервере не выполняется код, а пользователю отправляются только статические файлы.
Однако одним из недостатков этого является то, что Matrixer работает не во всех браузерах. До сих пор я обнаружил, что этот веб-сайт не работает в Internet Explorer 11. Ничего не происходит, когда я нажимаю кнопку «Рассчитать». Тем не менее, в любом другом браузере, который у меня был под рукой (Chrome, Firefox, Edge), калькулятор работал безупречно.
На сегодняшний день полный исходный код составляет около 7000 строк (включая комментарии и пустые строки). Сюда входят файлы JavaScript, HTML и CSS.
Я решил сделать весь проект открытым исходным кодом, и вы можете найти полный исходный код в этом репозитории GitHub. Он выпущен под лицензией GNU GPL V3.0, что означает, что вы можете повторно использовать этот код для своих собственных проектов, если вы указываете мое имя и публикуете свой код под той же лицензией.
И все!
Посмотрите мой калькулятор здесь, если вы еще этого не сделали, а также посмотрите на код, если хотите.








 — анимации
— анимации
 калькулятор может быстро решать уравнения, определяя опорные точки и
выполнение строковых операций для получения решений
калькулятор может быстро решать уравнения, определяя опорные точки и
выполнение строковых операций для получения решений Вам нужно только ввести свои матрицы, и
нажмите!
умножение двух матриц
Вам нужно только ввести свои матрицы, и
нажмите!
умножение двух матриц info
info Вы потеряли 16 граммов вещества, а в этой реакции этого просто не происходит! Куда делись 16 грамм?
Вы потеряли 16 граммов вещества, а в этой реакции этого просто не происходит! Куда делись 16 грамм? В этом приложении вам нужно будет выполнить три операции с матрицами:
В этом приложении вам нужно будет выполнить три операции с матрицами:
 Мы используем ту же технику для кислорода. Теперь у нас есть две матрицы (называемые Матрица A и Матрица B):
Мы используем ту же технику для кислорода. Теперь у нас есть две матрицы (называемые Матрица A и Матрица B): Теперь у вас должно быть: [A] -1 * [B] *det [A]
Теперь у вас должно быть: [A] -1 * [B] *det [A]

 1390 x –1 ] для доступа к сохраненной матрице. Смотрите первый экран.
1390 x –1 ] для доступа к сохраненной матрице. Смотрите первый экран.